Stabilizing electrochemical interfaces in viscoelastic liquid electrolytes

Viscoelastic liquid electrolytes composed of ultrahigh molecular weight polymer solutions stabilize electrodeposition of metals by suppressing electroconvection.

Abstract

Electrodeposition is a widely practiced method for creating metal, colloidal, and polymer coatings on conductive substrates. In the Newtonian liquid electrolytes typically used, the process is fundamentally unstable. The underlying instabilities have been linked to failure of microcircuits, dendrite formation on battery electrodes, and overlimiting conductance in ion-selective membranes. We report that viscoelastic electrolytes composed of semidilute solutions of very high–molecular weight neutral polymers suppress these instabilities by multiple mechanisms. The voltage window ΔV in which a liquid electrolyte can operate free of electroconvective instabilities is shown to be markedly extended in viscoelastic electrolytes and is a power-law function, ΔV : η^1/4, of electrolyte viscosity, η. This power-law relation is replicated in the resistance to ion transport at liquid/solid interfaces. We discuss consequences of our observations and show that viscoelastic electrolytes enable stable electrodeposition of many metals, with the most profound effects observed for reactive metals, such as sodium and lithium. This finding is of contemporary interest for high-energy electrochemical energy storage.

INTRODUCTION

Electrodeposition is a versatile electrochemical process used for creating metals/alloys (1, 2) and particulate (3, 4) and polymer (5) material coatings. The process also plays an important role in the shorting of microcircuits and in electrochemical energy storage technologies based on batteries. Therefore, it must be carefully managed to facilitate stable and safe operations over a range of operating temperatures and current rates and over many cycles of charge and discharge (6–10). In simple liquid electrolytes, deposition is subject to hydrodynamic and morphological instabilities, which drive strong convective processes near ion-selective interfaces. These instabilities have been studied intensively since the first reports of metal electroplating processes in the 1800s (10–24) and are in some cases beneficial because they promote mixing in the slow, inertia-less fluid flows typical in electrochemical systems. Mixing also enhances the efficiency of processes, such as electrodialysis, that rely on fast ion transport to ion-exchange membranes (13–15, 17, 22–26) or electrodeposition at battery electrodes (27), which requires large ionic currents to support high-power operations. In many other situations, including electroplating and emergent secondary batteries that use reactive metals (for example, lithium, sodium, and aluminum) as anodes, the instabilities are problematic because they produce complex flows that cause formation of rough, ramified metal electrodeposits known as dendrites at planar interfaces (12, 16, 18, 21, 28).

Unstable electrodeposition of metals that form chemically stable fluid/solid interfaces with liquid electrolytes (for example, silver, copper, and zinc) originates from electrohydrodynamic origins. In other metals, such as lithium, sodium, and aluminum, where the electrolyte reacts with the metal electrode to form a fragile interphase material, a combination of morphological and electrohydrodynamic instabilities is responsible for unstable electrodeposition (21). At low currents, dendrites arise naturally from nonuniform ionic conductivity of the heterogeneous interfaces electrolytes form in contact with many metals. Concentration of electric field lines on initial deposits/nucleates formed in high-conductivity regions of the interface promotes growth. Above a certain voltage, V_c ≈ 8RT/F, the ionic current in an electrolyte bounded by smooth, planar electrodes separated by distance l reaches a limiting value, i_L = 4FcD₊/l, which does not depend on applied voltage. At V_c, the ion migration rate exceeds that of diffusion, and electroneutrality of the bulk electrolyte cannot be maintained at planar interfaces with an electrode or membrane that is impermeable to anions (17, 21–24, 26). A space charge region is therefore formed at these interfaces that may extend many hundreds to thousands of ionic diameters into the electrolyte bulk (that is, well beyond the quasi-equilibrium space charge region that forms spontaneously at any charged substrate immersed in an electrolyte). At ionic currents above i_L, classical Nernst-Planck (N-P) theory predicts that the electric field near the electrodes diverges. A divergent electric field exerts a large electrical body force on fluid in the nonequilibrium space charge region, which drives a type of electroosmotic flow termed electroosmosis of the second kind, to distinguish it from normal electroosmotic slip generated when an electric field tangent to a charged surface acts on the quasi-equilibrium space charge to produce convection. The expression for i_L assumes a dilute electrolyte containing a binary monovalent symmetric salt; D₊ is the cation diffusivity; c is the electrolyte concentration; and F is the Faraday’s constant.

A substantial body of work has confirmed these observations and has shown that the instability plays a large role in both enhancing transport rates at ion-selective interfaces and in producing rough, dendritic deposition of metals in electroplating processes (10–24, 26, 29). These studies indicate that the instability drives the convective rolls that sweep ions away from regions surrounding a growing metal deposit and concentrates them on the deposit (12, 30). This enhances the rate of deposition of cations, but does so by promoting deposition at localized regions, leading to mossy or tree-like dendritic structures in certain circumstances. In liquid electrolytes bounded by ion-selective membranes, electroconvection has also been shown by means of theory (13, 14, 26), experiment (23, 24), and numerical simulations (17) to produce ionic current densities above the limiting value predicted by the N-P theory. In all of these studies, the fluid is typically a simple Newtonian liquid in which the resistance to large-scale electroconvective flow and small-scale ionic motions are determined by the liquid’s viscosity.

The linear stability analysis of electroconvection first discussed by Rubinstein and Zaltzman (13, 14) reveals that in an unsupported, symmetric, binary electrolyte, electroosmosis of the second kind is unstable. This analysis can be extended to show that at currents near i_L, small perturbations to the fluid velocity grow at a dimensionless rate

$$\mathrm{\sigma }={(\mathit{k}/\mathit{l})}^2{\mathit{V}}_0[{\mathit{V}}_0\mathit{P}\mathit{e}/8-\sqrt{\mathit{P}\mathit{e}(1-{\mathit{t}}_{+})}]$$ (1)

for k/l >> 1. Here, 2π/k is the wavelength of the perturbation; Pe≡Ul/D₊ = ε(RT/F)²/ηD₊ is a Peclet number based on a characteristic fluid velocity U = ε(RT/F)²/ηl, which captures the relative importance of convection and diffusion; V₀ is the dimensionless voltage; and t₊ is the fraction of the ionic transport due to the cations. This expression shows that although the growth rate of the instability is the largest on the smallest-length scales (largest k), it is nonnegligible on all length scales, meaning that the convective flow produced by the instability may extend to macroscopic-length scales in an electrochemical cell. The expression also shows that marginal stability (that is, a growth rate of zero) is achieved at a critical Peclet number, ${\mathit{P}\mathit{e}}_{\mathrm{c}}=64(1-{\mathit{t}}_{+})/{\mathit{V}}_0^2$, on all length scales. This condition allows a voltage range to be defined where stable interfacial ion transport should be observed in a Newtonian liquid

$${\mathit{V}}_0\le \frac{8\mathit{F}}{\mathit{R}\mathit{T}}\sqrt{\mathrm{\eta }{\mathit{D}}_{+}(1-{\mathit{t}}_{+})/\mathrm{\epsilon }}.$$ (2)

Therefore, in an electrolyte where the mechanisms for ion transport (conductivity) and momentum transport (electroconvection) can be separated, the width of the limiting current regime, $\mathrm{\Delta }\mathit{V}=\frac{\mathit{R}\mathit{T}}{\mathit{F}}{\mathit{V}}_0-{\mathit{V}}_{\mathrm{c}}$, can, in principle, be extended indefinitely.

RESULTS

The main results of this report are summarized in Fig. 1, which shows that the limiting current regime can be markedly extended by introducing moderate amounts of a high–molecular weight soluble polymer to a liquid electrolyte solvent and that the polymer achieves this feat by suppressing electroconvection. By means of tracer particle velocimetry using neutral micrometer-sized particles, we find that the source of the enhanced limiting current regime is the suppression of electroconvective flows in viscoelastic liquid electrolytes. Extending these findings to electrodeposition of metals, we report that even small amounts of an ultrahigh–molecular weight polymer dissolved in conventional liquid electrolytes can suppress nonuniform deposition, with the most dramatic effects apparent in softer, more reactive metals, such as lithium and sodium. The improved stability is discussed in terms of the polymer’s ability to suppress unstable secondary flows, without compromising ionic mobility. The viscosity thresholds at which the polymer begins to have beneficial effects are nevertheless calculated to be orders of magnitude lower than expected based on any current analysis of electroconvective instability in Newtonian liquids, implying that other features of the electrolytes, such as interfacial slip and fluid elasticity, particularly near the liquid/solid interface, may play an important role. In this regard, our observations bear qualitative similarities to the better-known Toms effect, in which small, even parts per million, quantities of ultrahigh–molecular weight flexible polymer additives in Newtonian fluids undergoing unstable turbulent flow produce large reductions in the frictional drag on surfaces wetted by the fluid (31, 32).

Fig. 1. Electrochemical characteristics of the viscoelastic electrolytes.

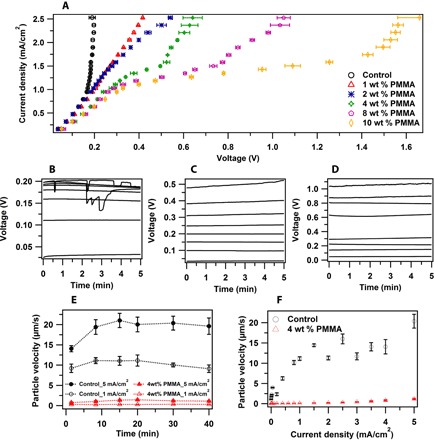
(A) I-V curves of electrolytes with different polymer concentrations. (B to D) Voltage versus time profiles measured in electrolytes with (B) no PMMA, (C) 2 wt % PMMA, and (D) 8 wt % PMMA at current densities ranging from 0.316 to 2.526 mA/cm². (E) Average tracer particle velocities measured in an optical lithium||stainless steel cell containing control (no polymer) and viscoelastic liquid electrolytes containing 4 wt % polymer. (F) Average tracer particle velocities measured in control and viscoelastic liquid electrolytes as a function of current density.

To create electrolytes in which ion and momentum transport pathways are uncoupled, we study semidilute solutions of high–molecular weight (M_w, ~1.5 × 10⁶ g/mol; M_w/M_n = 1.1) atactic poly(methyl methacrylate) (PMMA) (Agilent Technologies) dissolved in various solvents. High–molecular weight PMMA is chosen for at least three reasons. First, it is soluble in a wide variety of nonaqueous, high-dielectric constant liquid electrolytes, including carbonates [ethylene carbonate (EC), ε = 89.8; propylene carbonate (PC), ε = 64.9] and dimethyl sulfoxide (DMSO; ε = 46.7). Second, the polymer has low electrochemical activity, low-dielectric constant (ε = 2.6 to 3.6), and low affinity for the solvated metal cations we intend to study. We note that for this same reason, gel polymer electrolytes based on PMMA (33) and poly(ethylene oxide) (34) have been used in secondary batteries and super capacitors (35) for several decades. Finally, for high–molecular weight polymer, the critical concentration c* ~ M_w^−4/5(36) at which swollen polymer chains overlap and impart polymer-like physical properties to the electrolyte, is low.

The results summarized in Fig. 1A report current-voltage (I-V) response of PMMA–EC/PC–1 M bis(trifluoromethane) sulfonimide lithium (LiTFSI) electrolytes measured in the simple O-ring style symmetric Li||Li electrochemical cell depicted in fig. S1. For these experiments, the cell is mounted in the gravitational stable position (22, 37). We used current ramp measurements, which involved imposing a current on the electrolyte for a fixed period of time and recording the voltage response. By varying the measurement time at each current and by ramping the measurement current through a range of values, it is possible to record the I-V curve in electrolytes with different polymer concentrations at conditions that approach steady state (see Fig. 1, B to D). The limiting current for the control (no PMMA additive) is estimated to be 2.95 mA/cm² (table S1) in the dilute solution limit. Experiments show that the actual limiting current measured in dilute aqueous CuSO₄ solutions may be 1.5 to 4 times lower than theoretical estimates from the N-P theory (23, 24). At low current densities, an ohmic region is observed, and the slope of the I-V curve is a weak function of polymer concentration. In the control cells, the ohmic region is immediately followed by a second regime, in which the current increases much faster than linear with V, except for a slight change of slope at ca. i ≈ 1.6 mA/cm². This stands in sharp contrast to the I-V curve obtained upon the addition of just 1 weight % (wt %) of the polymer to the electrolyte, where the diffusion-controlled ohmic regime extends to voltages more than 10 times the thermal voltage (RT/F). At a PMMA concentration of 4 wt %, a plateau-like region is observed in which i varies little over a range of voltages, indicative of the ion depletion near the metal surface and the formation of the quiescent space charge region (38). At yet higher polymer concentration, the diffusion-limited transport regime extends further, becoming more than 40 times the thermal voltage at 10 wt % polymer, and the high-voltage slope of the I-V curve is lower.

Time-dependent voltage profiles (Fig. 1, B to D) measured at current densities bracketing the current where the change of slope is observed show that, beginning at current densities of around 1.6 mA/cm², the voltage profiles for the control electrolyte do not reach a steady value and, at higher current densities, large random transient voltage excursions are observed. Although these large transients are largely suppressed in electrolytes containing PMMA, there is a notable reappearance of a noise component at higher voltages, where the overlimiting conductance reemerges. A similar result is reported in fig. S2, where we characterize the effect of the measurement time on the shape of the I-V curve. Although it is plausible to attribute these behaviors to the increased noise associated in previous literature with overlimiting conductance and electroconvective instability, this designation is complicated in the present case by the fact that linear sweep voltammograms obtained from much faster voltage ramp measurements (1 mV/s) (fig. S3) show that there is a Faradic current maximum near 0.2 V in the control and viscoelastic electrolytes, corresponding to lithium stripping from the cathode. The fact that the position of this current maximum is unchanged in a viscoelastic liquid electrolyte indicates that the polymer produces negligible overpotential outside the transport-limited deposition regime.

It is possible to gain more direct information about electroconvection in the electrolytes from tracer particle velocimetry experiments. These measurements were made by dispersing 10 μm of uncharged polystyrene microparticles dyed blue in the electrolyte and tracking their time-dependent motions in an optical cell (fig. S4) interfaced with an optical microscope. We noted that in this cell configuration, the electric field and gravitational forces are perpendicular to each other, which can influence both the particle trajectories and the electroconvective flow pattern at the interface (37). A well-polished stainless steel electrode was used as the cathode for all experiments, while a range of anode materials (Li, Na, Zn, and Cu) were used. A fixed electrode spacing of 1.5 mm was maintained during all experiments. We analyzed videos using the ImageJ-based Fiji package (National Institutes of Health) and tracked particle motions using the TrackMate plugin. Particles were identified by the Laplacian of Gaussian detector, with an estimated blob diameter of 10 μm. Trajectories of particles were generated using the simple linear assignment problem tracker. Figure 1E reports the time-dependent average velocities in stainless steel||Li cells measured at current densities slightly below and above the experimentally determined i_L value and on time scales much larger than those probed in the I-V experiments discussed in the last section. Irrespective of the current density, tracer particles move far more slowly (by a factor of around 20) in the electrolyte containing PMMA than in the control. The results in Fig. 1F and fig. S5 show that the polymer-induced slowdown of tracer motions is observed at all current densities and voltages, with the largest effect observed at voltages in the range of 0.1 to 0.3 V.

Figure 2 (A and B) and fig. S6 report the rheological properties of the electrolytes used in the study measured at 25°C. Oscillatory shear measurements on a Rheometrics ARES rheometer outfitted with cone-plate fixtures were used for these measurements. It is apparent from the figure that the electrolytes that produce the largest effects in both the particle tracking and electrokinetics measurements are viscoelastic liquids, displaying dominant elastic properties, G′ > G″, over a range of time scales, t < 1/ω_c, where ω_c is the frequency at which G′ ≈ G″. Figure 2B reports the zero–shear rate, Newtonian shear viscosity for the electrolytes over the full range of PMMA concentrations studied (see fig. S6). At the lowest polymer concentration, the electrolyte viscosity is already 20 mPa·s, about 20 times that of the control electrolyte. In addition, at a concentration of 4 wt %, it is already more than three orders of magnitude higher than the viscosity of the control electrolyte. It is also apparent from the results in Fig. 2B that beginning at a polymer concentration of around 3 wt %, the polymer has a much larger effect on electrolyte viscosity. This transition is known to mark the onset of entanglement behavior in polymeric liquids, and its association with the strong suppression of overlimiting conductance and tracer particle migration is consistent with our hypothesis that the onset of entanglements would decouple ion and momentum transport in the electrolytes, meaning that the variable ηD₊ in Eq. 2 is not a constant. Under these conditions, this expression can be easily rearranged to show $\mathrm{\Delta }\mathit{V}:\sqrt{\mathrm{\eta }}$ for a Newtonian liquid electrolyte.

Fig. 2. Physical characteristics of viscoelastic liquid electrolytes.

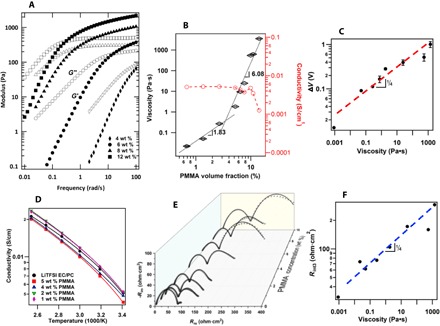
(A) Frequency-dependent dynamic storage G′ (filled symbols) and loss G″ (open symbol) moduli for PMMA–EC/PC (v/v, 1:1)–1 M LiTFSI electrolytes as a function of polymer concentration. (B) Concentration regimes of zero shear viscosity and conductivity at 25°C. (C) Extended stability regime (from Fig. 1A) in viscoelastic electrolytes as a function of electrolyte viscosity. The dashed line through the data shows that the experimental data can be approximated by the scaling relation, ΔV : η^1/4. (D) DC ionic conductivity of the viscoelastic liquid electrolytes as a function of temperature. The solid lines are Vogel-Fulcher-Tammann fits for the temperature-dependent ionic conductivity. (E) Nyquist plot obtained from EIS measurements in electrolytes with different polymer concentrations. The solid lines are fitted by an equivalent electrical circuit model shown in the supporting information (fig. S7). (F) Polymer contribution to the ASR of an electrolyte/Li interface as a function of electrolyte viscosity. The dashed line through the data shows that the experimental data obey an approximate scaling relation, R_int3 : η^1/4.

The results in Fig. 2A show that at a PMMA concentration of around 4 wt %, a significant elastic contribution is expected in electrolytes on time scales of the order 10 ms and at 8 wt %; elastic effects are evident on time scales of seconds. Optical birefringence measurements performed using a polarization modulation approach, reported elsewhere (39, 40), which allows both the orientation angle and birefringence of polymer chains to be quantified as a function of time, show that the electrolytes are nonbirefringent under the conditions of our polarization measurements. This means that PMMA molecules remain randomly oriented in the bulk electrolyte, indicating that the flow gradients in the bulk fluid are lower than the thresholds deduced from Fig. 2A. This behavior is quite different from what has been reported for drag-reducing polymer solutions (31).

As illustrated in Fig. 2C, the polymer shear viscosity has a noticeable effect on ΔV. The dashed line fitted to the data shows that over the range of concentrations where a plateau in the I-V data can be defined with the greatest certainty, the experimental results can be approximated by a power-law scaling form, ΔV : η^1/4, which is substantially weaker than the square root relation deduced from the marginal stability requirement. In addition, by rearranging variables in Eq. 2, the stability requirement can be written in terms of the electrolyte viscosity, η ≥ ε(V₀RT/F)²/64D₊(1 − t₊). Using typical values (ε ≈ 80; RT/F = 25.7 mV; V₀ ≈ 1; D₊ ≈ 2 × 10^{− 9} m²/s; t₊ ≈ 0.5), we estimate that a viscosity of at least 6.5 × 10⁵ Pa/s would be required to stabilize electroconvection.

Figure 2D reports temperature-dependent ionic conductivity of the electrolytes with various PMMA concentrations. These measurements were performed in symmetric stainless steel cells filled with the electrolytes and at temperatures ranging from 20° to 70°C. It is apparent that the DC ionic conductivity of the electrolytes changes little from the control (approximately 4 × 10⁻³ S/cm at 25°C; see Fig. 2B) at concentrations below the entanglement threshold, but thereafter, the electrolyte conductivity, κ, is a weak decreasing function of polymer concentration. However, because the viscosity is increasing markedly over this same range of concentration, the conductivity varies very weakly with electrolyte viscosity (at most as κ : η^{− 0.2}). This change is in fact far weaker than would be expected if small-scale Rouse-like polymer segment motions within their entanglement tubes control ion transport in the electrolyte (36). Thus, we conclude that even in the entangled state, ion transport in the solutions is governed by essentially the same process (solvent motion) as in electrolytes without polymer. Changes in conductivity produced by the addition of the polymer are for this reason negligible, at least in comparison to the changes in electrolyte viscosity and elasticity imparted by the polymer. Ion transport properties at the electrolyte/electrode interface reveal different features. Specifically, electrochemical impedance spectroscopy (EIS) was used to quantify the bulk and interfacial resistance in lithium symmetric cells. The resultant Nyquist plots are reported in Fig. 2E. It is apparent from the plots that even at the lowest concentration, the polymer contributes a well-defined second interface at the electrode that influences ion transport on longer time scales. The width of the second semicircle provides a rough measure of the resistance to interfacial ion transport imparted by the polymer. This width remains essentially constant up to a bulk polymer concentration of around 2 wt %, whereafter the contribution of the interfacial resistance from the second semicircle rises with polymer concentration. By fitting the equivalent circuit model illustrated in fig. S7A (41, 42) to these plots, more quantitative information about the bulk and interfacial resistances can be obtained (see fig. S7, B and C). The area squared resistance (ASR), R_int3, for the second interface correlates with the bulk polymer viscosity and is reported in Fig. 2F. It is apparent from the figure that R_int3 obeys a rough power-law relationship, R_int3 : η^1/4, essentially identical to that found previously for ΔV. We conclude that the polymer stabilizes electroconvection by delaying the onset of instability through its effect on the interfacial resistance. The weaker than predicted dependence of ΔV on η reflects the weaker than expected effect of polymer viscosity on R_int3. This conclusion is more important than it might at first appear because whereas the ΔV results are for electrolytes driven at high currents, where large levels of interfacial shear, orientation, and elastic effects are possible in an interfacial polymer layer (38, 39), the EIS experiments are performed for systems near equilibrium. That both measurements reveal that the electrolyte viscosity exhibits the same weak power-law effect indicates that interfacial elasticity of the deformed electrolyte at the fluid/solid interface does not play a significant role in our observations.

DISCUSSION

Our physical picture of the electrolyte/electrode interface is of a stratified structure: A polymer-depleted layer in contact with the electrode overlayed by a polymer-rich, bulk-like fluid layer. On reactive metal electrodes, such as lithium and sodium, the first layer is likely hosted in a nanoporous solid-electrolyte interphase formed by a chemical reaction of electrolyte components in contact with the electrode, the structure of which may be partly responsible for exclusion of the high–molecular weight polymer and the weak dependence of R_int3 on η (39, 41), under conditions where the bulk electrolyte conductivity is essentially independent of η. This perspective is supported by an x-ray photoelectron spectroscopy (XPS) depth profile analysis (fig. S8, A and B). In particular, we used an XPS high-resolution scan to analyze the composition profile of C 1s, O 1s, Li 1s, and F 1s on the surface of electrodes harvested from cells used for the electrokinetic measurements. These measurements show that the polymer component has an effect only on the XPS spectra in the uppermost layer, approximately 100-nm thick, associated with the bulk electrolyte (43, 44).

Figure 3 shows the consequences of suppressed electroconvective instability in viscoelastic liquid electrolytes on the stability of electrodepositon at an electrolyte/electrode interface, obtained by comparing electrodeposition of Li and Na in control electrolytes and in electrolytes containing 4 wt % PMMA at a fixed current density of 5 mA/cm²; analogous results at a lower current density (1 mA/cm²) are presented in the supporting materials (fig. S9, A to P). To facilitate these measurements, the sides and back of the cathode were covered by a polystyrene membrane to ensure that all the electrochemical processes occur on the anode-facing surface of the stainless steel cathode. As in the tracer visualization experiments, a small amount of blue polystyrene microspheres was added to the electrolyte to interrogate fluid motions in the vicinity of the evolving metal/electrolyte interface. The results reported in Fig. 3 (A to D) show that deposition in the control electrolyte quickly produces mossy and rough Li deposits at the stainless steel cathode. In contrast, more controlled, denser deposition is observed in the viscoelastic electrolytes. The analogous results for Na deposition are shown in Fig. 3 (I to P), where even more marked improvements in electrodeposit compactness and uniformity occurred. Similar observations of stabilized deposition in electrolytes containing 4 wt % PMMA are reported for Li and Na at lower current densities, as well as for Zn and Cu (fig. S9).

Fig. 3. Snapshots of interface evolution during electrodeposition in Li||stainless steel and Na||stainless steel optical cells operated above the limiting current.

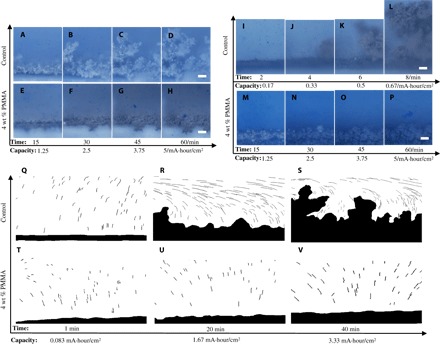
(A to D) Electrodeposition of Li in a Newtonian liquid control electrolyte (EC/PC–1 M LiTFSI). (E to H) Li electrodeposition in a viscoelastic liquid electrolyte (4 wt % PMMA in EC/PC–1 M LiTFSI). (I to L) Na deposition in a Newtonian liquid electrolyte [EC/PC–1 M sodium perchlorate (NaClO₄)]. (M to P) Na electrodeposition in a viscoelastic electrolyte (4 wt % PMMA in EC/PC–1 M NaClO₄). Scale bars, 100 μm. (Q to S) Flow patterns obtained by tracking tracer particle motions at different stages of the lithium electrodeposition in a Newtonian liquid EC/PC–1 M LiTFSI. (T to V) Flow patterns in a viscoelastic liquid electrolyte (4 wt % PMMA in EC/PC–1 M LiTFSI).

Figure 3 (Q to V) overlays evolution of the fluid velocity maps revealed by tracer particle motions with the evolution of the surface morphology in Li deposition. It is apparent from the figure that the particle trajectories for the control electrolyte evolve in an analogous manner as previously reported in the literature (30). At short times following imposition of the current, tracer motion is slow and primarily normal to the cathode surface. At longer times and higher deposition capacities, the flow becomes more complex, and there is a substantial velocity component tangential to the electrode surface. This flow pattern simultaneously confirms the nonlinear nature of electroconvection and shows that instabilities in the process are correlated with unstable deposition. Contrary to the experiments reported by Huth et al. (30), which show that streamlines always concentrate on dendrite tips, we find that tracer pathlines converge only on the fastest-growing, largest dendrite tips and may entirely bypass slow-growing dendrite tips in their vicinity. By promoting a runaway growth process for a few unstable growth modes, the observed flow pattern could explain why dendritic growth results in rapid short-circuiting of lithium metal anodes. Figure 3 (T to V) shows that these processes are completely eliminated in electrolytes containing polymer and that tracer particles move much more slowly (see Fig. 1E) and travel primarily perpendicular to the electrode surface.

Concentration of electric field lines on fast-growing dendrite tips means that analogous information about the stability of the electrodeposition process can be obtained by tracking time-dependent growth of the dendrite front, thereby quantifying the growth rate under a range of conditions. The main results for Li and Na are summarized in Fig. 4A and B, respectively. Whereas the polymer has a very large effect on dendrite growth rate for Li at a current density above i_L, the effect is initially more modest at a current density of 1 mA/cm², but grows with time. In contrast, for sodium electrodeposition under the same conditions, the polymer has a very noticeable and large effect on the growth rate of the dendritic front at both current densities studied and at all times. Figure 4C compares the dendrite growth rates extracted from the slopes of growth versus time plots for Li, Na, Cu, and Zn electrodeposition. Even at a concentration of 4 wt %, the polymer has a large and noticeable effect on dendritic growth, with the largest stabilization by far seen in Na deposition. This observation is significant because Na is commonly considered most prone to fail by dendritic deposition of all metals under consideration for energy storage in batteries both because of the higher reactivity and the softness of sodium metal (9, 29). The former feature makes it easier to create dendrite nuclei that grow as a result of morphological instability, whereas the latter makes the growing dendrite more prone to break away from the active electrode mass and to become electrochemically disconnected from the current collector in a battery.

Fig. 4. Analysis of electrodeposition of different metals in Newtonian and viscoelastic liquid electrolytes.

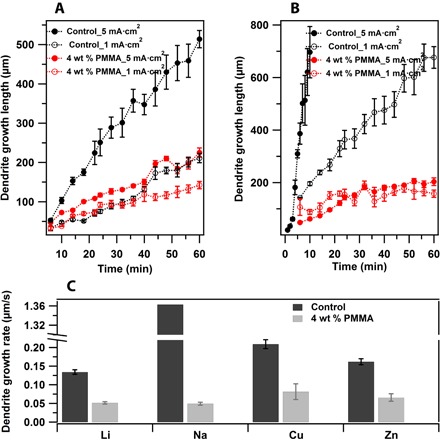
(A) Average lithium dendrite tip height as a function of time in the Newtonian control liquid electrolyte (EC/PC–1 M LiTFSI) and viscoelastic liquid electrolyte (4 wt % PMMA in EC/PC–1 M LiTFSI) at current densities below and above the limiting current. (B) Average sodium dendrite tip height as a function of time in the Newtonian control liquid electrolyte (EC/PC–1 M NaClO₄) and viscoelastic liquid electrolyte (4 wt % PMMA in EC/PC–1 M NaClO₄) at current densities below and above the limiting current. (C) Comparison of average dendrite growth rate for different metals in the Newtonian and viscoelastic liquid electrolytes at a fixed current density of 5 mA/cm².

MATERIALS AND METHODS

Electrolyte preparation

All chemicals were purchased from Sigma-Aldrich unless otherwise specified and used without purification. The desired amount of PMMA (Mp = 1,568,000, M_w/M_n = 1.07; Agilent Technologies) was dissolved in a mixture of EC and PC (v/v = 1:1), with 1 M LiTFSI salt for studying lithium electrodeposition or with 1 M NaClO₄ for studying sodium electrodeposition. PMMA (4 wt %) was dissolved in dry DMSO with 0.12 M copper(II) chloride or zinc chloride for studying copper and zinc deposition, respectively. All electrolyte preparations were performed in an argon-filled glove box (MBraun Labmaster) and dried vigorously before using.

Electrolyte characterization

Ionic conductivities of the electrolytes were measured using a Novocontrol N40 broadband dielectric spectrometer. Both Rheometrics ARES and Physica MCR501 rheometers were used to measure rheological properties of the electrolytes at room temperature. XPS measurements were performed with a Surface Science SSX-100 spectrometer using a monochromatic Al Kα source (1486.6 eV).

In situ visualization experiment

Visualization experiments were carried out in an airtight optical cuvette cell with two planar electrodes arranged parallel to each other. Metal ions were deposited at a constant current density on stainless steel (for lithium/sodium electrodeposition) or on the metals themselves (for copper/zinc electrodeposition). Deposition was monitored in real time by imaging the interface using an optical microscope outfitted with a video recorder.

Particle tracking

Electrodes were outlined in black against the electrolyte background via thresholding. Flow maps were formed by superimposing tracer particle trajectories on the images.

Electrochemical measurements

Cell assembly was carried out in an argon-filled glove box (MBraun Labmaster) by using coin cell 2032 type. The room temperature I-V characteristics of the cells were evaluated under galvanostatic conditions using Neware CT-3008 battery testers. Electrochemical impedance and lithium transference number measurement were conducted by using a Solartron Cell Test System model 1470E potentiostat/galvanostat.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/3/eaao6243/DC1

fig. S1. An illustration showing the lithium symmetric coin cell used for the I-V electrokinetic measurements.

fig. S2. Electrokinetic characteristics of viscoelastic electrolytes as a function of measurement time.

fig. S3. Linear sweep voltammetry as a function of PMMA concentration at a scan rate of 1 mV/s.

fig. S4. Schematic drawing of the experimental setup used to perform the visualization experiment for electrodeposition.

fig. S5. Tracer particle velocities in the Newtonian liquid electrolyte (EC/PC–1 M LiTFSI) and a representative viscoelastic electrolyte (4 wt % PMMA in EC/PC–1 M LiTFSI) as a function of voltage.

fig. S6. Complex shear viscosity at 25°C for viscoelastic liquid electrolytes containing varying concentrations of PMMA.

fig. S7. EIS measurements and analysis for viscoelastic electrolytes with different polymer concentrations.

fig. S8. Depth-profiling XPS spectra of a lithium metal surface after electrodeposition for 1 hour at a current density of 1 mA/cm².

fig. S9. Photographic images showing evolution of various metal electrode/electrolyte interfaces during electrodeposition.

table S1. Measured Li⁺ transference numbers and calculated limiting current densities [in the optical cell (J₁) and O-ring coin cell (J₂)] for electrolytes used in the study.