Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2019 Apr 1.
Published in final edited form as: Ophthalmology. 2017 Dec 2;125(4):569–577. doi: 10.1016/j.ophtha.2017.10.033

Personalized Prediction of Glaucoma Progression Under Different Target Intraocular Pressure Levels Using Filtered Forecasting Methods

Pooyan Kazemian 1,2, Mariel S Lavieri 3, Mark P Van Oyen 3, Chris Andrews 4,5, Joshua D Stein 4,5,6
PMCID: PMC5866175  NIHMSID: NIHMS917582  PMID: 29203067

Abstract

Purpose

To generate personalized forecasts of how patients with open-angle glaucoma (OAG) experience disease progression at different intraocular pressure (IOP) levels, to aid clinicians with setting personalized target IOPs.

Design

Secondary analyses using longitudinal data from 2 randomized controlled trials.

Participants

571 participants with moderate or advanced OAG from the Collaborative Initial Glaucoma Treatment Study (CIGTS) or the Advanced Glaucoma Intervention Study (AGIS).

Methods

Using perimetric and tonometric data from trial participants, we developed and validated Kalman filter models for fast-, slow-, and non-progressing patients with OAG. The Kalman filter can generate personalized and dynamically-updated forecasts of OAG progression under different target IOP levels. For each participant, we determined how mean deviation (MD) would change if the patient maintains his/her IOP at one of seven levels (6, 9, 12, 15, 18, 21, or 24 mmHg) over the next 5 years. We also model and predict changes to MD over the same time horizon if IOP is increased or decreased by 3, 6, and 9 mmHg from the level attained in the trials.

Main Outcome Measures

Personalized estimates of the change in MD under different target IOP levels.

Results

There were 571 participants (mean (standard deviation (SD)) age 64.2 (10.9) years) who were followed for a mean (SD) of 6.5 (2.8) years. Our models predicted that, on average, fast-progressors would lose 2.1, 6.7, and 11.2 dB MD under target IOPs of 6, 15, and 24 mmHg, respectively over 5 years. In contrast, on average, slow-progressors would lose 0.8, 2.1, and 4.1 dB MD under the same target IOPs and time frame. When using our tool to quantify the OAG progression dynamics for all 571 patients, we found no statistically significant differences over 5 years between progression for blacks vs. whites, males vs. females, and CIGTS vs. AGIS participants under different target IOPs (P>0.05 for all).

Conclusion

This is the first clinical decision-making tool we are aware of that generates personalized forecasts of the trajectory of OAG progression at different target IOP levels. This approach can help clinicians determine an appropriate and personalized target IOP for patients with OAG.

The American Academy of Ophthalmology (AAO) Preferred Practice Pattern for Primary Open-Angle Glaucoma (OAG) emphasizes the importance of setting a target level of intraocular pressure (IOP) for patients with glaucoma. By establishing a target IOP level, clinicians can gauge whether the interventions they are performing are effectively lowering the IOP to a level that is deemed safe or not and whether additional interventions are necessary.

While there is consensus among the glaucoma community that establishing a target IOP is useful in patient management, it is unclear what the optimal target IOP for a given patient should be. Traditionally, clinicians have used the results of landmark glaucoma clinical trials, past experience, and their gestalt to aid with target IOP selection. However, selecting a target IOP lower than what is required for a particular patient can lead to exposure to unnecessary medical and surgical interventions, which may have side effects, be fraught with complications, and be costly. Likewise, by selecting a target IOP higher than what is actually required, the patient is at risk for experiencing disease progression. Hence, improving the selection of the proper target IOP level can be very useful in managing patients with OAG.

An ideal method for selecting the proper target IOP would consider the glaucoma progression dynamics of a population of similar patients to capture how they progress at different IOP levels along with the unique disease progression dynamics of the particular patient in question. This would be used to generate personalized forecasts of disease progression under different IOP levels. These assessments can be dynamically updated each time the patient undergoes additional glaucoma testing. Furthermore, since patients vary from one another on a host of factors including sociodemographic characteristics, overall health and life expectancy, ability to tolerate different interventions, and preferences for aggressiveness of glaucoma control, a decision-making tool that informs clinicians about the glaucoma progression trajectories at different target IOP levels is more valuable than a tool that determines only one specific target IOP level for a particular patient. This would enable the clinician and patient to jointly decide on the most appropriate target IOP based on his or her unique circumstances and preferences.

We describe a novel technique using Kalman filtering (KF) to develop a personalized and dynamically updated menu of target IOPs for patients with OAG. Kalman filtering is a technique that has been used for decades by the aerospace industry to help guide flights1. More recently, this technique has been used to forecast disease progression in patients with conditions such as diabetes2,3 and prostate cancer4. It incorporates disease progression dynamics from an underlying population of patients with the condition of interest along with past measurements from the specific patient of interest to generate personalized disease forecasts. This technique also allows for updating of the forecasts each time additional readings are obtained.

METHODS

Data Sources

We used data from the Collaborative Initial Glaucoma Treatment Study (CIGTS) and the Advanced Glaucoma Intervention Study (AGIS) to parametrize and validate our models. Briefly, CIGTS is a multicenter clinical trial involving 607 participants with newly-diagnosed moderate OAG who were enrolled in 1993–1997 and followed for 5–9 years. The patients were randomized to either glaucoma medications or trabeculectomy. AGIS enrolled 591 participants with advanced OAG in 1988–1992 and followed them for 8–11 years. The patients were randomized to receive argon laser trabeculoplasty (ALT) or trabeculectomy. The participants in both trials were followed with tonometry and perimetry measurements obtained every 6 months during their follow-up time. Details about the study methodology of these trials have been described elsewhere5,6. CIGTS and AGIS data were de-identified prior to our accessing it, and the University of Michigan Institutional Review Board approved this study.

Inclusion/Exclusion Criteria

Both trials required participants to have a diagnosis of OAG in ≥1 eye, with elevated IOP at trial entry. For this study, we included only those persons from the trials who had been randomized to either receive medical therapy or ALT. Persons who had been randomized to trabeculectomy were excluded because incisional surgery can dramatically affect IOP and disease progression dynamics, and this adds complexity to the training of our forecasting algorithms. Furthermore, during follow-up, trial participants who later required incisional surgery were censored at the time they underwent trabeculectomy. We also excluded persons who had fewer than 4 IOP measurements or 4 visual field tests using a Humphrey Field Analyzer (Carl Zeiss Meditec, Dublin, CA). When both eyes of a participant met the eligibility criteria, we randomly selected one of the two eyes for inclusion in our analyses. After these exclusions, there were 571 eyes of 571 participants (266 from CIGTS and 305 from AGIS) who met the eligibility criteria.

Kalman Filter

At the heart of our decision support tool, we harnessed KF methodology7. A KF is a powerful statistical method that processes large amounts of quantitative data to forecast the trajectory of a system. This technology has been critical to aerospace engineering, including guiding Apollo missions to the moon1. More recently, it has been used to forecast the development or worsening of chronic diseases4,8–12, and we have used it to forecast OAG progression13.

The following example explains how this method works. Consider the prediction of where a spacecraft, presently in motion at point [x,y,z] in space, will be located in the future (e.g., 10, 20, 30, 40 seconds later) relative to a docking bay. Every 10 seconds, a new measurement of the spacecraft’s location [x,y,z] is obtained. All measurements possess some error (noise). Traditional regression models use a dataset of prior flights using similar spacecrafts and provide a linear relationship between independent (e.g., current location) and dependent (future location [x,y,z]) variables so as to minimize the mean squared error. However, these models were not designed for dynamic updates to the model as new measurements are taken. Instead, with KF each time a measurement is obtained, the model updates an estimate of the dependent variables based on input variables to minimize mean squared prediction error at each future stage. The effective estimates of current and future locations of the spacecraft require that the functions relating inputs (previously measured locations of the spacecraft) and outputs (future location) are connected over time. This is captured as a dynamic model of internal “state” variable transitions that describes how the process (motion of the spacecraft) changes over time. In addition to the [x,y,z] location, the internal state variables of a good model may include first and second derivatives on [x,y,z] position (velocity and acceleration, respectively). A set of equations relates the measured input variables to the full set of internal state variables, so that the system modeled (current and future motion of the spacecraft) can be optimally updated with each new measurement obtained. Such updating compares the newly obtained measurement (location of the modeled spacecraft) to what would have been expected from the population at that point in time (e.g., prior flights for similar spacecrafts) and what has been learned from the process modeled (e.g., as more measurements are obtained, the technique may reveal that the spacecraft being modeled is faster or slower than average similar spacecrafts). In addition, the method allows the model to include inherent randomness in the “motion” of the state and models of randomness in the observations specific to the measurements (the variability in manually measuring the spacecraft’s location).

Forecasting OAG trajectory is analogous to determining a spacecraft’s trajectory over time: the type of spacecraft is analogous to sociodemographic characteristics of the patient (e.g. age, sex, race), and other risk factors known to affect OAG progression. The position (or the state of the system) at the past, present, and future is analogous to the mean deviation (MD) and pattern standard deviation (PSD) on standard automated perimetry (SAP), and the IOP at different points in time. These variables help illuminate the disease’s current state and how it is changing over time. Moreover, the error or noise in the location measurements of our spacecraft analogy is akin to the error associated with SAP and IOP measurements. Randomness in the motion of the spacecraft (e.g., due to unmodeled friction) is akin to the inherent variability among patients on how OAG progresses. Additional information about our KF models is described in prior publications13,14.

Variables incorporated in our model for OAG

For each participant, we obtained all IOP, MD, and PSD measurements over the course of his/her participation in the trial. We incorporated these measurements together with their velocities and accelerations into the disease state vector so that interacting effects can be exploited, allowing the model to directly capture how changes in a given variable (e.g., IOP) affect the others (e.g., MD and PSD).

Parametrizing the Model

Eligible participants from CIGTS and AGIS were randomly divided into equally sized training and testing sets. We used the training set to parametrize and calibrate our KF models (described below); the testing set was used to evaluate the performance of our filtered forecasting technique. The two sets included similar numbers of (1) participants from CIGTS and AGIS, (2) persons with different OAG severities, (3) blacks and whites, and (4) males and females. We employed an expectation maximization algorithm15 to parametrize our KF model. We generated 25 different random sets of training and testing data; each time we parametrized the model on the training set and tested it on the testing set. The KF model exhibited unbiased error across all random sets, which means it is robust to the partition used to parameterize it. In the Results section, we present the results of one of these randomizations.

Characterizing Patients as Fast/Slow/Non-progressors

In addition to developing a KF model using data on all patients in the training set (called KA), we also trained 3 separate KF models to forecast OAG progression for fast (KF), slow (KS), and non-progressors (KN) in the training set. These customized models allow for more accurate prediction of OAG dynamics once a patient can be properly identified as a fast, slow, or non-progressor.

There is presently no gold standard for characterizing which patients with OAG are fast-progressors. As researchers have done previously, we defined fast progression as an MD loss of >1 dB/year16–19. The sensitivity loss associated with MD worsening at a rate of 1 dB/year is approximately 10 times greater than the normal age-related decline20. To integrate progression classification status into the KF, for each patient in the training set, we calculated the slope obtained from a linear regression of his/her entire history of MD readings and then classified the patient as a fast-progressor if the decline in MD was >1 dB/year, slow-progressor if the decline in MD was 0–1 dB/year, and non-progressor if there was no MD decline.

Using the first 5 six-month periods of follow-up for each patient, the KF adapts to the unique disease progression dynamics for that particular patient before it begins forecasting disease trajectory under different target IOP options. Previous research suggests that judgments about OAG progression should not be made without considering at least 5 SAP results due to fluctuating performance and other sources of noise18. Although the KF methodology is leveraged to reduce the measurement error, providing 5 data points to warm up and learn each patient’s specific disease dynamics enhances the model accuracy. After 5 sets of readings, each patient is classified as a fast-, slow-, or non-progressor based on the slope obtained from a linear regression of the patient’s first 5 MD readings. Thereafter, subsequent forecasts of future values of MD, PSD, and IOP are generated based on the corresponding specific KF model we developed for modeling fast (KF), slow (KS), and non-progressors (KN). Each time a new test result is obtained, the model reassesses a patient’s progression status by considering the slope of the last 5 MD measurements. Thus, a particular patient may transition between classification as a non-progressor, slow-progressor, and fast-progressor as she is followed over time, and the most appropriate of the 3 KF models is employed to make the next set of predictions.

Validation Method

After developing, parameterizing, and calibrating our models using data from the training dataset, we tested all patients in the testing dataset to determine the accuracy of our KF models for predicting the future OAG progression trajectory for each patient relative to actual values observed in the trials. We filtered the first 5 measurements of each patient using the KA model. Starting at period 5 (at which we first determine a patient’s progression classification status), we employed the more specific of the 3 KFs and predicted how the patient’s OAG was likely to progress over the following 5 periods (2.5 years) - i.e., periods 6 to 10 – along with computing the prediction error (defined as the predicted values minus the observed values) at each of those 5 periods. At the period 5 time point, the model identified 24 fast-progressors, 113 slow-progressors, and 58 non-progressors in the testing dataset.

Menu of Target Intraocular Pressures

Next, we integrated into our KF models a control variable which allowed us to modify one of the state variables in the model at each time period. This enabled us to forecast what would happen to MD at each future time period assuming the IOP were to remain constant at a specified level.

We analyzed the data on target IOP in two ways:

Pre-specified target IOP levels

In this analysis, for each patient in the testing dataset, we forecasted changes in MD, assuming that the IOP remained consistently at one of the following 7 target IOP levels over the next 5 years: 6, 9, 12, 15, 18, 21, and 24 mmHg. This enables the clinician and patient to have a menu of target IOP options to select from spanning from very aggressive IOP control to non-aggressive IOP control for which they can observe what will happen to MD over time. These predictions are tailored to each individual patient to generate personalized forecasts. In the Results section, we present sample output graphs for a fast and a slow-progressing patient from the testing dataset. Similar graphical output was generated for every patient in the testing dataset.

Relative changes to IOP

In this analysis, we used our KF models to assess how changing a patient’s IOP affected his/her MD over time. We did so by employing eight IOP control policies for all patients in the testing dataset: increasing a patient’s IOP by 3, 6, and 9 mmHg, keeping the IOP at the same level, and lowering the IOP by 3, 6, 9, and 12 mmHg compared to the IOP measured in period 5. For all 8 policies, we predicted how MD changed over the next 5 years and calculated the difference between the predicted values in periods 6 through 15 and the values at period 5. If the lowering of the IOP by the four specified levels above resulted in hypotony (an IOP <6 mmHg), we excluded such participants from those specific analyses (1, 9, 63, and 147 patients from the testing set were excluded under -3, -6, -9, and -12 mmHg IOP control policies with this additional criterion). This analysis generated graphical output that provides insight into how changing IOP (relative to its current value) affects MD. We compared MD progression under different IOP control policies for (1) fast vs. slow-progressors, (2) blacks vs. whites, (3) males vs. females, and (4) CIGTS vs. AGIS participants in the testing dataset. We calculated p-values for each two groups (e.g., blacks vs. whites) using 2-sample Student’s t-tests to compare the mean MD change under all eight IOP control policies. For all analyses, p-values <0.05 were considered statistically significant.

RESULTS

There were 571 eyes of 571 participants who met the study inclusion criteria. The mean (standard deviation (SD)) age of the participants at trial entry was 64.2 (10.9) years. There were 299 females (52%) in this study and the racial composition included 288 (50%) blacks, 263 (46%) whites, and 20 persons (4%) of other races/ethnicities. The sample included 305 participants (53%) from AGIS and 266 participants (47%) from CIGTS. The mean (SD) number of IOP measurements and SAP tests per participant was 11.2 (5.1). (Table 1)

Table 1.

Characteristics of Persons in the Training and Testing Datasets

Total Training Testing p-value*
No. or Mean % or SD No. or Mean % or SD No. or Mean % or SD
No. of participants † 571 100% 286 50% 285 50%
Trial 0.71
 CIGTS 266 100% 131 49% 135 51%
 AGIS 305 100% 155 51% 150 49%
Sex 0.87
 Male 272 48% 135 47% 137 48%
 Female 299 52% 151 53% 148 52%
Race 0.26
 Black 288 50% 154 54% 134 47%
 White 263 46% 123 43% 140 49%
 Other 20 4% 9 3% 11 4%
Mean (SD) no. of visits per patient‡ 11.2 5.1 11.0 5.0 11.3 5.3 0.49
Mean (SD) of age [years] 64.2 10.9 64.2 10.9 64.3 11.0 0.91
Mean (SD) of baseline MD [dB] −7.49 5.39 −7.39 5.53 −7.59 5.26 0.66
Mean (SD) of baseline PSD [dB] 6.42 3.69 6.45 3.68 6.39 3.70 0.85
Mean (SD) of baseline IOP [mmHg] 17.62 3.60 17.63 3.35 17.62 3.83 0.97
Progressor Status § 0.71
 Fast 121 21% 58 20% 63 22%
 Slow 267 47% 132 46% 135 47%
 Non 183 32% 96 34% 87 31%
Open in a new tab

IOP = intraocular pressure; MD = mean deviation; PSD = pattern standard deviation; SD = standard deviation; AGIS = Advanced Glaucoma Intervention Study; CIGTS = Collaborative Initial Glaucoma Treatment Study; mmHg = millimeter of mercury; dB = decibels.

*

Fisher Exact Test and Student’s t-test were used for categorical and continuous variables, respectively.

†

All participants contributed only one eye.

‡

Each visit includes tonometry and perimetric testing.

§

Designation of progression status for each patient was made based on all MD readings for that patient using the criteria described in the Methods section. Further, the fast-, slow-, and non-progressor patient sets are mutually exclusive subsets of the whole data set.

To calibrate, parameterize, and validate our models, we randomly split the 571 eyes into two similar sets: a training set consisting of 286 eyes (50%) and a testing set of 285 eyes (50%) twenty-five times. Table 1 shows the results of one of these 25 splits.

Validation of Kalman Filter Prediction

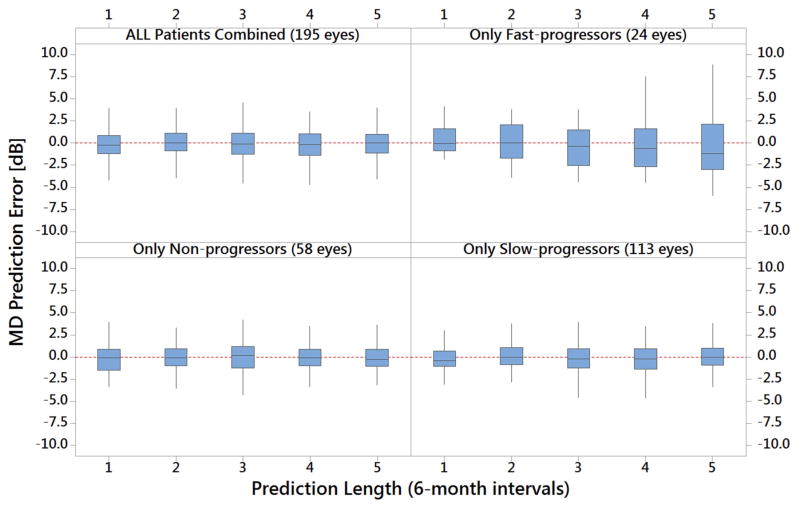
Figure 1 depicts the box and whisker plots for MD prediction error for all testing set patients and stratified by progression type. As the figure demonstrates, the mean prediction error is relatively small for the entire testing sample (−0.04 dB), as well as for patients designated fast-progressors (0.23 dB), slow-progressors (−0.06 dB), and non-progressors (−0.10 dB). Similar results were obtained for IOP (data not shown).

Figure 1. Prediction Errors of KF, KS, and KN Models for All Patients in the Testing Dataset after Stratification by Progression Status.

Figure 1

Open in a new tab

MD = mean deviation; dB = decibels. Each 6-month prediction interval is from Period 5.

The figure shows prediction errors for the three customized Kalman filter models separately, as well as all combined. It shows that overall and for all 3 progression status groups, the mean MD prediction error is rather small with the forecasts within 1 dB of the actual observations from the trial. The largest prediction errors were when the model forecasted far into the future for subset of patients who were fast-progressors. Patients were required to have 10 or more IOP, MD, and PSD measurements for inclusion in this analysis.

Menu of Target IOP Options

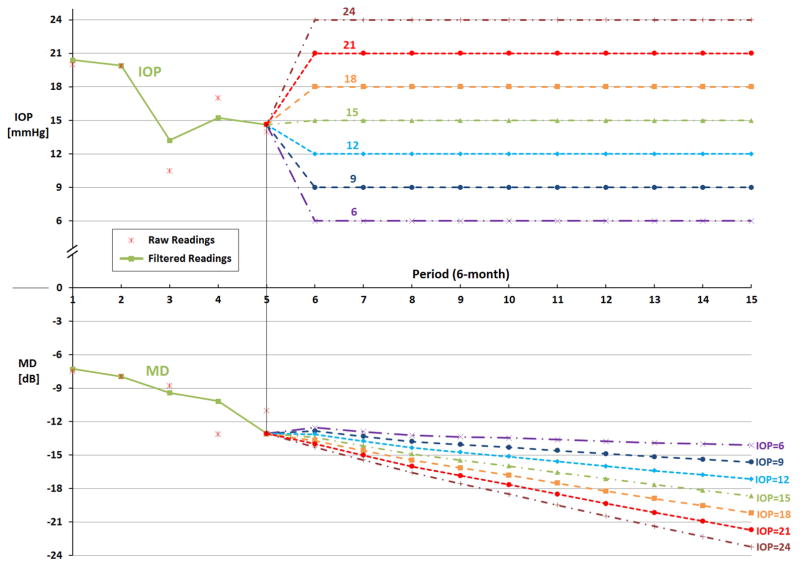
Figure 2 shows data for a sample fast-progressing patient from the AGIS trial. The first 5 readings are filtered using the KA model to identify that this particular patient fits our rule for classification as a fast-progressor. As the figure demonstrates, at entry into AGIS, the patient’s baseline IOP was 20 mmHg and her MD was −7.2 dB. By period 5, although the patient’s IOP had dropped to approximately 15 mmHg, her MD had declined to −13.0 dB. Our KF model predicts that if this patient were to maintain her IOP at 15 mmHg over the next 5 years, she would experience a further decline in her MD of about 5.7 dB over that time frame to a level of −18.7 dB in period 15. Our tool also shows what would happen to this patient’s MD should her IOP be maintained at different levels higher or lower than 15 mmHg. Lowering her IOP to 6 mmHg and maintaining it at that level over the 5 years of follow-up would result in a decline of MD of only 1.1 dB. However, if her IOP increased from 15 to 24 mmHg and was maintained at that level, she would lose 10.1 dB over the 5-year time frame.

Figure 2. Example of Forecasting Glaucoma Progression Under Different Target Intraocular Pressure Levels for a Fast Progressing Patient in the Sample.

Figure 2

Open in a new tab

IOP = intraocular pressure; MD = mean deviation; mmHg = millimeter of mercury; dB = decibels.

The figure shows the KF forecast of what would happen to MD over the next 5 years if this particular patient’s intraocular pressure were maintained at levels of 6, 9, 12, 15, 21, or 24 mm Hg beginning at period 6. Raw readings are observed values of IOP and MD from the AGIS and CIGTS trials. Filtered readings are the estimated values by our Kalman filter models.

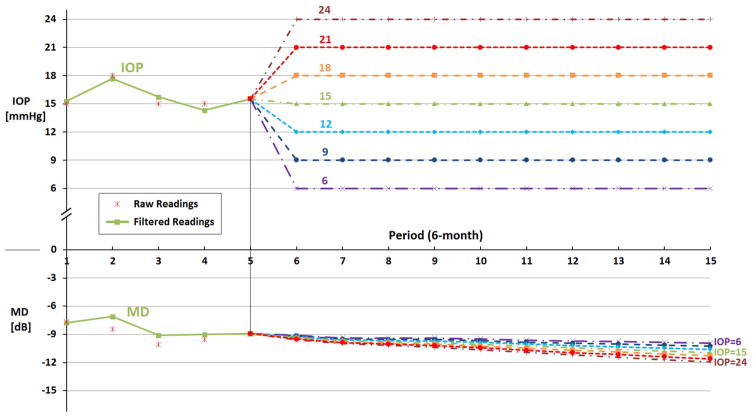
Figure 3 presents data for a slowly progressing patient from the CIGTS trial. For this patient, at period 5, his IOP was 15 mmHg and his MD was −8.9 dB. If the patient’s IOP was lowered to 6 mmHg and maintained there, our filtered forecasting model, KS, predicts his MD after 5 years will drop only 1.0 dB from −8.9 to −9.9 dB; if his IOP stayed at 15 mmHg during the next 5 years, his MD would drop 2.0 dB from −8.9 to −10.9 dB; and if his IOP were to rise from 15 to 24 mmHg and stay at that level over the 5 years, his MD would drop 3.0 dB from −8.9 to −11.9 dB. In contrast to the fast progressing patient described above who loses 1.1, 5.7, and 10.1 dB MD under target IOPs of 6, 15, and 24 mmHg, respectively, our models predict this second patient will only lose 1.0, 2.0, and 3.0 dB MD under the same target IOPs.

Figure 3. Example of Forecasting Glaucoma Progression Under Different Target Intraocular Pressure Levels for a Slow Progressing Patient in the Sample.

Figure 3

Open in a new tab

IOP = intraocular pressure; MD = mean deviation; mmHg = millimeter of mercury; dB = decibels.

The figure shows the KS forecast of what would happen to MD over the next 5 years if the patient’s intraocular pressure were maintained at levels of 6, 9, 12, 15, 21, or 24 mm Hg beginning at period 6. Raw readings are observed values of IOP and MD from the AGIS and CIGTS trials. Filtered readings are the estimated values by our Kalman filter models.

Our filtered forecasting tool predicts that, on average, fast-progressors in the testing set would lose 2.1, 6.7, and 11.2 dB MD under target IOPs of 6, 15, and 24 mmHg, respectively over 5 years. In contrast, on average, slow-progressors would only lose 0.8, 2.1, and 4.1 dB MD under the same target IOPs and time frame.

How Changes in Intraocular Pressure Affect Changes in Mean Deviation

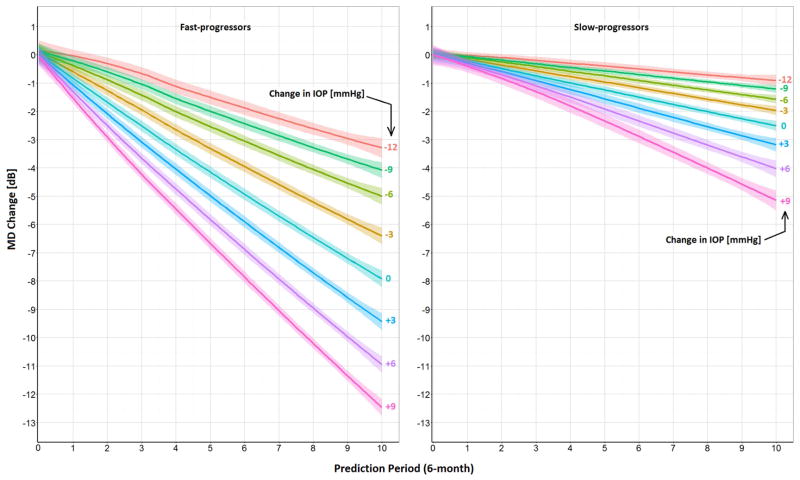
While Figures 2 and 3 present examples of the personalized output our tool provides to clinicians about specific patients, Figure 4 shows the average change in MD over the next 5 years for different levels of change in IOP for all the patients in our testing dataset. The mean MD in period 5 (i.e., prediction period 0) for fast (n=24) and slow-progressors (n=113) was −12.2 dB and −6.8 dB, respectively. Both groups have similar mean IOPs in period 5 of 17.5 mmHg. As expected, our tool shows that the MD declines more rapidly for the fast-progressor group than the slow-progressing patients under all different levels of IOP increase or decrease (Figure 4). For instance, Figure 4 shows that lowering the IOP by an additional 3 mmHg relative to the IOP value in period 5 causes a slow-progressing patient to lose 2 dB MD over 5 years, on average, whereas a fast-progressing patient loses, on average, 6.5 dB MD over the same follow-up period.

Figure 4. Kalman Filter Forecasts of How Changes in Intraocular Pressure of Different Magnitudes Affect Changes in Mean Deviation Over Time for Fast and Slow Progressing Patients.

Figure 4

Open in a new tab

MD = mean deviation; IOP = intraocular pressure; mmHg = millimeter of mercury; dB = decibels; Avg = average.

Prediction period 0 corresponds to 2.5 years after enrollment in the trials. The lines and the bounds around each line represent the mean and the 95% confidence interval around it, respectively. The mean starting MD (i.e., MD in prediction period 0) for fast and slow-progressors are −12.2 dB and −6.8 dB, respectively. Both groups have equal mean IOPs of 17.5 mmHg in prediction period 0. The figure shows forecasts of what would happen to MD over the next 5 years for fast and slow-progressors (using the KF and KS models, respectively) if their IOPs remained unchanged, increased 3, 6, or 9 mmHg or decreased 3, 6, 9, or 12 mmHg from the level measured at prediction period 0. For all levels of change in IOP, fast-progressors will have statistically significant lower MD after 5 years (P < 0.0001).

Figure 5 (available at www.aaojournal.org) demonstrates how MD changes when IOP is maintained at different levels over the 5 years of follow-up for (a) blacks vs. whites, (b) males vs. females, and (c) participants of CIGTS vs. AGIS in the testing dataset. Our prediction models found no statistically significant difference between these groups at the final time point (all p-values were >0.05).

DISCUSSION

Using an engineering technique called Kalman filtering, we parameterized, calibrated, and validated a novel glaucoma forecasting tool that can generate a menu of personalized and dynamically-updated target IOPs. The tool considers the underlying progression dynamics of a population of patients from AGIS and CIGTS along with past and current values of IOP, MD, and PSD from the patient of interest to forecast how each patient’s glaucoma will progress over time if the patient’s IOP was maintained at one of seven different target IOP levels. The resulting menu of target IOPs generated from the model can be used by clinicians to make informed decisions of how aggressively to lower IOP accounting for the unique circumstances and preferences of the patient. Likewise, clinicians can use the tool to educate patients with OAG of what will likely happen to their peripheral vision at different levels of IOP.

These analyses highlight the importance of recognizing and aggressively treating patients with OAG who are behaving like fast-progressors. As demonstrated in Figure 2, this rapidly progressing patient clearly needs a very low target IOP to prevent progression to blindness. Without a tool such as ours, clinicians might select an initial target IOP of 12 mmHg or higher for a patient such as this. Yet, our tool forecasts that if the IOP was lowered to and maintained at 12 mmHg, this particular patient would still lose 4.1 dB of MD over the next 5 years; so, depending on his circumstances, he likely would benefit from an even lower target IOP. Using a prediction tool such as ours to identify this early in the disease course might inform the clinician and patient to opt for more aggressive lowering of IOP with incisional surgery rather than treatment with medications.

In contrast to the fast progressing patient described above, our model shows that slow-progressors and non-progressing patients such as those who are behaving like the one depicted in Figure 3 may not require such aggressive IOP control. Without a tool like ours to help guide decision-making, a clinician might select an initial target IOP of mid-teens for a patient such as this one. Yet, our tool shows how, for this patient, if her IOP was maintained at 15 mmHg she would lose 2.0 dB of MD over the next 5 years, but if her IOP was instead maintained at 18 mmHg or 21 mm Hg, she would lose only slightly more MD (2.3 or 2.7 dB of MD, respectively) during that same time frame. Depending on the patient’s age and circumstances, the clinician and patient may decide that it is not worth subjecting her to the necessary medical, laser, or surgical interventions to maintain an IOP at 15 mmHg rather than one that is a few points higher.

Early identification of which patients with OAG would most benefit from aggressive lowering of IOP and which ones would fare well with minimal IOP reduction would benefit patients and society. Chronic use of glaucoma medications to lower IOP is known to cause ocular and systemic side effects and can be very costly21. Moreover, many common incisional glaucoma surgeries to lower IOP are fraught with complications, some of which can be sight-threatening22. Incisional glaucoma surgery is also expensive and burdensome to patients and their caregivers. Thus, strategies to minimize the unnecessary lowering of IOP in patients who do not require such a low IOP would be very useful. Likewise, studies have demonstrated that patients who progress from mild OAG to severe OAG experience a reduction in health-related quality of life23 and are at greater risk of falls and fractures24. The costs of caring for patients with advanced OAG are also considerably higher than persons with mild OAG. For all these reasons, it is important to employ tools such as KF to help clinicians and patients with selection of an appropriate target IOP considering their unique circumstances and preferences.

Our study has several limitations. First, we parameterized and validated our model using data on patients with moderate or advanced OAG. Further research is needed to study its effectiveness for patients with less severe disease. Second, we incorporated data from tonometry and perimetry into our models but have yet to consider structural data from optical coherence tonometry or other parameters known to be risk factors for disease progression such as central corneal thickness. Unfortunately, information on these factors was not adequately captured in AGIS and CIGTS for us to consider them in the models. We hope to perform additional testing on our forecasting tool using other data sources that have information on these important factors and, hopefully, this will enable us to refine the menu of target IOPs generated by our tool. Third, we limited our present analyses to trial participants who did not undergo incisional glaucoma surgery. Now that we have established that our tool is capable of generating reasonable target IOPs for those treated with medical and laser therapies, we plan to perform additional analyses to see whether it performs equally as well for patients undergoing incisional surgery, where there is often an abrupt change in IOP. Finally, our tool forecasts over a 5-year time frame. Ideally, forecasts would extend out 20 years or longer as disease progression can occur over decades. The CIGTS and AGIS trials did not follow patients that long, so it would be difficult to judge how well our tool forecasts beyond 5 years. We are in the process of incorporating our forecasting algorithms into a user-friendly decision support tool that will enable clinicians to upload tonometric and perimetric data on patients with OAG into the tool and it will generate a personalized real-time forecast of the trajectory of change in MD under different target IOP levels for each patient. Clinicians will be able to share these forecasts with the patients they are treating to determine an appropriate target IOP for each patient.

In conclusion, using KF we were able to generate a personalized, dynamically-updated menu of target IOPs that clinicians can use to enhance their ability to care for patients with OAG. The use of personalized menus of target IOPs may limit over- and under-treatment of disease and help clinicians and patients make more informed decisions about the level of aggressiveness to lower IOP in a given patient.

Supplementary Material

supplement. Online Figure 5: Kalman Filter Forecasts of Glaucoma Progression for Different Subsets of Patients from the Testing Dataset When Intraocular Pressures Are Raised or Lowered to Different Levels (available online only).

IOP = intraocular pressure; MD = mean deviation; mmHg = millimeter of mercury; dB = decibels; AGIS = Advanced Glaucoma Intervention Study; CIGTS = Collaborative Initial Glaucoma Treatment Study. Avg = average.

Average change in MD over the next 5 years under different levels of change in IOP graphed for (a) blacks vs. whites, (b) males vs. females, and (c) participants of CIGTS vs. AGIS. The lines and the bounds around each line represent the mean and the 95% confidence interval around it, respectively. Our models found no statistically significant difference between these groups of patients (all p-values were >0.05).

Acknowledgments

Financial Support: Funding to support this research comes from NEI R01 EY026641 (MSL/JDS/MPVO/CA), Glaucoma Research Foundation Shaffer Grant (JDS), and NSF CAREER: CMMI-1552525 (MSL). The funding organizations had no role in the design or conduct of this research.

The authors thank David C. Musch, PhD, MPH for allowing us access to data from CIGTS and Leslie Niziol, MS, for formatting the data from CIGTS, and Paul Van Veldhuisen, PhD, for allowing us to access data from AGIS for this study.

Footnotes

Presented, in part, at the American Glaucoma Society meeting, March 3, 2017, Coronado, CA.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  • 1.Lefferts EJ, Markley FL, Shuster MD. Kalman filtering for spacecraft attitude estimation. Journal of Guidance, Control, and Dynamics. 1982;5(5):417–29. [Google Scholar]
  • 2.Wang Q, Molenaar P, Harsh S, et al. Personalized state-space modeling of glucose dynamics for type 1 diabetes using continuously monitored glucose, insulin dose, and meal intake: An extended kalman filter approach. Journal of diabetes science and technology. 2014;8(2):331–45. doi: 10.1177/1932296814524080. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Eberle C, Ament C. The unscented Kalman filter estimates the plasma insulin from glucose measurement. Biosystems. 2011;103(1):67–72. doi: 10.1016/j.biosystems.2010.09.012. [DOI] [PubMed] [Google Scholar]
  • 4.Lavieri MS, Puterman ML, Tyldesley S, Morris WJ. When to treat prostate cancer patients based on their PSA dynamics. IIE Transactions on Healthcare Systems Engineering. 2012;2(1):62–77. [Google Scholar]
  • 5.Musch DC, Lichter PR, Guire KE, et al. The Collaborative Initial Glaucoma Treatment Study: study design, methods, and baseline characteristics of enrolled patients. Ophthalmology. 1999;106(4):653–62. doi: 10.1016/s0161-6420(99)90147-1. [DOI] [PubMed] [Google Scholar]
  • 6.AGIS Investigators. The Advanced Glaucoma Intervention Study (AGIS): 1. Study design and methods and baseline characteristics of study patients. Controlled clinical trials. 1994;15(4):299–325. doi: 10.1016/0197-2456(94)90046-9. [DOI] [PubMed] [Google Scholar]
  • 7.Kalman RE. A new approach to linear filtering and prediction problems. Journal of Fluids Engineering. 1960;82(1):35–45. [Google Scholar]
  • 8.Cunningham JP, Nuyujukian P, Gilja V, et al. A closed-loop human simulator for investigating the role of feedback control in brain-machine interfaces. J Neurophysiol. 2011;105(4):1932–49. doi: 10.1152/jn.00503.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Foussier J, Teichmann D, Jia J, et al. An adaptive Kalman filter approach for cardiorespiratory signal extraction and fusion of non-contacting sensors. BMC Med Inform Decis Mak. 2014;14:37. doi: 10.1186/1472-6947-14-37. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Kuure-Kinsey M, Palerm CC, Bequette BW. A dual-rate Kalman filter for continuous glucose monitoring. Conf Proc IEEE Eng Med Biol Soc. 2006;1:63–6. doi: 10.1109/IEMBS.2006.260057. [DOI] [PubMed] [Google Scholar]
  • 11.Bogaarts JG, Gommer ED, Hilkman DM, et al. EEG Feature Pre-processing for Neonatal Epileptic Seizure Detection. Ann Biomed Eng. 2014;42(11):2360–8. doi: 10.1007/s10439-014-1089-2. [DOI] [PubMed] [Google Scholar]
  • 12.Bukhari W, Hong SM. Real-time prediction and gating of respiratory motion using an extended Kalman filter and Gaussian process regression. Phys Med Biol. 2014;60(1):233–52. doi: 10.1088/0031-9155/60/1/233. [DOI] [PubMed] [Google Scholar]
  • 13.Kazemian P, Helm JE, Lavieri MS, et al. [Accessed on April 17, 2017];Dynamic Monitoring and Control of Irreversible Chronic Diseases with Application to Glaucoma. 2016 doi: 10.1111/poms.12975. Available at SSRN: http://ssrn.com/abstract=2733399. [DOI] [PMC free article] [PubMed]
  • 14.Helm JE, Lavieri MS, Van Oyen MP, et al. Dynamic Forecasting and Control Algorithms of Glaucoma Progression for Clinician Decision Support. Operations Research. 2015;63(5):979–99. [Google Scholar]
  • 15.Dempster AP, Laird NM, Rubin DB. Maximum Likelihood from Incomplete Data Via Em Algorithm. Journal of the Royal Statistical Society Series B-Methodological. 1977;39(1):1–38. [Google Scholar]
  • 16.Chauhan BC, Malik R, Shuba LM, et al. Rates of glaucomatous visual field change in a large clinical population. Invest Ophthalmol Vis Sci. 2014;55(7):4135–43. doi: 10.1167/iovs.14-14643. [DOI] [PubMed] [Google Scholar]
  • 17.Heijl A, Buchholz P, Norrgren G, Bengtsson B. Rates of visual field progression in clinical glaucoma care. Acta ophthalmologica. 2013;91(5):406–12. doi: 10.1111/j.1755-3768.2012.02492.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Gardiner SK, Crabb DP. Examination of different pointwise linear regression methods for determining visual field progression. Invest Ophthalmol Vis Sci. 2002;43(5):1400–7. [PubMed] [Google Scholar]
  • 19.De Moraes CG, Jasien JV, Simon-Zoula S, et al. Visual Field Change and 24-Hour IOP-Related Profile with a Contact Lens Sensor in Treated Glaucoma Patients. Ophthalmology. 2016;123(4):744–53. doi: 10.1016/j.ophtha.2015.11.020. [DOI] [PubMed] [Google Scholar]
  • 20.Heijl A, Lindgren G, Olsson J. Normal variability of static perimetric threshold values across the central visual field. Arch Ophthalmol. 1987;105(11):1544–9. doi: 10.1001/archopht.1987.01060110090039. [DOI] [PubMed] [Google Scholar]
  • 21.Azuara-Blanco A, Burr J. The rising cost of glaucoma drugs. Br J Ophthalmol. 2006;90(2):130–1. doi: 10.1136/bjo.2005.079996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Stein JD, Ruiz D, Jr, Belsky D, et al. Longitudinal rates of postoperative adverse outcomes after glaucoma surgery among medicare beneficiaries 1994 to 2005. Ophthalmology. 2008;115(7):1109–16. e7. doi: 10.1016/j.ophtha.2008.03.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Skalicky S, Goldberg I. Depression and quality of life in patients with glaucoma: a cross-sectional analysis using the Geriatric Depression Scale-15, assessment of function related to vision, and the Glaucoma Quality of Life-15. J Glaucoma. 2008;17(7):546–51. doi: 10.1097/IJG.0b013e318163bdd1. [DOI] [PubMed] [Google Scholar]
  • 24.Black AA, Wood JM, Lovie-Kitchin JE. Inferior field loss increases rate of falls in older adults with glaucoma. Optom Vis Sci. 2011;88(11):1275–82. doi: 10.1097/OPX.0b013e31822f4d6a. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

supplement. Online Figure 5: Kalman Filter Forecasts of Glaucoma Progression for Different Subsets of Patients from the Testing Dataset When Intraocular Pressures Are Raised or Lowered to Different Levels (available online only).

IOP = intraocular pressure; MD = mean deviation; mmHg = millimeter of mercury; dB = decibels; AGIS = Advanced Glaucoma Intervention Study; CIGTS = Collaborative Initial Glaucoma Treatment Study. Avg = average.

Average change in MD over the next 5 years under different levels of change in IOP graphed for (a) blacks vs. whites, (b) males vs. females, and (c) participants of CIGTS vs. AGIS. The lines and the bounds around each line represent the mean and the 95% confidence interval around it, respectively. Our models found no statistically significant difference between these groups of patients (all p-values were >0.05).

NIHMS917582-supplement.pdf (641.6KB, pdf)

RESOURCES