Neural mechanisms mediating motion sensitivity in parasol ganglion cells of the primate retina

SUMMARY

Considerable theoretical and experimental effort has been dedicated to understanding how neural circuits detect visual motion. In primates, much is known about the cortical circuits that contribute to motion processing, but the role of the retina in this fundamental neural computation is poorly understood. Here, we used a combination of extracellular and whole-cell recording to test for motion sensitivity in the two main classes of output neurons in the primate retina— midget (parvocellular-projecting) and parasol (magnocellular-projecting) ganglion cells. We report that parasol, but not midget, ganglion cells are motion sensitive. This motion sensitivity is present in synaptic excitation and disinhibition from presynaptic bipolar cells and amacrine cells, respectively. Moreover, electrical coupling between neighboring bipolar cells and the nonlinear nature of synaptic release contribute to the observed motion sensitivity. Our findings indicate that motion computations arise far earlier in the primate visual stream than previously thought.

INTRODUCTION

Motion estimation is crucial to an animal’s survival and success in the natural environment. Accordingly, the neural circuits that mediate motion computations have received a great deal of attention in the scientific literature (reviewed in Borst and Euler, 2011; Borst and Helmstaedter, 2015; Clark and Demb, 2016). Motion processing begins when specialized neural circuits extract local motion signals from visual inputs (Adelson and Bergen, 1985; Barlow and Levick, 1965; Hassenstein and Reichardt, 1956). In vertebrates, these circuits serve at least two distinct functions. First, specialized subcortical neural circuits compute object motion along specific cardinal axes that align with the axes of the semicircular canals of the inner ear. These visual signals, originating in direction-selective retinal ganglion cells, are combined with vestibular signals in the brainstem, thus bringing the visual and vestibular systems into register (Oyster et al., 1980; Sabbah et al., 2017; Simpson and Alley, 1974; Simpson et al., 1979; Taylor et al., 2000; Vaney et al., 2012). A separate system is responsible for real-time control of visually guided movements (Goodale and Milner, 1992). In humans and non-human primates, this latter system arises in part from retinal projections to the ‘magnocellular’ layers of the lateral geniculate nucleus (LGN) of the thalamus, which, in turn, provide input to the motion-sensitive neurons in the cortex that form the dorsal visual pathway (Kaplan and Benardete, 2001; Maunsell et al., 1990; Merigan et al., 1991b; Merigan and Maunsell, 1990; Schiller et al., 1990a, b). Despite this apparent link to motion vision, the contribution of parasol cells to motion processing has garnered remarkably little attention.

According to the orthodox view, the principal role of the retina is to provide a veridical representation of the visual environment. Similar to modern image compression algorithms, this representation is thought to arise by encoding visual inputs into distinct spatiotemporal channels that are realized at the level of different ganglion cell types (Campbell and Robson, 1968; Enroth-Cugell and Robson, 1966). In contrast to this view, work in the dominant retinal experimental systems indicates that the parallel ganglion cell pathways act as highly specialized feature detectors, performing functions that are far richer and more complex than simple spatiotemporal processing (reviewed in Gollisch and Meister, 2010; Masland and Martin, 2007). Indeed, ganglion cells have been found in several species that encode object versus background motion (Baccus et al., 2008; Ölveczky et al., 2003, 2007), direction of motion (Barlow et al., 1964; Barlow and Levick, 1965; Sabbah et al., 2017; Taylor and Vaney, 2002), orientation (Nath and Schwartz, 2016; Venkataramani and Taylor, 2010, 2016), and other very specific visual features (Baden et al., 2016; Mani and Schwartz, 2017; Sivyer et al., 2010). While the spatiotemporal-channels hypothesis has been all but abandoned in current theories of vision in nearly all vertebrate species (Gollisch and Meister, 2010; Masland and Martin, 2007), this hypothesis persists as the dominant model for visual processing in primates (Conway and Livingstone, 2003; Lennie and Movshon, 2005; Rust et al., 2005).

Based on their spatial receptive field sizes, temporal kinetics, and contrast sensitivity, parasol cells are thought to contribute to the general visual representation by bandpass filtering incoming visual signals in both space and time and by signaling changes in luminance relative to the background (Kaplan and Shapley, 1986; Lee et al., 1995; Purpura et al., 1988). It is commonly believed that specialized cortical circuits, then, use this general-purpose representation from parasol cells and other retinal ganglion cells to extract information about spatial form and visual motion (Adelson and Bergen, 1985; Lee et al., 1995; Movshon and Newsome, 1996). This view predicts that attenuating the signals arising from parasol (magnocellular) pathway would equally affect spatial/form and motion vision. However, inactivating or lesioning this pathway has little effect on spatial vision, but instead severely impairs an animal’s ability to detect motion (Maunsell et al., 1990; Merigan et al., 1991a; Schiller et al., 1990a, b), indicating that parasol cells principally contribute to motion vision.

Two earlier studies used multi-electrode array recording to demonstrate that the parasol cell population provides an incredibly precise readout of the speed and trajectory of moving objects (Chichilnisky and Kalmar, 2003; Frechette et al., 2005). This precision, however, was ascribed to the concerted activity of the population and the possibility that it originated in the properties of individual parasol cells or their presynaptic circuitries was not considered. Here, we performed a series of experiments to test for motion sensitivity in midget (parvocellular-projecting) and parasol (magnocellular-projecting) ganglion cells. While midget cells lacked motion sensitivity, parasol cell responses to motion were enhanced relative to other types of stimuli. This motion sensitivity in parasol cells was present across a wide range of contrasts and motion speeds, indicating that it was a general property of these cells. Further, we found that motion sensitivity was present at the level of glutamate release from presynaptic bipolar cells and disinhibition from amacrine cells and was mediated, in part, by electrical coupling between bipolar cell synaptic terminals. Taken together, our data indicate that motion processing begins far earlier in the primate visual stream than has been previously appreciated—at the second synapse of vision.

RESULTS

The canonical hypothesis of early visual processing in primates argues that the mosaic of parasol (magnocellular-projecting) ganglion cells contribute to a general-purpose representation of vision that is ultimately used by downstream cortical circuits to extract information about the structure/form of objects (spatial vision) as well as object motion (motion vision). Thus, our principal goal was to directly test whether these cells could distinguish between spatial form and visual motion. Inability to distinguish between the two would be taken as evidence in favor of the orthodox view. Likewise, greater sensitivity for motion would be evidence that individual parasol cells are, themselves, motion sensitive. We begin by demonstrating that parasol cells respond better to motion than to spatial form, a property which we term motion sensitivity.

Motion sensitivity of parasol ganglion cells

Do parasol ganglion cells exhibit motion sensitivity? Distinguishing a cell’s contribution to form and motion vision has proven an experimentally challenging task. For example, a white bar moving through a cell’s receptive field changes the intensity of light on the receptive field relative to the background (i.e., contrast). To separate parasol cell responses to spatial pattern versus motion, we employed an apparent-motion stimulus paradigm used previously to demonstrate motion sensitivity in the mouse retina (Kuo et al., 2016). The paradigm consisted of two interleaved stimuli: (1) an apparent-motion stimulus comprised of a bar shifting position incrementally through the receptive-field center and (2) a stimulus in which the bar positions were randomized. Except for the spatiotemporal sequence, both stimuli were identical, stimulating the same regions of the receptive-field center within the same time interval (Figure 1B, top).

Figure 1.

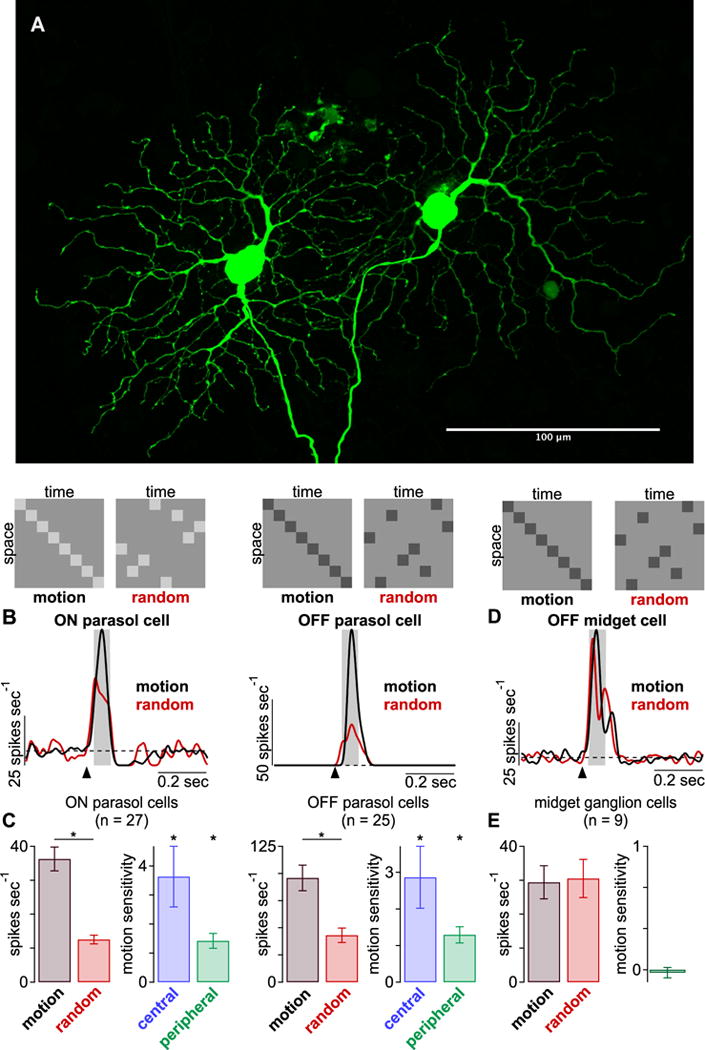
Parasol cells distinguish between apparent-motion and random-bar sequences. (A) Maximum projection of two neighboring ON parasol cells recorded for this study (scale bar, 100 μm). (B) Top, example spatiotemporal patterns are shown for the two stimulus classes. Mean spike responses from example ON and OFF parasol cells to the apparent-motion (black) and random-bar sequences (red). Arrow indicates stimulus onset; shaded regions indicate sampling windows. (C) Spike responses (left) and motion sensitivity (right) across ON (n = 27) and OFF (n = 25) cells. Motion sensitivity values are shown for central (blue, ≤3 mm) and more peripheral (green, >3 mm) eccentricities. Motion stimuli elicited significantly larger spike response than random sequence in both cell types (p < 0.05). Motion sensitivity was also significant for both types. (D) Same as (B) for an OFF midget ganglion cell. (E) Same as (C) for midget ganglion cells (n = 9). Bar plots indicate mean ± SEM.

We recorded the spike responses of ON and OFF parasol cells to repeated presentations of these stimuli. The average spike responses to these stimuli in example ON and OFF parasol cells are shown in Figure 1B. In both cell types, spike rates were higher for apparent motion than for the random-bar stimulus. We quantified these responses by calculating each cell’s average spike rate during the stimulus presentation (50-msec window) relative to the maintained spike rate immediately preceding the stimulus (500-msec window). The apparent-motion stimulus elicited higher spike rates than the random-bar stimulus in ON and OFF parasol cells, and these differences were statistically significant (n = 27 ON cells, p = 3.3 × 10⁻⁵; n = 25 OFF cells, p = 6.5 × 10⁻⁵).

To compare the relative response to the apparent-motion and random-bar stimuli across cells, we computed a motion sensitivity index for each neuron tested (Kuo et al., 2016):

$$\mathit{motion}\mathit{sensitivity}=\frac{R_{\mathit{motion}}-R_{\mathit{random}}}{R_{\mathit{random}}}$$

where R_motion and R_random are the responses to the apparent motion and random bar stimuli, respectively. Values greater than zero indicate a preference for the apparent-motion stimulus. The average motion sensitivity values for both cell types were greater than one, indicating that the apparent motion stimulus typically elicited more than twice as many spikes as the random bars (i.e., >100% increase; Figure 1C). The results of this experiment indicate that individual parasol ganglion cells can distinguish between motion and spatial form.

Major anatomical and physiological differences have been described between the central (macular) and peripheral regions of the primate retina and, in some cases, these differences are functionally relevant (Hecht and Verrijp, 1933; Rovamo and Raninen, 1988; Sinha et al., 2017; Tyler, 1985; Watanabe and Rodieck, 1989; Waugh and Hess, 1994). To determine whether motion sensitivity varied with retinal eccentricity, we separated the motion sensitivity of parasol cells located in or near the macula (<3 mm foveal eccentricity; n = 15 cells) from those located more peripherally (n = 37 cells). Surprisingly, we found that central cells showed, higher motion sensitivity than their more peripheral counterparts (central, 3.4 ± 0.7; peripheral, 1.4 ± 0.17; mean ± SEM; p = 2.6 × 10⁻⁴).

To assess the selectivity of our motion assay, we repeated this experiment in midget (parvocellular-projecting) ganglion cells. These cells contribute to chromatic and spatial vision and are not expected to show particular sensitivity to visual motion (reviewed in Neitz and Neitz, 2017; Wässle, 2004). Indeed, the apparent-motion and random-bar stimuli elicited similar spike responses from midget cells, indicating a lack of motion sensitivity (Figure 1D, E; n = 9 cells; p = 0.36).

Many neurons exhibit enhanced sensitivity to stimuli containing strong correlations (Rieke et al., 1995). Thus, an alternative interpretation of the results in Figure 1 is that parasol cells show enhanced sensitivity to spatiotemporal correlations, not necessarily motion. To test this possibility, we devised a stimulus containing strong correlations but lacking the spatiotemporal tilt or slant characteristic of visual motion (De Valois and Cottaris, 1998; De Valois et al., 2000; DeAngelis et al., 1993; McLean and Palmer, 1989; Movshon et al., 1978). The stimulus was a bar that alternated between two neighboring positions on every frame presentation, and the spatial location of the neighboring bars varied randomly on any given trial (Figure 2, top; see STAR Methods). Despite containing strong spatiotemporal correlations, the alternating stimulus elicited fewer spikes than the apparent-motion stimulus, producing significant motion sensitivity values for both ON (n = 10) and OFF (n = 14) cells (Figure 2; p < 1.0 × 10⁻⁴). These data indicate that the presence of spatiotemporal correlations alone is not sufficient to engage the mechanisms that mediate motion sensitivity in parasol cells. Further, these data show that motion computations arise far earlier in the visual stream of primates than previously recognized.

Figure 2.

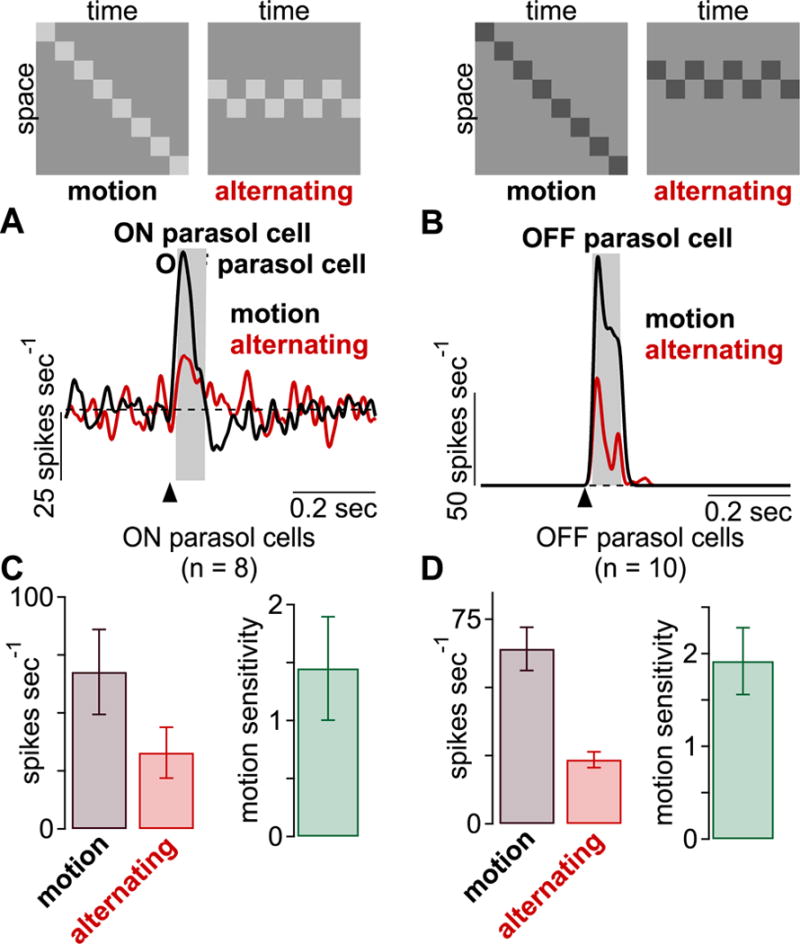
Responses to apparent-motion and alternating-bar sequences. Top, example spatiotemporal patterns for the two types of stimuli. (A-B) Average spike responses to motion (black) and alternating bar sequences (red). (C-D) Average spike rates to the two stimuli and motion sensitivity values in ON (n = 8) and OFF (n = 10) parasol cells.

Motion sensitivity present across contrasts and speeds

The experiments outlined above tested motion sensitivity at a single contrast and a single speed. To probe the generality of our results, we varied these two stimulus parameters. We determined whether motion sensitivity was present across a range of contrasts by repeating the apparent-motion/random-bar experiment at four contrasts between 25–100%—positive contrasts for ON parasol cells and negative contrasts for OFF parasol cells. The motion stimulus elicited more spiking than the random bar stimulus in both cell types at all contrasts (Figure 3A, B; p < 0.01). For ON parasol cells, motion sensitivity was similar at all contrasts tested, and OFF parasol cells showed higher motion sensitivity at lower contrasts (Figure 3B). We tested midget ganglion cells in the same way and found that, unlike parasol cells, the apparent-motion and random-bar stimuli elicited similar responses in midgets (Figure 3A, right). Accordingly, these cells lacked motion sensitivity at all contrasts tested (Figure 3B, right; p > 0.25).

Figure 3.

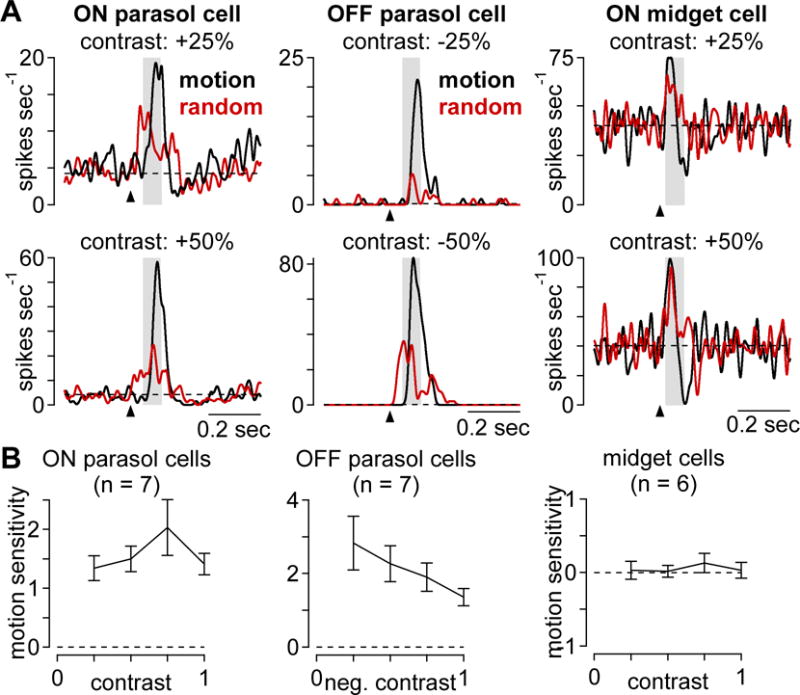
Motion sensitivity persists across a range of stimulus contrasts. (A) Example spike responses to the apparent-motion (black) and random-bar sequences (red) at 25% and 50% contrast. Arrow indicates stimulus onset and shaded region indicates sampling window. (B) Motion sensitivity values as function of contrast for ON parasol (n = 7), OFF parasol (n = 7), and midget ganglion cells (n = 6). Error bars indicate mean ± SEM.

If parasol cells contribute to visual motion coding, they should exhibit motion sensitivity across a range of stimulus speeds. We tested this by repeating the experiment at multiple speeds between 0.15–2.4 mm sec⁻¹ (~0.75–12 degrees sec⁻¹; Figure 4A, B; see STAR Methods). Stimulus speed was varied by altering the duration of bar presentations at a particular spatial location (i.e., by changing the update rate of the stimulus; see STAR Methods). Parasol cells showed poor selectivity for apparent motion at speeds below 3 degrees sec⁻¹ (p > 0.15) and robust motion sensitivity at higher speeds (p < 5.0 × 10⁻⁴). Midget cells, however, lacked a preference for motion at all of the speeds tested (Figure 4B, orange; p > 0.05).

Figure 4.

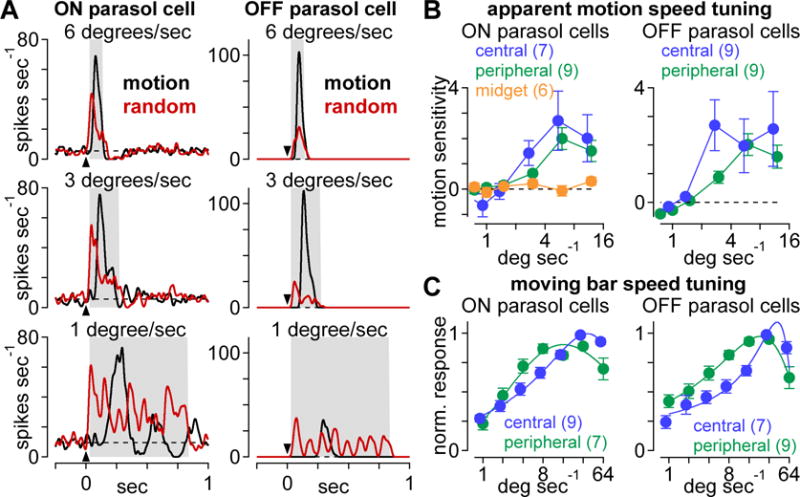
Parasol cells exhibit motion sensitivity across a range of speeds. (A) Example spike responses to apparent-motion (black) and random-bar sequences (red) at three different apparent motion speeds. Arrow indicates stimulus onset; shaded region indicates sampling window. (B) Motion sensitivity as a function of apparent motion speed in central parasol (blue), peripheral parasol (green), and midget (orange) ganglion cells. (C) Spike rate as function of speed for moving bar stimuli in central (blue) and peripheral (green) parasol cells. High refresh rates were used on the visual stimulator to simulate smooth motion at high speed. Solid line shows fit with bandpass speed tuning function. Error bars indicate mean ± SEM.

Given the apparent dependence of motion sensitivity on speed (Figure 4B), we sought a more comprehensive understanding of the speed tuning properties of parasol cells. We were particularly interested in whether speed tuning differed systematically between central and peripheral cells. Due to technical limitations, we were unable to test for motion sensitivity at speeds greater than 12 degrees sec⁻¹ (see STAR Methods). To obtain a more complete tuning curve that included faster speeds, we switched from the apparent-motion/random-bar stimulus paradigm to one in which bars were moved through the receptive-field center at different speeds (1–64 degrees sec⁻¹, 0.2–12.8 mm sec⁻¹).

The resulting speed tuning curves were fit well with a bandpass tuning function used to describe the speed tuning of motion-sensitive neurons in two cortical areas (Figure 4C, solid lines; Priebe et al., 2006). According to this function, the spike rate at a given speed, R(s), is a function of the cell’s preferred speed:

$$R(s)=A\lfloor \mathit{exp}\left(\frac{-{\left({\mathit{log}}_{2}s-{\mathit{log}}_2{s}_p\right)}^2}{2{\left(\beta +\zeta \left({\mathit{log}}_{2}s-{\mathit{log}}_2{s}_p\right)\right)}^2}\right)-\mathit{exp}\left(\frac{-1}{{\zeta }^2}\right)\rfloor$$

where A is the maximal spike rate (in spikes sec⁻¹), s_p is the preferred speed (in degrees sec⁻¹), β is the bandwidth, and ζ is the skew.

The resulting speed tuning curves showed two prominent features. First, responses varied systematically as a function of speed—spiking was highest at speeds between 8–32 degrees sec⁻¹ and decreased at higher and lower speeds (Figure 4C). Second, we observed differences in speed tuning between central and peripheral cells of the same type. On average, central cells showed higher peak speeds (ON central: 40.5 ± 6.5, n = 7; ON peripheral: 19.1 ± 5.9, n = 9; OFF central: 43.3 ± 3.8, n = 7; OFF peripheral: 25.9 ± 3.6; n = 9; mean ± SEM) and these differences were statistically significant (p_ON = 1.6 × 10⁻²; p_OFF = 2.6 × 10⁻³). Speed tuning bandwidth was also narrower for central OFF cells (in octaves; central: 1.2 ± 0.3; peripheral: 2.7 ± 0.2; p = 2.6 × 10⁻³), but the tuning bandwidth was similar between central and peripheral ON cells (central: 3.0 ± 0.5; peripheral: 2.9 ± 0.3; p = 0.42).

These experiments demonstrate a preference for motion in parasol cells across a range of stimulus contrasts and speeds, indicating that motion sensitivity is a robust property of these cells. Further, midget cells lacked substantial motion sensitivity at all contrasts and speeds tested. What gives rise to motion sensitivity in parasol cells? In the following section, we seek answers to this question by considering the synaptic inputs to parasol cells.

Motion sensitivity present in excitation and crossover inhibition

The experiments above found motion sensitivity in the spike output of parasol ganglion cells. Our next goal was to understand the circuit mechanisms mediating this motion sensitivity. Detecting visual motion requires mechanisms that compare at least two points in space at different points of time, and previous studies have identified excitatory and inhibitory circuits that perform this comparison (reviewed in Borst and Euler, 2011; Demb, 2007). To distinguish between these excitatory and inhibitory mechanisms, we recorded the direct synaptic input to parasol cells in voltage clamp. Excitatory currents were isolated by clamping a cell’s membrane voltage at the reversal potential for inhibition (−70 mV) and, likewise, inhibitory currents were recorded at the excitatory reversal potential (0 mV). An increase in excitatory input to a cell is manifest by a more negative current response relative to the leak current, whereas an increase in inhibition produces a more positive current response. Thus, to avoid potential difficulty in interpreting these results, we present summary data in terms of conductance (see STAR Methods). Figure 5 compares the relative sensitivity of the excitatory and inhibitory synaptic inputs to ON and OFF parasol cells to the apparent-motion and random-bar sequences. Just as was observed in the spike responses, apparent motion elicited significantly larger excitatory responses than the random-bar stimulus in both cell types (Figure 5A; n = 9 ON cells, p = 6.3 × 10⁻³; n = 16 OFF cells, p = 5.7 × 10⁻⁵). Thus, motion sensitivity was present at the synaptic output of bipolar cells.

Figure 5.

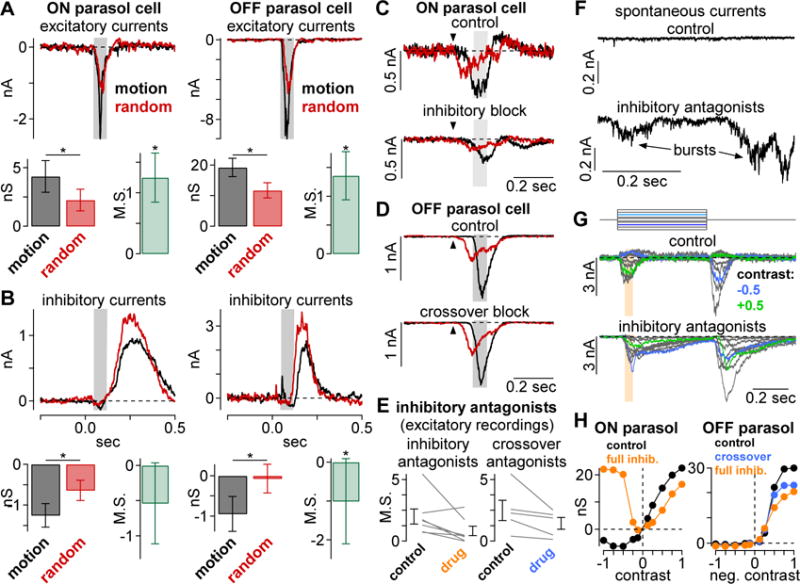
Motion sensitivity present in excitatory glutamate input and in disinhibition. (A) Apparent-motion stimuli (black) elicited larger inward excitatory currents than the random-bar sequences (red; V_hold, −70 mV). (B) Disinhibition was greater for apparent motion (black) than random bar sequences (red; V_hold, 0 mV). Population data (bottom) showing the change in conductance relative to gray background and motion sensitivity for excitation (A) and inhibition (B). Significance indicated by asterisks (*; p < 0.05). Arrows indicate stimulus onset and shaded regions show sample window. (C) Excitatory currents in an ON parasol cell recorded to the apparent-motion (black) and random-bar stimuli (red). Recordings were performed under control conditions (top) and with presynaptic inhibition blocked (bottom). (D) Excitatory currents in an OFF parasol cell as in (C) recorded under control conditions (top) and with presynaptic crossover inhibition blocked (bottom). (E) Effects of presynaptic inhibitory block (left; n = 7 cells) and crossover block (right; n = 5 cells) on motion sensitivity as measured in excitatory input to parasol cells. Individual cells shown in gray and population average shown in black. Error bars indicate mean ± SEM. (F) Excitatory currents recorded from an OFF parasol cell at a photopic background mean. Control recording shows a relatively small amount of spontaneous activity (top). Inhibitory antagonists increase spontaneous inward currents; several large bursts of activity are indicated with arrows (bottom). (G) Excitatory currents in response to contrast steps (top; duration, 0.5 sec) in an ON parasol cell under control conditions (top) and with synaptic inhibition blocked (bottom). (H) Contrast-response curves showing excitatory conductance as a function of contrast before and after drug application in the same cells.

Does synaptic inhibition contribute to motion sensitivity in parasol cells? To answer this question, we recorded inhibitory input to parasol cells in voltage clamp. The apparent-motion stimulus elicited a net removal of inhibition (disinhibition) relative to the mean background (Figure 5B) while the random-bar stimulus elicited less disinhibition (Figure 5B; p_ON = 3.1 × 10⁻²; p_OFF = 4.2 × 10⁻³). This disinhibition arises from circuits mediating crossover inhibition between the ON and OFF visual pathways—an ON amacrine cell provides direct inhibitory input to OFF parasol cell dendrites and an OFF amacrine cell inhibits ON parasol cells (Cafaro and Rieke, 2013; Manookin et al., 2008; Murphy and Rieke, 2006; Zaghloul et al., 2003). Thus, motion through the receptive field center elicits an increase in excitatory input and a simultaneous decrease in inhibitory input, causing parasol cells to spike (see Figure 8). Indeed, both of these circuit components were stronger for the apparent-motion than for the random-bar stimulus.

Figure 8.

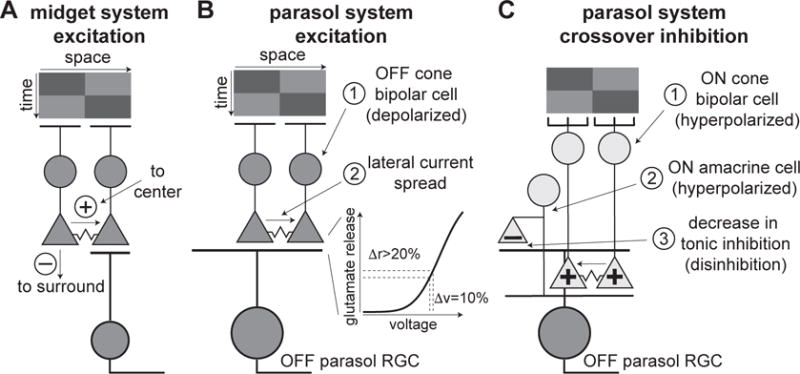
Proposed circuitry for motion responses in midget and parasol ganglion cells. (A) Working model for midget ganglion cells. Dark bar (top) stimulates left then right bipolar cells in sequence. Output of left bipolar cell falls in midget cell receptive-field surround. Portion of depolarization in left bipolar cell spreads to right bipolar cell, potentiating right bipolar cell located in midget cell receptive-field center. (B) Working model for motion sensitivity in synaptic excitation to parasol cells. Dark bar (top) stimulates left then right bipolar cells. Portion of depolarization in left bipolar cell spreads to right bipolar cell. Due to the nonlinear relationship between voltage and synaptic release in the terminal, increasing the voltage of the terminal in the second bipolar cell by an extra 10% could increase glutamate release by >20% (right). The left bipolar cell, thus, primes the right bipolar cell to subsequent stimulation within a brief time interval. (C) Model for motion sensitivity in disinhibition via suppression of crossover inhibition. Dark bar sequences strongly hyperpolarize ON cone bipolar cells; motion sequences enhance suppression of ON bipolar cells through the same junctional mechanism described in (B), resulting in strong removal of glutamate release (or hyperpolarization via junctional coupling) to an ON-type amacrine cell. The hyperpolarized amacrine cell, in turn, decreases inhibitory transmitter release onto OFF parasol cell dendrites relative to gray background, resulting in disinhibition.

These recordings assayed the direct excitatory and inhibitory input to parasol cells, but inner retinal inhibition, including crossover inhibition, can modulate glutamate release from bipolar cells (Asari and Meister, 2012; Eggers and Lukasiewicz, 2011; Eggers et al., 2007; Liang and Freed, 2010) and voltage-clamp recordings from parasol cells would not detect these interactions as they occur upstream of the parasol cell dendrites. To determine whether presynaptic inhibition contributes to motion sensitivity, we recorded excitatory currents in parasol cells before and after blocking inner retinal inhibition with a cocktail of glycine- and GABA-receptor antagonists (strychnine, 0.5 μM; GABAzine, 5 μM; TPMPA, 50 μM). Blocking presynaptic inhibition reduced motion sensitivity by ~60% (mean: control, 2.0 ± 0.6; drug, 0.8 ± 0.4; p = 2.3 × 10⁻²; n = 7 cells; Figure 5E, left). This result may indicate that presynaptic inhibition plays an important role in shaping motion sensitivity in bipolar cells, but we encourage great caution in interpreting these data as wholesale inhibitory blockade can produce many off-target effects. Indeed, during inhibitory block we observed an increase in the frequency and amplitude of spontaneous excitatory currents, consistent with a disruption in the resting state of bipolar cells (Figure 5F). Further, a previous study and our computational model suggest that releasing inner retinal inhibition could affect motion sensitivity simply by driving the bipolar cell output synapse into a more linear state (Kuo et al., 2016; see Figure 7).

Figure 7.

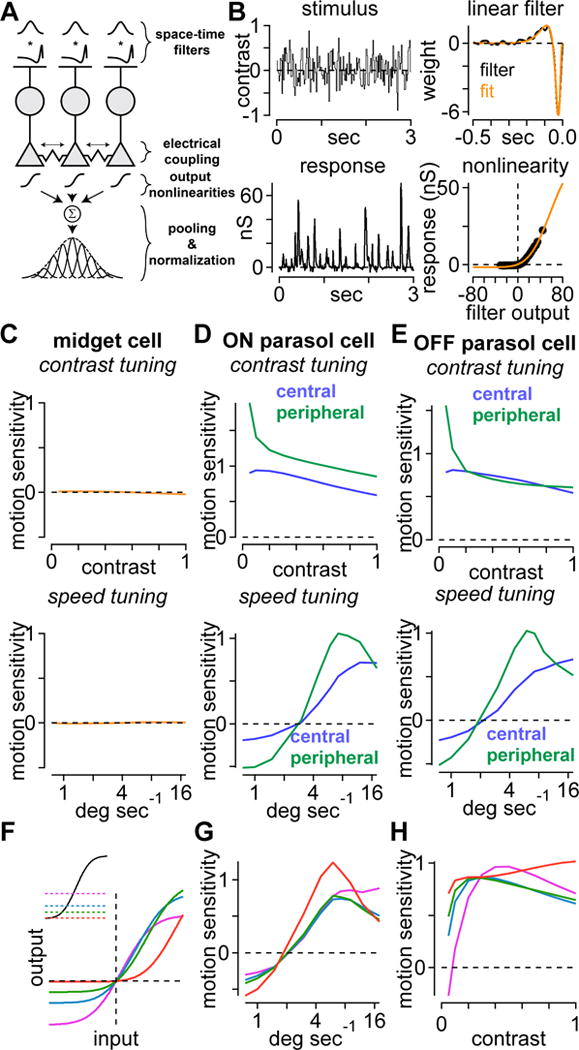
Computational model that includes bipolar cell coupling reproduces motion sensitivity observed in parasol cells and lack of motion sensitivity in midget cells. (A) Model structure. Spatiotemporal integration properties of bipolar cells were modeled as the product of a Gaussian in space and a biphasic linear filter in time. Light-driven signals were integrated at the synaptic terminal and a portion spread through gap junctions, depending on driving force, to neighboring bipolar cell terminals. Signals were then passed through a synaptic output nonlinearity before being pooled and normalized at the level of the ganglion cell dendrites. (B) Temporal filters and output nonlinearities were determined directly using temporal Gaussian flicker stimulus presented within the ganglion cell receptive-field center while recording excitatory responses in whole-cell voltage clamp. (C) Model output as a function of contrast and speed in midget ganglion cells. (D-E) Same as (C) for central and peripheral ON and OFF parasol cells. (F) Family of output nonlinearities (bottom) generated by shifting the y-axis of the nonlinearity to simulate changes in maintained glutamate release (inset). (G-H) Speed and contrast tuning curves generated by running the model using the family of output nonlinearities in (F).

To test for such confounding effects of inhibitory blockade on the bipolar cell output nonlinearity, we recorded contrast-response functions in the excitatory currents of the same cells before and after drug application (Figure 5G, H). Applying inhibitory antagonists changed the contrast-response relationship in both cell types. These effects were most striking in ON cells where inhibitory blockade unmasked an OFF excitatory input, which was greater in magnitude at high contrast than the inherent ON excitation (Figure 5H, left). Due to the clear unintended effects of full inhibitory block, we sought a more ideal pharmacological manipulation to assay the potential contribution of presynaptic inhibition to motion sensitivity.

The OFF visual pathway provides an opportunity to measure the contribution of presynaptic crossover inhibition without substantially shifting the resting state of OFF bipolar cells. This is achieved by applying an mGluR6 agonist (L-AP4, 5 μM) and antagonist (LY341495, 7.5 μM) in a ratio that strongly attenuates signal transmission between cones and ON bipolar cells without dramatically changing the resting state of the ON pathway (Ala-Laurila et al., 2011). Thus, we tested for contributions from presynaptic crossover inhibition to motion sensitivity in OFF parasol cells by recording excitatory currents before and after blocking crossover inhibition. Indeed, blocking crossover inhibition reduced motion sensitivity in each cell tested (mean: control, 2.5 ± 0.8; drug, 1.4 ± 0.5; p = 3.1 × 10⁻²; n = 5 cells; Figure 5E, right). Moreover, we did not observe the spontaneous bursting during crossover block that was present with the inhibitory blockade, indicating that the resting state of OFF bipolar cells was not strongly affected by the pharmacological manipulation. Thus, it appears that crossover inhibition contributes to motion sensitivity both presynaptically at the level of the bipolar cells and postsynaptically at the level of OFF parasol cell dendrites (Figure 5B). This mechanism may also contribute to motion sensitivity in ON parasol cells, but, unfortunately, an unequivocal pharmacological manipulation is not currently available to determine whether this is the case.

Collectively, these data indicate that motion sensitivity in parasol cells arises from an increase in excitatory input and simultaneous decrease in inhibitory input (disinhibition). Disinhibition may also act presynaptically at the level of bipolar cell terminals. Nonetheless, the magnitude of excitation was much larger than that of disinhibition. This, coupled with the larger driving force on excitation near the resting membrane potential, suggests that excitation from presynaptic bipolar cells provides the principal driver for motion sensitivity in parasol ganglion cells. We explored the neural mechanisms mediating motion sensitivity in bipolar cells with a series of experiments and computational model, described below.

Supralinear spatial summation supports a junctional mechanism

What mechanisms mediate the motion sensitivity observed in the excitatory bipolar cell input to parasol ganglion cells? Electrical coupling between bipolar cells via gap junctions mediates a similar type of motion sensitivity in the mouse retina (Kuo et al., 2016). Further, evidence for electrical coupling between diffuse bipolar cells has been found in marmoset (Luo et al., 1999), macaque (Dacey et al., 2000), and human retina (Kántor et al., 2017), including the type-3 bipolar cells that provide direct synaptic input to OFF parasol ganglion cells (Jacoby et al., 2000; Kántor et al., 2017; Luo et al., 1999). Thus, this mechanism is poised to contribute to motion sensitivity in parasol cells.

Gap junction blockers have been used in the past to test for contributions from junctional mechanisms, but these drugs have many off-target effects that greatly complicate data interpretation (Kuo et al., 2016). Instead, we tested whether presynaptic bipolar cells were electrically coupled using a paired-bar stimulus while recording from parasol cells (Kuo et al., 2016). The stimulus was comprised of a bar (width, 32–40 μm) presented at one of two spatial locations. On separate trials, bars were presented at one of the individual positions (‘bar 1’ or ‘bar 2’) or at both positions simultaneously (‘both bars’). The edges of the two bars were spaced sufficiently to avoid stimulating any single bipolar cell with both bars (separation, 32–40 μm; Figure 6A). The reasoning is that if bipolar cells were not electrically coupled, stimulation of one bipolar cell would not affect surrounding bipolar cells that were not, themselves, directly stimulated with the bar. Thus, both bars presented simultaneously should equal the linear sum of each of the bars presented individually (Figure 6A, top). Alternatively, if the bipolar cells were electrically coupled, depolarization would spread laterally and, in concert with the nonlinear nature of synaptic release, would result in glutamate release greater than the sum of individual bar presentations—supralinear spatial summation (Figure 6A, bottom).

Figure 6.

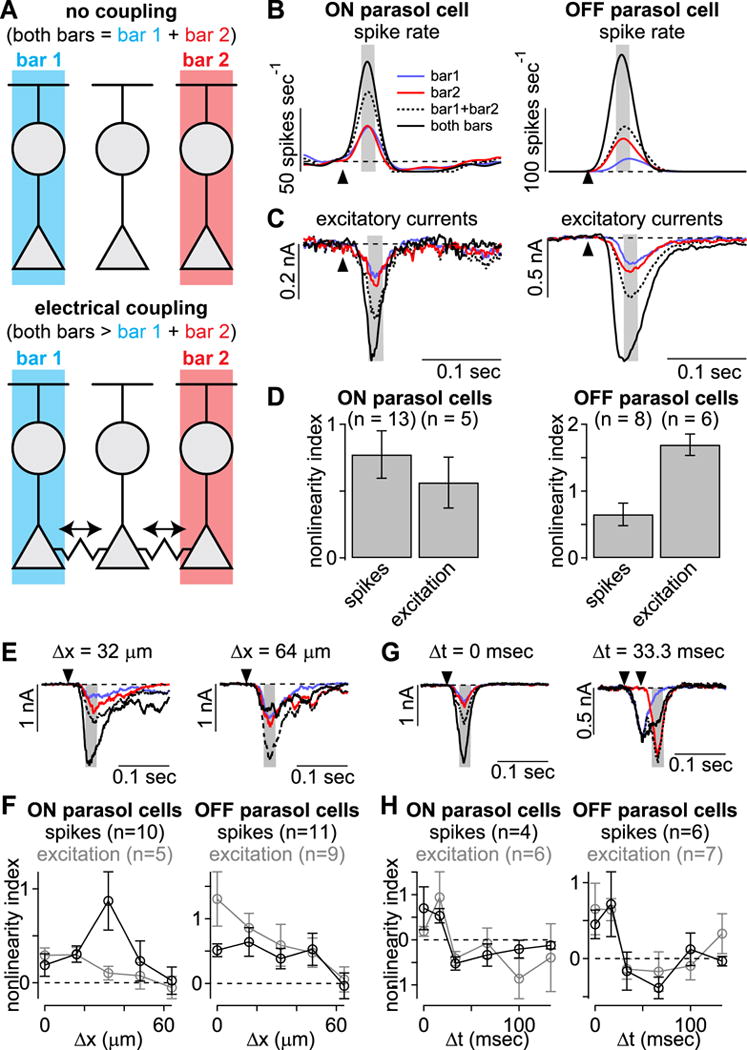
Parasol cells exhibit supralinear spatial summation. (A) Example stimulus configuration for paired-bar stimulation. (B) Spike rates elicited by single (blue, red) or paired (black) bars within the receptive-field center. Dashed line indicates the linear sum of the single bar stimuli. (C) Same format as (B) showing excitatory currents. Arrows indicate stimulus onset and shaded regions indicate sample windows. (D) Nonlinearity index for spike and excitatory responses. Bar plots indicate mean ± SEM. (E) Excitatory currents to paired-bar experiment when closest bar edges were spaced 32 μm or 64 μm apart. (F) Summary data for five different bar spacings in ON and OFF cells. Supralinear summation was absent for bar spacings of 64 μm in both cell types. (G) Data from paired bar experiments in which time between onset of first and second bar were varied. (H) Population data for six time lags. Supralinearity held for time lags of 0 and 17 msec, but dropped dramatically for greater time lags. Error bars indicate mean ± SEM.

When tested with this stimulus, simultaneous presentation of both bars elicited higher spike rates and larger excitatory currents than the linear sum of individual bar presentations (Figure 6B, C). We quantified the degree of supralinear summation using the ‘nonlinearity index’ (Kuo et al., 2016) defined as:

$$\mathit{nonlinearity}\mathit{index}=\frac{R_{\mathit{both}\mathit{bars}}-(R_{\mathit{bar}1}+R_{\mathit{bar}2})}{(R_{\mathit{bar}1}+R_{\mathit{bar}2})}$$

where R_x is the response of the cell in spike rate or excitatory current. Nonlinearity values were greater than zero for spiking and excitation in both cell types, indicating supralinear spatial summation (p < 0.05). These data are consistent with electrical coupling between the diffuse bipolar cells providing excitatory input to both ON and OFF parasol ganglion cells.

The conductances passing through gap junctions are generally considered passive. As a result, they should decay over short distances and times (Rall, 1969). To further test for a contribution from junctional coupling, we varied the parameters of the paired-bar stimulus in order to test these predictions. We examined spatial decay by varying the spacing between bars (Figure 6E, F). Supralinear summation was greatest when bars were spaced ≤32 μm apart and was absent at a spacing of 64 μm (~0.3 degrees), approximately twice the width of a diffuse bipolar cell dendritic tree at comparable retinal eccentricities (Boycott and Wässle, 1991; Dacey et al., 2000; Tsukamoto and Omi, 2015, 2016; Turner and Rieke, 2016). These data indicate that the neural interactions mediating supralinear summation occur on a narrow spatial scale and are likely limited to interactions between neighboring bipolar cells. These narrow spatial interactions would not be recruited well by stimuli lacking spatiotemporal correlations.

We next varied the time between bar presentations to determine whether supralinear summation decayed over time (Figure 6G, H). Nonlinearity indices were positive for time lags of 0 and 17 msec after which they declined below or near zero. These lags correspond to speeds of ≥6 degrees sec⁻¹, which is consistent with the speed tuning of motion sensitivity for these cells (Figure 4B).

Computational model predicts motion sensitivity

The pattern of supralinear spatial summation observed in the experiments, above, is consistent with significant electrical coupling between neighboring diffuse bipolar cells (Dacey et al., 2000; Kántor et al., 2017; Luo et al., 1999). Our working hypothesis is that this electrical coupling results in lateral interactions between neighboring bipolar cells, which contributes to motion sensitivity in bipolar cells (Kuo et al., 2016). Visual stimulation causes a bipolar cell to depolarize and some of this depolarization spreads laterally via gap junctions to neighboring bipolar cells. This spread potentiates these neighboring cells such that subsequent stimulation within a brief time interval produces a larger depolarization than if the cell were stimulated alone. This, combined with the highly nonlinear nature of synaptic release, biases the output of the bipolar cell mosaic to visual motion.

To further explore whether these mechanisms could explain the observed motion sensitivity, we created computational models of the bipolar cell mosaics presynaptic to midget, ON and OFF central parasol, and ON and OFF peripheral parasol cells. Spatiotemporal integration of visual inputs from cones was modeled as linear in which spatial integration was a two-dimensional Gaussian function and temporal integration was a biphasic impulse-response function (Figure 7A). Following linear spatiotemporal integration, a portion of the response spread laterally through gap junctions to neighboring bipolar cell terminals. This spread was based on the relative voltage of each of the bipolar cells and their relative distances. The resulting responses for each cell were then passed through a synaptic output nonlinearity (Figure 7B; Figure S1) before being pooled and normalized. Normalization was performed by modeling the ganglion cell receptive field as a two-dimensional Gaussian (see STAR Methods). The spatial properties of the model were based on measurements of midget and diffuse bipolar cell dendritic arbors in mid-peripheral macaque retina (Boycott and Wässle, 1991; Dacey et al., 2000; Polyak, 1941; Tsukamoto and Omi, 2015, 2016; Turner and Rieke, 2016). The temporal filters and synaptic output nonlinearities were measured directly by recording excitatory currents to a flickering uniform spot within the receptive field center; spot contrast was drawn pseudo-randomly from a Gaussian distribution on each frame presentation. These data were then used to calculate the temporal filters and output nonlinearities for the different bipolar cell types (Figure 7B; see STAR Methods).

Consistent with our direct recordings, the model predicted negligible motion sensitivity in the excitatory input to midget ganglion cells (Figure 7C). The model also showed a similar pattern of motion sensitivity to that observed from our direct recordings from parasol cells (compare Figure 7D-E to Figures 3, 4). Motion sensitivity was predicted at higher apparent motion speeds, but absent at lower speeds (Figure 7D). In addition, motion sensitivity was highest at low contrast and relatively flat at higher contrasts (Figure 7E). Further, it predicted a more high-pass speed tuning for central relative to peripheral parasol cells, similar to our direct recordings (Figure 4C, 7D-E). Overall, the model predictions were qualitatively similar to our physiological recordings, lending further support for a mechanism in which motion sensitivity arises at the level of glutamate release from diffuse bipolar cells and is mediated by electrical coupling between neighboring bipolar cells.

We next extended our model to investigate how motion sensitivity depended on the bipolar cell output nonlinearity. This was done by fixing the overall shape of the nonlinearity and varying the maintained glutamate release (i.e., release at zero contrast). This manipulation of the model emphasized different regions of the output nonlinearity, and we examined four different maintained release levels (Figure 7F). The highest maintained level was near the center of the nonlinearity and constituted a fairly linear region of the function for low stimulus contrasts. We then simulated the speed and contrast tuning curves for each nonlinearity; these simulations are shown in Figure 7G, H. The bandpass nature of speed tuning varied slightly with maintained release with the highest release level being the least bandpass (Figure 7G). The contrast simulations showed motion sensitivity for each of the nonlinearities at high contrast. At low contrast, however, motion sensitivity varied systematically with the degree of maintained release—motion sensitivity was highest at the lower release rates (Figure 7H). These simulations provide further support for the importance of electrical coupling between bipolar cells in motion sensitivity. Further, nonlinear release at the bipolar cell output synapse appears to play a particularly important role in motion sensitivity at low contrast.

DISCUSSION

We performed a series of experiments to directly address the long-standing question of whether motion computations arise in the primate retina. It is widely believed that the principal function of the early visual system in humans and non-human primates is to relay a veridical representation of the visual environment to cortical centers. The cortex, then, bears the bulk of the computational load, extracting spatial form, texture, and motion information from this rudimentary representation. In this view, the spike train of a single parasol cell represents achromatic spatial information, such as the contrast of an object, and is unconcerned about whether that object is moving. However, when measured directly, we found that visual motion elicited significantly larger responses than those produced by either uncorrelated or non-motion correlated spatiotemporal patterns (Figures 1–4). This striking motion sensitivity was also evident in the excitatory and inhibitory synaptic inputs to parasol cells (Figure 5).

Midget ganglion cells did not show significant motion sensitivity and this was true across a wide range of contrasts and speeds (Figures 1, 3, 4). What mechanisms account for this lack of motion sensitivity in midget ganglion cells? One possibility is that midget bipolar cells lack significant electrical coupling; it is clear, however, that OFF midget bipolar cells exhibit coupling both in their dendrites and in their axons (Kántor et al., 2017). Further, our model of the midget bipolar cells included electrical coupling and it, nonetheless, lacked significant motion sensitivity (Figure 7). Thus, we propose that the small receptive-field center size of midget ganglion cells plays a critical role in their lack of motion sensitivity. At the eccentricities that we typically record and in our computational model, midget ganglion cells collect from ~1–3 midget bipolar cells whereas a parasol ganglion cell collects from at least 30 bipolar cells in its receptive field center at comparable eccentricities. Thus, unlike the parasol cells, much of the enhanced responses from electrical coupling to motion falls in the midget cell receptive-field surround (see Figure 8A). Further, our direct recordings indicated that the midget bipolar cell output was more linear than that of diffuse bipolar cells, which likely also lessens their motion sensitivity (see Figure S1). Finally, fundamental asymmetries have been demonstrated in the inhibitory motifs of the midget and parasol pathways (Cafaro and Rieke, 2010, 2013), which may also contribute to the observed differences in motion sensitivity.

Bipolar cell coupling in primate retina

Previous studies have found evidence for extensive gap junctional coupling between bipolar cells in mouse and rabbit retina. Much of this coupling, particularly in ON-type bipolar cells, occurs through intervening amacrine cells, particularly the AII amacrine cell (reviewed in Bloomfield and Völgyi, 2009; Euler et al., 2014; Völgyi et al., 2013). Some OFF bipolar cells are also coupled and this coupling can occur at the level of their dendrites or axons (Feigenspan et al., 2004; Hilgen et al., 2011).

Far less is known about coupling patterns of primate bipolar cells, but the few key studies that have addressed this question found coupling in both ON and OFF bipolar cells (Dacey et al., 2000; Kántor et al., 2017; Kovács-Öller et al., 2017; Luo et al., 1999). Further, gap junctions were present in the axons of type-3 (OFF) bipolar cells that provide direct glutamatergic input to OFF parasol ganglion cells (Jacoby et al., 2000; Kántor et al., 2017; Luo et al., 1999). OFF parasol cells also receive synaptic input from type-2 bipolar cells, and ON parasol cells receive input from type-4 and type-5 bipolar cells (Jacoby et al., 2000; Marshak et al., 2002; Tsukamoto and Omi, 2015, 2016). However, further studies are needed to determine the coupling patterns in these bipolar cell types and to understand how these patterns contribute to information processing in the magnocellular visual pathway.

Motion sensitivity and retinal eccentricity

We found that motion sensitivity varied with retinal eccentricity—on average it was higher in the central retina than in the peripheral retina (Figure 1). What mechanisms account for this difference? Many cell types, including bipolar cells, show smaller dendritic tree diameters and closer spacing in the central versus the peripheral retina (Kolb et al., 1992; Rodieck, 1989; Watanabe and Rodieck, 1989). Given the exponential decay of passive conductances with distance, signals passing between electrically coupled bipolar cells would propagate most effectively when those cells were in close proximity (Rall, 1969). This would enhance the lateral spread of current through gap junctions, producing a concomitant enhancement of motion sensitivity. Thus, the enhanced motion sensitivity in central parasol cells may arise from closer spacing of their presynaptic bipolar cells. Counter to this hypothesis, however, our computational model was unable to replicate the higher motion sensitivity values for central versus peripheral cells (Figure 7D, E). Thus, other mechanisms, such as differences in inner retinal inhibition, may contribute to the enhanced motion sensitivity observed in central versus peripheral parasol cells and further studies will be required to elucidate these putative mechanisms.

Neural interactions within the receptive field center

Consistent with previous studies, our measurements indicate that different regions of the receptive field center of parasol cells interact, as evidenced by the observed supralinear summation (Figure 6; Crook et al., 2008; Freeman et al., 2015; Petrusca et al., 2007; Turner and Rieke, 2016). Our data further indicate that some of these interactions are mediated by electrical (gap) junctions between neighboring bipolar cells (Figure 6E-H). Indeed, including electrical coupling in our computational model of the bipolar cell mosaic reproduced the observed motion sensitivity (Figure 7).

Our working hypothesis for the synaptic mechanisms mediating motion sensitivity is shown in Figure 8B. Stimulation of a bipolar cell with light causes some of the current to spread laterally via gap junctions to neighboring bipolar cells, depolarizing their synaptic terminals. This depolarization enhances subsequent light-driven depolarization of the cell which, combined with the nonlinear nature of synaptic release, produces more glutamate release than if the cell were stimulated in isolation. For example, a 10% increase in voltage at the synaptic terminal can produce >20% increase in glutamate release. Thus, the combination of electrical coupling and the synaptic output nonlinearity biases parasol cells to visual motion (Kuo et al., 2016).

The disinhibition observed during bar motion arises from amacrine cells providing crossover inhibition to parasol cells (Manookin et al., 2008; Murphy and Rieke, 2006; van Wyk et al., 2009). We briefly summarize this mechanism for OFF parasol cells, but an analogous circuit mediates disinhibition in ON parasol cells (Cafaro and Rieke, 2010, 2013). The dark bars hyperpolarize ON cone bipolar cells which, in turn, decrease glutamate release onto ON amacrine cells. These amacrine cells, then, decrease inhibitory synaptic release onto OFF parasol cell dendrites, causing depolarization of the parasol cell (Figure 8B). Our measurements indicate that disinhibition plays a larger relative role in ON parasol cells than OFF parasol cells, but further experiments will be needed to determine whether this is the case across stimulus conditions.

Motion computations arise early in the primate visual stream

The fundamental importance of the magnocellular pathway to motion processing in primates was reported more than 25 years ago (Merigan et al., 1991a; Schiller et al., 1990a, b). These studies demonstrated that monkeys with lesions to the magnocellular LGN showed impaired motion perception. Moreover, inactivating the magnocellular, but not the parvocellular, pathway strongly attenuated neural activity in a cortical area that is critical for motion processing—the medial temporal (MT) area of cortex (Maunsell et al., 1990). Further evidence for the importance of parasol cells in motion vision comes from studies of neuronal connectivity. Cells in the magnocellular LGN that receive input from parasol cells provide input to cortical regions that contribute substantially to visual motion processing in the dorsal visual pathway of primates (Blasdel and Lund, 1983; Hawken et al., 1988; Maunsell et al., 1990; Maunsell and van Essen, 1983; Movshon and Newsome, 1996; Yabuta et al., 2001). Indeed, multi-electrode array recordings in macaque retina have demonstrated that the concerted output of the parasol cell mosaic provides a precise estimate of visual motion (Chichilnisky and Kalmar, 2003; Frechette et al., 2005). Our study adds to this previous work by demonstrating that individual parasol ganglion cells exhibit motion sensitivity and identifying the locus of motion sensitivity as the output of the diffuse bipolar cell mosaic. Moreover, our results indicate that visual cortex receives a far more informative representation of visual motion from the early visual system than has been previously recognized.

While our data indicate that parasol cells are motion sensitive, the response properties of these cells are clearly distinct from those of classical direction-selective retinal ganglion cells that respond selectively to motion in specific cardinal orientations of space (Barlow and Levick, 1965; Sabbah et al., 2017). Stimulating the receptive field centers of parasol cells produced no such selective motion preference and we expect that parasol cells contribute differently to motion vision than classical direction-selective ganglion cells. How, then, do parasol cells contribute to motion vision? To answer this question, future studies will need to determine whether these cells are sensitive to specific types of visual motion and how the receptive-field surround shapes motion sensitivity (Greschner et al., 2016; Manookin, 2016).

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Mike Manookin (manookin@uw.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Experiments were performed in an in vitro, pigment-epithelium attached preparation of the macaque monkey retina. Eyes were dissected from terminally anesthetized macaque monkeys of either sex (Macacca fascicularis, mulatta, and nemestrina) obtained through the Tissue Distribution Program of the National Primate Research Center at the University of Washington. All procedures were approved by the University of Washington Institutional Animal Care and Use Committee.

METHOD DETAILS

Tissue Preparation and electrophysiology

A detailed description of the preparation is given in our previous work (Manookin et al., 2015; Puller et al., 2015). Retina was superfused with warmed (32–35°C) Ames’ medium (Sigma) at ~6–8 mL min⁻¹. Additional D-glucose (14 mM) was added to the Ames’ medium. Recordings were performed from macular, midperipheral, or peripheral retina (2–8 mm, 10–30° foveal eccentricity). Physiological data were acquired at 10 kHz using a Multiclamp 700B amplifier (Molecular Devices), Bessel filtered at 3 kHz, digitized using an ITC-18 analog-digital board (HEKA Instruments), and acquired using the Symphony acquisition software package developed in Fred Rieke’s laboratory (http://symphony-das.github.io).

Recordings were performed using borosilicate glass pipettes containing Ames medium for extracellular spike recording or, for whole-cell recording, a cesium-based internal solution containing (in mM): 105 CsCH₃SO₃, 10 TEA-Cl, 20 HEPES, 10 EGTA, 2 QX-314, 5 Mg-ATP, and 0.5 Tris-GTP, pH ~7.3 with CsOH, ~280 mOsm. Series resistance (~3–9 MΩ) was compensated online by 50–75%. The membrane potential was corrected offline for the approximately –11 mV liquid junction potential between the intracellular solution and the extracellular medium. Excitatory and inhibitory currents were isolated by holding the cell at the reversal potentials for inhibition/chloride (~−70 mV) and excitation (0 mV), respectively. The pipette solution typically contained 0.5% EZ-Link biocytin (ThermoFisher) for later recovery of cellular morphology.

Visual stimuli and data analysis

Visual stimuli were generated using the Stage software package developed in the Rieke lab (http://stage-vss.github.io) and displayed on a digital light projector (Lightcrafter 4500; Texas Instruments) modified with custom LEDs with peak wavelengths of 405, 505 (or 475), and 640 nm. Stimuli were focused on the photoreceptor outer segments through the microscope objective. Mean light levels were in the low to medium photopic regimes (~3 × 10³ – 3.4 × 10⁴ photoisomerizations [R*] cone⁻¹ sec⁻¹). To simulate smooth motion at high speeds, the moving bar stimuli (Figure 4C) were presented at refresh rates of 360–720 Hz; otherwise, stimuli were presented at 60–120 Hz. Stimuli presented at rates >120 Hz required pre-rendering the stimulus, making this technique impractical for the apparent motion/random bar stimulus that required many repeats of the random stimuli. Contrast values are given in Weber contrast. All responses were analyzed in MATLAB (R2016a+, Mathworks).

Apparent-motion, random bar, and alternating bar stimuli were presented at a refresh rate of 120 Hz. Each bar was 16 × 128 μm and bars occupied non-overlapping regions of space. Speed was varied by changing the duration of individual bar presentations. For the alternating bar experiments (Figure 2), neighboring bars were presented in random regions of the receptive-field center on each trial such that, on average, the alternating bars stimulated the same regions as the apparent-motion and random bar stimuli. Thus, these three stimulus types varied only in their spatiotemporal correlation structure, allowing for a direct comparison.

Much of the previous work studying speed tuning in primates presented data in terms of visual angle (degrees sec⁻¹). In order to present our findings in the context of this previous work, we converted the speed of our visual stimuli from mm sec⁻¹ to degrees sec⁻¹. The macaque retina exhibits a nonlinear relationship between visual angle (in degrees) and retinal eccentricity (in mm)—one degree is 0.223 mm in the fovea and decreases to ~0.17 mm in the far periphery (Perry and Cowey, 1985). Thus, we used a value of 0.22 mm degree⁻¹ for cells recorded in the more central retina (≤3 mm foveal eccentricity) and 0.2 mm degree⁻¹ for peripheral cells (>3 mm eccentricity), making motion stimuli 10% slower for central relative to peripheral cells.

For extracellular recordings, currents were wavelet filtered to remove slow drift and amplify spikes relative to the noise (Wiltschko et al., 2008) and spikes were detected using either a custom k-means clustering algorithm or by choosing a manual threshold. Whole-cell records were leak subtracted and responses were measured relative to the median membrane currents immediately preceding stimulus onset (0.25–0.5 sec window). Summary data are presented in terms of conductance (g), which is the ratio of the current response (I) to the driving force:

$$g=\frac{I}{V_m-E}$$

where V_m is the holding potential (in mV) and E is the reversal potential (in mV). Reversal potentials of 0 mV and −70 mV were used for excitatory and inhibitory inputs, respectively.

To directly measure the input-output properties of diffuse bipolar cells for our computational model, we presented a flickering spot within the receptive field center of parasol and midget ganglion cells. On each frame, the spot contrast was drawn pseudo-randomly from a Gaussian distribution with a mean of zero and a standard deviation of 0.1–0.3 (i.e., 10–30% root-mean-squared [RMS] contrast). The linear filter (F) was then computed as the cross-correlation of the stimulus (S) and response (R).

$$F(t)={\displaystyle \int R(\tau )S(t+\tau )d\tau }$$

where τ is the temporal lag. In the Fourier domain, cross-correlation is accomplished by taking the dot product of the Fourier transform of the response and the complex conjugate of the Fourier transform of the stimulus:

$$\widehat{F}(\omega )=\frac{{\widehat{S}}^{\ast }(\omega )\widehat{R}(\omega )}{{\widehat{S}}^{\ast }(\omega )\widehat{S}(\omega )}$$

where $\widehat{S}(\omega )$ is the complex conjugate of the Fourier transform of S(t), $\widehat{R}(\omega )$ is the Fourier transform of R(t), and * denotes the complex conjugate. The denominator is the autocorrelation of the stimulus—normalizing by this value corrects for temporal correlations in the stimulus introduced by potential non-randomness in noise generation and by a finite presentation rate (60 Hz) as in (Baccus and Meister, 2002). The resulting temporal filters were modeled as a damped oscillator with an S-shaped onset as in (Schnapf et al., 1990) with the Gaussian decay replaced by an exponential decay (Angueyra and Rieke, 2013):

$$F(t)=A\frac{{\left(t/{\tau }_{\mathit{rise}}\right)}^3}{1+{\left(t/{\tau }_{\mathit{rise}}\right)}^3}{e}^{-\left(\frac{t}{{\tau }_{\mathit{decay}}}\right)}\cos \left(\frac{2\pi t}{{\tau }_{\mathit{period}}}+\phi \right)$$

where A is a scaling factor, τ_rise is the rising-phase time constant, τ_decay is the damping time constant, τ_period is the oscillator period, and φ is the phase (in degrees). Time and time constants are expressed in seconds. The best-fit parameters for the three cell types were used in the computational model, described below (midget: A, −105.3; τ_rise, 5.07 × 10⁻² ; τ_decay, 3.53 × 10⁻²; τ_period, −7.58 × 10⁻¹; φ, 222.4; ON parasol: A, 198.4; τ_rise, 4.86 × 10⁻²; τ_decay, 2.22 × 10⁻²; τ_period, 2.43 × 10⁻¹; φ, 9.3; OFF parasol: A, –51.08; τ_rise, 1.77 × 10⁻² ; τ_decay, 3.71 × 10⁻²; τ_period, −5.89 × 10⁻¹; φ, 123.3).

The output nonlinearity was then calculated by convolving the linear filter with the stimulus to generate a linear prediction (P):

$$P(t)={\displaystyle \int F(\tau )S(t-\tau )d\tau }$$

The contrasts in the noise stimulus were relatively low and we sought information about the shape of the nonlinearity at high contrast for our computational model. To obtain the complete output nonlinearity, we measured the excitatory contrast-response functions in the same cells by presenting spots that were the same size as the Gaussian noise stimulus (duration, 0.5 sec). The x-axis of the resulting contrast-response function was then multiplied by a scalar to bring it into alignment with the nonlinearity generated from Gaussian noise. The resulting nonlinearity (N) was described well by a normal cumulative distribution function (Chichilnisky, 2001; Turner and Rieke, 2016):

$$N(x)=\epsilon +\frac{\alpha }{\sqrt{2\pi }}{\displaystyle {\int }_{-\mathrm{\infty }}^x{e}^{\frac{-{(\beta t+\gamma )}^2}{2}}dt}$$

where α is the maximal response of the cell, ε is the offset along the y-axis, γ is the maintained drive to the cell, and β is the sensitivity of the nonlinearity to the filter output (x-axis). The best-fit parameters for the three cell types were used in the computational model, described below (midget: α, 4.3; β, 3.08 × 10⁻²; γ, –0.5; ε, −1.2; ON parasol: α, 56.7; β, 2.5 × 10⁻²; γ, −1.12; ε, −7.5; OFF parasol: α, 70.7; β, 3.3 × 10⁻²; γ, −1.9; ε, −1.6).

Immunostaining and confocal microscopy

Specimens were immersion-fixed in 4% paraformaldehyde in 0.1 M phosphate buffer (PB), pH 7.4, for 30–50 min at room temperature. Following fixation and washing in PB, samples were cryoprotected in a PB solution containing 30% sucrose and stored at −20°C until processing. Specimens were incubated free floating overnight at 4°C in Alexa-488-coupled streptavidin (1:1000, Invitrogen) and DAPI (1:2000, Invitrogen) in a PB solution containing 5% normal donkey serum, 1% bovine serum albumin, 1% Triton X-100. Following fixation, samples were washed in PB and mounted on glass slides using Vectashield mounting medium (Vector Laboratories) and cover-slipped. Confocal images were taken with a Leica TCS SB8 microscope using a 20X or 63X oil-immersion objective. Subsequent image analyses were done in Fiji/ImageJ (http://fiji.sc).

Modeling

We generated models of excitatory (bipolar cell) inputs to midget ganglion cells and central and peripheral parasol cells (Kuo et al., 2016; Schwartz et al., 2012). A previous study found that the parasol cell receptive-field diameter was approximately six times greater than that of the excitatory subunits at any given eccentricity (Turner and Rieke, 2016). We used receptive-field diameters (2-SD) of 96 μm and 192 μm for central and peripheral parasol cells, respectively. Diffuse bipolar cell receptive field diameters were 12.5 μm and 32 μm for central and peripheral eccentricities, respectively. The latter value agrees well with previous measurements from mid-peripheral macaque retina (Dacey et al., 2000; Tsukamoto and Omi, 2015, 2016; Turner and Rieke, 2016). A receptive-field center size of 25 μm and 12.5 μm was used for midget ganglion and bipolar cells, respectively (Polyak, 1941).

The location of each bipolar cell was randomly shifted in x and y spatial dimensions (SD: central, 3 μm; peripheral, 4 μm; midget, 2 μm). Each bipolar cell receptive field occupied two dimensions of space (x, y) and one dimension of time (t). The spatial dimensions were comprised of a circular Gaussian with a 2-SD width of the spatial receptive field and the temporal filter was the time axis. The model proceeded in four distinct stages. First, the stimulus (S) and spatiotemporal filter (F) were convolved to generate the linear response (R) for each bipolar cell in the mosaic.

$$R(t)={\displaystyle \int {\displaystyle \int {\displaystyle {\int }_{-\mathrm{\infty }}^{t}S(x,y,\tau )F(x,y,t-\tau )\mathit{dx}\mathit{dy}d\tau }}}$$

To simulate random fluctuations in membrane potential, noise was injected into each bipolar cell; this noise was calculated from the y-offset value (ε) of the output nonlinearity (described above). This value approximates the maintained excitatory conductance at zero-contrast. Assuming Poisson noise, by definition the mean and variance are equal. The noise value is, therefore, the square-root of the mean (ε):

$$\mathit{noise}=\sqrt{\mathit{variance}}=\sqrt{\mathit{mean}}=\sqrt{\epsilon }$$

Following noise injections, electrical coupling between bipolar cells was simulated by allowing a portion of the response to pass between the cells. The change in response in a given bipolar cell at each time point due to electrical coupling was defined as:

$$\mathrm{\Delta }{R}_i(t)={\displaystyle \sum _{j=1}^{n}g\left(R_i(t)-R_j(t)\right)e^{\left(\frac{-d_{i,j}}{\lambda }\right)}}$$

where g was the coupling gain (fraction of response shared by a given bipolar cell), λ was the decay constant for coupled signals over space, and d_i,j was the pair-wise Euclidean distance between bipolar cell (i) and the jth bipolar cell in the mosaic and n was the total number of bipolar cells. The resulting response in each cell after coupling (R_c) was then calculated as the sum of the response before coupling (R) and the response change due to coupling (ΔR):

$$R_{ci}(t)=R_i(t)+\mathrm{\Delta }{R}_i(t)$$

The output of each bipolar cell (b_i) was then calculated by passing the coupled response through the output nonlinearity (N):

$$b_i(t)=N\left(R_{ci}(t)\right)$$

The final stage consisted of normalizing the response of each bipolar cell relative to the center of the model ganglion cell receptive center and pooling the normalized responses to produce the time-dependent excitatory input to the model ganglion cell (E):

$$E(t)={\displaystyle \sum _{i=1}^n{b}_i(t)e^{-\left(\frac{d_i^2}{2{\sigma }^2}\right)}}$$

where σ is the 2-SD width of the ganglion cell receptive field center and d_i is the Euclidean distance between the bipolar cell and ganglion cell receptive field centers. The speed tuning simulations were run with a 30% stimulus contrast, and the contrast simulations were run at a speed of 12 degrees sec⁻¹. Motion sensitivity values were calculated by averaging the responses to the apparent motion and random bar stimuli across a sample window matched to the stimulus duration.

QUANTIFICATION AND STATISTICAL ANALYSIS

All statistical analyses were performed in MATLAB (R2016a+, Mathworks). Reported p-values in this study were calculated using either the Wilcoxon signed-rank test, for paired data, or the Mann-Whitney U test, for unpaired data. Final figures were created in MATLAB, Igor Pro, and Adobe Illustrator.

DATA AND SOFTWARE AVAILABILITY

Visual stimulation (http://stage-vss.github.io) and data acquisition (http://symphony-das.github.io) software are freely available.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Streptavidin, Alexa Fluor 488	ThermoFisher Cat# S11223	RRID:AB_2336881
Goat polyclonal anti-ChAT	EMD Millipore Cat# AB144P	RRID:AB_90650
Donkey anti-goat, Alexa Fluor 546	ThermoFisher Cat# A11056	RRID:AB_10584485
Chemicals
L-AP4	Tocris Cat# 0103	N/A
LY341495 disodium salt	Tocris Cat# 4062	N/A
Strychnine hydrochloride	Sigma Cat# S0532	N/A
GABAzine (SR-95531)	Sigma Cat# S106	N/A
TPMPA	Tocris Cat# 1040	N/A
Ames’ medium	Sigma Cat# 1420	N/A
Biological Tissue
Macaque retina	Regional Primate Research Center	N/A
Software and Algorithms
Stage	Rieke Lab, U. of Washington	N/A
Symphony	Rieke Lab, U. of Washington	N/A
MATLAB	Mathworks	N/A
Fiji/ImageJ	http://fiji.sc/Fiji	N/A
Igor Pro	Wavemetrics	N/A
Adobe Illustrator	Adobe	N/A