Attentional changes in either criterion or sensitivity are associated with robust modulations in lateral prefrontal cortex

Summary

Visual attention is associated with neuronal changes across the brain, and these widespread signals are generally assumed to underlie a unitary mechanism of attention. However, attention-related effects on performance can be partitioned using signal detection theory into changes in either the subject’s criterion or sensitivity. Neuronal modulations associated with only sensitivity changes were previously observed in visual cortex, raising the questions of which structures mediate attention-related changes in criterion and whether individual neurons are involved in multiple components of attention. Here we recorded from monkey lateral prefrontal cortex (LPFC) and found that in contrast to visual cortex, neurons in LPFC changed their firing rates, pairwise correlation, and Fano factor when the subject changed either its criterion or its sensitivity. These results indicate that attention-related neuronal modulations in separate brain regions are not a monolithic signal and instead can be linked to distinct behavioral changes.

eTOC Blurb

Luo and Maunsell show that the modulations in prefrontal cortex correspond to multiple components of attention and differ from modulations in visual cortex, indicating that different brain structures underlie distinct attentional mechanisms and that attention is not a unitary process.

Introduction

When attention is directed to a location in visual space, the activity of visually responsive neurons changes throughout the brain (Krauzlis et al., 2013; Maunsell, 2015; Moore and Zirnsak, 2017). When attention is directed within a neuron’s receptive field, its firing rate typically increases relative to when attention is elsewhere. Changes in firing rates associated with visuospatial attention are observed in the visual, parietal, and prefrontal regions of the cerebral cortex (Wurtz and Mohler, 1976; Lynch et al., 1977; Moran and Desimone, 1985), as well as in the superior colliculus and thalamus (Ignashchenkova et al., 2003; McAlonan et al., 2008; Briggs et al., 2013). Except for the retina, every brain region examined that contains neurons with spatially selective visual responses has been shown to contain signals related to visuospatial attention. While these modulations have been characterized by many studies since first observed in the superior colliculus (Goldberg and Wurtz, 1972), it remains unclear how they give rise to the behavioral effects associated with visuospatial attention. In particular, it is unknown whether distinct behavioral changes related to visuospatial attention depend on separate or the same brain areas.

When attention is directed to a visual location, an observer detects a higher proportion of targets at that location and responds to targets there with shorter delays (Posner et al., 1980; Bashinski and Bacharach, 1980). When the target is barely visible, attention can reliably make the difference between a successful detection and failure. In single-neuron recording studies, when an animal shows an increase in target detection rate (i.e., hit rate) without changes in the stimulus or eye movements, concomitant neuronal changes are considered to be correlates of visuospatial attention.

However, the attention-related improvement in hit rate can be partitioned into two independent components using signal detection theory: either changes in the subject’s criterion (c) or changes in the subject’s sensitivity (d′) (Figure 1A; Bashinski and Bacharach, 1980; Müller and Findlay, 1987; Downing, 1988; Hawkins et al., 1990; Müller and Humphreys, 1991; Wyart et al., 2012; Luo and Maunsell, 2015; Sridharan et al., 2017; Arcizet et al., 2017). A subject’s criterion corresponds to how readily the subject reports a target or withholds from such a report. Adopting a more liberal criterion (a decrease in c) at a visual location consists in responding more frequently at that location, resulting in more targets being detected there even when the stimulus is unchanged. A subject’s sensitivity corresponds to the ability to discriminate between a target and a nontarget. Enhancing sensitivity (increasing d′) at a location also results in more targets detected at that location. The distinction between criterion and sensitivity is crucial because any improvement in an observer’s hit rate can be equivalently brought about by a decrease in c or an increase in d′ (Figure 1B). These two changes are differentiated by the subject’s false alarm rate. An improvement in hit rate brought about by a decrease in c is associated with a higher false alarm rate, while the same increase in hit rate brought about by an increase in d′ is associated with a lower false alarm rate.

Figure 1. Visuospatial attention can be partitioned using signal detection theory.

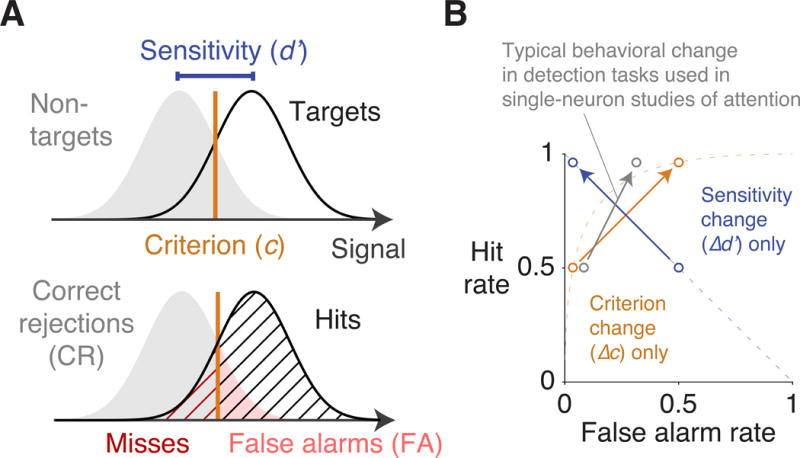
(A) In the signal detection model, each stimulus evokes a noisy internal signal. If the signal is stronger than the criterion (c), the stimulus is reported as a target. The distributions of internal signals evoked by the target and by the nontarget overlap, and the separation between these two distributions is indexed as sensitivity (d′). The subject’s response to each stimulus is categorized as a hit (H), miss (M), false alarm (FA), or correct rejection (CR), and the frequency of these responses are used to calculate c and d′. (B) An increase in hit rate, which is used to operationalize attention in many single-neuron studies, typically consists of a combination of changes in criterion and sensitivity (Luo and Maunsell, 2015). A typical behavioral change of this sort is shown (in gray), along with an isolated change in criterion (in orange) and an isolated change in sensitivity (in blue). The dashed orange line represents an isopleth along which d′ is constant and only c varies, and the dashed blue line represents the isopleth along which c is constant and only d′ varies. Any change in hit rate can be brought about by a change in criterion alone, a change in sensitivity alone, or both.

Because single-neuron studies typically have operationalized visuospatial attention using only hit rates, it is unclear how signals across the brain relate to these two components of attention. We previously designed a task for monkeys that isolated these two behavioral changes and found that neuronal modulations in visual cortical area V4 are associated with changes in sensitivity, but not with changes in criterion (Luo and Maunsell, 2015). This previous result indicates that at least in this task, changes in behavioral criterion depend on brain regions other than V4, and therefore suggests that separate brain regions contribute in distinct ways to visuospatial attention. Consistent with this interpretation, a recent study suggests that the superior colliculus contributes to visuospatial attention primarily through changes in the subject’s criterion rather than sensitivity (Sridharan et al., 2017).

Yet it remains unclear what neuronal signals are associated with attention-related changes in criterion, and whether criterion-related neuronal changes are qualitatively similar to the signals typically correlated with attention. To address these questions, we recorded from neurons in lateral prefrontal cortex (LPFC) while monkeys changed either their criterion or sensitivity at specific visual locations. Neuronal changes in LPFC have been correlated with spatially-selective changes in response readiness (Boch and Goldberg, 1989; Boussad and Wise, 1993) and in target detection (Lennert and Martinez-Trujillo, 2011). However, because previous studies recording from LPFC have not controlled the subject’s criterion and sensitivity, it is unknown to which component of attention the modulations in LPFC correspond.

We found that visual responses in LPFC were robustly modulated when the subject changed either criterion or sensitivity. Because the modulations in LPFC differ qualitatively from those in visual cortical area V4, which are correlated with changes only in sensitivity, the results demonstrate that attention-related modulations in different brain structures are not a unitary signal and instead relate to distinct behavioral components of attention.

Results

Isolation of behavioral changes in either criterion or sensitivity

We trained two monkeys on a change detection task that isolated spatially selective changes in either the subject’s criterion or its sensitivity (Figure 2A; Luo & Maunsell, 2015). In each trial, two stimuli (“samples”) appeared concurrently for 400 ms. After a delay of 150-250 ms, a single stimulus (“test”) appeared at one of the two sample locations selected at random. The monkey had to saccade to the test if it differed in orientation from the sample at the same location. The probability of an orientation change between the samples and the test was 0.5. If no change occurred, the monkey had to wait and saccade to a second test stimulus, which always differed from the sample. The response to the first test in each trial was categorized as a hit (H), miss (M), false alarm (FA), or correct rejection (CR), and these responses were used to compute c and d′.

Figure 2. Isolation of attentional changes in criterion and sensitivity.

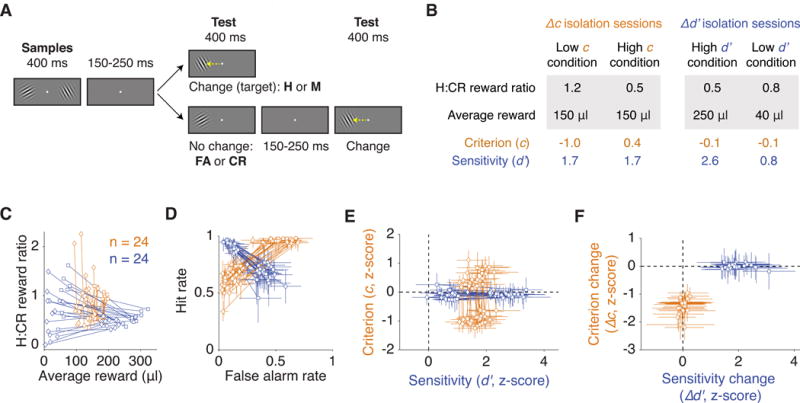
(A) Monkeys had to detect an orientation change that occurred on either the first or second test stimulus and report it with a saccade. If no change occurred on the first test, monkeys had to wait for a change that would always occur on the second test. In a trial in which a change occurred on the first test, the outcome was categorized as either a hit (H) or a miss (M), and when no change occurred on the first test, the outcome was either a false alarm (FA) or a correct rejection (CR). (B) Average reward parameters and behavioral indices across sessions. Each session consists of two task conditions, and isolation was achieved by varying reward sizes between the two conditions. Criterion was controlled primarily using the ratio of reward for a H to a reward for a CR (“H:CR reward ratio”), and sensitivity was controlled primarily using the average reward across H and CR. The task condition (high d′, low d′, low c, or high c) indicates the animal’s performance at the contralateral location. (C) Reward contingencies in each daily session. Each marker refers to one of the two task conditions of each session, and the pair of markers representing the same session are connected by a line. The data are from 24 Δc isolation sessions (shown in orange) and 24 Δd′ isolation sessions (in blue). Diamonds and squares represent monkeys C and Y, respectively. (D) Hit rates and false alarm rates of each task condition of each daily session. (E) Criterion and sensitivity of each task condition of each daily session. (F) Criterion change and sensitivity change in each session. Crosshairs in D-F represent 95% confidence intervals. See also Figure S1.

To control the subject’s criterion and sensitivity, we titrated the reward given for a H or a CR separately at each stimulus location. The subject’s criterion was primarily controlled by the ratio of the reward for a H to the reward for a CR (“H:CR reward ratio”, Figure 2B-C). A larger H:CR reward ratio at a location encouraged a more lenient criterion (i.e., lower or more negative c) at that location, while a smaller H:CR reward ratio encouraged a more stringent criterion (i.e., higher or more positive c). The subject’s sensitivity was primarily controlled by the average reward across H and CR. A larger average reward at a location results in a higher sensitivity at that location. These reward contingencies were varied between two task conditions of each daily session to isolate a change in either the subject’s criterion (in a “Δc isolation session”) or its sensitivity (in a “Δd′ isolation session”) at each stimulus location.

We isolated behavioral changes in 48 sessions: 12 sessions of criterion change and 12 sessions of sensitivity change performed by each of two monkeys (Figure 2C-F). Three other sessions in which we failed to adequately isolate a behavioral change were excluded. Behavioral changes were spatially specific, as demonstrated by the counterphase change in behavior between the two stimulus locations (Figure S1A), and therefore not due to global changes such as arousal. Similar changes in hit rate were obtained with sensitivity changes and criterion changes (Figure 2D). Behavioral control was prioritized at the stimulus location contralateral to the electrode array at the ipsilateral location (STAR Methods). Among the 48 sessions with satisfactory isolation at the contralateral location, 33 sessions also achieved isolation at the ipsilateral location (Figure S1B).

Neurons were recorded from lateral prefrontal cortex and tracked across days

In the right hemisphere of each monkey, we implanted a pair of 6×8 Utah microelectrode arrays anterior to the arcuate sulcus, either above or below the principal sulcus. The arrays overlapped with Walker’s areas 8A, 45, and 46 (Walker, 1940), and according to the map by Petrides and Pandya (1999), the areas 8Ad, 8Av, 9/46v, 45B, and 45A (Figure S2). We refer to these areas as lateral prefrontal cortex (LPFC).

We recorded from neuronal units during the 48 behavioral isolations described above. In each daily session, two Gabor stimuli were placed in opposite hemifields, and their positions and orientations were varied across days. On a typical day, we recorded from 94 units (11 fully-isolated single units and 83 partially-isolated units or multiunit clusters).

Because it is highly likely that the Utah arrays recorded from the same neurons across days (Dickey et al., 2009), we implemented the classification algorithm by Fraser and Schwartz (2012) to determine whether units in separate sessions represent the same neurons (STAR Methods). The classifier was calibrated to produce similar error rates for two types of errors: a decoy error in which different neurons were misclassified as the same neuron, and a drop error in which the same neuron was misclassified as two different neurons. The chosen classifier had a median decoy error rate of 0.0125 and drop error rate of 0.0121(Figure S3A-B). Sixty-two percent of units were recorded in more than one session, and the same unit could be recorded in sessions more than 30 days apart (Figure S3C-D). Among 4,843 units encountered, 1,088 were classified as unique.

Spatial selectivity was indexed using a memory-guided saccade task

Neurons in LPFC typically have extensive receptive fields that overlap with both visual hemifields (Funahashi et al., 1990). To study neuronal activity related to spatial attention, we measured the degree to which each neuron differentiated the two stimulus locations. At the start of each day, the animal performed a memory-guided saccade task. In this task, a target appeared for 400 ms in either the left or right hemifield, at the centers of the two Gabors subsequently displayed in the attention task. After a delay of 750 to 1000 ms, the fixation point disappeared, and the animal saccaded to the remembered target location for a reward.

We computed a spatial selectivity index (SSI) for each neuron based on its activity after the target onset (SSI_visual), during the delay period (SSI_delay), before the saccade (SSI_presac), and after the saccade (SSI_delay; Figures 3A-B). The SSI was equal to the area under the curve of a receiver operating characteristic analysis that classified the contralateral and ipsilateral responses during a given trial epoch. An SSI > 0.5 indicates stronger activity associated with the contralateral target or saccade than the corresponding ipsilateral event.

Figure 3. A memory-guided saccade task was used to index spatially selective.

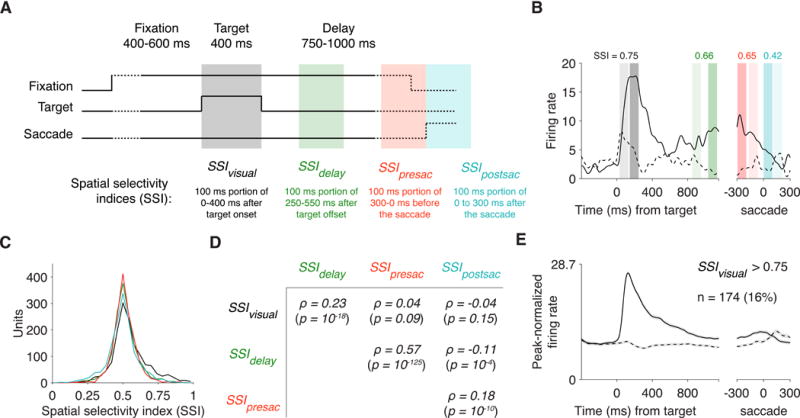
(A) After acquiring fixation, a target (0.4° white square) appeared for 400 ms in either the left or right hemifield. After a delay of 750-1000 ms, the fixation point disappeared to cue animal to saccade to the remembered location of the target. A spatial selectivity index (SSI) was computed for each neuron during each of four task periods. The 100 ms time window with the maximal firing rate was selected separately for events in the contralateral and ipsilateral hemifield. Contralateral and ipsilateral firing rates were then compared using a receiver operating characteristic (ROC) analysis, and the resulting area under the ROC curve was the SSI. SSI > 0.5 indicates stronger activity at the contralateral location. Shaded regions indicate the range of time windows that can be selected for computing SSI. (B) The peri-event time histogram (PETH) of an example unit was computed by convolving spikes with a Gaussian with σ = 25 ms. Solid lines correspond to trials with a contralateral target and saccade. Shaded bars indicate the time windows used to compute the SSI during each period. Darker shading corresponds to contralateral events and lighter to ipsilateral events. The example was selected by picking the unit that had the lowest SSI_visual among those with SSI_visual > 0.75. (C) Distributions of SSI were centered close to 0.5, but SSI_visual was skewed more towards 1 than other SSIs. N = 1,088. (D) Partial correlations between each pair of SSI’s. No reliable correlation was detected between SSI_visual and either SSI_presac or SSI_postsac. N = 1,088. (E) Contra-selective visual units with SSI_visual > 0.75. To compute the population-averaged PETH, each unit was normalized by the maximal value in its PETH. The maximum of the y-axis is 0.75 times the average peak firing rate across the population. Shading indicates mean ± SEM.

The distribution of SSI_visual was modestly skewed toward 1 (median = 0.526; p = 10⁻³⁷; Figure 3C), indicating that more neurons in LPFC prefer contralateral stimuli than ipsilateral stimuli, as observed previously (Funahashi et al., 1990; Lennert and Martinez-Trujillo, 2011). The distributions were also greater than 0.5, though very modestly, for SSI_delay (median = 0.505, p = 10⁻⁵) and SSI_presac (median = 0.504, p = 10⁻⁴). SSI_visual was larger than all other SSI (maximum p = 10⁻¹⁰ across pairwise comparisons; firing rates were distribution-matched using bin sizes of 1 Hz). These results indicate that neurons in LPFC show stronger contralateral preference in their visual responses than in their delay-related or saccade-related responses.

No reliable partial correlation was observed between SSI_visual and either SSI_presac or SSI_postsac (Figure 3D). A previous study reported overlap between visual receptive fields and presaccadic movement fields in LPFC (Bullock et al., 2017), which predicts a correlation between visual and presaccadic selectivity. Similarly, when we examined the correlation between SSI_visual and SSI_presac without controlling for selectivity in the delay period, we found a significant though modest correlation (ρ = 0.22, p = 10⁻¹⁵). Therefore, in our dataset, the correlation between visual selectivity and presaccadic selectivity was largely due to correlations between visual and delay-related selectivity and between delay-related and presaccadic selectivity.

For subsequent analyses, we use as an example the subset of units with reliable contralateral preference in their visual responses, with SSI_visual > 0.75 (Figure 3E), but we also show that results generalize for a broad range of SSI_visual thresholds for contralateral neurons. We focus on contralateral-preferring visual neurons because they outnumber ipsilateral-preferring cells and also because only 33/48 sessions had achieved behavioral isolation at ipsilateral location (Figure S1B). No difference in SSI was observed between neurons recorded during sessions isolating Δc and sessions isolating Δd′ (Wilcoxon rank-sum test: maximum across different types of SSI was p = 0.39).

Firing rates were modulated when the subject changed either its criterion or its sensitivity

Figure 4A shows peri-event time histograms (PETH) of visual, contra-selective neurons (SSI_visual > 0.75) aligned to three trial events: sample onset, test onset, and saccade. These neurons robustly increased their responses to the sample stimulus when the animal either lowered its criterion or elevated its sensitivity. To quantify the modulations in firing rates, we computed an index based on spike counts 80-480 ms after the onset of the sample (STAR Methods). The sample period was the most informative for assessing attention-related modulations because no behavioral decision or eye movement had yet occurred during this period. The modulation index associated with Δc, MI_Δc, was defined such that MI_Δc > 0 indicated a stronger response when the animal responded more frequently to the contralateral location. The modulation index associated with Δd′, MI_Δd′, was defined such that MI_Δd′ > 0 indicated a stronger response when the animal was more accurate in discriminating between orientation changes and matches at the contralateral position.

Figure 4. Visual responses increased when the subject either lowered its criterion or increased its sensitivity.

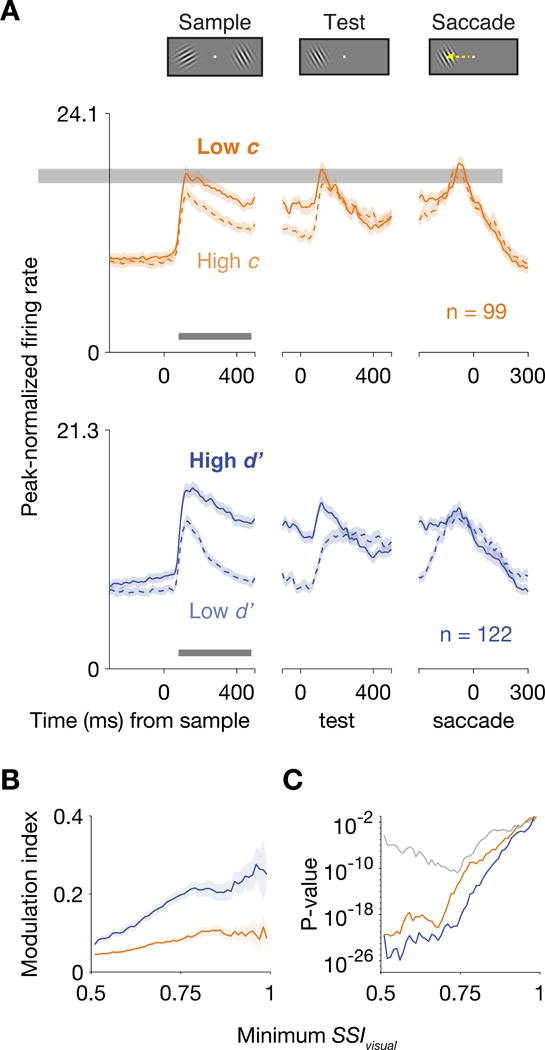
(A) PETH of units with SSI_visual > 0.75 during the attention task. Orange lines represent units recorded during Δc isolations, and blue lines represent units from Δd′ isolations. Spikes were convolved with a Gaussian with σ = 8 ms. The maxima of the y-axes are 0.75 times the average peak firing rate across the population. Shading indicates mean ± SEM. The bar near the x-axis indicates the sample period (80-480 ms after sample onset). Either lowering c or elevating d′ increased the firing rates of visual neurons throughout the sample period and into the test period. (B) Modulation index (MI) of firing rates during the period 80-480 ms after sample onset as function of the minimum SSI_visual of the units included for analysis. A Δc-related modulation index > 0 indicates stronger firing rates when the animal responded more frequently to the contralateral location. A Δd′-related MI > 0 indicates stronger firing rates when the animal was more accurate in discriminating between an orientation change and a match at the contralateral position. Shading indicates mean ± SEM across units. Modulation indices related to either Δc or Δd′ are greater than 0 regardless of the SSI_visual threshold. The sample sizes for minimum SSI_visual = 0.51 were 492 units from Δc isolations and 567 units from Δd′ isolations. (C) P-values were computed using the Wilcoxon signed-rank test for a zero median in the distribution of Δc-related modulation indices (orange) or Δd′-related indices (blue) and from the Wilcoxon rank-sum test of Δc- and Δd′-related indices having the same median (gray). See also Figure S4.

We found the modulation indices related to either Δc or Δd′ were substantially and reliably greater than zero (Figure 4B-C). The reliability of these effects held for a broad range of SSI_visual thresholds. Modulations related to Δd′ were stronger than modulations related to Δc, but the two types of modulations were qualitatively similar, indicating that previously documented modulations in LPFC could reflect either behavioral change. These results indicate that visual neurons in LPFC encode robust signals related to behavioral changes in either criterion or sensitivity.

We next examined how attention-related modulations depend on other spatial selectivity indices. The trial-averaged firing rates of all units during the attention task were computed in non-overlapping 200 ms bins. For each bin, we computed the partial correlation between the firing rate MI and each of Δ, while controlling for the other three SSIs (Figure 5). As expected from the previous analysis, there was reliable partial correlation between SSI_visual and either Δc- or Δd′-related MI during the sample period. This correlation became negative during the test period and after the saccade, indicating that attention-related modulations can reverse sign after the animal completed a decision. Spatial selectivity during the delay (SSI_delay) correlated modestly with the attention-related modulations during the test period. Also, presaccadic spatial selectivity (SSI_presac) correlated with attention-related modulation in the sample period. These findings indicate that attention-related modulations depend on spatial selectivity measured in multiple different periods of the memory-guided saccade task, though the dependency appears to be strongest for the period after target presentation (SSI_visual).

Figure 5. Firing rate modulations were correlated with spatial selectivity measured from multiple periods of the memory-guided saccade task.

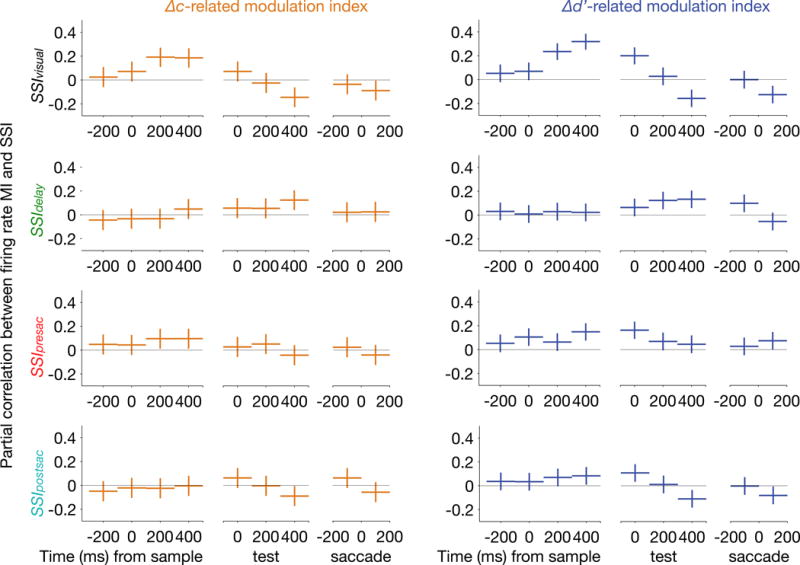
Partial correlation between firing rate MI and each SSI (among SSI_visual, SSI_delay, SSI_presac, and SSI_postsac) while controlling for the other three SSI. The left column of panels (orange) corresponds to Δc-related modulations and the right column (blue) to Δd′-related modulations. Only the 33/48 sessions in which behavior was isolated at both the ipsilateral and contralateral locations were included for this analysis. N = 559 units from Δc isolations and 667 units from Δd′ isolations. Vertical bars indicate 95% confidence interval. See also Table S1.

Lastly, we measured the extent to which firing rate modulations during the sample period (80-480 ms after sample onset) can be explained using the SSIs. We fitted linear models to Δc-related and Δd′-related firing rates modulations during the sample period and selected the best model for each type of modulation according to the Bayesian Information Criterion (Table S1). The proportion of variance explained by the optimal model was ~18% for Δd′-related modulations and ~13% for Δc-related modulations. The optimal models had a small intercept term (MI_Δc = 0.14, p = 10⁻⁴, MI_Δd′ = 0.01, p = 10⁻²¹, t-test), indicating that neurons in LPFC show lateralized Δc-related and Δd′-related modulation even if they display no spatial selectivity that could be detected in a memory-guided saccade task. We confirmed this to be the case by selecting neurons with SSI_visual, SSI_delay, SSI_presac, and SSI_postsac all within the interval of [0.4, 0.6] and subsampling this population until the population average for each of all four SSIs was within [0.49, 0.51]. This non-selective population indeed showed small but significant modulation (mean MI_Δc = 0.016, p = 0.05; mean MI_Δd′ = 0.019, p = 0.008; Wilcoxon signed-rank test).

Pairwise correlation and Fano factor were also modulated in association with either behavioral change

In addition to changes in firing rates, other attention-related neuronal modulations in visual cortex were found to be associated with behavioral changes in only sensitivity, but not criterion (Luo and Maunsell, 2015). These include reductions in spike count correlation between pairs of simultaneously recorded neurons (pairwise correlation) and across-trial variability in a neuron’s firing rate (indexed as Fano factor). Pairwise correlation in prefrontal cortex has been used to decode the animal’s trial-by-trial attentional state (Tremblay et al., 2015) and spatial working memory (Leavitt et al., 2017), but an attention-related reduction in correlation has not yet been reported in prefrontal cortex. Attention-related reductions in Fano factor were not observed in prefrontal cortex despite robust attention-related increases in firing rate, but these investigations focused on the frontal eye fields and not LPFC (Chang et al., 2012; Purcell et al., 2012).

Here we found that either lowering criterion or elevating sensitivity was associated with a reduction in both pairwise correlation and Fano factor among contra-selective visual neurons during the sample period (Figure 6). The information in the neural population for discriminating between the two orientations, measured as linear Fisher information (Kanitscheider et al., 2015), increased modestly in association with either a decrease in criterion or an increase in sensitivity, though these changes in population coding did not depend on changes in pairwise correlation (Figure S5). The changes in pairwise correlation and Fano factor further support the idea that robust neuronal signals associated with either component of visuospatial attention are present in LPFC.

Figure 6. Pairwise correlation and Fano factor decreased when the animal either lowered its criterion or elevated its sensitivity.

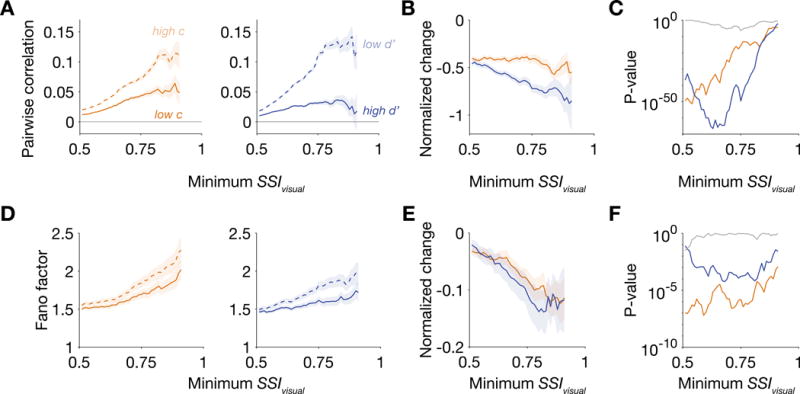
(A) Pairwise correlations between contra-selective visual units decreased when the animal performed with a lower criterion or a higher sensitivity at the contralateral hemifield. Correlations were computed using firing rates during the sample period (80-480 ms after sample onset). The sample sizes for minimum SSI_visual = 0.51 and 0.75 were 25273 and 988 pairs from Δc isolations and 26635 and 974 pairs from Δd′ isolations. (B) Changes in pairwise correlation were normalized by the population-averaged correlation in either high c contra condition (for Δc isolations) or the low d′ contra condition (for Δd′ isolations). (C) P-values were computed using the Wilcoxon signed-rank test for a zero median in the distribution of normalized changes related to either Δc (orange) or Δd′ (blue) and using the Wilcoxon rank-sum test of Δc- and Δd′-related correlation changes having the same median (gray). (D) Fano factor of contra-selective visual neurons also decreased when the animal performed with either a lower criterion or higher sensitivity. Fano factor was computed using spike counts during the sample period. The sample sizes for SSI_visual = 0.51 and 0.75 were 492 and 99 units from Δc isolations and 567 and 122 units from Δd′ isolations. (E) Normalized change in Fano factor. (F) P-values for normalized changes in Fano factor. See also Figure S5.

Reliable Δc-related modulations were observed in the population activity in LPFC but not in area V4

In a previous experiment (Luo and Maunsell, 2015), neuronal responses were recorded from area V4 in visual cortex while behavioral changes in either criterion or sensitivity were isolated using the same task as used here. We therefore directly compared the modulations in the activity of visual neurons between the two areas (Figure 7A). Both areas showed robust Δd′-related modulations in firing rates, pairwise correlation, and Fano factor. However, whereas LPFC had reliable Δc-related modulations, the Δc-related modulations in V4 in firing rate and Fano factor were weak. Moreover, the Δc-related modulations in pairwise correlation in V4 were opposite in sign to usual attention-related changes in correlation (Cohen and Maunsell, 2009; Mitchell et al., 2009).

Figure 7. Neuronal modulations related to Δc were reliably observed in the population activity of LPFC but not of area V4.

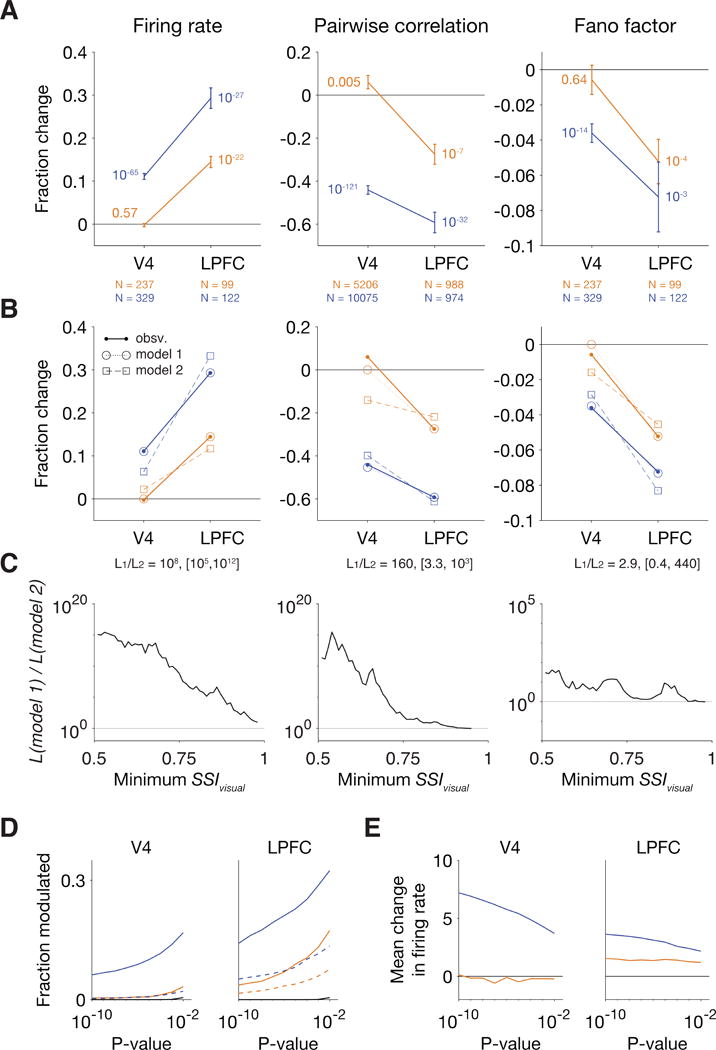
(A) Normalized change in firing rate, pairwise correlation, and Fano factor of neurons in LPFC and V4 with SSI_visual > 0.75. Error bars indicate mean ± SEM. P-values were computed using a Wilcoxon signed-rank test. (B) Maximum likelihood fits from model 1 (circles and dotted line) and from model 2 (squares and dashed lines). Model 1 assumes zero Δc-related modulations in V4, and model 2 assumes a multiplicative relationship between the modulations in V4 and LPFC. Each model has three parameters. The likelihood ratio and its bootstrapped 95% confidence intervals are indicated at the bottom of the panel. (C) The likelihood ratio of model 1 to model 2 across thresholds of SSI_visual. The likelihood ratio was greater than one (favoring model 1) for all thresholds of SSI_visual for all three measures. For firing rate and pairwise correlation, the bootstrapped 95% confidence interval (shading) of the likelihood ratio was greater than one for a broad range of SSI_visual. (D) The fraction of neurons whose firing rates were significantly modulated in association with either Δc (orange lines) or Δd′ (blue lines) plotted against the threshold for statistical significance. Solid lines indicate the fraction with significantly increased firing rates, and dashed lines indicate the fraction with a significant decrease. Black lines indicate the discovery rate at chance (p-value divided by two). (E) The mean firing rate change across all neurons with an individually significant increase or decrease in their firing rates.

It appears that neuronal responses in V4 are associated with only one component of visuospatial attention, while LPFC is associated with both. But it might instead be that Δc-related modulations were detectable in LPFC only because attentional modulations are generally stronger there, continuing the increase of attentional modulation with the level of visual cortical hierarchy (Maunsell and Cook, 2002). To evaluate these two possibilities, we fitted two models to the Δc- and Δd′-related modulations in the two brain areas (STAR Methods). In model 1, the mean of Δc-related changes across neurons in V4 was set to zero, while the population-means of Δd′-related modulations in V4 and of Δc- and Δd′-related modulations in LPFC were free to vary. In model 2, two parameters were assigned to the population-means of Δc- and Δd′-related modulations, and a third parameter determined the multiplicative relationship between the population-averaged modulations in V4 and LPFC. The two models were fitted using maximum likelihood estimation. Because the two models had the same number of parameters, they were compared using their maximized likelihoods (Figure 7B-C). Across a broad range of SSI_visual thresholds, the likelihood of model 1 was significantly higher than that of model 2 for firing rate and pairwise correlation. For Fano factor, the likelihood of model 1 was also larger, but it was significantly larger within only a limited range of SSI_visual thresholds, perhaps due to the typically smaller effect sizes of Fano factor modulations. This analysis indicates that the difference in attention-related changes between V4 and LPFC is not merely a stronger modulation in the latter, but that LPFC provides signals associated with a component of attention that were absent in population-averaged activity in V4.

However, individual neurons in V4 were modulated in association with Δc. A greater than expected fraction of V4 neurons significantly changed their firing rates in association with changes in behavioral criterion (6.5% of units at the p = 0.01 threshold), even though firing rates across these neurons averaged to near zero (Figure 7D-E). Therefore, when a subject changes its criterion, while firing rate changes are not detected in the population-averaged activity in V4, a small fraction of individual neurons significantly changed their firing rates.

Modulations related to criterion and sensitivity changes were correlated across LPFC neurons

Firing rate modulations related to either Δc or Δd′ were often observed for units recorded from the same electrodes (Figure S6), raising the question of the extent to which Δc- and Δd′-related modulations are correlated across LPFC neurons. A correlation would indicate that Δc- and Δd′-related modulations are combined within LPFC or in a common input, while a lack of correlation indicates that LPFC neurons receive independent Δc- and Δd′-related inputs. While we did not isolate Δc and Δd′ on the same day, we can measure the correlation across units that were recorded in multiple sessions and identified by the tracking algorithm to be putatively the same neuron.

Figure 8A plots the MIs of each putative unit with a SSI_visual > 0.75 from each pair of Δc-isolation and Δd′-isolation sessions in which that unit was recorded. Putative units showed a strong correlation between the two modulations, with the Δd′-related MI averaging about 1.7 times the Δc-related MI. The correlation suggests that Δc- and Δd′-related signals are at least partially combined within LPFC or have partially overlapping inputs.

Figure 8. Firing rate modulations related to Δc and Δd′ were correlated across neurons in LPFC.

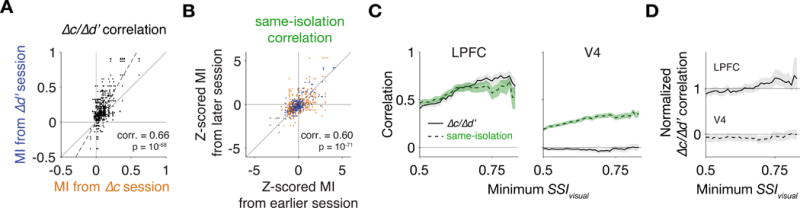
(A) Firing rate modulation indices (MI) from each pair of Δc-isolation session and Δd′-isolation session from each unit that was recorded in both sessions. Each marker indicates one pair of MI (576 pairs from 47 units that had a SSI_visual > 0.75). Both MIs of each pair belonged to the same unit. The slope of the regressed line (dashed, no intercept) was 1.72. (B) MIs from each pair of sessions with the same isolation from each unit that was recorded in both sessions. To combine MI pairs from Δc sessions (orange) and from Δd′ sessions (blue), MIs of each isolation type were z-scored (710 pairs from 79 units that had a SSI_visual > 0.75). (C) Correlations between Δc/Δd′ MI pairs and between same-isolation MI pairs. Correlations were calculated after distribution-matching the number of intervening sessions between each pair (Figure S7A-B). Shading indicates 95% confidence interval. (D) Normalized Δc/Δd′ correlations were computed by dividing Δc/Δd′ correlations by same-isolation correlations, and 95% confidence intervals were computed using a bootstrap procedure. Normalized correlations in LPFC were statistically indistinguishable from 1 and reliably different from normalized correlations in V4, which were indistinguishable from 0. See also Figure S7.

The measured correlation between Δc- and Δd′- related MIs should be considered a lower-bound, owing to noise arising from finite trial counts, error in tracking units across days, and uncontrolled behavioral difference between sessions. To assess how much these factors reduce the measured correlation, we sought to normalize the Δc/Δd′ correlation by the same-isolation correlation, i.e., the correlation between MIs related to the same behavioral change, which we assume to approximate the maximum correlation that can be extracted given the various measurement errors (STAR Methods).

Figure 8B plots the MIs from each pair of sessions with the same behavioral isolation for each putative unit with a SSI_visual > 0.75 that was recorded during both of those sessions. The correlation between same-isolation pairs was similar to that measured for Δc/Δd′ pairs, suggesting that the correlation in Figure 8A is about as strong as can be expected given the various sources of measurement error. Across a broad range of minimum SSI_visual, the Δc/Δd′ correlation was statistically indistinguishable from the same-isolation correlation (Figure 8C). Normalized by the same-isolation correlation, the Δc/Δd′ correlation was indistinguishable from one (Figure 8D). This result is consistent with LPFC neurons receiving a common input that combines Δc- and Δd′-related modulations or that separate Δc- and Δd′-related inputs are combined within LPFC.

In contrast to LPFC, the normalized Δc/Δd′ correlation within V4 pairs was indistinguishable from zero (slightly negative if a more liberal statistical criterion than p = 0.05 were used; Figure 8D). The normalized Δc/Δd′ correlations were reliably different between LPFC and V4 across thresholds of minimum SSI_visual. These findings support the idea that the attention-related modulations in LPFC and V4 are part of distinct mechanisms.

These results were verified by two additional analyses. First, because MI pairs sampled from different isolations were on average more separated in time than MI pairs sampled from the same isolation (Figure S7A), the correlations shown in Figure 8C-D were computed after matching the distributions of the number of intervening sessions between Δc/Δd′ pairs and same-isolation pairs (Figure S7B). The same analyses performed without distribution-matching showed qualitatively similar results (Figure S7C-D). A second analysis that computed correlations across units rather than pairs of MIs also showed a reliable difference in Δc/Δd′ correlations between LPFC and V4 (Figure S7E).

Discussion

A challenge in understanding visuospatial attention involves partitioning and organizing its related neuronal signals across the brain. Classical signal detection theory is useful for this purpose because it accurately describes performance in simple perceptual tasks using two orthogonal parameters (Green and Swets, 1966; Macmillan and Creelman, 2004). We hypothesized that the brain areas related with visuospatial attention can be distinguished according to whether the neuronal modulations therein correspond to behavioral changes in criterion, sensitivity, or both. This hypothesis was suggested by our previous result from visual cortex showing that attention-related signals in area V4 were associated with only changes in the subject’s sensitivity but not its criterion (Luo and Maunsell, 2015). This previous result suggests that other brain areas besides V4 underlie changes in the subject’s criterion. However, it was unclear what kind of neuronal signals are related to attention-related criterion changes.

We found that the responses of visual neurons in LPFC were robustly modulated in association with changes in the subject’s criterion. Criterion-related modulations were qualitatively similar to sensitivity-related modulations, and the two modulations were correlated on a cell-by-cell basis. These results are qualitatively different from previous results in area V4, therefore indicating that attention-related modulations in different brain areas can be meaningfully distinguished according to whether they correspond to behavioral changes in the subject’s sensitivity, criterion, or both. This scheme provides a step forward from treating neuronal changes related to attention as a monolithic signal, as has been often done in neurophysiological studies of visuospatial attention.

Is criterion change a component of visuospatial attention?

Changes in an observer’s criterion are consistent with an aspect shared by many definitions of attention: the “selection” of a stimulus to be perceived in greater detail, held in working memory, or acted on (Carrasco, 2011; Desimone and Duncan, 1995; Knudsen, 2007). This aspect of attention is consistent with the way criterion changes are operationalized here: when a subject lowers its criterion at a location, the subject “selects” the stimulus to be a likely target for an oculomotor response.

Considering criterion changes to be a component of attention provides an approach for partitioning the neuronal signals across different areas. The distinction between bottom-up and top-down attention (Buschman and Miller, 2007) and between spatial and feature attention (Bichot et al., 2015) have been useful in differentiating the contributions of different brain areas. However, even within the domain of top-down spatial attention, a large number of brain areas have been implicated (Desimone and Duncan, 1995). The distinction between criterion and sensitivity allows these areas to be functionally differentiated rather than viewed as homogeneous.

There is also a practical advantage in treating criterion change as a component of attention: many of the tasks that documented the neuronal signals related to visuospatial attention were designed such that the subject could have changed its criterion to improve its performance (Luo and Maunsell, 2015; Sridharan et al., 2017). To exclude behavioral criterion as a component of attention implies excluding or raising serious doubts regarding many studies included in the neurophysiological literature of attention. The potential contribution of changes in criterion or other decisional processes to the effects of attention is pervasive. The behavioral improvements in human observers performing the Posner cuing paradigm could depend entirely on decisional changes (Eckstein et al., 2002). The attention-related effects in not only detection tasks but also discrimination tasks could depend entirely on changes in criterion (Sridharan et al., 2017). Many current definitions of attention in the neurophysiological literature include (but do not necessarily emphasize) the decisional and oculomotor processes on which behavioral criterion likely depend (Desimone and Duncan, 1995; Knudsen, 2007; Krauzlis et al., 2014; Moore and Zirnsak, 2017).

Attention-related neuronal changes in prefrontal cortex

We found that firing rate modulations related to the two behavioral changes were highly correlated on a cell-by-cell basis. This finding suggests that Δc- and Δd′-related modulations arrive in a common signal in LPFC. However, it is also possible that Δc- and Δd′-related signals have separate origins, and that a mechanism within LPFC restricts the extent to which individual cells are modulated by either signal. Specifically, the variability in the size of attention-related modulations of firing rates across neurons in visual cortex are well explained by the strength of response normalization (Boynton, 2009; Lee and Maunsell, 2009; Ni and Maunsell, 2012; Reynolds and Heeger, 2009). The correlation in Δc- and Δd′-related modulations across neurons in LPFC might arise in part because both modulations depend on normalization mechanisms within LPFC.

This finding further raises the question of the extent to which the modulations in LPFC make up a generic attentional signal that does not distinguish between whether the animal has lowered its criterion, increased its sensitivity, or done both. A prominent view is that the firing rates of visual neurons in sensorimotor areas of the brain, such as the LPFC, frontal eye fields, and lateral intraparietal cortex, represents a generic “priority” or “salience” signal that can be used either guide a saccade or to allocate attention (Thompson and Bichot, 2005; Bisley and Goldberg, 2010). Our results indicate that the modulations in LPFC can be interpreted as a generic signal of this sort, and that sensitivity changes might be more closely coupled with such a signal than are criterion changes and are therefore associated with stronger modulations. However, further studies could reveal distinctions that make the notion of any generic signal untenable.

We observed reductions in the Fano factor and pairwise correlation of visual neurons when the animal changed either its criterion or its sensitivity. These two changes in spiking variability have been consistently observed in visual cortex when attention was manipulated (Cohen and Maunsell, 2009; Mitchell et al., 2007, 2009; Luo and Maunsell, 2015). In the FEF, attention-related Fano factor changes were not observed despite robust increases in firing rates (Chang et al., 2012; Purcell et al., 2012). While it is conceivable that the absence of Fano factor changes indicates different mechanisms underlying attentional changes in FEF and LPFC, reductions in Fano factor have small effect sizes. Even in visual cortex, changes in Fano factor may go undetected when increases in firing rate are readily apparent (McAdams and Maunsell, 1999). Attention-related decreases in pairwise correlation have not been reported in previous attention studies that performed multi-electrode recording in LPFC (e.g. Kadohisa et al., 2013; Tremblay et al., 2015). The association between criterion changes with changes in pairwise correlation is interesting because changes in pairwise correlation have been postulated as a mechanism for enhancing the animal’s perceptual sensitivity (Cohen and Maunsell, 2009; Mitchell et al., 2009). Our finding indicates that changes in pairwise correlation can occur even when there is no change in the animal’s perceptual sensitivity. A recent study indicates that attention-related changes in pairwise correlation in visual cortex can arise from response normalization mechanisms (Verhoef and Maunsell, 2017). Both changes in firing rate and in pairwise correlation related to behavioral changes in both criterion and sensitivity could depend to some extent on normalization mechanisms.

Brain structures associated with attentional changes in criterion and sensitivity

We found that the attention-related modulations in LPFC are associated with changes in both the subject’s criterion and its sensitivity, whereas such modulations in area V4 of visual cortex are associated only with sensitivity changes. Two recent studies examined whether the superior colliculus (SC) contributes to attention through changes in criterion or sensitivity (Sridharan et al., 2017; Lovejoy and Krauzlis, 2017). Both studies applied a multidimensional extension to classical signal detection theory. While the definitions of criterion are not identical across these studies (and our study), they represent likely overlapping neural processes. Together these two studies indicate that SC contributes to attention through changes in both criterion and sensitivity, but with criterion being the dominant contribution.

Sridharan et al., 2017 analyzed four previous studies in which the SC was perturbed, through either microstimulation or pharmacological inactivation, while subjects performed tasks that required spatial attention (Cavanaugh and Wurtz, 2004; Lovejoy and Krauzlis, 2009; Muller et al., 2004; Zénon and Krauzlis, 2012). For all the studies, the changes in behavioral performance resulting from collicular perturbation could be explained by a change in criterion without a change in sensitivity. Furthermore, for two studies in which models were directly fitted to the data, criterion changes alone (Zénon and Krauzlis, 2012) and a combination of changes in criterion and sensitivity (Lovejoy and Krauzlis, 2009) best accounted for the data. The analyses in Sridharan et al., 2017 therefore suggest that the predominant contribution of SC to spatial attention involves changing the subject’s criterion across different visual locations.

Lovejoy and Krauzlis (2017) trained monkeys to discriminate the direction of a moving stimulus that could appear at a random one of four locations (uncued condition) or appear at a cued location (cued condition). The effect of attention on performance was defined as the increase in d′ between the uncued and the cued conditions. When SC was pharmacologically inactivated, the cue-induced increase in d′ could not be detected in the affected region of visual space, indicating that SC is necessary for attention-related enhancement in behavioral sensitivity. During inactivation, the subject’s criterion was also affected by the inactivation such that subjects were less inclined to saccade to the affected region.

Given that both LPFC and SC are associated with both criterion changes and sensitivity changes, it is possible that no brain structure is entirely associated with only criterion changes. Some structures, such as V4 and LPFC, may be more strongly modulated in association with sensitivity changes than criterion changes, while others, possibly SC, are more closely linked to criterion changes. If this were the case, when animals are trained to change either only their criterion or only their sensitivity, overlapping groups of brain structures should be modulated, but to different extents.

Conclusion

Distinguishing and organizing the widespread attention-related signals in the brain is necessary for a deeper understanding of visuospatial attention. Our results indicate that neuronal changes in different brain areas related to attention can be partitioned using the indices of criterion and sensitivity from signal detection theory. Future work capitalizing on the distinction between criterion and sensitivity will likely provide insights into the mechanisms of visuospatial attention.

STAR Methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Thomas Zhihao Luo (thomas.zhihao.luo@gmail.com).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Animal use procedures were approved by The University of Chicago Institutional Care and Use Committee (IACUC) and carried out in accordance with National Institute of Health standards. Two male, eight-year-old, 9-11 kg rhesus macaques (Macaca mulatta) were used in the study. Access to water was scheduled to training or recording sessions that occurred 1-3 hours per day. Eye movements were tracked using a video system (EyeLink 1000, 500 Hz). Before training, each animal was implanted with a head post, and after training was completed, each animal was implanted with a pair of 6×8 Utah microelectrode arrays (Blackrock Microsystems) in lateral prefrontal cortex.

METHOD DETAILS

Criterion (c) and sensitivity (d′)

Criterion was indexed as criterion location (c) as described in (Macmillan and Creelman, 2004):

$$c=\frac{1}{2}[{\Phi }^{-1}(\mathit{hit}\mathit{rate})+{\Phi }^{-1}(\mathit{false}\mathit{alarm}\mathit{rate})]$$

Φ⁻¹ is the inverse normal cumulative distribution function. When c = 0, the subject shows no bias towards reporting either targets or nontargets. In the signal detection model (Figure 1A), this is the value on the x-axis where the two normal distributions intersect. When c < 0, the subject exhibits a bias towards reporting targets, and when c > 0, a bias towards nontargets.

Sensitivity was indexed as d′,

$$d\prime ={\Phi }^{-1}(\mathit{hit}\mathit{rate})-{\Phi }^{-1}(\mathit{false}\mathit{alarm}\mathit{rate})$$

In the signal detection model, d′ is the difference between the means of the target and nontarget distributions divided by the root mean square of their standard deviations. Because we assume the standard deviation to be equal between the nontarget and target distributions and equal to 1, d′ is simply the horizontal offset between the means of two standard normal distributions. A larger d′ indicates better sensitivity. The index d′ characteristically ranges from zero to infinity, though a negative d′ value can result from sampling errors.

The results here generalize for other indices of criterion (also known as response bias) used in signal detection theory, such the likelihood ratio (β). The index criterion location (c) has the advantages that c is orthogonal to d′, well-defined for d′ = 0, and measured in the same unit as that of d′ (z-scores) to facilitate comparison (Macmillan and Creelman, 1990).

Attention task

Two rhesus monkeys (C and Y) performed a variant of the Posner attention task that controls the subject’s criterion and sensitivity (Figure 2A). These animals were different from those used in a similar study of V4 (Luo and Maunsell 2015). The subject began each trial by fixating for 400-600 ms within a 2°×2° square window on a video display (57 cm away, 100 Hz frame rate). Two sample stimuli (full contrast Gabors with σ = 1.5° and spatial frequency = 0.7 cycle/°) appeared for 400 ms. Gabors were in opposite hemifields, diametrically opposed across the fixation point, and each 11° from the fixation point. Positions varie d from 30° above, 30° below, or directly on the horizontal meridian. After a delay of 150-250 ms, a single test stimulus appeared at a randomly chosen one of the two stimulus locations for 400 ms. The test was equally likely to be the same as the sample that appeared at the same location or different in orientation. If the test differed from the sample, the monkey had to saccade to it within 150-500 ms to receive a juice reward. If the test were the same as the sample, the monkey had to wait to saccade to a second test stimulus that appeared at the same location. The second test always differed from the sample, and it was used to ensure that the monkey was engaged during correct rejection trials. The monkey rarely failed to respond to the second test (<1%), and trials with such failures were excluded from analyses.

The size of the orientation change was same for all trials in each session and ranged from 45° to 90° across sessions. The sample and the test stimuli in each session could take on only two orientations. The orientation assigned to each sample was randomized on each trial so that the samples had to be inspected to achieve good performance. Stimulus orientation was independent between the two locations.

Each trial was categorized as a hit (H), miss (M), false alarm (FA), or correct rejection (CR) based on animal’s response to the first test. A target trial was a H if the monkey responded to the changed test and an M otherwise. A nontarget trial was a FA if the monkey incorrectly responded to the unchanged first test, and it was a CR if the monkey waited to respond to the changed second test. A hit rate (H/[H + M]) and a false alarm rate (FA/[FA + CR]) were computed for each stimulus location and for each attention condition. Trials with a break in fixation ended immediately and were excluded from analyses.

To control the subject’s criterion and sensitivity at each stimulus location, we titrated the reward given for a H and a CR separately at each location. The subject’s criterion was primarily influenced by the ratio of the reward for a H to the reward for a CR (“H:CR reward ratio”; Figure 2B-C). A larger H:CR reward ratio encouraged a lower criterion, while a lower ratio encouraged a higher criterion. Except for the low c condition, the ratio was typically < 1 because subjects preferred responding to the first test over waiting for the second test. The subject’s sensitivity at each location was primarily influenced by the average reward size (across H and CR) at that location. A larger average reward at a location resulted in a higher sensitivity at that location. Each day, reward contingencies were varied between two task conditions to isolate a behavioral change in either the subject’s criterion or its sensitivity.

The two task conditions of each session were alternated in blocks of 180 trials. In a Δc isolation session, the blocks in which the animal was performing with a lower (more negative) c at the stimulus location contralateral to the electrode array are referred to as the “low c contra” task condition, and the other blocks the “high c contra”. Similarly, in a Δd′ isolation session, blocks in which the subject was performing with a higher d′ at the contralateral location was referred to as the “high d′ contra” task condition, and the other blocks “low d′ contra” task condition. To encourage stable performance within each block, 50-100 priming trials at the beginning of each block cued the animal to the reward contingencies of that block. Priming trials probed the same stimulus condition 10-20 trials in a row rather than probing the two locations randomly. These trials were excluded from analysis.

After completing training, each monkey was implanted with a pair of 6×8 microelectrode arrays (Blackrock Microsystems) in its right cerebral hemisphere (Figure S2). Behavioral isolation in each recording session was considered satisfactory if the targeted behavioral change was at least four times the off-target behavioral change (median = 26:1). More priming trials were allocated toward stabilizing behavior at the contralateral location than at the ipsilateral location, and as a result, isolation was more consistent at the contralateral location. Behavioral isolation at the contralateral location was achieved in 48 sessions, and in 33 of those sessions, isolation was also considered satisfactory at the ipsilateral location (Figure S1D). Modulations of contra-selective visual neurons were similar between sessions in which the behavior for both stimuli were successfully controlled and sessions in which only the behavior at the contralateral stimulus was successfully controlled.

The 95% confidence intervals of c and d′ were computed through bootstrapping. In each of 10⁴ iterations, a random number of hits (H^rand) was drawn from a binomial distribution based on the observed number of H and M, and a random number of false alarms was similarly drawn.

$$H^{\mathit{rand}}~B\left(H+M,\frac{H}{H+M}\right)$$

$$F{A}^{\mathit{rand}}~B\left(FA+CR,\frac{FA}{FA+CR}\right)$$

A hit rate, computed by dividing H^rand by the sum of observed H and M, and false alarm rate, computed by dividing FA^rand by the sum of observed FA and CR, were used to compute a c and d′ for that iteration. The 2.5 and 97.5 percentile across iterations made up the confidence interval.

Memory-guided saccade task

Each recording session began with the animal performing a memory-guided saccade task. After fixating for 400-600 ms, a saccade target (0.4° white square) appeared for 400 ms in either the left or right hemifield at the center of the Gabors that were subsequently presented in the attention task. After a delay of 750-1000 ms, the fixation point disappeared to cue the animal to make a saccade to within 5° of the remembered location of the target. At least 20 correct trials were completed at each stimulus location in each session.

Tracking neurons across days

Electrophysiological signals were acquired at 200kHz. Spikes were sorted using the first and second principal components in OfflineSorter (Plexon). Fully isolated clusters were considered to be single units, but partially isolated units and small multiunit clusters were also sorted. All units were included in the tracking analysis regardless of isolation quality.

To track units across sessions, we used the algorithm by Fraser and Schwartz (2012) and the associated software package on MATLAB Central: “Tracking neurons over multiple days,” identification no. 30113. Four neurophysiological features—pairwise cross-correlograms, auto-correlogram, waveform shape, and mean firing rate—were used to compute similarity scores for each pair of units between two consecutive sessions. These neuronal metrics were computed using default parameters.

A linear correlation was computed between the average waveforms of the two units being evaluated. The maximum correlation across time shifts was Z-transformed and then taken as the similarity score. Auto-correlograms were computed from 0-100 ms in 5-ms bins, and the similarity score was the Z-transformed linear correlation between two units’ auto-correlogram. The similarity score for mean firing rate was the difference between the log of mean rates.

Cross-correlograms were computed from −500 to 500 ms in 100 ms bins. A cross-correlogram was calculated between each of the two units being evaluated and each of all other units present in both sessions. This results in one pair of cross-correlograms for each unit that was present in both sessions (besides the two units being evaluated). A linear correlation was computed between each pair of cross-correlogram and then Z-transformed. The mean z-score was the similarity score. Across the four neuronal metrics, the cross-correlogram provided the most useful information because many neurons were recorded simultaneously in each session, resulting in many cross-correlograms.

A classifier was trained to fit multivariate Gaussian densities to the four similarity scores using a partially supervised expectation-maximization procedure. The decision boundary of the classifier was titrated to achieve similar rates of decoy errors and drop errors (Figure S3A-B). A decoy error occurs when one neuron becomes undetectable and another appears, and they are classified as the same unit. A drop error occurs when the same neuron recorded across two consecutive sessions is misclassified as two different units. The decoy error rate was measured using pairs of units from separate microelectrodes, which were most likely different units because the spacing between electrodes was at least 400 μm. The decision boundary was set using the decoy error rate. The drop error was assessed by splitting each recording session into thirds and comparing the first and last thirds as though they were separate sessions. This was a lower bound estimate of the between-session drop error rate. Across a range of decoy error rate, we computed the corresponding drop error rate. Then, we selected the decoy error rate that was closest to the median drop error rate for the tracking procedure.

When multiple units were recorded from the same electrode, there might be multiple possible assignments of identity. When this occurred, an iterative procedure relabeled these units until the summed similarity scores converged to a maximum.

At least two sources of errors were not measured. First, a switch error occurs when the labels are switched between two units, but at least one unit is present on both days. For a switch error to occur, both a decoy error and a drop error would have to occur. Because decoy and drop error rates are close to 1%, the switch error rate is about two orders of magnitude lower than the other two error rates. The second unmeasured error arises when a neuron becomes undetectable for a session but reemerges later. Such a neuron would be given two labels. This error was not corrected because cross-correlograms, the most reliable metric of similarity, become less useful when there are few identical neurons between two sessions. In addition, tracking across non-consecutive sessions greatly increases the chance of decoy errors.

Spatial selectivity index (SSI)

Spatial selectivity indices (SSIs) were computed using correct trials in the memory-guided saccade task (at least 20 for each location in each session). SSI_visual was computed based on a neuron’s peak activity during visual target presentation. The 100 ms time window with the maximal firing rate was selected from among three hundred 100 ms windows ranging from [0, 100] ms to [300, 400] ms after the onset of the visual target. The time window of peak response was independently selected for contralateral target trials and ipsilateral target trials. The peak responses to the target at the two positions were compared using a receiver operating characteristic (ROC) analysis. The resulting area under the ROC curve was taken as the SSI.

Other SSIs were computed similarly but using different time windows. SSI_delay was computed based the peak firing rate in a 100 ms time window selected from [250, 350] ms to [550, 650] ms relative to target offset. SSI_presac was based on a window between [−300, −200] ms to [−100, 0] ms relative to saccade onset, which was defined as the time when the eyes left the fixation window. Finally, SSI_postsac was based on a window between [0, 100] ms to [200, 300] ms relative to saccade onset.

The SSI ranges from 0 to 1. SSI > 0.5 indicates a stronger response to the contralateral target or saccade than to the ipsilateral event and SSI < 0.5 indicates the reverse. The time window for indexing selectivity was varied for each neuron according to its peak response because neurons showed a range of visual and saccade-related latencies. This did not bias the SSI away from 0.5 because separate time windows were independently selected for contralateral and ipsilateral events. Varying the counting window for each neuron to select its maximal response has been used previously to characterize spatial selectivity of neuronal responses in prefrontal cortex (Bruce and Goldberg, 1985; Funahashi et al., 1991), though other studies used the same counting window for all neurons (Thompson et al., 2005; Gregoriou et al., 2012).

Modulation index (Ml) and peri-event time histogram (PETH)

A firing rate modulation index (MI) was computed for each neuron during the period 80-480 ms after the onset of the sample stimulus. The MI was computed using trial-averaged firing rates $(\overline{\mathit{FR}})$ from the pair of task conditions in each isolation session:

$$M{I}_{\mathit{\Delta }c}=\frac{\left({\overline{\mathit{FR}}}_{\mathit{low}c\mathit{contra}}-{\overline{\mathit{FR}}}_{\mathit{high}c\mathit{contra}}\right)}{\left({\overline{\mathit{FR}}}_{\mathit{low}c\mathit{contra}}+{\overline{\mathit{FR}}}_{\mathit{high}c\mathit{contra}}\right)}$$

$$M{I}_{\mathit{\Delta }d\prime }=\frac{\left({\overline{\mathit{FR}}}_{\mathit{high}d\prime \mathit{contra}}-{\overline{\mathit{FR}}}_{\mathit{low}d\prime \mathit{contra}}\right)}{\left({\overline{\mathit{FR}}}_{\mathit{high}d\prime \mathit{contra}}+{\overline{\mathit{FR}}}_{\mathit{low}d\prime \mathit{contra}}\right)}$$

MI_Δc > 0 indicates stronger firing rates when the animal responded more frequently to the contralateral location and less frequently to the ipsilateral location. MI_Δd′ > 0 indicates stronger firing rates when the animal was more accurate in discriminating between orientation changes and matches at the contralateral location and less accurate at the ipsilateral location. Modulation indices were computed separately for each of two orientations in each session and then averaged.

To compute the peri-event time histogram for each neuron, spikes were convolved with the trial-averaged histogram with a Gaussian kernel with σ = 8 ms. The PETH and modulation index for the sample period were computed using all complete trials (H, M, CR, FA). The PETH aligned to the test includes only trials in which the animal withheld from a response (CR and M), and the PETH aligned to the saccade included only trials in which the animal made a response (H and FA). PETHs and modulation indices were almost identical if only correct trials were used because they far outnumbered incorrect trials. We included error trials in neuronal measurements because our behavioral measurements required error trials. PETH for the test or saccade periods used trials in which the test or the saccade appeared in the neuron’s preferred stimulus location, as determined by its SSI_visual for the test period and SSI_presac for the saccade period.

In Figure 4, the MIs and PETHs of each unit that was recorded during multiple sessions were averaged across sessions of the same isolation.

Partial correlation between Ml and SSI

For the analyses in Figures 5 and Table S1, we included only neurons recorded from the 33/48 sessions in which we achieved behavioral isolation at both the ipsilateral and contralateral stimulus locations. For each unit that was recorded during multiple sessions, an SSI of each type (SSI_visual, SSI_delay, SSI_presac, or SSI_postsac) and a MI of each type (MI_Δc or MI_Δd′) was computed for that unit by averaging across sessions. The partial correlation coefficient between a MI and each SSI was computed by first fitting a linear model to explain the MI using the three SSIs being controlled and an intercept. A second model was fitted to explain the SSI that is being correlated using the SSIs being controlled and an intercept. The residuals from the two models were correlated to give the partial correlation.

The 95% confidence interval (CI) of each correlation coefficient was computed using the Fisher Z-transformation:

$$CI=[\mathit{tanh}(z-1.96\sigma ),\mathit{tanh}(z+1.96\sigma )]$$

$$z=0.5\mathit{log}\left(\frac{1+r}{1-r}\right)=\mathrm{\text{atanh}}(r)$$

$$\sigma =1/\sqrt{N-3}$$

where tanh is the hyperbolic tangent function, r is the correlation coefficient, N is the sample size, and atanh the inverse hyperbolic tangent function.

Pairwise correlation and Fano factor

Pairwise correlation was the linear correlation between the spike counts of pairs of simultaneously recorded neurons across trials. Fano factor was computed as each neuron’s spike count variance across trials divided by its spike count average across trials. Both pairwise correlation and Fano factor were based on spike counts during the period 80-480 ms after the onset of the sample stimulus during all complete trials (H, M, FA, and CR). Both were computed separately for each of the two sample orientations and then averaged. For each unit that was recorded during multiple sessions, Fano factor values were averaged across sessions of the same isolation. Similarly, for each pair of unit that was present in multiple sessions, correlation values were also averaged across sessions of the same isolation.

Because pairwise correlations can be negative, the standard modulation index was not used to index changes in correlations. Instead, differences in pairwise correlation between task conditions were normalized to the average correlation across pairs in either the high c contra condition (for pairs from Δc isolations) or the low d′ contra condition (for pairs from Δd′ isolations). Normalized differences were also computed for Fano factors, even though Fano factors are always positive, so that the size of Fano factor modulations can be compared to that of pairwise correlation modulations.

Comparison between LPFC and V4

In Figure 7, we compared the activity of contra-selective visual neurons in LPFC to the activity of V4 neurons that were recorded in the experiments described in Luo & Maunsell (2015). In the V4 dataset, the sample stimuli appeared for only 200 ms rather than 400 ms in the LPFC dataset and no memory-guided saccade task was performed. To facilitate comparison, firing rates of contra-selective visual neurons in LPFC were computed between 80 ms to 280 ms after sample onset. Moreover, we computed an approximate SSI_visual for each V4 unit. But because V4 neurons have entirely contralateral receptive fields, SSI_visual was approximated by performing a ROC analysis comparing firing rates to the sample stimulus (60 ms to 260 ms after sample onset) to the baseline response during the 200 ms before sample onset.

The attention-related change in firing rate or Fano factor of each neuron was normalized to the average across all neurons in that area in either the high c contra or low d′ contra task condition. Similarly, the change in the correlation of each neuronal pair was normalized to the average correlation across all pairs in that area in either the high c contra or low d′ contra task condition.

Two models were fitted to the normalized changes in firing rates in LPFC and V4 (Figure 7B-C). The distribution of normalized firing rate changes for each brain area and for each attention component was modeled as a normal distribution. In the first model, the means of Δd′-related changes in LPFC, Δc-related changes in LPFC, and Δd′-related changes in V4 were allowed to vary. However, the mean of Δc-related changes in V4 was constrained to be zero. The standard deviation (σ) of each distribution was constrained to be the sample standard deviation of each distribution. If σ were allowed to vary, the resulting log-likelihood ratios would be little changed and the fitted σ would be similar to the sample standard deviation.

$$\mathrm{\Delta }F{R^{\prime }}_{\mathrm{\Delta }d\prime ,\mathit{LPFC}}~\mathcal{N}({\beta }_1,{\sigma }_{\mathit{sample}})$$

$$\mathrm{\Delta }F{R^{\prime }}_{\mathrm{\Delta }c,\mathit{LPFC}}~\mathcal{N}({\beta }_2,{\sigma }_{\mathit{sample}})$$

$$\mathrm{\Delta }F{R^{\prime }}_{\mathrm{\Delta }d\prime ,V4}~\mathcal{N}({\beta }_3,{\sigma }_{\mathit{sample}})$$

$$\mathrm{\Delta }F{R^{\prime }}_{\mathrm{\Delta }c,V4}~\mathcal{N}(0,{\sigma }_{\mathit{sample}})$$

In the second model, the means of Δd′-related changes and Δc-related changes in LPFC are again allowed to vary. However, the means of changes in V4 are constrained to be related to the changes in LPFC by a multiplicative factor, which was allowed to vary.

$$\mathrm{\Delta }F{R^{\prime }}_{\mathrm{\Delta }d\prime ,\mathit{LPFC}}~\mathcal{N}({\beta }_1,{\sigma }_{\mathit{sample}})$$

$$\mathrm{\Delta }F{R^{\prime }}_{\mathrm{\Delta }c,\mathit{LPFC}}~\mathcal{N}({\beta }_2,{\sigma }_{\mathit{sample}})$$

$$\mathrm{\Delta }F{R^{\prime }}_{\mathrm{\Delta }d\prime ,V4}~\mathcal{N}({\beta }_3\ast {\beta }_1,{\sigma }_{\mathit{sample}})$$

$$\mathrm{\Delta }F{R^{\prime }}_{\mathrm{\Delta }c,V4}~\mathcal{N}({\beta }_3\ast {\beta }_2,{\sigma }_{\mathit{sample}})$$

Each model had three parameters, and they were fitted using maximum likelihood estimation and using the fminunc function in MATLAB. When fitting the models, because different numbers of neurons were recorded in different brain areas and in different types of behavioral isolation, we subsampled the neurons such that each combination of brain area and isolation type had the same number of neurons, which was the minimum across combinations. For example, for SSI_visual > 0.75, the minimum was 99 neurons recoded in LPFC during Δc isolations. Subsampling followed by model fitting were repeated for 10⁴ iterations, and we reported the median, 2.5 percentile, and 97.5 percentile of the bootstrapped distribution of likelihood ratios. These same analyses were performed for normalized changes in pairwise correlation and in Fano factor.

To determine whether individual units in V4 and LPFC were significantly modulated in correlation with either Δc or Δd′ (Figure 7D-E), we fitted a Poisson model to the neuron’s trial-by-trial spike count during the sample period. We did not simply perform a statistical test comparing the neuron’s firing rates across trials in the two different task conditions because many V4 units showed slow change in firing rates (either increase or decrease) over the course of a recording session. The probability of the number of spikes emitted by each neuron during the sample period in each trial was modeled as:

$$P(K)={\lambda }^K{e}^{-\lambda }/K!$$

$$\lambda ={\beta }_0+{\beta }_{1}t+{\beta }_2\theta +{\beta }_3\mathit{attention}$$

where K is the spike count, t is the trial number, θ is either a 0 or 1 indexing the orientation of the sample stimulus, and attention = 1 for either the low c contra condition or high d′ contra condition, and 0 otherwise. An additional restricted model was fitted to the trial-by-trial spike counts, with the constraint β₃ = 0. The restricted model and the unrestricted model were fitted using maximum likelihood estimation, and the two models were compared using a likelihood ratio test, thereby giving the p-value of a neuron being significantly modulated.

Correlation between Δc- and Δd′-related firing rate Ml

Firing rates modulation indices (MI) in Figure 8 were computed by counting spikes 80-280 ms after sample onset for units recorded in LPFC and 60-260 ms after sample onset for units in V4. For each unit that was recorded for multiple sessions, its MI from different sessions were paired. These pairs of MI were pooled across units and sorted according to whether a pair came from the same behavioral isolation (same-isolation MI pair) or different behavioral isolations (Δc/Δd′ MI pair).

Different number of sessions intervened between the earlier and later session of each MI pair (0-23 for LPFC; 0-43 for V4). On average, more sessions intervened between Δc/Δd′ MI pairs than between same-isolation MI pairs because the same behavioral isolation occurred at least five sessions in a row (Figure S7A-B). To control for this difference, we matched the distributions of intervening sessions between the two types of MI pairs. For each value of intervening session, the MI pairs of the type that had more pairs were subsampled to have the same number of pairs as the other type. Subsampled pairs across all values of intervening session were pooled to compute a correlation coefficient. Random subsampling was repeated 1000 times. The median correlation coefficient across the 1000 iterations and its associated confidence interval (computed using the Fisher Z-transform) were reported in Figure 8C.

The normalized Δc/Δd′ correlation was obtained by dividing the Δc/Δd′ correlation by the same-isolation correlation, and its 95% confidence interval was computed through bootstrapping. First, correlation coefficients (ρ) were Z-transformed:

$$z_{\mathit{\Delta }c/\mathit{\Delta }d\prime }=\mathrm{\text{atanh}}({\rho }_{\mathit{\Delta }c/\mathit{\Delta }d\prime })$$

$$z_{\mathit{same}-\mathit{iso}}=\mathrm{\text{atanh}}({\rho }_{\mathit{same}-\mathit{iso}})$$

Then, the standard error of the Z-transformed coefficient was computed as:

$$\sigma =1/\sqrt{N-3}$$

Because both types of MI pairs had the same sample size after distribution-matching, the two Z-transformed coefficients had the same standard error. Then, 10⁵ random samples were drawn from each of these normal distributions:

$$X_{c/\mathit{\Delta }d\prime }~N(z_{\mathit{\Delta }c/\mathit{\Delta }d\prime },\sigma )$$

$$X_{\mathit{same}-\mathit{iso}}~N(z_{\mathit{same}-\mathit{iso}},\sigma )$$

These random samples were transformed into correlation coefficients, and a ratio was taken between each pair of random samples:

$$r_{c/\mathit{\Delta }d\prime }~\tanh (X_{c/\mathit{\Delta }d\prime })$$

$$r_{\mathit{same}-\mathit{iso}}~\tanh (X_{\mathit{same}-\mathit{iso}})$$

$$R=\frac{r_{c/\mathit{\Delta }d\prime }}{r_{\mathit{same}-\mathit{iso}}}$$

The 2.5 and 97.5 percentiles of the resulting distribution of ratios was taken as the 95% confidence interval.

Linear Fisher information

In Figure S5, linear Fisher information was computed following the methods in Kantscheider et al. (2015). In each session, we computed the differences in the trial-averaged firing rates to the Gabor stimuli of two different orientations for all units with SSI_visual > 0.75.

$$d\mu \equiv \overline{\mathit{FR}}({\theta }^{+})-\overline{\mathit{FR}}({\theta }^{-})$$

dμ is a vector with a number of elements equal to the number of units with SSI_visual > 0.75 in that session. We further computed the inverse of the average of the covariance matrices for each orientation.

$$S^{-1}\equiv {\left(\frac{S^{+}+S^{-}}{2}\right)}^{-1}$$

Linear Fisher information was computed as

$$I=\frac{d{\mu }^T}{d\theta }{S}^{-1}\frac{d\mu }{d\theta }\left(\frac{2T-N-3}{2T-2}\right)-\frac{2N}{Td{\theta }^2}$$

where dθ is the difference in orientation between the two stimuli in radians, T is the number of trials, and N is the number of units. For sessions in which the number of trials differed for the two orientations, we subsampled the condition with more trials across 1000 iterations and averaged the estimated linear Fisher information across iterations.

Shuffled linear Fisher information was computed as

$$I_{\mathit{shuffle}}={\displaystyle \sum _i\frac{{(d{\mu }_i/d\theta )}^2}{s_i^2}}\left(\frac{T-2}{T-1}\right)-\frac{2N}{Td{\theta }^2}$$

where dμ_i is the trial-averaged firing rate difference between the two stimuli for neuron i and $s_i^2$ is its sample variance. Results were similar across a broad range of minimum SSI_visual (not shown).

QUANTIFICATION AND STATISTICAL ANALYSIS

The details of all statistical tests performed are describe in the Method Details section, in the main text, or in the figure captions. Details include the number of neuronal units and recording sessions used for each analysis. Error bars and shaded regions on plots indicate either mean ± SEM (Figures 3, 4, 6, 7A) or 95% confidence interval (Figures 2, 5, 7C, 8).

Highlights.

• Two behavioral components of visuospatial attention were isolated.

• Visual responses in lateral prefrontal cortex were robustly modulated by either component.

• Modulations in lateral prefrontal cortex and visual cortical area V4 were qualitatively different.

• The results indicate separate brain areas are associated with distinct mechanisms of attention.