Abstract
Burst firing in medial substantia nigra (mSN) dopamine (DA) neurons has been selectively linked to novelty-induced exploration behavior in mice. Burst firing in mSN DA neurons, in contrast to lateral SN DA neurons, requires functional ATP-sensitive potassium (K-ATP) channels both in vitro and in vivo. However, the precise role of K-ATP channels in promoting burst firing is unknown. We show experimentally that L-type calcium channel activity in mSN DA neurons enhances open probability of K-ATP channels. We then generate a mathematical model to study the role of Ca2+ dynamics driving K-ATP channel function in mSN DA neurons during bursting. In our model, Ca2+ influx leads to local accumulation of ADP due to Ca-ATPase activity, which in turn activates K-ATP channels. If K-ATP channel activation reaches levels sufficient to terminate spiking, rhythmic bursting occurs. The model explains the experimental observation that, in vitro, coapplication of NMDA and a selective K-ATP channel opener, NN414, is required to elicit bursting as follows. Simulated NMDA receptor activation increases the firing rate and the rate of Ca2+ influx, which increases the activation of K-ATP. The model suggests that additional sources of hyperpolarization, such as GABAergic synaptic input, are recruited in vivo for burst termination or rebound burst discharge. The model predicts that NN414 increases the sensitivity of the K-ATP channel to ADP, promoting burst firing in vitro, and that that high levels of Ca2+ buffering, as might be expected in the calbindin-positive SN DA neuron subpopulation, promote rhythmic bursting pattern, consistent with experimental observations in vivo.
NEW & NOTEWORTHY Recently identified distinct subpopulations of midbrain dopamine neurons exhibit differences in their two primary activity patterns in vivo: tonic (single spike) firing and phasic bursting. This study elucidates the biophysical basis of bursts specific to dopamine neurons in the medial substantia nigra, enabled by ATP-sensitive K+ channels and necessary for novelty-induced exploration. A better understanding of how dopaminergic signaling differs between subpopulations may lead to therapeutic strategies selectively targeted to specific subpopulations.
Keywords: bursting, calcium, dopamine, modeling, substantia nigra
INTRODUCTION
Dopamine (DA) neurons in vivo generally fire in either a tonic or a phasic pattern; tonic firing is a low-frequency (1–5 Hz) single action potential discharge, and phasic firing consists of transient high-frequency (>15 Hz) bursts of spikes, which have been widely hypothesized to signal reward-related information (Hyland et al. 2002; Schultz 1998, 2007). Unexpected rewards or stimuli that have been learned to predict subsequent rewards elicit single burst events consisting of three to eight action potentials. This type of phasic signaling is consistent with encoding of positive and negative prediction errors, which drive learning in the basal ganglia circuitry (Bromberg-Martin et al. 2010). An additional novel firing pattern (Schiemann et al. 2012) was recently identified in substantia nigra (SN) DA neurons in vivo: a rhythmic pattern of repetitive, sustained burst firing, distinct from the phasic mode described above, which generally refers only to individual burst events embedded in a background of single-spike activity. The sustained burst mode may be more appropriate for signaling nonphasic information, such as the presence of a novel environment or novel object. Rhythmic sustained bursting in vivo was observed only in those SN DA neurons that expressed the Ca2+-binding protein calbindin.
The functional diversity of subpopulations of DA neurons in both primates and rodents has begun to be appreciated (Roeper 2013), indicating that certain DA burst signals encode more than just reward prediction, depending upon the DA neuron subpopulation. Some burst in response to both aversive and rewarding stimuli, signaling motivational salience (Berridge 2007; Bromberg-Martin et al. 2010), while others may generate burst discharges to initiate or terminate learned action sequences (Jin and Costa 2010) or to initiate exploration of novelty (Schiemann et al. 2012). Very recent studies in songbirds demonstrated that the transient firing pattern of midbrain DA neurons also codes for performance errors (Gadagkar et al. 2016). Bursting in the medial, but not the lateral, SN is necessary for novelty-induced exploratory behavior, and both the bursts in the medial SN and the novelty-induced exploratory behavior require functional adenosine triphosphate-mediated K+ (K-ATP) channels (Schiemann et al. 2012).
Although SN DA neurons fire bursts in vivo, they spontaneously exhibit only regular, pacemaker-like firing in vitro (Grace and Onn 1989). Tonic activation of NMDA receptors has previously been shown to induce burst firing in SN DA neurons in vitro (Johnson et al. 1992) when accompanied by simultaneous injection of hyperpolarizing currents. Similarly, hyperpolarization provided by pharmacological activation of K-ATP channels enabled NMDA-induced burst firing in medial SN DA neurons in vitro (Schiemann et al. 2012). Application of 10 μM NN414, a K+ channel opener selective for SUR1/Kir6.2-mediated K-ATP channels, reduced the pacemaker firing rate to 75% of pre-NN414 levels, whereas application of 30 μM NMDA increased the firing rate from a baseline of 2.4 Hz to 6.4 Hz, with <10% of spikes fired in bursts. In contrast, coapplication of NMDA and NN414 induced a sustained burst firing pattern (60–70% spikes fired in bursts) in medial SN (Schiemann et al. 2012). Moreover, coapplication increases the average firing rate in the medial neurons to 7.2 Hz, so the application of the K+ channel opener can either increase or decrease the frequency, depending upon whether NMDA is present. K-ATP channels are known to link metabolic activity to excitability in neuroendocrine cells (Kanno et al. 2002). A recent model of bursting activity in pancreatic beta cells included an important contribution from slow cyclic changes in the activation of K-ATP channels, which were driven by slow changes in the ADP-to-ATP ratio. This ratio was itself modeled as dependent on cytosolic Ca2+, with the justification that this ratio depends on extrusion of Ca2+ via an ATPase (Watts et al. 2011). The role of K-ATP channels in neurons is less well understood. There is some evidence of a link between metabolic activity and electrical activity in neurons; for example, K-ATP channel open probability (Popen) was increased after a burst of action potentials in brain stem inspiratory neurons (Haller et al. 2001) and in dentate granule neurons (Tanner et al. 2011). Given the well-characterized regulation of K-ATP channels by cytosolic concentrations of the key metabolites ADP and ATP, the control of bursting discharge by energy metabolism is also an attractive candidate mechanism for medial SN DA neurons.
In this study, we develop a mechanistic, computational model of K-ATP channel-mediated bursting to explain our novel experimental results, which show that K-ATP channel Popen is controlled by the activity of voltage-gated calcium channels in metabolically intact SN DA neurons. We then apply the model to provide mechanistic explanations for the experimental observations of Schiemann et al. (2012) that pharmacologically enhanced Popen of K-ATP channels is necessary to mediate bursting in vitro, but not in vivo, and that a novel, sustained, rhythmic bursting mode is observed in calbindin-positive (CB+), but not -negative (CB−), DA SN neurons in vivo.
METHODS
Experimental
All animal experiments were approved by the regional council (Regierungspräsidium Darmstadt V54-19c20/15-F28/01). Adult (≥8 wk) male C57BL/6N mice were ordered from Charles River (Sulzfeld, Germany). Three or four 250-µm-thick coronal brain slices containing SN DA neurons per animal were prepared as previously described (Schiemann et al. 2012) with a vibratome (Leica VT 1200 S; Leica Biosystems, Wetzlar, Germany). Slices were held at 37°C during recordings. Kir6.2-knockout mice (Kir6.2−/−) were described in Schiemann et al., (2012), generated by Miki et al. (1998), and bred at mfd Diagnostics (Mainz, Germany). Kir6.2−/− have a 129/Sv background and were backcrossed over four generations with C57BL/6N mice. They have a general knockout for the pore-forming subunit Kir 6.2 and therefore lack functional K-ATP channels.
Single-channel recordings in cell-attached mode.
For on-cell recordings, membrane patches were held in cell-attached voltage-clamp mode at 0 mV to record both action currents and single K-ATP channels. Recordings were started >120 s after a stable gigaohm seal was established. For washin experiments, patches were constantly held at 0-mV holding potential. Spontaneous single-channel activity was recorded for at least 10 min. Patch ACSF (in mM: 125 NaCl, 3.5 KCl, 25 NaHCO3, 1.25 NaH2PO4, 2.5 glucose, 22.5 sucrose, 2 CaCl2, 2.06 MgCl2, and 1 sodium d-lactate) was exchanged with patch ACSF containing the corresponding pharmacological compound by bath perfusion. For single-channel recordings, synaptic blockers CGP 55845 (1 μM; Tocris), CNQX disodium salt (10 μM; Biotrend), dl-AP5 (50 μM), gabazine (SR 95531, 4 μM; Biotrend), and sulpiride (1 μM; Sigma-Aldrich) were added to the bath solution. Cell-attached pipette solution for single-channel K-ATP recordings contained (in mM) 140 KCl, 10 HEPES, 0.1 EGTA, and 2 MgCl2. The pipette solution contained 4-aminopyridine (1 mM; Sigma-Aldrich) and apamin (300 nM; Tocris) to block Kv4.3 and SK3 channels. Since the pipette contained physiological intracellular concentrations of K+, the Nernst potential for K+ through the patch is 0 mV, the same potential to which the patch was voltage-clamped. These cells are spontaneous pacemakers, so the average driving force for the K+ current during these experiments is the average value of the membrane potential during the interspike interval, which was about −50 mV.
Whole cell voltage-clamp recordings.
For whole cell voltage-clamp experiments, only recordings where series resistance (Rs) remained below 20 MΩ were used. Rs was compensated electronically between 50% and 80% with PATCHMASTER software. Voltage-clamp recordings enabled measurements of potassium currents through K-ATP channels. Therefore, cells were held at −50 mV in whole cell mode with an ATP-free pipette solution. For ATP washout experiments, 4 µM SR 95531 and 10 µM CNQX were added to the bath solution. Pipette solution for whole cell K-ATP washout recordings contained (in mM) 120 KGlu, 20 NaCl, 10 HEPES, 10 EGTA, and 2 MgCl2. Bath application of 300 nM isradipine (Tocris) was performed after 10 min of recording and 100 μM tolbutamide (Sigma-Aldrich) after 15 min.
Computational
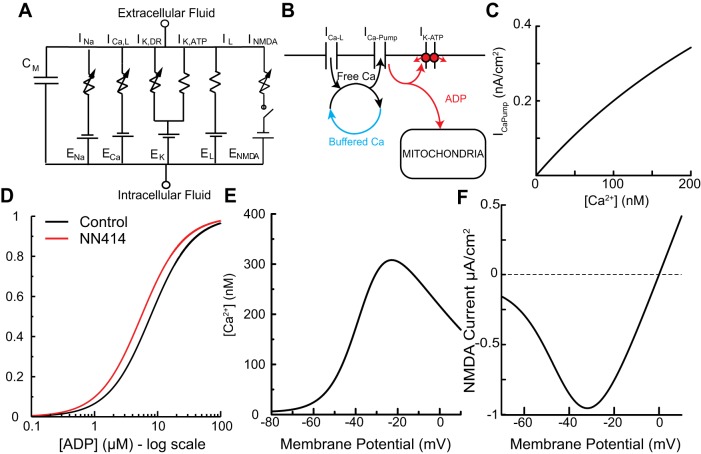
We built the simplest one-compartment Hodgkin-Huxley (Hodgkin and Huxley 1952)-style model of a DA neuron that allowed us to hypothesize a mechanism for how K-ATP channels enable burst firing. The electrical equivalent circuit (Fig. 1A) includes a fast voltage-gated Na+ current (INa) and a delayed-rectifier K+ current (IK,DR) to mediate spiking, a leak current (IL), a K-ATP current (IK,ATP), an L-type calcium current (ICa,L) to mediate voltage-gated calcium entry, and a synaptic NMDA current (INMDA), all parallel with a membrane capacitance Cm. Channel kinetics for the Na+, K+, and L-type calcium currents were taken from Ji et al. (2012). Activation curves for the NMDA channel (Fig. 1F) were adapted from Canavier (1999).
Fig. 1.
Model schematics. A: effective circuit diagram for single-compartment model containing sodium (INa), delayed-rectifying potassium (IK,DR), ATP-sensitive potassium (IK,ATP), leak (IL, which includes calcium component IL,Ca), L-type calcium (ICa,L), and NMDA (INMDA) currents all in parallel with the membrane capacitance. Variable resistors indicate time and voltage dependence. The DC voltage sources represent the Nernst reversal potentials. B: schematic of Ca2+ and ADP handling in the model. Ca2+ enters through the L-type voltage-sensitive Ca2+ channels as well as via components of the leak channels. The fraction of Ca2+ that is not free in the cytosol is presumed to instantaneously bind or be released from the buffer. Free Ca2+ is extruded through the action of an ATPase that acts as a nonelectrogenic calcium pump (ICa-Pump). The activity of these pumps converts ATP into ADP, which favors K-ATP channel opening. The mitochondria are modeled simply as an ADP sink. C: dependence of the pump current on free Ca2+. D: steady-state activation of the model K-ATP channel as a function of ADP concentration under control conditions and under the simulated application of the selective K-ATP channel opener NN414. E: Ca2+ nullcline (values of free Ca2+ and voltage for which d[Ca]/dt = 0). F: current per unit conductance of NMDA receptor vs. voltage. The voltage-dependent block of the channel by Mg2+ creates a negative slope conductance that allows for regenerative depolarization and hyperpolarization.
Current equations.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
Parameters for Eqs. 1–5 are given in Table 1.
Table 1.
Current equation parameters
| Cm, pF/cm2 | 1.0 |
| gNa, µS/cm2 | 1,500 |
| gK, µS/cm2 | 440 |
| gL,ns, µS/cm2 | 6.0 |
| gK,ATP, µS/cm2 | 45 |
| gL,Ca, µS/cm2 | 0.05 |
| gCa,L, µS/cm2 | 6.0 |
| gNMDA, µS/cm2 | 40 |
| EL,ns, mV | −60 |
| ENa, mV | 60 |
| EK, mV | −90 |
| ECa, mV | 60 |
| [Mg2+], mM | 1.2 |
| Shalf, µM | 7.7 |
Gating variable equations.
The gating variables m, h, l, and n obey equations of the form dx/dt = (x∞ − x)/τx, with , with parameters as given in Table 2.
Table 2.
Hodgkin-Huxley gating variable dynamics
| x | xhalf, mV | xk, mV | Time Constants τx, ms |
|---|---|---|---|
| m | −28.1 | 8.7 | |
| h | −54 | −8.77 | |
| n | −20 | 7.0 | |
| l | −40 | 7.5 |
Θ(x) is the Heaviside-theta step function, which was accidentally omitted from model description in earlier papers (Ji et al. 2012).
Calcium dynamics.
A schematic of the Ca2+ dynamics is given in Fig. 1B. Ca2+ enters via L-type (ICa,L) and leak channels (IL,Ca)
| (6) |
and is extruded by Ca-ATPase pumps (ICa,Pump) with Michaelis-Menten kinetics illustrated in Fig. 1C:
| (7) |
where F is the Faraday constant [F = 0.9648 C/(nM cm2 μm)], d is the effective compartment diameter (1.0 μm), and fca is the fraction of unbound calcium. The model is designed to be representative of a dendritic compartment, which has a diameter on the order of 1 μm (Vetter et al. 2001). This small compartment size is necessary to produce sufficient variation in calcium and ADP to produce deterministic, large-scale variations in K-ATP activation over the 100- to 1,000-ms timescales in pacing and bursting. It also is quite possible that a well-mixed bulk compartment model is not applicable but rather localized pools of Ca2+ and ADP drive the dynamics. Under these assumptions the removal of ADP would be more accurately attributed to diffusion/transport mechanisms than reuptake by mitochondria.
Ca2+ influx via NMDA channels was neglected, in part because previous work by Shen and Johnson (2010) indicated that the activation of NMDA channels does not increase the activation of K-ATP channels under voltage clamp in SN DA neurons and in part because the results are qualitatively the same whether Ca2+ entry is due solely to voltage-gated and leak channels or partially due to NMDA receptors. Fraction of free calcium was chosen to be 2%, consistent with the literature (Foehring et al. 2009). Ca2+ conductances (gCa,L and gL,Ca) and the maximal pump current (IPumpMax) were chosen to make the Ca2+ nullcline (Fig. 1E) for the model consistent with the measured Ca2+ nullcline of Wilson and Callaway (2000), except for a 100 nM offset that was also incorporated in their model. The nullcline shows the value of free Ca2+ at which Ca2+ influx and efflux are exactly balanced for each value of the membrane potential, with the gating variable l for the voltage-gated Ca2+ current set to its steady-state value as a function of voltage.
K-ATP dynamics.
The K-ATP channel (Aittoniemi et al. 2009) is an octameric complex with four inward-rectifying potassium channel Kir6.2 subunits forming a central pore and four sulfonylurea receptor SUR1 subunits surrounding them. Binding of ATP to sites on the Kir6.2 subunits of the K-ATP channel favors a conformational change that closes the central pore. MgADP binds to the adjacent SUR1 receptor, inducing a separate conformational change that is believed to reduce the affinity of Kir6.2 sites to ATP, resulting in an open pore (Burke et al. 2008; Proks et al. 2010). We neglect the reactions for binding and unbinding of the nucleotides to Mg2+ and refer simply to ADP and ATP, assuming that the interactions with Mg2+ are sufficiently fast to assume that the bound nucleotide can be treated as a constant fraction of total nucleotides. Since the concentration of cytosolic ATP is typically high in neuronal populations, of millimolar order (Ainscow et al. 2002), we assumed saturating levels of the inhibitory effect of ATP on the Kir6.2 subunit (Proks and Ashcroft 2009). Thus dynamic activation of the channel is modeled as a function solely of ADP acting at the SUR1 receptor. The activation of the K-ATP channel by ADP was based on the measured MgADP sensitivity (Proks et al. 2010), which was a Hill function with half activation of 7.7 μM and coefficient of 1.3 as given in Eq. 4 and plotted in Fig. 1D.
We modeled the conversion of ATP into ADP to be solely a function of the activity of Ca-ATPase. Other processes, such as the Na-K-ATPase (Tanner et al. 2011) and other internal ATP-consuming processes that might contribute as well, are neglected, because lumping these processes together is not likely to qualitatively affect the results. ADP is depleted by reuptake by the mitochondria and diffusion away from active regions, which we modeled with Michaelis-Menten dynamics:
| (8) |
where Km is the maximal clearance rate of ADP and ahalf is the half activation.
K-ATP antagonists, like the sulfonylureas glibenclamide and tolbutamide, and K-ATP channel openers, like diazoxide, bind directly to the regulatory subunit SUR1 (Ashcroft and Gribble 2000; Proks and Ashcroft 2009). NN414 has no effect in the absence of nucleotide (ADP or ATP); it also has no effect in the presence of a saturating concentration of ADP. One hundred micromolar MgATP reduced K-ATP currents by 80% compared with control solutions with no nucleotide in K-ATP channels expressed in oocytes (Dabrowski et al. 2003); subsequent addition of 100 μM NN414 in the presence of ATP reversed most of this reduction in conductance (Dabrowski et al. 2003). The absence of ADP in the bath does not imply that no ADP is present due to the ability of the SUR1 receptor to hydrolyze ATP. The increased conductance caused by NN414 could be due to an increase in single-channel conductance or to an increase in channel Popen. Since our model is deterministic, these two possibilities cannot be distinguished in our model. However, an increase in channel Popen is more likely in light of the results of Tanner et al. (2011), who found that 5 μM NN414 increased K-ATP channel Popen from 0.19% to 4.7% in mouse dentate granule cells.
Strikingly, in channels without functional SUR1 receptors, MgATP only reduced the K-ATP conductance by 40% and subsequent addition of NN414 did not reverse the reduction (Dabrowski et al. 2003). Given these findings, it seems clear that NN414 must exert its effect by increasing the ability of SUR1 to counter the inhibitory effect of ATP on Kir6.2, either directly or by increasing its affinity for ADP. The exact molecular mechanism is unknown, but the model was designed to capture the essence of this effect. Since we assume ATP concentrations are saturating, we modeled the effect of NN414 as an increase in affinity for ADP by shifting the half activation (Shalf) of the SUR1 subunit to ADP concentration from 7.7 μM to 5.0 μM (Fig. 1D).
The model has seven state variables: membrane potential, the four gating variables m, h, n, and l described in Table 2, cytosolic free Ca2+ concentration, and ADP concentration. The code was implemented in C with Python scripting. Model files are available at https://senselab.med.yale.edu/modeldb/ShowModel.cshtml?model=227678.
RESULTS
Voltage-Gated Ca2+ Influx Increases K-ATP Channel Open Probability
Given the well-characterized metabolic impact of pacemaker-dependent activity of voltage-gated L-type calcium channels on mitochondrial energy metabolism in SN DA neurons (Surmeier et al. 2011) and our own previous finding that K-ATP channel activity was controlled by mild uncoupling of the mitochondrial membrane potential (Liss et al. 2005), we probed for the role of voltage-gated L-type channels in regulating K-ATP channel activity in metabolically intact SN DA neurons. Single K-ATP channel recordings in the cell-attached patch-clamp configuration were conducted in spontaneously pacemaking DA neurons located predominantly in the medial SN. At 0-mV pipette holding potential, the mean single-channel current amplitudes were ~2.8 pA, consistent with an expected single-channel conductance of Kir6.2-SUR1-mediated K-ATP channels of ~60 pS. Only the membrane beneath the cell-attached patch is clamped to 0 mV. The cell is not impaled by the patch electrode or voltage clamped, and therefore the cell continues to exhibit pacemaking activity during the single-channel recordings in Fig. 2. Figure 2A shows that application of 300 nM isradipine significantly reduced the Popen of K-ATP channels compared with the control conditions. These results indicated that pacemaker-related activity of L-type calcium channels [most likely Cav1.3; see argument in Dragicevic et al. (2014)] induced metabolic consequences sufficient to facilitate K-ATP channel activity in metabolically intact cells. Inhibition of sodium channels with 300 nM TTX did not significantly reduce mean K-ATP channel Popen (control: 2.7 ± 0.61%; TTX: 2.4 ± 1.24%; P = 0.36; Wilcoxon signed-rank test; n = 14), with 64% of cells showing a decrease in Popen and 36% showing an increase, suggesting that sodium entry is less important than calcium entry in activating the K-ATP channel. In these experiments, some other relevant K+ channels were pharmacologically blocked (e.g., apamin in the pipette). Channel openings were greatly reduced in on-cell recordings from Kir6.2−/− (Fig. 2B) and inhibited by 1 µM glibenclamide (Fig. 2C). The remaining channel openings are likely not due to K-ATP channels but rather to other types of K+ channels with similar conductances. The massive reduction of the channel Popen in glibenclamide or in the Kir6.2−/− indicates that most of the channel openings observed with this protocol are indeed K-ATP channels.
Fig. 2.
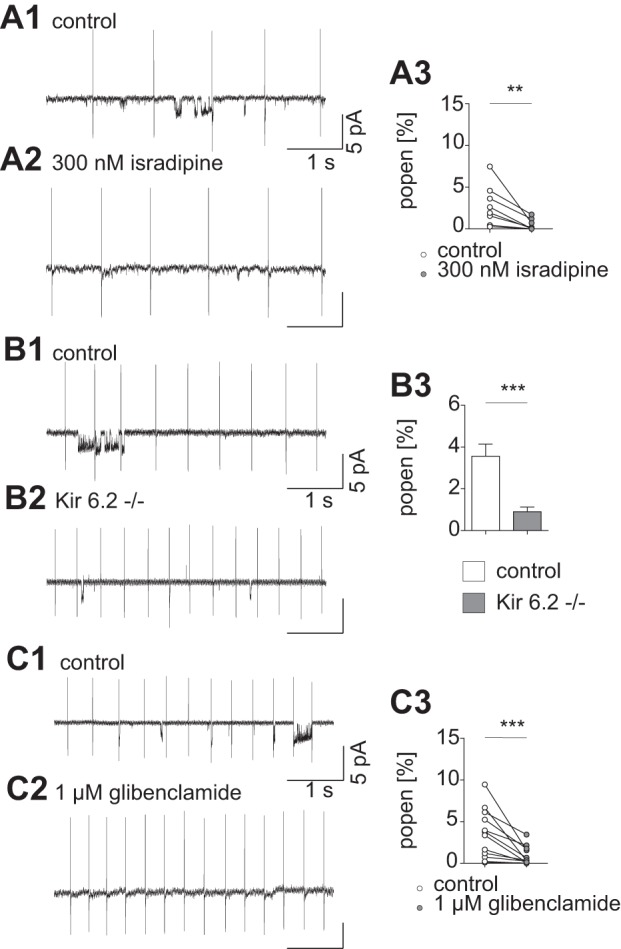
Single-ion channel activity is decreased after L-type calcium channel inhibition with 300 nM isradipine. A1: representative current trace before bath application of isradipine; short openings and clusters of channel activity can be detected. The current due to action potentials during pacemaking is clearly visible at regular intervals of several hundred milliseconds. A2: representative current trace during 300 nM isradipine bath application; channel openings appear rarely. A3: mean values for single-channel activity are reduced after isradipine application (Popen control: 2.8 ± 0.85%; Popen isradipine: 0.5 ± 0.24%, P = 0.0078; Wilcoxon signed-rank test; n = 8). B1: representative trace of an on-cell recording from a control animal. Openings of single channels appear in clusters. B2: current trace recorded in a Kir6.2−/− animal. Smaller event clusters can be detected. B3: average Popen recorded in control animals is significantly higher than in animals lacking functional K-ATP channels (Popen control: 3.6 ± 0.58%; Popen Kir6.2−/−: 0.9 ± 0.22%; P = 0.0003; Mann-Whitney test; n = 17). C1: control. C2: representative current trace in presence of the SUR1 subunit inhibitor glibenclamide. C3: glibenclamide causes a substantial drop in channel activation (Popen control: 3.5 ± 0.84%; Popen glibenclamide: 0.9 ± 0.32%; P = 0.0005; Wilcoxon-signed rank test; n = 12). The small 50-Hz oscillation in the current traces is an artifact of the ambient power. **P < 0.01; ***P < 0.001.
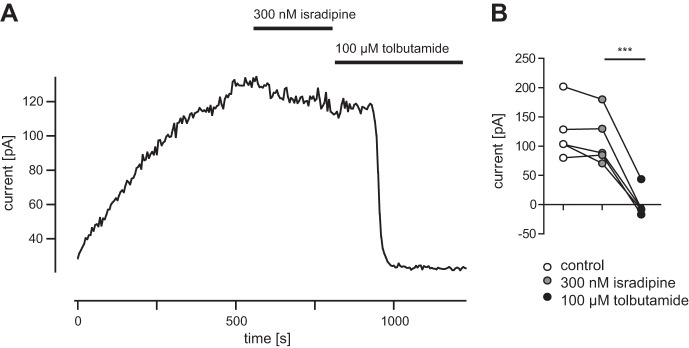
The results in Fig. 2 could potentially be explained if isradipine, in addition to blocking L-type Ca2+ channels, also directly blocked K-ATP channels. In the absence of nucleotides such as ATP and ADP, K-ATP channels have a much higher Popen than in their presence, because the inhibitory actions of the nucleotides predominate under physiological conditions (Ainscow et al. 2002; Proks and Ashcroft 2009). In whole cell recordings, no ATP or ADP is added to the pipette; therefore the concentration of nucleotides in the cell is depleted by dialysis during long experiments (Fig. 3). Under control conditions the ATP washout current was 123 ± 21.1 pA. In isradipine the washout current was 111 ± 19.9 (P = 0.14, not significant, t-test), demonstrating that this L-type channel blocker at 300 nM did not have any direct effect on K-ATP channel. The specific K-ATP channel blocker tolbutamide largely eliminated this current (1 ± 10.8, P = 0.0007, t-test). Thus isradipine mediates the Popen of these channels indirectly via reducing L-type channel-mediated calcium influx upstream of K-ATP channel activity.
Fig. 3.
Application of isradipine does not directly alter K-ATP channel activation. A: representative example for ATP washout current after performing whole cell configuration. Steady-state current is reached after ~20 min of recording; bath application of 300 nM isradipine does not change current amplitude; 2 min after 100 μM tolbutamide bath application washout current is completely blocked. B: isradipine does not significantly change ATP washout current; after tolbutamide application washout current is significantly reduced (n = 4).
These experimental results demonstrated that K-ATP channel activity was facilitated by L-type calcium channel activity during ongoing pacemaker activity in medial SN DA neurons, most likely by calcium channel-induced metabolic consequences. This type of functional coupling between electrical activity-driven calcium influx and its consequences for energy metabolism and in turn K-ATP channel activity inspired us to generate an electrical-metabolic pacemaker model of SN DA neurons to study the role of this coupling for control of different patterns of burst discharge in SN DA neurons.
Computational
We replicated the K-ATP-mediated burst firing evoked in medial SN DA neurons in vitro (Schiemann et al. 2012) Figure 4A shows control pacing at 3.2 Hz that is slowed to 2.5 Hz in Fig. 4B by reducing Shalf to simulate application of the K+ channel opener NN414. Simulated bath application of NMDA (gNMDA = 40 μS/cm2) increased the pacemaker firing rate to 8.2 Hz (Fig. 4C). Simulated coapplication of NMDA and NN414 induced regular bursting with an average firing rate of 11.7 Hz and an intraburst firing rate of 20 Hz (Fig. 4D). The main features we sought to capture in Fig. 4D were 1) a faster average frequency during bursting in the presence of NN414 and NMDA compared with NMDA alone, despite the presence of pauses during bursting, and 2) the plateaulike nature of the bursts.
Fig. 4.
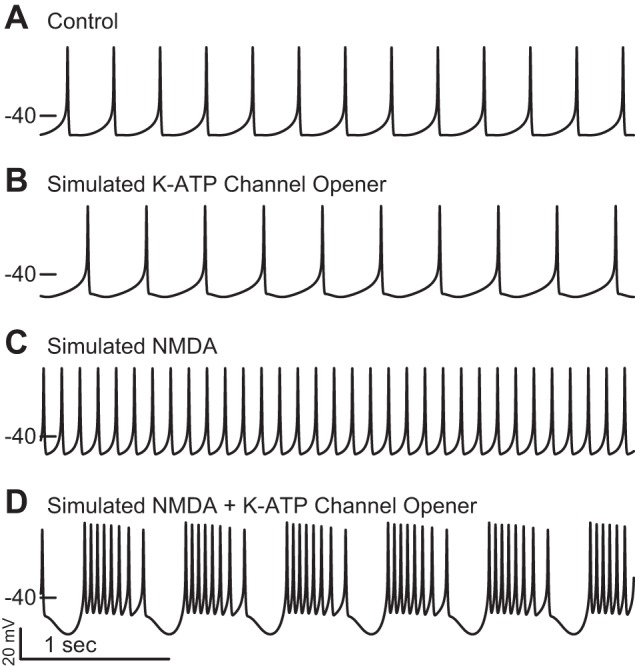
Simulation of the effects of bath application of NN414 and NMDA in vitro. A: the control pacemaking rate of the model was ~3.2 Hz. B: simulating the addition of the K-ATP channel opener NN414 decreased the firing rate to 2.5 Hz. C: simulating the addition of NMDA to the bath increased the firing rate to 8.2 Hz. D: simulating the addition of both NN414 and NMDA to the bath produced burst firing at an increased average firing rate of 11.7 Hz (intraburst average firing rate is 20 Hz).
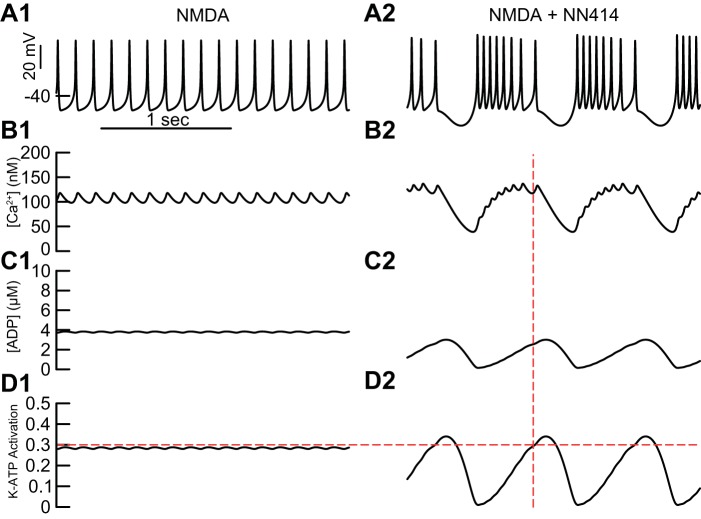
Figure 5A1 repeats the voltage trace of fast firing in the presence of NMDA from Fig. 4C. This regular, single-spike firing drives small-amplitude oscillations in Ca2+ (Fig. 5B1), ADP concentration ([ADP]) (Fig. 5C1), and activation of the K-ATP channel (Fig. 5D1); the horizontal dashed line corresponds to the fractional amount of steady-state K-ATP channel activation (0.3) required to terminate spiking; the dynamics oscillate below this threshold during pacemaker firing. Figure 5A2 repeats the voltage trace of burst firing in the presence of both NN414 and NMDA from Fig. 4D; the dashed vertical line intersects the voltage trajectory at the point at which spiking ceases. The oscillation in Ca2+ in Fig. 5B2 has a larger amplitude than that in Fig. 5B1, but a lower average value, and consequently evokes lower levels of ADP (Fig. 5C2) than in Fig. 5C1. NN414 increases the effectiveness of activation of the K-ATP channel via SUR1 (Dabrowski et al. 2003). We simulated the effects of NN414 by reducing Shalf to simulate application of NN414, which allows lower levels of ADP to more effectively activate K-ATP. Thus less ADP is required in the presence of NN414 to terminate spiking than in its absence. The levels of K-ATP activation (Fig. 5D2) reach both higher peaks and lower troughs during bursting compared with tonic firing in the presence of NMDA (Fig. 5D1). The peaks enable the pauses between bursts when spiking is terminated, and the troughs enable substantially faster intraburst firing. The average firing rate is higher during bursting in the presence of NN414 than in single spiking in the presence of only NMDA, consistent with experimental data (Schiemann et al. 2012). Essentially, whether the result is single spiking or bursting, the model only spikes when K-ATP activation is below the horizontal line in Fig. 5D, for reasons explained in Figs. 6 and 7. Bursting in the presence of NMDA and NN414, but not NMDA, was observed for ahalf ranging from 50 nM to 300 nM. Higher values of ahalf require less NMDA conductance to induce bursting. Conversely, lower values of Km require less NMDA conductance to induce bursting. Values of Km greater than ~50 μM/ms produce a distinct bursting mechanism dependent on depolarization block, due to inactivation of the Na+ channel. The basic mechanism of a transition from single-spike firing to bursting is fairly robust in the three-dimensional parameter space of ahalf, Km, and gNMDA.
Fig. 5.
Dynamics of bursting compared with regular single spiking. With simulated NMDA alone (A1 repeats Fig. 4C), single-spike firing drives small-amplitude oscillations in both [Ca2+] (B1) and [ADP] (C1) that cause the K-ATP activation (D1) to approach, but not overshoot, the level of static K-ATP activation required to terminate firing (0.3). With the addition of the simulated K-ATP channel agonist NN414 to the simulated NMDA, burst firing results (A2). The vertical dashed line at which spiking terminates corresponds to the point at which level of static K-ATP activation required to terminate firing (0.3, horizontal dashed line in D1 and D2) is achieved; however, Ca2+ is still elevated from the preceding burst, causing ADP and K-ATP activation to continue to accumulate. The oscillation amplitude of Ca2+ (B2) is larger than in B1, but it has a lower average value and consequently evokes lower levels of ADP (C2) but, due to the lower threshold for activation, a much larger amplitude oscillation in K-ATP activation (D2).
Fig. 6.
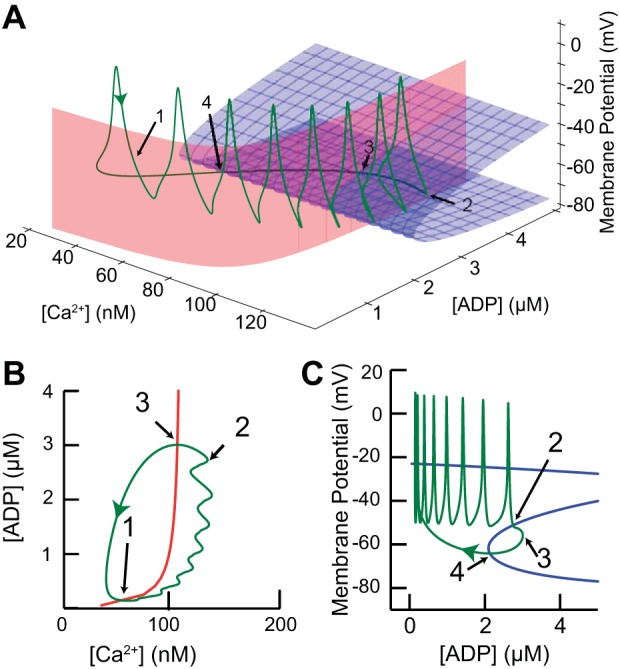
Phase space analysis explains the bursting mechanism. A: green curve represents a single cycle of the periodic bursting activity in Fig. 5B plotted in the state space. Blue surface comprises the lower 2 branches of the voltage nullcline (dV/dt = 0) in the V/ADP plane (all 3 branches are shown in C). Red surface is the ADP nullcline (dADP/dt = 0) in the ADP/Ca2+ plane (shown as red curve in B). The trajectory crosses the ADP nullcline at points 1 and 3 and the voltage nullcline at points 2 and 4. B: projection of ADP nullcline from A onto the ADP/Ca2+ plane. C: projection of V nullcline from A onto the V/ADP plane. In this view it is clear that the burst is terminated when the trajectory hits the middle branch of the voltage nullcline (dV/dt = 0, blue), then slowly repolarizes after exiting through the “knee.” Part of the Z is not visible on this scale, but the curve is continuous.
Fig. 7.
Distinct dynamic mechanisms for single spiking and bursting. Top: projection of the voltage nullcline from Fig. 6A unto the voltage/ADP plane in the same manner as in Fig. 6D. Bottom: voltage traces. A: in the absence of NN414, the tonic spiking trajectory (A1) from Fig. 5A does not interact with the middle branch of the voltage nullcline (dV/dADP = 0, black), enabling pacemaking (A2). B: addition of NN414 shifts the voltage nullcline left to lower ADP values, forcing a crossing that destabilizes the tonic mode (B1), resulting in bursting (B2). C: addition of a tonic GABAergic (10 μS/cm2) conductance causes a leftward shift in the voltage nullcline (C1) similar to NN414, allowing for stable bursting (C2). D: hyperpolarization due to a single simulated GABAergic IPSP can lead to a rebound burst (D2) because the hyperpolarization causes a crossing of the unstable middle branch in a downward direction (D1) and a period of quiescence.
Figure 6 explains the dynamics of bursting in the model with a three-dimensional space consisting of the membrane potential plus the two slow variables: the concentrations of free Ca2+ and ADP. We reduced the dimensionality of the full dynamical system, using the principle of separation of timescales (Somers and Kopell 1993; van der Pol 1926) by setting all gating variables (m, h, n, and l) to their steady-state values as a function of voltage, under the assumption that these variables change on a much faster timescale than the slow system comprised of free [Ca2+] and [ADP]. This reduction allowed us to obtain the red and blue nullcline surfaces in Fig. 6A that control the dynamics of the model system. The blue surface in Fig. 6A is the voltage nullcline comprised of the values of V and [ADP] for which the net current is zero (dV/dt = 0). The full Z shape of the voltage nullcline can be seen in the blue curve in Fig. 7C. The upper branch of the nullcline (see Fig. 7C) is suppressed in Fig. 6A to allow the middle branch to be seen clearly. The three nullcline branches are the same at each constant value of Ca2+ because membrane potential does not directly depend on Ca2+ (see Eq. 1). The red surface is the ADP nullcline comprised of the values for which the efflux and influx of ADP into the cytosolic compartment are equal (d[ADP]/dt = 0). The ADP nullcline is shown in Fig. 6B and is the same in Fig. 6A at each constant value of membrane potential, because the ADP concentration (Eq. 8) does not directly depend on membrane potential. The trajectory corresponding to a single cycle of the periodic bursting activity in Fig. 4D and Fig. 5B is replotted in this space (green curve, Fig. 6A). The slow variables move the trajectory between points 1 and 3 as explained in Fig. 6B below This moves the trajectory from regions in which the middle branch of the voltage nullcline is present to terminate spiking (point 2) as explained in Fig. 6C below to regions in which the middle branch is absent, where new bursts are initiated.
Figure 6B shows how the slow variables control the trajectory (green curve). The ADP nullcline (red curve) depends on the Ca2+ pump current, which in turn depends upon the level of Ca2+. This nullcline divides the plane into two regions: above the curve (after spike termination and just after burst initiation) ADP is decreasing because the level of pump activity is too low to sustain the concentration of ADP, whereas below the curve ADP is increasing because the level of pump activity can sustain a higher concentration of ADP. Points 1 and 3 in Fig. 6, A and B, show the intersections of the trajectory with the ADP nullcline. The slow cycle in this plane between points 1 and 3 moves the spiking trajectory toward the unstable middle branch of the voltage nullcline in Fig. 6A until spiking terminates when the trajectory touches this branch. Cessation of spiking causes Ca2+ to decrease until point 3 is crossed; then the slow cycle moves the trajectory away from the middle unstable branch of the nullcline surface while K-ATP current decreases (because ADP is decreasing). The decrease in K-ATP current depolarizes the membrane until spiking resumes, which causes Ca2+ to increase until the ADP nullcline is crossed at point 1, and ADP also begins to increase again.
Figure 6C explains the role of the voltage nullcline. The voltage nullcline divides the plane into two regions: to the left (and bottom) of the Z membrane potential increases, and to the right (and top) it decreases. The Z shape of the voltage nullcline (blue curve) results from the regenerative activation and deactivation of the NMDA receptor current (with an additional contribution by the L-type Ca2+ channel). On the top branch these channels are open, whereas on the bottom branch they are closed. On the unstable middle branch, positive feedback dominates, meaning that if the trajectory crosses this branch while the neuron is depolarizing, the depolarization accelerates because more channels are recruited by the depolarization and contribute to the depolarization. On the other hand, if this trajectory is crossed while the neuron is hyperpolarizing, the hyperpolarization will accelerate because more channels will close because of the hyperpolarization and thereby cause more hyperpolarization. This is precisely what happens at point 2, where the trajectory (green curve) intersects the middle branch and spiking is terminated as the membrane hyperpolarizes regeneratively. As explained above, cessation of spiking causes ADP to decrease, which causes the trajectory to cross the nullcline again at point 4, depolarizing the membrane potential and moving the trajectory away from the unstable middle branch.
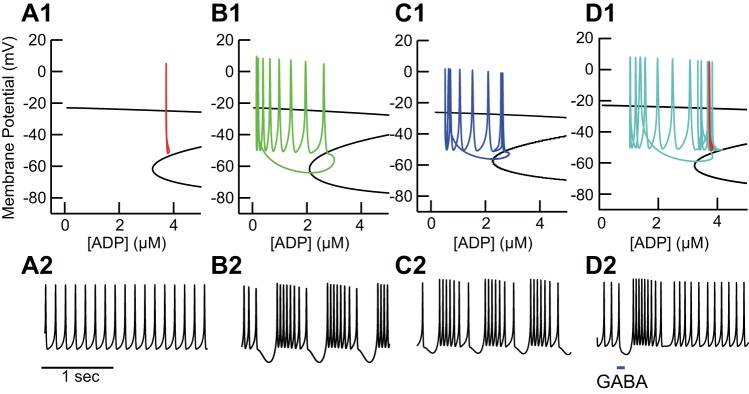
Figure 7 explains the mechanism that underlies transitions between single-spike firing and bursting. In the simulated presence of NMDA but not NN414 (Fig. 7A), the red trace in Fig. 7A1 corresponding to single-spike firing does not cross the middle branch of the voltage nullcline, allowing for stable pacemaking. The simulated addition of NN414 shifts the middle and lower branches of the nullcline leftward to lower ADP concentrations at each voltage (Fig. 7B). This forces a crossing of the unstable middle branch of the voltage nullcline, destabilizing pacemaking and enabling stable bursting as described in Fig. 6. Adding a tonic GABAergic conductance, instead of simulated NN414, to the presence of simulated NMDA similarly shifts the voltage nullcline leftward, again enabling bursting (Fig. 7C). Any additional outward current would have a similar effect. If the pacemaking trajectory is near the middle branch, a brief pulse of a GABAergic conductance can induce a rebound burst (Fig. 7D). (If the trajectory is farther to the left, a long hyperpolarization would be required to reduce ADP and move the trajectory toward the middle branch.) Obviously, burst firing in vivo does not require the exogenous channel opener NN414; these results suggest that GABAergic tone and/or random inhibitory postsynaptic potentials (IPSPs) in vivo might be sufficient to synergize with K-ATP activation for burst termination, leading to repetitive burst firing. Moreover, this suggests one possible explanation for why K-ATP mediated bursting is not observed in the lateral nigra: perhaps the contribution of other outward currents in those cells is sufficient for bursting in the presence of NMDA receptor activation.
The burst firing in Figs. 4–7 is more regular than that observed in vitro by Schiemann et al. (2012) and may correspond more closely to the novel, sustained, rhythmic mode that the same study observed in vivo but selectively in CB+ DA neurons. To better simulate physiological noise (as described in Stochastic Dynamics), we added 1 nA/cm2 Gaussian current noise in Fig. 8A to the bursting induced by NMDA and NN414 in Figs. 4D, 5B, and 6B. The minimal variation of the trajectory in Fig. 8A indicates that the deterministic model of bursting is robust with respect to modest channel noise. Since the model neuron in Figs. 4–6 exhibits rhythmic burst firing, we consider this parameter set to represent a CB+ neuron. We increased the fraction of free Ca2+ from 0.02 to 0.03 to simulate a CB− neuron (Fig. 8B) with presumably reduced buffering capacity. The reduction in Ca2+ buffering produced less regular bursting mode in the presence of the same level of current noise as in Fig. 8A, which may explain why only CB+ neurons exhibit regular bursting in vivo. Switches between single spiking and bursting may be mediated by bistability between bursting and single-spike firing (Butera 1998; Canavier et al. 1993, 1994), as is the case in this parameter set, by inducing burst terminations in neurons that in the absence of noise would be pacemakers or by inducing chaos in the transition between bursting and single-spike firing (Canavier et al. 1990). The key factor is that decreasing the buffer concentration speeds Ca2+ dynamics, which disrupts the slow rhythmic activity of [Ca2+] that underpins regular bursting as shown in Fig. 7B.
Fig. 8.
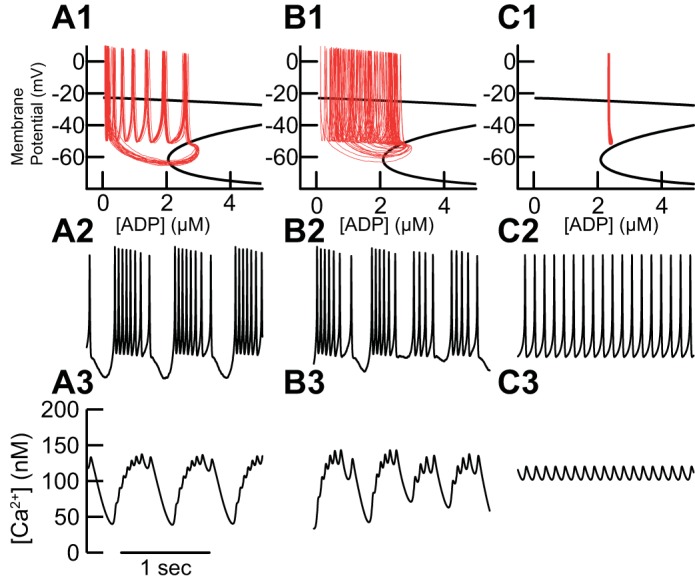
Effect of Ca2+ buffering and ADP clearance on K-ATP-mediated bursting. A: the simulated bursting in previous figures evoked by NN414 and NMDA remains regular with 1 nA/cm2 added Gaussian current noise as observed in the phase plane (A1), the membrane potential (A2), and free [Ca2+] (A3). B: the absence of calbindin was modeled as an increase in the fraction of free calcium (fca in Eq. 6). The decrease in buffering leads to a smearing of the trajectory in the phase plane (B1) and more irregular bursting including switching between single spiking and bursting (B2) in the presence of identical noise compared with A. Decreasing the buffer concentration speeds Ca2+ dynamics, disrupting the slow rhythmic activity of [Ca2+] that underpins regular bursting (B3). C: simply increasing the clearance rate of ADP (Km in Eq. 8) abolishes bursting in the presence of NMDA and NN414, as seen in the phase plane (C1), the voltage trace (C2), and [Ca2+] (C3).
Increasing the maximum rate of ADP clearance (Km) in Table 3 from 43 to 45 µM/ms in Fig. 8C eliminated burst firing in in the presence of NN414 and NMDA. This change prevents ADP accumulation during pacemaking and thus eliminates the bursting mode. There are no data regarding the dynamics of ADP clearance in midbrain dopamine neurons, but Fig. 8C suggests that differences in ADP clearance between medial and lateral neurons could explain the larger effect of inactivation of the K-ATP channel on burst reduction in medial vs. lateral nigra in vivo.
Table 3.
Parameters for calcium and ADP dynamics
| d, µm | 1.0 |
| IPumpMax, nA/cm2 | 1.2 |
| Chalf, nM | 500 |
| fca | 0.02 |
| ahalf, µM | 0.1 |
| Km, µM/ms | 43.0 |
DISCUSSION
Summary and Model Predictions
We used selective pharmacology to show that K-ATP single-channel Popen is increased by Ca2+ influx via voltage-gated channels. In our mathematical model, Ca2+ influx leads to local accumulation of ADP due to Ca-ATPase activity, which in turn activates K-ATP channels. Two slow variables ([Ca2+] and [ADP]) are required only because we postulate that the dependence of the K-ATP channel on Ca2+ is indirect, and it is well established that Ca2+ in these neurons varies slowly compared with the membrane potential (Wilson and Callaway 2000). Simulated NMDA receptor activation increased the firing rate and the rate of Ca2+ influx, which in turn increases the activation of K-ATP channels. For burst firing to occur, K-ATP channel activation must reach levels sufficient to terminate spiking. NN414 acts synergistically with local accumulation of ADP to boost the outward current to the level required for regenerative deactivation of the NMDA channels that terminates a burst. Here, phasic or tonic GABAergic inhibition could cooperate with K-ATP channel activation to facilitate burst firing. This prediction could be tested experimentally in vitro in the presence of NMDA, but not NN414, by applying a hyperpolarization to determine whether a rebound burst can be evoked (Fig. 7D) or by using the dynamic clamp to apply a tonic level of GABA conductance (Fig. 7C). Moreover, the model predicts that a faster rate of ADP clearance in lateral vs. medial nigra might account for the lack of K-ATP-mediated bursting laterally and that high levels of Ca2+ buffering, as might be expected in the CB+ population, could promote rhythmic bursting, consistent with experimental observations. Imaging for ADP clearance has not been performed on dopaminergic neurons, although existing imaging mechanisms having timescales on the order of seconds (Tantama et al. 2013) may be able to record ADP/ATP variation on the timescale of bursting.
Relevance of High Ca2+ Load of DA Neurons for K-ATP Function
Tanner et al. (2011) found that moderate action potential firing evoked K-ATP channel opening via Na+ influx and ATP depletion (or conversely, via ADP accumulation). However, they found that the increase in K-ATP channel opening largely disappeared in the presence of strophanthidin, a blocker of Na-K-ATPase, which implies that the Na-K-ATPases play a dominant role in activating K-ATP channels in mouse dentate gyrus neurons. Although we do not discount the role of Na-K-ATPase in activating K-ATP channels in SN DA neurons, our experimental data indicated a central role for Ca-ATPases. Ca2+ channels play a prominent role in the pacemaking mechanism (Bean 2007; Chan et al. 2007) of SN DA neurons, resulting in Ca2+ entry that is continuously maintained (Puopolo et al. 2007) during pacemaking. This in turn leads to a relatively high Ca2+ load in SN DA neurons, which has been blamed for their selective vulnerability in Parkinson disease (PD) (Surmeier et al. 2010, 2011, 2012). Here we suggest that this high Ca2+ load leads to local accumulation of ADP that recruits K-ATP channel opening, as suggested by experiment (Fig. 2) and the model schematic (Fig. 1B). In chronic mouse models of dopaminergic degeneration, the presence of functional K-ATP channels promotes cell death of SN DA (but not ventral tegmental area DA) neurons (Liss et al. 2005). Activation of K-ATP by Ca2+ influx may also contribute to neurodegeneration in humans; clinical trials are ongoing to test the efficacy of isradipine, an L-type Ca2+ channel blocker, in slowing the progress of PD (Ortner and Striessnig 2016; Surmeier et al. 2017).
Role of Hyperpolarization in Burst Firing
The first demonstration of burst firing in midbrain DA neurons in vitro (Johnson et al. 1992) revealed that bath application of NMDA could induce burst firing; however, additional hyperpolarization was required to unmask burst firing. The Na-K-ATPase channel blocker ouabain abolished burst firing, so a role for the outward electrogenic Na-K pump current in burst termination was hypothesized (a role of the Na-K-ATPase in activating K-ATP channels was not investigated). Burst firing often depends on a regime in which positive feedback leads to regenerative depolarization at the beginning of a burst and regenerative hyperpolarization at the end of a burst. If the neuron remains too depolarized, the outward currents never get the upper hand to start the regenerative hyperpolarization (Canavier 1999). This explains why hyperpolarizing current injection was required to unmask bursting in vitro (Johnson et al. 1992) and why the K-ATP channel opener NN414 was required to observe burst firing (Schiemann et al. 2012). Figure 7, C and D, show that phasic and tonic GABAergic inhibition can facilitate burst firing in vivo by helping the outward currents reach a level sufficient to engage the mechanism for regenerative hyperpolarization that terminates a burst. In addition to the K-ATP current and the electrogenic sodium pump, several other currents have been hypothesized to contribute to burst termination in DA neurons, including the M-type K+ current (Drion et al. 2010), the small-conductance (SK) Ca2+-activated K+ current (Amini et al. 1999), and the ether-à-go-go-related (ERG) K+ current (Ji et al. 2012). It is likely that the relative contribution of different outward currents to burst termination varies between subpopulations.
Role of SK vs. K-ATP in Bursts
The burst firing observed by Johnson et al. is likely distinct from that observed by Schiemann et al. (2012), because two of three neurons in their studies did not exhibit burst firing unless the SK channel blocker apamin was also applied (Seutin et al. 1993). The SK and K-ATP channels are both K+ channels gated by Ca2+, the former directly via calmodulin-mediated gating of the channel and the latter indirectly via metabolic coupling, yet they have opposite effects on burst firing in DA cells: the K-ATP channel promotes bursting (Schiemann et al. 2012), whereas the SK channel inhibits bursting (Drion et al. 2011; Seutin et al. 1993). We (Canavier and Landry 2006; Yu et al. 2014; Yu and Canavier 2015) and others (Drion et al. 2011) have shown that the SK Ca2+-activated K+ channel can inhibit bursting by deactivating currents that would otherwise lead to a more sustained depolarization, which could support a burst of multiple action potentials rather than just one. In contrast, the Ca2+ dependence of the K-ATP channel is delayed because of the intermediate dependence on ADP concentration and requires accumulation with multiple spikes to produce bursting. This difference in dynamics could explain the opposite effects of these currents on burst firing.
Stochastic Dynamics
In contrast to the regular bursting observed in Fig. 4, Schiemann et al. (2012) observed irregular rather than regular bursting in vitro. In the same study, regular bursting in vivo was selectively observed in CB+ SN DA neurons, which only constitute <20% of DA neurons within the SN (Liang et al. 1996); the regular bursting in Fig. 4 therefore may be more characteristic of CB+ neurons. For the irregular bursting observed in vitro, whole cell recordings were utilized, which allowed ADP and ATP washout of the cell, as well as changes in intrinsic calcium buffering. The irregular firing that was observed in vitro could therefore be due to this dialysis, to chaotic activity, or to stochastic channel openings. In Fig. 2, K-ATP channel openings are stochastic. We can estimate a total conductance of 2.4 nS from the 120-pA ATP washout current (Fig. 3) in the presence of a driving force of −50 mV (see methods). With our estimate of a single-channel conductance of 60 pS, this gives ∼40 open channels for this level of ATP washout current. Taking into account the Popen in the absence of nucleotide (0.15–0.37) (Proks et al. 2010; Vedovato et al. 2015), we can estimate the number of channels per neuron to be ~100–200. The law of large numbers is not likely to apply in this case; therefore we think it is likely that a stochastic model of the K-ATP channel would be required to accurately replicate the irregular bursting activity observed in vitro; however, the deterministic dynamics of the present model make the underlying mechanisms easier to discern.
CB+ vs. CB− SN DA Neurons
CB+ SN DA neurons have been consistently shown to preferentially survive the neurodegeneration in PD and in PD model systems compared with CB− SN DA neurons (German et al. 1992; Okamura et al. 1995; Rodríguez et al. 2001; Yamada et al. 1990). Here, we assume that CB+ SN DA neurons have a greater concentration of Ca2+ buffer, in line with the calbindin-established function as a Ca2+ buffering protein. We show (Fig. 8, A vs. B) that high buffering capacity promotes regular bursting, consistent with the observation that only CB+ SN DA neurons exhibited regular rhythmic burst firing in vivo (Schiemann et al. 2012). Although there may be other neuroprotective mechanisms operating in CB+ neurons (Canavier et al. 2016), the postulated higher buffering capacity may contribute to both the rhythmic, oscillatory bursting mode and their increased survival rate. Moreover, the rhythmic (bursty-oscillatory) form of repetitive burst firing observed in CB+ neurons in vivo (Schiemann et al. 2012) is sustained, (Fig. 8B1) and may therefore carry information about behavioral states (e.g., being in a novel environment) rather than single salient events such as unexpected reward delivery. Conversely, the lack of a sustained bursting mode in CB− populations may provide increased sensitivity to immediate stimuli and may therefore be more attuned to immediate reward signaling than behavioral states.
The major calcium-binding proteins in nigral DA neurons are thought to be calmodulin, calbindin, and calretinin (Hurley et al. 2013) There is heterogeneity in the expression of the proteins. For example, DA neurons expressing calretinin were mainly distributed in the dorsal SN pars compacta of mice, and <8% of the tyrosine hydroxylase-positive neurons were double labeled for calretinin (Yi et al. 2016). Similarly, CB+ DA neurons were located primarily in the dorsal tier and the CB− DA neurons in the ventral tier of the SN pars compacta in mice (Evans et al. 2017). Differential expression of the calcium-binding proteins correlates with differences in electrical activity (Evans et al. 2017) as well as with differential vulnerability in PD (Yi et al. 2016). The relative contributions of these three calcium-binding proteins to the buffering capacity of nigral DA neurons is not known but clearly must vary between subpopulations.
Role of Medial vs. Lateral Nigra
DA SN neurons in the medial SN project mainly to the dorsomedial striatum, while those in the lateral SN project predominantly to the dorsolateral striatum (Haber et al. 2000). The dorsomedial striatum is thought to play a role in goal-directed behavior, whereas the dorsolateral striatum is more closely associated with habitual acts (Yin and Knowlton 2006). The selective role of the medial nigra in novelty-induced exploration is consistent with a similar specialization for goal-directed vs. habitual activity in dopaminergic neurons of the medial vs. lateral nigra.
The expression of the K-ATP channel does not differ between the medial and lateral nigra (Liss et al. 2005). Therefore, the prevalence of K-ATP-mediated, novelty-induced bursting only in the medial nigra may indicate that, as in Fig. 8C, ADP clearance is slower in the medial SN DA neurons compared with those in the lateral SN, although there are at this time no data to support this hypothesis. Alternatively, there may be differences in colocalization of the K-ATP channel with ATP-consuming Ca2+-sensitive processes, also leading to differential kinetics of this channel in the two populations. Yet another possible explanation suggested by Fig. 7 is that other outward currents in lateral cells are sufficient for bursting in the presence of NMDA receptor activation without the need for a contribution of K-ATP.
Targeted Interventions
The theoretical framework guiding this research posits that SN DA neurons are diverse in their afferents, their projections, and their bursting mechanisms. Therefore the optimal burst-inducing stimuli likely differ between populations. Moreover, bursting in different subpopulations likely encodes different signals. Disordered dopaminergic signaling has been implicated in schizophrenia, addiction, PD, and attention deficit disorder. The long-term goal of describing diversity in dopaminergic signaling is to pave the way for the development of therapeutics targeted to specific types of burst signaling in distinct populations.
GRANTS
This work was funded by National Institutes of Health Grants R01 NS-61097 and R01 DA-041705 and a grant from the Alcohol and Drug Abuse Center of Excellence (ADACE) at the Louisiana State University Health Sciences Center to C. C. Canavier as well as by a CRC 1080 Deutsche Forschungsgemeinschaft grant to J. Roeper.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
C.J.K., S.K., J.R., and C.C.C. conceived and designed research; C.J.K., S.K., J.R., and C.C.C. performed experiments; C.J.K., S.K., J.R., and C.C.C. analyzed data; C.J.K., S.K., J.R., and C.C.C. interpreted results of experiments; C.J.K., S.K., J.R., and C.C.C. prepared figures; C.J.K., J.R., and C.C.C. drafted manuscript; C.J.K., J.R., and C.C.C. edited and revised manuscript; C.J.K., S.K., J.R., and C.C.C. approved final version of manuscript.
REFERENCES
- Ainscow EK, Mirshamsi S, Tang T, Ashford ML, Rutter GA. Dynamic imaging of free cytosolic ATP concentration during fuel sensing by rat hypothalamic neurones: evidence for ATP-independent control of ATP-sensitive K+ channels. J Physiol 544: 429–445, 2002. doi: 10.1113/jphysiol.2002.022434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aittoniemi J, Fotinou C, Craig TJ, de Wet H, Proks P, Ashcroft FM. SUR1: a unique ATP-binding cassette protein that functions as an ion channel regulator. Philos Trans R Soc Lond B Biol Sci 364: 257–267, 2009. doi: 10.1098/rstb.2008.0142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amini B, Clark JW Jr, Canavier CC. Calcium dynamics underlying pacemaker-like and burst firing oscillations in midbrain dopaminergic neurons: a computational study. J Neurophysiol 82: 2249–2261, 1999. [DOI] [PubMed] [Google Scholar]
- Ashcroft FM, Gribble FM. New windows on the mechanism of action of KATP channel openers. Trends Pharmacol Sci 21: 439–445, 2000. doi: 10.1016/S0165-6147(00)01563-7. [DOI] [PubMed] [Google Scholar]
- Bean BP. Neurophysiology: stressful pacemaking. Nature 447: 1059–1060, 2007. doi: 10.1038/4471059a. [DOI] [PubMed] [Google Scholar]
- Berridge KC. The debate over dopamine’s role in reward: the case for incentive salience. Psychopharmacology (Berl) 191: 391–431, 2007. doi: 10.1007/s00213-006-0578-x. [DOI] [PubMed] [Google Scholar]
- Bromberg-Martin ES, Matsumoto M, Hikosaka O. Dopamine in motivational control: rewarding, aversive, and alerting. Neuron 68: 815–834, 2010. doi: 10.1016/j.neuron.2010.11.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burke MA, Mutharasan RK, Ardehali H. The sulfonylurea receptor, an atypical ATP-binding cassette protein, and its regulation of the KATP channel. Circ Res 102: 164–176, 2008. doi: 10.1161/CIRCRESAHA.107.165324. [DOI] [PubMed] [Google Scholar]
- Butera RJ., Jr Multirhythmic bursting. Chaos 8: 274–284, 1998. doi: 10.1063/1.166358. [DOI] [PubMed] [Google Scholar]
- Canavier CC. Sodium dynamics underlying burst firing and putative mechanisms for the regulation of the firing pattern in midbrain dopamine neurons: a computational approach. J Comput Neurosci 6: 49–69, 1999. doi: 10.1023/A:1008809000182. [DOI] [PubMed] [Google Scholar]
- Canavier CC, Baxter DA, Clark JW, Byrne JH. Nonlinear dynamics in a model neuron provide a novel mechanism for transient synaptic inputs to produce long-term alterations of postsynaptic activity. J Neurophysiol 69: 2252–2257, 1993. [DOI] [PubMed] [Google Scholar]
- Canavier CC, Baxter DA, Clark JW, Byrne JH. Multiple modes of activity in a model neuron suggest a novel mechanism for the effects of neuromodulators. J Neurophysiol 72: 872–882, 1994. [DOI] [PubMed] [Google Scholar]
- Canavier CC, Clark JW, Byrne JH. Routes to chaos in a model of a bursting neuron. Biophys J 57: 1245–1251, 1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canavier CC, Evans RC, Oster AM, Pissadaki EK, Drion G, Kuznetsov AS, Gutkin BS. Implications of cellular models of dopamine neurons for disease. J Neurophysiol 116: 2815–2830, 2016. doi: 10.1152/jn.00530.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canavier CC, Landry RS. An increase in AMPA and a decrease in SK conductance increase burst firing by different mechanisms in a model of a dopamine neuron in vivo. J Neurophysiol 96: 2549–2563, 2006. doi: 10.1152/jn.00704.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan CS, Guzman JN, Ilijic E, Mercer JN, Rick C, Tkatch T, Meredith GE, Surmeier DJ. “Rejuvenation” protects neurons in mouse models of Parkinson’s disease. Nature 447: 1081–1086, 2007. doi: 10.1038/nature05865. [DOI] [PubMed] [Google Scholar]
- Dabrowski M, Larsen T, Ashcroft FM, Bondo Hansen J, Wahl P. Potent and selective activation of the pancreatic beta-cell type KATP channel by two novel diazoxide analogues. Diabetologia 46: 1375–1382, 2003. doi: 10.1007/s00125-003-1198-1. [DOI] [PubMed] [Google Scholar]
- Dragicevic E, Poetschke C, Duda J, Schlaudraff F, Lammel S, Schiemann J, Fauler M, Hetzel A, Watanabe M, Lujan R, Malenka RC, Striessnig J, Liss B. Cav1.3 channels control D2-autoreceptor responses via NCS-1 in substantia nigra dopamine neurons. Brain 137: 2287–2302, 2014. doi: 10.1093/brain/awu131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drion G, Bonjean M, Waroux O, Scuvée-Moreau J, Liégeois JF, Sejnowski TJ, Sepulchre R, Seutin V. M-type channels selectively control bursting in rat dopaminergic neurons. Eur J Neurosci 31: 827–835, 2010. doi: 10.1111/j.1460-9568.2010.07107.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drion G, Massotte L, Sepulchre R, Seutin V. How modeling can reconcile apparently discrepant experimental results: the case of pacemaking in dopaminergic neurons. PLoS Comput Biol 7: e1002050, 2011. doi: 10.1371/journal.pcbi.1002050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans RC, Zhu M, Khaliq ZM. Dopamine inhibition differentially controls excitability of substantia nigra dopamine neuron subpopulations through T-type calcium channels. J Neurosci 37: 3704–3720, 2017. doi: 10.1523/JNEUROSCI.0117-17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foehring RC, Zhang XF, Lee JC, Callaway JC. Endogenous calcium buffering capacity of substantia nigral dopamine neurons. J Neurophysiol 102: 2326–2333, 2009. doi: 10.1152/jn.00038.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gadagkar V, Puzerey PA, Chen R, Baird-Daniel E, Farhang AR, Goldberg JH. Dopamine neurons encode performance error in singing birds. Science 354: 1278–1282, 2016. doi: 10.1126/science.aah6837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- German DC, Manaye KF, Sonsalla PK, Brooks BA. Midbrain dopaminergic cell loss in Parkinson’s disease and MPTP-induced parkinsonism: sparing of calbindin-D28k-containing cells. Ann NY Acad Sci 648: 42–62, 1992. doi: 10.1111/j.1749-6632.1992.tb24523.x. [DOI] [PubMed] [Google Scholar]
- Grace AA, Onn SP. Morphology and electrophysiological properties of immunocytochemically identified rat dopamine neurons recorded in vitro. J Neurosci 9: 3463–3481, 1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haber SN, Fudge JL, McFarland NR. Striatonigrostriatal pathways in primates form an ascending spiral from the shell to the dorsolateral striatum. J Neurosci 20: 2369–2382, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haller M, Mironov SL, Karschin A, Richter DW. Dynamic activation of KATP channels in rhythmically active neurons. J Physiol 537: 69–81, 2001. doi: 10.1111/j.1469-7793.2001.0069k.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol 117: 500–544, 1952. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurley MJ, Brandon B, Gentleman SM, Dexter DT. Parkinson’s disease is associated with altered expression of CaV1 channels and calcium-binding proteins. Brain 136: 2077–2097, 2013. doi: 10.1093/brain/awt134. [DOI] [PubMed] [Google Scholar]
- Hyland BI, Reynolds JN, Hay J, Perk CG, Miller R. Firing modes of midbrain dopamine cells in the freely moving rat. Neuroscience 114: 475–492, 2002. doi: 10.1016/S0306-4522(02)00267-1. [DOI] [PubMed] [Google Scholar]
- Ji H, Tucker KR, Putzier I, Huertas MA, Horn JP, Canavier CC, Levitan ES, Shepard PD. Functional characterization of ether-à-go-go-related gene potassium channels in midbrain dopamine neurons—implications for a role in depolarization block. Eur J Neurosci 36: 2906–2916, 2012. doi: 10.1111/j.1460-9568.2012.08190.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin X, Costa RM. Start/stop signals emerge in nigrostriatal circuits during sequence learning. Nature 466: 457–462, 2010. doi: 10.1038/nature09263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson SW, Seutin V, North RA. Burst firing in dopamine neurons induced by N-methyl-d-aspartate: role of electrogenic sodium pump. Science 258: 665–667, 1992. doi: 10.1126/science.1329209. [DOI] [PubMed] [Google Scholar]
- Kanno T, Rorsman P, Göpel SO. Glucose-dependent regulation of rhythmic action potential firing in pancreatic β-cells by KATP-channel modulation. J Physiol 545: 501–507, 2002. doi: 10.1113/jphysiol.2002.031344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang CL, Sinton CM, Sonsalla PK, German DC. Midbrain dopaminergic neurons in the mouse that contain calbindin-D28k exhibit reduced vulnerability to MPTP-induced neurodegeneration. Neurodegeneration 5: 313–318, 1996. doi: 10.1006/neur.1996.0042. [DOI] [PubMed] [Google Scholar]
- Liss B, Haeckel O, Wildmann J, Miki T, Seino S, Roeper J. K-ATP channels promote the differential degeneration of dopaminergic midbrain neurons. Nat Neurosci 8: 1742–1751, 2005. doi: 10.1038/nn1570. [DOI] [PubMed] [Google Scholar]
- Miki T, Nagashima K, Tashiro F, Kotake K, Yoshitomi H, Tamamoto A, Gonoi T, Iwanaga T, Miyazaki J, Seino S. Defective insulin secretion and enhanced insulin action in KATP channel-deficient mice. Proc Natl Acad Sci USA 95: 10402–10406, 1998. doi: 10.1073/pnas.95.18.10402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okamura H, Yokoyama C, Ibata Y. Lateromedial gradient of the susceptibility of midbrain dopaminergic neurons to neonatal 6-hydroxydopamine toxicity. Exp Neurol 136: 136–142, 1995. doi: 10.1006/exnr.1995.1090. [DOI] [PubMed] [Google Scholar]
- Ortner NJ, Striessnig J. L-type calcium channels as drug targets in CNS disorders. Channels (Austin) 10: 7–13, 2016. doi: 10.1080/19336950.2015.1048936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Proks P, Ashcroft FM. Modeling KATP channel gating and its regulation. Prog Biophys Mol Biol 99: 7–19, 2009. doi: 10.1016/j.pbiomolbio.2008.10.002. [DOI] [PubMed] [Google Scholar]
- Proks P, de Wet H, Ashcroft FM. Activation of the KATP channel by Mg-nucleotide interaction with SUR1. J Gen Physiol 136: 389–405, 2010. doi: 10.1085/jgp.201010475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puopolo M, Raviola E, Bean BP. Roles of subthreshold calcium current and sodium current in spontaneous firing of mouse midbrain dopamine neurons. J Neurosci 27: 645–656, 2007. doi: 10.1523/JNEUROSCI.4341-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodríguez M, Barroso-Chinea P, Abdala P, Obeso J, González-Hernández T. Dopamine cell degeneration induced by intraventricular administration of 6-hydroxydopamine in the rat: similarities with cell loss in Parkinson’s disease. Exp Neurol 169: 163–181, 2001. doi: 10.1006/exnr.2000.7624. [DOI] [PubMed] [Google Scholar]
- Roeper J. Dissecting the diversity of midbrain dopamine neurons. Trends Neurosci 36: 336–342, 2013. doi: 10.1016/j.tins.2013.03.003. [DOI] [PubMed] [Google Scholar]
- Schiemann J, Schlaudraff F, Klose V, Bingmer M, Seino S, Magill PJ, Zaghloul KA, Schneider G, Liss B, Roeper J. K-ATP channels in dopamine substantia nigra neurons control bursting and novelty-induced exploration. Nat Neurosci 15: 1272–1280, 2012. doi: 10.1038/nn.3185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultz W. Predictive reward signal of dopamine neurons. J Neurophysiol 80: 1–27, 1998. [DOI] [PubMed] [Google Scholar]
- Schultz W. Multiple dopamine functions at different time courses. Annu Rev Neurosci 30: 259–288, 2007. doi: 10.1146/annurev.neuro.28.061604.135722. [DOI] [PubMed] [Google Scholar]
- Seutin V, Johnson SW, North RA. Apamin increases NMDA-induced burst-firing of rat mesencephalic dopamine neurons. Brain Res 630: 341–344, 1993. doi: 10.1016/0006-8993(93)90675-D. [DOI] [PubMed] [Google Scholar]
- Shen KZ, Johnson SW. Ca2+ influx through NMDA-gated channels activates ATP-sensitive K+ currents through a nitric oxide-cGMP pathway in subthalamic neurons. J Neurosci 30: 1882–1893, 2010. doi: 10.1523/JNEUROSCI.3200-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Somers D, Kopell N. Rapid synchronization through fast threshold modulation. Biol Cybern 68: 393–407, 1993. doi: 10.1007/BF00198772. [DOI] [PubMed] [Google Scholar]
- Surmeier DJ, Guzman JN, Sanchez J, Schumacker PT. Physiological phenotype and vulnerability in Parkinson’s disease. Cold Spring Harb Perspect Med 2: a009290, 2012. doi: 10.1101/cshperspect.a009290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Surmeier DJ, Guzman JN, Sanchez-Padilla J. Calcium, cellular aging, and selective neuronal vulnerability in Parkinson’s disease. Cell Calcium 47: 175–182, 2010. doi: 10.1016/j.ceca.2009.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Surmeier DJ, Guzman JN, Sanchez-Padilla J, Goldberg JA. The origins of oxidant stress in Parkinson’s disease and therapeutic strategies. Antioxid Redox Signal 14: 1289–1301, 2011. doi: 10.1089/ars.2010.3521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Surmeier DJ, Schumacker PT, Guzman JD, Ilijic E, Yang B, Zampese E. Calcium and Parkinson’s disease. Biochem Biophys Res Commun 483: 1013–1019, 2017. doi: 10.1016/j.bbrc.2016.08.168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanner GR, Lutas A, Martínez-François JR, Yellen G. Single KATP channel opening in response to action potential firing in mouse dentate granule neurons. J Neurosci 31: 8689–8696, 2011. doi: 10.1523/JNEUROSCI.5951-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tantama M, Martínez-François JR, Mongeon R, Yellen G. Imaging energy status in live cells with a fluorescent biosensor of the intracellular ATP-to-ADP ratio. Nat Commun 4: 2550, 2013. doi: 10.1038/ncomms3550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Pol B. On “relaxation-oscillations”. Lond Edinb Dubl Philos Mag J Sci 2: 978–992, 1926. doi: 10.1080/14786442608564127. [DOI] [Google Scholar]
- Vedovato N, Ashcroft FM, Puljung MC. The nucleotide-binding sites of SUR1: a mechanistic model. Biophys J 109: 2452–2460, 2015. doi: 10.1016/j.bpj.2015.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vetter P, Roth A, Häusser M. Propagation of action potentials in dendrites depends on dendritic morphology. J Neurophysiol 85: 926–937, 2001. [DOI] [PubMed] [Google Scholar]
- Watts M, Tabak J, Bertram R. Mathematical modeling demonstrates how multiple slow processes can provide adjustable control of islet bursting. Islets 3: 320–326, 2011. doi: 10.4161/isl.3.6.17636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson CJ, Callaway JC. Coupled oscillator model of the dopaminergic neuron of the substantia nigra. J Neurophysiol 83: 3084–3100, 2000. [DOI] [PubMed] [Google Scholar]
- Yamada T, McGeer PL, Baimbridge KG, McGeer EG. Relative sparing in Parkinson’s disease of substantia nigra dopamine neurons containing calbindin-D28K. Brain Res 526: 303–307, 1990. doi: 10.1016/0006-8993(90)91236-A. [DOI] [PubMed] [Google Scholar]
- Yi H, Bao X, Tang X, Fan X, Xu H. Estrogen modulation of calretinin and BDNF expression in midbrain dopaminergic neurons of ovariectomised mice. J Chem Neuroanat 77: 60–67, 2016. doi: 10.1016/j.jchemneu.2016.05.005. [DOI] [PubMed] [Google Scholar]
- Yin HH, Knowlton BJ. The role of the basal ganglia in habit formation. Nat Rev Neurosci 7: 464–476, 2006. doi: 10.1038/nrn1919. [DOI] [PubMed] [Google Scholar]
- Yu N, Canavier CC. A mathematical model of a midbrain dopamine neuron identifies two slow variables likely responsible for bursts evoked by SK channel antagonists and terminated by depolarization block. J Math Neurosci 5: 5, 2015. doi: 10.1186/s13408-015-0017-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu N, Tucker KR, Levitan ES, Shepard PD, Canavier CC. Implications of cellular models of dopamine neurons for schizophrenia. Prog Mol Biol Transl Sci 123: 53–82, 2014. doi: 10.1016/B978-0-12-397897-4.00011-5. [DOI] [PMC free article] [PubMed] [Google Scholar]