State-dependent rhythmogenesis and frequency control in a half-center locomotor CPG

Abstract

The spinal locomotor central pattern generator (CPG) generates rhythmic activity with alternating flexion and extension phases. This rhythmic pattern is likely to result from inhibitory interactions between neural populations representing flexor and extensor half-centers. However, it is unclear whether the flexor-extensor CPG has a quasi-symmetric organization with both half-centers critically involved in rhythm generation, features an asymmetric organization with flexor-driven rhythmogenesis, or comprises a pair of intrinsically rhythmic half-centers. There are experimental data that support each of the above concepts but appear to be inconsistent with the others. In this theoretical/modeling study, we present and analyze a CPG model architecture that can operate in different regimes consistent with the above three concepts depending on conditions, which are defined by external excitatory drives to CPG half-centers. We show that control of frequency and phase durations within each regime depends on network dynamics, defined by the regime-dependent expression of the half-centers' intrinsic rhythmic capabilities and the operating phase transition mechanisms (escape vs. release). Our study suggests state dependency in locomotor CPG operation and proposes explanations for seemingly contradictory experimental data.

NEW & NOTEWORTHY Our theoretical/modeling study focuses on the analysis of locomotor central pattern generators (CPGs) composed of conditionally bursting half-centers coupled with reciprocal inhibition and receiving independent external drives. We show that this CPG framework can operate in several regimes consistent with seemingly contradictory experimental data. In each regime, we study how intrinsic dynamics and phase-switching mechanisms control oscillation frequency and phase durations. Our results provide insights into the organization of spinal circuits controlling locomotion.

INTRODUCTION

Locomotor dynamics in limbed animals relies on the rhythmic alternation of flexor and extensor activity in each limb. It is well established that the basic flexion-extension alternating rhythmic pattern can be generated within the spinal cord; without rhythmic supraspinal or afferent inputs, by specially organized neural circuits called central pattern generators (CPGs) (Brown 1914; Grillner 1985, 2006). It is commonly accepted that the alternating flexor-extensor rhythmic activity generated by the CPG involves reciprocal inhibitory interactions between neural populations that represent flexor and extensor half-centers. However, the exact organization of the CPG circuit within the spinal cord and the mechanisms responsible for the rhythmogenesis and control of locomotor pattern and frequency remain largely unknown. A large body of experimental work completed over the last century or more addresses the organization of CPG circuits in multiple experimental models. The data provided by these studies led to the formulation of multiple general concepts of rhythm generation, each of which aims to provide a framework for a particular subset from the overall collection of seemingly contradictory experimental data.

The first hypothesis on locomotor CPG organization is based on the classical half-center concept originally proposed by Brown (1914). This hypothesis was derived from experiments in which cats with a transected spinal cord and cut dorsal roots demonstrated rhythmic alternating flexor and extensor activity, and the concept was further elaborated by others (Jankowska et al. 1967a, 1967b; Lundberg 1981). According to the classical half-center concept, both half-centers of the CPG do not necessarily exhibit intrinsic bursting capabilities. Alternating oscillations result from reciprocal inhibition between the half-centers combined with an adaptation mechanism that causes a slow reduction of activity in each half-center when it is active, which eventually results in phase switching (for review see McCrea and Rybak 2008; Stuart and Hultborn 2008). This concept suggests a quasi-symmetric organization of flexor and extensor half-centers and a critical importance of mutual inhibition not only for flexor-extensor alternation but for rhythmogenesis per se. Various recent experiments have provided support for the half-center hypothesis. For example, spontaneous or mesencephalic locomotor region (MLR)-evoked fictive locomotion in decerebrate cats can show either extensor or flexor phase dominance (Frigon and Gossard 2009; Yakovenko et al. 2005). Moreover, application of MLR stimulation during spontaneous locomotor episodes in the decerebrate cat could change the frequency of locomotor oscillations and switch the control of cycle period from extensor- to flexor-dominated (Frigon and Gossard 2009). Many additional experimental studies, including those based on fictive locomotion in cats, also support the classical half-center concept (Burke et al. 2001; Kriellaars et al. 1994; Lafreniere-Roula and McCrea 2005; Rybak et al. 2006a, 2006b; Yakovenko et al. 2005).

An alternative, principally asymmetric, flexor-driven concept for CPG organization and operation was proposed by Pearson and Duysens (“swing generator model,” Duysens 2006; Pearson and Duysens 1976; for review see Duysens et al. 2013) and used in a series of recent models (Danner et al. 2016, 2017; Shevtsova et al. 2015; Shevtsova and Rybak 2016; Zhong et al. 2012). In this concept, the flexor half-center is intrinsically rhythmic, unlike the extensor half-center, which exhibits rhythmic activity due to the rhythmic inhibition that it receives from the flexor half-center.

Recent studies in the isolated rodent spinal cord with drug-induced fictive locomotion have supported the notion of asymmetric flexor-dominated organization. Evidence comes for example from the existence of two types of nonresetting deletions: missing bursts in the flexor-dominated ventral root (L2) are accompanied by sustained activity in the ipsilateral extensor-dominated root (L5), whereas missing extensor bursts usually occur without obvious disturbances of the ipsilateral flexor rhythmic activity (Zhong et al. 2012). Furthermore, the responses of flexor and extensor phase durations to an increase in oscillation frequency during drug-evoked fictive locomotion in the isolated mouse spinal cord are asymmetric, such that the duration of the flexor phase changes much less than the duration of the extensor phase (Shevtsova et al. 2015; Talpalar et al. 2013), which also fits with similar phase measurements performed in cats in vivo (Frigon and Gossard 2009; Halbertsma 1983).

Finally, recent work has provided evidence that both flexor and extensor half-centers possess intrinsic rhythmogenic capabilities and can autonomously generate rhythmic activity (Hägglund et al. 2013). In the case when each half-center generates independent bursting, the role of mutual inhibition between half-centers is limited to ensuring coordinated alternation of flexor and extensor bursts.

Interestingly, each of the above conceptual frameworks has been explicitly or implicitly supported by particular sets of experimental data but cannot account for other data sets. One possible explanation for this disparity is that these different data were obtained using different experimental preparations (such as intact, in vivo, anesthetized, or decerebrate animals; different spinal preparations with or without limb movements; or the isolated spinal cord) or were obtained under different conditions with different methods used to evoke locomotor-like rhythmic activity (e.g., spontaneous, brain stem stimulation-evoked, or drug-evoked). The main aim of this study is to unify these experimental findings by suggesting that all of the mechanisms described above may operate in the same CPG, being engaged under different conditions. An important principle contributing to this unification, and a major message of this work, is that once half-center units are coupled into a network, their intrinsic dynamic properties may become overshadowed by emergent transition mechanisms that control switches between active and silent phases, and the same transition mechanisms can operate across synaptic pairings of units with different forms of intrinsic dynamics. At the same time, the units’ intrinsic dynamics may contribute to constrain which emergent mechanisms arise in the network.

We illustrate these principles using two distinct CPG models: 1) a population-based model with the flexor and extensor half-centers represented by populations of neurons with intrinsic bursting capabilities (modeled in the Hodgkin-Huxley style) and sparse excitatory interactions, which mutually inhibit each other via corresponding inhibitory populations, and 2) a reduced model, in which both half-center populations, again with conditional bursting properties, are represented by single nonspiking units that are coupled with mutual inhibition. The second model is used for qualitative analysis of the system dynamics. In both cases, oscillations are based on the slowly inactivating persistent sodium current (I_NaP). Due to the intrinsic rhythmogenic mechanism in each half-center, in the absence of coupling, an increase of excitatory drive causes a sequential transition from silence to rhythmic bursting and then to sustained (tonic) activity. Therefore, in both models, by changing drives to each half-center we could induce all three half-center mechanisms and analyze the transitions between them and the control of oscillation frequency and burst durations in each regime. In both models, stable rhythmic activity could occur in both symmetric and asymmetric networks. However, our analysis of the reduced model reveals that the changes in the oscillation frequency with changes in the excitatory drive to one or both half-centers or with changes in the strength of synaptic inhibition depend on the escape and release mechanisms that govern transitions between active and silent phases of each half-center within the network rhythm. Our study shows that even a simple half-center CPG can operate in multiple different regimes, which can explain some seemingly contradictory experimental data.

METHODS

Population Model

We implemented a population model of the CPG that consisted of two populations of excitatory neurons representing flexor (F) and extensor (E) half-centers that reciprocally inhibited each other via two populations of inhibitory interneurons, In-F and In-E (Fig. 1A). Each half-center population consisted of 200 neurons with intrinsic bursting properties and sparse excitatory synaptic interactions within the population; each inhibitory population comprised 100 inhibitory neurons without intrinsic bursting capabilities and mutual interactions. The number of neurons in the populations was selected to provide a reasonable compromise between the reproducibility of the simulation results (due to randomly distributed parameters) and simulation time. The number of neurons in the half-center populations was increased to 200 because of the low probability of interconnections within these populations (p = 0.1; see Table 1).

Fig. 1.

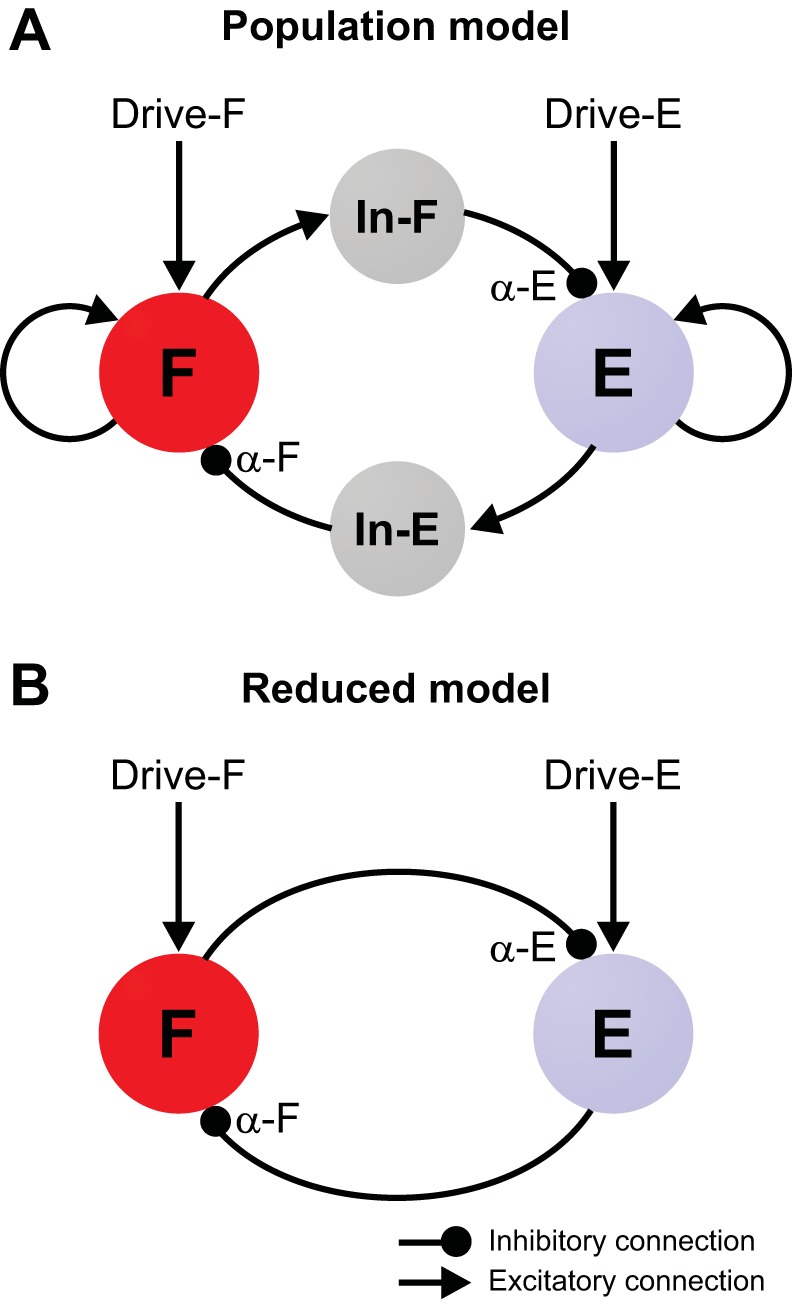
Model schematics. A: in the population model, the flexor (F) and extensor (E) half-centers represent populations of 200 neurons with I_NaP-dependent bursting properties and sparse mutually excitatory interconnections. These half-centers inhibit each other via corresponding populations of inhibitory neurons (In-E and In-F) each consisting of 100 neurons. α-F and α-E denote the overall strength of the mutual inhibition to each flexor and extensor neuron, respectively. Each half-center receives tonic external drive (Drive-F/E). All neurons are modeled in the Hodgkin-Huxley style (see methods). B: in the reduced model, the flexor and extensor half-centers are represented by two activity-based (nonspiking) units that mutually inhibit each other.

Table 1.

Steady-state functions for voltage-dependent activation and inactivation of ion channels and other parameter values for the two models

Ion channels
Fast sodium (Na)	m∞Na = {1 + exp[−(V + 34)/7.8]}−1
	τmNa = 0 ms
	h∞Na = {1 + exp[(V + 55)/7]}−1
	τhNa = 10/{exp[(V + 50)/15] + exp[−(V + 50)/16]} ms
	ḡNa = 500 nS
Persistent sodium (NaP)	m∞NaP = {1 + exp[−(V + 40)/6]}−1
	τmNaP = 0 ms
	h∞NaP = {1 + exp[(V + 55)/12]}−1
	τhNaP = 4,000/cosh[(V + 55)/24] ms
	ḡNaP = 5 nS
Potassium rectifier (K)	m∞K = {1 + exp[−(V + 28)/4]}−1
	τmK = 3.5/cosh[(V + 40)/40] ms
	ḡK = 40 nS
Leak (L)	gL = 2.8 nS
Neuron parameters
Reversal potentials	ENa = 50 mV; EK = −80 mV; ESynI = −75 mV
	Population model: ESynE = −10 mV; EL = −65 ± 0.325 mV
	Reduced model: ESynE = 0 mV; EL = −62.5 mV
Membrane capacitance	C = 20 pF
Synaptic/network parameters
Synaptic parameters	Population model ḡE = ḡI = 0.1 nS; τSynE = τSynI = 5 ms
	Reduced model: ḡSynE = ḡSynI = 1 nS; θ = 25 mV; σ = 5 mV
Synaptic connections	Population model (wji = w̄ji ± SD):
	F to F: 0.075 ± 0.00375, p = 0.1
	F to In-F: 0.175 ± 0.00875, p = 1
	E to E: 0.075 ± 0.00375, p = 0.1
	E to In-E: 0.175 ± 0.00875, p = 1
	In-F to E: 0.05 ± 0.005, p = 1 ($\Rightarrow$α-E = 5)
	In-E to F: 0.05 ± 0.005, p = 1 ($\Rightarrow$α-F = 5)
	Reduced model: α-F = α-E = 1

Parameter values are identical for the two models unless otherwise indicated. See methods for definitions.

All neurons were modeled in the Hodgkin-Huxley style. Each half-center population received a separate external excitatory drive (same as the other half-center or different), which defined whether the half-center when uncoupled generated rhythmic bursting or exhibited sustained activity. All neurons were silent at their respective resting potentials (see Table 1) when isolated.

All neurons in the population model were modeled as single-compartment neurons using Hodgkin-Huxley formal descriptions. The evolution of the neuronal membrane potential (V) of each neuron in the flexor (F) and extensor (E) populations was governed by the equation

$$C·\frac{\text{d}V}{\text{d}t}=-I_{Na}-I_{NaP}-I_K-I_L-I_{SynE}-I_{SynI},$$ (1)

with C representing membrane capacitance and t denoting time.

The evolution of the membrane potential of each neuron in each inhibitory population (In-F or In-E) was described by

$$C·\frac{dV}{dt}=-I_{Na}-I_K-I_L-I_{SynE}-I_{SynI}\mathrm{.}$$ (2)

The ionic currents on the right-hand sides of Eqs. 1 and 2 are fast sodium (I_Na), persistent (slowly inactivating) sodium (I_NaP) (not present in the inhibitory neurons), delayed rectifier potassium (I_K), and leak (I_L) currents. These currents were defined as

$$I_{Na}={\overline{g}}_{Na}·m_{Na}^3·h_{Na}·\left(V-E_{Na}\right);$$

$$I_{NaP}={\overline{g}}_{NaP}·m_{NaP}·h_{NaP}·\left(V-E_{Na}\right);$$ (3)

$$I_K={\overline{g}}_K·m_K^4·\left(V-E_K\right);\hspace{0.17em}{I}_L=g_L·\left(V-E_L\right),$$

where ḡ_x denotes the maximum conductance, E_X is the reversal potential, m_X is the activation variable, and h_X is the inactivation variable for the corresponding ionic current I_X.

Activation m_X and inactivation h_X of voltage-dependent ion channels in Eq. 3 evolved under the equations

$${\tau }_{mX}\left(V\right)·\frac{d}{dt}{m}_X=m_{\infty X}\left(V\right)-m_X;$$

$${\tau }_{hC}\left(V\right)·\frac{d}{dt}{h}_X=h_{\infty X}\left(V\right)-h_X,$$ (4)

where m_∞X(V) and h_∞X(V) denote the voltage-dependent steady-state activation and inactivation of the channel I_X, respectively. τ_mX(V) and τ_hX(V) define the corresponding time constants. Sodium channel activation was considered to be instantaneous (τ_mNa = τ_mNaP = 0). The expressions for the channel kinetics and model parameters (given in Table 1) were based on our previously published models (Rybak et al. 2006a, 2013; Shevtsova and Rybak 2016; Shevtsova et al. 2015).

The excitatory (I_SynE) and inhibitory (I_SynI) synaptic currents were modeled as

$$I_{SynE}=g_{SynE}·\left(V-E_{SynE}\right);$$

$$I_{SynI}=g_{SynI}·\left(V-E_{SynI}\right),$$ (5)

where g_SynE and g_SynI are the conductances and E_SynE and E_SynI the reversal potentials for the excitatory and inhibitory synaptic connections, respectively.

The conductances were equal to zero at rest and were activated by presynaptic input in the following manner:

$$g_{Syn{E}_i}\left(t\right)={\overline{g}}_E·\left[{\displaystyle \sum }_j{w}_{ji}·{\displaystyle \sum }_{t_{kj}<t}\exp \left(-\frac{t-t_{kj}}{{\tau }_{SynE}}\right)+Drive\right];$$

$$g_{Syn{I}_i}\left(t\right)={\overline{g}}_I·{\displaystyle \sum }_j{w}_{ji}·{\displaystyle \sum }_{t_{kj}<t}\exp \left(-\frac{t-t_{kj}}{{\tau }_{SynI}}\right),$$ (6)

where Drive represents the tonic external input that can be either applied to the flexor (Drive-F) or to the extensor (Drive-E). Each action potential at time t_kj from a neuron j of the presynaptic population increases the excitatory synaptic conductance in the postsynaptic neuron i by ḡ_E × w_ji or increases the inhibitory synaptic conductance by ḡ_I × w_ji. ḡ_E and ḡ_I define an increase in the excitatory or inhibitory synaptic conductance, respectively, produced by one arriving action potential at w_ji = 1 or by tonic external input when Drive = 1. τ_SynE and τ_SynI are the decay time constants for g_SynE and g_SynI, respectively. w_ji defines the strength of the synaptic input to the postsynaptic neuron i from the presynaptic neuron j.

Population Model Simulations

Neuronal heterogeneity within the 200 neurons of the rhythm generating (F and E) populations and 100 neurons of the inhibitory (In-F and In-E) populations was provided by randomly selecting values for the leak reversal potential E_L and initial conditions for the membrane potential and channel kinetics variables from Gaussian distributions (see mean values ± SD in Table 1). Results were only considered following an initial simulation period of 15 s to minimize the likelihood of incorporating transient dynamics.

Synaptic connections between the neurons of interacting populations were randomly assigned before each simulation based on a connection probability, p. If a population A was assigned to receive synaptic input from a population B, then each neuron in population A received the corresponding synaptic input from each neuron in population B with the probability p{A, B}. If p{A, B} < 1, then a random number generator was used to determine the existence of each synaptic connection. If p{A, B} = 1, then each neuron in population A received synaptic input from each neuron of population B. The average weights (w̄) ± SD and the probabilities (p) of connections are specified in Table 1.

To investigate the influence of changes in excitatory drives to the flexor and extensor rhythm generating populations (Drive-F and Drive-E, respectively), we ran a set of simulations where we varied the values of Drive-F and Drive-E independently. To study changes in model behavior when varying the strength of inhibitory connections (from In-F to E or from In-E to F) we introduced a parameter α characterizing the total inhibitory influence on a postsynaptic population as defined by α = w̄ × N, where N = 100 (the number of neurons in the inhibitory populations). In some simulations, synaptic strength from the extensor unit to the flexor unit (α-F) and vice versa (α-E) were varied independently or together to study the impact of inhibitory connection strength on oscillation frequency. The default value for this parameter was α = α-F = α-E = 5 (see Table 1) and when it was varied, we kept α ≤ 40. Our choices of α and of drive levels served to stabilize the flexor-extensor symmetric regime at high drives while producing a relatively wide range of oscillation frequencies with changes in α. Mutual interactions between inhibitory populations were not considered.

All simulations were performed using the simulation package NSM 4.0, developed at Drexel University by S. N. Markin, I. A. Rybak, and N. A. Shevtsova. Differential equations were solved using the exponential Euler integration method with a step width of 0.1 ms.

Reduced Model, Phase Planes, and Nullclines

In addition to the population model, we constructed a reduced model of the flexor-extensor rhythm generator, consisting of a flexor (F) and extensor (E) unit, mutually coupled by inhibitory synapses (Fig. 1B). Each unit in the reduced model represents a synchronized neural population (extensor or flexor) and was described by an activity-based (nonspiking) model, in which the unit membrane potential V represents an average voltage for that population and the population’s synaptic output f(V) [0 ≤ f(V) ≤ 1] represents the average or integrated population activity at the corresponding average voltage (Ermentrout 1994). At the same time, we included an explicit representation of some ionic currents into the model. In particular, we incorporated I_NaP to establish rhythmogenic properties of the flexor and extensor unit. The membrane potential V in the reduced model was governed by the equation

$$C·\frac{\text{d}V}{\text{d}t}=-I_{NaP}-I_L-I_{SynE}-I_{SynI},$$ (7)

where C represents the membrane capacitance of the unit and V is the voltage variable. The ionic currents included in this equation are the persistent sodium (I_NaP) and leak (I_L) currents. These currents were defined as in Eq. 3.

As in the population model, the I_NaP channel activation was considered to be instantaneous and the activation variable m_NaP in Eq. 3 was replaced by its steady state m_∞NaP (see Table 1). The inactivation variable h_NaP of the I_NaP channel evolved under the differential equation

$${\tau }_{hNaP}\left(V\right)·\frac{d}{dt}{h}_{NaP}=h_{\infty NaP}\left(V\right)-h_{NaP},$$ (8)

where h_∞NaP represents the voltage-dependent steady-state inactivation and τ_hNaP defines its time constant. The expressions for h_∞NaP and τ_hNaP and the ionic current parameters are given in Table 1.

The excitatory (I_SynE) and inhibitory (I_SynI) synaptic currents in the reduced model were defined as

$$I_{SynE}=g_{SynE}·Drive·\left(V-E_{SynE}\right);$$

$$I_{SynI}=g_{SynI}·\alpha ·f\left(V_{pre}\right)·\left(V-E_{SynI}\right),$$ (9)

where g_SynE and g_SynI are the conductances and E_SynE and E_SynI the reversal potentials for the excitatory and inhibitory synaptic currents, respectively. As in the population model, the tonic external drive was applied as an excitatory synaptic current. The inhibitory synaptic current includes an activation level that depends on the output of the presynaptic unit, f(V_pre), and a synaptic conductance, which was tuned with the strength parameter α. The output function was defined as

$$f\left(V_{pre}\right)={\left[1+\exp \left(-\frac{V_{pre}+\text{Θ}}{\sigma }\right)\right]}^{-1}\mathrm{.}$$ (10)

The function f converts the voltage level of the membrane potential of the presynaptic unit smoothly and instantaneously into a corresponding synaptic activation level.

As with the population model, we ran a series of simulations where we independently varied the strengths of excitatory drives to the flexor and extensor units (which we denoted as Drive-F and Drive-E, respectively). The synaptic strength parameters from the extensor unit to the flexor unit (α-F) or vice versa (α-E) were varied independently or together to study the impact of inhibitory connection strength on oscillation frequency. The default value was α = α-F = α-E = 1 and, when we studied the role of inhibition by varying this parameter, we kept α ≤ 6. Our choices of α and of drive levels served to stabilize the flexor-extensor symmetric regime at high drives while producing a relatively wide range of oscillation frequencies with changes in α.

Simulations of the reduced model unit were performed using the freely available software XPPAUT (Ermentrout 2002), in some cases with subsequent data processing done in MATLAB. In each simulation, an initial 15-s period was discarded, to avoid transient effects. Bifurcation diagrams (Fig. 7) were also generated using XPPAUT.

Fig. 7.

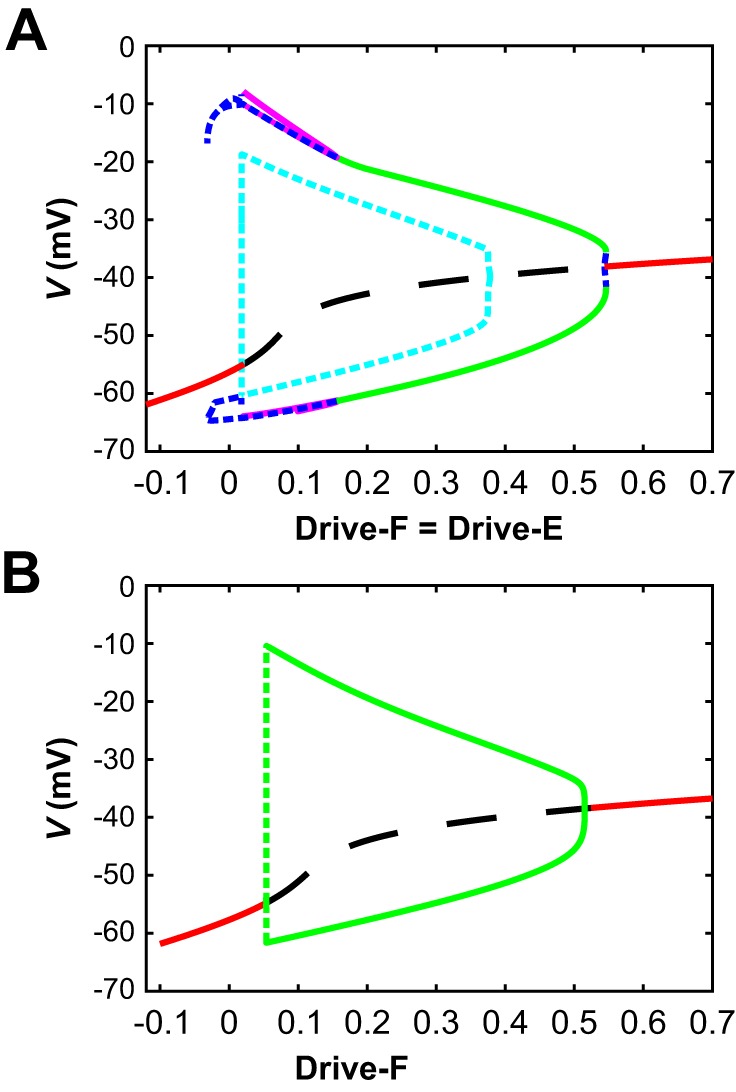
Bifurcation diagrams for the reduced model. A: diagram with drive levels to both units (Drive-F = Drive-E) used as the bifurcation parameter. At high and low drives, there are stable steady states (red solid curves) in which both units are tonically active (high drive) or silent (low drive) with equal voltages. These steady states both destabilize via Andronov-Hopf (AH) bifurcations, between which they are unstable (black dashed curve). The AH bifurcation near drive levels of 0.544 gives rise to a very small family of unstable periodic orbits (small blue dashed segment), which meets a family of stable periodic orbits (green curve shows maximal and minimal voltages along this family) corresponding to anti-phase oscillations (near Drive-F = Drive-E = 0.546) and extending to much lower drives. These oscillations destabilize in a pitchfork bifurcation (at Drive-F = Drive-E ≈0.155) that also gives rise to two new stable families of periodic orbits (magenta curves; outer curves show maximal and minimal voltages along one family, inner curves along the other, although the lower inner and outer curves largely lie on top of each other), which in turn destabilize around Drive-F = Drive-E = 0.018. The AH bifurcation near Drive-F = Drive-E = 0.018 gives rise to an unstable family of periodic orbits (cyan dashed curves show maximal and minimal voltages along these orbits) that terminate in another AH bifurcation around Drive-F = Drive-E = 0.38. B: diagram with Drive-E fixed at 0.6 and Drive-F used as the bifurcation parameter. Color conventions are as in A. In this case, there are just two AH bifurcations and one family of periodic orbits. Along the dashed part of the periodic orbit curve, the orbit amplitudes grow extremely rapidly and orbit stability could not accurately be resolved.

Because each model unit was described by a pair of differential equations for its voltage V and persistent sodium inactivation h, unit dynamics could be visualized in the phase plane, in which the h value for a unit is plotted against the V value for that unit as time evolves, starting from some initial condition, to generate a time-parameterized curve called a trajectory. In particular, if a unit was decoupled from the other unit, then we could plot its V-nullcline, where dV/dt = 0, and its h-nullcline, where dh/dt = 0, in the phase plane (Fig. 2). The relative positions and slopes of these nullclines organize the behavior of trajectories in the phase plane. Intersections of nullclines are equilibrium points, or steady states, where the variables for the unit do not change. Over most of the range of drives used in this work, the V-nullcline for a decoupled unit is cubic shaped, as in Fig. 2, consisting of three branches joined pairwise at twofold points or “knees,” a left knee at relatively high h and a right knee at relatively low h. For large enough drives, the V-nullcline becomes monotone increasing. When coupling between units is introduced at a fixed level, it alters the location of each unit’s V-nullcline, which can include changing its shape. As synaptic input to a unit evolves over time, it induces a corresponding time-dependent effect on that unit’s V-nullcline. Each unit’s h-nullcline is monotone decreasing, given by the shape of h_∞(V), and is independent of input from the other unit, since there is no coupling term in the differential equation for h.

Fig. 2.

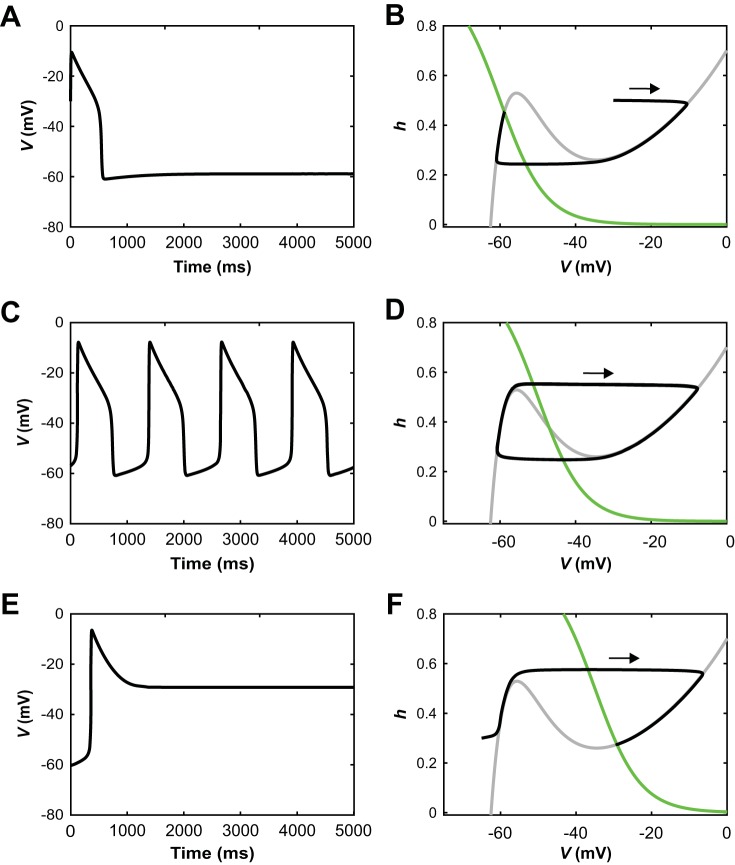
Schematic illustration of operating regimes for an uncoupled reduced model unit. A, C, and E: voltage time courses. B, D, and F: corresponding phase plane representations, each including V-nullcline (dV/dt = 0, gray), h-nullcline (dh/dt = 0, green), and trajectory (black). Each trajectory evolves clockwise. A and B: when the h-nullcline intersects the left branch of the V-nullcline, trajectories converge to a stable steady state at hyperpolarized voltage. C and D: when the h-nullcline intersects the middle branch of the V-nullcline, relaxation oscillations result. E and F: when the h-nullcline intersects the right branch of the V-nullcline, trajectories converge to a stable steady state at depolarized voltage.

Release/Escape Analysis

Classical relaxation oscillations occur in a planar system governed by one fast and one slow variable, such as the fast voltage V and slow recovery variable h in our reduced model. Assume that the fast V dynamics has one branch of stable equilibrium states over one interval of h values and another stable branch over another interval of h, such that these two h intervals overlap; this configuration can arise when the V-nullcline is cubic shaped as in Fig. 2. Relaxation oscillations can be understood by thinking of the dynamics as decomposed into fast transitions alternating with slow excursions. In the fast transitions, V evolves quickly, under the fast dynamics, to a small neighborhood of one of its equilibrium branches. Between transitions, h slowly drifts according to its differential equation, while V also drifts, following the equilibrium branch. A new transition occurs when the trajectory reaches the end of a stable equilibrium branch and the fast dynamics carries the trajectory to the other stable equilibrium branch. Importantly, in the relaxation oscillation regime, the true equilibrium state of the full 2D system is unstable and hence not relevant for the oscillatory state (Fig. 2D shows the phase plane representation for this regime, with corresponding voltage time course shown in Fig. 2C).

For two synaptically coupled model half-centers, the existence and stability of equilibria depend on the coupling between the half-centers units. The fully coupled system is 4D; however, we can think about the 4D system as a coupled pair of planar systems. That is, if both units are silent, then they do not inhibit each other, and the decomposition into two planar systems is clear. When one unit is active, it inhibits the other, which impacts the target unit’s voltage dynamics and the position of its V-nullcline as specified by Eqs. 7 and 9. Thus, the nature of the fast transitions in which one or both units switch between silent and active states can be analyzed based on the inhibition-dependent voltage-nullclines of the two units.

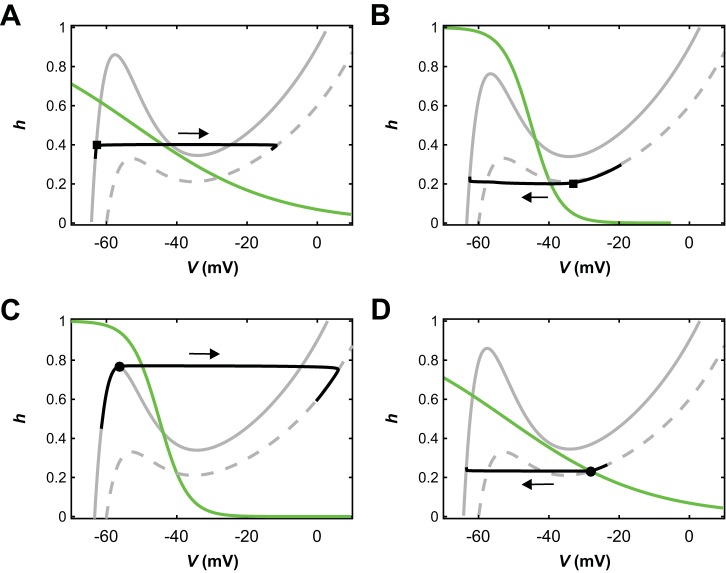
In half-center pairs with cubic-shaped voltage-nullclines and mutual synaptic inhibition, two fundamental classes of anti-phase active state transitions have been identified (Skinner et al. 1993; Wang and Rinzel 1992). In “release” transitions, the silent unit has a stable hyperpolarized equilibrium for the inhibition level it receives while the other unit is active. Thus, it is pinned in the silent state (Fig. 3A, solid V-nullcline). The active unit does not have a stable active phase equilibrium, however. Thus, its slow dynamics eventually causes it to transition out of the active state (Fig. 3B, square marker). When this happens, its voltage drops below the synaptic threshold and inhibition to the silent unit turns off. If the recovery variable h for the silent unit has deinactivated sufficiently, then this release from inhibition allows it to transition to the active phase (Fig. 3A, square marker). This transition mechanism is the one that occurs in the phenomenon known as postinhibitory rebound.

Fig. 3.

Transitions by escape and release in a pair of reduced model units coupled by mutual inhibition. Phase planes with V-nullclines corresponding to no inhibition (dashed gray) and maximal inhibition (solid gray), an h-nullcline (green), and a trajectory (black); the direction of evolution along each trajectory is indicated with an arrow. Fixed points lie where nullclines intersect. A: an inhibited unit that follows its inhibited V-nullcline is released from inhibition and thus transitions to the active phase (from the square), where it follows its no-inhibition V-nullcline. B: an active unit reaches its right knee (square) and transitions to the silent phase, thus releasing the other unit from inhibition. The released unit activates and crosses the synaptic threshold, such that the formerly active unit follows its inhibited V-nullcline in the silent phase. C: an inhibited unit reaches the left knee (circle) of its inhibited V-nullcline and escapes to become active. Its escape causes the other unit’s voltage to fall below the synaptic threshold, such that once the first unit becomes active, it follows its no-inhibition V-nullcline. D: an active unit approaches a fixed point (circle) along its uninhibited V-nullcline. Once it is in the neighborhood of the fixed point, it becomes inhibited by the escape of its partner and transitions to the silent phase (from the circle), where it follows its inhibited V-nullcline.

In “escape” transitions, the silent unit does not have a silent phase equilibrium state even when the other cell is active (Fig. 3C, solid V-nullclines), either for all levels of inhibition or once the inhibition from the active unit drops below some level. Thus, the silent unit can transition to the active phase despite the inhibition that it receives; that is, it escapes from inhibition (Fig. 3C, circle marker). Within this transition, the activating unit’s voltage crosses the synaptic threshold and thus it begins to inhibit the other unit, causing that unit to transition to the silent phase (Fig. 3D, circle marker).

For Figs. 9 and 11, we generated escape and release surfaces, based on locations of knees of appropriate V-nullclines. Knees were obtained by using continuation software built into XPPAUT (Ermentrout 2002) to follow fold points on V-nullclines as parameters were varied. The escape surface was a surface of left knees, corresponding to hyperpolarized V values and elevated (deinactivated) h values for a unit assumed to be a silent unit receiving synaptic input from another, active unit. The voltage level of the active unit (V_active) was used as a parameter, and the surface was defined by following the left knee location as this parameter and another parameter, either synaptic coupling strength or drive level to both units, were varied. The release surface was defined analogously, but using the right knees, corresponding to depolarized V values and lowered (inactivated) h values for a unit assumed to be an active unit inhibiting another, silent unit (which was coupled to the active unit in return). The voltage level of the silent unit (V_silent) was used as a parameter, and the surface was defined by following the right knee location as this parameter and another parameter, either synaptic coupling strength or drive level to both units, were varied. In the release case, although one unit was considered to be silent and one to be active to align with the concept of release, the mutual coupling did cause the synaptic coupling strength to impact the release surface when the silent voltage parameter was sufficiently depolarized. For Fig. 10, we generated curves of left and right knees following a similar procedure but assuming a fixed voltage for the other unit (i.e., the unit providing the synaptic input to the one for which the curve was being generated).

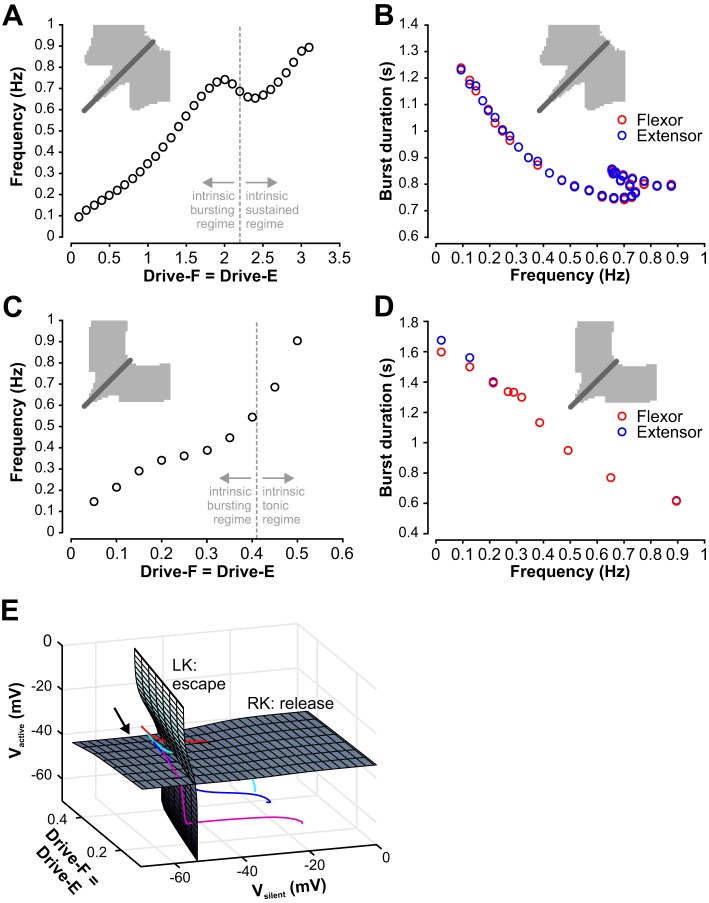
Fig. 9.

Control of frequency and burst durations with symmetric (equal) drives to both half-centers. A: for the population model, frequency increases with increasing drive but exhibits a drop at Drive-F = Drive-E≈2 that is followed by a subsequent increase in frequency when drive increases even more. The dashed line indicates the transition from the intrinsic bursting to the intrinsic sustained regime, which does not correspond to changes in the slope of the curve. B: flexor and extensor burst durations are equal over the whole frequency range for the population model. C: for the reduced model, frequency also increased with drive, over a similar range as for the population model. In an intermediate drive range the increase slowed, but no decline in frequency was observed. The dashed line indicates the transition from the intrinsic bursting to the intrinsic tonic regime, which does not correspond to changes in the slope of the curve. D: flexor and extensor burst durations are at least approximately equal over the whole frequency range for the original reduced model. E: knee surfaces derived from voltage nullclines for the reduced model. If the drive level to both units and the voltage level of one unit are fixed, then the other unit has a voltage nullcline (see methods, Fig. 2) with turning points at left (low V, high h) and right (high V, low h) knees. When the drive level or the voltage level of the fixed unit is varied, the nullcline and its knees move accordingly; see methods, Eqs. 7, 9, and 10. Gray surfaces are surfaces of left (LK) and right (RK) knees parameterized by drive level and by voltage of the fixed unit. Since the left knee surface is relevant when a unit is silent and the other unit is active, it is represented as a function of drive and the voltage level of the active unit (V_active). Since the right knee surface is relevant when a unit is active and the other unit is silent, it is represented as a function of drive and the voltage level of the silent unit (V_silent). Colored curves are trajectories of the coupled models for Drive-F = Drive-E = 0.15 (magenta), 0.25 (blue), 0.3 (cyan), 0.35 (red), each shown near a transition when one unit activates and the other falls silent. These evolve from upper left to lower right (arrow). In a transition by escape, a trajectory intersects the LK surface before the RK surface (red, cyan curves). This order is reversed in a transition by release (blue, magenta curves).

Fig. 11.

Dependence of oscillation frequency on the strength of mutual inhibition between the half-centers in the symmetric regime. A: in the symmetric regime with low drive to both half-centers, frequency is not sensitive to changes in the strength of the reciprocal inhibition for the population model. B: the reduced model also does not show strong frequency modulation with changing inhibition when drive is relatively low and transitions require release. C: the symmetric regime with high drive is highly sensitive to changes in inhibition for the population model. D: the reduced model shows a similarly strong frequency dependency on changes in inhibition when drive is relatively high and transitions occur by escape. E and F: surfaces of left (LK) and right (RK) knees, corresponding to transitions by escape and release, respectively, for the reduced model with low drive (0.2, E) and high drive (0.4, F). Colored curves are trajectories for various levels of inhibition strength α (orange, 1.5; pink, 2.5; red, 3.5; green, 4.5; cyan, 5.5; blue, 6.5). These evolve from upper left to lower right (arrows). E: with low drive, trajectories for all levels of α hit the RK surface before the LK surface, corresponding to transitions by release. F: with high drive, trajectories for all levels of α hit the LK surface before the RK surface, corresponding to transitions by escape.

Fig. 10.

Control of frequency and phase durations with asymmetric drives to the flexor and extensor half-centers. A: in the population model, with drive to the extensor half-center fixed at a level producing sustained activity, an increase in drive to the flexor half-center results in an increase in frequency until frequency reaches a plateau at high drives. The dashed line indicates the transition from the intrinsic bursting to the intrinsic sustained regime for the flexor. B: in the population model, the extensor phase duration decreases with increasing frequency, while flexor phase duration stays relatively constant. C: in the reduced model, with the strength of extensor drive maintained constant at a level for which the extensor half-center is in the tonic mode, an increase in strength of drive to the flexor half-center results in an increase in frequency until frequency slightly decreases at high drives. The dashed line indicates the transition from the intrinsic bursting to the intrinsic tonic regime for the flexor. D: in the reduced model, similar to the population model, the extensor phase duration decreases with increasing frequency, while flexor phase duration stays relatively constant. E: curve of flexor left knees (LK, black) and projection of trajectory segments (colored) for the reduced model for 4 values of Drive-F (0.1, 0.2, 0.3, 0.4). The direction of increasing time along each trajectory is from lower left to upper right. For each drive, the escape of the flexor from the silent phase occurs where the corresponding trajectory switches from sharply increasing in h to relatively flat in h. For larger drive, the escape occurs farther from the left knee, which corresponds to a shorter extensor active phase (see text). F: curve of extensor right knees (RK, black) and projection of trajectory segments (colored) for the reduced model for four values of Drive-F as in E. The direction of increasing time along each trajectory is from upper right to lower left. For each drive, the corresponding trajectory switches from sharply decreasing in h to relatively flat in h when the flexor escapes from the silent phase.

Burst Analysis

Symmetric case, Drive-F=Drive-E.

Since the flexor and extensor burst durations for Drive-F = Drive-E were equal and at low drives did not cover the full cycle period (see example traces in Figs. 5C and 6C), we could not interpret the model flexor and extensor burst durations as flexor and extensor phases, respectively. We thus analyzed burst durations in this case (Fig. 9, B and D) using a simple threshold burst detection. For the population model the threshold was set to 20% of the maximum amplitude for each individual simulation run. For the reduced model voltage increases and decreases through a threshold of −35 mV were used to determine burst onset and offset times for burst duration and network frequency calculations; activity patterns in which one or both units’ peak voltages were below −35 mV were not considered to be rhythmic.

Fig. 5.

Activity regimes depend on drive to half-center populations in the population model. A: frequency heat map obtained by independently varying flexor and extensor drives. Only frequencies where the flexor and extensor are bursting in strict alternation (1:1) are color coded. White areas are indicated where nonphysiological bursting occurs (1:n) (example with n = 3 shown in E) and where the flexor and/or extensor are tonic or silent (example for both tonic shown in H). B: alternating bursting (1:1) results from a wide range of drive combinations and underlying intrinsic (intr.) activity regimes of the flexor and extensor populations. Dashed lines indicate where the intrinsic activity state switches from bursting to sustained activity. C–H: examples of raster plots and histograms of flexor (red) and extensor (blue) population activities corresponding to different regimes of model activity. C: bursting activity of both half-centers with a gap between two bursts occurring at low, symmetric drives (Drive < 1.4). D: alternating bursting at intermediate, symmetric drives, when both half-centers operate in their intrinsic bursting mode. E: nonphysiological (1:n) bursting. F: oscillations based on intrinsic bursting of the flexor half-center with the extensor half-center exhibiting sustained activity if isolated. G: classical half-center oscillations, where both half-centers if isolated are in a sustained activity-mode. H: tonic activity that emerges at high symmetric drive.

Fig. 6.

Activity regimes depend on drive in the reduced model. A: frequency heat map obtained by independently changing drives to the flexor and extensor half-centers. Only frequencies where the flexor and extensor are rhythmically active in strict alternation (1:1) are color coded. White areas correspond to nonphysiological regimes of burst alternation (1:n or n:1) (example shown in E) and to the states when the flexor and/or extensor are tonically active or silent (example for both tonic shown in H). B: the alternating (1:1) oscillations result from a wide range of drive combinations and underlying intrinsic activity regimes of the flexor and extensor units. Dashed lines indicate where the intrinsic activity state switches from bursting to tonic. C–H: example traces of flexor (red) and extensor (blue) units generated at drive levels indicated by black squares in A, showing network activity at low, symmetric drives demonstrating the gap between two active states (C); intermediate, symmetric drives (D); asymmetric drives yielding nonphysiological (1:n) bursting (E); asymmetric drives yielding network oscillations due to intrinsic bursting in the flexor half-center with the extensor half-center in a tonic mode (F); high, symmetric drives for which the network exhibits half-center oscillations, although both flexor and extensor are intrinsically tonic (G); high symmetric drive yielding tonic network activity (represented by sustained elevated voltage) (H).

Asymmetric case, Drive-F≠Drive-E.

For the asymmetric case, no gaps between extensor and flexor activities were observed (see example traces in Figs. 5F and 6F) since the extensor was tuned to intrinsically produce sustained/tonic activity and hence was active unless it became inhibited by the rhythmic flexor activity. We thus could interpret flexor and extensor model activity (like extracellular ventral root recordings in animal experiments) as flexor and extensor phases and could assume that flexor phase duration + extensor phase duration = cycle period. To analyze phase durations in this case (Fig. 10, B and D), we determined the transition from flexor to extensor phase (and vice versa) by finding where the flexor and extensor voltage traces (normalized to their maximum amplitudes in the population case) intersected.

Link to Software

The executable files and scripts used to generate the simulations presented in this manuscript may be downloaded from http://neurobio.drexelmed.edu/rybakweb/software1.htm.

RESULTS

In this theoretical study, we used two complementary computational models with different levels of complexity, a large-scale population-based model and a mathematically tractable reduced model, to simulate and investigate the possible operational regimes in a relatively simple CPG architecture consisting of two conditionally bursting half-centers with mutual reciprocal inhibition (see methods and Fig. 1, A and B).

Population Model: Flexor and Extensor Half-Center Populations as Conditional Bursters

Recent studies using optogenetic activation of neuronal populations in the isolated mouse spinal cord have clearly demonstrated that flexor- and extensor-related rhythmic bursting can, under certain conditions, be evoked and maintained independently (Hägglund et al. 2013). However, it is unknown whether flexor and extensor bursting activities are independently generated in vivo and under what conditions. Following previous computational models of the mammalian spinal CPG (Brocard et al. 2013; Danner et al. 2016, 2017; McCrea and Rybak 2007; Rybak et al. 2006a, 2006b, 2014; Sherwood et al. 2011; Shevtsova and Rybak 2016; Zhong et al. 2012), we suggested that intrinsic bursting in neurons of both half-center populations is based on a persistent (slowly inactivating) sodium current (I_NaP) present in each neuron of these populations. This suggestion was previously indirectly supported by studies in several laboratories (Brocard et al. 2010, 2013; Tazerart et al. 2007, 2008; Zhong et al. 2007; Ziskind-Conhaim et al. 2008).

Previous theoretical and modeling studies have demonstrated that a population of neurons with I_NaP-dependent bursting properties and mutually excitatory synaptic interconnections can generate intrinsic bursting within a certain range of values of the tonic external excitatory drive to the population. A progressive increase of external drive to the population first leads to the onset of bursting with burst frequency increasing with drive and then to sustained activity (Best et al. 2005; Butera et al. 1999, 2005; Jasinski et al. 2013; Rybak et al. 2003, 2004, 2014; Smith et al. 2000).

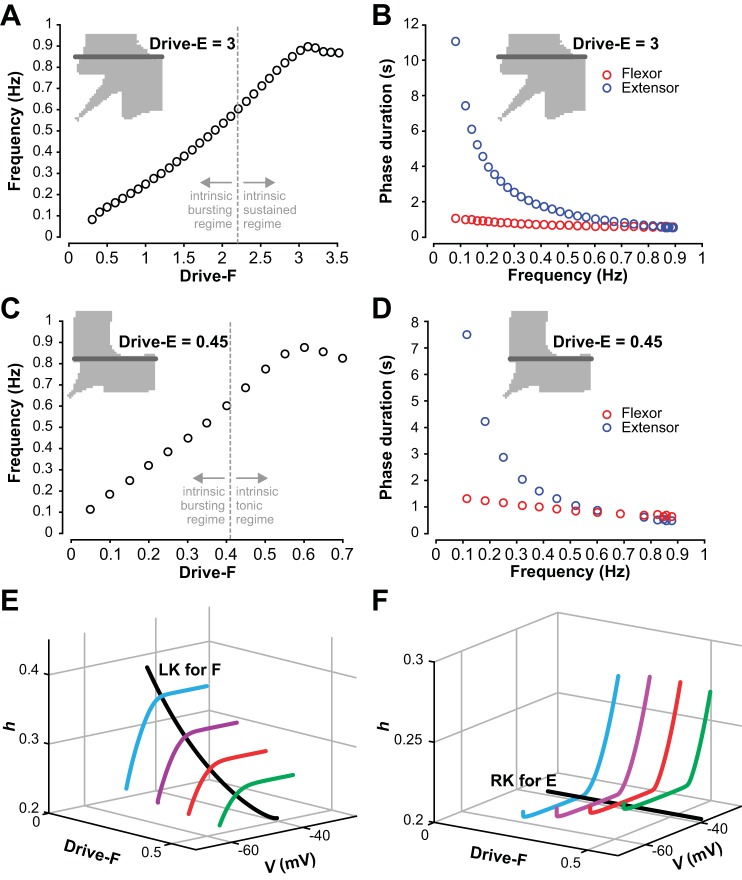
The probability of the sparse mutual interconnections within each half-center population in our model was set to 0.1 (Dougherty et al. 2013; Shevtsova et al. 2015; Table 1). Consistent with previous models, the isolated half-center population in our model was silent when the tonic drive was turned off. Intrinsic bursting activity emerged at a drive value of 0.1. Burst frequency then increased with an increase in drive until activity switched to sustained firing (at Drive = 2.2, Fig. 4, A–D). Both flexor and extensor half-centers in Fig. 1A were identical, and hence each half-center if isolated exhibited intrinsic bursting at drives between 0.1 and 2.2 and sustained firing when drive exceeded 2.2.

Fig. 4.

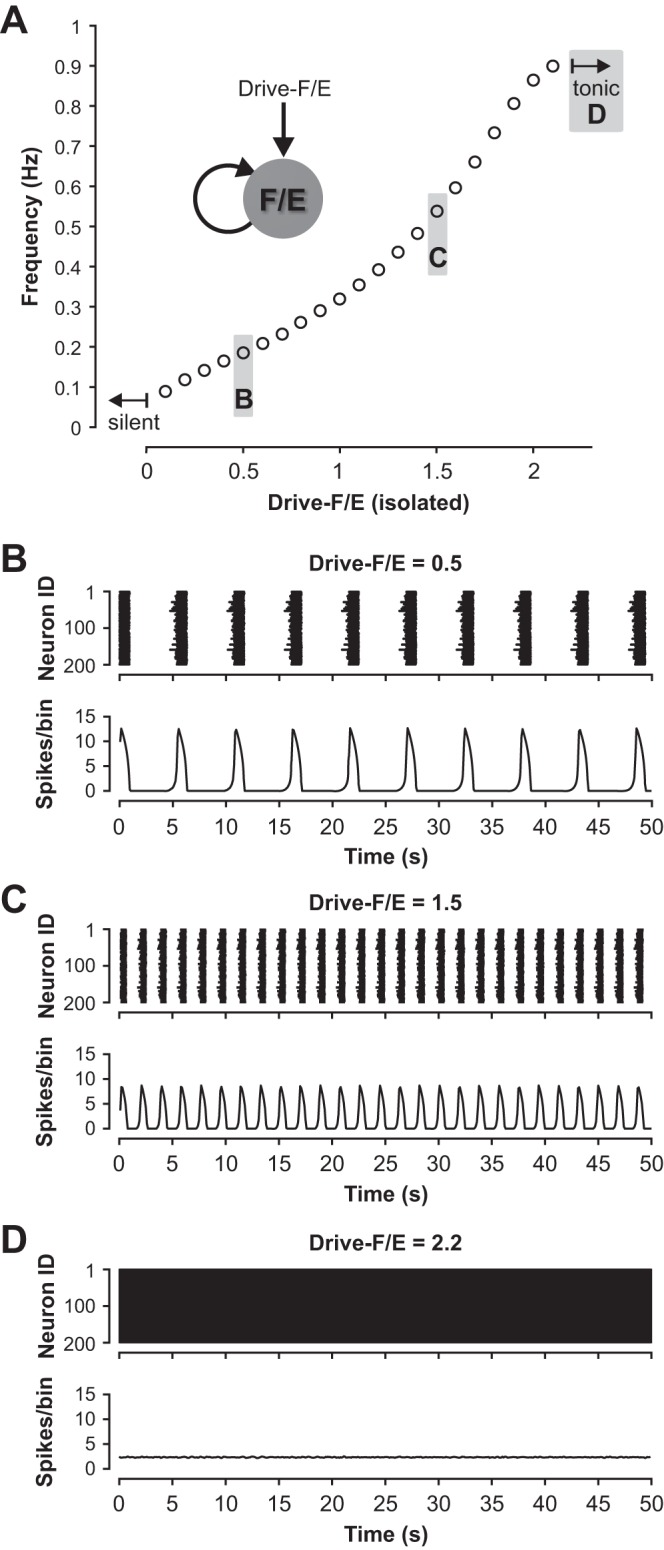
Conditional burst dynamics in the population model. A: with progressive increase of external excitatory drive, the activity of an isolated (flexor or extensor) population changes from silent (Drive < 0.1) to bursting (Drive ≥ 0.1) and to sustained activity (Drive ≥ 2.2). Example raster plots and histograms for the data points labeled with B–D are shown in panels B–D. B–D: example action potential raster plots (upper traces) for the 200 neurons in an isolated half-center population and histograms of population firing activity (lower traces) for three different drives to the isolated population that elicit low-frequency bursting (B), high-frequency bursting (C), and sustained activity (D). Population activity in B–D and following figures is represented by histograms showing the average number of spikes in the populations per 100-ms bin.

Distinct Activity Regimes Generated by the Flexor-Extensor CPG

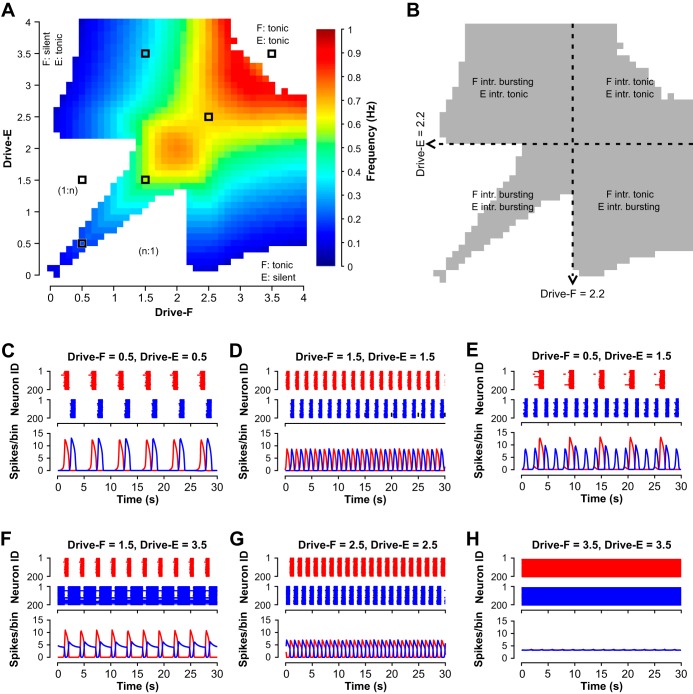
After synaptically connecting the half-center populations into a flexor-extensor network CPG (Fig. 1A), we could elicit a wide range of activity patterns by independently varying the drives to the flexor and extensor populations. We chose a range of drives that spanned from the silent regime, through the entire bursting regime, to the regime of sustained activity for an isolated population and monitored the resulting activity pattern of the network (Fig. 5). Varying drive may represent a change in descending supraspinal drive, a change in neuromodulatory state, or a change in afferent feedback to each population.

Since flexor and extensor populations as well as inhibitory populations and their interactions were almost identical (with only small variations due to randomly distributed parameters), the dynamics in the resulting parameter space was mirrored across the diagonal where the flexor drive was equal to the extensor drive. Figure 5 shows that different combinations of flexor and extensor drives resulted in multiple distinct regimes (and patterns) of network activity (see maps in Fig. 5, A and B). With changing drives, network activity changed from silence to an alternating (1:1) symmetric (Fig. 5, C, D, and G) or asymmetric (Fig. 5F) bursting, to “nonphysiological” (1:n) bursting (Fig. 5E), and to sustained activity (Fig. 5H). The color-coded area in Fig. 5A indicates the network frequency for strictly alternating (1:1) bursting that persisted beyond a 15-s transient period (see methods).

We found that alternating (1:1) bursting in the population (see color coded area in Fig. 5A and gray area in Fig. 5B) did not necessarily require intrinsic rhythmicity in the half-center components of the model. Indeed, 1:1 bursting arose in the subsets of parameter space that corresponded to three different combinations of intrinsic activity patterns for the flexor and extensor half-center populations: 1) both populations were intrinsically bursting, 2) only one population (e.g., flexor) was intrinsically bursting and the other (e.g., extensor) was in a sustained activity mode, and 3) both populations were in a sustained activity mode if isolated.

• When both the flexor and extensor populations were in intrinsic bursting mode (both drives < 2.2, see Fig. 5B), the network produced a 1:1 alternating bursting in the area close to the diagonal, where Drive-F≈Drive-E (example traces are shown in Fig. 5, C and D). The remaining area of the parameter space for both populations in intrinsic bursting mode was occupied by nonphysiological network activity (1:n or n:1 bursting, Fig. 5E). This finding suggests that if both flexor and extensor populations operate in bursting mode, then the drive to both populations has to be relatively tightly balanced to enable strictly alternating flexor-extensor bursting activity.

• When the extensor population received a drive sufficient to induce intrinsic sustained firing (Drive-E ≥ 2.2) while the flexor population operated in intrinsic bursting mode (Drive-F < 2.2), the network exhibited 1:1 bursting defined by the rhythmic flexor activity (Fig. 5F).

• With both populations in the intrinsic sustained activity mode (both drives ≥ 2.2), bursting activity resulted from reciprocal inhibitory network interactions and adaptive firing properties inherent to neurons in both half-center populations (Fig. 5G), instantiating the classical half-center oscillator concept. This bursting was always alternating (Fig. 5G), but the network switched to sustained activity when drives became too large (Fig. 5H).

We thus found that robust 1:1 bursting arises in a network where one population is in the intrinsic sustained activity mode while the other one’s activity is either bursting or sustained. It is also noteworthy that along the diagonal, when both drives were increased equally, low drives led to an activity pattern that, although characterized by 1:1 bursting, showed a pronounced gap between bursts (Fig. 5C). This gap diminished and then vanished with higher drives (≥ 1.4), preventing 1:n bursting and resulting in increases in network frequency (Fig. 5D).

A Reduced Model and Its Operational Regimes

To facilitate mathematical analysis of the dynamic mechanisms underlying the different activity regimes observed in the population model, we constructed a reduced model of the flexor-extensor rhythm generator, consisting of one flexor (F) and one extensor (E) unit, each represented by a nonspiking activity-based model (see methods), mutually coupled with inhibitory synapses (Fig. 1B). Similar to the population model described above, the flexor and extensor units in this model represent the flexor and extensor half-centers and were implemented with an adjusted I_NaP-dependent mechanism to enable intrinsic oscillations at certain levels of tonic external drive.

By design, with identical values of drive and symmetric inhibitory interactions, the extensor and flexor components in the reduced model are identical. We varied the drives (Drive-F and Drive-E) to the flexor and extensor half-centers independently and computed the frequency of the steady state oscillation, consisting of 1:1 activations of flexor and extensor units, over all drive values for which such oscillations were observed to persist beyond a 15-s transient period (see methods).

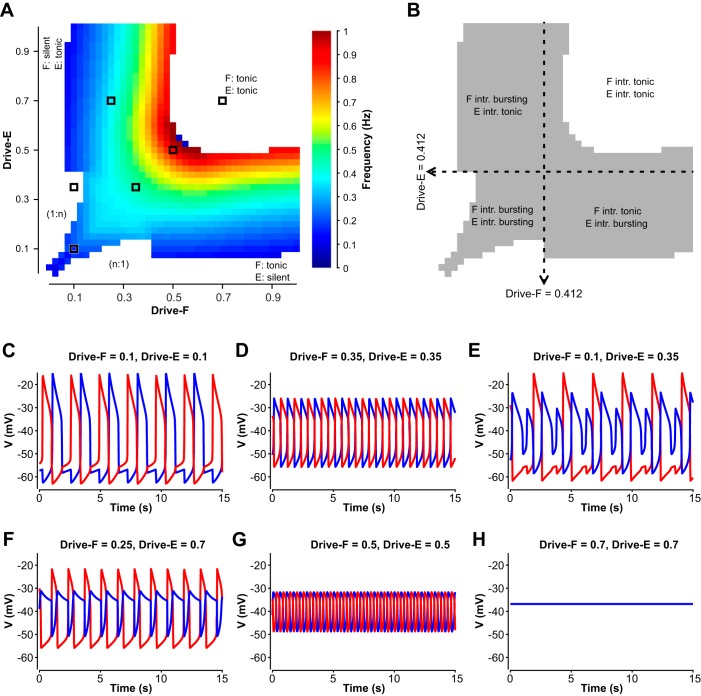
Maps representing how the dynamic regimes depend on the external drive values to the two coupled half-centers are shown in Fig. 6, A and B. As for the population model, 1:1 flexor-extensor oscillations were observed across a wide range of drive values, and specifically when Drive-F = Drive-E (Fig. 6, A–D and G) and when these drives were different but at least one unit was kept in the intrinsically tonic regime (Fig. 6F). With sufficient disparity in drive values in the regime in which both units are intrinsically bursting, the less driven component would only manage to activate once out of every n activations of the other component for n > 1, which was also similar to the population model (1:n, Fig. 6E). When the drives to the two units were made unequal, the oscillation frequency was selected by the smaller of the two drive values (Fig. 6A, colored bands). With high enough drive to both units, a tonic regime occurred in which both units converged to stable equilibrium states at depolarized voltages (Fig. 6, A and H). The general observations for the population model held in the reduced model as well, although there were some differences in details of frequency responses to drive, especially for Drive-F = Drive-E, which are described and analyzed in the following sections. Despite those differences, we found that for both models the transition from intrinsic oscillatory/bursting to intrinsic tonic/sustained activity did not seem to have an effect on changes in frequency with changes in drives (Figs. 5B and 6B, dashed lines). We thus used the reduced model to analyze the behavior of the coupled network in relation to the half-centers’ intrinsic states.

Bifurcations in the Reduced Model

As drive to a single, uncoupled unit was increased, the unit transitioned from a silent state (Fig. 2, A and B) to bursting (Drive ≥ 0.017; Fig. 2, C and D) and to tonic activity (Drive ≥ 0.412; Fig. 2, E and F). These regimes correspond to the stable states of the single-unit model, determined by its nullcline structure. Specifically, the model has a cubic-shaped voltage nullcline over a large range of drive values (Fig. 2, B, D, and F). For low drive, the model has a hyperpolarized equilibrium point, which lies on the left branch of its voltage nullcline (Fig. 2B). As drive was increased, this equilibrium moved to the middle nullcline branch and destabilized in an Andronov-Hopf (AH) bifurcation, and stable periodic orbits emerged, corresponding to bursting (Fig. 2D). In these bursting oscillations, the voltage alternated between silent phases spent near the hyperpolarized left branch of the voltage nullcline and active phases spent near the depolarized right branch of the voltage nullcline. These orbits were lost and the equilibrium restabilized, now at a depolarized voltage on the right branch of the voltage nullcline, in a second AH bifurcation as drive was increased further (Fig. 2F), and in this nonspiking modeling framework the stable depolarized equilibrium was the tonic activity state.

Once the units were reciprocally coupled with inhibitory synapses, the bifurcation diagram for the coupled pair with identical drives (Fig. 7A) showed a destabilization of the silent state at a small positive drive value, around Drive-F = Drive-E = 0.018, slightly above the value at which silence lost stability in a single unit. The bifurcation at which the silent state became unstable was an AH bifurcation, which gave rise to a family of unstable synchronized periodic solutions that terminated in another AH bifurcation at larger Drive-F = Drive-E (closed cyan loop in Fig. 7A). To understand the nature of the stable periodic solutions in this case, it is helpful to start not from low drives but from large values of Drive-F = Drive-E. For drive values above 0.544, the model exhibited a stable tonic activation steady state. As drive was decreased to 0.544, a much higher value than the drive level, 0.412, at which the intrinsic transition from oscillations to tonic activation occurred, another AH bifurcation produced a small amplitude unstable periodic orbit family (rightmost blue dashed curve in Fig. 7A). This family came together with a stable family of anti-phase periodic oscillations (green curve in Fig. 7A) in an event called a saddle-node of periodic orbits (SNPO) bifurcation at a drive value just slightly above 0.546, resulting in a very small window of bistability of oscillations and tonic activity (drive values from 0.544 to 0.546). The stable anti-phase oscillations (cf. Fig. 6D) continued for drive values well below the SNPO, down to approximately Drive-F = Drive-E = 0.155. There, a pitchfork bifurcation of periodic orbits occurred. In the pitchfork, the perfectly anti-phase oscillations became unstable and two stable periodic orbit branches of identical period were formed (magenta curves in Fig. 7A). One of these branches consisted of oscillations in which extensor activation was immediately followed by flexor activation, followed by a pause with neither unit active (e.g, Fig. 6C); the other branch was similar but with flexor activation preceding extensor activation. These branches destabilized around the same drive level, Drive-F = Drive-E = 0.018, where the silent state stability change occurred.

When drives to the two coupled units were not equal, if Drive-E was fixed, then as Drive-F was increased, the pair could transition from a steady state directly to anti-phase oscillations (for Drive-E sufficiently large) or from silence to 1:n oscillations to 1:1 oscillations (for smaller Drive-E); see Fig. 6A. In the former case, the bifurcation structure was straightforward. For example, with Drive-E = 0.6, when Drive-F was near 0, the network exhibited a stable steady state with Drive-F silent and Drive-E showing tonic activation (Fig. 7B). When Drive-F was increased to 0.054, this steady state destabilized, a family of periodic oscillations emerged and grew extremely rapidly in amplitude (green dashed curve in Fig. 7B), and a stable family of periodic oscillations appeared (green solid curve in Fig. 7B). This family continued up to approximately Drive-F = 0.515, where the oscillations terminated in an AH bifurcation and the steady state became stable again, now consisting of tonic activation of both units. With Drive-E fixed at small enough values to produce 1:n oscillations, the bifurcation diagram was much more complicated, with stable periodic branches of successively higher period and higher n (1:2, 1:3, and so on) existing for successively lower values of Drive-F, connected by unstable periodic branches and in some cases with very small windows of bistability (data not shown). These oscillations and further details of their bifurcation structure are outside the focus of this work.

The Reduced Model Reveals Phase Transitions by Escape and Release

An important concept that was revealed in the use of the reduced model is that transitions in which an active unit falls silent and a silent unit becomes active can occur by mechanisms known as escape and release (Skinner et al. 1993; Wang and Rinzel 1992; see Fig. 3 and methods); moreover, in some cases, a partial release or adaptation may help promote escape (Daun et al. 2009). When each unit was intrinsically bursting, it could transition from silent to active and from active to silent on its own in the absence of inhibition (Fig. 2D). In the coupled network, if one unit was active and the other was silent, then the silent unit was below synaptic threshold and did not inhibit the active unit. Thus, in the regime when the units were intrinsically bursting, the release mechanism was always available (e.g., Fig. 3B; note that the h-nullcline intersects the dashed V-nullcline on its middle branch, corresponding to the intrinsic bursting regime). A critical observation, however, is that for particular parameter sets, even in the symmetric, intrinsically bursting regime, transitions may actually occur by escape (Fig. 8A). Once units were intrinsically tonic, in contrast, the release mechanism was no longer available (Fig. 8B). Thus, transitions had to occur by escape. Putting these results together, we find that transitions by a single mechanism, escape, occur across part of the intrinsically bursting regime and all of the intrinsically tonic regime. That is, once the units are coupled into a network, their intrinsic dynamics may become masked by the occurrence of transition mechanisms that span across multiple intrinsic dynamic regimes.

Fig. 8.

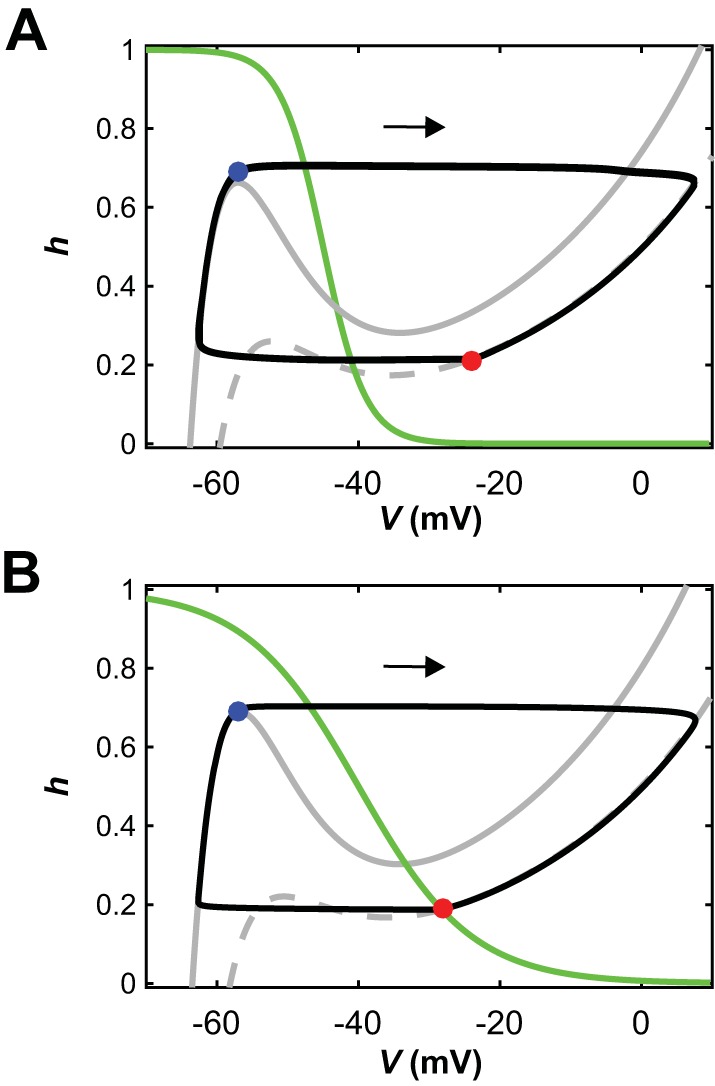
Escape transitions can occur when units are intrinsically oscillatory or tonic. A and B: with symmetric drives to both reduced model units, their nullclines and trajectories look identical in the phase plane, so we use a single phase plane diagram for both units (e.g., Rubin and Terman 2002). As in Fig. 3, gray curves are V-nullclines (solid, maximal inhibition; dashed, no inhibition), green are h-nullclines, and black are trajectories, which evolve clockwise (arrows). A: diagram when both units are intrinsically oscillatory. When one unit reaches the left knee of the maximal-inhibition V-nullcline, it initiates a phase transition by escaping from the silent phase (blue circle). The other unit becomes inhibited and jumps down to the silent phase (red circle). Although there is no fixed point in the active phase (right branch of V-nullclines), the transition is by escape rather than by release. B: when there is a fixed point in the active phase (red circle), transitions must occur by escape, which happens when a silent unit reaches the left knee of the maximal-inhibition V-nullcline (blue circle).

Effects of Changes in Equal Drive to Both Half-Centers on Oscillation Frequency and Phase Durations

The frequency maps in Figs. 5 and 6 show that as long as the drives applied to both flexor and extensor half-centers were equal, the network produced alternating (1:1) bursting until both drives became too large to generate network oscillations. In this case, we have investigated how frequency depends on the drive. In the population model, a symmetric increase in drive values (from 0.1 to 3.2) led to network oscillations with frequencies in the range from ~0.1–0.9 Hz (Fig. 9A). With equal drives to the flexor and extensor populations, the durations of flexor and extensor phases were equal and monotonically decreased with increases in frequency (Fig. 9B). However, frequency itself did not increase monotonically. There was a drop in frequency when both drives approached 2 (Fig. 9A) that was followed by a subsequent increase in frequency. Interestingly, the first change of sign for the slope of the frequency-drive curve occurred at a lower drive value than that at which individual half-center activity switches from intrinsically bursting to sustained activity (Fig. 9A, dashed line, Drive = 2.2), which lies within the decreasing segment of the frequency-drive curve. The mechanism underlying the slope changes relates to multiple model nonlinearities and cannot be easily explained in the framework of the population model.

In the reduced model, equal increases in the drives to the flexor and extensor units yielded a gradual increase in frequency over a range of drive values, similar to that seen in the population model (Fig. 9C). Also, as in the population model, the durations of bursts of the two units were quite similar over the full range of frequencies and decreased with increasing frequency (Fig. 9D). However, while the population model showed a nonmonotonic frequency-drive relationship when Drive-F = Drive-E (Fig. 9A), the reduced model’s frequency-drive curve featured variations in slope but did not show a negatively sloped region (Fig. 9C). Similar to the population model, changes in slope in the reduced model did not correlate with the transition from intrinsic bursting to intrinsic tonic activity (Fig. 9C, dashed line, Drive = 0.412). To understand the source of the slope variations in the frequency-drive curve, we turned to dynamical systems analysis of the reduced model.

The Impact of Drive on Frequency Depends on Phase Transition Mechanisms That Override Intrinsic Dynamics

In the reduced model, a unit will activate when its slow variable recovers (technically, deinactivates) enough to pull its trajectory above a threshold defined by the surface of left knees of its voltage nullcline (parameterized by drive and inhibition level; see methods). We have already seen that this activation may involve release, in which the active unit reaches the right knee of its voltage nullcline before the silent unit reaches the left knee surface, or may be driven by escape, in which the left knee surface is reached first (e.g., Fig. 3). By projecting the trajectory and comparing its position to those of the left and right knee surfaces, we could see that, for low drive, release occurred before the silent unit could activate (Fig. 9E, magenta trajectory). Indeed, in the low-drive end of the rhythmic regime, both models’ oscillations included phases where both units or populations were silent (Figs. 5C and 6C). In these phases, the leading oscillator had been fully released from inhibition, yet it still needed more time before it could activate.

As drive was increased, less recovery of the slow inactivation variable was needed for the leading silent unit to clear its left knee surface and activate, such that the overall time between cycles decreased, and hence cycle frequency increased. As drive increased more, there was a change in the qualitative nature of the network oscillation: the period when both units were silent was lost (Figs. 5D and 6D). Transitions were still based on full release (Fig. 9E, blue trajectory), but the increase in frequency with drive became weak. In fact, with all-or-none synapses, release transitions in mutually inhibitory networks are typically associated with negatively sloped frequency-drive curves (Daun et al. 2009; Shpiro et al. 2007; Skinner et al. 1993) because increased drive can prolong the active phase of the active unit before release occurs; however, the drive reversal potential (0 mV) prevented this effect from arising in our reduced model, such that the slope remained weakly positive (Fig. 9C, intermediate drive range). Eventually, with still more drive, the silent unit could reach the left knee surface and escape before full release had occurred (Fig. 9E, cyan trajectory for Drive-F = Drive-E = 0.3). This switch to escape occurred even though both units were still intrinsically in the bursting regime (cf. Fig. 8A).

Finally, with still more of an increase in drive, another qualitative change occurred. Eventually, the drive to the silent unit was enough to allow it to escape even with full inhibition from the active unit (Fig. 9E, red trajectory). Since the silent unit was in full control of the transition, while the inhibition from the active unit saturated at its maximum, frequency could grow more steeply with drive once again in this regime (Fig. 9C; Daun et al. 2009; Shpiro et al. 2007; Skinner et al. 1993). In brief, it is the switch from transitions by release, to transitions by escape assisted by release, to transitions entirely by escape that shapes the frequency-drive curve. In the population model, the same general trends occurred. However, in the intermediate case between the two regimes of strongly increasing frequency, the population model exhibited a more complicated frequency-drive relation than the reduced model due to its more complex adaptation mechanisms, which include spiking effects as well as gradual recruitment or termination of spiking within the active population. Importantly, in both of our models, the drive levels at which the transitions between regimes and changes in frequency-drive dependence occur do not correspond to the drive levels at which uncoupled units switch between bursting and tonically active dynamics. For drive values corresponding to both forms of intrinsic dynamics, units can activate on their own, and here this property allows escape to become important even at low enough drives that the units are still intrinsically bursting rather than intrinsically tonic. In the reduced model, for example, since the release-escape switch happens at lower drive (~0.3) than the switch from intrinsically oscillatory to tonic dynamics (~0.41), this latter switch has no effect on frequency when it occurs.

In summary, our analysis of the reduced model dynamics yields the following conclusions: 1) the network’s frequency response to changes in drives is determined by the phase transition mechanism operating in the network, which may be escape or release (Daun et al. 2009; Shpiro et al. 2007; Skinner et al. 1993), and 2) the intrinsic dynamics of the units define which transition mechanisms are available for the network to harness to achieve switches between active units. When half-center units are tonically active, only transitions by escape are possible (Fig. 8B) and hence frequency will increase appreciably with drive (Fig. 9, A and C). If a unit is intrinsically bursting, however, then both release and escape transitions are possible (Fig. 8A), and the network may switch between these mechanisms at drive levels that are not associated with any change in individual cell dynamics (Fig. 9E).

Asymmetric Regimes of Oscillations

Asymmetric regimes of oscillations in both models occurred when one half-center (e.g., extensor) received high drive that kept it in the mode of sustained/tonic activity, whereas the other half-center (in this case, the flexor) operated in bursting mode. For both the population model and the reduced model, increasing drive to the flexor half-center resulted in a monotone increase of oscillation frequency up to an approximate plateau just before network oscillations terminated (Fig. 10, A and C). Note that when the flexor population transitioned from bursting to tonic mode (population model: Drive-F = 2.2; reduced model: Drive-F = 0.412) there was no impact on the frequency-drive relation (Fig. 10, A and C, dashed lines). Changes in network frequency corresponded to alterations in the duration of extensor activation with little change in flexor active duration. While the duration of the extensor phase was generally longer than that of the flexor phase, the progressive reduction of extensor duration with increase in drive to the flexor eventually resulted in a symmetric locomotor pattern with approximately equal flexor and extensor phase durations (Fig. 10, B and D). These changes of phase durations and their ratio with increase of locomotor frequency look similar to those known from in vivo studies in cats (Frigon and Gossard 2009; Frigon et al. 2013; Halbertsma 1983). The following analysis of the reduced model looks further into the mechanisms underlying the frequency response and these asymmetric changes in phase durations.

In the Flexor-Driven Asymmetric Regime, Frequency Responses to Changes in Flexor Drive Are Defined by Flexor Half-Center Escape from Inhibition

As seen in Figs. 5A and 6A, maintaining a fixed high excitatory drive to the extensor unit allowed the network to produce 1:1 oscillations over a broad range of drive values to the flexor unit. It is interesting to note that we found 1:1 oscillations for low Drive-F only when the maintained drive to the extensor center was sufficiently large. When the extensor received intermediate drive, it was intrinsically oscillatory and it could produce several oscillations before the weakly driven flexor unit could finally activate. When Drive-E was larger, the extensor active phase became much longer. The prolonged extensor active phase allowed the flexor as much time as it needed to deinactivate, such that either it could escape on its own (if it had enough drive to do so) or, if the extensor was not fully tonic, it could manage to activate once the extensor finally released it.

The reduced model affords insights into the mechanisms underlying the characteristics of the frequency-drive relationship as seen in both models. Consider the situation when the extensor unit was active and the flexor was silent, such that the latter was inhibited and the former was not. For our fixed level of Drive-E, the uninhibited extensor unit had a fixed point in the active phase (cf. Fig. 2F). We used the voltage value at that fixed point to generate the synaptic input to the flexor unit. With that level of inhibition, the left knee of the flexor unit’s V-nullcline, which the unit must reach to activate, moved to lower values of h as Drive-F increased. A shorter time was needed for the flexor to reach a smaller h, yielding a shorter silent phase for the flexor and corresponding active phase for the extensor (Fig. 10D). A smaller h at flexor activation also yielded a lower maximal voltage, a smaller maximal inhibition to the extensor, and thus an earlier extensor escape at smaller h and a weaker maximal inhibition to the flexor. Thus, we observed a positive feedback cycle that resulted in an oscillation cycle with a smaller amplitude and higher frequency.

Figure 10, E and F show projections of trajectory segments for the flexor (Fig. 10E) and extensor (Fig. 10F), respectively, along with curves of flexor left knees and extensor right knees. The former were computed assuming that the extensor voltage was at its fixed point value, as described above, while the latter were computed assuming that there was no input from flexor to extensor and hence were independent of Drive-F. Note that for low Drive-F, the flexor trajectory reached its left knee and the extensor approached very close to its right knee, corresponding to a long extensor active phase in which the extensor reached a small neighborhood of its fixed point (near its right knee) before flexor escape finally occurred (Fig. 10, E and F, cyan curves). As Drive-F increased, the trajectories deviated more and more from the knee curves, meaning that the flexor was able to escape and terminate the extensor phase progressively earlier, with the extensor unit at larger voltages farther away from its right knee and fixed point, despite the stronger inhibition to the flexor associated with the larger extensor cell voltage (Fig. 10, E and F, magenta, red, and green curves).

Eventually, as Drive-F became large enough (in particular, larger than Drive-E), the flexor V-nullcline lost its cubic shape and became monotonic (data not shown). In this configuration, its fixed point in the silent phase was stable and therefore the flexor unit could not activate through standard escape. Its fixed point was at a large enough voltage, however, that the flexor could start to inhibit the extensor once it approached close enough to the fixed point, allowing a transition to occur. With increasing Drive-F, this approach could occur after a shorter flexor silent period. The overall frequency did not continue to increase with Drive-F, however, because increasing Drive-F also resulted in a higher flexor voltage and hence a stronger inhibition from the flexor to the extensor when the flexor was active, which delayed extensor escape. Thus, the oscillation frequency lost much of its dependence on Drive-F when it reached a high level (Fig. 10C, large Drive-F).

Therefore, in an asymmetric network with an intrinsically tonic extensor unit, increasing drive to the flexor can induce faster network oscillations by facilitating flexor escape from the silent phase and hence shortening the extensor active phase until, at sufficiently high drives, the flexor can no longer escape and hence the frequency plateaus.

The Role of Inhibition Between the Half-Centers in Control of Frequency

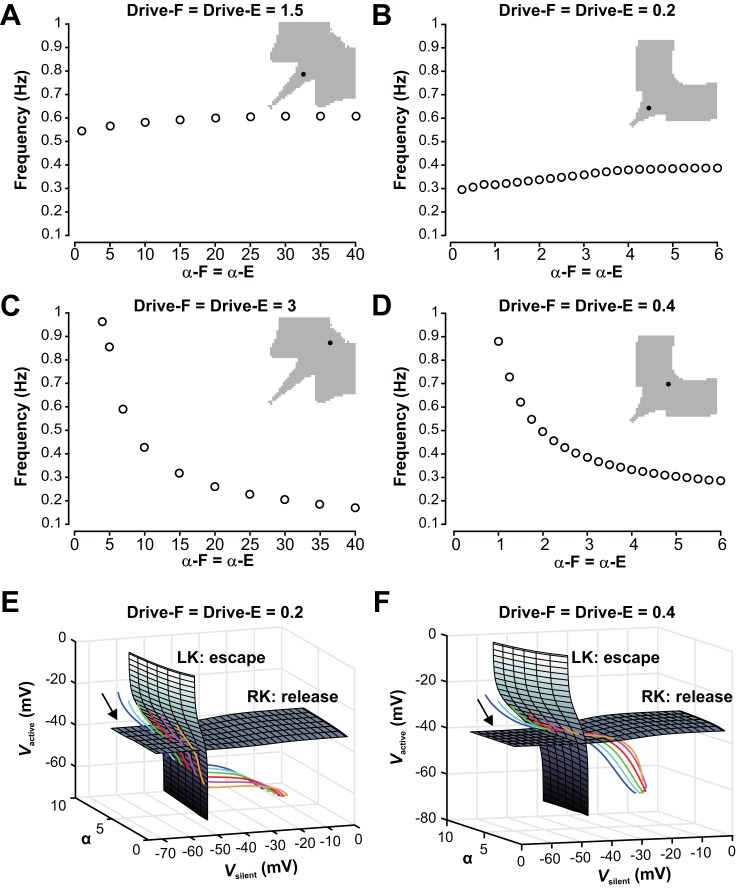
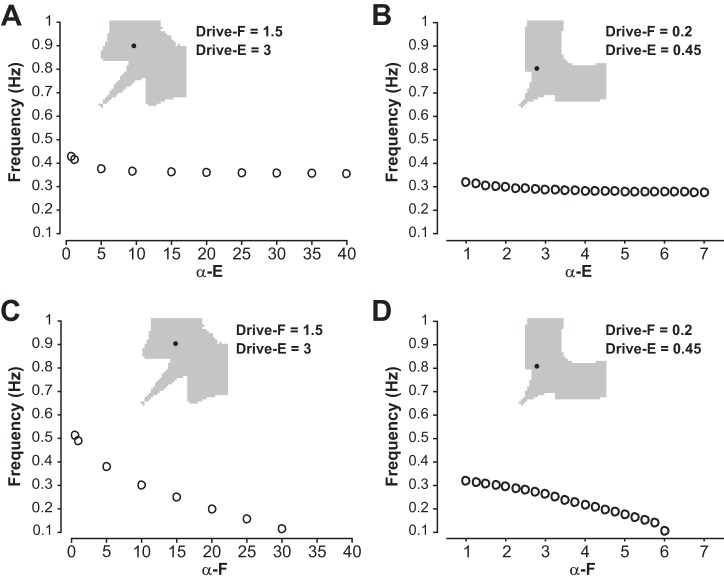
Another parameter that influences network frequency is the strength of inhibitory connections between the two half-center populations of the network. Using our models, we tested how inhibition strength α influences frequency in different network regimes described above. Its impact turned out to be quite different depending on the drive value selected but was qualitatively similar for the population model and the reduced model.

In models with equal but low drive (population model: Drive = 1.5; reduced model: Drive = 0.2) both populations were intrinsically oscillatory at a relatively low frequency. In this symmetric regime with low drive, frequency was not sensitive to changes in the strength of the reciprocal inhibition (Fig. 11, A and B).

Recall that for symmetric low drive, transitions between phases require at least partial release from inhibition (Fig. 9E). This requirement held even as the parameter α that defines the strength of inhibition (see methods) was varied (Fig. 11E). In this mode, the active unit was in control of the transition, since it had to do the releasing. Once the active unit’s transition to the silent phase was underway, its voltage started changing quickly; indeed, each unit was intrinsically oscillatory for this low drive and hence could transition to the silent phase on its own. Thus, a complete release occurred, regardless of the inhibition strength. Increasing α had very little impact on when the silent unit had been released enough that it could activate and hence did not significantly change the oscillation frequency (Fig. 11, A and B).

The situation changed when both half-centers were activated with a relatively high drive (Fig. 11, C and D; population model: Drive = 3; reduced model: Drive = 0.4), such that the transitions occurred by escape (Fig. 9E). With increases in α, transitions still occurred by escape (Fig. 11F), but additional deinactivation was required, escape was delayed, and hence frequency was significantly decreased (Fig. 11, C and D). Note that the drive did not need to reach the intensity that switches intrinsic dynamics from oscillatory to tonic in order for this regime change to occur, since escape remained an option even when the intrinsic dynamics were oscillatory (Fig. 8A); for example, Fig. 11, D and F show results for drive values below this transitional value (Drive = 0.4 < 0.412).

To investigate the impact of inhibition strength on the models with asymmetric drive, we fixed the drives to both units, selected such that the extensor unit was intrinsically tonically active (population model: Drive-E = 3, reduced model: Drive-E = 0.45) and the flexor unit was intrinsically oscillatory (population model: Drive-F = 1.5, reduced model: Drive-F = 0.2). Since, in the asymmetric case, the transitions from extensor active phase to flexor active phase and the transitions from flexor active phase to extensor active phase could occur by different mechanisms (escape vs. release) for a fixed parameter set, we varied the strength of the inhibitory synaptic conductance to each unit independently, holding that for the other unit fixed at its original value.

In the baseline rhythm for these parameter values, numerical simulations showed that the extensor escaped to initiate its active phase while the flexor, which received lower drive, did not escape until it was partially released. As inhibition α-E to the extensor increased, it became harder for the extensor unit to escape, leading to a longer flexor active phase and a slight decrease in frequency of the overall oscillation (Fig. 12, A and B). This effect continued with progressive increases in α-E until the transition required the extensor to be released by the flexor. Once that occurred, the oscillation was essentially independent of additional increases of α-E, since they did not affect the jump-down of the flexor to the silent phase.

Fig. 12.

Dependence of frequency on the strength of mutual inhibition between the half-centers in the asymmetric regime. A and B: for both the population (A) and reduced (B) models, changing inhibition strength to the extensor (α-E) produces almost no change in network frequency. C and D: for both the population (C) and reduced (D) models, varying the strength of inhibition to the flexor (α-F) does cause a frequency change but this effect is small relative to the case with strong symmetric drives (Fig. 11, C and D), especially in the reduced model.

On the other hand, increases in α-F had a stronger effect on frequency (Fig. 12, C and D). The key to this effect was that the extensor unit was intrinsically tonic and hence it would not fully release the flexor; that is, some component of flexor escape was always needed for the flexor to activate. Larger α-F yielded a significantly elevated h value at the left knee of the flexor V-nullcline, such that much more persistent sodium deinactivation was required for the flexor to escape, and this took much longer to achieve. Indeed, with larger α-F we observed a long extensor voltage plateau while the extensor was active before the flexor finally escaped and took over (similar to Fig. 6F but with more prolonged extensor activations; data not shown).

Thus, in the symmetric case at higher drives, when phase transitions occur based on the escape mechanism, the mutual inhibition becomes a highly effective parameter for frequency control. In the asymmetric case, similar principles imply that the inhibition level to the lower-drive unit impacts frequency more strongly than the inhibition level to the unit subject to higher drive. This result arises because the lower-drive unit must escape to activate, whereas the higher-drive unit can rely on release for its activation even when it is being strongly inhibited.

DISCUSSION

Different Views on CPG Organization: Do They Reflect Different CPGs or Different Regimes of the Same CPG?

Alternation of flexor and extensor activity represents a fundamental principle of motor control, providing coordinated alternating contraction of antagonistic flexor and extensor muscles necessary for the execution of any motor behavior including locomotion. A series of observations have shown that rhythmic alternation of flexor and extensor activity, similar to that generated during real locomotion, can be generated within the nervous system in the absence of rhythmic input signals. These observations led to the concept of a so-called half-center CPG consisting of flexor and extensor half-centers that reciprocally inhibit each other and undergo a fatigue/adaptation process that leads to sequential phase switching and flexor-extensor alternation (Brown 1914; Lundberg 1981; for review see Stuart and Hultborn 2008). This concept suggested a generally symmetric (or quasi-symmetric) organization of the half-centers and the interactions between them and did not count on the existence of intrinsic rhythmogenic properties in any of the half-centers or critical involvement of such properties in the generation of network oscillations. Despite its simplicity and obvious limitations, this “classical” concept of the half-center CPG is generally consistent with many experimental studies, including those based on fictive locomotion in cats (Burke et al. 2001; Kriellaars et al. 1994; Lafreniere-Roula and McCrea 2005; Rybak et al. 2006a, 2006b; Yakovenko et al. 2005).

An alternative asymmetric, flexor-driven organization of the locomotor CPG proposed by Pearson and Duysens (1976, “swing generator model”) suggested a dominant role of rhythmic flexor activity. According to this concept, the flexor half-center has intrinsic rhythmic capabilities while rhythmic activity of the extensor half-center results from its inhibition by the flexor half-center (Duysens et al. 2013; Pearson and Duysens 1976; Zhong et al. 2012). Recent evidence for a flexor-driven CPG organization came from studies of locomotor activity in isolated spinal cord preparations of neonatal rodents, where locomotor activity was induced by neuroactive drugs. Studies of nonresetting deletions (missing bursts) in these preparations showed two types of deletions: 1) deletions of flexor-related L2 ventral root bursts, which were accompanied by a sustained activity in the ipsilateral extensor-related L5 root, and 2) deletions of extensor-related L5 root bursts, during which the rhythmic activity in the flexor-related L2 root persisted without obvious changes (Zhong et al. 2012). Such asymmetric features of nonresetting deletions can be easily explained in terms of a flexor-driven organization of the locomotor CPG but are difficult to explain based on the symmetric half-center approach. Developmental and genetic studies also support the primacy of flexor activity in locomotor pattern generation (Britz et al. 2015; Machado et al. 2015). Measurements of how the durations of the flexion and extension phases change with frequency during drug-evoked locomotion in the isolated lumbar spinal cord (Molkov et al. 2015; Shevtsova et al. 2015; Talpalar et al. 2013) also support the flexor-driven hypothesis of the locomotor CPG. These changes of phase durations and their ratio are similar to those known from in vivo studies in cats (Frigon and Gossard 2009; Frigon et al. 2013; Halbertsma 1983).

In contrast to the above two concepts there is evidence that under certain conditions, rhythmic flexor and extensor activities can be independently evoked by optogenetic stimulation of selected areas within the isolated spinal cord (Hägglund et al. 2013), confirming that both half-centers can operate in the intrinsically rhythmic regime. The role of mutual inhibition between half-centers in this case is limited to ensuring coordinated alternation of flexor and extensor bursts.

The coexistence of these three contrasting views on CPG organization led to a situation in which some experimental data could be easily explained based on one concept but are not consistent with the other concepts. This discrepancy encouraged us to try to merge the above concepts into a common framework instantiating the principle that the same half-center CPG should be able to operate in all of the above regimes depending on conditions, such that these conditions can be changed by external inputs to the CPG without changing the CPG architecture.

In this study, we realized this framework using two modeling approaches. One approach included biologically realistic modeling of interacting populations of neurons described in the Hodgkin-Huxley style, and the second approach used a reduced activity-based description of neuron populations allowing us to use methods from dynamical systems theory to investigate network behaviors within different regimes and the transitions between them. Both models encompass different regimes, defined in terms of the intrinsic dynamics of model components, within a single framework. We show that within the relatively simple half-center network considered, rhythm-generating properties and responses to parameter changes emerge from network dynamics that override the intrinsic dynamics of each component and span across multiple dynamic regimes.

Both models had a half-center architecture. Each half-center was implemented as a conditional burster, whose intrinsic rhythmogenic properties were based on I_NaP as was suggested in previous models of the locomotor CPG (Brocard et al. 2013; Danner et al. 2016, 2017; McCrea and Rybak 2007; Rybak et al. 2006a, 2006b, 2014; Sherwood et al. 2011; Shevtsova et al. 2015; Shevtsova and Rybak 2016; Zhong et al. 2012) and supported by some experimental studies (Brocard et al. 2010, 2013; Tazerart et al. 2007, 2008; Zhong et al. 2007; Ziskind-Conhaim et al. 2008). Due to the implemented I_NaP-dependent mechanism, the expression of intrinsic bursting properties in each half-center was dependent on the neuronal excitability and hence on the external drives to the half-center. The two half-centers received independent external excitatory drives that could be either symmetric (equal) or asymmetric (unequal), which finally defined the regime of CPG operation. These control drives cannot only represent brain stem or other supraspinal inputs but can also include other sources of drive, such as afferent feedback, which could provide an additional activation of extensor circuits (Duysens et al. 2013; Pearson and Duysens 1976).

Both of our models reproduce, in the corresponding regions of the parameter space, the major distinguishing characteristics of the different CPG concepts: a classical half-center CPG, a flexor-driven asymmetric CPG, and a CPG consisting of two intrinsically bursting half-centers. Therefore, we suggest that many differences observed across the experimental results obtained from different model animals, preparations, and/or experimental conditions might not reflect fundamentally different CPG architectures, but rather represent different operational regimes of the same CPG, which are controlled and can be changed by supraspinal and afferent inputs to the CPG and by the strength of the synaptic coupling between its components.

Control of Frequency by External Drives in Different CPG Regimes

It is generally accepted that control of locomotor frequency in mammals is provided by external excitatory drive(s) conveyed to the spinal CPG via descending pathways from the brain stem and, specifically, from the MLR, whose electrical stimulation was shown to initiate locomotor oscillations in the spinal cord. An increase in the intensity of this stimulation led to an increase in locomotor frequency (Atsuta et al. 1990; Grillner 1985; Orlovsky and Shik 1976; Orlovsky et al. 1966; Shik et al. 1966; Skinner and Garcia-Rill 1984). Based on these studies, the control of oscillation frequency by external drives was implemented in many earlier and more recent models of locomotor CPGs (e.g., Danner et al. 2016, 2017; Daun et al. 2009; Yakovenko et al. 2011) including the present study.

Here we show that the control of frequency by external drives to the half-centers clearly depends on the regime of operation. Specifically, in the symmetric (or quasi-symmetric) regimes, the effectiveness and quality of this control at lower drives, for which the generation of network oscillations critically depends on the intrinsic bursting properties of both half-centers, differs from that at higher drives, for which oscillations are generated based on the classical half-center scenario not requiring intrinsic bursting capabilities in any of the half-centers (Fig. 9, A and C).

At low drives, both half-centers are intrinsically rhythmic and activation of the silent half-center occurs by release when firing of the active half-center is terminated by its own intrinsic mechanism. Initially within this regime, the frequency monotonically increases with increases in drives to both half-centers. However, the dependence of frequency on drives in this case is complicated and at some parameter sets may even have a negative slope (Fig. 9A).

In contrast, at higher drives, phase transitions from one half-center to the other occur by escape from inhibition, either because the silent half-center escapes from inhibition before it would be released by termination of firing of the active half-center, or when both half-centers become intrinsically tonic due to high enough drive. That is, escape transitions in the network can occur across both regimes of intrinsic half-center dynamics, rhythmic and tonic. The latter regime corresponds to the classical half-center framework (Brown 1914; Lundberg 1981, McCrea and Rybak 2008, Stuart and Hultborn 2008). Despite the switch in intrinsic dynamics, frequency exhibits a clear increase with drives throughout the escape case (cf. Shpiro et al. 2007; Skinner et al. 1993).

In the asymmetric (e,g. flexor-driven) regime, the network oscillations are generated due to intrinsic bursting in the flexor half-center, while the extensor half-center receives high enough drive to remain in the mode of intrinsic sustained/tonic activity. Throughout most of this regime, the onsets of flexor bursts occur by escape, since the extensor half-center will not release it. In this regime, with an increase of drive to the flexor half-center we always have a monotone increase of frequency. This regime corresponds to the “swing generator” concept (Duysens et al. 2013; Pearson and Duysens 1976). Finally, just before network oscillations are terminated, this dependency plateaus (Fig. 10, A and C), as the flexor nullcline becomes monotonic and standard release and escape are prevented.

Summarizing the above, the control of frequency by external drive is simpler and more effective in the asymmetric regime with intrinsic flexor oscillations and in the symmetric regime when phase switching occurs via an escape mechanism, which encompasses the classical half-center regime. Before the onset of the escape regime, the frequency control by drives is more complicated and may depend on intrinsic properties involved in the generation of half-center activity, such as adaptation mechanisms, rebound properties, and so on (Daun et al. 2009).

Control of Phase Durations in Different CPG Regimes

It is well established that, during normal overground or treadmill locomotion, a change in the locomotor speed, and hence in the cycle period, is mainly provided by a change in the stance phase duration (associated with extension), while the swing phase (associated with flexion) remains relatively unchanged over the range of locomotor frequencies (Frigon 2012; Gossard et al. 2011; Grillner 2006; Halbertsma 1983). In other words, the increase in frequency usually occurs due to the shortening of the stance (or extensor) phase. The mechanism providing this phase duration asymmetry is currently unknown and the proposed explanations can be split into two groups. One conceptual view is based on the idea that the CPG architecture underlying the generation of flexion and extension phases is symmetric when the CPG is isolated, and flexor-extensor phase duration asymmetry results from asymmetric inputs (supraspinal, afferent, or both) to the flexor and extensor half-centers (Armstrong 1988; Daun et al. 2009; Juvin et al. 2007; Markin et al. 2010; McCrea and Rybak 2007; Musselman and Yang 2007; Yakovenko et al. 2005). The opposite, competing view is that the flexor-extensor asymmetry is an inherent property of the CPG (Duysens et al. 2013; Frigon and Gossard 2009; Molkov et al. 2015; Pearson and Duysens 1976; Rybak et al. 2015; Shevtsova et al. 2015; Talpalar et al. 2013; Zhong et al. 2012), which was also indirectly supported by several recent studies (Britz et al. 2015; Machado et al. 2015).

One mode of operation for our CPG models is the classical half-center regime, in which both half-centers exhibit tonic intrinsic dynamics. In this regime, asymmetry in flexor-extensor phase durations can result from differences in drives to the half-centers, similar to that described in previous models based on the classical half-center idea (Daun et al. 2009; McCrea and Rybak 2007; Yakovenko et al. 2005). It has been shown previously that in such regimes, asymmetry in phase durations depends on the properties of the mechanisms defining the intrinsic half-center dynamics. Specifically, this phase-duration asymmetry was implemented by using I_NaP with slow inactivation to define the dynamics of each half-center, as we also have done in our current models; this implementation yielded asymmetry over a somewhat limited range of drives (Daun et al. 2009). In this case phase transitions occurred through the escape mechanism, such that an increased drive to one half-center shortened its silent phase (and thus shortened the active phase of the other half-center).

Another explanation for flexor-extensor asymmetry within the framework of the symmetric classical CPG architecture was recently proposed by Sobinov and Yakovenko (2017). Their model simulated a bilaterally interacting pair of half-center CPGs, in which flexor-extensor asymmetry could arise either from asymmetric drives or from asymmetric bilateral left-right interaction between the CPGs. However, the issue of bilateral interactions is outside the scope of the models considered in this paper.

At the same time, our CPG models can instantiate a qualitatively different regime in which the flexor half-center operates in the intrinsic bursting mode whereas the extensor half-center if isolated operates in the mode of sustained/tonic activity. In this fundamentally asymmetric regime, an increase of drive to the flexor half-center results in an increase of frequency that mostly occurs due to shortening of the extensor phase with a relatively constant flexor phase. This model behavior explicitly reproduces the speed-dependent changes of locomotor phase durations during locomotion in vivo (Frigon and Gossard 2009; Halbertsma 1983). The mechanism of this asymmetry in the model is based on the I_NaP-dependent intrinsic bursting mechanism operating in the flexor half-center, according to which the external drive affects the interburst interval much more strongly than it affects the burst duration. This regime also features transitions by escape and can extend over a broad range of drives encompassing a wide range of frequencies (e.g., most of the frequency range in Fig. 10, C and D). This type of flexor-extensor asymmetry was implemented in a series of recent models (Danner et al. 2016, 2017; Molkov et al. 2015; Shevtsova et al. 2015).

The Role of Inhibition in the Symmetric and Asymmetric Regimes

In addition to investigating the possibility of frequency and phase duration control by external drives, we have tested how oscillation frequency in each regime depends on the strength of mutual inhibition between the two half-centers. We found that the effect of changes in the strength of inhibition also depends on the network’s dynamic regime. Inhibition strength is more effective for the control of frequency in the symmetric modes at high external drives, which correspond to the classical CPG regime and employ the escape phase-transition mechanism (Fig. 11, C and D).

In the asymmetric regime, the strength of inhibition to the flexor half-center impacts frequency more strongly than the strength of inhibition to the extensor half-center, which is subject to higher drive (Fig. 12). This difference in frequency response is due to the fact that the flexor half-center must rely on escape to activate whereas the extensor half-center can rely on release even when inhibition is strong. Our models thus provide testable predictions for the activity of isolated spinal cords with selective manipulation of different types of inhibition mediated by two different groups of genetically identified, inhibitory interneurons, known as V1 and V2b. These two groups are critically involved in alternation of flexor and extensor activity with distinct roles in the control of the durations of flexor and extensor phases (Britz et al. 2015; Shevtsova and Rybak 2016; Zhang et al. 2014).

General Conclusions

In this theoretical study, we have developed and analyzed computational models of a half-center CPG consisting of two half-centers with conditional intrinsic bursting properties interacting through reciprocal inhibition. By manipulating external excitatory drives to each or both of the half-centers we could change the operating regimes of the CPG and reproduce several characteristic properties of the spinal locomotor network known from experimental studies. Using our models, we analyzed the control of CPG oscillation frequency and phase durations in different operating regimes. We show that control of frequency and phase durations by external drives to the half-centers in each regime depends primarily on the phase transition mechanisms operating within the network (escape or release) rather than on the intrinsic dynamics within the half-centers. Indeed, half-center dynamics are mostly masked within the network setting, although in some cases they do constrain which phase transition mechanisms are available. These results illustrate that even if the half-centers in two different CPGs exhibit different dynamics in isolation, the two CPGs may show similar frequency control and other properties. Our models show that seemingly contradictory experimental data on the generation of the locomotor rhythm, control of locomotor frequency, and frequency-dependent changes in locomotor phase durations can be reproduced within a simple half-center CPG and thus provide a common framework for uniting different contradicting concepts of CPG organization. This study may yield new insights into the organization of the locomotor CPG and its operation under different conditions.

GRANTS

This work was supported by the National Science Foundation [NSF Award 1612913 (J. E. Rubin)] and the National Institutes of Health [NIH grants: R01 NS081713 (I. A. Rybak), R01 NS090919 (I. A. Rybak), and R01 NS095366 (N. A. Shevtsova)].

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

J.A., I.A.R., and J.E.R. conceived and designed research; J.A., A.C.S., I.A.R., and J.E.R. performed experiments; J.A., A.C.S., N.A.S., I.A.R., and J.E.R. analyzed data; J.A., A.C.S., N.A.S., I.A.R., and J.E.R. interpreted results of experiments; J.A., A.C.S., I.A.R., and J.E.R. prepared figures; J.A., N.A.S., I.A.R., and J.E.R. drafted manuscript; J.A., N.A.S., I.A.R., and J.E.R. edited and revised manuscript; J.A., A.C.S., N.A.S., I.A.R., and J.E.R. approved final version of manuscript.