Manipulating thermal emission with spatially static fluctuating fields in arbitrarily shaped epsilon-near-zero bodies

Significance

Harnessing thermal fields is a current scientific challenge with far-reaching technological implications on heat and energy management, chemistry, and bioengineering. However, the random nature of thermal field sources, which eliminates phase information, hinders the use of interference-based conventional optical techniques. We propose an alternative route to control thermal fields based on epsilon-near-zero (ENZ) media, a medium with near-zero permittivity. We show how the effective enlargement of the wavelength on ENZ media results on intrinsically (material-based) enhanced spatial coherence, quite independently of the geometry of the ENZ body itself. This provides distinct opportunities in engineering thermal radiation, while maintaining flexibility on the geometrical degrees of freedom (shape of the body and/or position of the particles within it).

Abstract

The control and manipulation of thermal fields is a key scientific and technological challenge, usually addressed with nanophotonic structures with a carefully designed geometry. Here, we theoretically investigate a different strategy based on epsilon-near-zero (ENZ) media. We demonstrate that thermal emission from ENZ bodies is characterized by the excitation of spatially static fluctuating fields, which can be resonantly enhanced with the addition of dielectric particles. The “spatially static” character of these temporally dynamic fields leads to enhanced spatial coherence on the surface of the body, resulting in directive thermal emission. By contrast with other approaches, this property is intrinsic to ENZ media and it is not tied to its geometry. This point is illustrated with effects such as geometry-invariant resonant emission, beamforming by boundary deformation, and independence with respect to the position of internal particles. We numerically investigate a practical implementation based on a silicon carbide body containing a germanium rod.

The manipulation of the fluctuations of thermal fields as well as their radiation into the surrounding environment is central to the development of light sources (1, 2), heat management (3), thermophotovoltaics (4), bioengineering (5), and near-field energy transfer (6, 7). Thermal fields are inherently broadband and stochastic (8, 9), making them challenging to manipulate via traditional optical techniques, which ultimately resort to interference phenomena. However, different photonic nanostructures have been successfully utilized to address this challenge, including corrugated surfaces supporting surface plasmons (1, 9, 10), photonic crystals (4, 11–13), resonators (14, 15), metamaterials (16–19), graphene (20), transformation optics (21), and angle-selective filters (22, 23). In essence, these methodologies utilize structural degrees of freedom to either suppress (e.g., photonic bandgaps, angle-selective filters) or enhance (e.g., resonant cavities, corrugated surfaces) specific modes, thus leading to an enhanced spatial coherence that allows for a partial control of thermal fields.

Here, we investigate an alternative route in engineering thermal emission by using epsilon-near-zero (ENZ) media, that is, continuous media or metamaterials exhibiting a near-zero permittivity (24–27). The electromagnetic response of ENZ media is characterized by an effectively stretched wavelength and large phase velocity, resulting in spatially static fields dynamically oscillating in time (26). This behavior makes possible intriguing wave phenomena, including supercoupling (27–29), photonic doping (30), enhanced nonlinear response (31–33), geometry-invariant resonators (34), nonradiating modes (35–39), inhibition and enhancement of vacuum fluctuations (40, 41), etc. Here, we show that an effectively enlarged wavelength results in an intrinsically (material-based) enhanced spatial coherence, quite independently of the geometry of the ENZ body itself. Therefore, ENZ media offers the unique possibility of manipulating fluctuating fields and thermal emission while preserving several structural degrees of freedom. This point will be exemplified by effects such as geometry-invariant resonant emission, beamforming by boundary deformation, and independence with respect to the position of the internal particles.

Previous works have addressed thermal emission from ENZ media, particularly thin films and substrates, using structural resonances associated with the excitation of the so-called ENZ modes and/or enhanced longitudinal fields (42–44). As noted before, our work is fundamentally different as it does not rely on any particular geometry or structural resonance of the ENZ host. Previous works have also addressed other forms of emission in ENZ media. Typically, the enlargement of the wavelength is utilized to obtain a high directivity (26, 45). It also provides beamforming capabilities (46, 47) as well as enhanced collective emission (48–54). However, emission from thermal sources is qualitatively different from those studies since they consist of a random distribution directly impressed on ENZ media. In particular, radiation from thermal sources can be semiclassically described by a fluctuating current density whose frequency components, $\mathit{j}\left(\mathbf{r},\omega \right)$, obey the correlation function, $\langle j_p\left(\mathbf{r},\omega \right)j_q^{\ast }\left(\mathbf{r}\prime ,\omega \prime \right)\rangle =4\pi \omega {\epsilon }_0\mathrm{\Theta }\left(\omega ,T\right)\mathrm{Im}\left\{\epsilon \left(\mathbf{r},\omega \right)\right\}\delta \left(\omega -\omega \prime \right)\delta \left(\mathbf{r}-\mathbf{r}\prime \right){\delta }_{pq}$, consistent with the fluctuation dissipation theorem (9). Therefore, a careful analysis of the fields excited by sources directly impressed in ENZ media is required to elucidate its nontrivial thermal emission properties.

Theory of Thermal Emission in the ENZ Limit

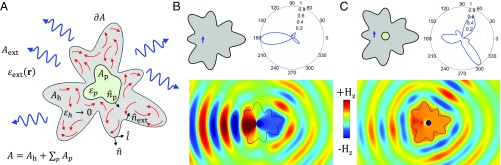
We consider a general scenario, schematically depicted in Fig. 1A, in which a 2D ENZ body of arbitrary shape and cross-sectional area $A$ is immersed in a photonic environment characterized by permittivity distribution ${\epsilon }_{\text{ext}}\left(\mathbf{r},\omega \right)$ on the external region $A_{\text{ext}}$. This body contains a number $N$ of 2D particles of arbitrary shape and cross-sectional area $A_p$, characterized by relative permittivity ${\epsilon }_p\left(\mathbf{r},\omega \right)$. Consequently, the remaining area of the ENZ host is $A_h=A-{\displaystyle {\sum }_p{A}_p}$. All materials are assumed to be nonmagnetic; thus, $\mu ={\mu }_0$.

Fig. 1.

(A) Sketch of the geometry: A 2D epsilon-near-zero (ENZ) (${\epsilon }_h\to 0$) body of cross-sectional area $A_h$ containing one or more 2D dielectric particles of cross-sectional area $A_p$ and relative permittivity ${\epsilon }_p$, is immersed in a photonic environment $A_{\text{ext}}$ characterized by relative permittivity ${\epsilon }_{\text{ext}}\left(\mathbf{r}\right)$. The permeability of all of the materials is taken to be that of free space. The body is assumed to be at thermal equilibrium at temperature $T$, resulting in thermal emission into the environment modeled as the radiation of fluctuating currents impressed on the body (shown as red arrows). (B) Sketch (Top Left), emission pattern (Top Right), and snapshot of the magnetic field distribution (Bottom) when the system is excited by a 2D line of point electric dipole (i.e., a line dipole) (shown as a blue arrow) directly impressed on the ENZ body. (C) Same as in B, but the body contains a dielectric rod of permittivity ${\epsilon }_p=10$ and radius $r_p=0.122{\lambda }_p$, designed resonantly to enhance the constant magnetic field. The numerical simulations ratify the excitation of spatially static fields on the ENZ host and the coupling to the environment in the form of directive emission.

We are interested in the radiation from a distribution of z-independent transversal currents $\mathit{j}\left(\mathit{\rho }\right)$, with $\widehat{\mathit{z}}\cdot \mathit{j}\left(\mathit{\rho }\right)=0$, directly impressed on the ENZ host (the z axis being parallel with the axis of all these 2D bodies). Without loss of generality, the magnetic field in each region is prescribed by the solution to the scalar Helmholtz equation (SHE), ${\nabla }^2{H}_z\left(\mathit{\rho },\omega \right)+k^2\left(\mathit{\rho },\omega \right)H_z\left(\mathit{\rho },\omega \right)=K_z\left(\mathit{\rho },\omega \right)$, where $k\left(\mathit{\rho },\omega \right)={\omega }^2/c^2\epsilon \left(\mathit{\rho },\omega \right)$ is the propagation constant and $K_z\left(\mathit{\rho },\omega \right)=-\widehat{\mathit{z}}\cdot \nabla \times \mathit{j}\left(\mathit{\rho }\right)$ is a source term. The general solution to SHE is constrained by the boundary conditions imposed by the continuity of $H_z$ and ${\epsilon }^{-1}\partial H_z/\partial n$ at every boundary. Crucially, in the ENZ limit (${\epsilon }_{\text{h}}\to 0$), SHE asymptotically collapses to Poisson’s equation (PE) ${\nabla }^2{H}_z\left(\mathit{\rho },\omega \right)=K_z\left(\mathit{\rho },\omega \right)$ and the second boundary condition reduces to $\partial H_z/\partial n=0$ on $\partial A_h$. Therefore, the magnetic field excited in the ENZ host is given by the solution to the Neumann problem of Poisson’s equation, which is known to exist and be unique up to an additive constant (55). Consequently, the magnetic field in the ENZ host can in general be written as follows:

$$H_z\left(\mathit{\rho },{\omega }_{\mathrm{ENZ}}\right)=H_z^{\mathrm{PE}}\left(\mathit{\rho }\right)+H_z^{\mathrm{cst}}\left({\omega }_{\mathrm{ENZ}}\right)\text{on}\hspace{0.17em}{A}_h.$$ [1]

The field distribution ([1]) formally justifies the excitation of spatially static fields dynamically oscillating in time. As anticipated, its spatially static character results in an enhanced spatial coherence, due to the lack of phase variation and extended range of these distributions in the ENZ region. In this equation, $H_z^{PE}\left(\mathit{\rho }\right)$ is the solution to PE under the Neumann boundary condition, which is a spatial distribution prescribed by the solution to the static problem, and not a function of the frequency at which the ENZ behavior takes place, ${\omega }_{\mathrm{ENZ}}$. $H_z^{\mathrm{cst}}\left({\omega }_{\mathrm{ENZ}}\right)$ is the constant term, which is simply independent of position in the ENZ volume.

Importantly, the solution ([1]) defines the field distribution on all of the other regions: $A_{\text{ext}}$ and $A_p$ for $p=1,\dots ,N$, which can be written by application of Green’s identities as follows (56):

$$\begin{array}{c}{H}_z\left(\mathit{\rho },{\omega }_{\mathrm{ENZ}}\right)={\displaystyle {\oint }_{\partial A_j}d{l}^{\prime }}\frac{\partial G_j\left(\mathit{\rho },{\mathit{\rho }}^{\prime },{\omega }_{\mathrm{ENZ}}\right)}{\partial n_j}{H}_z^{\mathrm{PE}}\left(\mathit{\rho }\prime \right)\\ +F_j\left(\mathit{\rho },{\omega }_{\mathrm{ENZ}}\right)H_z^{\mathrm{cst}}\left({\omega }_{\mathrm{ENZ}}\right)\hspace{1em}\text{on}\hspace{1em}{A}_j\hspace{0.17em}\text{with}\hspace{0.17em}j=\text{ext},1,\dots ,N.\end{array}$$ [2]

Here, $G_j\left(\mathit{\rho },{\mathit{\rho }}^{\prime },\omega \right)$ is the Green’s function for the SHE subject to $G_j\left(\mathit{\rho },{\mathit{\rho }}^{\prime },\omega \right)=0$ on $A_j$. $F_j\left(\mathit{\rho },{\omega }_{\mathrm{ENZ}}\right)={\displaystyle {\oint }_{\partial A_j}d{l}^{\prime }}\hspace{0.17em}\partial G_j\left(\mathit{\rho },{\mathit{\rho }}^{\prime },{\omega }_{\mathrm{ENZ}}\right)/\partial n_j$ is an auxiliary function describing the magnetic field at $\mathit{\rho }$ per unit of constant magnetic field on $\partial A_j$. Eq. 2 also serves to reemphasize how the spatially static distribution ([1]) couples to the external environment via the boundary $\partial A_{\text{ext}}$, exciting propagating waves in the form of directive thermal emission. This effect is further illustrated in Fig. 1B with a numerical simulation for the fields excited by a 2D point-dipole source.

Eqs. 1 and 2 define the complete solution to the problem, except for the value of the constant field $H_z^{\mathrm{cst}}\left({\omega }_{\mathrm{ENZ}}\right)$. This value can be found by noting that the field distribution ([1] and [2]) must be obviously consistent with Maxwell equations, where electric and magnetic fields are coupled via $\nabla \times \mathit{E}=i\omega {\mu }_0\mathit{H}$. By imposing Faraday’s law on the external boundary of the host: ${\mathrm{ℰ}}_{\partial A}=i\omega {\mathrm{\Phi }}_A$ [i.e., the electromotive force (emf) on $\partial A,\hspace{0.17em}{\mathrm{ℰ}}_{\partial A}={\displaystyle {\oint }_{\partial A}dl\prime \hspace{0.17em}\widehat{l}\cdot \mathit{E}}$, equals minus the time derivative of the flux on $A$], and rearranging the terms leads us to the following expression (Supporting Information):

$$H_z^{\mathrm{cst}}=\frac{i{\omega }_{\mathrm{ENZ}}{\mathrm{\Phi }}_A^{\mathrm{PE}}-{\mathrm{ℰ}}_{\partial A}^{\mathrm{PE}}}{{\mathcal{Z}}_{\partial A}-i{\omega }_{\mathrm{ENZ}}{\mathrm{ℒ}}_h+i{{\displaystyle \sum }}_p{X}_p}.$$ [3]

In this expression, ${\mathrm{\Phi }}_A^{\mathrm{PE}}={\mu }_0{\displaystyle {\int }_{A}dA}\hspace{0.17em}{H}_z^{\mathrm{PE}}\left(\mathit{\rho }\right)$ and ${\mathrm{ℰ}}_{\partial A}^{\mathrm{PE}}={\left(i{\omega }_{\mathrm{ENZ}}{\epsilon }_0\right)}^{-1}{\displaystyle {\oint }_{\partial A}dl{\displaystyle {\oint }_{\partial A_{\text{ext}}}d{l}^{\prime }}}{\partial }^2{G}_{\text{ext}}\left(\mathit{\rho },{\mathit{\rho }}^{\prime },{\omega }_{\mathrm{ENZ}}\right)/\partial n\partial n_{\text{ext}}{H}_z^{\mathrm{PE}}\left(\mathit{\rho }\prime \right)$ are the magnetic flux and electromotive force, respectively, associated with $H_z^{\mathrm{PE}}$. ${\mathcal{Z}}_{\partial A}={\left(i{\omega }_{\mathrm{ENZ}}{\epsilon }_0\right)}^{-1}{\displaystyle {\oint }_{\partial A}dl}\hspace{0.17em}\partial F_{\text{ext}}\left(\mathit{\rho },{\omega }_{\mathrm{ENZ}}\right)/\partial n$ is a surface impedance (per unit length in the z direction) relating the emf on $\partial A$ per unit of constant magnetic field. Similarly, ${\mathrm{ℒ}}_h={\mu }_0{A}_h$ is the inductance of the host and $X_p=-{\omega }_{\mathrm{ENZ}}{\mu }_0{\displaystyle {\int }_{A_p}dA}\hspace{0.17em}{F}_p\left(\mathit{\rho },{\omega }_{\mathrm{ENZ}}\right)$ is the 2D particle reactance.

Eq. 3 also suggests a strategy to resonantly enhance the constant field distribution, which will be maximized for ${\omega }_{\mathrm{ENZ}}{\mathrm{ℒ}}_h={\displaystyle {\sum }_p{X}_p}$. This resonance effect can be intuitively understood as follows: the solution to PE, $H_z^{\mathrm{PE}}\left(\mathit{\rho }\prime \right)$, and its associated electric field present an unbalanced Faraday’s law that must be compensated by the contribution of $H_z^{\mathrm{cst}}$. However, if the internal particles are designed such that the magnetic flux per unit of constant field is very small (i.e., for a vanishing effective reactance $-{\omega }_{\mathrm{ENZ}}{\mathrm{ℒ}}_h+{\displaystyle {\sum }_p{X}_p}\to 0$), a very strong $H_z^{\mathrm{cst}}$ will be required for a consistent solution. Under this condition, the field emitted by the sources is dominated by the contribution from $H_z^{\mathrm{cst}}$, that is, $H_z\left(\mathit{\rho },{\omega }_{\mathrm{ENZ}}\right)\approx F_{\text{ext}}\left(\mathit{\rho },{\omega }_{\mathrm{ENZ}}\right)H_z^{\mathrm{cst}}\left({\mathit{\rho }}_{\mathrm{ENZ}}\right)$. This effect is illustrated in Fig. 1C with a simple numerical simulation. Interestingly, this result indicates that even if the field is excited by a random distribution of sources, they will nevertheless radiate with a uniform field distribution (in magnitude and phase) on the surface of the object, resulting in an even more highly directive emission.

Our analysis up to this point has been focused on the magnetic field distribution, which is sufficient to determine the fields radiated by a directly impressed sources distribution. The associated electric field, characterized by a dominant nonradiating component, is discussed in Supporting Information.

Thermal Emission from SiC 2D Structure Augmented with Germanium Rods

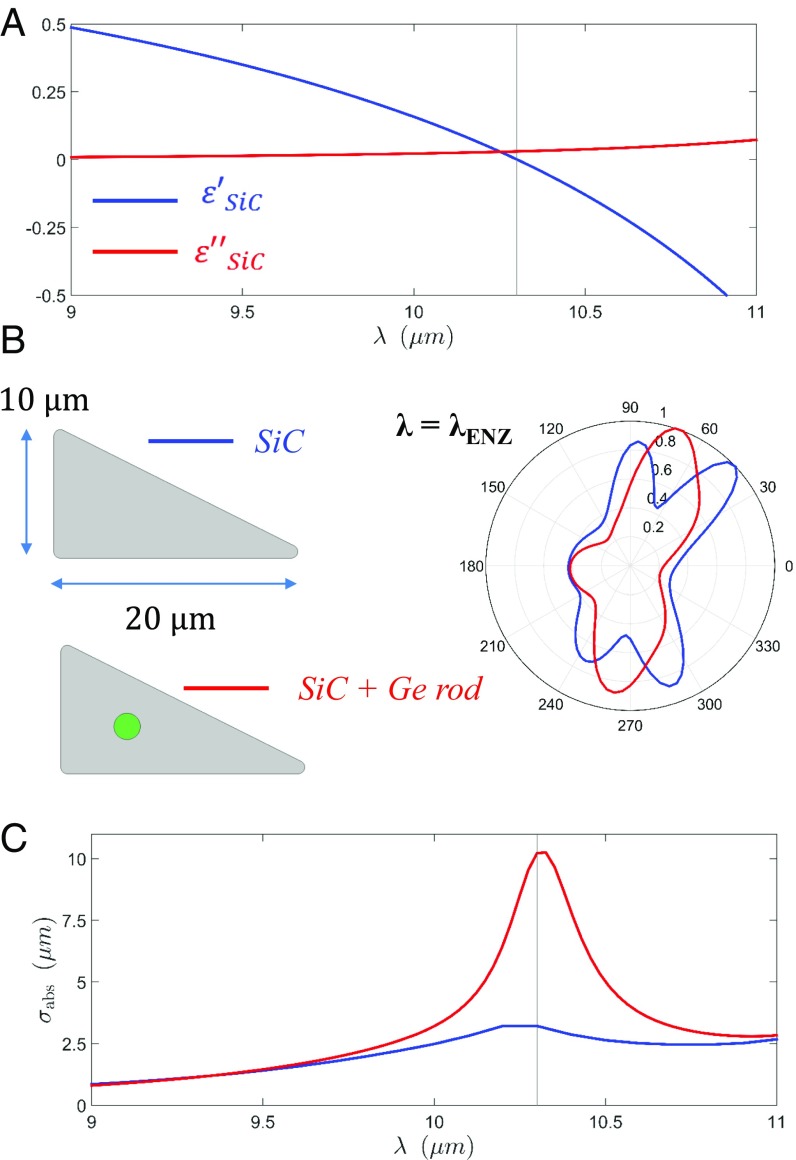
The previous theoretical analysis has been based on the asymptotic ENZ limit, and, even if exact, it remains to be demonstrated whether it can successfully describe systems with realistic material parameters including material loss. To this end, we investigate thermal emission from silicon carbide (SiC) 2D bodies containing germanium (Ge) rods. SiC provides a relatively high-quality ENZ response in the MIR [${\epsilon }_{\mathrm{SiC}}\approx i0.03$ at ${\lambda }_{\text{ENZ}}=10.3\hspace{0.5em}\mathrm{\mu }\text{m}$ (57, 58); Fig. 2A], while germanium (Ge) provides a low-loss high dielectric constant in the same frequency range [${\epsilon }_{\text{Ge}}\approx 16$ at ${\lambda }_{\text{ENZ}}=10.3\hspace{0.17em}\mathrm{\mu }\text{m}$ (59)]. As a case study, we consider thermal emission by a 2D SiC rod, whose cross-section is a right triangle with catheti $2{\lambda }_{\text{ENZ}}\times {\lambda }_{\text{ENZ}}$ and round corners. We emphasize that this body is not particularly optimized and it has been chosen for illustrative purposes and with area $A={\lambda }_{\text{ENZ}}^2$. To investigate the effect of resonant enhancement of the constant field, the body might optionally contain a Ge rod of circular cross-section, whose radius $r_p=0.096\hspace{0.17em}{\lambda }_{\text{ENZ}}$, and is designed to satisfy the above-mentioned resonant condition.

Fig. 2.

Thermal emission from 2D silicon carbide bodies augmented with dielectric rods. (A) Dielectric permittivity of silicon carbide (SiC) as a function of wavelength. Real part of the relative permittivity approaches zero at the wavelength ${\lambda }_{\text{ENZ}}=10.3\hspace{0.5em}\mathrm{\mu }\text{m}$ (highlighted by a vertical gray line) (57, 58). (B) Sketch (Left) and thermal emission pattern at ${\lambda }_{\text{ENZ}}$ (Right, computed by calculating the absorption and exploiting generalized Kirchhoff’s law). The 2D geometry consists of a right triangle (with round corners) with catheti of length 10 and 20 μm, with (red line) and without (blue line) containing a germanium rod (${\epsilon }_{\text{Ge}}\approx 16$) of radius $r_p=0.096\hspace{0.17em}{\lambda }_{\text{ENZ}}$. (C) Absorption cross-section for an incoming plane wave $\mathit{H}\left(\mathbf{r}\right)=\widehat{\mathit{z}}{H}_0\exp \left[-i{\omega }_{\text{ENZ}}\left(t-{\widehat{\mathbf{r}}}_{\text{inc}}\cdot \mathbf{r}/\text{c}\right)\right]$, corresponding to thermal emission in the −${\widehat{\mathbf{r}}}_{\text{inc}}$ direction (=63.4°). The numerical simulations ratify the resonant enhancement and directive thermal emission of 2D ENZ bodies augmented with dielectric particles.

Direct calculation of thermal emission requires from the computation of the field emitted by a random distribution of currents characterized by the aforementioned correlation function (9). Fortunately, direct application of reciprocity results in a generalized form of Kirchhoff’s law (60, 61) that links the emitted power with the absorption cross-section of the body $P_{\text{emit}}\left(\widehat{l},\widehat{r},\omega ,T\right)=1/2\hspace{0.17em}{I}_b\left(\omega ,T\right){\sigma }_{\text{abs}}\left(\widehat{l},-\widehat{r},\omega \right)$, which allows for an efficient calculation. The arguments should be read as power emitted by a body at temperature $T$ at frequency $\omega$ per unit of solid angle along the direction $\widehat{r}$, with polarization $\widehat{l}$. $I_b\left(\omega ,T\right)$ stands for the black-body radiance.

Fig. 2B depicts a comparison that the emission pattern of the SiC triangular 2D body at the ENZ wavelength with and without the Ge circular rod. In both cases, the emission pattern is found to be directive (for a body of size ∼λ_ENZ), as expected from the excitation of spatially static fields. In the bare SiC case, the emission is primarily constructed by the sum over the field intensities produced by distributions $H_z^{\mathrm{PE}}\left(\mathit{\rho }\right)$ for point sources at each $\mathit{\rho }\prime$, and therefore, the emission pattern has a nontrivial shape. On the other hand, when the body is augmented with the dielectric rod, the emission is dominated by a constant field distribution on the external surface, thus resulting in an emission pattern with three distinct lobes, one per each side of the body. Fig. 2C depicts the absorption cross-section for an incoming wave propagating along the $\widehat{\mathit{y}}$ direction (corresponding to the emission spectra that would be measured by a detector located in the $-\widehat{\mathit{y}}$ direction). The figure shows that the emission is locally enhanced around ${\lambda }_{\text{ENZ}}$ for the base SiC rod, and it is resonantly enhanced when the body is augmented with a dielectric rod.

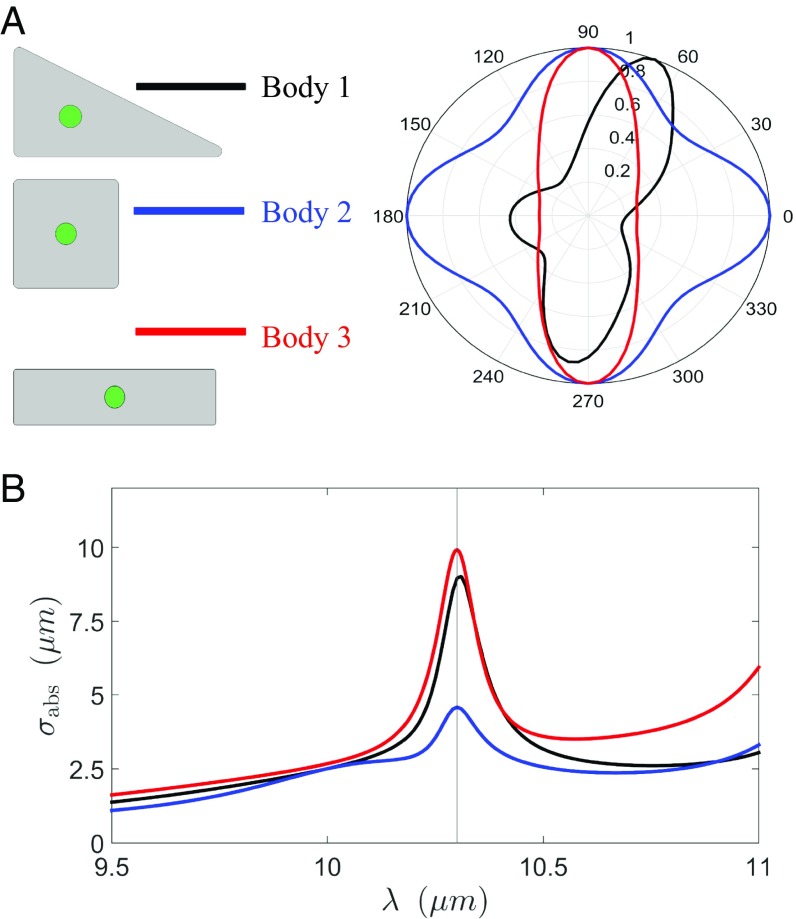
These numerical simulations illustrate that the theory of thermal emission in the ENZ limit could be observed in practice in SiC bodies, which could radiate at the ENZ wavelength as if supporting a uniform field distribution on its boundary. Moreover, thermal emission from these bodies would exhibit some of the exotic wave dynamics associated with zero-index media (24). For example, in full analogy with previously studied geometry-invariant resonant cavities (34), it is clear from the condition ${\omega }_{\mathrm{ENZ}}{\mathrm{ℒ}}_h={\displaystyle {\sum }_p{X}_p}$ that the resonant enhancement of the magnetic field occurs independently of the geometry of the external boundary of the host. Therefore, the body could be continuously deformed (while maintaining a constant area) and it will still exhibit a clear spectral feature at ${\lambda }_{\text{ENZ}}$ (Fig. 3). We emphasize that this is a collective resonant effect in which the entire body, and not the internal particle, is collectively excited and emits with a uniform field distribution on its surface. In turn, this enables a unique beamforming technique: one can simply change the number of sides and their length to add or remove, enhance, or mitigate, lobes in the emission pattern. As shown in Fig. 3, we simply find that a triangle cross-section will result in three distinct lobes, whereas square cross-section exhibits four lobes, and a rectangle will exhibit two dominant lobes. Larger directives would be obtained by increasing the size of the body and/or with smaller losses.

Fig. 3.

Geometry-invariant effects in ENZ thermal emission. (A) Sketch of the geometry and emission pattern at the ENZ wavelength, and (B) absorption cross-section for an incident plane-wave $\mathit{H}\left(\mathbf{r}\right)=\widehat{\mathit{z}}{H}_0\exp \left[-i{\omega }_{\text{ENZ}}\left(t-\widehat{y}\cdot \mathbf{r}/\text{c}\right)\right]$, corresponding to thermal emission in the −$\widehat{y}$ direction. The 2D geometry consists of a dielectric rod with three different cross-sections of area ${\lambda }_{\text{ENZ}}^2$ containing a germanium dielectric rod (${\epsilon }_{\text{Ge}}\approx 16$) of radius $r_p=0.096\hspace{0.17em}{\lambda }_{\text{ENZ}}$. Right triangle cross-section with catheti of length ${\lambda }_{\text{ENZ}}$ and $2{\lambda }_{\text{ENZ}}$ (black line), square cross-section of side ${\lambda }_{\text{ENZ}}$ (blue line), and $0.5{\lambda }_{\text{ENZ}}\times 2{\lambda }_{\text{ENZ}}$ rectangle cross-section (black line). The numerical results evidence geometry-invariant effects (a resonant spectral feature is observed at the same resonance frequency independently of the geometry of the external boundary keeping the same cross-sectional area) and beamforming capabilities (the emission patterns consist of one lobe per side of the body with emission strength proportional to the side of the triangle).

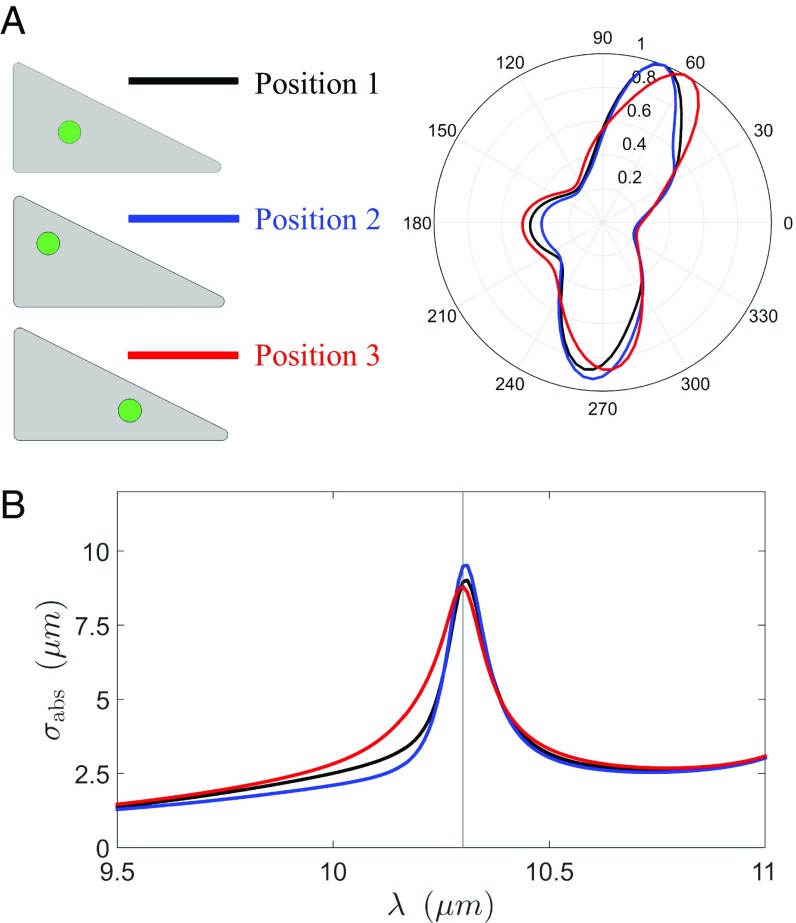
Another interesting effect associated with ENZ media is that of position independence, that is, the invariance of certain observables with respect to the position of particles in the host, also observed in related but different phenomena such as photonic doping (30). In our present study, since the resonant enhancement is triggered by the interaction of a constant field with dielectric particles, we could expect that the position of the particles play a small role in the process. We numerically test this property in Fig. 4 by analyzing the emission pattern and emission spectra for three different positions of the dielectric rod. The numerical simulations indeed confirm that, even with realistic materials parameters, the abortion cross-section/thermal emission is very robust against changes in the position of the particles.

Fig. 4.

Position-independent thermal emission. (A) Sketch of the geometry and emission pattern at the ENZ wavelength, and (B) absorption cross-section for an incident plane-wave $\mathit{H}\left(\mathbf{r}\right)=\widehat{\mathit{z}}{H}_0\exp \left[-i{\omega }_{\text{ENZ}}\left(t-\widehat{y}\cdot \mathbf{r}/\text{c}\right)\right]$, corresponding to thermal emission in the −$\widehat{y}$ direction. The 2D geometry consists of a dielectric rod with a right triangle cross-section with catheti of length 10 and 20 μm, containing a germanium dielectric rod (${\epsilon }_{\text{Ge}}\approx 16$) of radius $r_p=0.096\hspace{0.17em}{\lambda }_{\text{ENZ}}$ located at three different positions. The numerical simulations illustrate the robustness of thermal emission with respect to the position of the dielectric rod.

To finalize, although the main goal of this work is not to design a system for a specific application, we comment on the limits of directivity and bandwidth of the system, as well as the compromises to be addressed during the design process. In theory, since the excited magnetic field is dominated by a constant field term, the directivity of thermal emission would monotonically increase with the size of the body. On the other hand, as the size of the system progressively decreases, the response of the system would converge to the usual “quasistatic” (i.e., small-size) limit, as any other photonic structure would do, where the response of the system can be described by its polarizability. In practice, material loss deviates the behavior of the system from the theoretical ENZ limit, and there will be a threshold size beyond which the directivity stops increasing (Fig. S2). However, since the strength of the fluctuation currents is proportional to material loss, we find that, for a given geometry, there will be a compromise between directivity and emission rate. The design of a device optimizing this compromise for a given material, geometry, or application is out of the scope of the present study and is left for future investigation. Similarly, the bandwidth of enhanced thermal emission will be determined by the bandwidth of the resonance, whose quality factor is determined by damping mechanisms associated with material and radiation loss. In this manner, the bandwidth of the system can be controlled with material losses (imaginary part of the permittivity) and the size of the body (Fig. S3).

Extension to 3D Configurations

Although a 2D geometry has been assumed through this work, any physical implementation of the proposed theory will be necessarily constructed with a 3D body. For instance, we could extrude the body into the z direction to observe similar effects. Indeed, for an infinitely large 3D body, the electromagnetic emission can be decomposed into modes with out-of-plane propagation constants $k_z\in [-k_0,k_0]$. Evaluating the emitted field in the far zone using the stationary-phase approximation reveals that each mode corresponds to emission in the elevation angle $\theta =\cos \left(k_z/k_0\right)$ (62). Consequently, our analysis, corresponding to the $k_z=0$ case, is directly related to the emission by an 3D body in the azimuthal direction $\theta =\pi /2$. Naturally, any practical implementation will have a finite height. However, as the aspect ratio of the body increases, the emission in the azimuthal direction will converge to that of the 2D configuration. This effect is numerically studied in Fig. 5, which presents a comparison between the normalized emission patterns in the $\theta =\pi /2$ plane for the previously studied 2D configuration and 3D cases with increasing height. The numerical simulations confirm that the thermal emission in the azimuthal plane converges to the 2D case as the aspect ratio of the 3D case increases, and practically no difference when the body has a height of 80 µm.

Fig. 5.

Emission from 3D bodies. (Top) Sketch of the geometry, being identical to that in Fig. 2, except the 2D body has been extruded by a height L_z. (Bottom) Comparison of the numerical prediction of the normalized emission pattern at the ENZ wavelength, λ_ENZ = 10.3 μm, in the azimuthal plane (θ = π/2, H_z polarization), for the 2D case and 3D cases with heights L_z = 10, 20, and 80 μm. The numerical simulations confirm that the thermal emission in the azimuthal plane converges to the 2D case as the aspect ratio of the 3D case increases.

Conclusions

Our theoretical results suggest that ENZ media might provide an alternative route to controlling and shaping fluctuating fields and engineering thermal emission. We demonstrate that the excitation of spatially static fluctuating fields intrinsically result in directive thermal emission, accompanied by effects such as geometry-invariant resonant enhancement, beamforming by boundary deformation and position independence. Therefore, facilitated by the availability of ENZ media in the midinfrared, these results might find applications in energy management and the development of programmable and/or reconfigurable thermal light sources.

Methods

All numerical simulations were carried out with the commercially available full-wave electromagnetic simulator software COMSOL Multiphysics, version 5.2 (www.comsol.com/), using the frequency domain solver. The field distributions and emission patterns depicted in Fig. 1 and Fig. S1 were computed by exciting the system with a point 2D dipole. The emission patterns and absorption/emission spectra in Figs. 2–5 were obtained by exciting the system with a propagating plane wave, and scattering the incident angle over the XY plane. The absorption scattering cross-section was then obtained by means of field integration, and the thermal emitted power was obtained via the generalized Kirchhoff’s law (60, 61).