Abstract
Parkinson’s disease (PD) is an overwhelming neurodegenerative disorder caused by deterioration of a neurotransmitter, known as dopamine. Lack of this chemical messenger impairs several brain regions and yields various motor and non-motor symptoms. Incidence of PD is predicted to double in the next two decades, which urges more research to focus on its early diagnosis and treatment. In this paper, we propose an approach to diagnose PD using magnetic resonance imaging (MRI) data. Specifically, we first introduce a joint feature-sample selection (JFSS) method for selecting an optimal subset of samples and features, to learn a reliable diagnosis model. The proposed JFSS model effectively discards poor samples and irrelevant features. As a result, the selected features play an important role in PD characterization, which will help identify the most relevant and critical imaging biomarkers for PD. Then, a robust classification framework is proposed to simultaneously de-noise the selected subset of features and samples, and learn a classification model. Our model can also de-noise testing samples based on the cleaned training data. Unlike many previous works that perform de-noising in an unsupervised manner, we perform supervised de-noising for both training and testing data, thus boosting the diagnostic accuracy. Experimental results on both synthetic and publicly available PD datasets show promising results. To evaluate the proposed method, we use the popular Parkinson’s progression markers initiative (PPMI) database. Our results indicate that the proposed method can differentiate between PD and normal control (NC), and outperforms the competing methods by a relatively large margin. It is noteworthy to mention that our proposed framework can also be used for diagnosis of other brain disorders. To show this, we have also conducted experiments on the widely-used ADNI database. The obtained results indicate that our proposed method can identify the imaging biomarkers and diagnose the disease with favorable accuracies compared to the baseline methods.
Keywords: Parkinson’s disease, Diagnosis, Sparse regression, Joint feature-sample selection, Matrix completion, Robust linear discriminant analysis
Introduction
Diagnosis of neurodegenerative brain disorders using medical imaging is a challenging task due to different factors, including a wide variety of artifacts in the image acquisition procedure, the imposed errors due to preprocessing, and the large amount of intrinsic inter-subject variabilities. Among the neurodegenerative disorders, Parkinson’s disease (PD) is one of the most common ones, with a high socioeconomic impact. PD is provoked by progressive impairment and deterioration of brain neurons, caused by a gradual halt in the production of a vital chemical messenger.
PD symptoms start to appear with the loss of these neurotransmitters in the brain, notably dopamine. The neuropathology of PD is pinpointed by a selective loss of dopaminergic neurons in the substantia nigra (SN); nevertheless, in recent studies a widespread involvement of other structures and tissues is widely researched (Miller and OCallaghan, 2015). The degeneration of dopaminergic neurons results in decreased levels of dopamine in the putamen of the dorsolateral striatum, leading to dysfunction of direct and indirect pathways of movement control (Obeso et al., 2000). Furthermore, researchers have identified that it can also cause non-motor problems to the subjects (depression, anxiety, apathy/abulia) (Chaudhuri et al., 2006; Ziegler and Augustinack, 2013). People with PD may lose up to 80% of dopamine before symptoms appear (Braak et al., 2003; Duchesne et al., 2009; Miller and OCallaghan, 2015). Thus, early diagnosis and treatment are of great interest and are crucial to detain progression of PD in its initial stages.
Previous clinical studies (Braak et al., 2003) show that the disease is initiated in the brainstem and mid-brain regions; however, with time, it also affects many other brain regions. An illustration of PD progression is shown in Fig. 1, derived from the results achieved by Braak et al., (2003). In this figure, darker regions are those affected earlier in the process of PD progression.
Fig. 1.
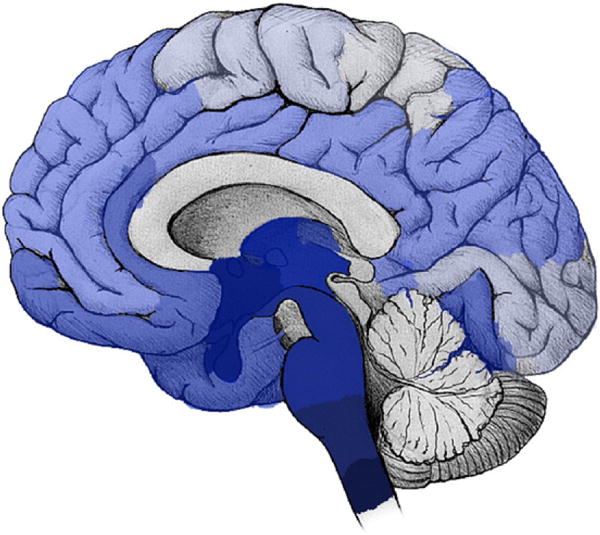
An illustration of the brain regions affected by PD in different stages of the disease. Darker blue denotes the earlier and more severely affected regions.
Current diagnosis of PD mainly depends on the clinical symptoms. But, the dopamine transporter positron emission computed tomography is very expensive and cannot be popularized on the clinical diagnosis of PD patients. Therefore, other neuro-imaging techniques could be crucial pathways for PD early diagnosis. For example, SPECT imaging is usually considered for the differential diagnosis of PD and often used for people with tremor (Duchesne et al., 2009; Prashanth et al., 2014). PET is utilized for PD diagnosis (Loane and Politis, 2011), while MRI is often employed for the differential diagnosis of PD syndromes (Duchesne et al., 2009; Marquand et al., 2013; Ziegler and Augustinack, 2013), as well as to analyze the structural changes in PD patients (Menke et al., 2009) and their differential diagnosis (Focke et al., 2011; Salvatore et al., 2014).
Thus, through analyzing the deep and mid-brain regions, along with cortical surfaces, we could potentially identify the imaging biomarkers for PD. Accordingly, we create a PD-specific atlas and further extract features by non-linearly registering this atlas to each subject’s brain image. The extracted features represent the tissue volumes of each labeled ROI.
Recently, with the advances in the area of machine learning and data-driven analysis methodologies, significant amount of research efforts have been dedicated to diagnosis and progression prediction of neurodegenerative diseases using different brain imaging modalities (Duchesne et al., 2009; Marquand et al., 2013; Prashanth et al., 2014; Rizk-Jackson et al., 2011; Thung et al., 2014). Automatic PD diagnosis and progression prediction could help physicians and patients avoid unnecessary medical examinations or therapies, as well as potential side effects and safety risks (Cummings et al., 2011). Machine learning and pattern recognition methods could simplify the development of these automatic PD diagnosis approaches. For instance, Prashanth et al. (2014) use intensity features extracted from SPECT images along with an SVM classifier, while Focke et al. (2011) use the voxel-based morphometry (VBM) on T1-weighted MRI with an SVM classifier to identify idiopathic Parkinson syndrome patients. In another work, Salvatore et al. (2014) proposes a method based on principal component analysis (PCA) on morphological T1-weighted MRI, in combination with an SVM for diagnosis of PD and progressive supranuclear palsy (PSP) patients. In the past several years, some research has exploited MRI in order to analyze changes in different brain regions in PD patients (Duchesne et al., 2009; Focke et al., 2011; Menke et al., 2009; Salvatore et al., 2014; Ziegler and Augustinack, 2013). Along with the impairment of the dopamine production process, many brain regions are also affected, leading to several movement problems and sometimes also a number of non-motor symptoms (Braak et al., 2003). Literature studies show that these influences could be characterized by the information acquired from the MRI data (Duchesne et al., 2009).
In this paper, we use MR images to diagnose PD and analyze the imaging biomarkers. To this end, we extract features from predefined brain regions and analyze changes and variations between PD and normal control (NC) subjects. In order to build a reliable system, we need to take several important issues into account. As mentioned earlier, the quality of MR images can be affected by different factors, like patient movements, radiations or device limitations. Most existing works manually discard poor subject images, which could eventually induce undesirable bias to the learned model. Therefore, it is of great interest to automatically select the most reliable samples, boosting up robustness of the method and its application under a clinical setting. On the other hand, many studies analyze MR images by parcellating them into several pre-defined regions of interest (ROIs) and then extracting features from each ROI (Djamanakova et al., 2014; Thung et al., 2014; Tzourio-Mazoyer et al., 2002). It is noted that PD, like many other neurodegenerative diseases, highly affects a number of brain regions (Braak et al., 2003). Therefore, it is also desirable to select the most important and relevant regions for our diagnosis procedure. This also leads to identifying the biomarkers for the disease, as well as initiating studies to the future clinical analysis. Similar studies for identification of biomarkers for Alzheimer’s disease (AD) are previously conducted in many works (Bron et al., 2014; Oh et al., 2007; Thung et al., 2014). But, such studies are scarce for PD, in the literature.
Considering all these factors, we seek to automatically select both a subset of the subjects and the most discriminative brain ROIs to construct a robust model for PD diagnosis. Each subject will form a sample in our classification task. Samples are described by the features extracted from their ROIs. In many previous works, either feature selection (Bron et al., 2014; Oh et al., 2007) or sample selection (Rohlfing et al., 2004) was performed individually, or both were considered sequentially (Thung et al., 2014). We observe that these two processes (or two sub-problems) affect each other, and that performing one before the other does not guarantee the selection of the best overall subsets for both features and samples. Thus, these two sub-problems are overlapping, but do not have optimal sub-structures (Cormen et al., 2009). In other words, optimal overall solution is not composed of optimal solution to each sub-problem. This motivates us to jointly search for the best subsets for both features and samples. Specifically, in this paper, we introduce a novel joint feature-sample selection (JFSS) method based on how well the training labels could be represented sparsely by different numbers of features and samples. Then, we further introduce a robust classification scheme, specially designed to enhance the robustness to noise. The proposed robust classification framework follows the least-squares linear discriminant analysis (LS-LDA) (De la Torre, 2012) formulation and the robust regression scheme (Huang et al., 2012).
Many previous researches have been conducted on feature and sample selection (Coates et al., 2011; Nie et al., 2010; Peng et al., 2005; Thung et al., 2014). But, few of them consider a joint formulation (Mohsenzadeh et al., 2013). Authors in Mohsenzadeh et al. (2013) extend the classic relevance vector machine (RVM) formulation by adding two parameter sets for feature and sample selection in a Bayesian graphical inference model. They consider sparsity in both feature and sample domains, as we do, but instead they solve the problem in a marginal likelihood maximization procedure. In contrast, we develop a single optimization problem for jointly selecting features and samples. Our formulation is reduced to two simple and convex problems and therefore can be efficiently solved.
Fig. 2 illustrates an overview of our proposed method. After preprocessing the subjects’ MRI scans, we extract features from their predefined brain ROIs, and select the best subsets of features and samples through our proposed JFSS. The joint feature-sample selection procedure is able to simultaneously discard irrelevant samples and redundant features. After JFSS, there may still be some random noise in the remaining data. To further clean the data, we decompose it into two parts, cleaned data and its noise component. This is done in conjugation with the classification process, in a supervised manner, to increase the classification robustness to noise. Additionally, the testing data is also de-noised through representing the data as a locally compact linear combination of the cleaned training data.
Fig. 2.
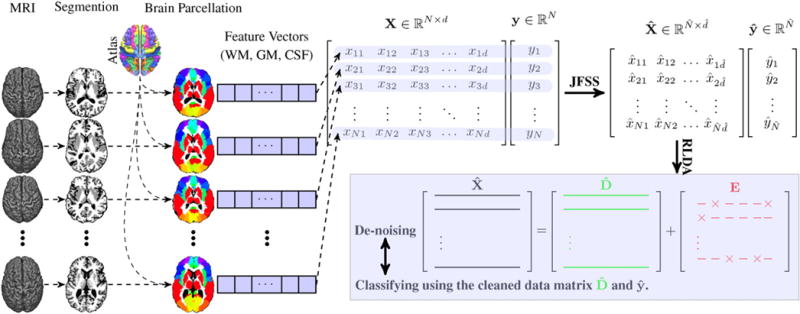
Overview of our proposed method. First, the MR images are processed and tissue-segmented. Then, the anatomical automatic labeling (AAL) atlas is non-linearly registered to each subject’s original MR image, and then the WM, GM and CSF volumes of each ROI are calculated as features. These features form X and the corresponding labels form Y. Through our proposed joint feature-sample selection (JFSS), we discard some uninformative features and samples, leading to and . Then, we train a robust classifier (i.e.,, Robust LDA), in which we jointly decompose into cleaned data and its noise component E, and classify the cleaned data.
The key methodological contributions in our work are multi-fold: (1) We propose a new joint feature-sample selection (JFSS) procedure, which jointly selects the best subset of most discriminative features and best samples to build a classification model. (2) We utilize the robust regression method in Huang et al. (2012) and further develop a robust classification model. In addition, we propose to de-noise the testing data based on the supervised cleaned training samples. (3) We apply our method for PD diagnosis, as the diagnosis methods for PD are scarce. (4) In order to extract useful features for PD diagnosis, we specifically define some new clinically-relevant ROIs for PD. Therefore, finally the automated data-driven methods can be developed for PD diagnosis or further analyses.
Data acquisition and preprocessing
The data used in this paper was obtained from the Parkinson’s progression markers initiative (PPMI) database1 (Marek et al., 2011). PPMI is the first substantial study for identifying PD progression markers to advance the overall understanding of the disease. PPMI is an international study with multiple centers around the world designated to identify the progression of PD markers, to enhance the understanding of the disease, and to provide crucial tools for succeeding in PD modifying therapeutic trials. They seek to establish standardized protocols for acquisition, transfer and analysis of clinical, imaging and biospecimen data, and investigate novel methods that demonstrate interval changes in PD patients, compared to normal controls. All these could be used by the PD research community to elevate knowledge about the disease and an understanding of how to cure or slow down its progression.
PD subjects in the PPMI study are de novo PD patients, newly diagnosed and unmedicated. The healthy/normal control subjects are both age- and gender-matched with the PD subjects. The subjects and their stagings are evaluated using the widely used Hoehn and Yahr (H&Y) scale (Hoehn and Yahr, 1967). H&Y scale defines board categories, which rate the motor function for PD patients. H&Y stages correlate with motor decline, neuroimaging studies of dopaminergic loss and deterioration in quality of life (Bhidayasiri and Tarsy, 2012). The original version has a 5-point scale (Stages 1–5) measurement. Most of the studies in PD evaluated disease progression through analyzing patients and the time taken for them to reach one of the H&Y stages. The subjects in the first stage have unilateral involvement only, often with the least or no functional impairment. They have mild symptoms, which are inconvenient but not disabling. The second stage has bilateral or midline involvements, but still with no impairment of balance. For these subjects, the posture and gait are usually affected. Stage three shows the first signs of impaired reflexes. The patient will show significant slowing of the body movements and moderately severe dysfunction. In the fourth stage, the disease is fully developed and is severely disabling; the patient can still walk but to a limited extent, and might not be able to live alone any longer. In the fifth (final) stage, the patient will have a confinement to bed or will be bound to a wheelchair. The PD subjects in this study are mostly in the first two H&Y stages. As reported by the studies2 in PPMI (Marek et al., 2011), among the PD patients at the time of their baseline image acquisition, 43% of the subjects were in stage 1, 56% in stage 2 and the rest in stages 3 to 5.
In this research, we use the MRI data acquired by the PPMI study, in which a T1-weighted, 3D sequence (i.e., MPRAGE) is acquired for each subject using 3 T SIEMENS MAGNETOM TrioTim syngo scanners. This gives us 374 PD and 169 NC scans. The T1-weighted images were acquired for 176 sagittal slices, with the following parameters: repetition time (TR) = 2300ms, echo time (TE) = 2.98ms, flip angle = 9°, and voxel size = 1×1×1mm3.
All the MR images were preprocessed by skull stripping (Wang et al., 2011), cerebellum removal, and tissue segmentation into white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) (Lim and Pfefferbaum, 1989). The anatomical automatic labeling (AAL) atlas (Tzourio-Mazoyer et al., 2002), parcellated with 90 predefined regions, was registered using HAMMER3 (Shen and Davatzikos, 2002; Wang et al., 2011) to the native space of each subject. We further added eight regions in the template to be transferred to the subject native space using the deformation fields obtained in the previous step. Those regions include four regions in the brainstem such as midbrain, pons, medulla oblongata and superior cerebellar peduncle (see Fig. 3b), together with the left and right red nucleus and the left and right SN (see Fig. 3c). These regions have been shown as clinically important regions for PD. All the 98 ROIs are depicted in Fig. 3.
Fig. 3.
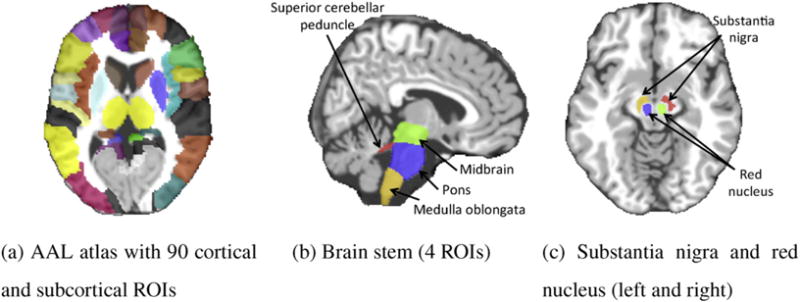
All 98 ROIs used in this study: 90 ROIs from the AAL atlas (Tzourio-Mazoyer et al., 2002), 4 ROIs defined in brainstem, 2 ROIs in substantial nigra (L/R), and 2 ROIs in red nucleus (L/R).
We, then, computed WM, GM and CSF tissue volumes in each of the regions and used them as features, leading to 98 WM, 98 GM and 98 CSF features, for each subject. Table 1 shows the details of the subjects used in our experiments. As can be seen, subjects from PD and NC groups have closely similar distributions of age and education characteristics.
Table 1.
Details of the subjects from the PPMI dataset used in our study. ‘Age’ indicates the mean ± standard deviation (std) of the subject ages (in years) in that category. Similarly, ‘Education’ denotes the mean ± std of the amount education (in years) of the subjects.
| Total | Gender
|
Age (years) | Education (years) | ||
|---|---|---|---|---|---|
| Female | Male | ||||
| PD | 374 | 132 | 242 | 61.50 ± 9.62 | 15.58 ± 2.93 |
| NC | 169 | 59 | 110 | 60.42 ± 11.43 | 16.09 ± 2.87 |
Overview of the method
As discussed earlier, we first process the MR images and obtain tissue segmented images, after which the anatomical automatic labeling (AAL) atlas is non-linearly registered to the original MR image space of each subject. From each of the ROIs, we extract the WM, GM and CSF volumes as features. These features form, and the corresponding labels form. To formulate the problem, we consider N training samples, each with d=98×3=294 dimensional feature vector. Note that we have 98 ROIs, each of which are represented by 3 tissue-volume features. Let X ∈ ℝN×d denote the training data, in which each row indicates a training sample, and y∈ℝN their corresponding labels. The goal is to determine the labels for the testing samples, .
Using our proposed joint feature-sample selection (JFSS), some uninformative features and samples are discarded, leading to and . Note samples and features are selected, resulting in a new data matrix, and training labels, . It is important to remark that the same Ntst testing samples will now have features each,. . After obtaining the subset of features and samples, we train a robust linear discriminant analysis (RLDA) to learn a classification model. In this process, we jointly decompose into cleaned data, and its noise component, E. The classification model is learned on the cleaned data, in order to avoid any probable noise effects. This procedure is visualized in Fig. 2.
Note that, throughout this paper, bold capital letters denote matrices (e.g., X). All non-bold letters denote scalar variables. xij denotes the scalar in the row i and column j of X. 〈x1,x2〉 denotes the inner product between two vectors x1 and denotes the squared Euclidean Norm of x. ‖X‖* designates the nuclear norm (sum of singular values) of X. ‖x‖1=Σi |xi| denotes the ℓ1 norm of the vector x.
The proposed joint feature-sample selection (JFSS) algorithm
The first task is to reliably select the most discriminative features, along with the best samples to build a classification model. During this process, since the poorly shaped samples are discarded and most discriminative features are selected, it can not only improve the generalization capability of the learned model, but also speed up the learning process. In many real-world applications, it is a cumbersome task to acquire samples and features for the learning task. Particularly in our application, feature vectors extracted from MRI data are quite prone to noise. Therefore, the data from some of the subjects might not be useful and might mislead the learning procedure. This motivates us to select the best samples for learning a diagnosis model. On the other hand, as described before, we parcellate brain images into a number of ROIs and represent each subject by concatenating the features from these ROIs. However, brain neurodegenerative diseases are not reflected on all these ROIs. This further motivates us to select the most discriminative features. Since, features are extracted from ROIs, selecting the most discriminative features also reveals the most crucial brain ROIs related to the specific disease (such as PD in our case).
Formulation
As discussed earlier, these two sub-problems (feature selection and sample selection) were generally targeted separately. However, feature selection and sample selection affect each other, making separate selections open to more defective feature-sample subsets. In other words, separate selections might limit the subsequent classification performance in terms of overall learning model accuracy. In this subsection, we propose a novel feature-sample selection framework in a joint formulation, to guarantee the selection of best and most discriminative subsets in both domains.
To this end, the selected samples and features should best describe a regression model, in terms of the overall accuracy. Without the loss of generality, we employ a linear regression model. In order to select the most discriminative subset, we consider sparsity both in feature and sample domains. Recently, the linear sparse regression model has been widely used for feature selection (Nie et al., 2010), in which a sparse weight vector β is learned to best predict the training labels. More formally, we would like to minimize , while keeping the coefficient vector, β, sparse. But, this feature selection procedure might be misled if there were noisy features and poor samples. In this way, we propose to jointly select features and samples through constructing a linear regression model. This would account for the noisy/redundant information in both domains, simultaneously.
For this purpose, we introduce two vectors α and β, used to select samples and features, respectively. To get the most compact and sparse set in both domains, we need to impose ℓ0 regularizations on both α and β Our joint feature-sample selection (JFSS) is thus formulated as
| (1) |
The first term controls the overall data fitting error only for the selected samples indicated by α. The second and third terms are to ensure the selection of the smallest number of the most meaningful samples and features. λ1,λ2>0 are the optimization hyperparameters, controlling the level of contribution of each term in the entire optimization process.
The minimization process of the objective function in (1) is not computationally tractable. This is because the ℓ0 term is not a convex function and optimizing its associated variable is as difficult as trying all possible subsets of the measurements. Therefore, we need to consider approximations of the ‘0 norms. One of the most common approximations of the ℓ0 regularization for sparse representation is the ℓ1 norm (Wright et al., 2009). Another feasible approximation is to project the solution onto a simplex (Duchi et al., 2008). As a result, the above objective function could be rewritten as the following, using ℓ1 approximations for sparsity:
| (2) |
As we would like our method to at least select a minimum number of samples, to avoid overfitting and prevent from getting trivial solutions, we propose to interpret the coefficients in α as probabilities and impose the condition that ∀i αi ≥0 and . This is equal to projecting the ℓ1-ball onto the simplex as in (Duchi et al., 2008; Huang et al., 2013). Moreover, this constraint makes the third regularization term in (2) constant, and thus the problem reduces to:
| (3) |
Note that the solution to the above objective function for α is indeed sparse, because of the simplex constraints (Duchi et al., 2008; Huang et al., 2013). It is also noteworthy that with this formulation, the algorithm is dependent on less hyperparameters, making it quite appealing for applications with large and diverse data, in which selecting the hyperparameter is burdensome.
Optimization
The solution to the objective function in (3) is not very easy to achieve, as the first term introduces a quadratic optimization term. In order to solve the optimization problem, we use an alternating optimization procedure, in which we break the problem down into two sub-problems and then solve them iteratively. When fixing each of the associated variables, the resulting sub-problems would be convex. As studied in the literature, in such problems, the main objective function can converge to the optimal point (Gorski et al., 2007).
In each iteration, we optimize the objective function by fixing one of the optimization variables, while solving for the other, until convergence. Specifically, optimizing for β, while fixing α and therefore would reduce to
| (4) |
Similarly, the optimization step for α, while fixing β, is:
| (5) |
The first sub-problem is similar to the standard sparse regression formulation, and very easy to solve with any standard solver or with the alternating direction method of multipliers (ADMM) (Boyd et al., 2011). We introduce an auxiliary variable, b, and form the Lagrangian function as below:
| (6) |
where γ1 is the Lagrangian multiplier and ρ1> 0 is a penalty hyperparameter. Therefore, the optimization steps would be formulated as
| (7) |
Here, is the soft thresholding operator or the proximal operator for the ℓ1 norm (Boyd et al., 2011), and is the identity matrix. Note that r+= max(r,0).
In order to solve the second sub-problem, (5), we rewrite it as the following:
| (8) |
The most critical step is the projection of the solution onto the probabilistic simplex, which is formulated as:
| (9) |
where is the probabilistic simplex, onto which we want to project the α weight vector, as also defined in Duchi et al. (2008), Huang et al. (2013), and Michelot (1986). This can be solved using the accelerated projected gradient, as in Duchi et al. (2008), and Michelot (1986), by writing the Lagrangian function as:
| (10) |
Solving for α while keeping the K.K.T. conditions would give us the optimal projection onto the probabilistic simplex (Duchi et al., 2008; Huang et al., 2013). Therefore, the objective function in the sub-problem (8) could be optimized through the projected quasi-Newton algorithm proposed in Schmidt et al. (2009). We initialize the vector α inversely related to the prediction power of the samples:
| (11) |
where δ is a small positive number to avoid devision by zeros and σ is a scaling factor. In the experiments, these two parameters are fixed as δ= 0.0001 and σ=0.01, respectively.
Subsequently, the solution to the main problem, as in Eq. (3), is obtained by alternatively solving each of the sub-problems until convergence. The stopping criterion is that the changes in the two variables α and β in two consecutive iterations is less than a threshold (‖αk−αk−1‖ < ε and ‖βk − βk−1‖< ε). The penalty hyperparameter ρ1 in (6) controls the convergence rate of the optimization process. It serves as a step size on how fast to move towards the optimum. If we select a very small value, the solution will converge very slowly, whereas, if it has a large value, the step will be very big and might jump over the optimum. Therefore, a good choice of this hyperparameter could reduce the convergence time. Many different strategies are used in the literature to deal with this hyperparameter. Similar to Adeli-Mosabbeb et al. (2015) and Liu et al. (2013), we first set the hyperparameter to a small value to take small steps at the beginning. In each next iteration, we increase its value by , so that we take a larger step towards the optimum. This is because, at the beginning, the optimization process starts with randomly initialized variables and, if we take a larger step, we might mislead the direction to the optimum and increase the convergence time. But, after a number of iterations, larger steps would lead to faster convergence.
JFSS as a classifier (JFSS-C)
The above procedure of selecting features and samples could also be used directly for the classification task. As it is obvious, the first term learns a linear regression model, in which the weights β construct the mapping from the features spaces, X, to the space of the labels, y. This could be used as a classification tool by discretizing the values y into classes.
To build the linear classification model (i.e., y=Xβ +b, where b is the bias), we add a single column of 1s to the matrix X (i.e., X=[X 1]). This classification scheme is used as a baseline method in the experiments, referred to as JFSS-C.
Robust classification (robust LDA)
Even with selection of the most discriminative features and best samples, there might still be some noises present in the data. These noise elements of data can adversely influence the classifier learning process. This is the case for almost all real-world applications, where the data is precepted through inaccurate or noise-prone sensors. This issue has been recently explored in the areas of subspace methods (De la Torre, 2012; Liu et al., 2013), machine learning (Goldberg et al., 2010) and computer vision (Huang et al., 2012).
In this section, we introduce a robust classification technique based on the least-squares formulation of linear disciriminant analysis (LS-LDA). Then, we will apply it to learn a model, classifying our selected samples and features. Note that the feature and sample selections were performed on the training data. This procedure discarded the entire features or samples (columns or rows) in X. But the selected subset might still have some amounts of noisy elements. Furthermore, it is quite probable that the testing data were also contaminated with noise. Therefore, a de-noising procedure, for both training and testing data, could play a very important role on the testing stage and the overall performance. Note that the de-noising of testing samples is less studied in the literature, or is simply performed in an unsupervised manner. We introduce a procedure to de-noise the testing samples based on the cleaned training data.
Training
To suppress the possible noise in the data, while learning the classification model, we need to model the noise in the feature matrix. In other words, we account for the intra-sample outliers in to further reduce the influences of noise elements in the data. For this purpose, following Goldberg et al. (2010) and Liu et al. (2013), we assume that the data matrix could be spanned on a low-rank subspace and, therefore, should be rank-deficient. This assumption supports the fact that samples from the same class are correlated (Goldberg et al., 2010; Huang et al., 2012). In order to achieve a robust classifier, we use a similar idea as in Huang et al. (2012), which was proposed for robust regression. In our case, classification is posed as a binary regression problem, in which a transform, w, maps each sample in to a binary label in . In the linear case, this could be modeled with a linear discriminant analysis (LDA) through learning a linear mapping to minimize the intra-class discrimination and maximize the inter-class variation. An extension of LDA, namely LS-LDA (De la Torre, 2012), models the LDA problem in a least-squares formulation:
| (12) |
where w∈ℝd is a projection of
to the space of labels, . Note that is a weighing factor to compensate for an unbalanced number of samples in each of the two classes (De la Torre, 2012).
If the data matrix is corrupted by noise, we can model the noise by considering , where is the underlying noise-free component and is the noise component. To model this noise in the above formulation and learn the mapping w from the clean data, D, we utilize the scenario in Huang et al. (2012). Analogous to the robust principal component analysis (RPCA) formulation (Candès et al., 2011), it could be assumed that the noise-free component of the data is spanned on a low-rank subspace. Correspondingly, the error matrix is assumed to be a sparse matrix, as we are not expecting a huge amount of elements to be contaminated by noise. This is because the JFSS procedure selects the most relevant features and the best samples. Therefore, lots of original data contaminated with noise are already removed. The remaining data are those with the most correlation to the labels. But, there is still a possibility that some random noise is remaining in the selected features. Considering these, we can rewrite our problem as:
| (13) |
where the first term learns the mapping from the clean data and projects the samples to the label space. The second and the third terms guarantee the rank-deficiency of the data matrix D and the sparsity of the matrix E, respectively. These two terms are similar to RPCA (Candès et al., 2011).
Note that RPCA is an unsupervised method, which de-noises the data matrix without considering the data labels. Whereas, the above formulation cleans the data in a supervised manner. Particularly, matrix D retains the subspace of , which is most correlated to the labels .
The solution to problem (13) could be achieved by writing the Lagrangian function, and iteratively solving for, w, D, , E and one at a time, while fixing others (Huang et al., 2012), using the augmented Lagrangian method (ALM) of multipliers technique.
Testing
In the testing phase, the probable noise present in the samples can dramatically affect the classification accuracy. De-noising the testing samples is a challenging task, as we do not have any label and class information for them; thus we cannot perform the supervised de-noising procedure, as we did for the training samples.
To clean the testing data, one can use RPCA (Candès et al., 2011; Huang et al., 2016), but as discussed before, it is an unsupervised approach. To this end, we utilize the samples cleaned in the training stage, D, in a supervised manner. The de-noising procedure for the testing data, , would consist of representing the testing sample as a linear combination of the training data samples:
| (14) |
where Ztst is the coefficient matrix for the combination. But, to account for the noise in the testing samples, we add a noise element and reformulate the combination as:
| (15) |
where is the noise component of the testing data. To acquire the best linear combination, for representing the testing samples, it is important to ensure that each sample is represented only by a small number of the training samples. Because samples come from different classes and the samples could best be de-noised if they are represented by the most similar samples to them. As a result, in order for the linear combination to be locally compact, we further impose the low-rank constraint on the coefficients, as in Lin et al. (2011) and Liu et al. (2013):
| (16) |
This optimization problem could be solved using linearized ALM method as in (Lin et al., 2011). After cleaning the testing data, the prediction for the classification output is calculated as
| (17) |
Same as in LS-LDA (De la Torre, 2012), ytst is used as the decision value, and the binary class labels are produced using the k-nearest neighbor strategy.
Experiments
As discussed earlier, the proposed JFSS discards poor samples and irrelevant features to build a linear regression model that can predict subject categories. In order to validate the proposed JFSS procedure, we first construct a set of synthetic data to evaluate the behavior of the method against noisy samples and redundant features. Then, the proposed procedure is used to diagnose PD patients. As described earlier, subjects from the PPMI database are used for this study.
All results are generated using a 10-fold cross validation strategy. The best hyperparameters for our method are selected using a grid search with all possible values for each hyperparameter. To be fair, the results for the baseline methods were also generated using a similar 10-fold cross validation strategy and, similar to our method, the best hyperparameters for each of the methods were selected. Specifically, the hyperparameters were set using an inner 10-fold cross validation, where the training data itself was split into 10 partitions and then a 10-fold cross validation procedure determined the best set of the hyperparameters for the method. The best values for each of the hyperparameters in Eqs. (3), (13) and (16) are separately optimized in the range [10−5, 1].
In order to evaluate the proposed approach, different baseline methods are incorporated. Baseline classifiers under comparison include linear support vector machines (SVM), sparse SVM (Bi et al., 2003), matrix completion (MC) (Goldberg et al., 2010), sparse regression (SR), JFSS as a classifier (JFSS-C) as described in Section 4, and the original least-squares linear discriminant analysis (LS-LDA) (De la Torre, 2012). Matrix completion is a transductive classification approach that deals with the noise in feature values and can suppress a controlled amount of sparse noise in both training and testing feature vectors (Goldberg et al., 2010). It has shown a good performance in many applications recently (Adeli-Mosabbeb and Fathy, 2015; Cabral et al., 2015). MC, like our method, incorporates a sparse noise model to de-noise the data. On the other hand, it de-noises both training and testing data. Therefore, in order to provide extensive and fair comparative studies, we compare the results from MC against the results obtained by our approach.
As for feature and sample selection, to evaluate the proposed JFSS procedure, we compare the results with separate feature and sample selections (FSS), sparse feature selection (SFS), and no feature sample selection (no FSS). These three methods provide direct baseline methods for the proposed JFSS, since they use a similar approach for selecting samples and features. Note that for the SR classification scheme, as described above, we only report results for FSS and SFS. Furthermore, we report results using other prominent methods for feature transform or reduction like the popular min-redundancy max-relevance (mRMR) (Peng et al., 2005), principal component analysis (PCA), robust principal component analysis (RPCA) (Candès et al., 2011), autoencoder-restricted Boltzmann machine (AE-RBM) (Coates et al., 2011), and non-negative matrix factorization (NNMF) (Berry et al., 2007). These five methods are of the state-of-the-art methods widely used for feature reduction or transformation, compared to which we can demonstrate the significant improvements by the proposed method.
An important characteristics of the proposed JFSS method was to select the best set of samples (along with features) to build a classification model. One of the most popular approaches for removing outliers is RANSAC (Fischler and Bolles, 1981). RANSAC is a consensus resampling technique, which randomly subsamples the input data and constructs models, iteratively. In each iteration, if the selected samples result in a smaller inlier error, the classification model parameters are updated. The procedure starts by randomly selecting the minimum number of samples (denoted by m) required to build the classification model, after which the classifier is trained, using the randomly selected samples. Then, the whole set of samples from the training set is examined with the built model and the number of inliers is determined. If the fraction of the number of inliers over the total number of samples exceeds a certain threshold τ, the classifier is again built using all the identified inliers and the procedure is terminated. Otherwise, this procedure is iterated at least times to ensure the selection of an appropriate set of samples. is chosen as a high enough number, such that, with probability p = 0.99, at least one set of the selected samples does not include an outlier (Fischler and Bolles, 1981). Let u represent the probability of a sample being an inlier. , the number of iterations, is set by:
| (18) |
The hyperparameters for RANSAC are chosen with the same strategy as all other methods, through 10-fold cross-validation. m is set to 1/4 of the total number of samples , and the hyperparameters τ and u are optimized in the sets [0.5,1.0] and [0.1,1.0], respectively. As a baseline method, we also report results on RANSAC to demonstrate the JFSS ability in removing poor samples.
Synthetic data
The first set of experiments runs on the synthetically created toy data to observe behavior of the proposed method against different levels of noise in both samples and features. We first sample some data points from a number of subspaces and then gradually add noisy features and samples, comparing the performance of the proposed method with the competing methods. This experiment creates a good testbed to analyze how our method can select the best samples and features and suppress noise, compared to different baseline methods.
To this end, we construct two independent subspaces of dimensionality 100, same as described in Liu et al. (2013), and sample 500 samples from each subspace, which could create a binary classification problem. The two subspaces S1, S2 are constructed with bases U1 and U2. U1 ∈ℝ100×100 is a random orthogonal matrix and U2=TU1, in which is T a random rotation matrix. Then, 500 vectors are sampled from each subspace through Xi=UiQi,i={1,2} with Qi, a 100×500 matrix, independent and identically distributed (i.i.d.) from to (0, 1).
In order to evaluate the robustness of the method in both sample and feature spaces, we gradually add a certain number of additional noisy samples and features to the data. Specifically, we add ρ randomly generated features and ρ randomly generated samples to the data, and then run the proposed and the baseline methods. All noisy data are drawn i.i.d. from (0, 1). Since our method jointly performs both and feature selections, we increase the noise level in both domains. Fig. 4 shows the mean accuracy results of three different runs, as a function of the additional number of noisy features and samples, with a 10-fold cross-validation strategy. The mean and standard deviation values could be found in Table 2, as well. The reported results for all the methods are achieved with their best tuned hyperparameters. To analyze the effects of the only hyperparameter (λ1) associated with JFSS, we plot the accuracy of two classification techniques (SVM and RLDA) as a function of the parameter in Fig. 5. The diagram is plotted for the case that the number of added noisy features and sample, ρ, is equal to 100. As can be seen, the classification performance is partially independent from the hyperparameter and, in a sensible range of the values for the hyperparameter, we consistently achieve reasonable results.
Fig. 4.
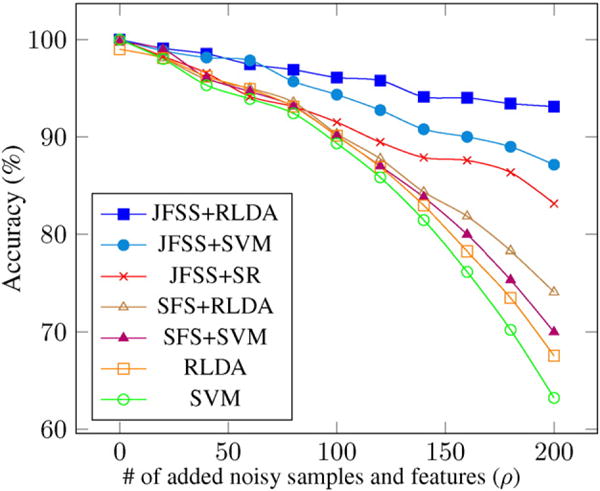
Comparisons of results on synthetic data, for three different runs. The diagram shows the mean accuracy for different methods as a function of ρ.
Table 2.
Results comparisons on synthetic data, for three different runs. Mean and standard deviation for different number of added noisy samples and features (ρ).
| Method | ρ | mean ± std | ρ | mean ± std |
|---|---|---|---|---|
| JFSS + RLDA | 100 | 96.1 ± 1.0 | 200 | 93.1 ± 1.9 |
| JFSS + SVM | 100 | 94.3 ± 1.5 | 200 | 87.2 ± 2.7 |
| JFSS + SR | 100 | 91.5 ± 2.4 | 200 | 83.1 ± 4.1 |
| SFS + RLDA | 100 | 90.3 ± 2.3 | 200 | 74.1 ± 3.9 |
| SFS + SVM | 100 | 90.1 ± 1.4 | 200 | 70.0 ± 2.1 |
| RLDA | 100 | 90.1 ± 2.6 | 200 | 67.6 ± 4.4 |
| SVM | 100 | 89.3 ± 2.1 | 200 | 63.2 ± 4.3 |
Fig. 5.
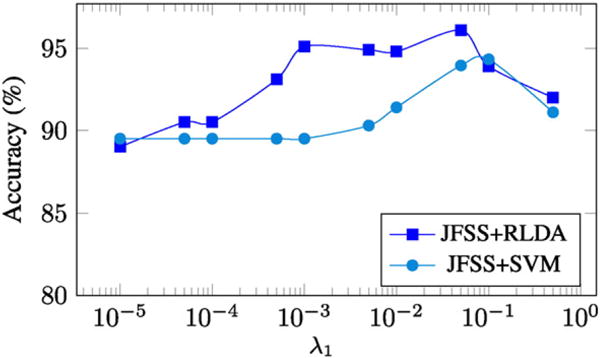
Accuracy as a function of the JFSS hyperparameter (λ1), experimented on synthetic data, with ρ=100.
Our JFSS coupled with any of the classifiers has the ability to select better subset of features and samples and achieve satisfactory results. However, when the RLDA classification scheme is used, it acts more robust against the increase of noise elements (as can be seen in Fig. 4). This is attributed to the de-noising process introduced by our RLDA. As discussed earlier, with RLDA, we de-noise the testing samples as well, while for other classifiers the testing samples are intact. Note that, these testing samples do not go through the JFSS procedure, and outlier samples cannot be discarded, as we did for the training samples. Therefore, de-noising the data plays an important role in achieving better overall performance.
Parkinson’s disease diagnosis
For this experiment, we have used the subjects acquired from the PPMI dataset. The details of the data are described in Section 2. For quantitative evaluations, we first compare our proposed JFSS and robust LDA on this dataset in terms of accuracy, true positive rate (TPR), false positive rate (FPR) and area under the ROC curve (AUC). TPR is a measure indicating the proportion of positive subjects with PD that are correctly categorized as such. On the other hand, FPR is the rate of occurrence of positive testing results in subjects known to be free of the disease (normal controls or NC in our case). These two measurements are very important for disease diagnosis applications. Fig. 6 depicts the results for all these four metrics, in comparisons to the baseline methods. As could be seen, the proposed JFSS coupled with our RLDA outperforms all other methods with a significant margin.
Fig. 6.
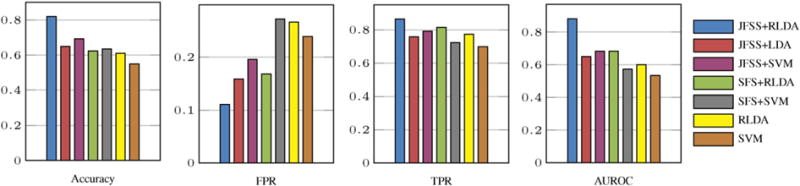
Comparisons of results by the proposed (JFSS + RLDA) and the baseline methods.
In a more comprehensive set of comparisons, Table 3 shows the diagnosis accuracy of the proposed technique (RLDA + JFSS) against different approaches for feature or sample selection, reduction or transformation. All experiments are conducted through a 10-fold cross-validation strategy. The optimization hyperparameters are chosen by a grid search for the best performance, using the same cross-validation strategy on the training data. The proposed method outperforms all other approaches.
Table 3.
Accuracy of the PD/NC classification, compared among baseline classifiers and different feature-sample selection or reduction techniques. First column shows the results for the proposed joint feature-sample selection method. The second, third and fourth columns include the results with separate feature and sample selection, sparse feature selection, and no feature or sample selections, respectively. The next five columns show the results for some state-of-the-art feature reduction techniques, and finally the last column shows the results for the well-known RANSAC algorithm for outlier sample removal.
| Classifier | Selection/Reduction method
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| JFSS | FSS | SFS | no FSS | mRMR | PCA | RPCA | AE-RBM | NNMF | RANSAC | |
| Robust LDA | 81.9 | 78.0* | 67.7† | 61.5† | 70.5† | 65.0† | N/A | 76.8* | 64.5† | 74.7† |
| MC | 78.9* | 73.5 | 66.0† | 56.2† | 69.2† | 62.4† | N/A | 73.1† | 64.1† | 72.3† |
| LDA | 65.9† | 62.1† | 61.5† | 56.0† | 60.9† | 56.0† | 60.5† | 65.1† | 58.1† | 66.0† |
| SVM | 69.1† | 61.9† | 61.1† | 55.5† | 58.8† | 58.5† | 61.0† | 66.6† | 59.1† | 71.2† |
| Sparse SVM | 70.1† | 62.8† | 6.15† | 59.5† | 60.0† | 59.3† | 61.8† | 68.7† | 63.1† | 73.1† |
| SR | N/A | 61.6† | 59.6† | N/A | 60.5† | 59.9† | 60.6† | 63.7† | 61.5† | 64.2† |
| JFSS-C | 68.7† | N/A | N/A | N/A | 67.5† | 68.8† | 71.9† | 72.8† | 67.0† | 69.9† |
Note that
stands for the case with p<0.05 and
for p<0.01 in a cross-validated 5×2 t-test against the proposed method (RLDA + JFSS). Bold indicates best achieved results.
The Second, third and fourth columns in Table 3 include the results from feature or sample selection techniques, which can be regarded as direct baseline methods for the proposed JFSS approach. Clearly, one can conclude that the joint selection of the features and samples (JFSS: first column in the table) results in better accuracies than selecting features and samples separately (FSS: second column in the table). The fifth through ninth columns include results with some state-of-the-art feature reduction/transformations. It is evident from the results that our JFFS outperforms all these methods as well. This is simply attributed to the fact that our method performs the selection in both feature and sample domains in a supervised manner, while all other methods included here are unsupervised feature reduction or transformation techniques. Furthermore, for our application, the features come from the brain ROIs. Since not all the brain regions are associated with PD, many of the features are redundant. This is why these feature reduction techniques perform worse than our feature selection scheme. In the context of feature selection, we only select the most relevant features, while the feature reduction techniques transform the whole set of features (all with equal contributions) to a lower dimension space. The last column in the table shows the results from the RANSAC technique for outlier sample removal (Fischler and Bolles, 1981). Again, the proposed JFSS shows to select a much better set of samples along with their respective features for the task of PD diagnosis.
It is worth noting that the SR classification technique, which is used as a baseline method, is directly derived from the weights learned in FSS and SFS. Therefore, when using SFS and FSS, we can report results for SR. We further ran the sparse regression on the outputs of other feature reduction techniques and reported results in Table 3. In addition, the last row of the table contains results form JFSS as a classifier (JFSS-C), explained in Section 4. JFSS-C is, in fact, the original JFSS, which can be directly used to build the classification model. So, JFSS and JFSS-C are not two separate procedures, and that’s why we do not couple JFSS-C with other feature selection methods. As can be seen, JFSS-C can produce comparable results with LDA or SVM coupled with our JFSS, while it is much better than LDA, SVM or even RLDA when no feature or sample selection is conducted.
One of the most important baselines to the de-nosing aspect of the proposed method could be the RPCA approach, which de-noises the data through the same low-rank assumption on the data matrix. Therefore, we apply RPCA on the training data to de-noise the samples and their feature vectors and then apply a variety of classifiers to classify them. The results could be seen in the seventh row of Table 3. The RLDA and MC classifiers implicitly de-noise the data through a same low-rank minimization procedure, and therefore we did not couple RPCA with them.
Additionally, a statistical analysis is performed on the results and reported in Table 3. In order to statistically analyze the significance of the achieved results, a cross-validated 5×2 t-test (Dietterich, 1998) is performed on the accuracy results of each competing method against our proposed method (JFSS + RLDA). As discussed in detail in Dietterich (1998), Ojala and Garriga (2010) and Stelzer et al. (2013), this statistical test yields more reliable results for statistically analyzing the classifier performances, compared to the conventional paired t-tests. In particular, we perform 5 different replications of a 2-fold cross-validation. In each of the replications, the data is randomly split into two sets. The results from the first set of the five replications are used to estimate the mean difference, and the results of all folds are incorporated to estimate the variance. Then, a t-statistic is calculated to achieve the p-value, showing the significance of the comparison on the results. The details of the test are explained in Dietterich (1998). In Table 3, the methods with a p-value of p<0.05 are indicated with a * symbol and the results with p<0.01 are indicated with a † symbol. As can be seen, our proposed method achieves statistically significant results compared to all other methods. Furthermore, we also perform a permutation test (Ojala and Garriga, 2010) on the proposed method, which is a non-parametric method without assuming any data distribution, to assess whether the proposed classifier has found a class structure (a connection between the data and their respective class labels), or the observed accuracy was obtained by chance. In order to perform this test, we repeat the classification procedure by randomly permuting the class labels for τ different times (τ=100, in our experiments). The p-value can then be calculated as the percentage of runs for which the obtained classification error is better than the original classification error. After performing the test, we get a p-value smaller than 0.05, which indicates that the classification error on the original data is indeed significantly small and, therefore, the classifier is not randomly generating those results (Ojala and Garriga, 2010).
In addition, to analyze the effect of the hyperparameter on the accuracy of the methods, the proposed JFSS method was put together with all classifiers and the best achieved accuracy for each set of hyperparameters and classifiers is plotted in Fig. 7. As can be seen, the first two methods, which perform de-noising while learning the classifier model, behave similarly, while JFSS + RLDA leads to a better performance. In general, changing the hyperparameter influences the selected features, and that is why the classifiers perform differently under different hyperparameter settings. In order to further investigate the effect of the hyperparameters, we plot the performance of the competing classifiers, with the JFSS parameters fixed, as a function of their respective hyperparameter.
Fig. 7.
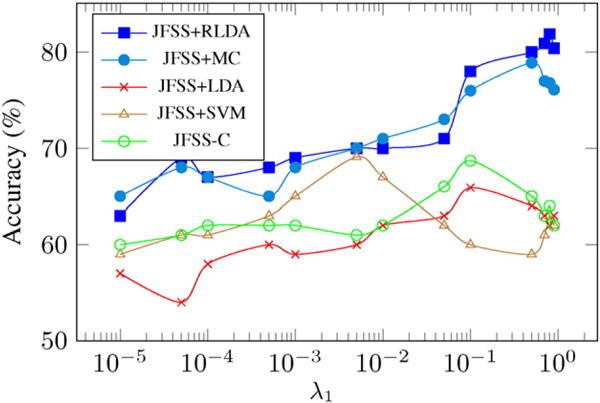
Accuracy as a function of the JFSS hyperparameter (λ1), for the Parkinson’s disease diagnosis experiment.
Fig. 8 shows these results for three major methods in comparison. Specifically, the diagram on the left analyzes the hyperparameter λ of matrix completion, as in Goldberg et al. (2010). This hyperparameter controls the amount of induced noise in the data. The middle diagram shows the performance of the sparse SVM (Bi et al., 2003) classifier, with respect to the hyperparameter λ, which controls the amount of sparseness in the learned weight vector. Finally, the diagram on the right shows the performance of the conventional SVM classifier as a function of its hyperparameter C, which is a trade-off hyperparameter affecting the generalization capability of SVM.
Fig. 8.
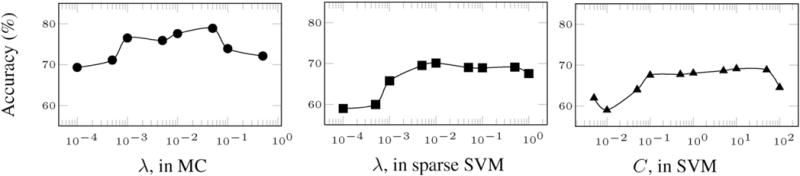
Accuracy of the competing methods, as a function of their hyperparameter.
Discussions
The clinical symptoms of PD start to emerge after the degeneration of a considerable number of dopaminergic neurons. Therefore, at this stage, it could already be counted as the nearly-advanced stage. As a result, the disease-modifying therapies might be ineffective to hinder the neurodegeneration progression. Accordingly, identification of specific and sensitive biomarkers is extremely important to facilitate early and differential diagnosis by monitoring the disease progression and assessing effectiveness of current and future treatments. Hence, there is a calling need of automated approaches and techniques as prior tools to detect gray and white matter alterations in the cortex (Patenaude et al., 2011). Our method provides a detailed analysis on each single ROI in the brain and opens the path for further analysis and early diagnosis of PD.
To analyze the most relevant brain regions for PD, we setup a new experiment. In this experiment, the JFSS hyperparameter is set such that the best performance in terms of diagnosis rate is achieved. As discussed earlier, with the parameters set, we perform a 10-fold cross validation, where, for each fold, 9 other folds are considered as training data and the test is conducted on that left-out fold. The final accuracy reported is the average of all these 10 different runs, which usually has better generalization capabilities. With this setting, for each separate fold we possibly get different sets of features. We observe that the selected features for each of the folds using JFSS is almost consistent in most folds. The most frequently selected ROIs in the process of joint feature-sample selection for PD diagnosis are the red nucleus (left and right), substantial nigra (left and right), pons, middle frontal gyrus (left and right), superior temporal gyrus (left), which are also visualized in Fig. 9. These regions are the ones that were selected at least for 80% of the times in 10 repetitions of the 10-fold cross validation runs. These selected regions are consistent with previously reported results (Braak et al., 2003; Worker et al., 2014), and are also shown to be the important regions for PD diagnosis. In order to have a closer look at the regions and their tissue types, the detailed set of ROIs and their tissue types selected by at least 10% of the 10 repetitions of the 10-fold cross validation runs are also listed in Table 4. As can be seen, the gray matter tissue densities play the most important role for most regions. In the deep brain regions, the white matter tissue densities also contribute to the classification and improve the overall performance. The selected brain regions could be further investigated in future clinical studies.
Fig. 9.
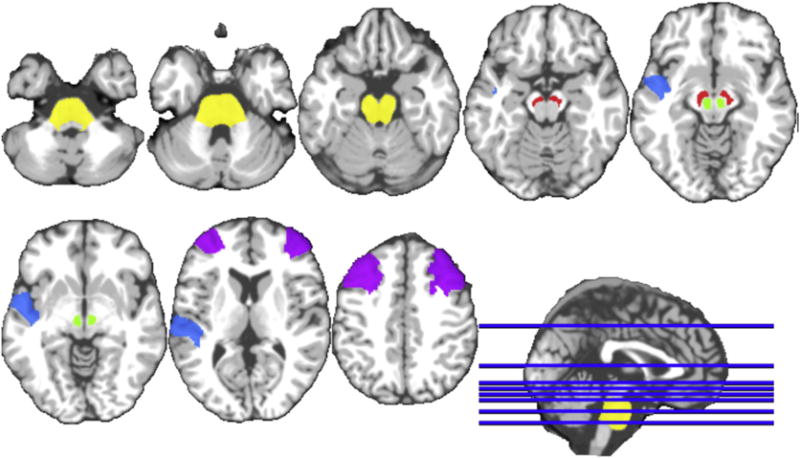
Top and most frequent selected ROIs by our method.
Table 4.
The ROIs and their tissue types that were selected at least once in the 10-fold cross validation strategy.
| Region of Interest (ROI) | WM | GM | CSF | Region of Interest (ROI) | WM | GM | CSF |
|---|---|---|---|---|---|---|---|
| Precentral gyrus right | ✓ | Putamen right | ✓ | ✓ | |||
| Suplementary motor area right | ✓ | ✓ | Pallidum left | ✓ | ✓ | ||
| Superior frontal gyrus (media) left | ✓ | Thalamus left | ✓ | ✓ | |||
| Insula left | ✓ | Superior temporal gyrus left | ✓ | ||||
| Middle cingulate gyrus left | ✓ | ✓ | Superior temporal gyrus right | ✓ | |||
| Middle cingulate gyrus right | ✓ | Superior temporal gyrus right | ✓ | ||||
| Calcarine cortex right | ✓ | Middle temporal gyrus left | ✓ | ||||
| Lingual gyrus right | ✓ | Middle temporal gyrus right | ✓ | ||||
| Middle occipital gyrus right | ✓ | Inferior temporal left | ✓ | ✓ | |||
| Fusiform gyrus left | ✓ | Midbrain | ✓ | ✓ | |||
| Postcentral gyrus left | ✓ | Pons | ✓ | ||||
| Superior parietal gyrus right | ✓ | Substantia nigra left | ✓ | ||||
| Inferior parietal lobule left | ✓ | Substantia nigra right | ✓ | ||||
| Caudate left | ✓ | Red nucleus left | ✓ | ✓ | |||
| Putamen left | ✓ | Red nucleus right | ✓ |
It is worth noting that RLDA alone does not provide very good performance, as the results in Table 3 suggest. This could be caused by the large amount of noisy and irrelevant features in the data. RLDA and most robust methods can deal with a controlled amount of noise, as they assume a sparse noise element in the data, and model it with an ℓ1 regularization. That may be the reason why RLDA with no FSS does not achieve satisfactory results. Furthermore, if we apply RLDA before our proposed JFSS-C, the obtained accuracy is 73.6% for PD classification. This lower accuracy can be attributed to the fact that the ℓ1 regularization on the noise element in RLDA fails to discard the huge amount of noise in the original data. On the other hand, RLDA de-noises the testing data (Section 5.2), while JFSS-C does not. This could be another reason why RLDA results in a better classification model. Using JFSS, we first discard the redundant features and poor samples, and then utilize RLDA to de-noise the remaining features, while classifying the data.
The PD-related pathology studies showed that the progression of the lesions are initiated in the brainstem (which includes pons), and substantial nigra (Braak et al., 2003). Our research also confirms that the morphological changes of red nucleus are important in the initial PD pathology course (Colpan and Slavin, 2010; Habas and Cabanis, 2006). The brainstem pathology takes an upward course to the temporal lobe, and then to the frontal lobe areas. It should be noted that the most frequently selected brain ROIs for PD diagnosis in our research are associated with the initial PD-related pathology, which makes early diagnosis of PD possible.
Furthermore, as confirmed by the results, we can distinguish PD from NC using only MRI. With the progression of PD, patients’ brains are affected heavily with time. So, these data-driven methods could be of great use for early diagnosis, or prediction of the disease progression. MRI techniques could be used to monitor disease progression and to detect brain changes in preclinical patients or in patients at risk of developing PD. However, to date, these techniques suffer from the lack of standardization, particularly the methods for extracting quantitative information from images, and the lack of validation in large cohorts of subjects in longitudinal studies. Our research partly resolved the bottleneck restriction.
Our proposed method for classifying the neuroimaging data could be easily employed for analysis and identification of other brain diseases. To demonstrate that, we setup another experiment using the widely researched Alzheimer’s disease neuroimaging initiative (ADNI) database4. The aim is to identify the subjects status, diagnosing AD and its prodormal stage, known as mild cognitive impairment (MCI). For this purpose, we used 396 subjects (93 AD patients, 202 MCI patients and 101 NC subjects) from the database, which had complete MRI and FDG-PET data. To process the data, tools in Dai et al. (2013) and Wang et al. (2014) are used for spatial distortion, skull-stripping, and cerebellum removing. Then, the FSL package Zhang et al. (2011) was used to segment each MR image into three different tissues, gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF). The subjects are further processed with 93 ROIs (Kabani et al., 1998) parcellated for each (Shen and Davatzikos, 2002) with atlas warping. The volume of GM tissue in each ROI was calculated as the image feature. For FDG-PET images, a rigid transformation was employed to align it to the corresponding MR image and the mean intensity of each ROI was calculated as the feature. All these features were further normalized in a similar way as in Zhang et al. (2011). As a results, each subject has 2×93=186 features. Table 5 lists the results achieved by our proposed method (JFSS + RLDA) on this data, compared with some baseline methods. Two different sets of experiments are conducted to first discriminate NC from MCI subjects and then NC from AD subjects. Therefore, NC subjects form our negative class, while the positive class is defined as AD in one experiment and MCI in another experiment. Table 5 shows the results for the two separate experiments, AD NC and MCI NC classifications.
Table 5.
The accuracy (ACC) and the area under ROC curve (AUC) results of AD diagnosis on the ADNI database, with comparison to some baseline methods. Bold indicates best achieved results.
| JFSS + RLDA | JFSS + LDA | JFSS + SVM | RPCA + LDA | RPCA + SVM | RLDA | LDA | SVM | ||
|---|---|---|---|---|---|---|---|---|---|
| AD/NC | ACC | 91.5 | 89.4 | 89.0 | 89.5 | 86.1 | 87.8 | 82.7 | 85.4 |
| AUC | 0.94 | 0.90 | 0.90 | 0.92 | 0.88 | 0.90 | 0.84 | 0.85 | |
| MCI/NC | ACC | 81.9 | 79.1 | 77.3 | 78.1 | 80.1 | 80.3 | 66.1 | 74.1 |
| AUC | 0.83 | 0.80 | 0.75 | 0.72 | 0.78 | 0.82 | 0.69 | 0.74 | |
Similar to the experiment conducted on PD, the top selected regions with the best parameters are listed in Table 6. The top selected regions are defined as those selected by at least 50% of the times in 10 repetitions of the 10-fold cross validation runs. Note that these selected regions are consistently reported as important in the previous AD/MCI studies (Pearce et al., 1985; Thung et al., 2014), as well.
Conclusions
In this paper, we have introduced a joint feature-sample selection (JFSS) framework, along with a robust classification approach for PD diagnosis. We have established robustness in both training and testing phases. We verified our method using subjects excerpted from the PPMI dataset, a first large-scale longitudinal study of PD. Our method outperforms several baseline methods on both synthetic data and the PD/NC classification problem, in terms of the accuracy of the classification task. Furthermore, we investigated the biomarkers for PD and have also confirmed the results reported in the recent and ongoing researches. As a direction for future work, one can use clinical scores and other imaging modalities to predict PD progression, or to improve prediction accuracy. More effective features can also be extracted to further enhance the diagnosis accuracy.
Appendix A. Augmented Lagrangian method (ALM)
Augmented Lagrangian methods are sets of algorithms for solving problems of constrained optimization (Boyd et al., 2011). In these methods, usually the constrained optimization objective is replaced with one or a series of unconstrained objectives, by adding penalty terms. These terms are added to mimic a Lagrange multiplier. The general form of an equality-constrained convex optimization problem would be
| (A:1) |
where x∈ℝn, A∈ℝm×n, b∈ℝm and f: ℝn→ℝ is a convex function. The Lagrangian function for the above objective would form as follows, by incorporating a Lagrangian multiplier or a so-called dual variable, y∈ℝm:
| (A:2) |
This problem could be solved using the dual ascent method (Boyd et al., 2011; Boyd and Vandenberghe, 2004), by writing the dual function and solving for that. But to ensure the convergence, f should be strictly convex and finite. To solve the problem under more relaxed conditions, the augmented Lagrangian method of multipliers could be incorporated, by adding a penalty term to the Lagrangian:
| (A:3) |
where ρ >0 is a penalty hyperparameter that controls the rate of convergence towards the satisfaction of the constraint, used as a step size. Note that when ρ = 0, is the standard Lagrangian function. The advantages of considering the penalty term is that the dual function would be differentiable under rather mild conditions for problem Eq. (A.1). Therefore, applying dual ascent to the new problem with the penalty term leads to the following optimization steps on each variable, at each kth iteration:
| (A:4) |
| (A:5) |
A.1. Alternating direction method of multipliers (ADMM)
When there are more than one optimization variables associated with the problem, we can take advantage of the decomposability of the dual ascent (Boyd et al., 2011) method and the convergence superiority of the ALM to solve the problem in a similar way. Suppose we have a problem modeled as:
| (A:6) |
where x∈ℝn, z∈ℝm, A∈ℝp×n, B∈ℝp×m and c∈ℝp. The two functions f: ℝn→ℝ and g: ℝm→ℝ are assumed to be the convex functions. As can be seen in Eq. (A.6), there are two variables to be optimized in this new formulation. Similarly, we can write the augmented Lagrangian as:
| (A:7) |
Here, to optimize the above function, we need to iteratively update each variable while keeping others fixed. Therefore, the x-minimization, z-minimization, and Lagranigiuan multiplier update steps at the kth iteration have the following forms:
| (A:8) |
| (A:9) |
| (A:10) |
In this method, the augmented Lagrangian function is minimized jointly with respect to the two associated variables. Each of the variables is updated in a sequential order or a so-called alternating fashion. If we have more variables, same strategy can be incorporated, as long as the problem can be decomposed into sub-problems and the sub-problems (like in Eqs. (A.8) and (A.9)) are convex. The stopping criterion in this situation would the convergence of the main objective, while the constraint(s) are satisfied. For a more detailed discussion on the methods and their convergence properties, please refer to Boyd et al. (2011) and Boyd and Vandenberghe (2004).
Table 6.
Top selected ROIs for the ADNI experiments.
| MRI | FDG-PET | |
|---|---|---|
| AD/NC | Hippocampal formation right, hippocampal formation left, middle temporal gyrus left, middle frontal gyrus right, middle temporal gyrus left, perirhinal cortex left, superior parietal lobule left, lateral occipitotemporal gyrus right, inferior frontal gyrus left | Precuneus right, precuneus left, globus palladus left, temporal pole right, frontal lobe WM left, middle temporal gyrus left, postcentral gyrus left, temporal lobe WM left, postcentral gyrus right, medial frontal gyrus right, amygdala left, amygdala right, thalamus right, occipital pole left |
| MCI/NC | Middle frontal gyrus right, lateral front-orbital gyrus right, precuneus right, precuneus left, medial front-orbital gyrus right, inferior frontal gyrus left, inferior occipital gyrus left, inferior frontal gyrus right, precentral gyrus left, temporal pole left | Globus palladus right, frontal lobe WM right, subthalamic nucleus left, inferior occipital gyrus left, superior occipital gyrus right, supramarginal gyrus left, caudate nucleus right, lingual gyrus left, postcentral gyrus left, parietal lobe WM right, postcentral gyrus right, angular gyrus left |
Footnotes
References
- Adeli-Mosabbeb E, Fathy M. Non-negative matrix completion for action detection. Image Vis Comput. 2015;39:38–51. [Google Scholar]
- Adeli-Mosabbeb E, Thung KH, An L, Shi F, Shen D. Robust feature-sample linear discriminant analysis for brain disorders diagnosis. Neural Information Processing Systems (NIPS) 2015 [Google Scholar]
- Berry MW, Browne M, Langville AN, Pauca VP, Plemmons RJ. Algorithms and applications for approximate nonnegative matrix factorization. Comput Stat Data Anal. 2007;52(1):155–173. [Google Scholar]
- Bhidayasiri R, Tarsy D. Movement disorders. A Video Atlas: Springer; 2012. [Google Scholar]
- Bi J, Bennett K, Embrechts M, Breneman C, Song M. Dimensionality reduction via sparse support vector machines. J Mach Learn Res. 2003;3:1229–1243. [Google Scholar]
- Boyd S, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found Trends Mach Learn. 2011;3(1):1–122. [Google Scholar]
- Boyd S, Vandenberghe L. Convex Optimization. Cambridge University Press; New York, NY, USA: 2004. [Google Scholar]
- Braak H, Tredici K, Rub U, de Vos R, Steur EJ, Braak E. Staging of brain pathology related to sporadic Parkinson’s disease. Neurobiol Aging. 2003;24(2):197–211. doi: 10.1016/s0197-4580(02)00065-9. [DOI] [PubMed] [Google Scholar]
- Bron E, Smits M, van Swieten J, Niessen W, Klein S. Feature selection based on svm significance maps for classification of dementia. Machine Learning in Medical Imaging. 2014;8679:272–279. [Google Scholar]
- Cabral R, Torre FDI, Costeira JP, Bernardino A. Matrix completion for weakly-supervised multi-label image classification. IEEE Trans Pattern Anal Mach Intell. 2015;37(1):121–135. doi: 10.1109/TPAMI.2014.2343234. [DOI] [PubMed] [Google Scholar]
- Candès EJ, Li X, Ma Y, Wright J. Robust principal component analysis? J ACM. 2011;58(3):11:1–11:37. [Google Scholar]
- Chaudhuri KR, Healy DG, Schapira AH. Non-motor symptoms of Parkinson’s disease: diagnosis and management. Lancet Neurol. 2006;5(3):235–245. doi: 10.1016/S1474-4422(06)70373-8. [DOI] [PubMed] [Google Scholar]
- Coates A, Lee H, Ng A. An analysis of single-layer networks in unsupervised feature learning, in: AI and Stat. J Mach Learn Res. 2011;15:215–223. [Google Scholar]
- Colpan ME, Slavin KV. Subthalamic and red nucleus volumes in patients with parkinson’s disease: do they change with disease progression? Parkinsonism Relat Disord. 2010;16(6):398–403. doi: 10.1016/j.parkreldis.2010.03.008. [DOI] [PubMed] [Google Scholar]
- Cormen TH, Leiserson CE, Rivest RL, Stein C. Introduction to Algorithms. Third The MIT Press; 2009. [Google Scholar]
- Cummings JL, Henchcliffe C, Schaier S, Simuni T, Waxman A, Kemp P. The role of dopaminergic imaging in patients with symptoms of dopaminergic system neurodegeneration. Brain. 2011;134(11):3146–3166. doi: 10.1093/brain/awr177. [DOI] [PubMed] [Google Scholar]
- Dai Y, Wang Y, Wang L, Wu G, Shi F, Shen D. abeat: a toolbox for consistent analysis of longitudinal adult brain MRI. PLoS One. 2013;8(4):e60344. doi: 10.1371/journal.pone.0060344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De la Torre F. A least-squares framework for component analysis. IEEE Trans Pattern Anal Mach Intell. 2012;34(6):1041–1055. doi: 10.1109/TPAMI.2011.184. [DOI] [PubMed] [Google Scholar]
- Dietterich TG. Approximate statistical tests for comparing supervised classification learning algorithms. Neural Comput. 1998;10(7):1895–1923. doi: 10.1162/089976698300017197. [DOI] [PubMed] [Google Scholar]
- Djamanakova A, Tang X, Li X, Faria AV, Ceritoglu C, Oishi K, Hillis AE, Albert MS, Lyketsos C, Miller MI, Mori S. Tools for multiple granularity analysis of brain MRI data for individualized image analysis. NeuroImage. 2014;101(0):168–176. doi: 10.1016/j.neuroimage.2014.06.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duchesne S, Rolland Y, Varin M. Automated computer differential classification in parkinsonian syndromes via pattern analysis on MRI. Acad Radiol. 2009;16(1):61–70. doi: 10.1016/j.acra.2008.05.024. [DOI] [PubMed] [Google Scholar]
- Duchi J, Shalev-Shwartz S, Singer Y, Chandra T. Efficient projections onto the l1-ball for learning in high dimensions. International Conference on Machine Learning. 2008:272–279. [Google Scholar]
- Fischler MA, Bolles RC. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Commun ACM. 1981;24(6):381–395. [Google Scholar]
- Focke NK, Helms G, Scheewe S, Pantel PM, Bachmann CG, Dechent P, Ebentheuer J, Mohr A, Paulus W, Trenkwalder C. Individual voxel-based subtype prediction can differentiate progressive supranuclear palsy from idiopathic parkinson syndrome and healthy controls. Hum Brain Mapp. 2011;32(11):1905–1915. doi: 10.1002/hbm.21161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberg AB, Zhu X, Recht B, Xu JM, Nowak RD. Transduction with matrix completion: three birds with one stone. Neural Information Processing Systems. 2010:757–765. [Google Scholar]
- Gorski J, Pfeuffer F, Klamroth K. Biconvex sets and optimization with biconvex functions: a survey and extensions. Math Meth Oper Res. 2007;66(3):373–407. [Google Scholar]
- Habas C, Cabanis EA. Cortical projections to the human red nucleus: a diffusion tensor tractography study with a 1.5-T MRI machine. Neuroradiology. 2006;48(10):755–762. doi: 10.1007/s00234-006-0117-9. [DOI] [PubMed] [Google Scholar]
- Hoehn M, Yahr M. Parkinsonism: onset, progression and mortality. Neurology. 1967;17:427–442. doi: 10.1212/wnl.17.5.427. [DOI] [PubMed] [Google Scholar]
- Huang D, Cabral R, De la Torre F. Robust regression. European Conference on Computer Vision. 2012:616–630. [Google Scholar]
- Huang H, Yan J, Nie F, Huang J, Cai W, Saykin A, Shen L. Medical Image Computing and Computer-Assisted Intervention (MICCAI), Vol 8150 of Lecture Notes in Computer Science. Springer Berlin Heidelberg; 2013. A new sparse simplex model for brain anatomical and genetic network analysis; pp. 625–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang D, Cabral R, Torre FDI. Robust regression. IEEE Trans Pattern Anal Mach Intell. 2016;38(2):363–375. doi: 10.1109/TPAMI.2015.2448091. [DOI] [PubMed] [Google Scholar]
- Kabani NJ, Macdonald DJ, Holmes CJ, Evans AC. 3D anatomical atlas of the human brain; 20th Annual Meeting of the Organization for Human Brain Mapping.1998. [Google Scholar]
- Lim K, Pfefferbaum A. Segmentation of MR brain images into cerebrospinal fluid spaces, white and gray matter. J Comput Assist Tomogr. 1989;13:588–593. doi: 10.1097/00004728-198907000-00006. [DOI] [PubMed] [Google Scholar]
- Lin Z, Liu R, Su Z. Linearized alternating direction method with adaptive penalty for low-rank representation. Neural Information Processing Systems. 2011:612–620. [Google Scholar]
- Liu G, Lin Z, Yan S, Sun J, Yu Y, Ma Y. Robust recovery of subspace structures by low-rank representation. IEEE Trans Pattern Anal Mach Intell. 2013;35(1):171–184. doi: 10.1109/TPAMI.2012.88. [DOI] [PubMed] [Google Scholar]
- Loane C, Politis M. Positron emission tomography neuroimaging in Parkinson’s disease. Am J Transl Res. 2011;3(4):323–341. [PMC free article] [PubMed] [Google Scholar]
- Marek K, et al. The Parkinson Progression Marker Initiative (PPMI) Prog Neurobiol. 2011;95(4):629–635. doi: 10.1016/j.pneurobio.2011.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marquand A, Filippone M, Ashburner J, Girolami M, Mourao-Miranda J, GJ B, Williams S, Leigh P, Blain C. Automated, high accuracy classification of parkinsonian disorders: a pattern recognition approach. PLoS One. 2013;8(7):e69237. doi: 10.1371/journal.pone.0069237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menke RA, Scholz J, Miller KL, Deoni S, Jbabdi S, Matthews PM, Zarei M. MRI characteristics of the substantia nigra in Parkinson’s disease: a combined quantitative T1 and DTI study. NeuroImage. 2009;47(2):435–441. doi: 10.1016/j.neuroimage.2009.05.017. [DOI] [PubMed] [Google Scholar]
- Michelot C. A finite algorithm for finding the projection of a point onto the canonical simplex of ℝn. J Optim Theory Appl. 1986;50(1):195–200. [Google Scholar]
- Miller DB, OCallaghan JP. Biomarkers of parkinsons disease: present and future. Metabolism. 2015;64(3 Supplement 1):S40–S46. doi: 10.1016/j.metabol.2014.10.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohsenzadeh Y, Sheikhzadeh H, Reza AM, Bathaee N, Kalayeh MM. The relevance sample-feature machine: a sparse Bayesian learning approach to joint feature-sample selection. IEEE Trans Cybern. 2013;43(6):2241–2254. doi: 10.1109/TCYB.2013.2260736. [DOI] [PubMed] [Google Scholar]
- Nie F, Huang H, Cai X, Ding CH. Efficient and robust feature selection via joint ℓ2,1-norms minimization. Neural Information Processing Systems. 2010:1813–1821. [Google Scholar]
- Obeso JA, Rodriguez-Oroz MC, Rodriguez M, Lanciego JL, Artieda J, Gonzalo N, Olanow CW. Pathophysiology of the basal ganglia in Parkinson’s disease. Trends Neurosci. 2000;23(Supplement 1):S8–S19. doi: 10.1016/s1471-1931(00)00028-8. [DOI] [PubMed] [Google Scholar]
- Oh JH, Kim YB, Gurnani P, Rosenblatt K, Gao J. Biomarker selection for predicting Alzheimer disease using high-resolution maldi-tof data; IEEE International Conference on Bioinformatics and Bioengineering; 2007. pp. 464–471. [Google Scholar]
- Ojala M, Garriga GC. Permutation tests for studying classifier performance. J Mach Learn Res. 2010;11:1833–1863. [Google Scholar]
- Patenaude B, Smith SM, Kennedy DN, Jenkinson M. A Bayesian model of shape and appearance for subcortical brain segmentation. NeuroImage. 2011;56(3):907–922. doi: 10.1016/j.neuroimage.2011.02.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearce B, Palmer A, Bowen D, Wilcock G, Esiri M, Davison A. Neurotransmitter dysfunction and atrophy of the caudate nucleus in Alzheimer’s disease. Neurochem Pathol. 1985;2(4):221–232. [PubMed] [Google Scholar]
- Peng H, Long F, Ding C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans Pattern Anal Mach Intell. 2005;27(8):1226–1238. doi: 10.1109/TPAMI.2005.159. [DOI] [PubMed] [Google Scholar]
- Prashanth R, Roy SD, Mandal PK, Ghosh S. Automatic classification and prediction models for early Parkinson’s disease diagnosis from SPECT imaging. Expert Syst Appl. 2014;41(7):3333–3342. [Google Scholar]
- Rizk-Jackson A, Stoffers D, Sheldon S, Kuperman J, Dale A, Goldstein J, Corey-Bloom J, Poldrack RA, Aron AR. Evaluating imaging biomarkers for neurodegeneration in pre-symptomatic Huntington’s disease using machine learning techniques. NeuroImage. 2011;56(2):788–796. doi: 10.1016/j.neuroimage.2010.04.273. [DOI] [PubMed] [Google Scholar]
- Rohlfing T, Brandt R, Menzel RM, Maurer CR., Jr Evaluation of atlas selection strategies for atlas-based image segmentation with application to confocal microscopy images of bee brains. NeuroImage. 2004;21(4):1428–1442. doi: 10.1016/j.neuroimage.2003.11.010. [DOI] [PubMed] [Google Scholar]
- Salvatore C, Cerasa A, Castiglioni I, Gallivanone F, Augimeri A, Lopez M, Arabia G, Morelli M, Gilardi M, Quattrone A. Machine learning on brain MRI data for differential diagnosis of Parkinson’s disease and progressive supranuclear palsy. J Neurosci Methods. 2014;222:230–237. doi: 10.1016/j.jneumeth.2013.11.016. [DOI] [PubMed] [Google Scholar]
- Schmidt MW, van den Berg E, Friedlander MP, Murphy KP. Optimizing costly functions with simple constraints: a limited-memory projected quasi-newton algorithm. AISTATS, Vol. 5 of JMLR Proceedings. 2009:456–463. [Google Scholar]
- Shen D, Davatzikos C. HAMMER: hierarchical attribute matching mechanism for elastic registration. IEEE Trans Med Imaging. 2002;21:1421–1439. doi: 10.1109/TMI.2002.803111. [DOI] [PubMed] [Google Scholar]
- Stelzer J, Chen Y, Turner R. Statistical inference and multiple testing correction in classification-based multi-voxel pattern analysis (mvpa): random permutations and cluster size control. NeuroImage. 2013;65:69–82. doi: 10.1016/j.neuroimage.2012.09.063. [DOI] [PubMed] [Google Scholar]
- Thung KH, Wee CY, Yap PT, Shen D. Neurodegenerative disease diagnosis using incomplete multi-modality data via matrix shrinkage and completion. NeuroImage. 2014;91:386–400. doi: 10.1016/j.neuroimage.2014.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. NeuroImage. 2002;15(1):273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
- Wang Y, Nie J, Yap PT, Shi F, Guo L, Shen D. Robust deformable-surface-based skull-stripping for large-scale studies. Medical Image Computing and Computer-Assisted Intervention (MICCAI) 2011;6893:635–642. doi: 10.1007/978-3-642-23626-6_78. [DOI] [PubMed] [Google Scholar]
- Wang Y, Nie J, Yap PT, Li G, Shi F, Geng X, Guo L, Shen D, ADNI et al. Knowledge-guided robust MRI brain extraction for diverse large-scale neuroimaging studies on humans and non-human primates. PLoS One. 2014;9(1):e77810. doi: 10.1371/journal.pone.0077810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worker A, et al. Cortical thickness, surface area and volume measures in Parkinson’s disease, multiple system atrophy and progressive supranuclear palsy. PLoS ONE. 2014;9(12):e114167. doi: 10.1371/journal.pone.0114167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright J, Yang AY, Ganesh A, Sastry SS, Ma Y. Robust face recognition via sparse representation. IEEE Trans Pattern Anal Mach Intell. 2009;31(2):210–227. doi: 10.1109/TPAMI.2008.79. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE TMI. 2001;20(1):45–57. doi: 10.1109/42.906424. [DOI] [PubMed] [Google Scholar]
- Zhang D, Wang Y, Zhou L, Yuan H, Shen D, ADNI et al. Multimodal classification of Alzheimer’s disease and mild cognitive impairment. NeuroImage. 2011;55(3):856–867. doi: 10.1016/j.neuroimage.2011.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ziegler DA, Augustinack JC. Harnessing advances in structural MRI to enhance research on Parkinson’s disease. Imaging Med. 2013;5(2):91–94. doi: 10.2217/iim.13.8. [DOI] [PMC free article] [PubMed] [Google Scholar]


