Determination of protein oligomeric structure from small‐angle X‐ray scattering

Abstract

Small‐angle X‐ray scattering (SAXS) is useful for determining the oligomeric states and quaternary structures of proteins in solution. The average molecular mass in solution can be calculated directly from a single SAXS curve collected on an arbitrary scale from a sample of unknown protein concentration without the need for beamline calibration or protein standards. The quaternary structure in solution can be deduced by comparing the experimental SAXS curve to theoretical curves calculated from proposed models of the oligomer. This approach is especially robust when the crystal structure of the target protein is known, and the candidate oligomer models are derived from the crystal lattice. When SAXS data are obtained at multiple protein concentrations, this analysis can provide insight into dynamic self‐association equilibria. Herein, we summarize the computational methods that are used to determine protein molecular mass and quaternary structure from SAXS data. These methods are organized into a workflow and demonstrated with four case studies using experimental SAXS data from the published literature.

Introduction

Small‐angle X‐ray scattering (SAXS) has emerged as an important method for studying the solution structural properties of proteins, nucleic acids, and macromolecular complexes. A search of PubMed for “protein” and “small angle X‐ray scattering” returns fewer than 30 articles per year during the 40 years spanning 1956 to 1997. The same search returns over 300 articles per year during the last five years. The increased use of SAXS likely reflects a combination of factors, including improved access to SAXS synchrotron beam lines, advances in software for processing and analyzing SAXS data, and a recognition by the structural biology community of the value of SAXS as a complementary technique to X‐ray crystallography.

Because SAXS is a low‐resolution technique (12–20 Å), it is best suited for addressing questions about the last level of the protein structure hierarchy: quaternary structure. As a result of the low‐resolution nature of the technique, SAXS is not ideal for tertiary structure determination or protein fold recognition. Conversely, deducing quaternary structure from X‐ray crystallography can be challenging and potentially misleading. Because the conditions used for crystallization are designed to induce protein–protein interactions, crystal structures may contain nonphysiological protein–protein interfaces that are stabilized by crystal packing.1 In particular, the high protein concentration used in crystallization favors high‐order assembles, and it can be difficult to determine from the crystal lattice alone whether such assembles are stable in solution, despite significant advances in the computational analysis of protein–protein interfaces in crystals.2, 3, 4, 5, 6 SAXS avoids some of these pitfalls because sample composition is interrogated in solution. The protein concentration used in SAXS, however, is still relatively high (>1 mg/mL) compared to other assays, such as enzyme kinetics, analytical ultracentrifugation, or electron microscopy, which may still result in overrepresentation of high‐order assemblies. Nevertheless, SAXS has become a powerful tool for determining the oligomeric structures of biological macromolecules in solution, particularly when used in combination with X‐ray crystallography and computational analysis of crystal packing.

The purpose of this review is to demonstrate the use of SAXS for determining the oligomeric states and quaternary structures of proteins in solution. It does not cover the mathematical foundations of SAXS, the experimental setup and data collection, the merging and scaling of SAXS data, or the assessment of data quality. These topics are reviewed elsewhere.7, 8, 9, 10 Accordingly, it is assumed that users have high‐quality, background‐subtracted SAXS curves ready for input into the data analysis and interpretation pipeline.

Determination of the Molecular Mass in Solution from SAXS

The oligomeric structure of a protein has two components: the oligomeric state and the quaternary structure. The oligomeric state is the number of protomers in the oligomer and is also known as the degree of oligomerization (n). Quaternary structure refers to the spatial arrangement of the protomers in the oligomer and includes a description of the protein–protein interfaces within the oligomer. In this section, we discuss how n can be determined from SAXS.

The degree of oligomerization can be deduced from the molecular mass (M _r) of the protein in solution and the M _r of the protomer. The former is obtained from SAXS, while the latter is typically calculated from the protein sequence. One can approximate the M _r of the protomer as 110 Da times the number of residues in the polypeptide chain. This formula is based on the average M _r of an amino acid residue and the average occurrence of the 20 amino acids in proteins. A more accurate value of the protomer M _r can be calculated from the protein sequence using servers such as ProtParam.11 For highest accuracy, specify the exact sequence of the protein that was used in the SAXS experiments, including cloning artifacts, mutations, affinity tags, etc.

For clarity of presentation, we divide the methods for determining the M _r from SAXS into three categories: (1) empirical methods, (2) I(0)‐based methods, and (3) methods based on SAXS invariants. Empirical methods provide qualitative estimates of M _r (or equivalently, n) from a SAXS structural parameter. They are easy to implement, can be used with SAXS data measured on an arbitrary scale, do not require reference to a standard curve, and the protein concentration need not be known. The main disadvantages are modest accuracy (∼25% error) and limitation to large proteins (>100 kDa), as described in more detail below. The I(0)‐based methods provide better accuracy (∼10% error) than empirical methods. Potential disadvantages are that the concentration of the sample must be accurately known, and the SAXS data must be referenced to known protein standards or collected on an absolute scale. The methods based on SAXS invariants are the most useful tools for typical protein SAXS users. They give accurate results (expected error <10%), can be used with SAXS data collected on an arbitrary scale, do not require the sample concentration to be known, and have been implemented in web servers and software packages.

Empirical Methods for Estimating M _r from SAXS

The V _p/1.6 rule

An early idea from Svergun's group is that M _r is approximately one‐half of the excluded (i.e., hydrated) particle volume, also known as the Porod volume (V _p).12, 13 The rule was later updated using theoretical SAXS data calculated from 53 protein structures obtained from the PDB.14 The updated formula is

$$M_{\mathrm{r}}\left(\text{in} \text{kDa}\right)\hspace{0.17em}=V_{\mathrm{p}}\left({\text{in} \text{nm}}^3\right)/1.6.$$ (1)

A fast way to implement Eq. (1) is to calculate V _p from the SAXS curve using the GNOM15 utility of PRIMUS,16 which is part of the ATSAS package.17 Alternatively, the excluded volume can be obtained from shape reconstruction calculations using DAMMIF18 or DAMMIN.19 These programs report the excluded particle volume in the header of the dummy atom model. Because it is customary to average and filter many (10–50) dummy atom models resulting from independent shape reconstructions, the V _p used in Eq. (1) should be the filtered volume listed in the header of the averaged and filtered dummy atom model output by DAMAVER20 (i.e., dammif.pdb). Note the filtered volume in dammif.pdb has units of Å3, whereas Eq. (1) has V _p in nm³. Also, it is advised that the factor of 1.6 in the denominator of Eq. (1) should be 1.7 if the volume is obtained from DAMMIN (see Supporting Information Table S1 of Petoukhov et al.14). One advantage to obtaining V _p from a shape reconstruction is the variation of the excluded volume in the ensemble of dummy atom models can be used to estimate the uncertainty in the calculated M _r.

Porod–Debye estimate of n

Rambo and Tainer21 also developed a method based on V _p. The user assumes a trial value for n and estimates the particle density from V _p as

$$d\left(\text{in} \mathrm{g}/\text{mL}\right)\hspace{0.17em}=\hspace{0.17em}1.66\hspace{0.17em}n M_{\mathrm{r},1}\left(\text{in} \text{Da}\right)/V_{\mathrm{p}}\left(\text{in} {\AA }^3\right),$$ (2)

where M _r,1 is the molecular mass of the protomer in Da and V _p has units of ų. The trial density is compared with a histogram of protein particle densities (Fig. 8 of Rambo and Tainer21), and n is varied until the calculated density is within the bounds of the histogram (0.8–1.5 g/mL). If n is overestimated, the predicted particle density is impossibly high, whereas underestimation of n leads to unrealistically low densities. This trial‐and‐error procedure allows one to identify the most plausible n, and hence, M _r of the protein in solution.

Power law rule

The radius of gyration (R _g) is a fundamental structural parameter that is readily obtained from SAXS. Because R _g reports on the size of the protein, it is reasonable to think that R _g contains information about the in‐solution M _r. A survey of 23,699 protein structures from the PDB showed that the R _g of protein monomers and oligomers exhibits power law behavior:

$$R_{\mathrm{g}}\left(\text{in} \AA \right)\hspace{0.17em}=\hspace{0.17em}2.0N^{0.4},$$ (3)

where N is the number of residues in the oligomer.22 Rearrangement of Eq. (3), along with appropriate units conversion and assuming 110 Da/residue, yields the following:

$$M_{\mathrm{r}}\left(\text{in} \text{kDa}\right)\hspace{0.17em}=\hspace{0.17em}0.0194\hspace{0.17em}{R}_{\mathrm{g}}{}^{2.5}$$ (4)

Note R _g in Eq. (4) has units of Å. Users are cautioned that the power law equation works best for large, spherical proteins. For highly elongated proteins, the true R _g is larger than that predicted by the power law [Eq. (3)], which results in an overestimation of M _r.

Limits and uncertainties of empirical methods

It is wise to appreciate the limitations of the empirical methods for estimating M _r from SAXS. We studied this problem using structures from the PDB to estimate the error incurred when using Eqs. (1) and (4). The database for this analysis consisted of 21,967 protein assemblies having maximum pairwise identity of 50% and crystallographic resolution better than 2.5 Å. The M _r of each structure (including implicit H atoms) was calculated with CNS.23 Theoretical SAXS curves with maximum q of 0.32 Å⁻¹ were calculated with FoXS24 using default parameters. GNOM .out files were calculated from the SAXS curves with datgnom.25 Porod volumes were calculated from the GNOM .out files with datporod.17

Figure 1(A) shows the percent error incurred when using the V _p/1.6 rule [Eq. (1)]. Figure 1(B) shows the corresponding data for the power law equation [Eq. (4)]. In both cases, the error has a strong dependence on M _r. Very large errors are evident for M _r < 100 kDa. However, the error is generally less than 50% for proteins with M _r > 100 kDa. The average percent error for proteins with M _r > 100 kDa is 23% for the V _p/1.6 rule, and 24% for the power law rule. These results provide quantitative support for the conventional wisdom that Eq. (1) works best for large proteins (section 5.3 of Putnam et al.8). In summary, the V _p/1.6 and power law methods are generally applicable to large proteins (>100 kDa), and one can expect an uncertainty in the predicted M _r of approximately 25%.

Figure 1.

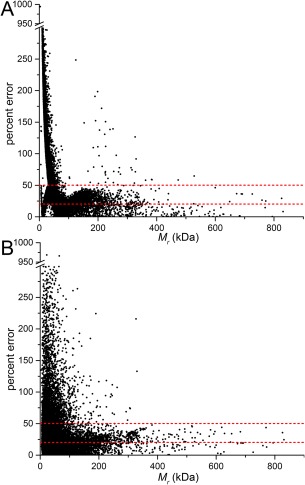
Analysis of the uncertainty in the molecular mass from empirical methods. (A) A scatterplot showing the percent error between total M _r of the biological assembly and the M _r calculated using the V_p/1.6 rule [Eq. (1)]. (B) A scatterplot of percent error between total M _r of the biological assembly and the M _r calculated using the power law rule [Eq. (4)]. The dashed lines are drawn at 20 and 50% error.

I(0)‐based methods

The M _r of the solute can be estimated from the extrapolated scattering intensity at zero angle, I(0). This is the traditional approach for determining M _r from SAXS data. Although I(0) cannot be measured because it is coincident with the direct beam, it can be estimated as the y‐intercept in Guinier analysis or by calculation of the distance distribution function. I(0)‐based methods require calibration of the SAXS data using protein standards of known concentrations or by placing the data on an absolute scale by reference to the scattering of a pure substance of known electron density, such as water.7 When using protein standards for calibration, M _r is obtained as follows:26

$$M_{\mathrm{r}}=M_{\mathrm{r},\text{st}}\left[I\left(0\right)/\mathrm{C}\right]/\left[I{\left(0\right)}_{\text{st}}/{\mathrm{C}}_{\text{st}}\right]$$ (5)

where I(0)_st is I(0) measured from a solution of a protein standard with molecular mass M _r,st present and concentration C _st. I(0) and C are the corresponding values for the protein under study. Alternatively, if the SAXS data are measured on an absolute scale, M _r is obtained from the following equation:7

$$M_{\mathrm{r}}\left(\text{in} \text{Da}\right)\hspace{0.17em}=I\left(0\right)N_{\mathrm{A}}{\mathrm{C}}^{-1}{(\Delta \rho \nu )}^{-2}.$$ (6)

where I(0) has units of cm⁻¹, N _A is Avogadro's number, C is the protein concentration in g/cm³, Δρ is the mean difference between the particle and solvent scattering density (“contrast”, in units of cm⁻²), and ν is the partial specific volume in cm³/g. Jacques and Trewhella7 and Mylonas and Svergun26 describe how to estimate the contrast. The partial specific volume for proteins can be estimated from the amino acid sequence and is typically close to 0.73 cm³/g.

The main advantage of these methods is that M _r can be determined with an accuracy of about 10%,26 which rivals analytical ultracentrifugation. The main disadvantages are that protein concentrations must be accurately known (5–10% error) and instrument calibration requires effort, time, and dedicated resources.

Determination of M _r from SAXS Invariants

SAXSMoW

Fischer and coworkers27 developed a convenient and accurate method for estimating M _r from a single SAXS curve measured on a relative scale. Their approach starts with the Q invariant, which can be calculated directly from SAXS data:

$$Q=\hspace{0.17em}{\int }_0^{\mathrm{\infty }}I\left(q\right)q^2\mathrm{d}q.$$ (7)

The Q invariant is related to the volume of the scattering particle and I(0) as follows:

$$V_{\mathrm{p}}=\hspace{0.17em}2{\pi }^{2}I\left(0\right)/Q.$$ (8)

Because density relates mass and volume, the molecular mass can be obtained as M _r = V _p/ν, where the numerator is obtained from Eq. (8), and ν is the protein partial specific volume.

A challenge to implementation is that the Q integral must be necessarily truncated at the maximum q of the experimental data, which leads to errors in the calculation of the particle volume. Fischer et al. developed an approximate method for calculating V by calibration with structures in the PDB. The uncertainty of M _r from this method is estimated to be less than 10%, with the average error from the test set of structures being only 5.3%. The method appears to be applicable to proteins with M _r > 10 kDa. Importantly, the method works well even for proteins that deviate from spherical shape. The method is available online as the SAXSMoW2 server (http://saxs.ifsc.usp.br/).

Volume of correlation

Rambo and Tainer28 defined the volume of correlation (V _c) as

$$V_{\mathrm{c}}=\hspace{0.17em}I\left(0\right)/{\int }_0^{\mathrm{\infty }}I\left(q\right)q\mathrm{d}q.$$ (9)

V _c is analogous to V _p [Eq. (8)], except the integrand in the V _c formula has q rather than q‐squared. Thus, V _c has units of area rather than volume. In fact, V _c is proportional to the ratio of V _p to the particle correlation length. An advantage of V _c is that the integral in its denominator has better convergence than Q, especially for partially unfolded proteins. Because V _c is not a true volume, it cannot be converted easily to M _r using the partial specific volume. Therefore, Rambo and Tainer empirically tested various ratios involving V _c to find a parameter that scales with M _r, ultimately discovering that the square of V _c divided by R _g, known as Q _R, provides an estimate of the M _r for proteins:

$$M_{\mathrm{r}}=Q_{\mathrm{R}}/0.1231\hspace{0.17em}=\hspace{0.17em}{V}_{\mathrm{c}}^2{R}_{\mathrm{g}}^{-1}/0.1231.$$ (10)

A similar equation is provided for RNA.28 The average mass error for the V _c method was estimated to be 5% based on analysis of theoretical SAXS data calculated from 9446 protein structures from the PDB. Equations (9) and (10) are implemented in the SAXS analysis package Scatter.29

Determination of Protein Quaternary Structure from SAXS

In this section, we describe how to determine protein quaternary structure using SAXS data. We will focus on the specific case in which SAXS data have been measured for a protein whose crystal structure is known. The SAXS data and crystal structures are integrated into a workflow of calculations that outputs a description of the oligomeric structure in solution (Fig. 2). We first describe the major stages of the workflow, then demonstrate it with case studies.

Figure 2.

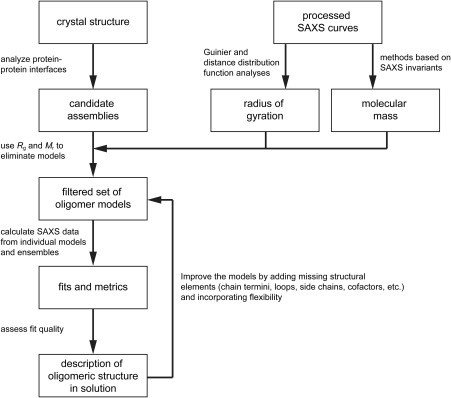
A workflow for determining protein oligomeric structure from SAXS and X‐ray crystallography.

Generate candidate assemblies

The best‐case scenario is when the crystal structure of the target protein is known. In this case, candidate assemblies are generated by in silico and manual inspection of protein–protein interfaces in the crystal lattice. Because the crystallographic asymmetric unit often does not represent the true biological assembly or range of oligomers formed in solution, assembles generated by crystallographic and noncrystallographic symmetry must be considered. Although the PDB provides “biological assemblies” for each entry, users are cautioned that these assemblies are sometimes incorrect.30, 31 Therefore, one should use additional methods for generating models from the lattice. For example, the servers PDBePISA2, 3 and Eppic5 extract plausible assemblies from crystal structures.

Crystal structures are often less complete than the in‐solution proteins they represent. For example, chain termini, loops, surface side chains, and cofactors may have been omitted due to lack of electron density. Because the absence of these atoms can affect the SAXS analysis, they should be added to the crystal structure at some point in the analysis. For expediency, we recommend that an initial pass through the workflow be done using the models extracted directly from the crystal structure. This often provides a good indication of which oligomers are present in solution and may suffice for some purposes. Next, a second set of calculations should be done with models that include features absent in the crystal structure. One convenient way to add missing sections of the polypeptide chain and disordered side chains is to run a homology modeling server using a protomer from the crystal structure as the template. This is possible, for example, with SWISS‐MODEL.32 The resulting model is replicated and superimposed onto the crystallographic oligomers. Missing cofactors can be docked into the structure by analogy to a related protein. The goodness‐of‐fit parameters calculated with the more complete models should be compared with those from the initial calculations to determine whether adding the missing elements improved the fit to the experimental data.

Although not covered in this article, if the crystal structure is unknown, homology modeling can be used to generate a model of the protomer. Several homology modeling servers are available, including SWISS‐MODEL,32 MODELLER,33 Phyre2,34 I‐TASSER,35 RaptorX,36 and MULTICOM37 Also, precalculated models are available from ModBase.38 Some homology modeling servers, such as SWISS‐MODEL, will generate an oligomer based on the template structure. Alternatively, oligomeric models can be generated by superimposing copies of the protomer model onto oligomers of homologous proteins. Another option for oligomer generation is to use the SAXS data directly to build models, rather than generating models independent of the SAXS data. For example, GLOBSYMM39 builds symmetric homooligomers from identical protomers, and FoXSDock40 can be used for dimers.

Use the SAXS R _g and M _r to eliminate models

In some cases, certain assemblies can be eliminated from further consideration using knowledge of the R _g and M _r calculated from the SAXS data. Oligomers with R _g or M _r that deviate substantially from the SAXS‐derived values are likely absent in solution or in low population (see case studies 1, 2, and 4 below). Several servers and programs calculate R _g from atomic coordinates, including FoXS,24, 41 CRYSOL,17, 42 CNS,23 and MOLEMAN.43 Note that it is possible for the SAXS R _g to lie between those of two oligomers with different n values; this could indicate either the presence of a self‐association equilibrium (see case study 3 below), that the models used are insufficient to represent in‐solution behavior, or simply that R _g is unable to discriminate between the models. In summary, consideration of R _g coupled with knowledge of the M _r in solution often eliminates certain models from further consideration, resulting in a filtered set of plausible models that is input to the next stage of analysis.

Comparison of experimental and theoretical SAXS curves

The definitive method for determining quaternary structure is by comparing the experimental SAXS curves to theoretical ones calculated from trial models. The mathematical foundations of these calculations and their implementation have been discussed elsewhere.41, 42 The programs CRYSOL42 and FoXS41 are commonly used for this analysis. Both are available via servers and downloadable programs.

Assessing the fits of the theoretical SAXS curves to the experimental data is a crucial step in quaternary structure determination from SAXS data. SAXS fitting programs output statistics that express the quality of the fit, and these statistics are used to identify the correct model from a set of candidate models. For example, in the case studies below, we report the goodness‐of‐fit parameter output by FoXS, χ (essentially the square root of the reduced χ² statistic). Users should be aware of the limitations of χ and similar metrics output by other programs. Because the experimental errors of the intensity measurements, σ(I _exp(q)), appear in the denominator of the χ formula,41 SAXS data with small errors will lead to fits with relatively high χ values, whereas data with larger errors will result in lower χ values. Therefore, χ generally is not useful for judging the fits of a particular model to different experimental SAXS curves. On the other hand, χ is useful for comparing the fits of different models to a single experimental SAXS curve. Franke et al. recently discussed the limitations of goodness‐of‐fit metrics in SAXS analysis and proposed a new statistic, CorMap.44 Hura et al. also developed the volatility of ratio difference metric as an alternative to χ.45

The oligomer models are static and cannot accurately represent the flexibility of the in‐solution oligomer, which can result in poor fits to the experimental SAXS data. Programs such as AllosMod‐FoXS46 and BILBOMD47 perform in silico sampling of conformations with various degrees of restraint. It can be helpful to use AllosMod‐FoXS, for example, when flexible termini are disordered in a crystal structure model. Conveniently, AllosMod‐FoXS will build missing residues, generate models with alternate conformations, and submit each model to the FoXS server. This approach can help generate a model to improve the fit of the theoretical curve to the experimental data. As with the model incompleteness issue described above, we recommend omitting conformational sampling in the first pass through the workflow.

Case 1: Distinguishing between monomer and dimer

Structures of the small calcium‐binding protein polcalcin phl p7 were determined independently using NMR48 (PDB ID 2LVK) and X‐ray crystallography49 (PDB ID 1K9U). The NMR structure is a compact, globular monomer with R _g of 11.4 Å [Fig. 3(A)]. In contrast, the crystal structure features an interlocked, domain‐swapped dimer with R _g of 15.1 Å that is predicted by PDBePISA to be stable in solution [Fig. 3(B)]. Each protomer of the crystallographic dimer is highly elongated (R _g of 14.7 Å) compared to the NMR monomer. The SAXS R _g of 12.91 ± 0.03 Å differs by ∼2 Å from both the R _g of the NMR monomer (11.4 Å) and crystallographic dimer (15.1 Å) [Fig. 3(B), inset]. Thus, in this particular case, consideration of R _g was not useful for identifying the correct in‐solution oligomer.

Figure 3.

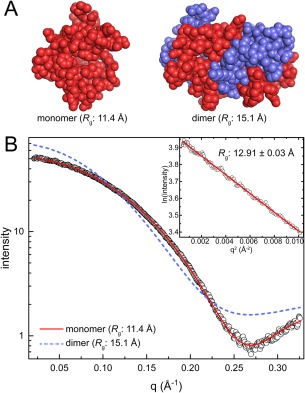
Case 1: distinguishing between a monomer and a dimer. (A) Models of the polcalcin phl p7 monomer from NMR (PDB ID 2LVK) and the crystallographic dimer (PDB ID 1K9U). Protomers in the dimer model are colored differently for clarity. (B) Experimental SAXS data (open circles) collected at a single concentration of polcalcin phl p7. The inset shows the Guinier plot. Theoretical curves calculated from the polcalcin NMR monomer (red solid line; FoXS χ: 1.5) or dimer (slate dashed line; FoXS χ: 24) are shown.

In contrast to R _g analysis, estimation of M _r from the SAXS data together with the calculation of SAXS curves from the models clearly shows that the protein is monomeric in solution. The M _r from the SAXSMoW2 server is within only 11% of the monomer. Moreover, the scattering profile calculated from an NMR monomer model shows excellent agreement with the experimental curve [Fig. 3(B)]. The good agreement is characterized by the FoXS goodness‐of‐fit parameter (χ) of 1.5. In contrast, the SAXS curve calculated from the crystallographic dimer deviates substantially from the experimental curve throughout the entire q region of the data and has a very high χ of 24. In conclusion, the calculation of scattering profiles was the litmus test for distinguishing between two competing models of polcalcin.

Case 2: Identifying the correct oligomer from several crystallographic assemblies

The crystal structure of Aspergillus fumigatus UDP‐galactopyranose mutase (PDB ID 3UTE) has a dimer‐of‐dimers bow tie‐shaped tetramer in the asymmetric unit.50 Interestingly, the analysis of crystal packing using PDBePISA predicted several potentially stable assemblies, including an octamer (R _g = 51.6 Å), the bow tie tetramer (R _g = 46.9 Å, tetramer 1), a different tetramer (R _g = 48.7 Å, tetramer 2), and three dimers (R _g = 33.6 Å, 35.5 Å, 43.0 Å). The structures of these potential oligomers are depicted in Figure 4(A).

Figure 4.

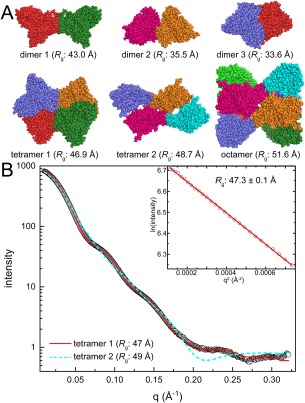
Case 2: Identifying the correct oligomer from several models. (A) Assembles of the UDP‐galactopyranose mutase from Aspergillus fumigatus derived from PDBePISA analysis of crystal packing (PDB ID 3UTE). Protomers are colored differently for clarity. (B) Experimental SAXS data (open circles) collected at a single protein concentration. The inset shows the Guinier plot. Theoretical curves calculated from tetramer 1 (red solid line; FoXS χ: 3.5) or tetramer 2 (cyan dashed line; FoXS χ: 21) are shown.

Analysis of R _g and M _r reduces the number of possible models. The Guinier R _g of 47.3 ± 0.1 Å is strong evidence against the two smallest dimers, which have R _g of only 34–35 Å. However, all the other models have an R _g within 10% of the experimental R _g, so additional criteria are needed to identify the correct oligomer(s). At this point, it is useful to estimate M _r from the SAXS curve. The SAXSMoW2 server returns M _r of 232.3 kDa, which is within 2% of the M _r of a tetramer. Thus, R _g and M _r suggest one of the tetramer models represents the major species in solution.

The calculation of scattering profiles identifies the correct tetramer. Comparison of the theoretical scattering curves of the two tetrameric models to the experimental data reveals χ values of 3.5 and 21 for the bow tie tetramer and tetramer 2, respectively [Fig. 4(B)]. This result shows that the statistically better fit is clearly the bow tie tetramer model. Therefore, here, the calculation of scattering curves was able to differentiate between two models of similar R_g to determine the correct in‐solution assembly.

Case 3: An obvious monomer–dimer equilibrium

The crystal structure of proline utilization A from Sinorhizobium meliloti was determined in monoclinic and trigonal crystal forms.51 The monoclinic form has a dimer with R _g of 40.3 Å in the asymmetric unit [Fig. 5(A); PDB ID 5KF6]. The trigonal asymmetric unit (PDB ID 5KF7) contains only a monomer (R _g = 32.7 Å), but crystallographic symmetry generates the same dimer that is in the monoclinic asymmetric unit [Fig. 5(A)]. Because the observation of the same assembly in multiple crystal forms is strong evidence that it may be a true structural assembly, it is tempting to assume the protein is dimeric in solution. However, SAXS analysis revealed a more interesting situation.

Figure 5.

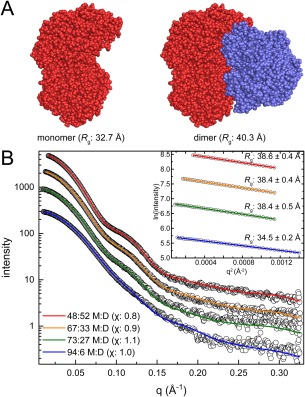
Case 3: An obvious monomer–dimer equilibrium. (A) Monomer and dimer models of proline utilization A from Sinorhizobium meliloti (PDB ID 5KF6). Protomers in the dimer model are colored differently for clarity. (B) Experimental SAXS data (open circles) collected at four increasing protein concentrations. The inset shows the Guinier plots for each concentration. MultiFoXS fits using a monomer‐dimer ensemble model are shown for each concentration. The optimal monomer:dimer (M:D) ratios determined by MultiFoXS are indicated in the legend, with the χ value for the each fit in parentheses.

SAXS data were collected at four different protein concentrations [Fig. 5(B)]. A distinguishing aspect of case 3 is that qualitative features of the SAXS curve vary with protein concentration. In particular, a bump appears in the curve at q = 0.10–0.14 Å⁻¹ as protein concentration is increased. The prominence of the bump correlates with an increase in R _g. The Guinier R _g increases from 34.5 ± 0.2 Å at the lowest concentration to 38.6 ± 0.4 Å at the highest concentration [Fig. 5(B), inset]. Note this range of R _g falls between the R _g values calculated from the monomer and dimer models (32.7 and 40.3 Å). These observations suggest the presence of a concentration‐dependent self‐association phenomenon. Consistent with this hypothesis, the M _r from the SAXSMoW2 server ranges from 123 kDa for the lowest concentration sample, to 208 kDa for the highest concentration sample. The lower value is close to the monomer M _r of 131.8 kDa, whereas the higher value approaches the M _r of a dimer (263.6 kDa). These observations are consistent with a concentration‐dependent monomer–dimer equilibrium.

To determine the relative effect of concentration on oligomeric state, MultiFoXS was used to fit ensembles of the monomer and dimer crystal structure models [Fig. 5(A)] to the experimental SAXS data. The ensemble approach yields statistically excellent fits over the entire concentration range [Fig. 5(B), χ: 0.8–1.1]. Consistent with dependence of R _g and M _r on protein concentration, the MultiFoXS analysis implies that the proportion of dimer increases with increasing protein concentration. At the lowest protein concentration, the monomer predominates (94:6 monomer:dimer), while at the highest protein concentration, the monomer and dimer contribute equally to the scattering (48:52 monomer:dimer). Overall, this case study is an excellent example of a concentration‐dependent self‐association equilibrium revealed by SAXS.

Case 4: A subtle dimer–tetramer equilibrium

The crystal structure of Bradyrhizobium japonicum proline utilization A has a domain‐swapped dimer with R _g of 44.8 Å in the C2 asymmetric unit [Fig. 6(A), PDB ID 3HAZ].52 Inspection of crystal packing using PDBePISA suggests three potentially stable oligomers: the domain‐swapped dimer (dimer 1), a different dimer (R _g = 44.1 Å, dimer 2), and a ring‐shaped dimer‐of‐dimers tetramer (R _g = 51.2 Å).

Figure 6.

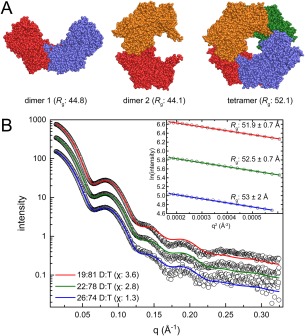
Case 4: A subtle dimer–tetramer equilibrium. (A) Models of proline utilization A from Bradyrhizobium japonicum derived from the crystal lattice (PDB ID 3HAZ). Protomers are colored differently for clarity. (B) Experimental SAXS data (open circles) collected at three increasing protein concentrations. The inset shows the Guinier plots for each concentration. MultiFoXS fits using an ensemble model of dimer 1 and the tetramer are shown for each concentration. The dimer 1:tetramer (D:T) ratios determined by MultiFoXS are indicated in the legend with the χ value for the each fit in parentheses.

SAXS data were collected at three different protein concentrations [Fig. 6(B)]. The Guinier R _g from the three curves is 52–53 Å consistent with the tetramer model. This result suggests the possibility of eliminating the two dimer models. The M _r estimated from the SAXSMoW2 server is within 1% of the tetramer (430.2 kDa) for all three curves, thereby effectively eliminating the possibility of dimer in‐solution. Thus, case 4 seems to be a straightforward example of a monodisperse tetramer, similar to case 2.

Thus, initial fitting to the experimental curves was carried out using only the tetramer model. The χ values obtained from fits to the crystallographic tetramer alone were in the range of 4.1–8.5, and there was a noticeable mismatch between the theoretical and experimental curves in both the Guinier region and the valley near q of 0.05–0.075.53 This result indicated that the tetramer alone may not be sufficient to explain the experimental data. To address this issue, MultiFoXS fitting was employed using all three models (dimer 1, dimer 2, and tetramer). Interestingly, 2‐body ensembles containing the tetramer and a small contribution of dimer 1 (20–25%) yielded markedly improved fits (χ: 1.3–3.6) [Fig. 6(B)]. This improvement suggests the presence of a dimer‐tetramer equilibrium despite M _r estimations suggesting a monodisperse solution.

It is noteworthy that the optimal ensembles from MultiFoXS always favored dimer 1 over dimer 2. These results agree with other studies showing that dimer 1 is conserved within this class of protein.53 Thus, SAXS ensemble fitting was able to differentiate between physiological and non‐physiological assemblies.

Conclusions

Over the past decade, SAXS has emerged as a powerful tool for analysis of the in‐solution structural properties of proteins, including molecular mass and quaternary structure. The use of SAXS to understand protein oligomeric structure works best when the researcher provides additional data and expert knowledge about the system under study, such as crystal structures and information about conservation of quaternary structure. Advances in computational tools have enabled the development of a well‐defined work flow consisting of three main tasks: (1) generating candidate oligomer models, (2) filtering the models based on SAXS‐derived structural parameters, and (3) analyzing single‐body and multibody simulations of the SAXS data (Fig. 2). Assuming the SAXS data are of high‐quality, implementation of this workflow results in reliable determination of oligomeric structure.

Small Angle Scattering Biological Data Bank (SASBDB) Accession Codes

The SAXS curves shown in the case studies have been deposited in the SASBDB54 under the following accession codes: case study 1—SASDDJ2; case study 2—SASDDK2, case study 3—SASDDL2, SASDDM2, SASDDN2, SASDDP2; case 4—SASDCS3, SASDCT3, SASDCU3.