Impact of the Local Public Hospital Reform on the Efficiency of Medium‐Sized Hospitals in Japan: An Improved Slacks‐Based Measure Data Envelopment Analysis Approach

Abstract

Objective

To assess the change in efficiency and total factor productivity (TFP) of the local public hospitals in Japan after the local public hospital reform launched in late 2007, which was aimed at improving the financial capability and operational efficiency of hospitals.

Data Sources and Data Collection

Secondary data were collected from the Ministry of Internal Affairs and Communications on 213 eligible medium‐sized hospitals, each operating 100–400 beds from FY2006 to FY2011.

Study Design

The improved slacks‐based measure nonoriented data envelopment analysis models (Quasi‐Max SBM nonoriented DEA models) were used to estimate dynamic efficiency score and Malmquist Index.

Principal Findings

The dynamic efficiency measure indicated an efficiency gain in the first several years of the reform and then was followed by a decrease. Malmquist Index analysis showed a significant decline in the TFP between 2006 and 2011. The financial improvement of medium‐sized hospitals was not associated with enhancement of efficiency. Hospital efficiency was not significantly different among ownership structure and law‐application system groups, but it was significantly affected by hospital location.

Conclusions

The results indicate a need for region‐tailored health care policies and for a more comprehensive reform to overcome the systemic constraints that might contribute to the decline of the TFP.

Local public hospitals in Japan are an essential component of the nation's quality health care system: They were established with the objective of improving public welfare, and they focus primarily on implementing the so‐called policy‐based medical services. These services include high‐technological medical care for complicated diseases; nonprofit health care; services for less densely populated and remote areas; and support for disaster relief and other emergencies. Data from the Ministry of Health, Labor and Welfare show that although local public hospitals accounted for only approximately 11 percent of the total number of hospitals and only 15 percent of total beds in 2010, they were intensively engaged in various public functions. They accounted for approximately 70 percent of the hospitals designated for serving remote areas; 40 percent of the emergency centers and 40 percent of regional cancer centers; and operated more than 60 percent of infectious beds, 20 percent of emergency beds, and 30 percent of tuberculosis beds. The Ministry of Internal Affairs and Communications launched the local public hospital reform in late 2007 because of their lackluster financial performance. The objective of this study was to investigate the impact of the reform on the efficiency of the hospitals.

Local Public Hospital Reform

During the first decade of the 21st century, the local public hospital system, one of the largest industries owned by the local government, faced many challenges threatening the soundness of the health care system in Japan.

First, substantial government subsidies, huge debts, and high operating costs raised obstacles for the hospitals. Despite substantial government subsidies, the financial conditions of the hospitals continued to worsen. The annual government subsidy for the hospitals was the second largest among all local public industries, but the annual net loss of the hospitals increased by more than 50 percent between 2003 and 2007.

Second, ambiguous functions of local public hospitals created misallocation of health care resources. In some areas, especially remote areas, the local public hospitals were not well equipped to provide sufficient policy‐based medical service to the local residents because of their fiscal constraints and typical brain drain. However, in other areas where health resources were more concentrated, the hospitals directly competed with primary health care facilities due to the absence of a gatekeeper system in Japan.

Third, lack of autonomy challenged local public hospitals. Managers of the hospitals were only authorized to manage daily operations. Several important management functions were controlled by the local governments, and bureaucratic constraints led to weak responsiveness by hospitals in the competitive health care market (Hashimoto et al. 2011).

To respond to the challenges, especially the financial challenges, the reform was implemented by the Ministry of Internal Affairs and Communications in late 2007. Local governments were required to formulate a three‐part, five‐year performance improvement plan, starting in FY2008: first, monitoring of three key performance indicators; second, reorganization of the local health care delivery system (concentrating beds in well‐functioning “magnet hospitals” and building “satellite clinics”) to ensure sufficient health care services in rural areas; third, initiating organizational reform. The guidelines also stipulated that hospitals operating below the minimum occupancy rate will face downsizing or replacement by clinics (MIC 2007).

Surveillance data from the Ministry of Internal Affairs and Communications show that the financial performance of hospitals substantially improved after 2008 (see Figure 1). The ratio of ordinary revenues to ordinary expenditures increased substantially, from 95.2 to 100.2 between 2006 and 2011. However, previous studies indicate that financial indicators have little association with the efficiency of hospitals and some financial incentives, like government subsidy, even reduce the efficiency (Luoma et al. 1996; Wilson et al. 2012). Examination of all available indicators is not sufficient to determine what change in efficiency, if any, occurred.

Figure 1.

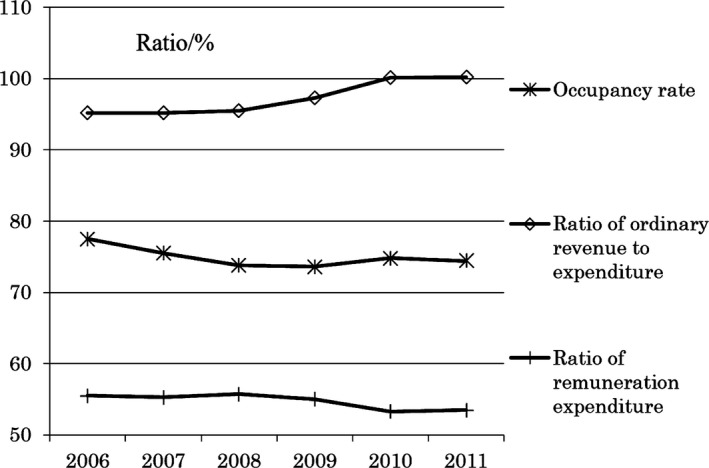
Changes in Monitored Indicators

Hospital Efficiency Analysis

There are two schemes in efficiency analysis, parametric and nonparametric ones (Hollingsworth 2003). Compared with a parametric scheme like stochastic frontier analysis, the nonparametric data envelopment analysis (DEA) approach does not require information on relative prices and assumptions about the specific functional form for the production possibility frontier (PPF; Worthington 2004; O'Neill et al. 2008). The DEA approach also provides a convenient method for calculating the Malmquist Index, which is used to measure productivity changes and identify the sources of inefficiency between two periods (Färe et al. 1994).

The DEA approach has been used widely for evaluating efficiencies in health care systems (Hollingsworth 2003, 2008; Worthington 2004; O'Neill et al. 2008). It operationalizes the measure of efficiency for the organizational unit under analysis, also known as a decision making unit (DMU), with multiple inputs and outputs in the form of an efficiency score that represents the relative distance from the objective DMU to the PPF formed by efficient peer DMUs. The closer a DMU is to PPF, the greater productivity it has.

Orientation in the DEA model describes the strategy of DMUs to achieve the PPF. Input‐oriented models are those where DMUs are considered to produce a given amount of output with the smallest possible amount of input, whereas output‐oriented models are those where the DMU with a given amount of inputs are deemed to produce the highest possible amount of outputs. For nonoriented models, DMUs are considered to produce the optimal mix of inputs and outputs. Different orientation models in a single input and single output production system are described in Figure 2.

Figure 2.

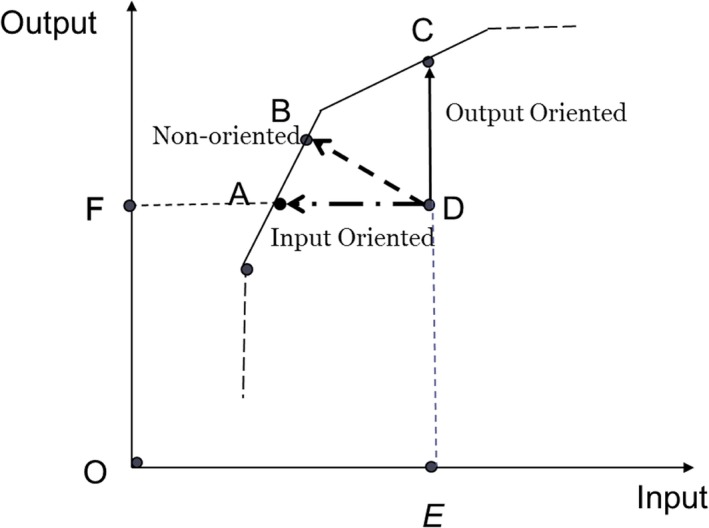
Different Orientation Models [Color figure can be viewed at wileyonlinelibrary.com]

The PPF in the DEA approach differs depending on the scale assumption that underpins the model. Two scale assumptions are commonly applied: constant returns to scale (CRS) and variable returns to scale (VRS). CRS reflects the fact that output will change proportionally as inputs are changed, for example, a doubling of all inputs will double the outputs; VRS reflects the fact that production technology may exhibit increasing, constant, and decreasing returns to scale.

There are typically two schemes in DEA, the radial scheme represented by the models CCR (Charnes, Cooper, and Rhodes 1978) and BCC (Banker, Charnes, and Cooper 1984); and the nonradial scheme represented by the slacks‐based measure (SBM) model (Tone 2001). The difference between the radial and nonradial schemes is that the radial models assume proportional change in input or output resources and usually ignore the remaining nonradial slacks, while the SBM model does not adopt the assumption of proportional change but aims to obtain maximum rates of change of inputs and/or outputs (Tone 2001; Avkiran, Tone, and Tsutsui 2008).

The study aimed to evaluate efficiency and total factor productivity (TFP) change before and after the local hospital reform launched in late 2007 and to analyze factors, including ownership, law application, and location of hospitals, which influence the efficiency and TFP. In so doing, a nonradial scheme, the nonoriented Quasi‐Max SBM method, was applied to estimate dynamic efficiency scores and the Malmquist Index (Tone 2001, 2004, 2010; Tone and Tsutsui 2010). We make three noteworthy contributions as follows.

First, the SBM model has the following advantages. It can eliminate nonradial slacks. Remaining nonradial slacks in radial models may mislead decision making when the efficiency score was used as the only index for evaluating the performance of DMUs (Torgersen, Førsund, and Kittelsen 1996; Tone 2001). Furthermore, the SBM model can be used to construct nonoriented models which assume that decision makers can control the inputs and outputs simultaneously (Ozcan 2008; Tone 2011; Bilsel and Davutyan 2014; Du et al. 2014; Zhu 2014; Sommersguter‐Reichmann and Stepan 2015). This scenario is more suitable in Japan's practices (Okamura, Kobayashi, and Sakamaki 2005; Hashimoto et al. 2011; Besstremyannaya 2013). Lastly, based on the nonoriented SBM model, infeasible linear programming issues are solved when intertemporal linear programming is used to calculate the Malmquist Index under variable returns to scale (VRS) models (Tone 2002, 2004). For more details, please refer to Appendix 3 in Appendix SA2.

Second, the efficiency measure of the original SBM model was improved using the “Variation I” proposed in the previous study (Tone 2010). The original SBM model evaluates the efficiency of DMUs relative to the furthest point on the PPF within a range. This problem leads to the hardest score and an inappropriate reference for the objective DMU. Using the “Variation I” (Quasi‐Max SBM model), each DMU is evaluated by the nearest point on the same facet of the production possibility set identified by the original SBM model. It depicts the differences among the CCR model, original SBM, and Quasi‐Max SBM models under single output and double input production system as shown in Figure 3. The original SBM model eliminates the nonradial slacks compared to the CCR model. The Quasi‐Max SBM model can help a DMU to attain an efficient status with less effort (less input reduction in this case) than the original SBM model does. The projection by the Quasi‐Max SBM model can be considered as a more practical improvement for a DMU. It should be noted that the distance identified by the “Variation I,” however, is not necessarily the real shortest distance. Therefore, we refer to it as the Quasi‐Max SBM model (Tone 2010).

Figure 3.

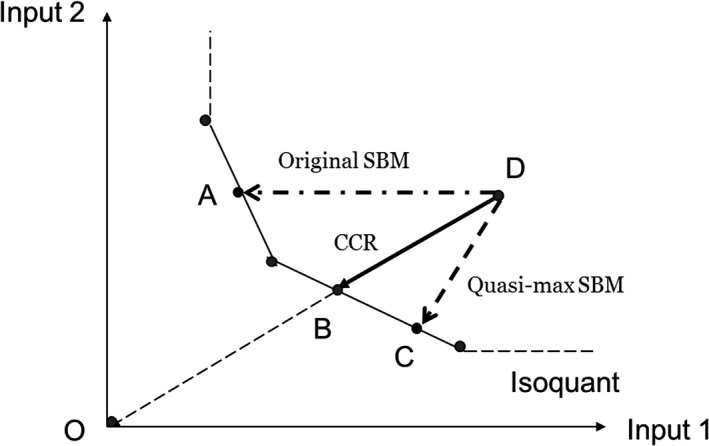
Differences among the CCR, Original SBM, and Quasi‐Max SBM Models

Third, besides the strict exclusion criteria, hospital selection was limited to those with 100 to 400 beds. The homogeneity of the outputs of hospitals was improved compared with other hospital efficiency studies conducted in Japan (Besstremyannaya 2011; Kawaguchi, Tone, and Tsutsui 2014).

Methods

Data Collection

This study collected data from the Ministry of Internal Affairs and Communications and included six annual surveys of all local public hospitals in Japan from FY 2006 to 2011 (MIC 2006–2011). According to the Local Public Enterprise Law, local governments are required to submit to the ministry annual audited financial statements of the local public enterprises under their governance. The ministry discloses this information on its website on a yearly basis, with Japan's fiscal year running from April 1 to the following March 31.

In FY2011, there were 652 local public enterprises running 863 hospitals. Among these 863 hospitals, 816 had successfully reported their operational and financial statement to the Ministry of Internal Affairs and Communications during the research period. We set rigorous exclusion criteria to improve the problem of heterogeneity of outputs among hospitals, because the local public hospital data lacked inherent case‐mix information, which has been demonstrated to be a factor contributing to hospital efficiency (Magnussen 1996; Rosen et al. 2003; Ozcan 2008; Vitikainen, Street, and Linna 2009).

One tuberculosis‐specialized hospital, 33 psychiatric hospitals and 36 other hospitals specializing in cancer, rehabilitation, rheumatics, and cerebrovascular and other diseases were excluded. A total of 289 hospitals with less than 80 percent general beds or with an average length of stay of either more than 70 days or <6 days in any of the 6 years examined were also excluded. With usual hospitalizations in Japan lasting at least 1 week, shorter stays might be associated with negative diagnoses or preliminary diagnostics which often lead to subsequent transfer to a specialized hospital (Evans et al. 2007; Besstremyannaya 2011). Furthermore, we excluded those with fewer than 100 or more than 400 beds. Finally, 213 eligible hospitals with complete and consecutive 6‐year data were selected for analysis.

Efficiency and Productivity Models

The nonoriented SBM model is explained in Appendix 1 in Appendix SA2, which is the basis of calculating the dynamic DEA model and Malmquist Index. The method to improve efficiency measure is also explained (Quasi‐Max SBM DEA model). Readers can refer to other articles for more information (Tone 2001, 2011; Ozcan 2008).

Dynamic Quasi‐Max SBM DEA Model

With regard to production, there are various factors that can lead to carryover of resources or finished products from one period to the next. Thus, it is not sufficient to assume that only inputs acquired in a particular period contribute to the production of outputs in that period. The dynamic SBM DEA model can handle the problem more precisely, because it can integrate the effect of carryover activities into efficiency measure, classify carryovers according to their respective characteristics, and calculate the efficiency scores overall and for each period (Tone and Tsutsui 2010). To use the dynamic SBM DEA model, data in initial and final periods are sacrificed. Thus, dynamic efficiency score is only reported from 2007 to 2010 in this study. For the way to calculate the dynamic Quasi‐Max SBM DEA model, refer to Appendix 2 in Appendix SA2.

Quasi‐Max SBM Malmquist Index

The DEA model provides a convenient approach for calculating the Malmquist Index, which is used to estimate the TFP change and identify the sources of inefficiency between two periods (Malmquist 1953; Färe et al. 1994). The index is calculated as follows:

$$\text{MI}={\left[\frac{{\mathit{\delta }}^p\left({\left(x_o,y_o\right)}^q\right)}{{\mathit{\delta }}^p\left({\left(x_o,y_o\right)}^p\right)}\times \frac{{\mathit{\delta }}^q\left({\left(x_o,y_o\right)}^q\right)}{{\mathit{\delta }}^q\left({\left(x_o,y_o\right)}^p\right)}\right]}^{\frac{1}{2}},$$

where δ and $\left(x_o,y_o\right)$ indicate the efficiency score and DMU_o, respectively_, and the superscripts indicate the time periods p and q. For instance, ${\mathit{\delta }}^p\left({\left(x_o,y_o\right)}^q\right)$ indicates the efficiency score of DMU$\left(x_o,y_o\right)$ in period q, as measured by the frontier technology for period p.

The Malmquist Index can be further broken down into two components:

$$\begin{array}{cc}\hfill \text{MI}& =\frac{{\mathit{\delta }}^q\left({\left(x_o,y_o\right)}^q\right)}{{\mathit{\delta }}^p\left({\left(x_o,y_o\right)}^p\right)}\times {\left[\frac{{\mathit{\delta }}^p\left({\left(x_o,y_o\right)}^p\right)}{{\mathit{\delta }}^q\left({\left(x_o,y_o\right)}^p\right)}\times \frac{{\mathit{\delta }}^p\left({\left(x_o,y_o\right)}^q\right)}{{\mathit{\delta }}^q\left({\left(x_o,y_o\right)}^q\right)}\right]}^{\frac{1}{2}}\hfill \\ \hfill \text{Or}\text{MI}& =\text{Catch‐up}\times \text{Frontier‐shift}\hfill \end{array}$$

The first component (the ratio outside the square brackets) represents the “Catch‐up,” which is related to the DMU attained for improving its technical efficiency. The second component (the Frontier‐shift) reflects changes in the TFP levels due to the frontier‐shift between two periods or, in other words, reflects technological changes or innovation (Färe et al. 1994).

A value of Malmquist Index >1 indicates TFP progress, <1 represents regression, and equal to 1 implies no change.

The method of calculating nonoriented SBM Malmquist Index was introduced by Tone (2004). Refinement of efficiency measure following Quasi‐Max approach is explained in Appendix 3 in Appendix SA2.

Model Specification

It is challenging to measure efficiency of health care institutions. Challenges come not only from how to determine proper inputs and outputs, but also from how to appropriately weigh the quality of outputs in efficiency measurement, which is known in clinical situations to vary widely by patients, conditions, providers, and other factors (Hussey et al. 2009). It is worth noting that our models have several limitations. For instance, capital inputs and quality information of outputs are omitted in the government database. However, various methods have been adopted to reduce potential biases in this study.

This article followed previous studies on variable selection (Hollingsworth, Dawson, and Maniadakis 1999; Hollingsworth 2003, 2008; O'Neill et al. 2008; Cook, Tone, and Zhu 2014; Kawaguchi, Tone, and Tsutsui 2014).The input, output, and carryover variables are shown in Table 1. For the inputs, numbers of doctors, nurses, and other personnel were used as proxy variables of labor resources; number of operational beds and building area were used to measure the complexity and size of hospitals. To more accurately measure the number of treatments completed by a hospital, we used the annual average of admissions and discharges, which was not reported in the surveys of the Ministry of Internal Affairs and Communications, as one of the outputs. However, we can calculate the annual average of admissions and discharges for the general beds by means of the following formulation:

$$\begin{array}{c}\hfill \text{average}\text{of}\text{admissions}\text{and}\text{discharges}\\ & =\frac{\text{annual}\text{admissions}\text{+}\text{annual}\text{discharges}}{2}\hfill \\ & =\text{no.}\text{of}\text{general}\text{beds}\times \frac{\text{utilization}\text{rate}}{\text{average}\text{length}\text{of}\text{stay}}\hfill \\ & \times \frac{\text{no.}\text{of}\text{calendar}\text{days}\mathrm{a}\text{year}}{100}.\hfill \end{array}$$

Table 1.

Specification of Different Models

	Variables	Dynamic SBM DEA Model	Malmquist Index Model
Inputs	Doctors	X	X
	Nurses	X	X
	Other staff	X	X
	Total beds	X	X
	Structure area	X	X
Outputs	Outpatients per day	X	X
	Annual average of admissions and discharges	X	X
	Emergency beds	X	X
Carryovers	Total revenue	X
	Total expenditure	X

For carryover variables, the net income is considered as a proper carryover for a hospital. However, the net income of a large number of local public hospitals in Japan is negative. The dynamic SBM DEA model cannot analyze negative values. Thus, we took total revenue and expenditure as a “desirable (good) carryover” variable and an “undesirable (bad) carryover” variable instead, respectively. We assume that based on the current data, hospital managers could predict hospital revenue and expenditure in the coming year and then draw up operational strategy.

Statistical Analysis

We analyzed the effects of contextual factors such as hospital location, ownership, and management aspects, which have been proven to impact on the success of quality improvement (Kaplan et al. 2010). The selected hospitals were divided into three groups according to their location: North group, including the Hokkaido and Tohoku regions; Center group, including the Kanto, Chubu, and Kinki regions; and South group, including the Chugoku, Shikoku, and Kyushu regions. In light of ownership, hospitals were categorized as (1) prefecture‐owned, that is, those owned by prefectures or designated cities; and (2) nonprefecture‐owned, that is, those owned by cities, towns, and villages (these hospitals are comparatively small). Hospitals were also categorized into full law‐application and partial law‐application groups. Local public hospitals are owned by the local governments and are thus subject to some or all of the Local Public Enterprise Law stipulations regarding the organizational, financial, and personnel administration of public enterprises. Theoretically, the autonomy of hospitals with full law‐application is guaranteed by the law, and thus, these hospitals tend to be more free from intervention by local governments.

The dynamic efficiency measures and Malmquist Index for all medium‐sized hospitals were classified into geographic, ownership, and law‐application groups, respectively. The Kruskal–Wallis one‐way ANOVA or Mann–Whitney U‐test were used to examine the distribution and median of the efficiency score among different groups. The bias‐corrected and accelerated (BCa) bootstrap was used to estimate the 95 percent confidence interval (CI 95 percent) of the geometric mean of the Malmquist Index (Efron 1987; Atkinson and Wilson 1995; Burgess and Wilson 1995). The efficiency scores and the Malmquist Index were calculated based on DEA‐Solver Pro 12 software package (SAITECH, Inc 2015), and SPSS 22.0 (IBMCorp 2013) was used to perform those statistical tests and to apply the BCa bootstrap.

Results

Overview of the Medium‐Sized Hospitals

There was no significant difference between the efficiency scores of ownership and law‐application groups. Thus, the results are displayed here only on the basis of geographic groupings.

Table 2 shows the statistics of input, output, and carryover variables. The means of doctors, nurses, and other staff decreased from 26.8, 149.9, and 65.7 in 2006 to 26.4, 149.2, and 64.0 in 2008, and then increased to 27.7, 156.3, and 64.7 in 2011, respectively. During the same period, number of beds continued to decrease from 254.5 to 246.1, and the building area slightly increased from 16.8 to 17.4 thousand square meters, respectively. The number of outpatients per day fell continuously from 2006, while annual average admissions and discharges decreased between 2006 and 2008 and then increased from 3,960 to 4,150 between 2009 and 2011. The number of emergency beds continued to increase during the research period. Both revenues and expenditures, in billion yen, increased from 4.25 and 4.55 in 2008 to 4.66 and 4.70 in 2011, respectively. The difference between expenditures and revenues continued to decrease, from 0.33 billion yen in 2006 to 0.04 billion yen in 2011.

Table 2.

Descriptive Statistics of Input, Output, and Carryover Variables

	2006		2007		2008		2009		2010		2011
	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
Input variables
Doctors (FTE)	26.8	14.0	26.4	14.5	26.4	15.1	26.8	16.0	27.1	16.3	27.7	17.3
Nurses (FTE)	149.9	64.2	150.1	67.2	149.2	68.1	150.8	70.4	154.0	74.0	156.3	76.2
Other staff (FTE)	65.7	27.5	65.2	27.9	64.0	27.8	63.9	28.0	64.3	28.9	64.7	29.9
Total beds	254.5	86.7	252.6	86.3	250.5	88.1	248.1	88.5	247.1	88.8	246.1	88.8
Structure area (thousand m2)	16.8	7.0	16.8	7.0	16.9	7.1	17.1	7.2	17.2	7.2	17.4	7.4
Output variables
Number of outpatients per day	555.4	217.8	523.9	206.6	495.8	200.6	488.3	195.5	481.5	197.6	472.9	198.4
Average annual admissions and discharges (thousand cases)	4.06	2.06	3.97	2.07	3.91	2.16	3.96	2.20	4.10	2.28	4.15	2.38
Emergency beds	7.25	6.84	7.36	6.81	7.35	6.78	7.38	6.77	7.46	6.79	7.65	6.70
Carryover variables
Total revenue (billion yen)	4.28	1.98	4.25	2.01	4.25	2.08	4.38	2.19	4.60	2.35	4.66	2.45
Total expenditure (billion yen)	4.61	2.09	4.57	2.12	4.55	2.19	4.59	2.25	4.67	2.34	4.70	2.41

Dynamic Efficiency Measures

The dynamic efficiency scores are reported in Table 3. The median of efficiency score under constant returns to scale (CRS) for all medium‐sized hospitals increased from 0.744 to 0.837 between 2007 and 2009 and then decreased to 0.732 in 2010. The overall dynamic efficiency score for the North group was the highest, 0.933, followed by the South group with a score of 0.855, and by the Center group at 0.717. Both the distribution and median for the three groups were significantly different at the 1 percent confidence level. Regarding yearly dynamic efficiency measures, the North group had the highest median, constant at 1 until 2009 and then decreasing to 0.990 in 2010. The Center group had the lowest median. Both Center and South groups had an initial efficiency gain after the reform, followed by a decrease in subsequent years. It is important to note that the South group medians of dynamic efficiency scores increased from 0.909 in 2007 to 1.000 in 2008 and then dramatically dropped to 0.759 in 2010.

Table 3.

Dynamic Efficiency Measure for Geographic Groups

	North N = 39		Center N = 123		South N = 51		Total N = 213
	Median	Min	Median	Min	Median	Min	Median	Min
Dynamic efficiency score under CRS
2007 ** , ##	1.000	0.301	0.681	0.127	0.909	0.239	0.744	0.127
2008* , ##	1.000	0.342	0.754	0.115	1.000	0.408	0.801	0.115
2009* , #	1.000	0.347	0.715	0.116	0.881	0.413	0.837	0.116
2010	0.990	0.265	0.682	0.279	0.759	0.295	0.732	0.265
Overall** , ##	0.933	0.348	0.717	0.291	0.855	0.435	0.789	0.291
Dynamic efficiency score under VRS
2007* , #	1.000	0.328	0.751	0.244	1.000	0.214	0.834	0.214
2008##	1.000	0.315	0.832	0.233	1.000	0.437	1.000	0.233
2009##	1.000	0.313	0.861	0.300	1.000	0.420	1.000	0.300
2010** , ##	1.000	0.307	0.861	0.303	0.847	0.325	0.899	0.303
Overall** , ##	1.000	0.316	0.802	0.314	0.903	0.445	0.889	0.314

^†The maximum of all groups is 1.

For median: *p < .05, **p < .01; for distribution: ^# p < .05, ^## p < .01.

The dynamic efficiency estimates for all medium‐sized hospitals under VRS, however, show a significant efficiency gain from 0.834 in 2007 to 1.000 in 2008 and then decreased to 0.899 in 2010.

Malmquist Index

The results of the Malmquist Index with a 95% CI are shown in Table 4. For Malmquist Index under CRS, a significant regress of TFP, 2.1 percent (0.979[0.961–0.997]), was observed between 2006 and 2011, with a significant Catch‐up efficiency gain of 3.9 percent (1.039[1.016–1.060]) but a significant Frontier‐shift regress of 5.0 percent (0.950[0.937–0.962]). The regress of the PPF actually offset the Catch‐up efficiency gain and led to a TFP regression for medium‐sized hospitals. No significant change in yearly TFP was observed over the study periods, except for a significant decrease of 1.4 percent during the period 2006–2007. The Catch‐up efficiency increased significantly and the Frontier‐shift decreased significantly in the first fiscal years (2007–2009) after local public hospital reform guidelines went into effect. The Frontier‐shift increased significantly, while the Catch‐up efficiency started to decrease in the period 2010–2011.

Table 4.

Malmquist Index for Geographic Groups

		North			Center			South			Total
		G.M.*	Lower¶	Upper¶	G.M.	Lower	Upper	G.M.	Lower	Upper	G.M.	Lower	Upper
Malmquist Index under CRS
	MI†	0.998	0.954	1.035	0.985	0.971	1.000	0.981	0.960	1.000	0.986	0.975	0.998
06/07	CMI‡	1.028	0.985	1.069	0.994	0.975	1.014	0.982	0.946	1.014	0.997	0.982	1.013
	FMI§	0.976	0.953	1.000	0.999	0.983	1.018	1.008	0.980	1.038	0.997	0.985	1.010
	MI	0.958	0.935	0.977	1.021	1.005	1.037	0.983	0.964	1.001	1.000	0.988	1.012
07/08	CMI	1.017	0.990	1.044	1.081	1.059	1.101	1.058	1.029	1.086	1.064	1.049	1.079
	FMI	0.944	0.927	0.962	0.951	0.935	0.965	0.933	0.916	0.950	0.945	0.935	0.956
	MI	0.998	0.967	1.032	1.013	0.999	1.027	1.011	0.992	1.033	1.010	0.999	1.020
08/09	CMI	1.023	0.988	1.062	1.038	1.015	1.060	1.043	1.014	1.073	1.036	1.019	1.053
	CFM	0.979	0.960	1.001	0.984	0.970	0.999	0.974	0.955	0.993	0.981	0.971	0.991
	MI	0.993	0.971	1.015	1.015	1.002	1.027	0.993	0.965	1.016	1.006	0.995	1.015
09/10	CMI	0.999	0.975	1.022	1.017	1.000	1.034	1.003	0.974	1.029	1.010	0.997	1.023
	FMI	0.997	0.977	1.014	1.003	0.991	1.014	0.992	0.978	1.005	0.999	0.991	1.007
	MI	1.017	0.982	1.050	0.991	0.981	1.002	1.000	0.978	1.022	0.998	0.988	1.008
10/11	CMI	0.976	0.940	1.013	0.944	0.929	0.958	0.951	0.920	0.983	0.952	0.938	0.966
	FMI	1.045	1.026	1.067	1.055	1.042	1.069	1.058	1.033	1.085	1.054	1.044	1.064
	MI	0.941	0.901	0.976	0.991	0.970	1.013	0.978	0.939	1.021	0.979	0.961	0.997
06/11	CMI	1.026	0.974	1.075	1.051	1.023	1.079	1.019	0.975	1.067	1.039	1.016	1.060
	FMI	0.923	0.898	0.949	0.951	0.934	0.966	0.967	0.939	0.993	0.950	0.937	0.962
Malmquist Index under VRS
	MI	0.985	0.954	1.013	0.975	0.962	0.988	0.995	0.972	1.019	0.982	0.971	0.992
06/07	CMI	1.008	0.973	1.043	0.992	0.974	1.011	1.010	0.986	1.035	1.000	0.985	1.013
	FMI	0.980	0.964	1.000	0.988	0.975	1.003	0.990	0.968	1.014	0.987	0.977	0.998
	MI	0.969	0.943	0.996	1.015	0.998	1.035	0.985	0.965	1.007	1.000	0.987	1.013
07/08	CMI	0.988	0.960	1.016	1.051	1.031	1.073	1.041	1.009	1.075	1.037	1.021	1.053
	FMI	0.982	0.965	1.000	0.972	0.956	0.987	0.954	0.933	0.974	0.969	0.959	0.980
	MI	1.008	0.983	1.039	1.010	0.994	1.026	1.003	0.985	1.022	1.008	0.997	1.019
08/09	CMI	1.040	1.017	1.066	1.032	1.011	1.053	1.012	0.985	1.038	1.028	1.014	1.043
	CFM	0.970	0.955	0.985	0.985	0.972	0.997	0.996	0.977	1.013	0.985	0.976	0.993
	MI	1.004	0.983	1.023	1.010	1.000	1.020	0.997	0.972	1.019	1.006	0.997	1.015
09/10	CMI	1.006	0.980	1.031	1.021	1.007	1.036	1.007	0.977	1.034	1.015	1.002	1.027
	FMI	1.000	0.988	1.013	0.995	0.982	1.007	0.993	0.980	1.008	0.995	0.986	1.004
	MI	1.010	0.974	1.045	0.992	0.983	1.001	1.010	0.991	1.030	1.000	0.989	1.009
10/11	CMI	1.001	0.959	1.040	0.962	0.948	0.974	0.991	0.967	1.012	0.976	0.962	0.987
	FMI	1.014	0.996	1.033	1.037	1.024	1.051	1.023	1.005	1.040	1.029	1.020	1.039
	MI	0.967	0.927	1.007	0.994	0.972	1.016	0.982	0.943	1.022	0.986	0.968	1.004
06/11	CMI	1.029	0.982	1.077	1.039	1.011	1.065	1.046	0.999	1.088	1.039	1.017	1.060
	FMI	0.946	0.910	0.979	0.963	0.948	0.976	0.943	0.921	0.963	0.955	0.944	0.966

*Geometric mean.

†Malmquist Index.

‡Catch‐up component.

§Frontier‐shift component.

¶Lower and upper indicate boundary of 95% confidence interval.

Among the geographic groups, between 2006 and 2011 the North group showed the greatest decline in TFP, 5.9 percent (0.941 [0.901–0.976]). The South group had the second largest decrease, 2.2 percent (0.978 [0.939–1.021]), whereas Center group had the lowest decrease, 0.9 percent (0.991 [0.970–1.013]). Catch‐up efficiency increased, whereas Frontier‐shift decreased significantly for all geographic groups (see Table 4).

For the yearly TFP change measures, the Malmquist Index for the Center group was highest in 2007–2010 and was greater than 1, indicating progress in TFP, whereas the Malmquist Index for North group was always <1 in that period (see Table 4). The geometric mean of the Catch‐up efficiency for the North group remained above 1 until the period 2008–2009, when it decreased to <1 in the following periods. The Catch‐up efficiency for the Center and South groups, respectively, increased from 0.994 (0.975–1.014) and 0.982 (0.946–1.014) in 2006–2007 to 1.081(1.059–1.101) and 1.058 (1.029–1.086) in 2007–2008 and subsequently decreased for several periods. The Catch‐up efficiency for the Center and South groups remained above 1 until the period 09/10. In contrast, the Frontier‐shift for the Center and South groups decreased in 2006–2008 and subsequently increased. The Frontier‐shift of all three groups exceeded 1 in the period 2010–2011.

The Malmquist Index under VRS (see Table 4) showed the same trend as those under CRS. Between 2006 and 2011, medium‐sized hospitals had 1.4 percent (0986[0.968–1.004]) TFP regress with 3.9 percent (1.039[1.017–1.060]) Catch‐up efficiency gain and 4.5 percent (0.955[0.944–0.966]) Frontier‐shift regress. TFP measures among different groups between 2006 and 2011 showed a general gain in Catch‐up efficiency and a deterioration in Frontier‐shift. For yearly TFP measures, what should be noticed was that the North group had a significant Catch‐up efficiency increase (1.040[1.017–1.066]) and Frontier‐shift decrease (0.970[0.955–0.985]) in period 08/09.

A visualization of the Malmquist Index change during the different periods is shown in Appendix 4 in Appendix SA2.

Discussion

The reform of law‐application system was not sufficiently effective to enhance hospitals' efficiency. Furthermore, the improvement of financial conditions did not lead to corresponding improvement in efficiency. The results indicate that there were no significant differences in efficiency of hospitals with full and partial law‐application systems. Previous studies suggested that publicizing performance indicators could help hospitals to improve their focused activities (Marshall et al. 2000; Hibbard, Stockard, and Tusler 2003). The three publicized fiscal focused indicators might have contributed to the continuous improvement of financial conditions but had little effect on the efficiency of hospitals.

The impact of the reform on efficiency was temporary, and policy makers need to reflect on the reasons behind the efficiency decrease. The dynamic SBM model showed an efficiency gain in the first several years of the reform, followed by a decrease. The Great East Japan Earthquake on March 11, 2011, might have caused the decrease of efficiency in the North group (Shibuya et al. 2011), while the decrease in efficiency in the Center and South groups still need to be further investigated.

The efficiency and TFP change of medium‐sized hospitals were found here to vary considerably among geographic regions. The results of application of dynamic models reveal that the hospitals in the North group had the highest efficiency score, whereas those in the Center group had the lowest. The Malmquist Index results, however, found the greatest TFP decrease in the North group and least decrease in the Center group. The delivery of local health care services of the prefectures in northern parts of Japan is heavily dependent on local public hospitals; for example, the hospitals accounted for approximately 40 percent of total hospital beds in Yamagata prefecture in 2011, and thus, an efficiency and TFP change might have a greater than average impact on the local health care system effectiveness in that area. Regress of efficiency and TFP indicate possible compromised accessibility in those areas. Zhang and Oyama (2016) indicate that patients in the prefectures carrying more local public hospital burden tend to seek health care in those bearing less burden. These imbalances substantially increase after the local public hospital reform.

A significant regress of the Frontier‐shift between 2006 and 2011 was found in this study. It may result from two factors. First, the local public hospital reform emphasized functions of policy‐based medical service provision and quality of care in hospitals. Both policy foci required more resources, but the demand side was unstable. As the results showed, local governments increased nurse staffing, one of the health care quality indicators (Aiken et al. 2002; Harless and Mark 2010), even though the number of hospital beds has decreased during the study period. Second, the Frontier‐shift may have resulted in part from constraints of systemic mechanisms, such as provider payment regimens and incentive mechanisms (Smith 2010). The report from OECD shows that Japan was the second largest pharmaceutical consumer after the USA, but there was a longer time lag in drug and medical devices provision than that in other OECD counterparts (Jones 2009). The long lag for approval and the high regulatory cost discouraged manufacturers from entering. Furthermore, the government‐controlled fee schedule system has also diminished the attractiveness of Japan's drug and medical device market as a result of price‐control or even exclusion of them from fee schedules (Ikegami and Campbell 2004; Hashimoto et al. 2011). In the long term, this may constrain technology progress in Japan's health care system. The assumptions, however, need to be further investigated.

As nonradial DEA models have not been used frequently in previous health care–related research, the results of related studies should be interpreted and treated with great caution (Newhouse 1994; Hollingsworth 2008; Hussey et al. 2009). The following are noteworthy limitations of this study. First, there was no information about case‐mixing and quality of service in our database. Certain biases could have been introduced into the research: the efficiency of small hospitals might be overestimated because smaller hospitals tend to treat simpler cases that need fewer health care resources, whereas cases in larger hospitals tend to be more complicated and need more health care resources for treatment. Second, to guarantee the homogeneity of the inputs and outputs, our subjects were limited to medium‐sized hospitals. Thus, the effect of economies of scale was not addressed in this study. Finally, several organizational reform measures were introduced into the local public hospitals, but most hospitals undergoing those organizational reforms were excluded from our study because of missing key variables. Thus, the impact of the local public hospital reform on efficiency might have been underestimated.

Conclusion

A newly developed nonoriented Quasi‐Max SBM approach is applied in this study. The approach integrates nonradial slacks into the efficiency measurements and alleviates the problem of inappropriate reference in the original SBM models. Furthermore, nonoriented models provide additional options for researchers to analyze production where both input and output could be controlled simultaneously.

The local public hospital reform was followed by a temporary efficiency gain and then a decrease for the medium‐sized hospitals in Japan. The results of the Malmquist Index analysis indicate a significant decline in TFP between 2006 and 2011, stemming from changes in technology or service quality. The examination of Japanese local public hospital reform has implications for international policy makers: First, financial performance–oriented reform in public hospitals does not result in efficiency improvement. Also limited empowerment of public hospitals, such as change of law‐application system, is not effective to improve the efficiency. Last but not least, our results point to a need for region‐tailored health care policies and suggest the necessity of a more comprehensive plan to overcome systemic constraints when an efficiency improvement–focused reform is initiated.

There is a need for further studies in this area. Particularly, in the new era of value‐based health care that is embodied in Japan's vision for health care in 2035 (Miyata et al. 2015), improvement in quality and efficiency is required to be implemented to drive better care at lower costs worldwide. It is important to continue to monitor hospitals' efficiency and concurrently to investigate the use of efficiency models that integrate quality dimensions. Measures such as mortality, readmission rate, and satisfaction of patients can be considered for inclusion in future studies.

Supporting information

Appendix SA1: Author Matrix.

Appendix SA2:

Appendix 1: Non‐Oriented Quasi‐Max SBM DEA Model.

Appendix 2: Non‐Oriented Quasi‐Max Dynamic SBM DEA Model.

Appendix 3: Non‐Oriented Quasi‐Max SBM Malmquist Index.

Appendix 4: Malmquist Index for Geographic Groups.