Replacing iterative algorithms with single-pass algorithms

Consider the rather mundane question: what is the distance from point A to point B? Of course, in Euclidean geometry, the answer is trivial, but what if A and B are cities, and we are taking ground transportation? Seeking the optimal path is now more challenging because we must consider terrain conditions. In other words, the optimal path depends on the rate of speed that is possible at each point. This problem is considered isotropic because the rate of speed at each point is independent of direction. It can be solved by using existing single-pass algorithms such as those by Dijkstra (1), Tsitsiklis (2), and Sethian (3). Of course, a more realistic problem also would take into account that the possible speed at a given point also depends on the direction we are traveling (uphill/downhill, with/against traffic, etc.). This is the anisotropic version of the problem and is substantially more complicated. The algorithm of Sethian and Vladimirsky (4) in this issue of PNAS successfully generalizes Sethian's fast marching method (3) to make it the only single-pass algorithm able to solve the anisotropic path planning problem.

But in principle, the notion that information is essentially starting from point A, emanating in some sense radially outward from A, and eventually striking the point B is apparent.

To illustrate the greater complication of the anisotropic problem, I begin by describing how to solve the isotropic problem. To solve this problem, it is necessary to consider all possible routes from A to B. For example, consider all paths from A to B that pass through a given point x. Let the function T(x) represent the time elapsed to travel on the optimal path from A to x. Because the problem involves varying driving conditions, s(x) is designated as the driving speed at each point x. If the optimal path from A to B passes through the point x, then it follows that this path is also the optimal path from A to x (for otherwise, the optimal path from A to B would have been chosen differently). Now, consider a small distance from the point x given by x − δx. For small δx, assume s(x − δx) is approximately constant. Then it is clear that if x − δx is also on the optimal path, then

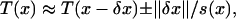1

where the ± corresponds to whether x − δx is before (+) or after (−) x on the optimal path. To see why this equation holds, note that to get from x − δx to x any quicker would exceed the local speed limit s(x). Letting δx → 0, Eq. 1 reduces to an Eikonal equation

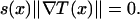2

This derivation is an application of Bellman's optimality condition (5) where I have assumed that the time T(x) is a differentiable function. One can show that the differentiability assumption is not necessary by using a viscosity solution formulation introduced by Crandall and Lions (6).

The question now becomes, how does one solve Eq. 2? If an iterative approach is considered, Eq. 2 can be suitably discretized so that T is approximated at a set of nodes x_i. Each pass through the data the iteration updates the value of T(x_i) to reflect the shortest time to reach x_i from its neighbors. Of course, the values at the neighbors do not necessarily give the correct shortest time. Suppose, however, that each of the nodes x_i could be marked in such a way that after each iteration x_i is marked if the value of T(x_i) is correct (no further iteration necessary). One could imagine how the marked nodes would expand from the starting point A outward until eventually filling the domain including the terminal point B. In the first iteration all of the nodes immediately adjacent to A would be correct. In the second pass, the next neighboring nodes would be correct, and so forth. Of course, such a marking technique is not possible in this iterative framework, because simply standing at some intermediate node x_i there is no a priori way of knowing whether the value of T(x_i) is now correct or will be modified in some future iteration. But in principle, the notion that information is essentially starting from point A, emanating in some sense radially outward from A, and eventually striking the point B is apparent. It is this basic concept that is the foundation for single-pass methods for solving the optimal path problem. Three such single-pass methods are the algorithms given by Dijkstra (1), which solves the optimal path problem on a discrete network and the motion is confined to links between nodes, and Tsitsiklis (2) and Sethian (3), both of which focus on continuous solutions of the Eikonal equation and that motion can occur in any direction. Although these three algorithms use different variations of the same theme to solve different formulations and equations, they share a common principle of dynamically determining the order in which the values of T(x_i) need to be computed to get the correct value without iterating.

These single-pass methods have had a significant impact in a broad range of applications. Dijkstra's original article (1), according to the Web Of Science (http://www.webofscience.com), has been cited nearly 1,000 times. It has been applied to circuit design (7), image processing (8), transportation (9, 10), and water distribution (11) to name a few. The much more recent papers by Tsitsiklis (2) and Sethian (3) have been used for numerous applications; in particular, Sethian's fast marching method has been used for shape recovery in medical imaging (12), computation of seismic travel times (13), and fatigue crack propagation (N. Sukumar, D.L.C., and B. Moran, unpublished work) and acts as an integral part of the popular level set method of Osher and Sethian (14) for general problems of moving interfaces.

Let us now return to the optimal path problem. A more genuine path planning problem would recognize that the possible speed at a given point x also may depend on the direction of travel. For example, if x were a point on a highway, traveling along the road would be much faster than crossing it. This additional possibility defeats both single-pass algorithms for the continuous problem, because they rely on the condition that the optimal path coincides with the gradient ∇T. This is clearly not the case for point x on the highway because ∇T would be more orthogonal to the direction of the road. Suppose that this highway may meander a bit. If it were to connect A to B, then standing at point x in between, we can no longer rely on the gradient to tell us from where the optimal path is coming, a crucial bit of information when computing T(x).

This is where the work by Sethian and Vladimirsky (4) takes a leap forward. If one doesn't know the direction from which the optimal path is arriving, one is essentially forced back to the original slower iterative methods, which require no insight into the behavior of the optimal path. However, Sethian and Vladimirsky use Bellman's optimality principle (5) to make the observation that the range of points from which the optimal path must pass before arriving at point x is limited by the local range of speed values. Therefore, in the single-pass framework, the value of T(x_i) depends only on a small subset of the nodes of already computed values of T(x_j). The larger the ratio between the maximum and minimum local speed with respect to direction, the wider the net must be cast to capture the optimal path. Nonetheless, this is enough to restore the single-pass construction for solving the larger class of static Hamilton-Jacobi equations

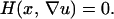3

Sethian and Vladimirsky demonstrate the viability of their techniques by applying them to problems in anisotropic seismic travel times, in which the speed of wave propagation depends on orientation, problems in optimal control, and problems of finding the shortest geodesic path on a manifold.

Although the discussion in this commentary has been confined to construction of optimal paths, static Hamilton–Jacobi equations, and the related Hamilton–Jacobi–Bellman equations appear in a variety of places, including general problems in control theory (see, for example ref. 15) and anisotropic front propagation (W. Symes and I. Qian, personal communication). Many of these applications require fast computation for real-time interactivity such as robotic arm motion, image processing, and optimal control. The application of Sethian and Vladimirsky's ordered upwind method will provide a quantum improvement over the existing solution methods, which still rely on large numbers of iterations.