Log Odds and the Interpretation of Logit Models

Abstract

Objective

We discuss how to interpret coefficients from logit models, focusing on the importance of the standard deviation (σ) of the error term to that interpretation.

Study Design

We show how odds ratios are computed, how they depend on the standard deviation (σ) of the error term, and their sensitivity to different model specifications. We also discuss alternatives to odds ratios.

Principal Findings

There is no single odds ratio; instead, any estimated odds ratio is conditional on the data and the model specification. Odds ratios should not be compared across different studies using different samples from different populations. Nor should they be compared across models with different sets of explanatory variables.

Conclusions

To communicate information regarding the effect of explanatory variables on binary {0,1} dependent variables, average marginal effects are generally preferable to odds ratios, unless the data are from a case–control study.

Researchers often struggle with how to estimate a model with a binary {0,1} dependent variable and present the results in a meaningful way. The choices for estimation and presentation approaches tend to fall along disciplinary lines. Epidemiologists and clinical researchers often estimate logit models and report odds ratios. Economists might estimate logit, probit, or linear probability models, but they tend to report marginal effects. There is an increasing recognition that model specification—particularly the inclusion or exclusion of additional explanatory variables—affects the interpretation of the results from nonlinear models, even when the explanatory variables are independent of each other (e.g., Yatchew and Griliches, 1985; Mroz and Zayats 2008; Mood 2010).

This is in contrast to linear regression models, where the inclusion or exclusion of truly independent variables affects only the standard errors of the coefficients, not their magnitude or marginal effects. To be clear, throughout this article, we are referring to the inclusion or exclusion of additional explanatory variables that are independent of the variables already in the equation. If the additional variables are correlated with the previously included variables, such as confounders, then leaving those additional variables out of the model can create endogeneity bias, which is a different problem. With endogeneity, the estimated coefficients will be biased and inconsistent, as will all marginal effects, odds ratios, and any other statistic derived from the estimated parameters.

This article focuses specifically on the effect of additional explanatory variables on the estimation and interpretation of odds ratios. Odds ratios have some convenient properties: they are simple to calculate; they are applicable to both continuous and discrete explanatory variables of interest. In some cases, such as case–control studies, they are indispensable. If the sign of the effect is what the research wants to test, then odds ratios are sufficient. However, depending on the research question, the researcher may also care about the magnitude of the effect, and the magnitude of odds ratios is easy to misinterpret. For example, they, sometimes, are misinterpreted as risk ratios, yet mathematically, they diverge significantly from risk ratios when the baseline risk exceeds about 10 percentage points (Greenland 1987; Sackett, Deeks, and Altman 1996; Altman, Deeks, and Sackett 1998; Schwartz, Woloshin, and Welch 1999; Walter 2000; Kleinman and Norton 2009; Tajeu et al. 2012).

More recent critiques have identified a more serious problem with odds ratios. Allison (1999) explained why odds ratios cannot be compared across samples. Mood (2010) extended this work nicely to show that odds ratios cannot be interpreted as absolute effects, nor can they be compared across models or across groups within models. Several authors have pointed out that odds ratios will change if variables are added to the model, even if those additional variables are independent from the other variables (Gail, Wieand, and Piantadosi 1984; Yatchew and Griliches, 1985; Allison 1999; Mood 2010). Mroz and Zayats (2008) also discussed the effect of omitted variables on the interpretation of odds ratios in logit models.

The first section of this article derives odds ratios in a way that explicitly shows the importance of the standard deviation (σ) of the error term in a logit or probit model. We then discuss five implications of estimating coefficients in a logit (or probit) model that are normalized by σ. For any given dataset and dependent variable, and any given explanatory variable of interest, there is no single odds ratio. There are many odds ratios, conditional on what other explanatory variables are included in the estimated model. Unless accompanied by a detailed description of the explanatory variables included in the model, odds ratios cannot be compared across different model specifications or across different study samples, for example, in meta‐analyses. When comparing odds ratios across models that progressively add covariates to test for robustness, the odds ratios are expected to increase. In summary, these important issues of interpretation are in addition to concerns about the misinterpretation of odds ratios as risk ratios. The final section of the article discusses the advantages of some alternatives to odds ratios, including marginal and incremental effects and risk ratios.

Logit and Probit Models

Derivation of Odds Ratio

We start by deriving the odds ratio in a way that makes explicit the relationship between the estimated logit parameters β and the error term ε _i. Suppose that a continuous latent variable $y_i^{\ast }$ can be modeled as a linear function of K explanatory variables (covariates), x _ki, for k = 1, … , K for individuals i = 1 … N. The equation for $y_i^{\ast }$ can be written as

$$y_i^{\ast }={\mathit{\beta }}_0+{\mathit{\beta }}_1{x}_{1i}+{\mathit{\beta }}_2{x}_{2i}+\dots +{\mathit{\beta }}_{Ki}{x}_{Ki}+{\mathit{\epsilon }}_i$$ (1)

If we allow the explanatory variables, including the constant term, to be represented by the vector ${\mathit{x}}_i^{\prime }$, then equation 1 can be represented in matrix notation as

$$y_i^{\ast }={\mathit{x}}_i^{\prime }\mathit{\beta }+{\mathit{\epsilon }}_i$$ (2)

However, the researcher observes only the explanatory variables and a binary {0,1} variable y _i, which indicate whether $y_i^{\ast }$ exceeds the threshold of zero.

$$y_i=\left\{\begin{array}{cc}1& \mathrm{if}{y}_i^{\ast }>0\\ 0& \mathrm{otherwise}\end{array}\right.$$ (3)

To make statements about the probability that y _i  = 1 (or equivalently, $y_i^{\ast }$ > 0), we need to express the probability in terms of an error term with a known distribution. Substituting ${\mathit{x}}_i^{\prime }\mathit{\beta }+{\mathit{\epsilon }}_i$ for $y_i^{\ast }$ allows us to write the probability that y _i  > 0 in terms of the probability that the error term takes on a range of values.

$$\text{Pr}(y_i^{\ast }>0|{\mathit{x}}_i)=\text{Pr}({\mathit{x}}_i^{\prime }\mathit{\beta }+{\mathit{\epsilon }}_i>0|{\mathit{x}}_i)=\text{Pr}({\mathit{\epsilon }}_i>-{\mathit{x}}_i^{\prime }\mathit{\beta }|{\mathit{x}}_i)$$ (4)

If the error term has mean zero and is symmetric (which is true for both the standard logistic and standard normal distributions), then

$$\text{Pr}(y_i>1|{\mathit{x}}_i)=\text{Pr}(y_i^{\ast }>0|{\mathit{x}}_i)=\text{Pr}({\mathit{\epsilon }}_i<{\mathit{x}}_i^{\prime }\mathit{\beta }|{\mathit{x}}_i)$$ (5)

Equation 5 holds for any arbitrary scaling of ε and β (e.g., ε/3 and β/3). Thus, because the distribution of ε is unknown, the Pr (y _i  = 1|x _i) cannot be evaluated without an additional step (Greene and Hensher 2010). To address that problem, the typical solution is to divide both ε and β by the standard deviation of ε: ε/σ and β/σ. Those transformations makes Pr (y _i  = 1|x _i) a cumulative distribution function (CDF) of a standard logistic (logit) or normal (probit) variable, which is easy to calculate for logistic and normal distributions.

For the probit model, the standard deviation of ε/σ = 1. The cumulative distribution function for the probit model is

$$\text{Pr}(y_i=1|\text{normal},{\mathit{x}}_i)=\text{Pr}\left(\frac{{\mathit{\epsilon }}_i}{\mathit{\sigma }}<{\mathit{x}}_i^{\prime }\frac{\mathit{\beta }}{\mathit{\sigma }}\right)=\left(\mathit{\varphi }{\mathit{x}}_i^{\prime }\frac{\mathit{\beta }}{\mathit{\sigma }}\right)$$ (6)

For the logit model, the standard deviation of ε/σ = $\mathit{\pi }/\sqrt{3}$. The cumulative distribution function for the logit model is

$$\text{Pr}(y_i=1|\text{logistic},{\mathit{x}}_i)=\text{Pr}\left(\frac{{\mathit{\epsilon }}_i}{\mathit{\sigma }}<{\mathit{x}}_i^{\prime }\frac{\mathit{\beta }}{\mathit{\sigma }}\right)=\frac{1}{1+\text{exp}(-{\mathit{x}}_i^{\prime }\frac{\mathit{\beta }}{\mathit{\sigma }})}$$ (7)

This derivation explicitly shows the important role of σ in making any statements about probabilities.

Many researchers prefer to estimate logit rather than probit models because of the odds ratio interpretation of the logit coefficients. The odds for individual i are expressed as the ratio of the probability p _i to 1–p _i, where p _i  = Pr(y _i = 1|logistic, x _i).

$$\text{odds}=\frac{p_i}{1-p_i}=\frac{\frac{\frac{1}{1+\text{exp}(-{\mathit{x}}_i^{\prime }\frac{\mathit{\beta }}{\mathit{\sigma }})}}{\frac{1}{\text{exp}(-{\mathit{x}}_i^{\prime }\frac{\mathit{\beta }}{\mathit{\sigma }})}}}{1+\frac{1}{\text{exp}(-{\mathit{x}}_i^{\prime }\frac{\mathit{\beta }}{\mathit{\sigma }})}}=\text{exp}\left(-{\mathit{x}}_i^{\prime }\frac{\mathit{\beta }}{\mathit{\sigma }}\right)$$ (8)

The odds ratio is the ratio of the odds in equation 8 for two different values of an explanatory variable. This is easiest to derive for a binary variable. For example, consider a study in which the dependent variable is the probability that the subject dies before age 65, and the primary explanatory variable of interest is whether the person smoked (at all) in the years prior to age 65. Let smoke_1i be an indicator for smoking status, and β _smoke be the corresponding coefficient. The odds of mortality by age 65 if individual i was a smoker (smoke_1i = 1) and the odds if individual i was a nonsmoker (smoke_1i = 0) are:

$$\text{odds for smoker}=\text{exp}\left(\frac{{\mathit{\beta }}_0+{\mathit{\beta }}_{\mathrm{smoke}}{\text{smoke}}_{1i}+{\mathit{\beta }}_2{x}_{2i}+\dots {\mathit{\beta }}_K{x}_{K_i}}{\mathit{\sigma }}\right)$$ (9)

$$\text{odds for non smoker}=\text{exp}\left(\frac{{\mathit{\beta }}_0+{\mathit{\beta }}_2{x}_{2i}+\dots {\mathit{\beta }}_K{x}_{K_i}}{\mathit{\sigma }}\right)$$ (10)

Therefore, the odds ratio is the ratio of the odds, which simplifies to the exponentiated coefficient.

$$\text{OR}=\text{odds ratio}=\frac{\text{odds for smoker}}{\text{odds for nonsmoker}}=\text{exp}\left(\frac{{\mathit{\beta }}_{\mathrm{smoke}}}{\mathit{\sigma }}\right)$$ (11)

The log odds are the logarithm of the odds ratio, in other words, the coefficient (normalized by the standard error).

$$\text{Log odds}=\text{exp}\left(\frac{{\mathit{\beta }}_{\mathrm{smoke}}}{\mathit{\sigma }}\right)$$ (12)

Although most textbooks and published papers write the odds ratio as the exponentiated coefficient, in this case exp (β _smoke), we purposefully leave in σ. The crux of the issues raised by this article arise because logit (and probit) models do not estimate the coefficients β; instead, they estimate β/σ.

Sigma

Next, we discuss in more detail what σ is and how the estimated β/σ is affected by the estimated model. In general, σ is the standard deviation of the error term. It is a measure of the variation in the latent dependent variable that remains unexplained after inclusion of the explanatory variables (covariates). However, σ cannot be estimated directly because the continuous y* on which an estimate of σ could be based also only in theory. Only y = 1 and y = 0 are observed. In logit (and probit) models, only the ratio β/σ is identified (although it is still useful to postulate a model containing these parameters to show the relationship among models with different parameters).

Although this article focuses on how σ is related to changes in model specification, there is another way in which σ can change without changing any explanatory variables. Consider a model where the continuous underlying latent variable y* is continuous birth weight. In a linear regression model, the magnitude of σ depends on both the scale, or unit, of y* (grams or ounces in this example) and the fraction of the variance in the dependent variable that is accounted for by the explanatory variables in the model. Fortunately, changes in σ associated with changes in the scale of the latent dependent variable are offset by changes in estimated coefficients (β); that is, the interpretation and statistical significance in a linear regression model are not dependent on whether birth weight is measured in metric or imperial units.

However, in a logit or probit model, the analyst observes only a binary indicator for whether the baby has low birth weight or not. Therefore, in a logit or probit model, the ratio β/σ is invariant to changes in scale of the latent dependent variable.

As mentioned above, the logit and probit models postulate error distributions with different values of σ (the standard normal distribution has a variance of 1, the standard logistic distribution has a variance of π ²/3). This explains why the estimated logit and probit coefficients are different. The normalizations are different. A rule of thumb is that logit coefficients are larger by a factor of about 1.6.

Changes in σ resulting from adding or removing covariates to the model are more problematic. Any change in the covariates that improves the model fit makes σ smaller and β/σ bigger. Conversely, omitting variables that should be included in the model (because they affect the dependent variable) increases σ. This is true even if the additional variables are independent from the explanatory variables that are already in the model. Unlike changes in the scale of the latent dependent variable, changes in the covariates included in the model change β/σ, meaning that logit (and probit) coefficient estimates are not invariant to model specification.

In mathematical terms, the derivative of the odds ratio with respect to σ is not zero. The derivative of the odds ratio for variable x ₁ with respect to a percentage change in σ, denoted ∂ σ/σ, is:

$$\frac{\mathit{\partial }[\mathrm{OR}]}{\frac{\mathit{\partial }\mathit{\sigma }}{\mathit{\sigma }}}=-\left(\frac{{\mathit{\beta }}_1}{\mathit{\sigma }}\right){\mathrm{e}}^{(\frac{{\mathit{\beta }}_1}{\mathit{\sigma }})}=-\left(\frac{{\mathit{\beta }}_1}{\mathit{\sigma }}\right)\mathrm{OR}$$ (13)

This expression always is opposite in sign to β ₁. For a positive β ₁, an increase in σ (e.g., due to dropping variables from the model specification) will reduce the odds ratio. This expression does not depend on the values of the other covariates and, so, is the same for all observations in the dataset. However, it does depend on which covariates are included in the model specification. This feature is both a strength and a weakness. A strength of the odds ratio is its invariance with respect to the values of the other explanatory variables, but that strength also is a weakness because there is no averaging over observations to attenuate the effect of dividing the coefficients by σ as discussed in the section on “Alternatives”.

Implications

Several implications follow from understanding that logit models estimate β/σ instead of β. First, there is no single odds ratio. An odds ratio is not an absolute number, like π. An odds ratio estimated from a multivariate logit model is conditional on the sample and on the model specification (Allison 1999; Mood 2010). A study that aims or claims to estimate the odds ratio, even in a single dataset, is misguided. The odds ratio is primarily useful to show the sign and statistical significance of an effect, but the same can be said about the estimated coefficient β/σ.

Second, an estimated odds ratio does have a specific interpretation, but the correct interpretation is far more complex than commonly believed or reported (Mood 2010). Unless accompanied by an explanation of the model specification, a statement like “The estimated odds ratio is 1.5” is factually incorrect. A more accurate, but imprecise, statement would be “An estimated odds ratio is 1.5.” A correct precise interpretation might be: “The estimated odds ratio is 1.5, conditional on age, gender, race, and income, but a different odds ratio would be found if the model included a different set of explanatory variables. The 1.5 estimated odds ratio should not be compared to odds ratios estimated from other datasets with the same set of explanatory variables, or to odds ratios estimated from this same dataset with a different set of explanatory variables.”

Third, it is not possible to compare odds ratios from different studies that use different datasets or even subpopulations within the same dataset, even if they have the same model specification (Allison 1999; Mood 2010). Any observed differences in coefficients across datasets could be due to differences in residual variation σ, or to differences in effects β, or both. These two effects are confounded because the estimated coefficient is their ratio, β/σ.

Fourth, in some studies, authors compare odds ratios from models that progressively add more and more explanatory variables. The reason for making these comparisons is to see whether the coefficient (or odds ratio) changes with the addition of more explanatory variables. Authors implicitly assume that if the odds ratio remains the same, that the estimated odds ratio for a specific variable is robust to the inclusion of additional explanatory variables which might represent confounders. However, unless the additional variables explain none of the variance in the dependent variable, their addition to the model will decrease σ and the odds ratio will increase. Therefore, even when the model is robust to different model specifications, the estimated odds ratios will change. As more variables are added to the model, changes in the odds ratio do not isolate or identify the presence or absence of confounder variables.

Fifth, this understanding of the importance of σ in β/σ enhances the already strong criticism of reporting odds ratios on the basis of misunderstanding by others (Greenland 1987; Sackett, Deeks, and Altman 1996; Altman, Deeks, and Sackett 1998; Kleinman and Norton 2009; Tajeu et al. 2012). Most prior arguments have focused on the difference between risk ratios and odds ratios, and how people mistakenly interpret odds ratios as risk ratios (Sackett, Deeks, and Altman 1996 also discuss other points). However, the correct interpretation of odds ratios also requires an understanding of the specification of the model that produced the odds ratio. This makes the correct interpretation of an odds ratio and comparability across studies even harder.

These five implications are not widely appreciated in the literature. Papers frequently report findings of the odds ratio, as if it were an absolute number that could be estimated without explicit conditioning on the model and covariates. Having made these points, we now turn to alternative ways of reporting and interpreting results from logit models.

Alternatives

How should researchers report and interpret results when the dependent variable is binary? The answer depends on the research question. There is no single right way for all studies. Nonlinear models are inherently complicated. Although odds ratios commonly are reported, the magnitude of an odds ratio depends on the sample and model specification. Researchers, however, have several alternatives to odds ratios for models with binary dependent variables. Mood (2010) has a comprehensive discussion of alternatives.

One popular alternative to the odds ratio is the marginal or incremental effect (sometimes these are called partial effects) of an explanatory variable on the probability that y _i equals 1 versus 0. The marginal effect is defined as the effect of a tiny change in a single continuous explanatory variable x _1i on the probability that y _i  = 1, or $\mathrm{\partial }$Pr(y _i = 1|x _i)/$\mathrm{\partial }$ x _1i. The incremental effect is defined as the effect of a discrete change from zero to one of a binary explanatory variable on the probability that y _i  = 1:

$$\text{Incremental effect}=\text{Pr}(y_i=1|{\mathit{x}}_i,x_{1i}=1)-\text{Pr}(y_i=1|{\mathit{x}}_i,x_{1i}=0)$$ (14)

The marginal effect is less sensitive to changes in the model specification than the odds ratio. First, this has been proved rigorously for the case of independent omitted variables for the logit, probit, and multinomial logit models (Lee 1982; Yatchew and Griliches 1985; Wooldridge 2010).

Second, unlike the odds ratio, the change in the marginal effect (ME) with respect to a change in sigma has parts that can be either positive or negative, depending on the baseline probability where the change is evaluated. These positive and negative effects may cancel out when computing an average marginal effect across the sample. For the logit model, the marginal effect of a continuous variable x ₁ is

$${\text{ME}}_i^{Logit}=\frac{\mathit{\partial }\text{Pr}(y_i=1|{\mathit{x}}_i)}{\mathit{\partial }{x}_{1i}}=\left(\frac{{\mathit{\beta }}_1}{\mathit{\sigma }}\right)\times p_i\times (1-p_i)$$ (15)

The derivative of the marginal effect for observation i with respect to a percentage change in σ is

$$\frac{\mathit{\delta }[{\mathrm{ME}}_i^{Logit}]}{\frac{\mathit{\delta }\mathit{\sigma }}{\mathit{\sigma }}}={\mathrm{ME}}_i^{Logit}\times [\mathrm{In}(\frac{p_i}{1-p_i})(2{\mathrm{p}}_i-1)-1]$$ (16)

which can be positive or negative, depending on the value of p _i. If p _i is less than about 0.176 or greater than about 0.823, then the term in brackets is positive; otherwise it is negative. Therefore, the average marginal effect, which is averaged over the values of p _i for all observations in a sample, may not be that sensitive to changes in σ. However, in specific situations, one could have all the predicted probabilities above or below these bounds. The same is true of incremental effects in the logit model.

In contrast, because the odds ratio for x _i is invariant with respect to the values of the other explanatory variables, there is no such averaging effect.

The same is also true for both marginal and incremental effects in the probit model. For the probit model, the marginal effect of x ₁ is

$$\frac{\mathit{\delta }\text{Pr}(y_i=1|x_i^{\prime })]}{\mathit{\delta }{x}_{1i}}=(\frac{{\mathit{\beta }}_1}{\mathit{\sigma }})\times \mathit{\varphi }({\mathit{x}}^{\prime }\frac{\mathit{\beta }}{\mathit{\sigma }})$$ (17)

where ϕ (·) is the normal probability density function. The derivative of the marginal effect for observation i with respect to a percentage change in σ can be written either as a function of the probability p _i or the index function.

$$\frac{\mathit{\delta }[{\text{ME}}_i^{Probit}]}{\frac{\mathit{\delta }\mathit{\sigma }}{\mathit{\sigma }}}={\text{ME}}_i^{Probit}[{(x^{\prime }\frac{\mathit{\beta }}{\mathit{\sigma }})}^2-1]$$ (18)

which can be positive or negative, depending on the value of (${\mathit{x}}^{\prime }\frac{\mathit{\beta }}{\mathit{\sigma }}$). If p _i is less than about 0.159 or greater than about 0.841, then this derivative is positive; otherwise it is negative. Again, because we usually care about average marginal effects, what matters is how marginal effects change over the whole sample. Changes in σ also have little effect on the average marginal effect for the probit model.

We can see that the response functions for logit and probit models are virtually the same, by graphing the cumulative distribution functions (CDF, appropriately scaled) against the linear index function (see Figure 1). The logit CDF has slightly fatter tails, but the difference is small. The linear probability response function is similar to the logit and probit functions only in a narrow range, unless, of course, a more flexible functional form is used.

Figure 1.

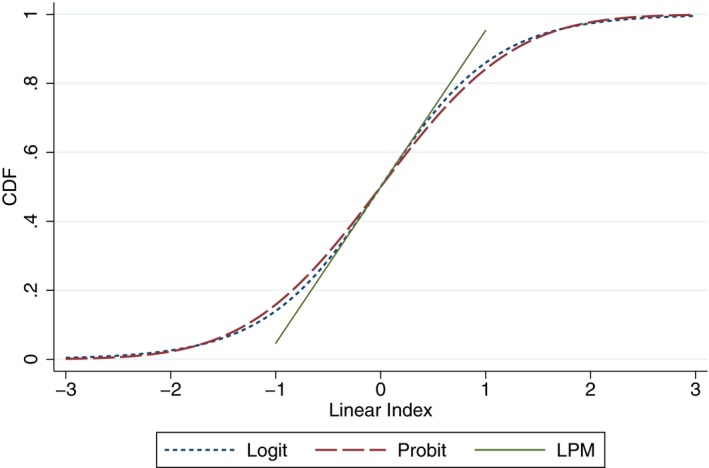
Scaled Response Functions for Logit, Probit, LPM [Color figure can be viewed at wileyonlinelibrary.com]

Third, we conducted a simulation to demonstrate how changing the model specification changes the odds ratio in a predictable way, but has no effect on the marginal effects for the linear probability model, and barely alters the average marginal effects for either logit or probit models. In the simulated dataset, the continuous dependent variable y is a linear function of a dummy variable x _d and four continuous variables x ₁ through x ₄. For these illustrative examples (N = 10,000), the variables of interest are the dummy variable (x _d) and the first two continuous covariates (x ₁ and x ₂). The covariates are independent of each other. When independent variables x ₃ and x ₄ are added to the simple model specification, the coefficients in the linear probability model remain essentially the same, as expected (see Table 1). The corresponding probit and logit models show that, unlike the linear probability model, the coefficients change when adding variables—because σ becomes smaller, the coefficients in the full model specification are larger. The corresponding marginal and incremental effects remain virtually identical (see Table 1). In contrast, the odds ratios are vastly different; they increase by orders of magnitude.

Table 1.

Comparison of Coefficient Estimates, Marginal Effects, and Odds Ratios for the Linear Probability, Logit, and Probit Models for Two Different Model Specifications

Variables	LPM		Logit		Probit
	Simple	Full	Simple	Full	Simple	Full
Constant
β/σ	0.5062 (0.0063)	0.5039 (0.0044)	0.032 (0.032)	0.109 (0.062)	0.020 (0.019)	0.057 (0.034)
x d
β/σ	0.0478 (0.0089)	0.0485 (0.0064)	0.244 (0.045)	0.827 (0.087)	0.145 (0.027)	0.468 (0.048)
IE			0.0482	0.0459	0.0476	0.0465
OR			1.276	2.285
x 1
β/σ	0.1081 (0.0043)	0.1037 (0.0032)	0.551 (0.024)	1.8424 (0.059)	0.331 (0.014)	1.033 (0.031)
ME			0.1085	0.1021	0.1084	0.1024
OR			1.734	6.312
x 2
β/σ	0.1968 (0.0037)	0.2014 (0.0031)	1.000 (0.026)	3.655 (0.089)	0.603 (0.015)	2.046 (0.048)
ME			0.1972	0.2025	0.1977	0.2027
OR			2.719	38.66
x 3
β/σ		0.0963 (0.0032)		1.678 (0.058)		0.938 (0.031)
x 4
β/σ		0.2959 (0.0030)		5.40 (0.12)		3.018 (0.066)
RMSE	0.45	0.32
R 2	0.20	0.59
Pseudo R 2			0.17	0.74	0.17	0.74

Notes. Robust standard errors are in parentheses. 10,000 observations of simulated data, based on the formula for the underlying latent dependent variable: y* = 0.5x _d + x ₁+2x ₂ + x ₃+ 3x ₄ with covariates normally distributed, except x _d which is a dummy variable.

IE, incremental effect; ME, marginal effect; OR, odds ratio; RMSE, root mean squared error.

When the research question is about how a change in a continuous independent variable affects the probability, we recommend presenting the results in terms of the marginal or the average marginal effects. Virtually, all statistical software packages compute odds ratios either as an option or as the default output from a logit model. Karaca‐Mandic, Norton, and Dowd (2012) and Ai and Norton (2003) discuss the computation of marginal effects in nonlinear models, and Dowd, Greene, and Norton (2014) explain how to compute the standard errors of nonlinear functions of estimated coefficients, including marginal effects in nonlinear models.

We want to emphasize several points about the magnitudes of odd ratios and marginal effects, because researchers usually care about the magnitude of a policy effect, not just its sign. The magnitude of the odds ratio is the same for all observations. The same is not true for marginal effects, which vary across observations depending on the values of the covariates. Average marginal effects for subgroups can differ from each other, and this could lead to different policy conclusions for different groups. This point—that marginal effects vary by subgroup but that odds ratios do not—is so important in the context of heterogeneous treatment effects and personalized medicine that we show it with a simple example with real data.

We use a sample of 16,278 nonelderly adults (age 18–64) from the 2004 Medical Expenditure Panel Survey to predict whether they currently take any prescription drugs. We estimate a logit model that controls for age, gender, and whether the person is uninsured. Those three variables are highly statistically significant, with the probability of taking any prescription drugs being higher for persons who are older, female, and insured (see Table 2). Consider how to report the magnitude of the effect of age. The estimated coefficient is 0.0388, the odds ratio is 1.04, and the overall average marginal effect is 0.0078. However, the marginal effect of one additional year of age is not constant, and it varies not only by age, but also across the four types of persons (men and women, insured, and uninsured). The differences can be seen in Figure 2, which show that the variation in marginal effects is up to threefold across the age range for these four types. Even with the age coefficient constrained to be constant across all groups, there are still differences in marginal effects because the logit model assumes a nonlinear relationship between the covariates and the probability that the dependent variable equals one. Uninsured men are presumably the least likely to take prescription drugs when young, and so their consumption will increase fastest during adulthood. The magnitude of the effect on the predicted probability corresponding to a given odds ratio is a function of both the predicted probability and the odds ratio, with the largest effects around predicted probability 0.5.

Table 2.

Logit Model Results to Predict Probability of Taking Any Prescription Drugs, Using MEPS Data from 2004

Variables	Logit
Constant
β/σ	−1.205 (0.062)
Age
β/σ	0.0388 (0.0014)
ME	0.0078
OR	1.0396
Female
β/σ	0.842 (0.035)
IE	0.170
OR	2.320
Uninsured
β/σ	−1.256 (0.043)
IE	−0.253
OR	0.285
Pseudo R 2	0.12

Notes. Robust standard errors are in parentheses. There are 16,278 observations of Medical Expenditure Panel Survey data.

IE, incremental effect; ME, marginal effect; OR, odds ratio.

Figure 2.

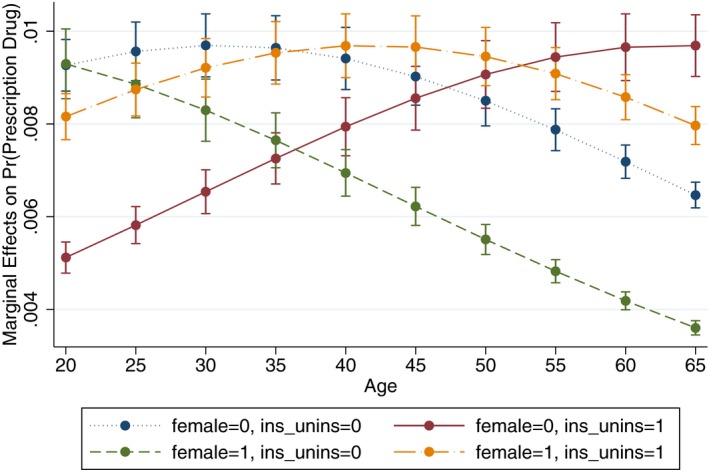
Conditional Marginal Effects of Age with 95% CIs [Color figure can be viewed at wileyonlinelibrary.com]

This simple example illustrates that the magnitude of the marginal effect of a variable depends on the subgroup (the conditioning set). Policy conclusions therefore could differ for different subgroups, and this important interpretation never would be revealed from a standard discussion of odds ratios.

Another way to drive home the point that magnitudes matter is to graph how marginal effects depend on the log odds (β/σ) and on the baseline probability (e.g., the probability of mortality for a nonsmoker). Marginal effects are largest when the probability is close to one‐half and are proportional to the magnitude of the log odds (see Figure 3). Conversely, if the marginal effect is known, the corresponding log odds increase as the probability moves to the extremes of zero and one (see Figure 4).

Figure 3.

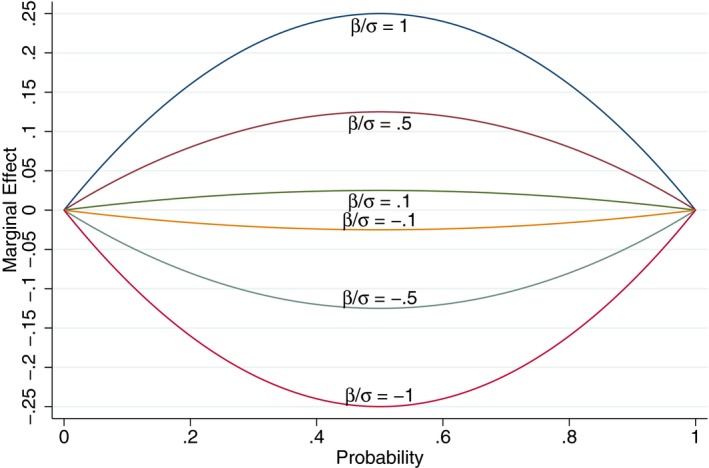
Marginal Effects as a Function of P and Log Odds (β/σ) [Color figure can be viewed at wileyonlinelibrary.com]

Figure 4.

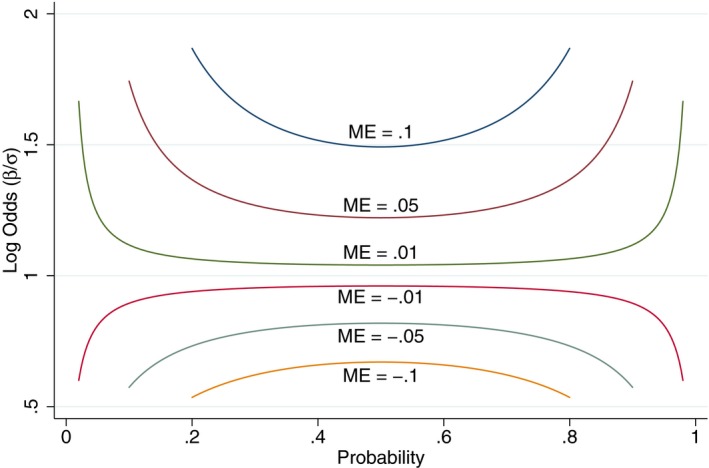
Log Odds as a Function of P and Marginal Effects [Color figure can be viewed at wileyonlinelibrary.com]

The researcher should report the magnitude of the results that best answers the research question. Returning to alternative ways of expressing the results, if the research question is about the ratio of probabilities, then risk ratios may be preferable to odds ratios for reasons of interpretation (Kleinman and Norton 2009; Norton, Miller, and Kleinman 2013). While the incremental effect is a difference between two probabilities, the risk ratio for an explanatory variable x _i is the probability that y _i = 1 given x _i = 1 divided by the probability that y _i = 1 given x _i = 0. For the logit model, the risk ratio for x _1i is a function of all the explanatory variables:

$$\mathrm{risk}\mathrm{ratio}=\frac{Pr(y_i=1|x_{1i}=1)}{Pr(y_i=1|x_{1i}=0)}=\frac{{[1+exp(\frac{-{\mathit{\beta }}_0-{\mathit{\beta }}_1{x}_{1i}-{\mathit{\beta }}_2{x}_{2i}-···-{\mathit{\beta }}_K{x}_{Ki}}{\mathit{\sigma }})]}^{-1}}{{[1+exp(\frac{-{\mathit{\beta }}_0-{\mathit{\beta }}_2{x}_{2i}-···-{\mathit{\beta }}_K{x}_{Ki}}{\mathit{\sigma }})]}^{-1}}$$ (19)

A linear probability model can be useful if the goal is an overall average marginal effect (Angrist 2001). However, the linear probability model can produce predictions outside of the feasible range of [0, 1], negative variances of the error terms, and coefficient estimates that are heavily influenced by outliers. If the sample size is large enough, in principle, one could estimate a linear probability model (ordinary least squares with an index function that is linear in the coefficients) with a functional form that is sufficiently flexible to overcome this problem and to mimic the results from any other flexible probability model.

It is worth emphasizing that there are some models where the odds ratio interpretation is preferred, in spite of the issues described in this article. In a case–control study, subjects with a disease are matched to subjects without the disease in order to identify important risk factors (causes of effects). However, one cannot compute marginal effects of the risk factors on the probability of having the disease directly from the model without imposing additional assumptions because the probability of having the disease in the sample does not mirror the probability of having the disease in the population. The group fixed effects sweep out not only common factors to the group, but also any hope of measuring a baseline rate for that group within the model. The researcher is left with the odds ratio interpretation or must assume the baseline rate from other data sources and use that to approximate the marginal effect.

The Chamberlain conditional fixed‐effects logit model is widely used in economics to sweep out group‐level fixed effects (but also any observations with no within‐group variation in the dependent variable). This model also appropriately uses an odds ratio interpretation. To compute predicted probabilities or marginal effects, the fixed‐effects logit model requires making additional assumptions, as with case–control studies. Because the fixed effects soak up much of the otherwise unexplained variation, σ will decrease and the estimated β/σ will increase. This increase in β/σ is consistent with its interpretation in a model that is conditional on fixed effects: the odds ratio for the variable of interest is the effect after holding constant many other factors, leaving a much more homogeneous comparison group. A similar effect appears in random effects models. One advantage of the Chamberlain conditional fixed‐effects logit model is not having to estimate the group fixed effects, also called incidental parameters, but one disadvantage is not being able to estimate a baseline rate.

Finally, measures that are the ratio of estimated coefficients, such as marginal rates of substitution (including willingness to pay and values of time), are not affected by σ because that parameter drops out of the ratio (Train, 2009). Train also discusses how one could conduct a meta‐analysis, while allowing the σ to differ in each substudy. The ratio of the variances would need to be estimated, in addition to all the β parameters, to make the appropriate adjustment (see Ben‐Akiva and Morikawa 1990, Swait and Louviere 1993, and Train 2009 for details).

Conclusions

Given the voluminous literature in health services research, epidemiology, clinical research, and other social sciences that estimates and reports odds ratios without proper discussion of conditioning, arbitrary normalization of parameters, or heterogeneity, there is a long way to go to improve best practice and translation of results. The correct interpretation of odds ratios acknowledges that the magnitude of the odds ratio is conditional on the data and the model specification. When more independent variables are included in the model, the error variance is reduced and the odds ratio (exp(β/σ)) increases. An odds ratio estimated from one multivariate logit model cannot be directly compared to odds ratios estimated from another sample from the same dataset, from other datasets, or from using a different model specification.

There are alternatives to odds ratios that do not share the property of being as sensitive to inclusion of additional variables. Average marginal or incremental effects and risk ratios are preferred ways of interpreting the results from logistic regression models when the model is not a case–control or fixed‐effects model. Clear communication of the meaning of the estimated parameters generally requires changing habits and using average marginal effects, unless estimating a case–control model.

Supporting information

Appendix SA1: Author Matrix.

Appendix S1: Appendix with Proofs and Stata Code.