Summary
Purpose
To develop and validate a REE prediction equation for young adults.
Methods
Baseline data from two studies were pooled (N = 318; women = 52%) and randomly divided into development (n = 159) and validation samples (n = 159). REE was measured by indirect calorimetry. Stepwise regression was used to develop an equation to predict REE (University of Kansas (KU) equation). The KU equation and 5 additional REE prediction equations used in clinical practice (Mifflin–St. Jeor, Harris–Benedict, Owens, Frankenfield (2 equations)) were evaluated in the validation sample.
Results
There were no significant differences between predicted and measured REE using the KU equation for either men or women. The Mifflin–St. Jeor equation showed a non-significant mean bias in men; however, mean bias was statistically significant in women. The Harris–Benedict equation significantly over-predicted REE in both men and women. The Owens equation showed a significant mean bias in both men and women. Frankenfield equations #1 and #2 both significantly over-predicted REE in non-obese men and women. We found no significant differences between measured REE and REE predicted by the Frankenfield #2 equations in obese men and women.
Conclusion
The KU equation, which uses easily assessed characteristics (age, sex, weight) may offer better estimates of REE in young adults compared with the 5 other equations. The KU equation demonstrated adequate prediction accuracy, with approximately equal rates of over and under-prediction. However, enthusiasm for recommending any REE prediction equations evaluated for use in clinical weight management is damped by the highly variable individual prediction error evident with all these equations.
Keywords: Resting energy expenditure, Indirect calorimetry, Weight management, Young adults
Introduction
Data from the National Health and Nutrition Survey (2011–2012) indicated that the prevalence of overweight and obesity (BMI ≥ 25 kg/m2) in young adults age 20–39 years was 60.3%, with 30.3% classified as obese (BMI ≥ 30 kg/m2) [1]. Thus, young adults represent a large segment of the population in need of weight management. Successful weight management is aided by the establishment of realistic goals for energy intake and energy expenditure based on resting energy expenditure (REE), which represents the largest component of total daily energy expenditure. Although REE can be accurately assessed using indirect calorimetry, the costs of equipment, the need for trained personnel, and the logistics associated with this assessment make its use impractical in the majority of clinical settings.
In lieu of directly assessed REE, weight management clinics typically utilize equations, based on easily assessed parameters such as age, height, and weight, to predict REE. Several REE prediction equations are frequently used in clinical practice. However, information relative to the validity of these equations in young adults across the weight spectrum in limited [2–9]. Several of these studies have been conducted in only women [2,3,5,8] only normal weight individuals [6,7] or in specific population sub-groups including Hispanics [2] and Chinese [6,7]. To date, there is no prediction equation developed specifically for use in young adults across the weight spectrum. Therefore, the purpose of this analysis was to develop and evaluate the accuracy of an equation that uses easily assessed physical characteristics (age, height, weight, sex) to predict REE in a sample that includes normal, overweight and obese young adults, and to compare the accuracy of this equation with other prediction equations frequently used in clinical practice including: Mifflin–St. Jeor [10], Harris–Benedict [11], Owens [12], and Frankenfield [9].
Methods
Participants
Baseline data from two recently completed randomized trials conducted at University of Kansas Energy Balance Lab, that used similar inclusion/exclusion criteria (age 18–30 yrs, healthy, non-smoking, planned physical activity <500 kcal/wk) were pooled and served as the basis for this analysis: Trial 1: n = 173, age = 22.2 ± 2.8 yrs, BMI = 25.7 ± 4.6 kg/m2 [13]; trial 2: n = 145, age = 22.8 ± 3.2 yrs, BMI = 30.7 ± 4.6 kg/m2 [14]. The pooled sample was then divided randomly into 2 equal samples; a development (n = 159) and a validation sample (n = 159). The University of Kansas–Lawrence Institutional Review Board approved the research protocols for both trials. All participants provided written informed consent prior to the initiation of study procedures.
Weight/height
Participants were weighed on a digital scale accurate to ±0.1 kg (PS6600, Befour Inc., Saukville, WI) while wearing in a standard hospital gown. Weight was assessed between 7 and 10 a.m., prior to breakfast, and after attempting to void. Height was measured to the nearest 0.125 cm on a standardized, wall-mounted stadiometer. Body mass index (BMI) was calculated as weight in kg/height in m2. Height and weight were measured during the same laboratory visit where REE was assessed and were used in all prediction equations.
Measured REE
REE was measured using a ParvoMedics TrueOne 2400 (ParvoMedics Inc., Sandy, UT) indirect calorimetry system. This system has been shown to provide accurate measures of REE when compared with the Douglas bag technique [15]. All assessments were completed in the morning (7–10 a.m.), following a 12 h fast and >36 h abstention from exercise, in accordance with recommended protocol [16]. Following 15 min of supine rest in an isolated temperature controlled (21–24°C) room; participants were placed under a ventilated hood for a minimum of 35 min. The first 5 min of measurement were eliminated. REE (kcal/day) was calculated from measured oxygen consumption and carbon dioxide production using the Weir equation [17]. REE calculated from values averaged over 30 min of steady state (<10% fluctuation in minute-to-minute ventilation, oxygen consumption, and respiratory quotient) served as our criterion measure.
Predicted REE
Stepwise multiple-regression was used to develop an equation to predict REE (kcal/day) in 159 participants in the development sample. Independent variables considered included height (cm), weight (kg), BMI (kg/m2), age (yrs), sex (1 = men, 0 = women), and ethnicity (1 = white, 2 = minority). The final equation was: REE (kcal/day) = 11.2 (weight) −7.2 (age) + 237.6 (sex) + 780.3 (Model R2 = 0.77). This analysis, and all other analyses statistical analyses, were performed using SAS version 9.3 (SAS Institute Inc., Cary, NC).
Prediction equations evaluated (Table 1)
Table 1.
Resting energy expenditure (kcal/day) prediction equations evaluated.
| Equation name | Sex or obesity status | Equationa |
|---|---|---|
| University of Kansas | Men/women | 11.2 (weight) − 7.2 (age) + 237.6 (sex) + 780.3 |
| Mifflin–St. Jeor [10] | Men | 10 (weight) + 879 |
| Women | 7.18 (weight) + 795 | |
| Harris–Benedict [11] | Men | 66.5 + 13.8 (weight) + 5 (height) − 6.8 (age) |
| Women | 655 + 9.6 (weight) + 1.8 (height) − 4.7 (age) | |
| Owens [12] | Men | 10.2 (weight) + 879 |
| Women | 7.18 (weight) + 795 | |
| Frankenfield #1 [9] | Non-obese men/women | 10 (weight) + 3 (height) − 5 (age) + 207 (sex) + 454 |
| Obese men/women | 10 (weight) + 3 (height) − 5 (age) + 244 (sex) + 440 | |
| Frankenfield #2 [9] | Non-obese men/women | 10 (weight) − 6 (age) + 230 (sex) + 838 |
| Obese men/women | 10 (weight) − 5 (age) + 274 (sex) + 865 |
Weight in kg, height in cm, age in years, sex (1 = men, 0 = women).
We evaluated the accuracy of the new equation, hereafter referred to as the University of Kansas (KU) equation, and the Mifflin–St. Jeor [10], Harris–Benedict [11], Owens [12] and two Frankenfield [9] equations in 159 individuals in the validation sample. Mifflin–St. Jeor, Harris–Benedict, and Owens provide separate prediction equations for men and women and vary slightly in the predictor variables utilized: Mifflin–St. Jeor (weight, age), Harris–Benedict (weight, height, age), Owens (weight). Frankenfield provided REE prediction equations using two sets of variables; equation #1 included weight, height, age and sex and equation #2 included weight, age and sex. Frankenfield provided separate equations for obese and non-obese individuals using each set of variables.
Analysis
The differences between predicted and measured REE were calculated as predicted minus measured. Therefore, a negative difference indicates an under-prediction while a positive difference indicates an over-prediction. Paired t-tests were used to determine the significance of differences between predicted and measured REE. Pearson correlations were used to assess the association between predicted and measured values. Additionally, agreement between predicted and measured REE was evaluated using the Bland–Altman method [18] which plots the difference between predicted and measured REE versus the mean of predicted and measured REE. Limits of agreement were calculated as the mean difference between predicted and measured REE ±2 standard deviations of the difference. A prediction equation was considered accurate if predicted and measured REE were within ±10% [19]. The percent of the sample in which REE was under predicted (predicted <10% of measured) and over predicted (predicted >10% of measured) was calculated.
Results
The study sample consisted of overweight and obese (mean BMI ∼ 28 kg/m2, range = 21–41 kg/m2) young adults (mean age ∼ 22 yrs, range = 18–30 yrs) (Table 2). Approximately 64% of the sample was overweight and obese (BMI ≥ 25 kg/m2) with ∼ 24% classified as obese (BMI ≥ 30 kg/m2), reflecting the weight distribution of young adults in the general population [1]. There were no significant differences in descriptive characteristics been participants randomly assigned to the development (n = 159, 75 women, 84 men, 39 obese, 120 non-obese) or validation samples (n = 159, 89 women, 70 men, 37 obese, 122 non-obese).
Table 2.
Sample characteristics values are mean ±SD unless otherwise stated.
| Variable | Development sample (n = 159) | Validation sample (n = 159) | p-Between |
|---|---|---|---|
| Age (yrs) | 22.5 ± 3.0 | 22.3 ± 3.0 | 0.60 |
| Height (cm) | 172.4 ± 9.5 | 171.9 ± 9.0 | 0.64 |
| Weight (kg) | 83.1 ± 17.8 | 81.4 ± 15.2 | 0.38 |
| BMI (kg/m2) | 27.8 ± 4.7 | 27.5 ± 4.4 | 0.54 |
| REE (kcal/day) | 1673 ± 316 | 1642 ± 310 | 0.81 |
| Female (%) | 46.8 | 56.0 | 0.27 |
| Minority (%) | 8.2 | 6.3 | 0.57 |
| Overweight/obese (%) | 62.9 | 65.4 | 0.95 |
REE = resting energy expenditure.
A summary of comparisons between REE measured by indirect calorimetry and estimated by the KU equation, as well as the Mifflin–St. Jeor, Harris-Benedict, Owens, and Frankenfield equations are presented in Table 3. Bland–Altman plots for the combined sample of men and women for the KU equation, Mifflin–St. Jeor, Harris-Benedict, Owens and by obesity status for the Frankenfield are presented in Fig. 1. A detailed description of the results for each equation is presented below.
Table 3.
Results summary
| Prediction equation | Sex | Bias kcal/day (%)a | Prediction accuracy (%)b |
Under prediction (%)c |
Over prediction (%)d |
|---|---|---|---|---|---|
| University of Kansas | Men | −21 ± 162 (−0.3 ± 9%) | 69 | 17 | 14 |
| Women | 5 ± 151 (1.6 ± 11%) | 70 | 12 | 18 | |
| Mifflin–St. Jeor | Men | 31 ± 165 (2.5 ± 9%) | 70 | 9 | 21 |
| Women | 62 ± 157 (5.5 ± 12%)** | 62 | 8 | 30 | |
| Harris–Benedict | Men | 159 ± 159 (9.3 ± 9%)*** | 56 | 0 | 44 |
| Women | 119 ± 156 (9.7 ± 12%)*** | 47 | 3 | 50 | |
| Owens | Men | −85 ± 160 (−3.7 ± 8%)*** | 73 | 24 | 3 |
| Women | −126 ± 169 (−7.2 ± 11%)* | 51 | 44 | 5 | |
| Frankenfield #1e (non-obese) | Men | 137 ± 150 (8.4 ± 9%)*** | 55 | 2 | 43 |
| Women | 146 ± 181 (11.8 ± 12%)*** | 45 | 1 | 54 | |
| Frankenfield #1 (obese) | Men | 24 ± 164 (1.9 ± 8%) | 76 | 0 | 24 |
| Women | 84 ± 185 (6.1 ± 11%) | 45 | 10 | 45 | |
| Frankenfield #2f (non-obese) | Men | 64 ± 151 (4.3 ± 9%)** | 68 | 4 | 28 |
| Women | 81 ± 143 (7.1 ± 12%)*** | 58 | 3 | 39 | |
| Frankenfield #2 (obese) | Men | −51 ± 175 (−1.6 ± 8%) | 76 | 18 | 6 |
| Women | 6 ± 182 (1.5 ± 10%) | 75 | 10 | 15 |
Values are mean ± standard deviation,
p < 0.01,
p < 0.001,
p < 0.0001.
Predicted minus measured resting energy expenditure (REE).
Percentage of the sample with predicted and measured REE within ±10%.
Percentage of the sample with predicted REE <10% of measured REE.
Percentage of the sample with predicted REE >10% of measured REE.
Equation using weight, height, age, and sex.
Equation using weight, age, and sex.
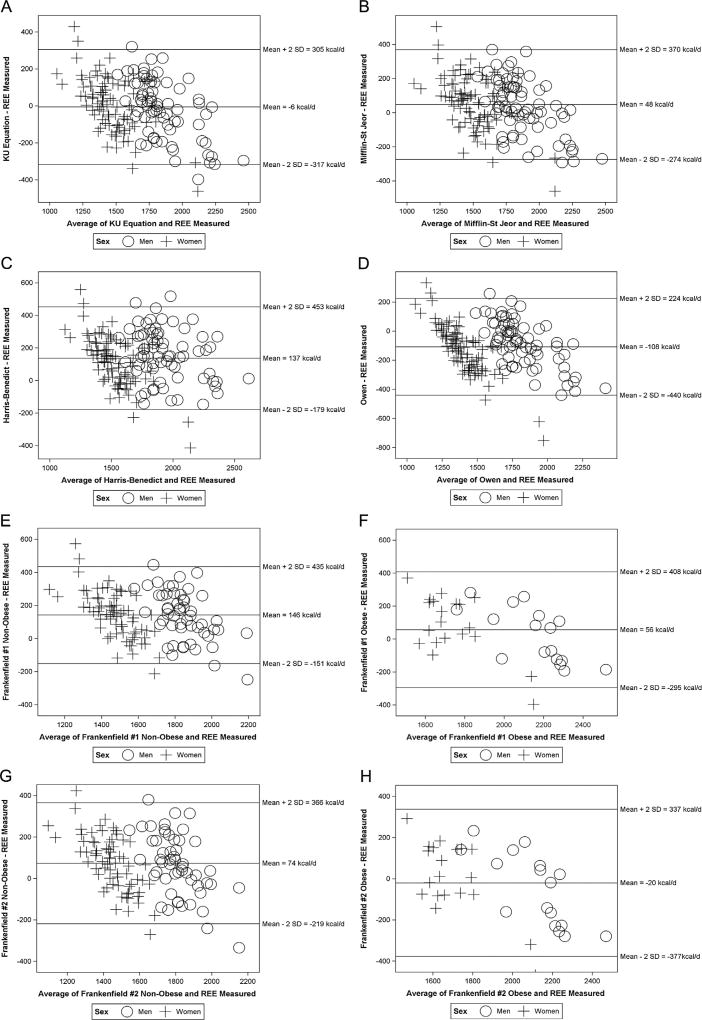
Figure 1.
Comparison of resting energy expenditure (REE) estimated by REE prediction equations and assessed by indirect calorimetry. (A) University of Kansas equation, (B) Mifflin–St. Jeor, (C) Harris–Benedict, (D) Owen, (E) Frankenfield #1 non-obese, (F) Frankenfield #1 obese, (G) Frankenfield #2 non-obese, (H) Frankenfield #2 obese.
KU equation (Fig. 1A)
There were no significant differences between predicted and measured REE using the KU equation for either men (predicted = 1845 ± 163 kcal/day, measured = 1866 ± 251 kcal/day, p = 0.29) or women (predicted = 1472 ± 151 kcal/day, measured = 1466 ± 228 kcal/day, p = 0.735). The correlation between predicted and measured REE was 0.78 in men and 0.87 in women. On average, the KU equation under-predicted REE by −21 ± 161 kcal/day (−0.3 ± 9.0%) in men and over-predicted REE by 5 ± 151 kcal/day (1.6 ± −11%) in women. The limits of agreement were large in both men (−344 to +302 kcal/day) and women (−296 to +306 kcal/day). There was an inverse association between the magnitude of measured REE and the difference between predicted and measured REE in both men (r = −0.58, p < 0.001) and women (r = −0.54, p < 0.001). REE tended to be over-predicted in the lower and under-predicted at upper ranges of REE. Predicted and measured REE were within ±10% in 69% of men and 70% of women. The percentage of participants in which the KU equation under and over-predicted REE were similar in both men (under = 17%, over = 14%) and women (under = 12%, over = 18%).
Mifflin–St. Jeor equations (Fig. 1B)
There was no significant difference between predicted and measured REE in men (predicted = 1896 ± 162 kcal/day, measured = 1866 ± 251 kcal/day, p = 0.125). However, in women, predicted REE (1528 ± 155 kcal/day) was significantly higher than REE measured by indirect calorimetry (1466 ± 228 kcal/day, p < 0.001). The correlation between predicted and measured REE was 0.76 in men and 0.86 in women. On average, the mean REE was over-predicted by 31 ± 165 kcal/day (2.5 ± 9%) in men and 62 ± 157 kcal/day (5.5 ± 12%) in women. The limits of agreement were large in both men (−299 to +361) and women (−252 to +376). There was an inverse association between the magnitude of REE and the difference between predicted and measured REE in both men (r = −0.57, p < 0.0001) and women (r = −0.50, p < 0.0001). REE tended to be over-predicted in lower and under-predicted in the higher ranges of REE. Predicted and measured REE were within ±10% in 70% of men and 62% of women. REE was over-predicted by the Mifflin–St. Jeor equation in 30% of women and 21% of men and under-predicted in 8% of women and 9% of men.
Harris–Benedict equations (Fig. 1C)
Predicted REE was significantly higher than measured REE in both men (predicted = 2025 ± 212 kcal/day, measured = 1866 ± 251 kcal/day, p < 0.0001) and women (predicted = 1585 ± 134 kcal/day, measured = 1466 ± 228 kcal/day, p < 0.0001). The correlation between predicted and measured REE was 0.78 in men and 0.75 in women. On average, the Harris–Benedict equations over-predicted mean REE by 159 ± 159 kcal/day (9.3 ± 9%) in men and 119 ± 156 kcal/day (9.7 ± 12%) in women. The limits of agreement were large in both men (−159 to +477 kcal/day) and women (−192 to +430 kcal/day). There was an inverse association between the magnitude of REE and the difference between predicted and measured REE in both men (r = −0.26, p = 0.03) and women (r = −0.64, p < 0.0001). REE tended to be over-predicted in the lower and under-estimated in the higher range of REE. Predicted and measured REE were within ±10% in 56% of men and 47% of women. REE was over-predicted in 44% of men and 50% of women and under-predicted in 0% of men and 3% of women.
Owens equations (Fig. 1D)
Predicted REE was significantly lower than measured REE in both men (predicted = 1781 ± 149 kcal/day, measured = 1866 ± 251 kcal/day, p < 0.0001) and women (predicted = 1340 ± 95 kcal/day, measured = 1466 ± 228 kcal/day, p = 0.005). The correlation between predicted and measured REE was 0.80 in men and 0.85 in women. On average, the Owens equations under-predicted mean REE by −85 ± 160 kcal/day (−3.7 ± 8%) in men and −126 ± 169 kcal/day (−7.2 ± 11%) in women. The limits of agreement were large in both men (−406 to +236 kcal/day) and women (−465 to +213 kcal/day). There was an inverse association between the magnitude of REE and the difference between predicted and measured REE in both men (r = −0.67, p < 0.0001) and women (r = −0.83, p < 0.0001). REE tended to be over-predicted in the lower and under-predicted in the higher ranges of REE. Predicted and measured REE were within ±10% in 73% of men and 51% of women. The Owens equations over-predicted REE in 3% of men and 5% of women and under-predicted REE in 24% of men and 44% of women.
Frankenfield equation #1 (weight, height, age, sex) – non-obese (Fig. 1E)
Predicted REE was significantly higher than measured REE in both men (predicted = 1914 ± 105 kcal/day, measured = 1777 ± 175 kcal/day, p < 0.0001) and women (predicted = 1546 ± 91 kcal/day, measured = 1400 ± 178 kcal/day, p < 0.0001). The correlation between predicted and measured REE was 0.52 in non-obese men and 0.59 in non-obese women. On average, Frankenfield equation #1 over-predicted REE by 137 ± 150 kcal/day (8.5 ± 9%) in men and 146 ± 181 kcal/day (11.8 ± 12%) in women. The limits of agreement were large in both men (−164 to +437 kcal/day) and women (−142 to +435 kcal/day). There was an inverse association between the magnitude of REE and the difference between predicted and measured REE in both men (r = −0.53, p < 0.0001) and women (r = −0.67, p < 0.0001). REE tended to be over-predicted in the lower and under-predicted in the higher ranges of REE. Predicted and measured REE were within ±10% in 55% of men and 45% of women. The Frankenfield equation under-predicted REE in 2% of men and 1% of women and over-predicted REE in 43% of men and 54% of women.
Frankenfield equation #1 (weight, height, age, sex) – obese (Fig. 1F)
Predicted and measured REE were not significantly different in obese men (predicted = 2166 ± 148 kcal/day, measured = 2143 ± 254 kcal/day, p > 0.05) or obese women (predicted = 1780 ± 126 kcal/day, measured = 1695 ± 238 kcal/day, p > 0.05). The correlation between predicted and measured REE was 0.79 in obese men and 0.64 in obese women. On average, Frankenfield equation #1 over-predicted REE by 24 ± 164 kcal/day (1.9 ± 8%) in men and 84 ± 185 kcal/day (6.1 ± 11%) in women. The limits of agreement were large in both men (−304 to +351 kcal/day) and women (−286 to +454 kcal/day). There was an inverse association between the magnitude of REE and the difference between predicted and measured REE in both men (r = −0.68, p < 0.01) and women (r = −0.66, p < 0.01). REE tended to be over-predicted in the lower and under-predicted in the higher ranges of REE. Predicted and measured REE were within ±10% in 76% of men and 45% of women. In obese participants the Frankenfield equation #1 under-predicted REE in 0% of men and 10% of women and over-predicted REE in 24% of men and 45% of women.
Frankenfield equation #2 (weight, age, sex) – non-obese (Fig. 1G)
Predicted REE was significantly higher than measured REE in both men (predicted = 1841 ± 102 kcal/day, measured = 1777 ± 175 kcal/day, p < 0.001) and women (predicted = 1481 ± 91 kcal/day, measured = 1400 ± 178 kcal/day, p < 0.0001). The correlation between predicted and measured REE was 0.51 in non-obese men and 0.60 in non-obese women. On average, Frankenfield equation #2 over-predicted REE by 64 ± 151 kcal/day (4.3 ± 9%) in men and 81 ± 143 kcal/day (7.1 ± 12%) in women. The limits of agreement were large in both men (−238 to +366 kcal/day) and women (−205 to +367 kcal/day). There was an inverse association between the magnitude of REE and the difference between predicted and measured REE in both men (r = −0.55, p < 0.0001) and women (r = −70, p < 0.0001). REE tended to be over-predicted in the lower and under-predicted in the higher ranges of REE. Predicted and measured REE were within ±10% in 68% of men and 58% of women. In non-obese participants the Frankenfield equation #2 under-predicted REE in 4% of men and 3% of women, and over-predicted REE in 28% of men and 39% of women.
Frankenfield equation #2 (weight, age, sex) – obese (Fig. 1H)
Predicted and measured REE were not significantly different in obese men (predicted = 2091 ± 131 kcal/day, measured = 2143 ± 254 kcal/day, p > 0.05) or obese women (predicted = 1702 ± 118 kcal/day, measured = 1695 ± 238 kcal/day, p > 0.05). The correlation between predicted and measured REE was 0.77 in obese men and 0.67 in obese women. On average, Frankenfield equation #2 under-predicted REE by −51 ± 175 kcal/day (−1.6 ± 8%) in men and over-predicted REE by 6 ± 182 kcal/day (1.5 ± 10%) in women. The limits of agreement were large in both men (−401 to +300 kcal/day) and women (−357 to +369 kcal/day). There was an inverse association between the magnitude of REE and the difference between predicted and measured REE in both men (r = −0.74, p < 0.001) and women (r = −0.71, p < 0.001). REE tended to be over-predicted in the lower and under-predicted in the higher ranges of REE. Predicted and measured REE were within ±10% in 76% of men and 75% of women. In obese participants, the Frankenfield equation #2 under-predicted REE in 18% of men and 10% of women, and over-predicted REE in 6% of men and 15% of women.
Discussion
We developed the KU equation specifically for the prediction of REE in young adults across the weight spectrum, and evaluated the accuracy of this equation and 5 other REE prediction equations commonly used in clinical practice. We found that the mean REE predicted using the KU equation was not significantly different from REE measured by indirect calorimetry (i.e., mean bias <2.0%). Similar results were noted for both Frankenfield equations in obese participants, and for the Mifflin–St. Jeor equation in men, where predicted and measured REE did not differ significantly (mean bias range −6.1 to +2.5%). In contrast, the Mifflin–St. Jeor (women), and Harris-Benedict equations (men/women) significantly over-predicted REE (range ∼ + 6% to 10%) while the Owens (men/women) and both Frankenfield equations (non-obese men/women) under-predicted REE (mean bias range ∼−12% to −4%). REE predicted by the KU equation was within ±10% of measured REE (i.e. accurate) in 69% of men and 70% of women. Similar accuracy rates were observed for other equations including the Mifflin–St. Jeor (men/women), Owens (men), Frankenfield #1 (obese men), and Frankenfield # 2 (non-obese men, obese men/women). However, only the KU and Frankenfield #2 equations provided relatively equal rates of over and under-prediction, whereas, the Mifflin–St. Jeor, Frankenfield #1 (obese men), and Frankenfield #2 (non-obese men) tended to over-predict and the Owens equation tended to under-predict measured RMR. Thus, in our sample of young adult men and women, with a percentage of overweight and obese participants similar to that of the general population, the KU equation predicted mean REE with a level of bias and percent accuracy similar or superior to the 5 other equations evaluated. However, the magnitude of error in predicting REE on an individual level, for the KU equation, and all other equations evaluated was considerable, and inconsistent across the range of measured REE. REE was over-predicted at lower levels and under-predicted at higher levels of measured REE, an observation consistent with previous studies [7,20].
The 2005 Evidence Analysis Working Group report from the American Dietetic Association, concluded that the Mifflin–St. Jeor equation was “more likely than other equations tested to estimate RMR within 10% of that measured, but noteworthy errors and limitations exist when it is applied to individuals and possibly when it is generalized to certain age and ethnic groups.” In the current analysis, both the KU and the Mifflin–St. Jeor equations demonstrated similar levels of accuracy (range 62–70%) in both men and women. REE was over and under-predicted for a similar percentage of both men and women using the KU equation. By comparison, the rates of over-prediction of mean REE using the Mifflin–St. Jeor equation were higher than the rates of under-prediction. Thus, our results provide some evidence to recommend the KU equation over the Mifflin–St. Jeor for prediction of mean REE in groups of young adults, particularly women. However, enthusiasm for recommending either the KU or Mifflin–St. Jeor equations for predicting individual REE in a clinical weight management setting is damped by the large individual error evident with both equations.
The results of previous reports regarding predictions of REE in young adults using the Mifflin–St. Jeor equations are mixed [2–9,21], with accuracy varying from 37% [6] to 80% [7,9,21]. Several studies reported accuracy ≥70% [3,7,9,21]; however accuracy ≤60% has also been reported [2,4,6]. The Mifflin–St. Jeor equations tend to over, rather than under-predict REE. For example, Siervo et al. [5] reported the Mifflin–St. Jeor equation significantly over-predicted mean REE ranging from 6.4% in normal weight, 5.3% in overweight and 3.1% in obese, young adult (18–35 yrs) women (n = 157), with large individual error. Significant over-predictions of mean REE have also been reported in a small sample (n = 30) of young adult Hispanic overweight women (+10.7%) [2], a large sample (n = 124) of European American women (9.1%)[8], a small sample (n = 43) of young (∼ 23 yrs), normal weight (BMI ∼ 21 kg/m2) Chinese men and women (+9.0%) [6] and a sample of Singaporean Chinese men (n = 96, age 18–40 yrs, BMI ∼ 23 kg/m2) (2.4%) [7]. Although the 2005 Evidence Working Group concluded that the Mifflin–St. Jeor equations were more likely to predict REE within 10% of measured values [19], the results of our study and other more recent studies, suggest that the Mifflin–St. Jeor equations may be inappropriate for use in young adults, particularly young adult women.
In our sample of young adults, the Harris-Benedict equations significantly overestimated REE (∼10%) in both men and women. Prediction accuracy was poor with a tendency to over rather than under-predict REE in both men and women. This finding is in agreement with the preponderance of the literature evaluating the Harris-Benedict equation which suggests poor accuracy and the tendency to over-predict REE in young adults. Prediction accuracy of the Harris-Benedict equation has been reported to range ∼ 13% [2] to 75% [21] with several studies reporting accuracy <60% [2,4,6,8] and ≤30% [2,6]. Significant over-prediction of REE has been reported in both normal, overweight and obese, young adult, men and women. For example, Siervo et al. [5] reported the Harris-Benedict equation significantly over-predicted mean REE ranging from 12.8% in normal weight, 10.8% in overweight and 7.6% in obese, young adult (18–35 yrs) women (n = 157), with large individual error. Over-predictions of mean REE have also been reported in a small sample (n = 30) of young adult Hispanic overweight women (+17%) [2], a large sample (n = 124) of European American women (10.3%) [8], a small sample (n = 43) of young (∼23 yrs), normal weight (BMI ∼ 21 kg/m2) Chinese men and women (+19.7%) [6], a sample of Singaporean Chinese men (n = 96, age 18–40 yrs, BMI ∼ 23 kg/m2) (6.5%) [7], and in a sample of 86 obese (BMI = 33.9 kg/m2), young adult women (∼37 yrs) (4.6%) [3]. Across studies [2–4,6,7,21] REE was over-predicted in between 24% [21] and 87% of participants [2]. Thus, our results, as well as previous reports, suggest that the Harris-Benedict equations should not be used to estimate REE in young adults.
The Owens equations significantly under-predicted REE for both men and women in our sample. However, prediction accuracy in our sample was relatively high in men (70%), but not in women (51%). Others have reported prediction accuracy using the Owens equation in young adults ranging from 8% [4] to 84% [2], with accuracy <60% in several studies [3,4,6,8,21] and >70% in fewer studies [2,7]. Some reports have indicated no significant differences between measured and REE predicted using the Owens equations [5–7]. For example, Siervo et al. [5] reported that mean REE estimated using the Owens equation was not significantly different from REE measured by indirect calorimetry (−0.75%) in normal weight young adult women; however, REE was significantly under-predicted in both overweight (−3.7%) and obese (−9.4%) women. In agreement with the results of Siervo et al. [5], Song et al. [7] reported a small non-significant difference between measured and predicted REE using the Owens equation (−0.4%) in a sample of normal weight Singaporean Chinese men, while Rao et al. [6] reported a small and non-significant underestimation of mean REE (−0.7%) in normal weight Chinese men and women. Interestingly, while the Owens equation provided a reasonable estimate of mean REE in both the studies of Song et al. [7] and Rao et al. [6], the accuracy of estimation was only 73% and 42% in the Song and Rao studies, respectively. Across studies, rates of over-prediction of REE ranged from 0% to 52% while rates of under-prediction ranged from 15% to 56% [2–4,6,7,21]. Potential difference is prediction accuracy by sex, and the tendency for under-prediction of REE in overweight or obese subjects, argues against the use of the Owens equations for overweight or obese young adults, especially women.
We are unaware of previous reports regarding the predictive characteristics of Frankenfield REE equations [9]. In our sample of young adults, both Frankenfield equations #1 (weight, height, age, sex) and #2 (weight, age, sex) significantly over-predicted REE in non-obese men and women, with accuracy rates ranging from 45% to 68%. We found no significant differences between measured REE and REE predicted by the Frankenfield #2 equations in obese men and women. Accuracy rates were similar in obese men and women for Frankenfield equation #2 (∼75%); however, accuracy rates were higher for obese men (76%) than in obese women (45%) for Frankenfield equation #1. Our results suggest that the Frankenfield equations may be useful for predicting REE in obese young adults. However, these results should be interpreted cautiously, as the number of obese participants in our sample was small (n = 37) and thus require confirmation in larger samples.
In conclusion, the KU equation, which uses easily assessed characteristics (age, sex, weight) may offer better estimates of REE in young adults across the weight spectrum, compared with the 5 other equations evaluated in this analysis. That is, the KU equation demonstrated relatively low mean bias and adequate prediction accuracy, with approximately equal rates of over and under-prediction, as compared with the Mifflin–St. Jeor, Harris–Benedict, Owens or Frankenfield equations. Additionally, error using the KU equation was equally distributed between over and underestimation. REE tended to be over-predicted using the Mifflin–St. Jeor, Harris–Benedict and Frankenfield equations and under-predicted by the Owens equations. However, the utility of the KU equation, or any of the other REE prediction equations evaluated in our analysis, for use in clinical weight management, is questionable, given the potentially large individual error of estimation associated with their use. Clinicians need to carefully consider selection of REE prediction equations. Only equations that have been developed and evaluated in samples with demographic characteristics (age, weight, sex, ethnicity, etc.) similar to those in which they are intended to be used should be considered. Additionally, clinicians should consider limitations in terms of accuracy, and over and under-prediction rates associated with any specific prediction equation. It is important to consider that these equations only provide “estimates” of REE which may be useful as a starting point for the prescription of energy intake for weight loss, which may need to be adjusted subsequently, based on clinical judgment. Although portable, relatively inexpensive indirect calorimetry devices are currently available, the validity of these devices for the assessment of REE is questionable [22–25]. Additionally, evidence suggests that the bias and accuracy of REE assessed with these devices may offer little or no improvement over REE estimated using available equations. Therefore, when accurate assessments are needed, REE should be assessed using standard indirect calorimetry techniques.
Acknowledgments
Disclosure of funding
This study was supported by the National Institutes of Health (DK049181 and DK080832).
Footnotes
Conflict of interest
The authors have disclosed that they have no significant relationships with, or financial interest in, any commercial companies pertaining to this article.
References
- 1.Ogden CL, Carroll MD, Curtin LR, Lamb MM, Flegal KM. Prevalence of high body mass index in US children and adolescents, 2007–2008. J Am Med Assoc. 2010;303:241–9. doi: 10.1001/jama.2009.2012. [DOI] [PubMed] [Google Scholar]
- 2.Miller S, Milliron BJ, Woolf K. Common prediction equations overestimate measured resting metabolic rate in young Hispanic women. Top Clin Nutr. 2013;28:120–35. doi: 10.1097/TIN.0b013e31828d7a1b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ruiz JR, Ortega FB, Rodriguez G, Alkorta P, Labayen I. Validity of resting energy expenditure predictive equations before and after an energy-restricted diet intervention in obese women. PLoS ONE. 2011;6:e23759. doi: 10.1371/journal.pone.0023759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hasson RE, Howe CA, Jones BL, Freedson PS. Accuracy of four resting metabolic rate prediction equations: effects of sex, body mass index, age, and race/ethnicity. J Sci Med Sport. 2011;14:344–51. doi: 10.1016/j.jsams.2011.02.010. [DOI] [PubMed] [Google Scholar]
- 5.Siervo M, Boschi V, Falconi C. Which REE prediction equation should we use in normal-weight, overweight and obese women. Clin Nutr. 2003;22:193–204. doi: 10.1054/clnu.2002.0625. [DOI] [PubMed] [Google Scholar]
- 6.Rao ZY, Wu XT, Liang BM, Wang MY, Hu W. Comparison of five equations for estimating resting energy expenditure in Chinese young, normal weight healthy adults. Eur J Med Res. 2012;17:26. doi: 10.1186/2047-783X-17-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Song T, Venkataraman K, Gluckman P, Seng CY, Meng KC, Khoo EY, et al. Validation of prediction equations for resting energy expenditure in Singaporean Chinese men. Obes Res Clin Pract. 2014;8:e201–98. doi: 10.1016/j.orcp.2013.05.002. [DOI] [PubMed] [Google Scholar]
- 8.Vander Weg M, Watson J, Klesges R, Clemens LE, Slawson D, McClanahan B. Development and cross-validation of a prediction equation for estimating resting energy expenditure in healthy African-American and European-American women. Eur J Clin Nutr. 2004;58:474–80. doi: 10.1038/sj.ejcn.1601833. [DOI] [PubMed] [Google Scholar]
- 9.Frankenfield DC. Bias and accuracy of resting metabolic rate equations in non-obese and obese adults. Clin Nutr. 2013;32:976–82. doi: 10.1016/j.clnu.2013.03.022. [DOI] [PubMed] [Google Scholar]
- 10.Mifflin MD, St Jeor ST, Hill LA, Scott BJ, Daugherty SA, Koh YO. A new predictive equation for resting energy expenditure in healthy individuals. Am J Clin Nutr. 1990;51:241–7. doi: 10.1093/ajcn/51.2.241. [DOI] [PubMed] [Google Scholar]
- 11.Harris JA, Benedict FG. A biometric study of human basal metabolism. Proc Natl Acad Sci USA. 1918;4:370–3. doi: 10.1073/pnas.4.12.370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Owen OE, Holup JL, D’Alessio DA, Craig ES, Polansky M, Smalley KJ, et al. A reappraisal of the caloric requirements of men. Am J Clin Nutr. 1987;46:875–85. doi: 10.1093/ajcn/46.6.875. [DOI] [PubMed] [Google Scholar]
- 13.Washburn RA, Donnelly JE, Smith BK, Sullivan DK, Marquis J, Herrmann SD. Resistance training volume, energy balance and weight management: rationale and design of a 9 month trial. Contemp Clin Trials. 2012;33:749–58. doi: 10.1016/j.cct.2012.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Donnelly JE, Washburn RA, Smith BK, Sullivan DK, Gibson C, Honas JJ, et al. A randomized, controlled, supervised, exercise trial in young overweight men and women: the Midwest Exercise Trial II (MET2) Contemp Clin Trials. 2012;33:804–10. doi: 10.1016/j.cct.2012.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Crouter SE, Antczak A, Hudak JR, DellaValle DM, Haas JD. Accuracy and reliability of the ParvoMedics TrueOne 2400 and MedGraphics VO2000 metabolic systems. Eur J Appl Physiol. 2006;98:139–51. doi: 10.1007/s00421-006-0255-0. [DOI] [PubMed] [Google Scholar]
- 16.Compher C, Frankenfield D, Keim N, Roth-Yousey L, Group EAW. Best practice methods to apply to measurement of resting metabolic rate in adults: a systematic review. J Am Diet Assoc. 2006;106:881–903. doi: 10.1016/j.jada.2006.02.009. [DOI] [PubMed] [Google Scholar]
- 17.Weir JdV. New methods for calculating metabolic rate with special reference to protein metabolism. J Physiol. 1949;109:1–9. doi: 10.1113/jphysiol.1949.sp004363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Martin Bland J, Altman D. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;327:307–10. [PubMed] [Google Scholar]
- 19.Frankenfield D, Roth-Yousey L, Compher C. Comparison of predictive equations for resting metabolic rate in healthy nonobese and obese adults: a systematic review. J Am Diet Assoc. 2005;105:775–89. doi: 10.1016/j.jada.2005.02.005. [DOI] [PubMed] [Google Scholar]
- 20.Rodriguez G, Moreno LA, Sarria A, Fleta J, Bueno M. Resting energy expenditure in children and adolescents: agreement between calorimetry and prediction equations. Clin Nutr. 2002;21:255–60. doi: 10.1054/clnu.2001.0531. [DOI] [PubMed] [Google Scholar]
- 21.Namazi N, Aliasgharzadeh S, Mahdavi R, Kolahdooz F. Accuracy of the common predictive equations for estimating resting energy expenditure among normal and overweight girl university students. J Am Coll Nutr. 2015:1–7. doi: 10.1080/07315724.2014.938280. [DOI] [PubMed] [Google Scholar]
- 22.Melanson EL, Coelho LB, Tran ZV, Haugen HA, Kearney JT, Hill JO. Validation of the BodyGem hand-held calorimeter. Int J Obes Relat Metab Disord. 2004;28:1479–84. doi: 10.1038/sj.ijo.0802643. [DOI] [PubMed] [Google Scholar]
- 23.Compher C, Hise M, Sternberg A, Kinosian BP. Comparison between Medgem and Deltatrac resting metabolic rate measurements. Eur J Clin Nutr. 2005;59:1136–41. doi: 10.1038/sj.ejcn.1602223. [DOI] [PubMed] [Google Scholar]
- 24.Frankenfield DC, Ashcraft CM, Galvan DA. Prediction of resting metabolic rate in critically ill patients at the extremes of body mass index. J Parenter Enter Nutr. 2013;37:361–7. doi: 10.1177/0148607112457423. [DOI] [PubMed] [Google Scholar]
- 25.Anderson EJ, Sylvia LG, Lynch M, Sonnenberg L, Lee H, Nathan DM. Comparison of energy assessment methods in overweight individuals. J Acad Nutr Diet. 2014;114:273–8. doi: 10.1016/j.jand.2013.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]