Abstract
Variation in the relative biological effectiveness (RBE) within the irradiation field of a carbon beam makes carbon-ion radiotherapy unique and advantageous in delivering the therapeutic dose to a deep-seated tumor, while sparing surrounding normal tissues. However, it is crucial to consider the RBE, not only in designing the dose distribution during treatment planning, but also in analyzing the clinical response retrospectively. At the National Institute of Radiological Sciences, the RBE model was established based on the response of human salivary gland cells. The response was originally handled with a linear–quadratic model, and later with a microdosimetric kinetic model. Retrospective analysis with a tumor-control probability model of non–small cell cancer treatment revealed a steep dose response in the tumor, and that the RBE of the tumor was adequately estimated using the model. A commonly used normal tissue complication probability model has not yet fully been accountable for the variable RBE of carbon ions; however, analysis of rectum injury after prostate cancer treatment suggested a highly serial-organ structure for the rectum, and a steep dose response similar to that observed for tumors.
Keywords: carbon-ion radiotherapy, relative biological effectiveness, microdosimetric kinetic model, tumor control probability, normal tissue complication probability
INTRODUCTION
The National Institute of Radiological Sciences (NIRS) of National Institutes for Quantum and Radiological Sciences (QST) has treated more than 10 000 patients by carbon-ion radiotherapy (CIRT), starting in 1994 [1], taking over the pioneering study conducted at the Lawrence Berkeley National Laboratory in the USA [2].
The stopping power of ions is inversely proportional to their energy when traveling through matter toward their range end, and the graph of this relationship, known as the Bragg curve, indicates the usefulness of this characteristic in radiotherapy. By associating the Bragg peak position close to the tumor, concentrated dose delivery to deep-seated radioresistant tumors can be realized, while sparing the surrounding normal tissues. For heavier ions such as carbon, the extent of the concentration toward the Bragg peak is further enhanced both physically and biologically due to less significant multiple scattering compared with that of lighter ions, and a pronounced increased biological effectiveness results. The change in the relative biological effectiveness (RBE), especially, means that consideration of the RBE is indispensable in treatment planning with an appropriate model, as it is in retrospective analysis of clinical outcomes. The approach of RBE consideration in CIRT at NIRS is explained below.
MODEL FOR RBE
Variation in the biological effectiveness of carbon ion beams can be attributed to significant variation in the density of energy deposited by an individual incident ion in a biological target on a micrometer scale.
LET (linear energy transfer) has conventionally been used as an index of the deposited energy density. LET expresses the expected value for the amount of energy deposition of radiation (dE) in a unit length (dx) (i.e. dE/dx). When an incident beam heavier than a proton travels through matter, some of the primary particles break into fragmentary particles when they collide with target nucleii. In addition, the energy of the primary particles is often modulated to deliver the required amount of energy to the target volume. As a result, the therapeutic beam contains various particle species of various energies [3].
Absorbed dose D can be expressed as a product of LET and particle fluence, as below:
| (1) |
Here, shows the particle fluence of and ρ represents the density of the matter. The absorbed dose does not represent the individual energy loss but the gross amount of energy deposited by the incident beam. RBE is defined as the ratio of the absorbed dose of a radiation required in order to cause the same biological effect compared with that of a reference radiation, and the following RBE-weighted dose Dw shows the absorbed dose of a reference radiation required to cause the biological effect of concern.
| (2) |
If Dw is uniform, uniform biological effect is expected.
When expressing RBE in relation to X-rays as the reference radiation, RBE as a function of LET is almost 1.0 at <10 keV/μm, then tends to increase gradually until it comes to the maximum at around LET = 150 keV/μm, and finally decreases. The latter decrease is known as the overkill effect. In the case of carbon ions, as the ions slow down, the LET value increases from about 10 to 100 keV/μm. The corresponding RBE value varies in the ‘ascending slope’, i.e. <2.0 at the entrance of the Bragg curve to >3.0 at the Bragg peak (see Fig. 1).
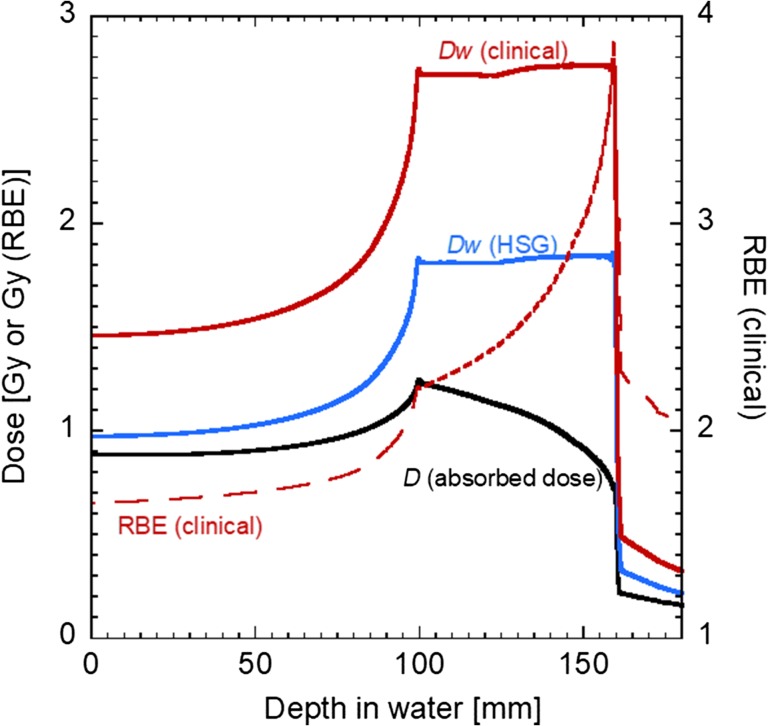
Fig. 1.
Depth–dose distribution of a therapeutic carbon beam by passive-beam delivery (290 MeV/n, 60 mm SOBP) [5]. Black, blue and red solid lines correspond to absorbed dose, dose weighted with HSG, and clinical RBE values, respectively. The clinical RBE value is plotted as a red dashed line.
The LET of a proton beam also increases in the irradiation field toward the Bragg peak but ranges below 10 keV/μm. The RBE of a proton beam is slightly higher than that of X-rays; as comprehensively reviewed by Paganetti in 2014 [4], recent studies have reported an obvious increase in RBE around the distal end, and the resultant extended effective range of the RBE-weighted dose. However, for the therapeutic purpose a constant value of 1.1 is widely used as the proton RBE, and its variation has generally not yet been taken into consideration in treatment planning. Strictly speaking, LET is not constant, even in the field of X-rays, due to the beam-hardening effect; however, the extent of the change is considered negligible, and therefore a constant RBE of 1.0 has been adopted in X-ray RT. As a result, in treatment planning of ongoing X-ray RT or proton therapy, it is not mandatory to consider the change in RBE- as RBE-weighted dose Dw explicitly, but the absorbed dose D under constant RBE is treated as the objective quantity to optimize.
On the contrary, it is necessary to make not the absorbed dose D but the RBE-weighted dose Dw uniform in the target in CIRT treatment planning. In the original model at NIRS [5], initially the RBE value of clonogenic cell survival for human salivary gland (HSG) cells was chosen as the reference biological endpoint. The HSG cell survival probability as a function of absorbed dose was experimentally studied for various energies of pristine carbon-ion beams [6]. In the study, the corresponding LET was calculated, and the derived dose–survival relationship was fitted with a commonly used linear–quadratic (LQ) model as:
| (3) |
where S and D are the cell survival probability and the absorbed dose, respectively, and α and β are the so-called LQ parameters. The derived LQ parameters were tabulated as a function of LET in the treatment planning system.
In treatment planning, the incident pristine beam is modulated to cover the target area in a spread-out Bragg peak (SOBP) with a uniform RBE-weighted dose. The shape of the SOBP follows the mechanical shape of a ridge filter, and therefore is not adjustable in the passive-beam delivery. The target biological effectiveness in the SOBP was fixed at 10% survival level of the HSG cells, irrespective of the prescribed dose. The biological effectiveness of the modulated beam was estimated using the dose-averaged α and β parameters in the literature for the LET value of each beam at the point. Finally, the planned dose distribution was scaled according to the clinical RBE value of fast-neutron therapy 3.0 at the point where the dose-averaged LET value is 80 keV/μm, so that the biological effectiveness would be comparable with that of fast neutron therapy. Figure 1 shows an example of the dose distribution of a therapeutic carbon beam. The therapeutic dose was prescribed in terms of the RBE-weighted dose to the target.
This framework of the RBE model was further enhanced when an active 3D scanning delivery system was installed in 2011 [7]. The scanning technique enables optimization of the shape of the depth–dose distribution individually with respect to the dose prescribed to the target. The Microdosimetric Kinetic Model (MKM) [8] was introduced into the RBE model for active 3D scanning. The MKM was developed to extend the concept of the theory of dual radiation action (TDRA) [9] in microdosimetry. The model is based on the energy deposition in a micrometre-scale unit region ‘domain’. Instead of the dual use of absorbed dose and LET in the original model, the amount of energy deposited in the domain over its mass, the so-called specific energy z, is used as the sole physical parameter. The number of biological lesions L produced in the domain is associated with the specific energy as L = Az + Bz2 in the MKM, while L = Bz2 in the original TDRA.
A cell nucleus is tiled up with the domains, and its survival probability is given from Poisson statistics when none of the domains in the cell nucleus receives any single lethal lesion. The dose–survival relationship by MKM can be expressed with using absorbed dose D according to the following equation.
| (4) |
Here is a saturation-corrected dose-averaged single-event specific energy. is a LQ parameter extrapolated to radiation. is treated as a constant parameter in the MKM.
As shown in Equation (4), the dose–survival relationship according to the MKM still shows a LQ dependency on the absorbed dose. However, the parameters can be given as a function of the physical quantity , which is measurable or calculable. Then, once the other parameters are fixed, MKM makes it possible to estimate the biological effectiveness of any radiation of a specific energy. The versatile and causal estimation of the RBE according to the MKM is regarded as suitable, especially for treatment planning with scanning delivery, where the resultant irradiation field is highly complex and optimized for each individual plan.
In ongoing CIRT at NIRS, MKM has been applied routinely in treatment planning [10, 11]. HSG cells have been used as the reference cells, and the RBE-weighted dose for HSG cells according to the MKM is scaled to become the clinical dose at the point where the radiation quality would be the same as that at the middle of the most frequently used beam (350 MeV/n, SOBP 60 mm) in past therapeutic irradiations. With this approach, the prescribed dose is consistent with dose prescription under the original model, and the shape of the beam exactly reflects the biological effectiveness of the beam equivalent to the reference beam delivering the amount of the RBE-weighted dose at the specified point (see figure 1 in [12]).
Tumor response
In analyzing the clinical outcomes after CIRT, the tumor control probability (TCP) has been examined with a conventional TCP model [13], as shown below.
| (5) |
With this model, TCP is estimated using the fractional absorbed dose d, the α and β value of the tumor with deviation σ on α, number of clonogens in the tumor N, number of fractionations n, tumor doubling time Td, total length of therapeutic irradiation T and kick-off time in tumor multiplication Tkick.
As radiation quality such as LET continuously changes in the irradiation field, the α(LET)/β(LET) value and the absorbed dose d is not unique within the target. Here, as mentioned, CIRT was started with passive-beam delivery where the depth–dose distribution is determined by the ridge filter, and the relationship between the absorbed dose and the RBE-weighted dose is fixed.
In the analysis of non-small-cell lung cancer (NSCLC) [14], CIRT was started with 18 fractions in 6 weeks by passive-beam delivery at NIRS in a dose-escalation manner to find the optimum dose realizing satisfactory tumor control while maintaining tolerable side effects. As the prescribed dose was given in terms of the RBE-weighted dose, the fractional absorbed dose d needed in the TCP formalism was derived by dividing the prescribed RBE-weighted dose by the RBE value at the middle of the 60 mm SOBP that has been most frequently used in NSCLC irradiation. Because the parameter β of the HSG cells is almost constant (see fig. 8 in [14]) and has little effect on cell survival response in a fractional dose range, β was assumed fixed and the same as that for the HSG cells (0.076). The remaining parameter α and its deviation σ was estimated through the fitting. In this approach, σ can be regarded as including not only individual differences in radiosensitivity between patients but also variation in the α value in the irradiation field.
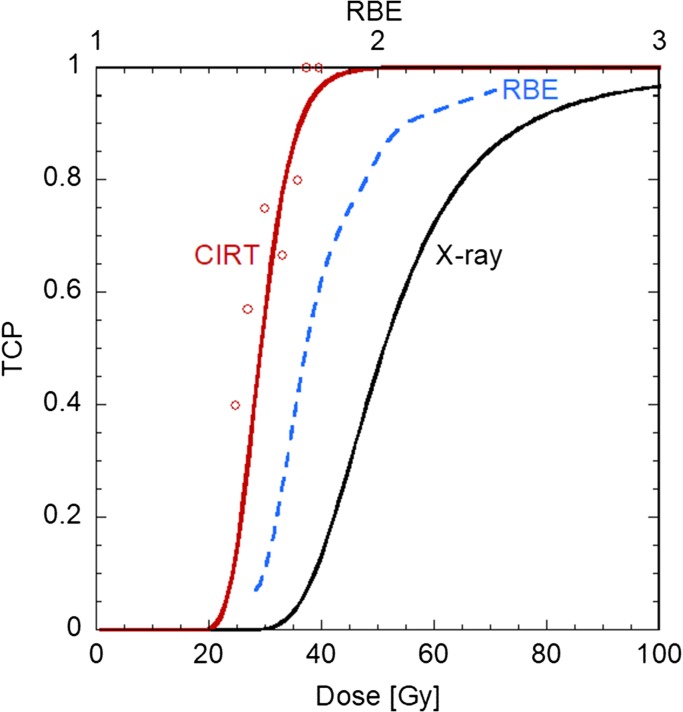
By comparing the derived TCP curve with that of X-rays, it was found that the RBE value estimated using the model in the treatment planning in Fig. 1 was appropriate at a high TCP level, as shown in Fig. 2. The increase in RBE as a function of TCP corresponds to the fact that the TCP curve of CIRT is steeper than that of X-ray RT. This suggests that the TCP after CIRT can be predicted with little concern for individual difference in radiosensitivity.
Fig. 2.
TCP of NSCLCs by CIRT (red) and X-ray (black) in 18Fx [14]. The dashed blue line in the figure shows RBE in terms of TCP.
Normal-tissue response
While the cell survival model and the TCP model are based on mechanistic considerations of the incident radiation and causal response, commonly used normal-tissue complication probability (NTCP) models represent numerical expressions of the macroscopic dose–response of the organ at risk (OAR) from a phenomenological viewpoint. It can be attributed to the vast variation of the endpoint of ‘complication’, depending on the OAR, in contrast to comparably obvious cell survival or tumor control. This makes it difficult to treat the RBE issue of CIRT in NTCP analysis.
Equation 6 shows the most commonly used Lymann–Kutcher–Bermann NTCP model [15, 16]. This model makes use of the error function to reproduce the sigmoidal dose–response for a given dose d, and m and TD50 as an index to show the steepness of the curve and the dose required to achieve 50% of the complication of interest in 50% of the population.
| (6) |
with
| (7) |
In general, dose distribution in the OAR becomes highly heterogeneous, even in X-ray radiotherapy. In treating the heterogeneity, the dose distribution within the OAR is often replaced with the EUD (equivalent uniform dose) [17], a representative dose postulated to cause the same OAR response as the actual dose distribution.
| (8) |
D i and N represent the dose at the i-th voxel and the number of total voxels, respectively. The parameter n describes the extent of the volume effect of the OAR. If n = 0, EUD corresponds to the maximum dose within the target; the OAR is regarded to be made up with serial connection of functional sub units (FSU) while the EUD is equal to the mean dose if n = 1, in which case the OAR responds as a parallel structure.
The direct use of the EUD for NTCP analysis is controversial in CIRT. As stated, treatment planning for CIRT calculates the RBE-weighted dose Dw instead of the absorbed dose D. In contrast to TCP analysis, because the dose deposited to the OAR drastically varies case by case, it is not easy to simply translate the RBE-weighted dose to the absorbed dose in the OAR retrospectively. In addition, even if the RBE-weighted dose distribution is reduced to the absorbed dose distribution, it is still necessary to consider the radiation quality dependence of the OAR response in the NTCP analysis.
Due to this problem, instead of differentiating the RBE-weighted dose from the absorbed dose and related radiation-quality index, we have tried to analyze the normal-tissue response with the LKB NTCP model using the EUD estimated directly from the RBE-weighted dose in treatment planning. With this approach, it should be noted, the EUD value of the OAR is weighted with the HSG-based RBE a priori. In addition, as the EUD is modulated using the volume index n, care should be paid when comparing the EUD-based NTCP response with other radiation modalities of different n value.
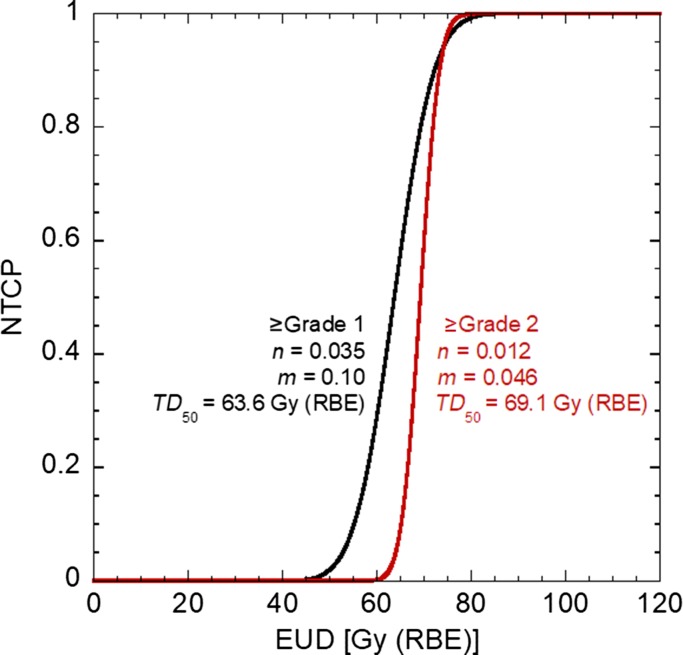
With these points in mind, late rectum injury after prostate cancer therapy was examined [18]. Figure 3 shows the NTCP curve for rectum injury classified as Grade 1 or higher, or Grade 2 or higher. The parameters n and m drawn in the figure were determined by the maximum likelihood method. The results indicate that the rectum exhibited a significant serial-like response, and that the hot spot for dose within the rectum had a strong correlation with the incidence of the rectum injury. The steep dose–response curve suggests that the variation in individual radiosensitivity only plays a limited role and that the occurrence of normal-tissue injury is predictable.
Fig. 3.
NTCP of rectum injury after CIRT for prostate cancer for Grade 1 or higher (black) and Grade 2 or higher (red) [18]. Derived NTCP parameters n, m and TD50 are shown in the figure.
Equivalent Uniform Effect (EUE) is a concept that has recently been proposed [19] to take into account changing biological effectiveness in the analysis of CIRT. Instead of the dose used in the EUD, the EUE represents a uniform biological effect comparable with that of the real complex biological effect .
| (9) |
n′ corresponds to the volume index n in the EUD. The biological effect is determined as follows (e.g. in the case of the LQ model):
| (10) |
Because modern biological models for CIRT, such as the MKM or the Local Effect Model (LEM) developed at GSI [20], enable prediction of the parameters and from the radiation quality at a given point and the biological parameters under the reference conditions, once the parameters are adequately set, analysis using the EUE may be beneficial in terms of handling the variation in the biological effectiveness in the irradiation field.
CONCLUSION
The high dose localization to tumours and the high RBE within tumours is an attractive characteristic of CIRT. In more than two decades of experience with the RBE model in relation to CIRT, the clinical efficacy of CIRT has been confirmed, especially for treating radioresistant tumours such as bone and soft-tissue sarcomas, as has the safety of completing the course of therapy, even with the hypofractionation regime [1]. Due to superior clinical outcomes, 10 CIRT facilities are in operation in the world as at the end of 2017 [21]. In order to make the modality pervasive further, it will be necessary to evaluate QOL and clinical effectiveness to be comparable with other therapeutic modalities. Our current analysis of tumour response and normal-tissue response shows that CIRT tends to realize a steep, and therefore a predictable, level of tissue response irrespective of individual difference in radiosensitivity. However, the existing models, especially for normal-tissue response, are not developed enough to fully account for the RBE characteristics of CIRT. In addition to accumulating comparable clinical data, it will be necessary to establish a versatile response model suitable for use with various types of radiation by adequately taking into account the dependence on radiation quality.
ACKNOWLEDGEMENTS
The author would like to thank Dr Tatsuaki Kanai of Osaka Heavy Ion Therapy Center (HIMAK) who developed the original biological model for CIRT at NIRS. The staff of NIRS are also appreciated for their substantial help, especially Drs Nobuyuki Kanematsu, Taku Inaniwa and Mai Fukahori.
CONFLICT OF INTEREST
The author has no conflict of interest.
References
- 1. Kamada T, Tsujii H, Blakely EA et al. . Carbon ion radiotherapy in Japan: an assessment of 20 years of clinical experience. Lancet Oncol 2015;16:e93–100. [DOI] [PubMed] [Google Scholar]
- 2. Castro JR. Results of heavy ion radiotherapy. Radiat Environ Biophys 1995;34:45–8. [DOI] [PubMed] [Google Scholar]
- 3. Matsufuji N, Fukumura A, Komori M et al. . Influence of fragment reaction of relativistic heavy charged particles on heavy-ion radiotherapy. Phys Med Biol 2003;48:1605–23. [DOI] [PubMed] [Google Scholar]
- 4. Paganetti H. Relative biological effectiveness (RBE) values for proton beam therapy. Variations as a function of biological endpoint, dose, and linear energy transfer. Phys Med Biol 2014;59:R419–72. [DOI] [PubMed] [Google Scholar]
- 5. Kanai T, Endo M, Minohara S et al. . Biophysical characteristics of HIMAC clinical irradiation system for heavy-ion radiation therapy. Int J Radiat Oncol Biol Phys 1999;44:201–10. [DOI] [PubMed] [Google Scholar]
- 6. Furusawa Y, Fukutsu K, Aoki M et al. . Inactivation of aerobic and hypoxic cells from three different cell lines by accelerated 3He-, 12C- and 20Ne-ion beams. Radiat Res 2000;154:485–96. [DOI] [PubMed] [Google Scholar]
- 7. Furukawa T, Inaniwa T, Sato S et al. . Performance of the NIRS fast scanning system for heavy-ion radiotherapy. Med Phys 2010;37:5672–82. [DOI] [PubMed] [Google Scholar]
- 8. Hawkins RB. A statistical theory of cell killing by radiation of varying linear energy transfer. Radiat Res 1994;140:366–47. [PubMed] [Google Scholar]
- 9. Kellerer M, Rossi HH. A generalized formation of dual radiation action. Radiat Res 1978;75:471–88. [Google Scholar]
- 10. Kase Y, Kanai T, Matsufuji N et al. . Biophysical calculation of cell survival probabilities using amorphous track structure models for heavy-ion irradiation. Phys Med Biol 2008;53:37–9. [DOI] [PubMed] [Google Scholar]
- 11. Inaniwa T, Furukawa T, Kase Y et al. . Treatment planning for a scanned carbon beam with a modified microdosimetric kinetic model. Phys Med Biol 2010;55:6721–37. [DOI] [PubMed] [Google Scholar]
- 12. Inaniwa T, Kanematsu N, Matsufuji N et al. . Reformulation of a clinical-dose system for carbon-ion radiotherapy treatment planning at the National Institute of Radiological Sciences, Japan. Phys Med Biol 2015;60:3271–86. [DOI] [PubMed] [Google Scholar]
- 13. Webb S, Nahum AE. A model for calculating tumour control probability in radiotherapy including the effects of inhomogeneous distributions of dose and clonogenic cell density. Phys Med Biol 1993;38:653–66. [DOI] [PubMed] [Google Scholar]
- 14. Kanai T, Matsufuji N, Miyamoto T et al. . Examination of GyE system for HIMAC carbon therapy. Int J Radiat Oncol Biol Phys 2006;64:650–6. [DOI] [PubMed] [Google Scholar]
- 15. Lyman JT. Complication probability as assessed from dose–volume histograms. Radiat Res 1985;104:S13–9. [PubMed] [Google Scholar]
- 16. Burman C, Kutcher GJ, Emami B et al. . Fitting of normal tissue tolerance data to an analytic function. Int J Radiat Oncol Biol Phys 1991;21:123–35. [DOI] [PubMed] [Google Scholar]
- 17. Niemierko A. A generalized concept of equivalent uniform dose (EUD). Med Phys 1999;26:1100. [Google Scholar]
- 18. Fukahori M, Matsufuji N, Himukai T et al. . Estimation of late rectal normal tissue complication probability parameters in carbon ion therapy for prostate cancer. Radiother Oncol 2016;118:136–40. [DOI] [PubMed] [Google Scholar]
- 19. Brüningk SC, Kamp F, Wilkens JJ. EUD-based biological optimization for carbon ion therapy. Med Phys 2015;42:6248–57. [DOI] [PubMed] [Google Scholar]
- 20. Scholz M, Kellerer AM, Kraft-Weyrather W et al. . Computation of cell survival in heavy ion beams for therapy. Radiat Environ Biophys 1997;36:59–6. [DOI] [PubMed] [Google Scholar]
- 21.Particle Therapy Co-Operative Group (PTCOG). https://www.ptcog.ch/ (23 February 2018, date last accessed).