Thermodynamic characterization of the multivalent interactions underlying rapid and selective translocation through the nuclear pore complex

Abstract

Intrinsically disordered proteins (IDPs) play important roles in many biological systems. Given the vast conformational space that IDPs can explore, the thermodynamics of the interactions with their partners is closely linked to their biological functions. Intrinsically disordered regions of Phe–Gly nucleoporins (FG Nups) that contain multiple phenylalanine–glycine repeats are of particular interest, as their interactions with transport factors (TFs) underlie the paradoxically rapid yet also highly selective transport of macromolecules mediated by the nuclear pore complex. Here, we used NMR and isothermal titration calorimetry to thermodynamically characterize these multivalent interactions. These analyses revealed that a combination of low per-FG motif affinity and the enthalpy–entropy balance prevents high-avidity interaction between FG Nups and TFs, whereas the large number of FG motifs promotes frequent FG–TF contacts, resulting in enhanced selectivity. Our thermodynamic model underlines the importance of functional disorder of FG Nups. It helps explain the rapid and selective translocation of TFs through the nuclear pore complex and further expands our understanding of the mechanisms of “fuzzy” interactions involving IDPs.

Introduction

Intrinsically disordered proteins (IDPs)⁶ and proteins with intrinsically disordered regions (IDRs) constitute ∼30–40% of the human proteome and are involved in many protein signaling and regulation processes (1). IDPs/IDRs can interact with their targets with high specificity, yet often with low affinity and high reversibility. There is a broad interest in quantifying the thermodynamic driving forces governing IDP interactions. Many IDPs undergo a disorder-to-order transition upon binding to their targets (2), whereas others form “fuzzy complexes” (3), where significant residual disorder is maintained in the interacting state. Due to their essential role in many biological processes, a better understanding of the energetics of IDP interactions is needed (4).

Many IDP interactions are mediated by short linear motifs (SLiMs) that engage with receptor molecules. Because SLiMs do not have extensive interaction interfaces to induce high enthalpy, SLiM-containing IDPs often utilize multiple motifs to participate in multivalent interactions (5). This mitigates the conformational entropy loss upon binding and enhances individually weak monovalent interactions, resulting in higher overall affinity (avidity) and specificity (6, 7). One example of an IDR that utilizes multiple short linear motifs are disordered domains of Phe–Gly nucleoporins (FG Nups) that line the central channel of the nuclear pore complex (NPC) (Fig. 1A). FG Nups typically contain 5–50 FG motifs separated by spacer residues (8). These FG repeat regions collectively form a selectively permeable barrier for macromolecular transport through the NPC. Specific cargoes can translocate rapidly and efficiently through the NPC by binding to cognate transport factors (TFs). TFs make contacts with multiple FG repeat motifs, allowing them to diffuse rapidly and selectively through the central channel (9, 10). The passage of nonspecific macromolecules, which lack similar interactions, is impeded (11). Selectivity for TFs arises, in part, because the surface of TFs contains multiple hydrophobic pockets for FG motif interaction. However, the binding of multiple FG motifs to a TF containing multiple interaction sites could lead to high avidity complexation and thus long residence times, and such interactions would be incompatible with the rapid transport rates observed in vivo (∼5–10 ms) (12, 13). The thermodynamics underlying FG–TF interactions that enable TFs to translocate rapidly yet selectively through the NPC (often referred to as the “transport paradox” (14)) has been poorly characterized, so it remains unclear what mechanism prevents TFs from “sticking” to multiple FG motifs through such avidity effects.

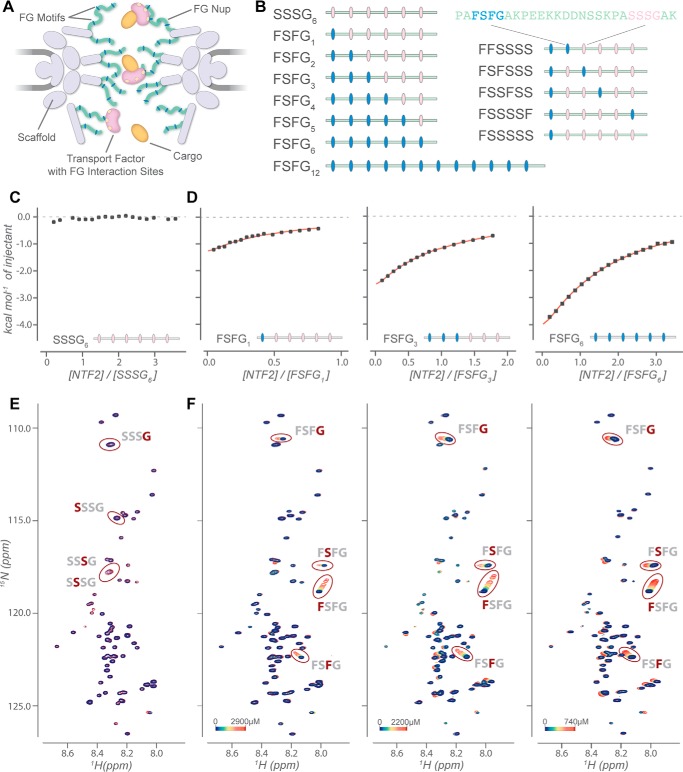
Figure 1.

Systematic analysis of multivalent interaction between FSFG constructs and NTF2. A, schematic diagram of the NPC-mediated transport. B, design of FSFG constructs with varying degrees of valency (left) and with varying distance between two FSFG motifs (right). C–F, characterization of the interaction between NTF2 and SSSG₆, FSFG₁, FSFG₃, and FSFG₆ by ITC (C and D) and NMR HSQC titration experiments (E and F). The ITC curves represent the baseline-corrected, normalized, and reference-subtracted data set (see Fig. S3 for details and Table S2 for experimental conditions). HSQC spectra containing [¹⁵N]SSSG₆ (100 μm) (E) were obtained at 900 MHz, in the presence (blue) and absence (red) of 150 μm NTF2. HSQC titrations of [¹⁵N]FSFG₁, [¹⁵N]FSFG₃, and [¹⁵N]FSFG₆ were performed at a fixed concentration of 120 μm, 40 μm, and 20 μm, respectively. The concentrations for NTF2 vary with the maximum concentrated tested, indicated by the color bar. Titrations were acquired at 800 MHz.

Results

We characterized the interaction between FG Nups and NTF2 with a series of constructs containing a variable number of FSFG motifs by sequentially replacing FSFG motifs with SSSG motifs (Fig. 1B). This Phe → Ser mutation is known to negate interaction with TFs (15, 16). We characterized their interaction with NTF2 by both NMR and ITC. We first titrated NTF2 against each FSFG construct. Control titrations with the SSSG₆ variant yielded no observable heat (Fig. 1C), no chemical shift perturbations (CSPs), and no peak intensity changes (Fig. 1E), confirming that the SSSG motif and the spacer regions display no affinity to NTF2. In contrast, heteronuclear single quantum coherence (HSQC) peaks corresponding to FSFG motif residues underwent selective chemical shift changes upon increasing concentration of NTF2, although the spacer residues remained largely unperturbed, consistent with previous observations (Fig. 1F) (17, 18).

Affinity measurements by NMR and ITC were consistent for each construct (Fig. 2 (A and B), Figs. S1 and S2, and Table S1), demonstrating that they reported on the same chemical reactions. Data from both methods fit to a simple binding model and did not require the use of more complex equilibrium models. The affinity of the single FG-motif construct (FSFG₁) to NTF2 was very weak (K_D = 4.35 mm observed by NMR). This is consistent with the affinity measured for the interaction between importin-β and a human Nup153 Phe → Ala mutant with only a single phenylalanine residue (K_D = 7.3 mm) (18). Although the accumulated strength of multivalent interactions could substantially increase avidity (6), the affinity of NTF2 for the divalent construct FSFG₂ was only ∼2-fold greater than for the monovalent FSFG₁. As the FSFG valency increased further, the apparent affinity continued a modest increase, plateauing after four motifs; even 12 FSFG repeats (FSFG₁₂) exhibited a similar affinity to that of FSFG₆ (Fig. 2B and Table S1). Thus, multivalency had a much weaker effect on the overall affinity than might be expected.

Figure 2.

Quantitative analysis of NTF2 interaction with various FSFG constructs. A, titration curves derived from NMR titration experiments in Fig. 1F, displaying changes in chemical shifts (Δδ) versus concentration of NTF2. Solid line, the fit to Equation 2 used to determine the apparent dissociation constant (K_D) (see Fig. S1 and Table S3 for final saturation achieved). B, K_D values for each of the FSFG₁–FSFG₁₂ constructs (Fig. 1B, left) by NMR and ITC. S.E. of the curve fitting and S.E. of the mean are plotted for NMR and ITC, respectively (see Table S1). C, K_D values determined by NMR titration experiments of FSFG constructs with varying distance between two FSFG motifs (Fig. 1B, right). Concentrations of [¹⁵N]FSFG constructs were fixed at 60 μm for all titrations. The infinity sign indicates the K_D for the FSFG₁ construct. D, schematic diagram of the local concentration effect promoting the “interacting state.”

Importantly, titrations with FSFG₁ yield the per-motif affinity to an NTF2 molecule (which contains multiple FG contact sites). For multivalent FSFG constructs, this per-motif affinity would remain constant in the absence of cooperativity, and the overall molecular K_D values would reflect the ensemble of all equivalent FSFG motifs interacting and rebinding to NTF2 before escaping to bulk by diffusion (19). Our experiments lacked temporal resolution to fully describe such microstates in the ensemble. Thus, we emphasize that the measured K_D values reflect equilibria between the two time-averaged ensembles: the non-interacting and the interacting state ensembles. For respective FSFG valency, the measured K_D accounts for contributions made by all underlying microscopic interaction equilibria with distinct individual K_D values, including ones involving simultaneous engagement of multiple FG motifs to a single NTF2. Affinity measurements indicate that FSFG displays modest avidity to NTF2, implying that even the divalently interacting state is at best scarcely or transiently populated.

The interaction of a TF with any of the FG motifs in a construct localizes the rest of the FG chain into the vicinity of the TF, increasing the concentration of FG motifs available for subsequent interactions or rebinding events. If the additional enthalpy from the intramolecular interaction significantly exceeds the loss of conformational entropy of the chain, strong avidity would result (6, 20). To assess how changes in the local concentration of FSFG motifs would affect the overall affinity, we tested a set of FSFG₂ variants, altering the distance between the two FSFG motifs (Fig. 1B (right) and Table S3). The affinity for NTF2 decreased toward that of FSFG1 with increased intermotif distance (Fig. 2C). Separations larger than two repeats induced no significant binding enhancement. Thus, the modest affinity gain observed in Fig. 2B can be described as the result of increased intramolecular contacts induced by the local concentration of FSFG motifs (Fig. 2C). This excludes an interaction mechanism where each FSFG motif binds independently to a different molecule of NTF2, where no change in the measured affinity would be expected. Our results also suggest that FSFG motifs proximal to the initially bound FG motif more effectively contribute to the enhancement of overall affinity than those that are distant. Importantly, the effect of large local concentration increases the probability that an FG molecule will be in the “interacting” state through rebinding (Fig. 2D) (19).

To explore the effect of increased local concentration on the NTF2 interaction surface, we mapped the NTF2 residues interacting with our FSFG constructs by NMR. As observed previously (21), CSPs were observed at, but not limited to, the crystallographically observed site around Phe-5 of NTF2 (22) and extended along the hydrophobic groove bridging the two monomers (Fig. 3A and Fig. S4). TROSY-HSQC titrations with FSFG₁, FSFG₃, and FSFG₆ showed the same residues of [²H,¹⁵N]NTF2 were involved in the interaction (Fig. 3B), and the affected residues shifted linearly regardless of the valency of the FSFG constructs, indicating a single binding mode regardless of FG valency. To determine the number of spectrally distinguishable binding modes contributing to the CSPs, singular value decomposition (SVD) analysis was used (23). SVD analysis from each titration produced only two non-noise components (free and interacting), indicating an apparent two-state reaction (Fig. S5). We calculated NTF2 site affinity for all significantly perturbed residues, collectively representing the interaction surface (Fig. 3A and Figs. S4–S7), using the raw and SVD noise-filtered data, the latter of which yielded better precision in the derived K_D (Fig. S7). Surprisingly, for [²H,¹⁵N]NTF2 titrations with varying concentration of FSFG₁, fitting of the 61 residues displaying significant CSPs to a global K_D value yielded 19.9 ± 0.4 mm (Fig. S7A). This dissociation constant is probably a lower bound in our assay conditions, as we were limited by the solubility of the FSFG₁ construct. Higher solubility was achieved using a single-repeat FSFG peptide; nevertheless, a similar result to that of FSFG₁ was obtained with this peptide (Figs. S4–S7). These titrations probed the saturation of spatially distinct, independent interaction sites.

Figure 3.

NMR analysis of NTF2. A, chemical shift perturbations at ∼1:1 molar ratio of [²H,¹⁵N]NTF2/FSFG₆ mapped onto the structure of NTF2 (Protein Data Bank code 1GYB). Several selected residues are shown in ball and stick representations with their associated titration curves and K_D (locally fit) from the reconstructed data set after noise filtering by SVD. See Figs. S4–S7 for additional information. B, chemical shift perturbations observed at the indicated concentrations for each assigned residue in NTF2 from experiments with FSFG₆ (top), FSFG₃ (middle), and FSFG₁ (bottom) as the titrant.

Our results indicate that residues on NTF2, in different areas of the molecule (Fig. S4E), have individual K_D values of similar values and can be fit to a single global value with high precision (Fig. S7). Our previous simulations demonstrated that FSFG motifs make multiple transient and exploratory contacts with the interaction surface of NTF2 (24). Taken together, the single binding mode detectable by SVD suggests that the exchange rates of FG motifs contacting the NTF2 surface are faster than the experimental detection (in the range of milliseconds), such that the observed CSPs reflect a single time-averaged binding mode. In other words, whereas multiple interactions and rebinding events occur rapidly, we only detect average bulk behavior in the timescale of our experiments. The difference in observed K_D between this titration of NTF2 sites and the titration of [¹⁵N]FSFG₁ (above) (Fig. 2B and Table S1) further suggests that the NTF2 interaction surface is composed of multiple contact sites. This difference is illustrated by a simple kinetic modeling of FSFG₁–NTF2 interaction (supporting information and Fig. S8).

The NTF2 per-site K_D decreased with FSFG valency (Figs. S6 and S7), with FSFG₃ and FSFG₆ displaying ∼7.5- and ∼60-fold increases, respectively, compared with FSFG1. As there was neither an emergence of additional residues involved in the interaction at higher valency (Fig. 3B) nor additional binding modes appearing by SVD analysis (Fig. S5), multivalency appears to simply induce an additive effect. The increased frequency of contacts formed enhances specificity but without significantly changing the mode of interaction. Taken together, FSFG motifs interact with a large surface patch with nearly uniformly distributed low interaction potentials, lacking a well-defined energy minimum.

To understand what factors prevent strong avidity, we examined the energetics of interactions by ITC. The increase in negative ΔG with higher valency was modest, with only a ∼27% gain with FSFG₆ relative to FSFG₁ (Fig. 4A and Table S1). We observed enthalpy-driven interactions for each FSFG construct. Because the interactions are both low-affinity and low-enthalpy, we had to balance the sensitivity and the degree of complexation to maintain the data quality. As a result, these ITC experiments were performed at low c values (c = n[M₀]/K_D, where [M₀] is the concentration of the titrand and n is the molecular stoichiometry). However, low c values are not necessarily limiting, as long as sufficient saturation is achieved and the value of n or of ΔH is separately determined by other methods (25, 26). Moreover, NMR measurements can cross-validate the K_D determined by ITC. Due to lack of sufficient saturation, the lower-affinity constructs (FSFG₁–FSFG₃) were excluded from thermodynamic analysis (Table S1). For FSFG₄–FSFG₆, we set n = 1 based on dynamic light scattering (DLS) titration measurements, which indicated that FSFG₆ and NTF2 predominantly form a complex of 1:1 molecular stoichiometry at high sample concentrations (Fig. S9). This confirms that the local concentration effect favors intra- rather than intermolecular FG Nup–TF interaction (Fig. 2C). For FSFG₁₂, DLS indicates that two molecules of NTF2 can interact simultaneously with a single FSFG₁₂ polypeptide (Fig. S9); thus, we set n = 2. This indicates that after some number of FSFG motifs (greater than six), a second TF molecule would be able to interact, probably due to the loss of steric and/or excluded volume constraints. Importantly, the K_D values of FSFG₆ and FSFG₁₂ were similar, suggesting that the linkage between the two adjacent TF interactions is minimal beyond a certain distance. Thus, the affinity of TF interactions with FG Nups can remain weak even in the NPC milieu, where a large number of FG motifs are clustered on single FG Nups.

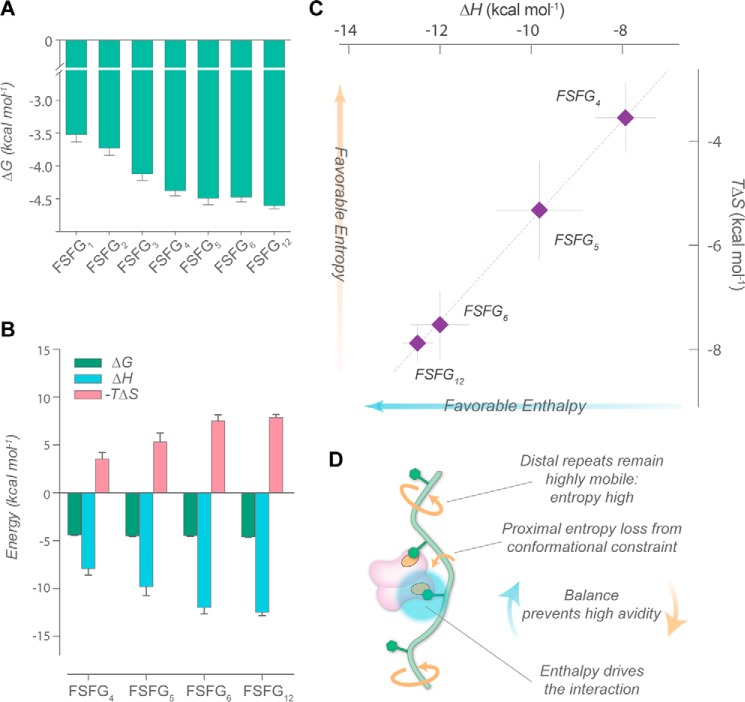
Figure 4.

Thermodynamics of FSFG–NTF2 interaction. A, Gibbs free energy (ΔG) for the interactions between FSFG constructs and NTF2. B, ΔG, enthalpy (ΔH), and entropy (−TΔS) for the interactions between FSFG₄–FSFG₁₂ constructs and NTF2 measured by ITC. C, enthalpy–entropy compensation curve for interactions for the aforementioned constructs, with a linear fit (see Fig. S11). D, schematic diagram of the enthalpy–entropy balance that prevents high-avidity interactions.

The overall heat released increased with valency, as expected (Fig. S2). A prominent negative ΔH for higher-valency constructs further indicates that more frequent intramolecular contacts form (Fig. 4B and Table S1) as the local concentrations of FSFG motifs increase (supporting information, Fig. S10, and Table S3). Notably, although hydrophobic associations are usually driven by a favorable change in solvent entropy, FSFG–NTF2 interactions instead display a “non-classical” hydrophobic interaction driven by enthalpy (27). This type of interaction has been attributed to water molecules at hydrophobic surfaces participating in weaker hydrogen bonding relative to bulk solvent, and therefore their displacement (by potentially enthalpically favorable contacts between the interaction partners) is overall enthalpically favorable (27). Our result suggests an unexpected and important role of protein hydration and solvent dynamics in FG–TF interaction, raising an interesting question regarding the origin of the enthalpy in FG–TF interactions.

Many multivalent interactions involve ligands with relatively rigid spacers, at lengths similar to the distances between receptor interaction sites, resulting in large cumulative enthalpy with minimal loss in conformational entropy and consequently, strong avidities (28). In our system, the magnitude of ΔH that increased with increasing FSFG valency was almost perfectly offset by an increasing −TΔS (Fig. 4C), exhibiting apparent enthalpy–entropy compensation (29). This trend again reflects the additive nature of the system (30) (i.e. the frequency of qualitatively similar contacts increases with valency). We conclude that this modest avidity is maintained because the effect of increased local concentration of FSFG motifs around NTF2 is countered by the entropic costs of restricting the conformational freedom of the chain, preventing stable multibound states (Fig. 4D).

Discussion

The inherent issue in IDP interactions is how they cope with the loss of conformational entropy upon binding. High entropy state of IDPs may appear as a considerable energetic obstacle to their functions. Here, we propose instead that FG Nups exploit this entropy loss for functionality. The weak single FG motif affinity and the enthalpy–entropy balance operative at higher valency states prevent strong avidity, enabling rapid and reversible interactions. Simultaneously, enhanced specificity is achieved through high local concentration of FG motifs, permitting higher frequency of contacts (longer global residence time at a high rate of exchange). We propose this combined effect as a reasonable explanation to the “transport paradox” (14).

Our results also provide new details for NPC transport models that describe the NPC as a virtual energetic gate (31, 32) By providing microscopic details, our work, along with other recent studies, indicates that collective low-affinity FG–TF interactions are functionally relevant to the transport mechanism (17, 18). This contrasts with models assigning emphasis on high avidity ones (33).

Importantly, high concentration of FG motifs in the NPC and their fluctuations around a TF probably facilitate TF hopping between different FG Nups. When multiple FG motifs from two or more different FG Nups simultaneously engage to a TF at different sites (i.e. intermolecular interaction), the interactions at those sites are very weak (K_D in the millimolar range), and individual FG motifs would have short residence times, τ, on a single interaction site (τ = 1/k_off, where k_off is the off-rate constant). τ is estimated to be <1 μs, assuming K_D = 1 mm and based on limits of the on-rate constant, k_on, from stopped-flow analysis (∼10⁹ m⁻¹ s⁻¹) (18). Thus, the lifespan of such a multivalent complexation would be short (i.e. a few microseconds). When multiple FG motifs from the same chain engage with an NTF2 molecule at different sites (intramolecular interaction), the enthalpy–entropy balance disfavors divalent and higher-valency (high-avidity) interactions because of the entropic penalty associated with the intramolecular interaction. In both scenarios, FG motifs would easily undergo rapid exchange due to competition from other FG Nups. Thus, it appears that the combination of multivalency and low per-NTF2-site affinity provides a balance between the selectivity achieved through increased avidity and the fast exchange rates required for transport. Whereas other effects, such as sequence heterogeneity among FG Nups, end-tethering to the NPC scaffold, and inter-FG Nup cohesiveness (34–36), may additionally modulate the FG–TF interactions, entropic resistance to static complexes would still play a fundamental role in the selective translocation.

Our study also expands our mechanistic understanding of “fuzzy” interactions involving IDPs (3). The design principle characterized here could be extended to chemical applications, such as artificial molecular sorting machines (37) and steric inhibitors utilizing multivalency (6).

Experimental procedures

Plasmids

FSFG₆ and SSSG₆ DNA constructs codon-optimized for bacterial expression were synthesized (IDT). Gene fragments from the synthesized plasmids were ligated into pET21b or pET24a vector. The FSFG₁₂ plasmid was created by inserting a FSFG₆ fragment into a FSFG₆ plasmid. Other FSFG variants were created by site-directed mutagenesis from the two parental constructs. For NTF2, the genomic sequence from Saccharomyces cerevisiae was used. All of the proteins were C-terminally tagged with hexahistidine. Their primary sequences are listed in the supporting information.

Protein purification

FSFG constructs were purified as described previously (17) (see supporting information), and NTF2 was expressed and purified in an identical manner except that urea was removed from all of the buffers.

U-¹⁵N and U-¹³C,¹⁵N samples were prepared using M9 media containing [¹⁵N]NH₄Cl and [U-¹³C]glucose (Cambridge Isotopes) as needed. For [²H,¹⁵N]NTF2, the sample was prepared in M9 media containing 99% D₂O and [¹⁵N]NH₄Cl with natural-abundance glucose as the sole carbon source (38). The purification of NMR-labeled samples was identical to the protocol for their natural-abundance counterparts. However, for [²H,¹⁵N]NTF2, additional steps were needed to exchange the unobservable N²H to N¹Hs (see supporting information). Protein concentrations were measured by BCA assay kit (Thermo Scientific), following the product instructions. Amino acid analysis was conducted for select FSFG constructs and NTF2, and the measured concentrations were consistent with those measured by a BCA assay.

Nuclear magnetic resonance

All NMR experiments were conducted on Bruker spectrometers at 800 MHz and 298 K with samples prepared in Buffer A (20 mm HEPES-KOH, pH 6.8, 150 mm KCl, 2 mm MgCl₂), unless otherwise noted. NMR data were analyzed using NMRPipe (39) and CCPNMR analysis (40). Titration experiments were performed in Buffer A using a fixed concentration of ¹⁵N-labeled sample and by preparation of separate samples for each titration point. Sample concentrations for [²H,¹⁵N] NTF2 were either 250 or 500 μm, whereas concentrations for [¹⁵N] FSFG_x ranged from 20 to 120 μm. A majority of our experimental conditions were within the optimal range of titrant concentrations suggested by Granot (41) with the exception of titrations involving FSFG₁ as well as [²H,¹⁵N]NTF2 titration with FSFG₃ due to the very low-affinity nature and limited solubility of both components. As a result, derived K_D values for those titrations should be considered as lower-bound estimates. Chemical shifts for the FSFG residues and all of the assigned NTF2 residues were extracted from each titration point, and the CSPs were calculated as follows,

$$\sqrt{{\left({\delta }^{15}\text{N}\times 0.11\right)}^2+{\left({\delta }^1\text{H}\right)}^2}$$ (1)

where δ¹⁵N and δ¹H are the ¹⁵N and ¹H chemical shift changes with respect to the free state (42). The CSP was plotted as a function of titrant concentration and fit to a standard equation (42),

$$\Delta \delta =\Delta {\delta }_{\max }\left(\left(P_0+X+K_D\right)-\sqrt{{\left(P_0+X+K_D\right)}^2-\left(4\times P_0\times X\right)}\right)/\left(2\times P_0\right)$$ (2)

where Δδ_max is the maximum chemical shift change, P₀ is the fixed protein concentration, and X is the titrant concentration. The fitting was performed by Prism (GraphPad Software) with the above equation to derive K_D. This general equation was also used to calculate the final saturation using the protein concentrations at the last titration point,

$$\text{Final}\hspace{0.17em}\text{saturation}=\left(\left(P_0+X_{\max }+K_D\right)-\sqrt{{\left(P_0+X_{\max }+K_D\right)}^2-\left(4\times P_0\times X_{\max }\right)}\right)/\left(2\times P_0\right)$$ (3)

Final saturations for the ITC experiments were calculated in the same manner. Assignments of NTF2 used standard triple resonance approaches (43, 44), including HNCO, HNCACO, HNCACB, CBCACONH, HNCA, and HNCOCA.

The single-repeat FSFG peptide was synthesized and reverse-phase HPLC–purified by the Proteomic Resource Center at Rockefeller University. A stock solution was prepared by dissolving the lyophilized sample into Buffer A.

Isothermal titration calorimetry

All ITC experiments were conducted in Buffer A at 25 °C on a MicroCal Auto-iTC200 (Malvern). In all experiments, the concentration of FSFG construct was fixed, and NTF2 was titrated in (see Table S2). See the supporting information for additional details.

The raw heat evolution data were integrated and analyzed by the ITC module (Malvern) within the Origin program (OriginLab). Heats of dilution of FSFG constructs and NTF2 were separately measured for each experiment (see Fig. S3) before curve fitting. The corrected curves were fitted using Origin software, using a non-linear least squares algorithm based on a model with a single class of independent, equivalent sites to determine the molecular stoichiometry n, the K_D, and the enthalpy (ΔH). For FSFG₄–FSFG₆, n was set at 1, and for FSFG₁₂, n was set at 2, based on the molecular stoichiometry determined by DLS (see Fig. S9), whereas the K_D and the ΔH were allowed to freely float in the fitting procedure. For the constructs with very low affinity and low enthalpy (i.e. FSFG₁–FSFG₃), fixing n at 1 yielded poor fits to the experimental data, and curve fitting also failed to converge on single n and ΔH values when n was freely fit. This is due to the low degree of complexation (Table S2) limited by the low affinity and the low enthalpy of interactions as well as the limitations of NTF2 solubility. Thus, for those constructs, n and ΔH could not be determined separately, although during the fitting procedure, the products of n and ΔH (nΔH, total enthalpy change) can be calculated and were reported because they are known to stay approximately normal in low c-value systems (25, 26). However, K_D values are insensitive to errors in n at low c values (26) and were reliably obtained for those constructs by ITC, as demonstrated by the cross-validation with the NMR results (Fig. 2B and Table S1).

Gibbs free energy (ΔG) and its entropic component (TΔS) were calculated using the following equations,

$$\Delta G=RT\ln \left(K_D\right)$$ (4)

$$\Delta G=\Delta H-T\Delta S$$ (5)

where R is the ideal gas constant and T is the absolute temperature (298 K). Means and S.E. values of the thermodynamic parameters were calculated for each FSFG construct and are reported in Table S1.

Author contributions

R. H., S. S., D. C., and M. R. conceived the project. R. H., S. S., L. H., and K. D. performed experiments and R. H., S. S., L. H., and C. C. prepared the samples. R. H., S. S., J. M. K., and D. C. analyzed the data and R. H., S. S., and M. R. made figures and wrote the manuscript with D. C.