Respiratory sinus arrhythmia: Modeling longitudinal change from 6 weeks to 2 years of age among low-income Mexican Americans

Abstract

Parasympathetically-mediated heart rate variability (HRV), commonly indexed via respiratory sinus arrhythmia (RSA), is theorized to support the physiological regulation of emotion; however, little is known about the trajectory of change in resting RSA across early development among high-risk populations for whom emotion regulation is crucial. This study characterized resting RSA change from 6 weeks to 2 years of age among 312 low-income Mexican American infants. RSA was assessed longitudinally at 6, 12, 18, 24, 52, 78, and 104 weeks of age. On average, resting RSA increased as infants aged, and this change accelerated over time. There was significant variance between infants in resting RSA at 6 weeks of age, and in the slope, and acceleration of resting RSA change. Intraclass correlation among infants’ resting RSA measures was minimal, indicating that resting RSA may not be “trait-like” during infancy. Results characterize early RSA development among a high-risk sample, which can inform theoretical understanding of the development of emotional, and behavioral self-regulation in a high-risk population, as well as efforts to promote wellbeing across early childhood.

1 | INTRODUCTION

Throughout the first 2 years of life, infants undergo rapid physiological development. Multiple systems involved in early co- and self-regulation undergo development, including the parasympathetic nervous system (PNS). The PNS coordinates with other neurological systems to help the body regulate in the face of varied environmental demands (e.g., stress, social interaction). In particular, the PNS acts via the vagus nerve to speed up or slow down the heart in response to social, and environmental stimuli. With these adjustments, heart rate becomes more variable, which facilitates effective emotional, and social responses to the environment (Porges, 1997). Although overall variability in heart rate is influenced by multiple systems (Appelhans & Luecken, 2006), PNS influence alone can be measured via quantifying respiratory sinus arrhythmia (RSA), which is a naturally occurring rhythm in the heart rate pattern that oscillates at approximately the frequency of spontaneous breathing (Porges & Furman, 2011).

RSA is theorized to play a crucial role in regulation of emotion and effective interpersonal interactions and can be thought of as a measure of the physiological capacity to regulate emotions. Resting RSA has been associated with multiple early indicators of infant emotional and behavioral well-being. Infants and children with higher RSA are more easily soothed (Huffman et al., 1998) and display less withdrawn, depressed, or aggressive behavior (Porges, Doussard-Roosevelt, Portales, & Greenspan, 1996). Additionally, measures of resting RSA in early infancy and childhood predict later child outcomes. Children with low resting RSA from 5 to 48 months of age display greater behavior problems in multiple domains at 48 months of age (e.g., aggressive behavior, oppositional defiant problems; Patriquin, Lorenzi, Scarpa, Calkins, & Bell, 2015).

In general, previous work suggests that resting RSA is “trait-like” in adulthood. Even over periods of a year or longer, there is little change in resting HRV, and rank ordering of resting HRV across individuals changes very little (Burleson et al., 2003). However, the extent to which resting RSA changes with development or is stable and “trait-like” in infancy is unclear, and RSA development has not yet been well characterized, particularly among infants in adverse environments (e.g., poverty) who are at higher risk for emotional, and behavioral problems related to poor self-regulation (Flouri, Midouhas, & Joshi, 2014). One of the few studies assessing parasympathetic activity among low-income Latino infants found that resting RSA increased across time from 6 to 60 months, and found a weak positive longitudinal intraclass correlation coefficient (Alkon, Boyce, Davis, & Eskenazi, 2011). However, no previous work has assessed resting RSA beginning earlier in infancy in a low-income Mexican American sample, or assessed whether increases in RSA follow a linear or quadratic pattern as infants’ neurological systems develop. Models of developmental change often identify non-linear patterns; for example, trajectories of body mass index across childhood are best described quadratically (Boyer, Nelson, & Holub, 2015).

An improved understanding of the parasympathetic nervous system’s development has implications for theory on the development of regulatory ability, future longitudinal research of early predictors of emotion regulation outcomes, and targeted efforts to improve wellbeing in infancy, and across the lifespan among high-risk populations. The current paper seeks to characterize developmental change in RSA across infancy (from 6 weeks to 2 years of age) among impoverished Mexican American infants, using data from a longitudinal study of low-income Mexican-origin mothers and their infants to model changes in infant resting RSA over the first 2 years of life. We hypothesized that infant resting RSA would increase across the postpartum period, and that this increase would accelerate over time.

2 | METHODS

2.1 | Participants and procedure

Participants included 312 mothers (mean age = 27.8, SD = 6.5, range = 18–45) and their 312 infants (54% female, mean gestational age = 39.3 weeks). Data were collected during home visits at 6, 12, 18, and 24 weeks, and during visits to the Arizona State University lab at 52, 78, and 104 weeks. Mothers were recruited from a hospital-based prenatal clinic that serves low-income and uninsured women from the surrounding community in the southwest United States. Eligibility criteria for mothers included: (1) self-identification as Mexican or Mexican American, (2) fluency in English or Spanish, (3) age 18 or older, (4) low-income status (family income below $25,000 or eligibility for Medicaid or Federal Emergency Services coverage for the birth), and (5) anticipated delivery of a singlet baby with no prenatal evidence of a serious health or developmental problem. One child was removed from analyses due to being born significantly preterm (26-weeks gestation). Three children whose mothers reported that they had been diagnosed with heart problems were removed from the sample for these analyses. One child became ineligible for the overall study due to early emergence of cognitive and regulatory deficits. Children with other health concerns which were not relevant to the current study (e.g., anemia) were retained in the sample for analyses; the removal of their data did not significantly affect the pattern or statistical significance of results.

2.2 | Retention

A planned missingness design was used to lower participant burden while retaining statistical power. All mother-infant dyads were assigned to complete the 6 week home visit, but each dyad was randomly assigned to complete 2 of the 3 remaining home visits. 312 dyads (100%) completed the 6 week visit, 205 dyads (95%) completed the 12 week visit, 210 dyads (93%) completed the 18 week visit, and 210 dyads (93%) completed the 24 week visit. The remaining visits were completed in the lab; 206 dyads (66%) completed the 52 week visit, 237 (76%) completed the 78 week visit, and 244 (78%) completed the 104 week visit.

2.3 | Measures

2.3.1 | Time

Time was measured in weeks since birth. The exact number of weeks when the visit was completed was used in data analyses, but visits are referred to by their targeted date of completion (e.g., 6-week visit, 12-week visit) in table, figures, and discussion of results for convenience. The time variable was centered at 6 weeks to aid in interpretation (i.e., the intercept at time = 0 refers to 6 weeks postpartum). Because analyses include data across 2 years (104 weeks), the time variable was divided by 10 to avoid non-convergence in estimation due to a large variance in the time variable, and small week to week changes in RSA. Thus, the results provide estimates of the change in RSA across 10-week periods in development.

2.3.2 | Respiratory sinus arrhythmia

Infant heart rate data were recorded across a 7 min baseline period at 256 Hz with electrocardiography (ECG) equipment from Forest Medical, LLC (Trillium 5000; East Syracuse, NY). During the home visits, infants were seated upright in a car seat, while during the lab visits, infants were seated on their mothers’ laps. Mothers were instructed to “relax quietly…without moving”. Electrodes were placed on infants’ left shoulder and right and left waist in a standard three-lead configuration. Electrodes were placed approximately 2–3 min prior the beginning of baseline data collection. The first 5 min of the 7 min baseline period were used.

Resting RSA (ln[ms²]) was calculated consistent with the Porges method (Porges, 1986), which quantifies RSA amplitude using age-specific parameters of breathing frequency. First, QRSTool software 1.2.2 (Allen, Chambers, & Towers, 2007) was used to process the ECG data and automatically identify R-waves in the ECG data. QRSTool and CardioEdit software (Brain-Body Center, 2007) were then used by trained coders to manually correct misidentified or unidentified R-waves, and obtain R-R time interval data and produce a time series of sequential heart periods. If sections of ECG data were not valid per commonly used guidelines (e.g., R-waves could not be identified at all or over 5% of beats required manual correction; Quintana, Alvarez, & Heathers, 2016), files were cropped to retain the valid sections of data in analyses. Files without at least two continuous minutes of valid HR data were not coded. Using CardioBatch software (Brain-Body Center, 2007), a moving polynomial filter was applied to the R-R time interval data to extract heart period variance in the frequency band of RSA (for infants, 0.3–1.3 Hz; Porges & Byrne, 1992; Riniolo & Porges, 1997). These heart period variances within the frequency band of RSA were then natural log-transformed to obtain a measure of the amplitude of RSA (in ln[ms²]), and a mean resting RSA value averaged from 30 s epochs across the 5-min baseline period was obtained for use in analyses.

2.3.3 | Covariates

Infant sex and gestational age were obtained from medical records at the birth hospital for consideration as statistical covariates.

2.4 | Data analytic plan

RSA data were analyzed using Mplus 7.4 (Muthén & Muthén, 1998), which allowed for multilevel modeling accounting for both between-infant variance in RSA as well as within-infant change in RSA over time. Full information maximum likelihood (FIML) estimation was used to handle missing data. Several increasingly complex growth curve models were fitted, in order to find a model that can best describe the pattern of RSA growth as infants develop over the first 2 years of life, and to assess whether there was between-infant variability in their RSA growth trajectories. Likelihood ratio chi-square tests were employed to compare different models and the test results are displayed in Table 1. Infant sex and gestational age were considered as covariates, but were nonsignificant, and so neither were included in the final analyses.

TABLE 1.

Likelihood ratio chi-square tests comparing models

	Unconditional model	Linear model with random intercept and fixed linear slope	Linear model with random intercept and random linear slope	Quadratic model with random intercept, random linear slope, and fixed quadratic slope	Quadratic model with random intercept, random linear slope, and random quadratic slope
Log likelihood	−2390.541	−1831.260	−1827.688	−1790.110	−1780.979
χ2		1118.562	7.144	75.156	18.262
df		1	2	1	3
P		<.001	.028	<.001	<.001

Each model except for the unconditional model is compared to the preceding model.

3 | RESULTS

3.1 | Demographics

The majority of mothers were born in Mexico (87%), primarily spoke Spanish (82%), were married or living with a partner (78%), and were low educated (59% had obtained less than a high school education, and 27% were high school graduates). The median family income was in the 15,000–25,000 dollars per year range.

3.2 | Preliminary analyses

Means and correlations for the infants’ heart rate and heart rate variability at each time point are displayed in Table 2. The average heart rate variability increased at each time point, ranging from a mean of 2.51 (SD = 0.97) at the 6- week visit, to a mean of 6.23 (SD = 1.12) at the 104-week visit. Means and standard deviations of RSA at the 6-and 12- month visits were comparable to those obtained among low-income Latino infants in previous research (3.11 [0.85] vs. 3.32 [0.82] at 6 months, and 3.66 [0.95] vs. 3.74 [0.93] at 12 months; Alkon et al., 2011).

TABLE 2.

Variable descriptives and correlations

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
1. Infant sex (54% female)
2. Infant gest. age	0.04
3. Infant RSA, 6 weeks	−0.02	−.01
4. Infant RSA, 12 weeks	0.08	−.07	.30**
5. Infant RSA, 18 weeks	−.13	−.10	.21”	.30**
6. Infant RSA, 24 weeks	−.13	−.01	.24”	.30**	.51**
7. Infant RSA, 12 months	.01	.04	.15	.37**	.31**	.38**
8. Infant RSA, 18 months	.05	.07	.14	.06	.13	.37**	.49**
9. Infant RSA, 24 months	.03	.01	−.01	.07	.19*	−.13	.05	.04
10. Infant HR, 6 weeks	−.08	.01	−.50**	.01	.08	−.15	.11	−.05	.01
11. Infant HR, 12 weeks	−.10	−.03	−.18*	−.73**	−.06	−.17	−.28*	−.04	−.09	.11
12. Infant HR 18 weeks	.04	.12	−.08	−.01	−.62**	−.13	−.10	−.11	−.11	.13	.17
13. Infant HR, 24 weeks	.06	−.08	−.10	−.03	−.26*	−.55**	−.10	−.18	.11	.13	.17	.20
14. Infant HR, 12 months	.02	−.03	−.08	−.23	−.17	−.17	−.73**	−.13	.04	−.11	.24*	.28**	.18
15. Infant HR, 18 months	.02	−.15	−.01	−.07	.11	−.20*	−.40*	−.62**	−.06	−.03	.26*	−.01	.30**	.36**
16. Infant HR, 24 months	.14	.05	−.02	.07	−.09	−.35**	−.08	−.16	−.21*	.03	.12	−.03	.25*	.07	.14	1.0
Mean / (SD)		39.34 (1.17)	2.50 (0.97)	2.81 (1.00)	2.86 (0.94)	3.10 (0.85)	3.66 (0.95)	4.25 (0.98)	6.23 (1.12)	157.5 (17.2)	150.6 (17.9)	153.2 (16.0)	146.7 (12.1)	132.3 (2.09)	124.2 (11.9)	116.1 (13.4)

“HR” = heart rate; “Gest. age” = gestational age.

^*p < .05.

^**p<.01.

3.3 | Primary analyses

We began by fitting an unconditional model, or a random ANOVA model, to calculate the intraclass correlation coefficient (ICC). In an unconditional model, the total variability in infants’ RSA decomposes into two parts: variation due to between-person differences and variation due to within-person change. A higher ICC indicates that more variability is attributable to individual differences rather than change over time within infants. Therefore, the ICC tells us whether the independence assumption of traditional statistical analyses is satisfied or not. Many traditional statistical analyses including linear regression and ANOVA require the independence assumption be met. The independence assumption indicates that each observation is not related to any other observations in the data set. In other words, observations belonging to the same person are no more similar than observations belonging to different persons. The ICC value of 0 indicates that the independence assumption is satisfied, and that traditional statistical analyses assuming independence can be used. However, when the independence assumption is not met, that is, observations belonging to the same person are more similar than observations belonging to different persons, the ICC is greater than 0. In such cases, using traditional statistical analyses assuming independence can lead to an elevated type I error rate, and multilevel models (or mixed-effects models) are needed to obtain more accurate results (Raudenbush & Bryk, 2002; Snijders & Bosker, 2012).

The obtained ICC for our data was 0.005 meaning that only 0.5% of the total variation in infants’ RSA is due to between-person differences. Even though the ICC value was relatively small compared to typical ICC values ranging .2–.4 observed in intensive longitudinal studies (Bolger & Laurenceau, 2013, p.30), we decided to use multilevel modeling to take into account the nested structure of our data (observations are nested within infants, and thus observations belonging to the same infant can be more similar than observations belonging to different infants) and potential increase in type I error rate.

We fitted the following four models as well as the unconditional model: (a) linear growth curve model with random intercept and fixed linear slope, (b) linear growth curve model with random intercept and random linear slope, (c) quadratic growth curve model with random intercept, random linear slope and fixed quadratic slope, and (d) quadratic growth curve model with random intercept, random linear slope, and random quadratic slope.

We first fitted the model (a) that assumes the RSA linearly increases (or decreases) over time in such a way that the RSA at the starting time (6 weeks postpartum) varies across infants but the growth rate is the same for all infants. The model (a) was significantly better than the unconditional model (χ²(1) = 1118.562, p < .001), indicating that the RSA trajectories significantly change over time. Then we fitted the model (b) that assumes the RSA linearly increases (or decreases) over time in such a way that the RSA at the starting time (6 weeks postpartum) varies across infants and the growth rate also varies across infants. The model (b) was significantly better than the model (a) (χ²(2) = 7.144, p = .028) indicating that the RSA growth rate significantly varies across infants. Then we fitted the model (c) in which the RSA is assumed to change quadratically over time in such a way that the RSA at the starting time (6 weeks postpartum) and the linear growth rate vary across infants but the quadratic slope is the same for all infants. Model (c) was significantly better than the model (b) (χ²(1) = 75.156, p < .001) indicating that the RSA growth accelerates over time. Finally, we fitted the model (d) that assumes the RSA changes quadratically over time, and all growth parameters including the RSA at the starting time (6 weeks postpartum), the linear slope, and the quadratic slope vary across infants. The model (d) was significantly better than the model (c) (χ²(3) = 18.262, p < .001) meaning that the growth acceleration significantly varies across infants as well.

Based on the likelihood ratio tests, the best-fitting model was model (d), in which the intercept and both the linear, and quadratic slopes vary across individuals. See Table 3 for parameter estimates from the final quadratic growth model. On average, infant’s resting RSA was 2.698 at 6 weeks of age. On average, the linear slope, or initial rate of change in infants’ resting RSA (at age of week 6) was .069 per 10 weeks. The estimated mean quadratic slope was .026, indicating that the rate of change increased by .026 every 10 weeks, on average. That is, in general infants’ resting RSA increased slowly early in the postpartum period, but increased more quickly as time went on. See Figure 1 for the average trajectory of infants’ resting RSA across the first two postpartum years.

TABLE 3.

Estimated fixed effects and variance components in the final quadratic growth model for infant’s resting RSA

Parameter	Estimate	Est/S.E.	p-value
Residual variance	0.673	16.630	<.001
Mean intercept	2.698	55.419	<.001
Mean linear slope	0.069	2.208	.027
Mean quadratic slope	.026	7.924	<.001
Intercept variance	.267	4.307	<.001
Linear slope variance	.059	2.379	.017
Quadratic slope variance	.001	2.890	.004
Intercept/linear slope covariance	−.039	−1.225	.220
Intercept/quadratic slope covariance	.002	0.794	.427
Linear slope/quadratic slope covariance	−.007	−2.588	.010

FIGURE 1.

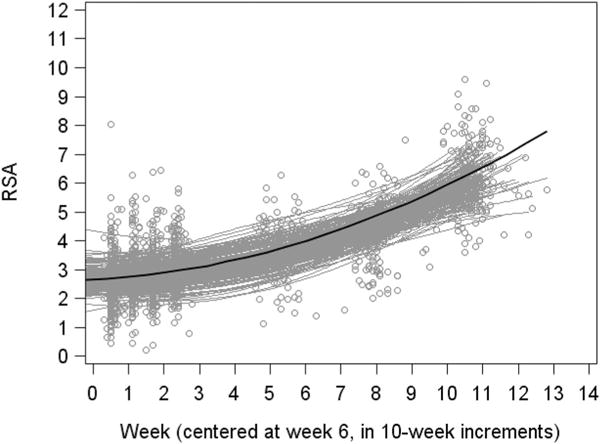
Change in infant resting RSA from 6 weeks to 2 years.

Note. Gray circles indicate individual data points. Gray curves indicate individuals’ predicted quadratic curves. Black curve is the predicted mean quadratic curve, plotted at the mean on gestational age

The parameters assessed in the final model also indicated that there was significant variance across infants in the initial resting RSA value at 6 weeks postpartum (estimate = 0.267, p < .001), as well as in the slope of resting RSA change (estimate = .061, p = .015), and in terms of acceleration of resting RSA change across the postpartum period (estimate =.001, p = .004). The slope of resting RSA change and acceleration of resting RSA change across the postpartum period significantly covaried (estimate = −.007, p = .010), such that those with a flatter initial rate of change accelerated at a higher rate. See Figure 1 for display of estimated individual trajectories of RSA.

4 | DISCUSSION

Using data from Las Madres Nuevas, a longitudinal study of low-income Mexican-origin mothers and their infants, the current study modeled changes in infant resting RSA over the first 2 years of life. In line with hypotheses, infant resting RSA was found to increase across the postpartum period, and change accelerated over time, best described by a quadratic model. Significant variability was evident in both infant resting RSA levels at 6 weeks, as well as in the pattern of change in infant resting RSA over the first 2 years of life. The results suggest that, across the first 2 years of life, development of the physiological capacity to regulate emotions starts to develop and grow slowly, followed by an accelerating increase. The developmental process of change in infant resting RSA, however, appears to differ across individuals, with some infants starting with a higher capacity, and developing at a faster rate than others, even after statistically adjusting for gestational age.

Interestingly, there was little intra-class correlation among different resting RSA measures among the infants in our sample. In contrast, previous work has found positive weak correlations among measures of resting RSA from 6 to 60 months of age (Alkon et al., 2011). Although the age range captured by Alkon et al. (2011) occurs later in development than the range in the current study, limiting direct comparison, this discrepancy in ICC may imply that stronger intra-class correlations can be found later in development. It may also be the case that unique features of the current sample (e.g., economic instability, housing changes) may be contributing to lower intra-class correlation among different resting RSA measures than found in other studies. Future work identifying the age range at which resting RSA measures become stable, as well as predictors of stability, and age at which resting RSA becomes stable, would help to further understand how infants gain the consistent physiological capacity to regulate their emotions. Additionally, future research using measures of RSA to predict psychological outcomes should carefully consider the influence of development and age at the time of RSA collection in study planning and interpretations of results.

The current study has a number of strengths and provides an expansion on previous cross-sectional studies and longitudinal studies conducted later in infancy and childhood. The study focuses on a high-risk sample which has been understudied in research on early physiological development, but which could benefit greatly from effective, and targeted intervention efforts. However, there are limitations to the conclusions that can be drawn from the results. All infants had mothers who were of low socioeconomic status, and as such can be considered “high-risk”. As this sample did not include high socioeconomic status, “low risk” infants, the results should not be generalized across risk group status. Future work should examine how risk may differentially impact developmental trajectories of RSA. Furthermore, all infants had mothers who identified as Mexican-origin. Some studies have suggested ethnic differences in infant RSA (Propper et al., 2008), and the results might not be generalizable to other ethnic groups. In addition, the current study focused on resting RSA; results may differ when RSA is assessed during exposure to a stimulus or in different states of arousal. Assessing developmental change in reactive RSA would complement the current findings and provide a fuller picture of development of emotional regulation ability.

Additional factors, not assessed in the current study, may also influence the rate of development of RSA. Evaluation of the influence of hereditary factors, prenatal exposures, or postnatal environmental factors such as parenting quality, could highlight individual differences in the development of resting RSA among low-income Mexican American infants (e.g., Alkon et al., 2011). For example, previous work has shown that more positive maternal responsivity predicts a steeper RSA trajectory from 1 to 5 years of age among Mexican American infants (Johnson et al., 2017). Future work should also extend the current findings by assessing developmental changes in resting RSA alongside cognitive and behavioral correlates (e.g., social competence) in order to better understand emotional development.

The current study characterizes longitudinal change in infant resting RSA from 6 weeks to 2 years of age among low-income Mexican American infants. Resting RSA became increasingly higher across the first 2 years of life, and growth accelerated over time fitting a quadratic model, potentially indicating growth in the development of physiological capacity to regulate one’s emotions. Variability was evident between infants in both initial levels of resting RSA, as well as growth, and acceleration over time. However, we found little intra-class correlation among infants’ RSA measurements at differing time points. Although future research is needed to identify predictors of patterns of RSA development, knowledge from the current study will inform further research on the development of co- and self-regulatory ability, as well as inform efforts to promote wellbeing among this high-risk population.