Deep-Earth reactor: Nuclear fission, helium, and the geomagnetic field

Abstract

Geomagnetic field reversals and changes in intensity are understandable from an energy standpoint as natural consequences of intermittent and/or variable nuclear fission chain reactions deep within the Earth. Moreover, deep-Earth production of helium, having ³He/⁴He ratios within the range observed from deep-mantle sources, is demonstrated to be a consequence of nuclear fission. Numerical simulations of a planetary-scale geo-reactor were made by using the SCALE sequence of codes. The results clearly demonstrate that such a geo-reactor (i) would function as a fast-neutron fuel breeder reactor; (ii) could, under appropriate conditions, operate over the entire period of geologic time; and (iii) would function in such a manner as to yield variable and/or intermittent output power.

The geomagnetic field is evidence of a powerful energy source at or near the center of the Earth. Traditional geophysical models of energy sources for the geomagnetic field invoke the decay energy of naturally occurring long-lived radionuclides (mainly U, Th, ⁴⁰K) or are based upon the assumed ongoing growth of the inner core by cooling, presumably releasing gravitational potential energy and latent heat of crystallization (1). These energy sources, however, generally are capable of changing only gradually and in only one direction over time. The Earth's magnetic field, by contrast, varies in intensity and reverses polarity frequently (2), but quite irregularly, with an average interval between reversals of about 200,000 years. Lacking a variable and/or intermittent energy source, geophysicists have for decades hypothesized geomagnetic reversals as arising solely from geo-dynamo instabilities (3).

Variations in the Earth's magnetic field, however, are readily understandable strictly from an energy standpoint given the presence of naturally varying self-sustaining nuclear fission chain reactions occurring deep within the Earth (4–6). Indeed, the variable and/or intermittent energy output of a deep-Earth nuclear reactor, serving as the major energy source for geomagnetic field production, will inevitably lead to variations in the Earth's magnetic field whether the geomagnetic field arises from a self-excited dynamo mechanism, as widely believed, or from some other yet unknown mechanism.

Nuclear fission chain reactions occur in nature. In 1972, scientists at the French Atomic Energy Establishment at Pierrelatte discovered the nearly intact remains of a natural nuclear fission reactor in a 0.5-m-thick seam of uranium ore located at Oklo, in the Republic of Gabon (7). Subsequently, other reactor zones were discovered in the region and appear to have functioned as self-sustained nuclear fission reactors about 1,800 million years ago (8).

At the time that the Oklo reactor was active, the proportion of ²³⁵U in natural uranium was sufficiently great for nuclear fission chain reactions to occur in a thick mass of natural uranium ore. In addition to functioning as a thermal neutron reactor moderated by ground water, the Oklo reactor also functioned as a fast-neutron breeder reactor, producing additional fissile material in the form of plutonium and other transuranic elements (9).

In setting forth the fundamental concepts and underlying basis for planetary-scale nuclear fission reactors, Herndon (4–6, 10) recognized that fuel breeding was necessary for reactor functioning over the most recent 2,000 million years. From evidence of fuel breeding in the Oklo reactor, fuel breeding was assumed possible for planetary-scale reactors, but it was not demonstrated quantitatively in previous publications. This communication presents the results of calculations made by using the SCALE code sequence for nuclear reactor fuel-depletion studies (11). These calculations demonstrate quantitatively that, under appropriate conditions, a planetary-scale nuclear fission reactor can operate throughout the entire period of geologic time as a fast-neutron breeder reactor. Moreover, the calculations show that production of helium with ³He/⁴He ratios within the range observed from deep-mantle sources is an expected consequence of deep-Earth nuclear fission.

Background

Knowledge of the structure and physical states of the interior regions of the Earth is derived mainly from seismic data augmented by moment-of-inertia considerations. The chemical compositions of those regions, however, are primarily obtained as implications from meteorite data. The Earth's fluid core comprises 30.8% of the mass of the Earth and is thought to consist of iron and one or more light elements, such as sulfur. A small, apparently solid object, about the size of the moon and three times its mass, called the inner core, comprises 1.65% of the mass of the Earth and resides at the center. The composition of the inner core is inextricably connected to ideas as to the energy source that powers the geomagnetic field as described below.

Four years after Lehmann (12) discovered the inner core in 1936, Birch (13) considered the abundances of the elements in coming to the idea that the inner core is partially crystallized iron metal. Birch realized, from the relative abundances of the elements, that the sum of all elements heavier than nickel and iron would not be enough to comprise a mass as great as the inner core, and one would not expect a pure nickel inner core because nickel and iron, Birch thought, are invariably alloyed in meteorites. Birch could not possibly have known that the presence of silicon in the nickel–iron alloy can lead to the precipitation of nickel silicide. Meteoritic nickel silicide (a compound of nickel and silicon found in enstatite meteorites) was not discovered until the 1960s. In 1979, Herndon (14) suggested that the inner core is not iron metal but nickel silicide.

In the Birch view of the inner core, which has been widely discussed for six decades, one must assume that the boundary of the inner core is maintained at the melting point of iron at the respective pressure throughout most of the time that the Earth has existed, and, during the same period, the inner core has consistently grown so as to energize a geomagnetic field powered by the latent heat of fusion of iron metal. Such a situation would seem to demand tight thermodynamic constraints.

Birch's idea about the composition of the inner core was based on observations of ordinary chondrites and iron meteorites. Those meteorites are sufficiently oxidized, as indicated by the FeO content of their silicates or silicate inclusions, to preclude the occurrence of appreciable amounts of uranium in an Earth core of similar composition. However, suggestions have been made that the deep interior of the Earth is similar to the matter of certain rare, highly reduced, enstatite chondrite meteorites (15–17). Of the various chondritic meteorites, only the enstatite chondrites have oxygen isotopic compositions indistinguishable from the Earth (18).

There are reasons to associate the highly reduced matter of enstatite chondrites with the inner regions of the solar system and with the Earth. E-type asteroids (based on reflectance spectra, polarization, and albedo), the presumed source of enstatite meteorites, are radially from the sun, the innermost of the asteroids (19). The regolith of the planet Mercury, from reflectance spectroscopic investigations, appears to be highly reduced, essentially devoid of FeO—like the silicates of certain enstatite chondrites, such as the Abee meteorite (20). Moreover, the relative mass of the Earth's core is consistent with the Earth having been derived from highly reduced matter like that of certain enstatite chondrites (4, 17). Likewise, the constituents of the Earth's core, specifically the inner core and the “islands” of matter at the core boundary (21), are understandable in a causally related manner as precipitates from a highly reduced core gravitationally differentiated from enstatite-chondrite-like matter (14, 22). Because of the highly reduced state of oxidation of the Abee meteorite, only part of its uranium is lithophile. Much of the uranium and some thorium occur in the alloy portion (4) of the Abee meteorite that corresponds to the Earth's core (23).

In the Herndon view of the inner core, a fully crystallized inner core of nickel silicide would have precisely the mass measured for the inner core. It is not necessary to postulate a growing inner core, because, if the core of the Earth is like the alloy portion of certain highly reduced enstatite chondrites, major proportions of uranium and, presumably, thorium will exist within the Earth's core; high-temperature precipitation and gravitationally driven accumulation will inevitably lead to a fissionable mass. The geochemical and geophysical basis for uranium and thorium occurring in the Earth's core precipitating and accumulating at the planet's center has been discussed in detail in previous communications (4–6) and is mentioned here only briefly for background reference.

At the pressures that prevail in the Earth's core, density is a function almost exclusively of atomic mass and atomic number. Uranium, thorium, and other actinides, being high-temperature precipitates and the densest substances, by the action of gravity, would tend to concentrate, possibly scavenged by other precipitates, ultimately forming a fissionable, critical mass (4–6). The same mechanism for concentrating the actinides (i.e., gravitational separation by density at high pressure) should cause the lighter fission products to separate from the heavier actinides, thus helping to maintain a nuclear-reactor-critical configuration.

The frequent, but irregular, variability in intensity and direction of the Earth's magnetic field may be understandable from a fissionogenic energy-production standpoint—a consequence of fission-product accumulation with concomitant nuclear fuel dilution and the subsequent gravitationally driven fission product separation with nuclear fuel reconcentration. Unlike other globally significant energy sources, nuclear reactor output can be variable or intermittent, depending on changes in composition and/or the position of fuel, moderators, and neutron absorbers. For example, one might imagine instances in which the rate of production of fission products exceeds their rate of removal by gravitationally driven diffusion. In such an instance, the power output of the geo-reactor would decrease and the reactor might eventually shut down, thereby diminishing and ultimately shutting down the Earth's magnetic field. As the fission products diffuse out of the reactor region to a region of lower density and the actinide fuel diffuses inward, the reactor restarts. As the reactor increases in power, the geomagnetic field reestablishes itself, either in the same direction or in the reverse direction.

Analytical Methodology

Calculations were made using the SAS2 analysis sequence contained in the SCALE Code Package from Oak Ridge National Laboratory (11). SAS2 is used primarily for calculating the time-dependent isotopic inventories in nuclear power reactor fuel as a function of reactor power history. SAS2 invokes the ORIGEN-S isotopic generation and depletion code to calculate concentrations of actinides, fission products, and activation products simultaneously generated through fission, neutron absorption, and radioactive decay. SAS2 performs the one-dimensional transport analyses at selected time intervals, calculating an energy flux spectrum, updating the time-dependent weighted cross-sections for the depletion analysis, and calculating the neutron multiplication of the system.

SAS2 is widely used throughout the nuclear industry to calculate reactor fuel end-of-life fuel isotopic compositions and radiological decay properties for use in fuel design, spent fuel cask design, and nuclear accident analyses. The code has been extensively validated against analyses of isotopic assay measurements for commercial reactor fuels (24–28).

Although SAS2 was designed primarily to characterize the spent fuel inventories for a wide variety of reactor types, the code is sufficiently general to allow simulations of many nuclear systems provided they can be accurately represented with a one-dimensional transport model. Because of its simple (spherical one region) geometry, it is possible to represent the main neutronic features of a planetary-scale geo-reactor by using SAS2.

For the calculations performed in this paper, the initial material compositions and abundances are contained in Table 1. Three separate calculations were performed to more clearly understand the reactor behavior under different conditions. In the first calculation, the fission power was assumed to be zero. This represents the case where no fission occurs. In the second calculation, the fission power was a constant 3 Terra-watts (TW; 1 TW = 10¹² W), but fission products were removed from the system at the end of each time step. This represents the case with a steady-state fission power and fission products migrating out of the reactor region. In the third calculation, the fission power was a constant 3 TW and the fission products remained in the system. This represents the case with a steady-state fission power and no migration of fission products.

Table 1.

Initial values of the deep-Earth reactor

Isotope	Initial mass, g	Initial density, g/cm3	Relative atom abundances
235U	4.867  × 1018	8.568	0.233
238U	1.606  × 1019	28.272	0.767
Uranium	2.0927  × 1019	36.84	1.0

Values are those used as input to SAS2. Initial volume of the uranium is 5.6807 × 10¹⁷ cm³. Steady-state fission power: 3.0 TW (3.0 × 10¹⁹ ergs/s). The uranium values are taken from Herndon (4), based on the uranium concentration of the alloy portion of the Abee enstatite chondrite, corresponding to the Earth's core, multiplied by Earth core mass. The uranium density is from equation of state calculations (4). 

Results and Discussion

Terrestrial heat flow is about 45 TW. Geophysicists believe that not more than about 10 to 11 TW comes from the core, and most geophysicists are more comfortable with a figure of about 4 or 5 TW. Part of the core's heat flow is thought to represent power dissipated by the geo-dynamo that is thought to produce the geomagnetic field (1).

The uranium fission geo-reactor simulation discussed in the present paper was constrained to operate at a constant power level of 3 TW. Additional heat production from the natural radioactive decay of ²³⁵U and ²³⁸U would increase the power level at the time of Earth formation to 4.3 TW, decreasing over time to a present-day level of 3.5 TW. The power level adopted for the simulation was chosen to permit continuous reactor operation over the entire lifetime of the Earth without prematurely consuming all of the actinide fuel. Had thorium been included, those power levels might have been as much as about three times as great.

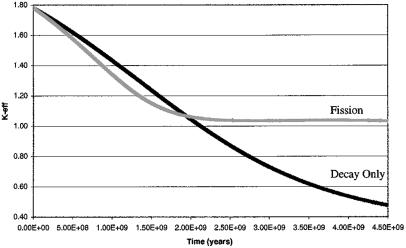
From nuclear reactor theory (29), the defining condition for self-sustaining nuclear fission chain reactions is that k_eff = 1.0. The value of k_eff represents the number of fission neutrons in the current population over the number of fission neutrons in the previous population. If k_eff > 1.0, the neutron population and energy output are increasing and will continue to increase until geometry and material effects cause k_eff to decrease to 1.0. If k_eff < 1.0, the neutron population and energy output are decreasing and will eventually decrease to zero. If k_eff = 1.0, the neutron population and energy output are constant.

The curves in Fig. 1 [k_eff vs. time] show the calculated values of k_eff over the entire period of geologic time as obtained from the geo-reactor numerical simulation with and without (Decay Only) fission power, made by using parameters set forth in Table 1. The curve labeled Fission shows how the k_eff of the system varies over time as a result of fission at a steady-state power of 3 TW, natural radioactive decay, and continuous removal of fission products. Obviously, k_eff could not remain over 1.0 for the last 4.5 billion years. A more complex model involving a mechanism for fission product removal, which would allow the k_eff of the system to fluctuate, is discussed below. The curve labeled Decay Only, which is presented for reference purposes, shows how in the absence of fission, the k_eff of the system would vary solely as a result of natural radioactive decay. The Decay Only curve, which strictly speaking is only applicable for a noncritical mass, nevertheless illustrates that if fission has not occurred before about 2 billion years ago, fission will never occur. Given the parameters of this simulation, the Fission curve in Fig. 1 shows that a self-sustaining chain reaction could have existed over the ≈4.5-billion-year life of the Earth.

Figure 1.

The effective multiplication constant, k_eff, for the geo-reactor simulation as a function of time for two different fission power levels. For the curve labeled Fission, starting with the initial isotopes and fission power listed in Table 1, the isotopes in the simulation change because of fission and radioactive decay. For the curve labeled Decay Only, starting with the initial isotopes listed in Table 1, the isotopes in the simulation change because of natural radioactive decay only; fission power is zero. A critical system is present when k_eff = 1.00.

The reason a self-sustaining chain reaction is possible throughout the entire period of geologic time is that ²³⁵U, ²³⁹Pu, and other higher order fissile actinides are produced from ²³⁸U as follows. When ²³⁸U absorbs a neutron, it eventually transmutes to ²³⁹Pu, which is a fissile nuclide. The ²³⁹Pu fissions, decays to ²³⁵U, or absorbs a neutron, forming a higher-mass actinide, which is also fissile. In a long-lived breeding fission reactor, the majority of ²³⁸U is converted to fissile actinides that help sustain the self-sustained chain reaction.

In a neutron flux, ²³⁵U, which is referred to as a fissile nuclide, absorbs neutrons and either fissions or forms ²³⁶U. Fission produces energy and additional neutrons that cause more fission. The ²³⁶U that is formed decays to ²³²Th, which has characteristics similar to those of ²³⁸U in a fission reactor. When ²³²Th absorbs a neutron, it is eventually converted to ²³³U, which also can fission. The neutrons that are not absorbed by ²³⁵U are either absorbed by another isotope or leak from the system. The geo-reactor system is so large that only an insignificantly small percentage of neutrons leak from the system. Table 2 contains the mass of selected actinides at the initial time (reactor startup), 1.5 billion years, 3.0 billion years, and 4.5 billion years (the present). As shown in Fig. 1 and Table 2, the presence of the neutron flux produced by fission enables sufficient fuel to breed through actinide transmutation to sustain the nuclear fission chain reaction.

Table 2.

Selected isotope mass existing at specified time

Isotope	Initial mass, g	Mass at 1.5 × 109 years, g	Mass at 3.0 × 109 years, g	Mass at 4.5 × 109 years, g
230Th	0.0	1.896  × 1014	1.160  × 1014	6.157  × 1013
232Th	0.0	2.392  × 1017	3.664  × 1017	3.896  × 1017
231Pa	0.0	4.048  × 1013	2.100  × 1013	1.277  × 1013
233Pa	0.0	4.696  × 106	1.039  × 107	1.581  × 107
232U	0.0	4.339  × 106	3.966  × 106	3.641  × 106
233U	0.0	1.011  × 1013	2.237  × 1013	3.403  × 1013
234U	0.0	6.209  × 1014	3.798  × 1014	2.015  × 1014
235U	4.867 × 1018	8.844  × 1017	4.585  × 1017	2.782  × 1017
236U	0.0	5.940  × 1015	5.312  × 1015	4.941  × 1015
237U	0.0	3.339  × 105	3.533  × 105	3.283  × 105
238U	1.606  × 1019	1.148  × 1019	7.024  × 1018	3.726  × 1018
237Np	0.0	3.855  × 1013	4.032  × 1013	3.911  × 1013
238Pu	0.0	2.338  × 106	4.303  × 106	6.296  × 106
239Pu	0.0	3.969  × 1013	4.288  × 1013	3.498  × 1013
240Pu	0.0	4.937  × 107	9.399  × 107	1.154  × 108
241Pu	0.0	1.792  × 10−1	5.986  × 10−1	1.111  × 100
241Am	0.0	5.402  × 100	1.805  × 101	3.348  × 101

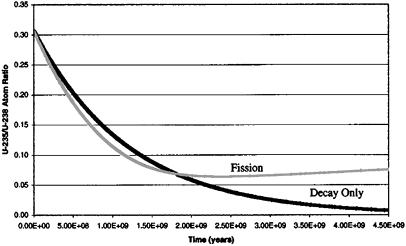
Fig. 2 shows the ²³⁵U/²³⁸U ratio during the lifetime for two geo-reactor numerical simulations. The curve labeled Decay Only represents the ²³⁵U/²³⁸U ratio of a natural, noncritical (i.e., non-fissioning, radioactive decay only) mass of uranium and is shown for reference purposes. The other curve, labeled “Fission,” represents the ²³⁵U/²³⁸U ratio for the initial conditions stated in Table 1, with fission products continuously removed. In the constant-power level geo-reactor simulation, fast neutron fission and fuel breeding reactions keep the ²³⁵U/²³⁸U ratio nearly constant after 1.5 billion years and appropriate for critical reactor operation. By contrast, in the absence of fission and breeding, radioactive decay alone decreases the ²³⁵U/²³⁸U ratio to such a point that the natural initiation of nuclear chain reactions for natural uranium in recent geologic times is impossible.

Figure 2.

The ²³⁵U/²³⁸U atom ratio as a function of time for the geo-reactor simulation as indicated by the curve labeled Fission. Note that fuel breeding causes the ²³⁵U/²³⁸U ratio to be maintained at essentially a constant level, rather than decreasing because of natural radioactive decay, as indicated for the Decay Only reference case.

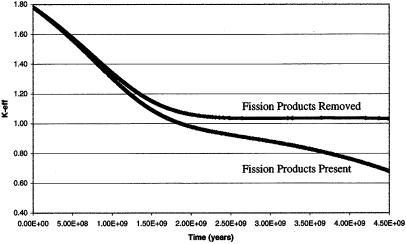
Fig. 3 shows the ²³⁵U/²³⁸U ratio during the lifetime for two geo-reactor numerical simulations for the initial conditions stated in Table 1. The curve labeled Fission Products Removed presents the system k_eff with fission products removed. The other curve, labeled Fission Products Present, represents the same system with fission products remaining in the reactor. This figure indicates the necessity for some fission product removal mechanism in order for the geo-reactor to operate over the life of the Earth. The fission process itself provides a natural mechanism for removing fission products through gravitational separation by converting dense actinide fuel to fission products that are on average about 60% as dense as uranium. The natural process for generating and removing fission products represents the controlling mechanism that could alternately shut down and start up the reactor.

Figure 3.

The effective multiplication constant, k_eff, as a function of time for two geo-reactor simulations, one with fission products instantaneously removed and the other with fission products remaining in place. Criticality is indicated by the line at k_eff = 1.00. Note that the accumulation of fission products can shut down the chain reaction and that their removal could restart the geo-reactor.

The rate that the ²³⁵U burns and fission products are produced is a function of the initial ²³⁵U/²³⁸U ratio, the power density (power/total uranium mass), and the fission product removal rate. The system power is a function of power density and total uranium mass. The initial uranium mass is only needed to determine the system power or total output energy. For the geo-reactor simulation, the initial fuel consisted solely of uranium. Had thorium been included, the results would have been substantially the same, except that the reactor could have operated for a longer time or at a higher power density, producing a larger total output energy.

The geo-reactor numerical simulation, although based on the specific parameters shown in Table 1, is nevertheless sufficiently general with respect to nuclear reactivity to have validity. In the absence of historical data, particularly power output data, the specification of constant fission power generation is taken as a reasonably objective alternative to different assumed choices that might otherwise seem to tailor results to predetermined objectives. In reality, one might expect nuclear reactions to be neither homogeneous throughout the entire reactor nor uniform in output over time. Far more potential variations exist than can reasonably be modeled within the framework of the present investigation.

The lower curve in Fig. 3, labeled Fission Products Present, is calculated with all fission products retained. Notably, according to the numerical simulation, during the first 1.5 billion years after the formation of the Earth, accumulation of fission products alone would not shut down the reactor by making k_eff ≤ 1. Other material, geometric, or neutronic effects not considered in the simplified models present in this paper could still shut down the reactor during the first 1.5 billion years. One might speculate, however, that the frequency of nuclear-reactor-induced geomagnetic field reversals might be less than the frequency during the most recent 2.5 billion years of geologic time. Current paleomagnetic data on the most ancient rocks, all of which are extensively altered, are too imprecise to serve as a guide.

An independent verification of the presence of fission deep inside the Earth would be the detection of fission and decay products from sources deep inside the Earth. The density gradient deep inside the Earth would cause light elements to migrate out of the core. Helium, being the second lightest element and a noble gas, would be the most likely of these elements to be detected at the surface.

An actinide nucleus typically splits into two fragments when it fissions. But once in approximately every 10⁴ binary fission events, an actinide nucleus splits into three fragments. Tritium, ³H, is a major ternary fission product that beta decays with a 12.32-year half-life to form ³He. ⁴He, by contrast, is produced, not by fission, but through the natural radioactive decay of actinides (and their daughters) to isotopes of lead.

³H has a very low neutron-absorption cross-section and therefore is relatively unaffected by the neutron flux of the reactor zone. ³He, on the other hand, has a high neutron-absorption cross-section and, if formed within the neutron flux field of the reactor zone, will readily absorb a neutron, transforming to ⁴He. Hydrogen is an extremely mobile element and the least-dense substance within the geo-reactor. With the relatively long half-life of 12.32 years, one might reasonably expect a large fraction of the ³H to migrate several km to escape the reactor zone. Outside the neutron flux field of the reactor zone, ³H will beta decay to form stable ³He. In the absence of a detailed structure of the reactor zone and relevant diffusion coefficients, the numerical simulation was calculated under the assumption that all ³H escapes the reactor zone before it beta decays to ³He.

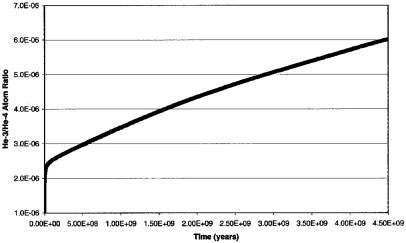
Fig. 4 shows the cumulative ³He/⁴He atom ratio as a function of time for the reactor simulation, with the initial conditions stated in Table 1 and with fission products removed. In this constant-power density case, production of the ³H progenitor of ³He is constant over time, whereas ⁴He production decreases over time because of actinide depletion by natural radioactive decay and by fission. Under the simulation conditions, the instantaneous ³He/⁴He ratio varied from just above the value for the Earth's atmosphere (1.37 × 10⁻⁶) to 6.7 times that value. These values should not be considered as limits. Generally, the relative production of ³He and ⁴He depends on the reactor power-to-actinide ratio; the higher the power-to-actinide ratio, the higher the ³He/⁴He ratio being produced.

Figure 4.

Cumulative ³He/⁴He atom ratio as a function of time for the geo-reactor simulation of the occurrence of fission and the removal of fission products. The instantaneous ratio at present is about 6.7 times the atmospheric ratio. The values shown are for this simulation and are not limits. Generally, the ³He/⁴He atom ratio depends on the reactor-power-to-actinide ratio.

Deep-mantle magma sources [e.g., Hawaiian volcanic lavas (30)] have ³He/⁴He ratios in excess of the atmospheric ratio, by a large factor, sometimes as great as 34. Lacking a viable production mechanism, scientists attribute the observed ³He from deep-mantle sources to be from helium trapped at the time of Earth formation some 4.5 billion years ago. Most elements are produced by fission. Light elements that could migrate out of the Earth's core are of special interest. Regrettably, fission yield data for neon isotopes, the next lightest noble gas, were not available for the present investigation.

Beryllium is produced by nuclear fission with a ¹⁰Be/⁹Be ratio of 6. One might speculate on the possibility of beryllium escaping the geo-reactor zone and the Earth's core (because of its low atomic number and low atomic weight) and finding transport in some volcanic system to the Earth's surface. ¹⁰Be has a half-life of only 1.5 × 10⁶ years, which may possibly be too short for transport from the inner core to the Earth's surface. ¹⁰Be should, nevertheless, be sought in deep-mantle magma sources as a possible ¹⁰Be/⁹Be dating method for deep-Earth-to-surface transport time.

Conclusions

A steady-state, planetary-scale reactor, continuously operating throughout geologic time, was maintained in the numerical simulation through the instantaneous removal of fission products. In a reactor deep inside the Earth, one would expect fission products, having an average density about 60% that of actinides, to diffuse radially outward as the fuel reconcentrates radially inward because of gravity. Variable and/or intermittent reactor operation would be the natural and expected consequence. Nuclear fission reactor variability, we suggest, is evidenced by the observed reversals of direction and changes in intensity of the geomagnetic field (2). Preliminary results suggest that, during the first 1.5 billion years after the formation of the Earth, geomagnetic reversals might have been less prevalent than in recent times. Clearly, further investigations, both nuclear and paleomagnetic, are necessary for a more precise characterization.

Nuclear fission, as shown in the present paper, provides a viable mechanism for the deep-Earth production of ³He, rather than the assumed origin from a yet non-degassed part of the Earth. The helium observed in such geological samples, the authors suggest, may be evidence of deep-Earth nuclear fission. The absence of cross-section data for neon, the next lightest noble gas, precluded calculating fission and decay yields for this element. Comparison of calculated and measured results for neon may provide further evidence. Detection of ¹⁰Be in rock originating from deep-mantle magma would provide strong evidence of deep-Earth nuclear fission because of its relatively short half-life and the fact that the only other significant mechanism for ¹⁰Be production takes place in the upper atmosphere.

In terms of energy production, a nuclear fission geo-reactor is clearly an acceptable alternative to previously postulated energy sources for the geomagnetic field, mainly, the latent heat of fusion presumably released during the assumed growth of the inner core (31). But unlike release of the latent heat of fusion from inner core growth, nuclear fission geo-reactor output can be variable and/or intermittent, a fact that is quite consistent with the observed variability of the geomagnetic field.

A nuclear reactor actinide subcore, surrounded by a subshell, possibly fluid or slurry, composed of fission products and lead from radioactive decay is expected to exist at the center of the inner core of the Earth (6). Moving charges create magnetic fields. A nuclear fission geo-reactor will produce a plethora of charged particles and copious amounts of ionizing radiation. One might wonder whether the geomagnetic field might originate, in some yet unspecified manner, from this assemblage rather than from fluid motions in the main core of the Earth.