flexsurv: A Platform for Parametric Survival Modeling in R

Abstract

flexsurv is an R package for fully-parametric modeling of survival data. Any parametric time-to-event distribution may be fitted if the user supplies a probability density or hazard function, and ideally also their cumulative versions. Standard survival distributions are built in, including the three and four-parameter generalized gamma and F distributions. Any parameter of any distribution can be modeled as a linear or log-linear function of covariates. The package also includes the spline model of Royston and Parmar (2002), in which both baseline survival and covariate effects can be arbitrarily flexible parametric functions of time. The main model-fitting function, flexsurvreg, uses the familiar syntax of survreg from the standard survival package (Therneau 2016). Censoring or left-truncation are specified in ‘Surv’ objects. The models are fitted by maximizing the full log-likelihood, and estimates and confidence intervals for any function of the model parameters can be printed or plotted. flexsurv also provides functions for fitting and predicting from fully-parametric multi-state models, and connects with the mstate package (de Wreede, Fiocco, and Putter 2011). This article explains the methods and design principles of the package, giving several worked examples of its use.

1. Motivation and design

The Cox model for survival data is ubiquitous in medical research, since the effects of predictors can be estimated without needing to supply a baseline survival distribution that might be inaccurate. However, fully-parametric models have many advantages, and even the originator of the Cox model has expressed a preference for parametric modeling (see Reid 1994). Fully-specified models can be more convenient for representing complex data structures and processes (Aalen, Borgan, and Gjessing 2008), e.g., hazards that vary predictably, interval censoring, frailties, multiple responses, datasets or time scales, and can help with out-of-sample prediction. For example, the mean survival $\mathtt{\text{E}}(T)={\int }_0^{\infty }S(t)dt,$ used in health economic evaluations (Latimer 2013), needs the survivor function S(t) to be fully-specified for all times t, and parametric models that combine data from multiple time periods can facilitate this (Benaglia, Jackson, and Sharples 2015).

Package flexsurv (Jackson 2016) for R (R Core Team 2016) allows parametric distributions of arbitrary complexity to be fitted to survival data, gaining the convenience of parametric modeling, while avoiding the risk of model misspecification. Built-in choices include spline-based models with any number of knots (Royston and Parmar 2002) and 3–4 parameter generalized gamma and F distribution families. Any user-defined model may be employed by supplying at minimum an R function to compute the probability density or hazard, and ideally also its cumulative form. Any parameters may be modeled in terms of covariates, and any function of the parameters may be printed or plotted in model summaries.

flexsurv is intended as a general platform for survival modeling in R. The survreg function in the R package survival (Therneau 2016) only supports two-parameter (location/scale) distributions, though users can supply their own distributions if they can be parameterized in this form. Some other contributed R packages can fit survival models, e.g., eha (Broström 2015) and VGAM (Yee and Wild 1996), though these are either limited to specific distribution families, or not specifically designed for survival analysis. Others, e.g., ActuDistns (Nadarajah and Bakar 2013), contain only the definitions of distribution functions. flexsurv enables such functions to be used in survival models.

It is similar in spirit to the Stata packages stpm2 (Lambert and Royston 2009) for spline-based survival modeling, and stgenreg (Crowther and Lambert 2013) for fitting survival models with user-defined hazard functions using numerical integration. Though in flexsurv, slow numerical integration can be avoided if the analytic cumulative distribution or hazard can be supplied, and optimization can also be speeded by supplying analytic derivatives. flexsurv also has features for multi-state modeling and interval censoring, and general output reporting. It employs functional programming to work with user-defined or existing R functions.

Section 2 explains the general model that flexsurv is based on. Section 3 gives examples of its use for fitting built-in survival distributions with a fixed number of parameters, and Section 4 explains how users can define new distributions. Section 5 concentrates on classes of models where the number of parameters can be chosen arbitrarily, such as splines. In Section 6 flexsurv is used for fitting and predicting from fully-parametric multi-state models. Finally Section 7 suggests some potential future extensions.

2. General parametric survival model

The general model that flexsurv fits has probability density for death at time t:

$$f(t|\mu (\mathbf{\text{z}}),\mathit{\alpha }(\mathbf{\text{z}})),t\ge 0.$$ (1)

The cumulative distribution function F(t), survivor function S(t) = 1 − F(t), cumulative hazard H(t) = − log S(t) and hazard h(t) = f(t)/S(t) are also defined (suppressing the conditioning for clarity). μ = α₀ is the parameter of primary interest, which usually governs the mean or location of the distribution. Other parameters α = (α₁, . . . , α_R) are called “ancillary” and determine the shape, variance or higher moments.

Covariates

All parameters may depend on a vector of covariates z through link-transformed linear models $g_0(\mu (\mathbf{\text{z}}))={\gamma }_0+{\mathit{\beta }}_0^{\text{⊤}}\text{z}\text{and}{g}_r({\alpha }_r(\mathbf{\text{z}}))={\gamma }_r+{\mathit{\beta }}_{\gamma }^{\text{⊤}}\mathbf{\text{z}}.$ g() will typically be log() if the parameter is defined to be positive, or the identity function if the parameter is unrestricted.

Suppose that the location parameter, but not the ancillary parameters, depends on covariates. If the hazard function factorizes as h(t|α, μ(z)) = μ(z)h₀(t|α), then this is a proportional hazards (PH) model, so that the hazard ratio between two groups (defined by two different values of z) is constant over time t.

Alternatively, if S(t|μ(z), α) = S₀(μ(z)t|α) then it is an accelerated failure time (AFT) model, so that the effect of covariates is to speed or slow the passage of time. For example, doubling the value of a covariate with coefficient β = log(2) would give half the expected survival time.

Data and likelihood

Let t_i : i = 1, . . . , n be a sample of times from individuals i. Let c_i = 1 if t_i is an observed death time, or c_i = 0 if this is censored. Most commonly, t_i may be right-censored, thus the true death time is known only to be greater than t_i. More generally, the survival time may be interval-censored on $(t_i^{\text{min}},t_i^{\text{max}}).$

Also let s_i be corresponding left-truncation (or delayed-entry) times, meaning that the ith survival time is only observed conditionally on the individual having survived up to s_i, thus s_i = 0 if there is no left-truncation. Time-dependent covariates (Section 3.1) and some multi-state models (Section 6) can be represented through left-truncation.

With at most right-censoring, the likelihood for the parameters θ = {γ, β} in Equation 1, given the corresponding data vectors, is

$$l(\mathit{\theta }|\mathbf{\text{t}},\mathbf{\text{c}},\mathbf{\text{s}})=\left\{{\displaystyle \prod _{i:c_i=1}{f}_i(t_i)}{\displaystyle \prod _{i:c_i=0}{S}_i(t_i)}\right\}/{\displaystyle \prod _i{S}_i(s_i)},$$ (2)

where f_i(t_i) is shorthand for f(t_i|μ(z_i), α(z_i)), S_i(t_i) is S(t_i|μ(z_i), α(z_i)), and μ, α are related to γ, β, and z_i via the link functions defined above. The log-likelihood also has a concise form in terms of hazards and cumulative hazards, as

$$\text{log}l(\mathit{\theta }|\mathbf{\text{t}},\mathbf{\text{c}},\mathbf{\text{s}})={\displaystyle \sum _{i:c_i=1}\{\text{log}(h_i(t_i))-H_i(t_i)\}-{\displaystyle \sum _{i:c_i=0}{H}_i(t_i)+{\displaystyle \sum _i{H}_i(s_i)}}}.$$

With interval-censoring, the likelihood is

$$l(\mathit{\theta }|{\mathbf{\text{t}}}^{\text{min}},{\mathbf{\text{t}}}^{\text{max}},\mathbf{\text{c}},\mathbf{\text{s}})=\left\{{\displaystyle \prod _{i:c_i=1}{f}_i(t_i)}{\displaystyle \prod _{i:c_i=0}\left(S_i(t_i^{\text{min}})-S_i(t_i^{\text{max}})\right)}\right\}/{\displaystyle \prod _i{S}_i(s_i)}.$$ (3)

These likelihoods assume that the times of censoring are fixed or otherwise distributed independently of the parameters θ that govern the survival times (see, e.g., Aalen et al. 2008). The individual survival times are also independent, so that flexsurv does not currently support shared frailty, clustered or random effects models (see Section 7).

The parameters are estimated by maximizing the full log-likelihood with respect to θ, as detailed further in Section 3.6.

3. Fitting standard parametric survival models

An example dataset used throughout this paper is from 686 patients with primary node positive breast cancer, available in the package as bc. This was originally provided with package stpm (Royston 2001), and analyzed in much more detail by Sauerbrei and Royston (1999) and Royston and Parmar (2002).¹ The first two records are shown by:

R> library("flexsurv")
R> head(bc, 2)

  censrec rectime group   recyrs
1       0    1342  Good 3.676712
2       0    1578  Good 4.323288

The main model-fitting function is called flexsurvreg. Its first argument is an R ‘formula’ object. The left hand side of the formula gives the response as a survival object, using the Surv function from the survival package.

R> fs1 <- flexsurvreg(Surv(recyrs, censrec) ~ group, data = bc,
+    dist = "weibull")

Here, this indicates that the response variable is recyrs. This represents the time (in years) of death or cancer recurrence when censrec is 1, or (right-)censoring when censrec is 0. The covariate group is a factor representing a prognostic score, with three levels "Good" (the baseline), "Medium" and "Poor". All of these variables are in the data frame bc. If the argument dist is a string, this denotes a built-in survival distribution. In this case we fit a Weibull survival model.

Printing the fitted model object gives estimates and confidence intervals for the model parameters and other useful information. Note that these are the same parameters as represented by the R distribution function dweibull: The shape α and the scale μ of the survivor function S(t) = exp(−(t/μ)^α), and group has a linear effect on log(μ).

R> fs1

Call:
flexsurvreg(formula = Surv(recyrs, censrec) ~ group, data = bc,
    dist = "weibull")

Estimates:
             data mean  est      L95%     U95%     se
shape             NA     1.3797   1.2548   1.5170   0.0668
scale             NA    11.4229   9.1818  14.2110   1.2728
groupMedium   0.3338    −0.6136  −0.8623  −0.3649   0.1269
groupPoor     0.3324    −1.2122  −1.4583  −0.9661   0.1256

             exp(est)  L95%     U95%
shape             NA        NA       NA
scale             NA        NA       NA
groupMedium   0.5414    0.4222   0.6943
groupPoor     0.2975    0.2326   0.3806

N = 686,  Events: 299,  Censored: 387
Total time at risk: 2113.425
Log-likelihood = −811.9419, df = 4
AIC = 1631.884

For the Weibull (and exponential, log-normal and log-logistic) distribution, flexsurvreg simply acts as a wrapper for survreg: The maximum likelihood estimates are obtained by survreg, checked by flexsurvreg for optimization convergence, and converted to flexsurvreg’s preferred parameterization. Therefore the same model can be fitted more directly as

R> survreg(Surv(recyrs, censrec) ~ group, data = bc, dist = "weibull")

Call:
survreg(formula = Surv(recyrs, censrec) ~ group, data = bc, dist = "weibull")

Coefficients:
(Intercept) groupMedium   groupPoor
  2.4356168  −0.6135892  −1.2122137

Scale= 0.7248206

Loglik(model)= −811.9   Loglik(intercept only)= −873.2
        Chisq= 122.53 on 2 degrees of freedom, p= 0
n= 686

The maximized log-likelihoods are the same, however the parameterization is different: The first coefficient (Intercept) reported by survreg is log(μ), and survreg’s "scale" is dweibull’s (thus flexsurvreg)’s 1 / shape. The covariate effects β, however, have the same “accelerated failure time” interpretation, as linear effects on log(μ). The multiplicative effects exp(β) are printed in the output as exp(est).

The same model can be fitted with package eha, also by maximum likelihood:

R> library("eha")
R> aftreg(Surv(recyrs, censrec) ~ group, data = bc, dist = "weibull")

The results are presented in the same parameterization as flexsurvreg, except that the shape and scale parameters are log-transformed, and (unless the argument param = "lifeExp" is supplied) the covariate effects have the opposite sign.

3.1. Additional modeling features

If we also had left-truncation times in a variable called start, the response would be Surv(start, recyrs, censrec). Or if all responses were interval-censored between lower and upper bounds tmin and tmax, then we would write Surv(tmin, tmax, type = "interval2").

Time-dependent covariates can be represented in “counting process” form – as a series of left-truncated survival times, which may also be right-censored. For each individual there would be multiple records, each corresponding to an interval where the covariate is assumed to be constant. The response would be of the form Surv(start, stop, censrec), where start and stop are the limits of each interval, and censrec indicates whether a death was observed at stop.

Relative survival models (Nelson, Lambert, Squire, and Jones 2007) can be implemented by supplying the variable in the data that represents the expected mortality rate in the bhazard argument to flexsurvreg. Case weights and data subsets can also be specified, as in standard R modeling functions, using weights or subset arguments.

3.2. Built-in models

flexsurvreg’s currently built-in distributions are listed in Table 1. In each case, the probability density f() and parameters of the fitted model are taken from an existing R function of the same name but beginning with the letter d. For the Weibull, exponential (dexp), gamma (dgamma) and log-normal (dlnorm), the density functions are provided with standard installations of R. These density functions, and the corresponding cumulative distribution functions (with first letter p instead of d) are used internally in flexsurvreg to compute the likelihood.

Table 1.

Built-in parametric survival distributions in flexsurv.

	Parameters (location in italics)	Density R function	dist
Exponential	rate	dexp	"exp"
Weibull	shape, scale	dweibull	"weibull"
Gamma	shape, rate	dgamma	"gamma"
Log-normal	meanlog, sdlog	dlnorm	"lnorm"
Gompertz	shape, rate	dgompertz	"gompertz"
Log-logistic	shape, scale	dllogis	"llogis"
Generalized gamma (Prentice 1975)	mu, sigma, Q	dgengamma	"gengamma"
Generalized gamma (Stacy 1962)	shape, scale, k	dgengamma.orig	"gengamma.orig"
Generalized F (stable)	mu, sigma, Q, P	dgenf	"genf"
Generalized F (original)	mu, sigma, s1, s2	dgenf.orig	"genf.orig"

flexsurv provides some additional survival distributions, including a Gompertz distribution with unrestricted shape parameter (dist = "gompertz"), log-logistic, and the three- and four-parameter families described below. For all built-in distributions, flexsurv also defines functions beginning with h giving the hazard, and H for the cumulative hazard.

Generalized gamma

This three-parameter distribution includes the Weibull, gamma and log-normal as special cases. The original parameterization from Stacy (1962) is available as dist = "gengamma.orig", however the newer parameterization (Prentice 1974) is preferred: dist = "gengamma". This has parameters (μ,σ,q), and survivor function

$$\begin{array}{ll}1-I(\gamma ,u)\hfill & (q>0),\hfill \\ 1-\Phi (z)\hfill & (q=0),\hfill \end{array}$$

where $I(\gamma ,u)={\int }_0^u{x}^{\gamma -1}\exp (-x)/\Gamma (\gamma )$ is the incomplete gamma function (the cumulative gamma distribution with shape γ and scale 1), Φ is the standard normal cumulative distribution, u = γ exp(|q|z), z = (log(t) − μ)/σ, and γ = q⁻². The Prentice (1974) parameterization extends the original one to include a further class of models with negative q, and survivor function I(γ, u), where z is replaced by −z. This stabilizes estimation when the distribution is close to log-normal, since q = 0 is no longer near the boundary of the parameter space. In R notation,² the parameter values corresponding to the three special cases are

dgengamma(x, mu, sigma, Q = 0)     == dlnorm(x, mu, sigma)
dgengamma(x, mu, sigma, Q = 1)     == dweibull(x, shape = 1 / sigma,
                                               scale = exp(mu))
dgengamma(x, mu, sigma, Q = sigma) == dgamma(x, shape = 1 / sigma^2,
                                             rate = exp(-mu) / sigma^2)

Generalized F

This four-parameter distribution includes the generalized gamma, and also the log-logistic, as special cases. The variety of hazard shapes that can be represented is discussed by Cox (2008). It is provided here in alternative “original” (dist = "genf.orig") and “stable” parameterizations (dist = "genf") as presented by Prentice (1975). See help("GenF") and help("GenF.orig") in the package documentation for the exact definitions.

3.3. Covariates on ancillary parameters

The generalized gamma model is fitted to the breast cancer survival data. fs2 is an AFT model, where only the parameter μ depends on the prognostic covariate group. In a second model fs3, the first ancillary parameter sigma (α₁) also depends on this covariate, giving a model with a time-dependent effect that is neither PH nor AFT. The second ancillary parameter Q is still common between prognostic groups.

R> fs2 <- flexsurvreg(Surv(recyrs, censrec) ~ group, data = bc,
+    dist = "gengamma")
R> fs3 <- flexsurvreg(Surv(recyrs, censrec) ~ group + sigma(group),
+    data = bc, dist = "gengamma")

Ancillary covariates can alternatively be supplied using the anc argument to flexsurvreg. This syntax is required if any parameter names clash with the names of functions used in model formulae (e.g., factor() or I()).

R> fs3 <- flexsurvreg(Surv(recyrs, censrec) ~ group, data = bc,
+    anc = list(sigma = ~ group), dist = "gengamma")

Table 3 compares all the models fitted to the breast cancer data, showing absolute fit to the data as measured by the maximized −2× log likelihood −2LL, number of parameters p, and Akaike’s information criterion −2LL + 2p (AIC). The model fs2 has the lowest AIC, indicating the best estimated predictive ability.

Table 3.

Comparison of parametric survival models fitted to the breast cancer data.

	-2 log likelihood	Parameters	AIC
Weibull (fs1)	1623.8	4	1631.9
Generalized gamma (fs2)	1575.2	5	1585.1
Generalized gamma (fs3)	1572.4	7	1586.4
Log-logistic (fs4)	1598.2	4	1606.1
Spline (sp1)	1578.0	5	1588.0
Spline (sp2)	1574.8	7	1588.8
Spline (sp3)	1585.8	5	1595.7
Spline (sp4)	1571.4	9	1589.3

3.4. Plotting outputs

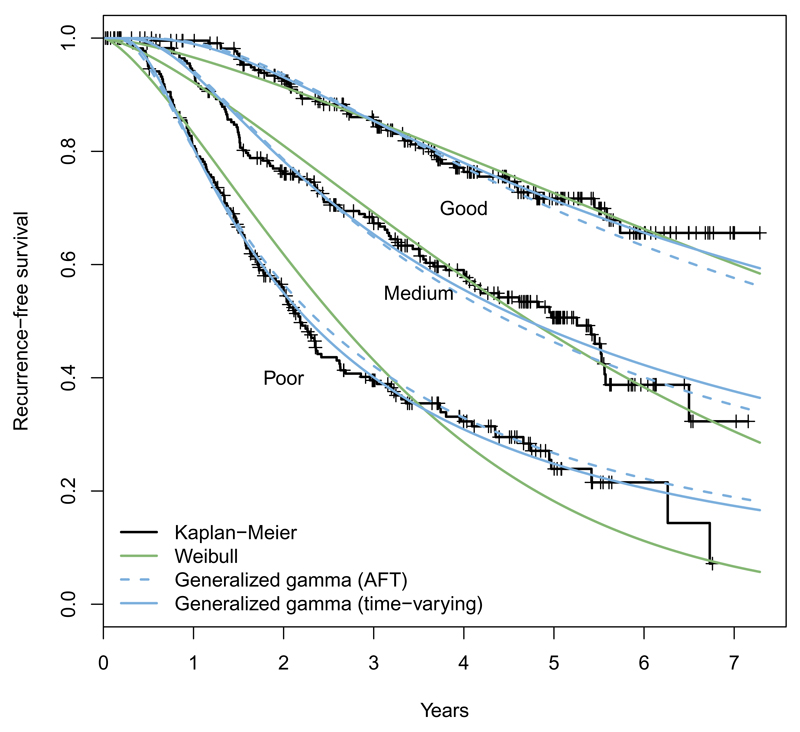
The plot() method for ‘flexsurvreg’ objects is used as a quick check of model fit. By default, this draws a Kaplan-Meier estimate of the survivor function S(t), one for each combination of categorical covariates, or just a single “population average” curve if there are no categorical covariates (Figure 1). The corresponding estimates from the fitted model are overlaid. Fitted values from further models can be added with the lines() method.

Figure 1.

Survival by prognostic group from the breast cancer data: Fitted from alternative parametric models and Kaplan-Meier estimates.

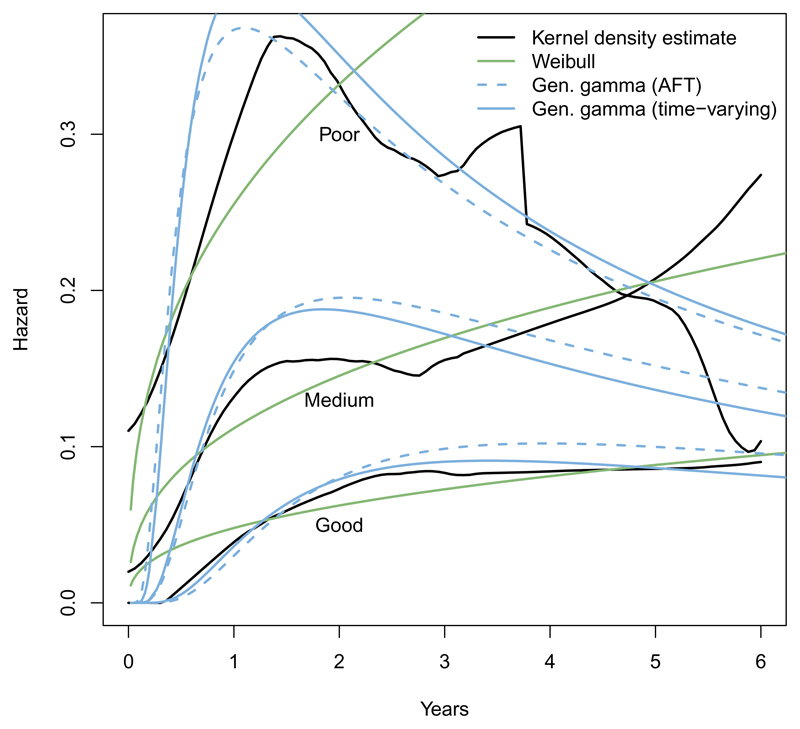
The argument type = "hazard" can be set to plot hazards from parametric models against kernel density estimates obtained from muhaz (Hess 2014; Müller and Wang 1994). Figure 2 shows more clearly that the Weibull model is inadequate for the breast cancer data: The hazard must be increasing or decreasing – while the generalized gamma distribution can represent the increase and subsequent decline in hazard seen in the data. Similarly, type = "cumhaz" plots cumulative hazards.

Figure 2.

Hazards by prognostic group from the breast cancer data: Fitted from alternative parametric models and kernel density estimates.

The numbers plotted are available from the summary method for ‘flexsurvreg’ objects. Confidence intervals are produced by simulating a large sample from the asymptotic normal distribution of the maximum likelihood estimates of {β_r : r = 0, . . . , R} (Mandel 2013), via the function normboot.flexsurvreg. This very general method allows confidence intervals to be obtained for arbitrary functions of the parameters, as described in the next section.

In this example, there is only a single categorical covariate, and the plot and summary methods return one observed and fitted trajectory for each level of that covariate. For more complicated models, users should specify what covariate values they want summaries for, rather than relying on the default.³ This is done by supplying the newdata argument, a data frame or list containing covariate values, just as in standard R functions like the predict method for ‘lm’ objects. Time-dependent covariates are not understood by these functions.

This plot() method is only for casual exploratory use. For publication-standard figures, it is preferable to set up the axes beforehand (plot(..., type = "n")), and use the lines() methods for ‘flexsurvreg’ objects, or construct plots by hand using the data available from the summary method for ‘flexsurvreg’ objects.

3.5. Custom model summaries

Any function of the parameters of a fitted model can be summarized or plotted by supplying the argument fn to the summary or plot methods for ‘flexsurvreg’ objects. This should be an R function, with optional first two arguments t representing time, and start representing a left-truncation point (if the result is conditional on survival up to that time). Any remaining arguments must be the parameters of the survival distribution. For example, median survival under the Weibull model fs1 can be summarized as follows

R> median.weibull <- function(shape, scale)
+    qweibull(0.5, shape = shape, scale = scale)
R> set.seed(1460)
R> summary(fs1, fn = median.weibull, t = 1, B = 10000)

group=Good
  time     est      lcl      ucl
1    1 8.75794 7.097961 10.77422

group=Medium
  time      est      lcl      ucl
1    1 4.741585 4.106213 5.475475

group=Poor
  time      est      lcl      ucl
1    1 2.605819 2.316097 2.936309

Although the median of the Weibull has an analytic form as μ log(2)^1/α, the form of the code given here generalizes to other distributions. The argument t (or start) can be omitted from median.weibull, because the median is a time-constant function of the parameters, unlike the survival or hazard.

10000 random samples are drawn to produce a slightly more precise confidence interval than the default – users should adjust this until the desired level of precision is obtained. A useful future extension of the package would be to employ user-supplied (or built-in) derivatives of summary functions if possible, so that the delta method can be used to obtain approximate confidence intervals without simulation.

3.6. Computation

The likelihood is maximized in flexsurvreg using the optimization methods available through the standard R optim function. By default, this is the "BFGS" method (Nash 1990) using the analytic derivatives of the likelihood with respect to the model parameters, if these are available, to improve the speed of convergence to the maximum. These derivatives are built-in for the exponential, Weibull, Gompertz, log-logistic, and hazard- and odds-based spline models (see Section 5.1). For custom distributions (see Section 4), the user can optionally supply functions with names beginning "DLd" and "DLS" respectively (e.g., DLdweibull, DLSweibull) to calculate the derivatives of the log density and log survivor functions with respect to the transformed baseline parameters γ (then the derivatives with respect to β are obtained automatically). Arguments to optim can be passed to flexsurvreg – in particular, control options, such as convergence tolerance, iteration limit or function or parameter scaling, may need to be adjusted to achieve convergence.

4. Custom survival distributions

flexsurv is not limited to its built-in distributions. Any survival model of the form (1–3) can be fitted if the user can provide either the density function f() or the hazard h(). Many contributed R packages provide probability density and cumulative distribution functions for positive distributions. Though survival models may be more naturally characterized by their hazard function, representing the changing risk of death through time. For example, for survival following major surgery we may want a “U-shaped” hazard curve, representing a high risk soon after the operation, which then decreases, but increases naturally as survivors grow older.

To supply a custom distribution, the dist argument to flexsurvreg is defined to be an R list object, rather than a character string. The list has the following elements.

name: Name of the distribution. In the first example below, we use a log-logistic distribution, and the name is "llogis"⁴. Then there is assumed to be at least available either

• a function to compute the probability density, which would be called dllogis here, or

• a function to compute the hazard, called hllogis.

  There should also be a function called pllogis for the cumulative distribution (if d is given), or H for the cumulative hazard (to complement h), if analytic forms for these are available. If not, then flexsurv can compute them internally by numerical integration, as in package stgenreg (Crowther and Lambert 2013). The default options of the built-in R routine integrate for adaptive quadrature are used, though these may be changed using the integ.opts argument to flexsurvreg. Models specified this way will take an order of magnitude more time to fit, and the fitting procedure may be unstable. An example is given in Section 5.2.

  These functions must be vectorized, and the density function must also accept an argument log, which when TRUE, returns the log density. See the examples below.

  In some cases, R’s scoping rules may not find the functions in the working environment. They may then be supplied through the dfns argument to flexsurvreg.

pars: Character vector naming the parameters of the distribution μ, α₁, . . . , α_R. These must match the arguments of the R distribution function or functions, in the same order.

location: Character; quoted name of the location parameter μ. The location parameter will not necessarily be the first one, e.g., in dweibull the scale comes after the shape.

transforms: A list of functions g() which transform the parameters from their natural ranges to the real line, for example, c(log, identity) if the first is positive and the second unrestricted.⁵

inv.transforms: List of corresponding inverse functions.

inits: A function which provides plausible initial values of the parameters for maximum likelihood estimation. This is optional, but if not provided, then each call to flexsurvreg must have an inits argument containing a vector of initial values, which is inconvenient. Implausible initial values may produce a likelihood of zero, and a fatal error message (initial value in ‘vmmin’ is not finite) from the optimizer.

Each distribution will ideally have a heuristic for initializing parameters from summaries of the data. For example, since the median of the Weibull is μ log(2)^1/α, a sensible estimate of μ might be the median log survival time divided by log(2), with α = 1, assuming that in practice the true value of α is not far from 1. Then we would define the function, of one argument t giving the survival or censoring times, returning the initial values for the Weibull shape and scale respectively.⁶

inits = function(t) c(1, median(t[t > 0]) / log(2))

More complicated initial value functions may use other data such as the covariate values and censoring indicators: For an example, see the function flexsurv.splineinits in the package source that computes initial values for spline models (Section 5.1).

Example: Using functions from a contributed package

The following custom model uses the log-logistic distribution functions (dllogis and pllogis) available in the package eha. The survivor function is S(t|μ, α) = 1/(1 + (t/μ)^α), so that the log odds log((1 − S(t))/S(t)) of having died are a linear function of log time.

R> custom.llogis <- list(name = "llogis", pars = c("shape", "scale"),
+    location = "scale", transforms = c(log, log),
+    inv.transforms = c(exp, exp), inits = function(t) c(1, median(t)))
R> fs4 <- flexsurvreg(Surv(recyrs, censrec) ~ group, data = bc,
+    dist = custom.llogis)

This fits the breast cancer data better than the Weibull, since it can represent a peaked hazard, but less well than the generalized gamma (Table 3).

Example: Wrapping functions from a contributed package

Sometimes there may be probability density and similar functions in a contributed package, but in a different format. For example, eha also provides a three-parameter Gompertz-Makeham distribution with hazard h(t|μ, α₁, α₂) = α₂ + α₁ exp(t/μ). The shape parameters α₁, α₂ are provided to dmakeham as a vector argument of length two. However, flexsurvreg expects distribution functions to have one argument for each parameter. Therefore we write our own functions that wrap around the third-party functions.

R> dmakeham3 <- function(x, shape1, shape2, scale, ...)
+    dmakeham(x, shape = c(shape1, shape2), scale = scale, ...)
R> pmakeham3 <- function(q, shape1, shape2, scale, ...)
+    pmakeham(q, shape = c(shape1, shape2), scale = scale, ...)

flexsurvreg also requires these functions to be vectorized, as the standard distribution functions in R are. That is, we can supply a vector of alternative values for one or more arguments, and expect a vector of the same length to be returned. The R base function Vectorize can be used to do this here.

R> dmakeham3 <- Vectorize(dmakeham3)
R> pmakeham3 <- Vectorize(pmakeham3)

and this allows us to write, for example,

R> pmakeham3(c(0, 1, 1, Inf), 1, c(1, 1, 2, 1), 1)

[1] 0.0000000 0.9340120 0.9757244 1.0000000

When fitting the model with flexsurvreg we could use dist = list(name = "makeham3", pars = c("shape1", "shape2", "scale"), ...), though in the breast cancer example, the second shape parameter is poorly identifiable.

Example: Changing the parameterization of a distribution

We may want to fit a Weibull model like fs1, but with the proportional hazards (PH) parameterization S(t) = exp(−μt^α), so that the covariate effects reported in the printed ‘flexsurvreg’ object can be interpreted as hazard ratios or log hazard ratios without any further transformation. Here instead of the density and cumulative distribution functions, we provide the hazard and cumulative hazard.⁷

R> detach("package:eha")
R> hweibullPH <- function(x, shape, scale = 1, log = FALSE)
+    hweibull(x, shape = shape, scale = scale ^ {-1 / shape}, log = log)
R> HweibullPH <- function(x, shape, scale = 1, log = FALSE)
+    Hweibull(x, shape = shape, scale = scale ^ {-1 / shape}, log = log)
R> custom.weibullPH <- list(name = "weibullPH", pars = c("shape", "scale"),
+    location = "scale", transforms = c(log, log),
+    inv.transforms = c(exp, exp), inits = function(t)
+      c(1, median(t[t > 0]) / log(2)))
R> fs6 <- flexsurvreg(Surv(recyrs, censrec) ~ group, data = bc,
+    dist = custom.weibullPH)
R> fs6$res["scale", "est"] ^ {-1 / fs6$res["shape", "est"]}

[1] 11.42286

R> - fs6$res["groupMedium", "est"] / fs6$res["shape", "est"]

[1] -0.6135897

R> - fs6$res["groupPoor", "est"] / fs6$res["shape", "est"]

[1] -1.212215

The fitted model is the same as fs1, therefore the maximized likelihood is the same. The parameter estimates of fs6 can be transformed to those of fs1 as shown. The shape α is common to both models, the scale μ′ in the AFT model is related to the PH scale μ as μ′ = μ^−1/α. The effects β′ on life expectancy in the AFT model are related to the hazard ratios β as β′ = −β/α.

A slightly more complicated example is given in the package vignette flexsurv-examples of constructing a proportional hazards generalized gamma model. Note that phreg in eha also fits the Weibull and other proportional hazards models, though again the parameterization is slightly different.

5. Arbitrary-dimension models

flexsurv also supports models where the number of parameters is arbitrary. In the models discussed previously, the number of parameters in the model family is fixed (e.g., three for the generalized gamma). In this section, the model complexity can be chosen by the user, given the model family. We may want to represent more irregular hazard curves by more flexible functions, or use bigger models if a bigger sample size makes it feasible to estimate more parameters.

5.1. Royston and Parmar spline model

In the spline-based survival model of Royston and Parmar (2002), a transformation g(S(t, z)) of the survival function is modeled as a natural cubic spline function of log time: g(S(t, z)) = s(x, γ) where x = log(t). This model can be fitted in flexsurv using the function flexsurvspline, and is also available in the Stata package stpm2 (Lambert and Royston 2009) (historically stpm; Royston 2001, 2004).

Typically we use g(S(t, z)) = log(− log(S(t, z))) = log(H(t, z)), the log cumulative hazard, giving a proportional hazards model.

Spline parameterization

The complexity of the model, thus the dimension of γ, is governed by the number of knots in the spline function s(). Natural cubic splines are piecewise cubic polynomials defined to be continuous, with continuous first and second derivatives at the knots, and also constrained to be linear beyond boundary knots k_min, k_max. As well as the boundary knots there may be up to m ≥ 0 internal knots k₁, . . . , k_m. Various spline parameterizations exist – the one used here is from Royston and Parmar (2002).

$$s(x,\gamma )={\gamma }_0+{\gamma }_{1}x+{\gamma }_2{\upsilon }_1(x)+\dots +{\gamma }_{m+1}{\upsilon }_m(x)$$ (4)

where υ_j(x) is the jth basis function

$$\begin{array}{ll}{\upsilon }_j(x)={(x-k_j)}_{+}^3-{\lambda }_j{(x-k_{\text{min}})}_{+}^3-(1-{\lambda }_j){(x-k_{\text{max}})}_{+}^3,\hfill & {\lambda }_j=\frac{k_{\text{max}}-k_j}{k_{\text{max}}-k_{\text{min}}}\hfill \end{array}$$

and (x − a)₊ = max(0, x − a). If m = 0 then there are only two parameters γ₀, γ₁, and this is a Weibull model if g() is the log cumulative hazard. Table 2 explains two further choices of g(), and the parameter values and distributions they simplify to for m = 0. The probability density and cumulative distribution functions for all these models are available as dsurvspline and psurvspline.

Table 2.

Alternative modeling scales for flexsurvspline, and equivalent distributions for m = 0 (with parameter definitions as in the R d functions referred to elsewhere in the paper).

Model	g(S(t, z))	In flexsurvspline	With m = 0
Proportional hazards	log(− log(S(t, z))) (log cumulative hazard)	scale = "hazard"	Weibull shape γ1, scale exp(−γ0/γ1)
Proportional odds	log(S(t, z)−1 − 1) (log cumulative odds)	scale = "odds"	Log-logistic shape γ1, scale exp(−γ0/γ1)
Normal / probit	Φ−1(S(t, z)) (inverse normal CDF, qnorm)	scale = "normal"	Log-normal meanlog − γ0/γ1, sdlog 1/γ1

Covariates on spline parameters

Covariates can be placed on any parameter γ through a linear model (with identity link function). Most straightforwardly, we can let the intercept γ₀ vary with covariates z, giving a proportional hazards or odds model (depending on g()).

$$g(S(t,z))=s(\text{log}(t),\gamma )+{\beta }^{\text{⊤}}\mathbf{\text{z}}$$

The spline coefficients γ_j : j = 1, 2 . . ., the “ancillary” parameters, may also be modeled as linear functions of covariates z, as

$${\gamma }_j(\mathbf{\text{z}})={\gamma }_{j0}+{\gamma }_{j1}{z}_1+{\gamma }_{j2}{z}_2+\dots$$

giving a model where the effects of covariates are arbitrarily flexible functions of time: a non-proportional hazards or odds model.

Spline models in flexsurv

The argument k to flexsurvspline defines the number of internal knots m. Knot locations are chosen by default from quantiles of the log uncensored death times, or users can supply their own locations in the knots argument. Initial values for numerical likelihood maximization are chosen using the method described by Royston and Parmar (2002) of Cox regression combined with transforming an empirical survival estimate.

For example, the best-fitting model for the breast cancer dataset identified in Royston and Parmar (2002), a proportional odds model with one internal spline knot, is

R> sp1 <- flexsurvspline(Surv(recyrs, censrec) ~ group, data = bc, k = 1,
+    scale = "odds")

A further model where the first ancillary parameter also depends on the prognostic group, giving a time-varying odds ratio, is fitted as

R> sp2 <- flexsurvspline(Surv(recyrs, censrec) ~ group + gamma1(group),
+    data = bc, k = 1, scale = "odds")

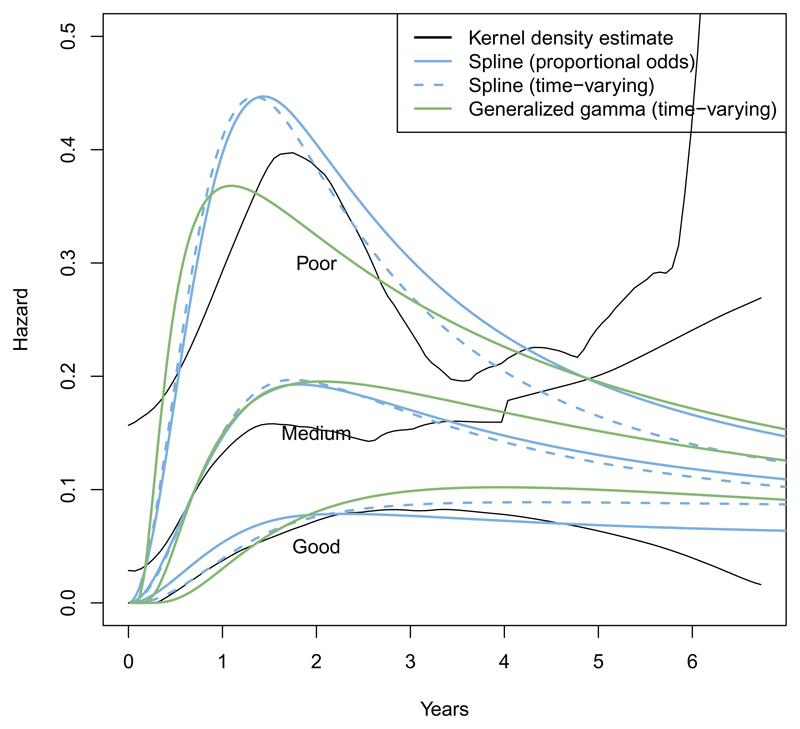
These models give qualitatively similar results to the generalized gamma in this dataset (Figure 3), and have similar predictive ability as measured by AIC (Table 3). Though in general, an advantage of spline models is that extra flexibility is available where necessary.

Figure 3.

Comparison of spline and generalized gamma fitted hazards for the breast cancer survival data by prognostic group.

In this example, proportional odds models (scale = "odds") are better-fitting than proportional hazards models (scale = "hazard") (Table 3). Note also that under a proportional hazards spline model with one internal knot (sp3), the log hazard ratios, and their standard errors, are substantively the same as under a standard Cox model (cox3). This illustrates that this class of flexible fully-parametric models may be a reasonable alternative to the (semi-parametric) Cox model. See Royston and Parmar (2002) for more discussion of these issues.

R> sp3 <- flexsurvspline(Surv(recyrs, censrec) ~ group, data = bc, k = 1,
+    scale = "hazard")
R> sp3$res[c("groupMedium", "groupPoor"), c("est", "se")]

                  est        se
groupMedium 0.8334517 0.1712042
groupPoor   1.6111788 0.1640933

R> cox3 <- coxph(Surv(recyrs, censrec) ~ group, data = bc)
R> coef(summary(cox3))[ , c("coef", "se(coef)")]

                 coef  se(coef)
groupMedium 0.8401002 0.1713926
groupPoor   1.6180720 0.1645443

An equivalent of a “stratified" Cox model may be obtained by allowing all the spline parameters to vary with the categorical covariate that defines the strata. In this case, this covariate might be group. With k = m internal knots, the formula should then include group, representing γ₀, and m + 1 further terms representing the parameters γ₁, . . . , γ_m+1, named as follows.

R> sp4 <- flexsurvspline(Surv(recyrs, censrec) ~ group + gamma1(group) +
+    gamma2(group), data = bc, k = 1, scale = "hazard")

Other covariates might be added to this formula – if placed on the intercept, these will be modeled through proportional hazards, as in sp1. If placed on higher-order parameters, these will represent time-varying hazard ratios. For example, if there were a covariate treat representing treatment, then

R> flexsurvspline(Surv(recyrs, censrec) ~ group + gamma1(group) +
+    gamma2(group) + treat + gamma1(treat), data = bc, k = 1,
+    scale = "hazard")

would represent a model stratified by group, where the hazard ratio for treatment is time-varying, but the model is not fully stratified by treatment.

R> res <- t(sapply(list(fs1, fs2, fs3, fs4, sp1, sp2, sp3, sp4),
+    function(x) rbind(-2 * round(x$loglik, 1), x$npars, round(x$AIC, 1))))
R> rownames(res) <- c("Weibull (fs1)", "Generalized gamma (fs2)",
+    "Generalized gamma (fs3)", "Log-logistic (fs4)",
+    "Spline (sp1)", "Spline (sp2)", "Spline (sp3)", "Spline (sp4)")
R> colnames(res) <- c("-2 log likelihood", "Parameters", "AIC")
R> res

These results are shown in Table 3.

5.2. Implementing new general-dimension models

The spline model above is an example of the general parametric form (Equation 1), but the number of parameters, R + 1 in Equation 1, m + 2 in Equation 4, is arbitrary. flexsurv has the tools to deal with any model of this form. flexsurvspline works internally by building a custom distribution and then calling flexsurvreg. Similar models may in principle be built by users using the same method. This relies on a functional programming trick.

Creating distribution functions dynamically

The R distribution functions supplied to custom models are expected to have a fixed number of arguments, including one for each scalar parameter. However, the distribution functions for the spline model (e.g., dsurvspline) have an argument gamma representing the vector of parameters γ, whose length is determined by choosing the number of knots. Just as the scalar parameters of conventional distribution functions can be supplied as vector arguments (as explained in Section 4), similarly, the vector parameters of spline-like distribution functions can be supplied as matrix arguments, representing alternative parameter values.

To convert a spline-like distribution function into the correct form, flexsurv provides the utility unroll.function. This converts a function with one (or more) vector parameters (matrix arguments) to a function with an arbitrary number of scalar parameters (vector arguments). For example, the 5-year survival probability for the baseline group under the model sp1 is

R> gamma <- sp1$res[c("gamma0", "gamma1", "gamma2"), "est"]
R> 1 - psurvspline(5, gamma = gamma, knots = sp1$knots)

[1] 0.6896969

An alternative function to compute this can be built by unroll.function. We tell it that the vector parameter gamma should be provided instead as three scalar parameters named gamma0, gamma1, gamma2. The resulting function pfn is in the correct form for a custom flexsurvreg distribution.

R> pfn <- unroll.function(psurvspline, gamma = 0:2)
R> 1 - pfn(5, gamma0 = gamma[1], gamma1 = gamma[2], gamma2 = gamma[3],
+    knots = sp1$knots)

[1] 0.6896969

Users wishing to fit a new spline-like model with a known number of parameters could just as easily write distribution functions specific to that number of parameters, and use the methods in Section 4. However the unroll.function method is intended to simplify the process of extending the flexsurv package to implement new model families, through wrappers similar to flexsurvspline.

Example: Splines on alternative scales

An alternative to the Royston-Parmar spline model is to model the log hazard as a function of time instead of the log cumulative hazard. Crowther and Lambert (2013) demonstrate this model using the Stata package stgenreg. An advantage explained by Royston and Lambert (2011) is that when there are multiple time-dependent effects, time-dependent hazard ratios can be interpreted independently of the values of other covariates.

This can also be implemented in flexsurvreg using unroll.function. A disadvantage of this model is that the cumulative hazard (hence the survivor function) has no analytic form, therefore to compute the likelihood, the hazard function needs to be integrated numerically. This is done automatically in flexsurvreg (just as in stgenreg) if the cumulative hazard is not supplied.

Firstly, a function must be written to compute the hazard as a function of time x, the vector of parameters gamma (which can be supplied as a matrix argument so the function can give a vector of results), and a vector of knot locations. This uses flexsurv’s function basis to compute the natural cubic spline basis (Equation 4), and replicates x and gamma to the length of the longest one.

R> hsurvspline.lh <- function(x, gamma, knots) {
+    if (!is.matrix(gamma)) gamma <- matrix(gamma, nrow = 1)
+    lg <- nrow(gamma)
+    nret <- max(length(x), lg)
+    gamma <- apply(gamma, 2, function(x) rep(x, length.out = nret))
+    x <- rep(x, length.out = nret)
+    loghaz <- rowSums(basis(knots, log(x)) * gamma)
+    exp(loghaz)
+ }

The equivalent function is then created for a three-knot example of this model (one internal and two boundary knots) that has arguments gamma0, gamma1 and gamma2 corresponding to the three columns of gamma,

R> hsurvspline.lh3 <- unroll.function(hsurvspline.lh, gamma = 0:2)

To complete the model, the custom distribution list is formed, the internal knot is placed at the median uncensored log survival time, and the boundary knots are placed at the minimum and maximum. These are passed to hsurvspline.lh through the aux argument of flexsurvreg.

R> custom.hsurvspline.lh3 <- list(name = "survspline.lh3",
+    pars = c("gamma0", "gamma1", "gamma2"), location = "gamma0",
+    transforms = rep(c(identity), 3), inv.transforms = rep(c(identity), 3))
R> dtime <- log(bc$recyrs)[bc$censrec == 1]
R> ak <- list(knots = quantile(dtime, c(0, 0.5, 1)))

Initial values must be provided in the call to flexsurvreg, since the custom distribution list did not include an inits component. For this example, “default” initial values of zero suffice, but the permitted values of γ₂ are fairly tightly constrained (from −0.5 to 0.5 here) using the "L-BFGS-B" bounded optimizer from R’s optim (Nash 1990). Without the constraint, extreme values of γ₂, visited by the optimizer, cause the numerical integration of the hazard function to fail.

R> sp5 <- flexsurvreg(Surv(recyrs, censrec) ~ group, data = bc, aux = ak,
+    inits = c(0, 0, 0, 0, 0),
+    dist = custom.hsurvspline.lh3,
+    method = "L-BFGS-B", lower = c(-Inf, -Inf, -0.5),
+    upper = c(Inf, Inf, 0.5),
+    control = list(trace = 1, REPORT = 1))

This takes around ten minutes to converge, so is not presented here, though the fit is poorer than the equivalent spline model for the cumulative hazard. The 95% confidence interval for γ₂ of (0.16, 0.37) is firmly within the constraint. Crowther and Lambert (2014) present a combined analytic / numerical integration method for this model that may make fitting it more stable.

Other arbitrary-dimension models

Another potential application is to fractional polynomials (Royston and Altman 1994). These are of the form ${\sum }_{m=1}^M{\alpha }_m{x}^{p_m}\log {(x)}^n$ where the power p_m is in the standard set {2, −1, −0.5, 0, 0.5, 1, 2, 3} (except that log(x) is used instead of x⁰), and n is a non-negative integer. They are similar to splines in that they can give arbitrarily close approximations to a nonlinear function, such as a hazard curve, and are particularly useful for expressing the effects of continuous predictors in regression models. See e.g., Sauerbrei, Royston, and Binder (2007), and several other publications by the same authors, for applications and discussion of their advantages over splines. The R package gamlss (Rigby and Stasinopoulos 2005) has a function to construct a fractional polynomial basis that might be employed in flexsurv models.

Polyhazard models (Louzada-Neto 1999) are another potential use of this technique. These express an overall hazard as a sum of latent cause-specific hazards, each one typically from the same class of distribution, e.g., a poly-Weibull model if they are all Weibull. For example, a U-shaped hazard curve following surgery may be the sum of early hazards from surgical mortality and later deaths from natural causes. However, such models may not always be identifiable without external information to fix or constrain the parameters of particular hazards (Demiris, Lunn, and Sharples 2015).

6. Multi-state models

A multi-state model represents how an individual moves between multiple states in continuous time. Survival analysis is a special case with two states, “alive” and “dead”. Competing risks are a further special case, where there are multiple causes of death, that is, one starting state and multiple possible destination states.

Given that an individual is in state X(t) at time t, their next state, and the time of the change, are governed by a set of transition intensities

$$q_{rs}(t,\mathbf{\text{z}}(t),{ℱ}_t)=\underset{\delta t\to 0}{\text{lim}}\text{P}(X(t+\delta t)=s|X(t)=r,\mathbf{\text{z}}(t),{ℱ}_t)/\delta t$$

for states r, s = 1, . . . , R, which for a survival model are equivalent to the hazard h(t). The intensity represents the instantaneous risk of moving from state r to state s, and is zero if the transition is impossible. It may depend on covariates z(t), the time t itself, and possibly also the “history” of the process up to that time, ℱ_t: the states previously visited or the length of time spent in them.

Data. Instead of a single event time, there may now be a series of event times t₁, . . . , t_n for an individual, corresponding to changes of state. The last of these may be an observed or right-censored event time. Note panel data are not considered here – that is, observations of the state of the process at an arbitrary set of times (Kalbfleisch and Lawless 1985). In panel data, we do not necessarily know the time of each transition, or even whether transitions of a certain type have occurred at all between a pair of observations. Multi-state models for that type of data (and also exact event times) can be fitted with the msm package for R (Jackson 2011), but are restricted to (piecewise) exponential event time distributions. Knowing the exact event times enables much more flexible models, which flexsurv can fit.

Alternative time scales. In semi-Markov (clock-reset) models, q_rs(t) depends on the time t since entry into the current state, but otherwise, the time since the beginning of the process is forgotten. Any software to fit survival models can also fit this kind of multi-state model, as the following sections will explain.

In an inhomogeneous Markov (clock-forward) model, t represents the time since the beginning of the process, but the intensity q_rs(t) does not depend further on ℱ_t. Again, standard survival modeling software can be used, with the additional requirement that it can deal with left-truncation or counting process data, which survreg, for example, does not currently support.

These approaches are equivalent for competing risks models, since there is at most one transition for each individual, so that the time since the beginning of the process equals the time spent in the current state. Therefore no left-truncation is necessary.

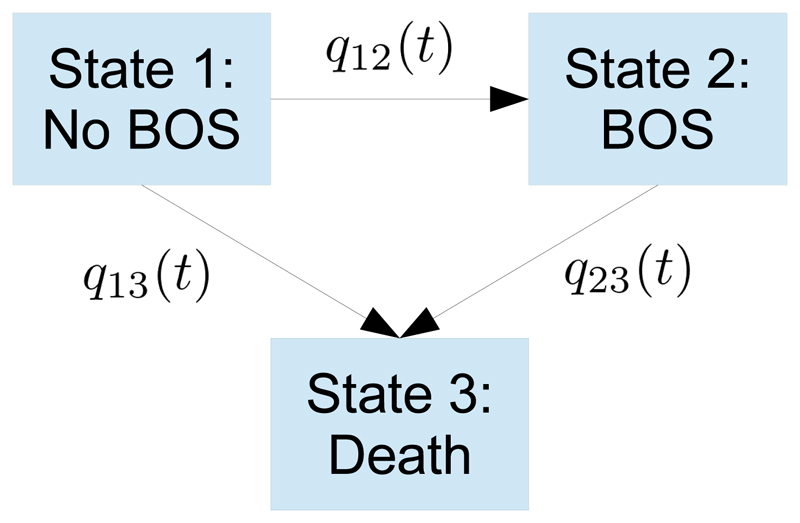
Example. For illustration, consider a simple three-state example, previously studied by Heng, Sharples, McNeil, Stewart, Wreghitt, and Wallwork (1998). Recipients of lung transplants are at risk of bronchiolitis obliterans syndrome (BOS). This was defined as a decrease in lung function to below 80% of a baseline value defined in the six months following transplant. A three-state “illness-death” model represents the risk of developing BOS, the risk of dying before developing BOS, and the risk of death after BOS. BOS is assumed to be irreversible, so there are only three allowed transitions (Figure 4), each with an intensity function q_rs(t).

Figure 4.

Three-state multi-state model for bronchiolitis obliterans syndrome (BOS).

6.1. Representing multi-state data as survival data

Andersen and Keiding (2002) and Putter, Fiocco, and Geskus (2007) explain how to implement multi-state models by manipulating the data into a suitable form for survival modeling software – an overview is given here. For each permitted r → s transition in the multi-state model, there is a corresponding “survival” (time-to-event) model, with hazard rates defined by q_rs(t). For a patient who enters state r at time t_j, their next event at t_j+1 is defined by the model structure to be one of a set of competing events s₁, . . . , s_nr . This implies there are n_r corresponding survival models for this state r, and Σ_r n_r models over all states r. In the BOS example, there are n₁ = 2, n₂ = 1 and n₃ = 0 possible transitions from states 1, 2 and 3 respectively.

The data to inform the n_r models from state r consists firstly of an indicator for whether the transition to the corresponding state s₁, . . . , s_nr is observed or censored at t_j+1. If the individual moves to state s_k , the transitions to all other states in this set are censored at this time. This indicator is coupled with:

• (for a semi-Markov model) the time elapsed dt_j = t_j+1 − t_j from state r entry to state s entry. The “survival” model for the r → s transition is fitted to this time.

• (for an inhomogeneous Markov model) the start and stop time (t_j, t_j+1), as in Section 3.1. The r → s model is fitted to the right-censored time t_j+1 from the start of the process, but is conditional on not experiencing the r → s transition until after the state r entry time. In other words, the r → s transition model is left-truncated at the state r entry time.

In this form, the outcomes of two patients in the BOS data are

R> bosms3[18:22, ]

   id from to    Tstart     Tstop     years status trans
18  7    1  2 0.0000000 0.1697467 0.1697467      1     1
19  7    1  3 0.0000000 0.1697467 0.1697467      0     2
20  7    2  3 0.1697467 0.6297057 0.4599589      1     3
21  8    1  2 0.0000000 8.1615332 8.1615332      0     1
22  8    1  3 0.0000000 8.1615332 8.1615332      1     2

Each row represents an observed (status = 1) or censored (status = 0) transition time for one of three time-to-event models indicated by the categorical variable trans (defined as a factor). Times are expressed in years, with the baseline time 0 representing six months after transplant. Values of trans of 1, 2, 3 correspond to no BOS → BOS, no BOS → death and BOS → death respectively. The first row indicates that the patient (id 7) moved from state 1 (no BOS) to state 2 (BOS) at 0.17 years, but (second row) this is also interpreted as a censored time of moving from state 1 to state 3, potential death before BOS onset. This patient then died, given by the third row with status 1 for trans 3. Patient 8 died before BOS onset, therefore at 8.2 years their potential BOS onset is censored (fourth row), but their death before BOS is observed (fifth row).

The mstate R package (de Wreede, Fiocco, and Putter 2010; de Wreede et al. 2011) has a utility msprep to produce data of this form from “wide-format” datasets where rows represent individuals, and times of different events appear in different columns. msm has a similar utility msm2Surv for producing the required form given longitudinal data where rows represent state observations.

6.2. Multi-state model likelihood

After forming survival data as described above, a multi-state model can be fitted by maximizing the standard survival model likelihood (2), l(θ|x) = ∏_i l_i(θ|x_i), where x is the data, and i now indexes multiple observations for multiple individuals. This can also be written as a product over the K = Σ_r n_r transitions k, and the m_k observations j pertaining to the kth transition. The transition type will typically enter this model as a categorical covariate – see the examples in the next section.

$$l(\mathit{\theta }|\mathbf{\text{x}})={\displaystyle \prod _{k=1}^K{\displaystyle \prod _{j=1}^{m_k}{l}_{jk}(\mathit{\theta }|{\mathbf{\text{x}}}_{jk})}}$$ (5)

Therefore if the parameter vector θ can be partitioned as (θ₁| . . . |θ_K), independent components for each transition k, the likelihood becomes the product of K independent transition-specific likelihoods (Andersen and Keiding 2002). The full multi-state model can then be fitted by maximizing each of these independently, using K separate calls to a survival modeling function such as flexsurvreg. This can give vast computational savings over maximizing the joint likelihood for θ with a single fit. For example, Ieva, Jackson, and Sharples (2015) used flexsurv to fit a parametric multi-state model with 21 transitions and 84 parameters for over 30,000 observations, which was computationally impractical via the joint likelihood, whereas it only took about a minute to perform 21 transition-specific fits.

On the other hand, if any parameters are constrained between transitions (e.g., if hazards are proportional between transitions, or the effects of covariates on different transitions are the same) then it is necessary to maximize the joint likelihood (5) with a single call.

6.3. Fitting parametric multi-state models

Joint likelihood

Three multi-state models are fitted to the BOS data using flexsurvreg, firstly using a single likelihood maximization for each model. The first two use the “clock-reset” time scale. crexp is a simple time-homogeneous Markov model where all transition intensities are constant through time, so that the clock-forward and clock-reset scales are identical. The time to the next event is exponentially-distributed, but with a different rate q_rs for each transition type trans. crwei is a semi-Markov model where the times to BOS onset, death without BOS and the time from BOS onset to death all have Weibull distributions, with a different shape and scale for each transition type. cfwei is a clock-forward, inhomogeneous Markov version of the Weibull model: The 1 → 2 and 1 → 3 transition models are the same, but the third has a different interpretation, now the time from baseline to death with BOS has a Weibull distribution.

R> crexp <- flexsurvreg(Surv(years, status) ~ trans, data = bosms3,
+    dist = "exp")
R> crwei <- flexsurvreg(Surv(years, status) ~ trans + shape(trans),
+    data = bosms3, dist = "weibull")
R> cfwei <- flexsurvreg(Surv(Tstart, Tstop, status) ~ trans + shape(trans),
+    data = bosms3, dist = "weibull")

Semi-parametric equivalents

The equivalent Cox models are also fitted using coxph from the survival package. These specify a different baseline hazard for each transition type through a function strata in the formula, so since there are no other covariates, they are essentially non-parametric. Note that the strata function is not currently understood by flexsurvreg – the user must say explicitly what parameters, if any, vary with the transition type, as in crwei.

R> crcox <- coxph(Surv(years, status) ~ strata(trans), data = bosms3)
R> cfcox <- coxph(Surv(Tstart, Tstop, status) ~ strata(trans),
+    data = bosms3)

In all cases, if there were other covariates, they could simply be included in the model formula. Typically, covariate effects will vary with the transition type, so that an interaction term with trans would be included. Some post-processing might then be needed to combine the main covariate effects and interaction terms into an easily-interpretable quantity (such as the hazard ratio for the r, s transition). Alternatively, mstate has a utility expand.covs to expand a single covariate in the data into a set of transition-specific covariates, to aid interpretation (see de Wreede et al. 2011).

Transition-specific models

In this small example, the joint likelihood can be maximized easily with a single function call, but for larger models and datasets, this may be unfeasible. A more computationally-efficient approach is to fit a list of transition-specific models, as follows.

R> crwei.list <- vector(3, mode = "list")
R> for (i in 1:3) {
+    crwei.list[[i]] <- flexsurvreg(Surv(years, status) ~ 1,
+      subset = (trans == i), data = bosms3, dist = "weibull")
+  }

This list of ‘flexsurvreg’ objects can be supplied as the first argument to the output and prediction functions described in the subsequent sections, instead of a single ‘flexsurvreg’ object. However, this approach is not possible if there are constraints in the parameters across transitions, such as common covariate effects.

Any parametric distribution can be employed in a multi-state model, just as for standard survival models, with flexsurvreg. Spline models may also be fitted with flexsurvspline, and if hazards are assumed proportional, they are expected to give similar results to the Cox model. A restriction (currently even when fitting a list of models) is that all transition-specific models must be from the same parametric family. Though to enable a mixture of simpler and more complex models, we could choose a very flexible family, such as the generalized gamma or a spline, and use the fixedpars argument to flexsurvreg to fix parameters for certain transitions at values for which the flexible family collapses to a simpler one (e.g., Section 3.2, Table 2).

6.4. Obtaining cumulative transition-specific hazards

Multi-state models are often characterized by their cumulative r → s transition-specific hazard functions $H_{rs}(t)={\int }_0^t{q}_{rs}(u)du.$ For semi-parametric multi-state models fitted with coxph, the function msfit in mstate (de Wreede et al. 2010, 2011) provides piecewise-constant estimates and covariances for H_rs(t). For the Cox models for the BOS data,

R> library("mstate")
R> tmat <- rbind(c(NA, 1, 2), c(NA, NA, 3), c(NA, NA, NA))
R> mrcox <- msfit(crcox, trans = tmat)
R> mfcox <- msfit(cfcox, trans = tmat)

tmat describes the transition structure, as a matrix of integers whose r, s entry is i if the ith transition type is r, s, and has NAs on the diagonal and where the r, s transition is disallowed. flexsurv provides an analogous function msfit.flexsurvreg to produce cumulative hazards from fully-parametric multi-state models in the same format. This is a short wrapper around summary(..., type = "cumhaz") for ‘flexsurvreg’ objects, previously mentioned in Section 3.4. The difference from mstate’s method is that hazard estimates can be produced for any grid of times t, at any level of detail and even beyond the range of the data, since the model is fully parametric. The argument newdata can be used in the same way to specify a desired covariate category, though in this example there are no covariates in addition to the transition type. The name of the (factor) covariate indicating the transition type can also be supplied through the tvar argument, in this case it is the default, "trans".

R> tgrid <- seq(0, 14, by = 0.1)
R> mrwei <- msfit.flexsurvreg(crwei, t = tgrid, trans = tmat)
R> mrexp <- msfit.flexsurvreg(crexp, t = tgrid, trans = tmat)
R> mfwei <- msfit.flexsurvreg(cfwei, t = tgrid, trans = tmat)

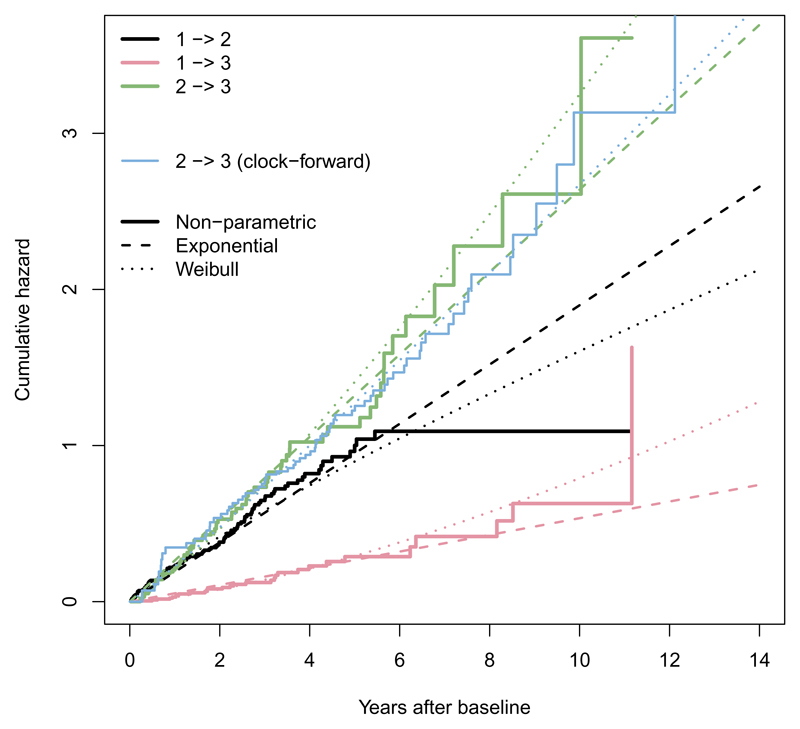
These can be plotted (Figure 5) to show the fit of the parametric models compared to the non-parametric estimates. Both models appear to fit adequately, though give diverging extrapolations after around 6 years when the data become sparse. The Weibull clock-reset model has an improved AIC of 1091, compared to 1099 for the exponential model. For the 2 → 3 transition, the clock-forward and clock-reset models give slightly different hazard trajectories.

Figure 5.

Cumulative hazards for three transitions in the BOS multi-state model (clock-reset), under non-parametric, exponential and Weibull models. For the 2 → 3 transition, an alternative clock-forward scale is shown for the non-parametric and Weibull models.

6.5. Prediction from parametric multi-state models

The transition probabilities of the multi-state model are the probabilities of occupying each state s at time t > t₀, given that the individual is in state r at time t₀.

$$P(t_0,t)=\text{P}(X(t)=s|X(t_0)=r)$$

Markov models

For a time-inhomogeneous Markov model, these are related to the transition intensities via the Kolmogorov forward equation

$$\frac{dP(t_0,t)}{dt}=P(t_0,t)Q(t)$$

with initial condition P() = I (Cox and Miller 1965). This can be solved numerically, as in Titman (2011). This is implemented in the function pmatrix.fs, using the deSolve package (Soetaert, Petzoldt, and Setzer 2010). This returns the full transition probability matrix P(t₀, t) from time t₀ = 0 to a time or set of times t specified in the call. Under the Weibull model, the probability of remaining alive and free of BOS is estimated at 0.3 at 5 years and 0.09 at 10 years:

R> pmatrix.fs(cfwei, t = c(5, 10), trans = tmat)

$`5` 
[1,]  0.3042166  0.2521698  0.4436136
[2,]  0.0000000  0.2804130  0.7195870
[3,]  0.0000000  0.0000000  1.0000000

$`10`
            [,1]        [,2]       [,3]
[1,]  0.09116592  0.12048155  0.7883525
[2,]  0.00000000  0.06903971  0.9309603
[3,]  0.00000000  0.00000000  1.0000000

Confidence intervals can be obtained by simulation from the asymptotic distribution of the maximum likelihood estimates – see help("pmatrix.fs") for full details. A similar function totlos.fs is provided to estimate the expected total amount of time spent in state s up to time t for a process that starts in state r, defined as ${\int }_{u=0}^{t}P{(0,u)}_{rs}du.$

Semi-Markov models

For semi-Markov models, the Kolmogorov equation does not apply, since the transition intensity matrix Q(t) is no longer a deterministic function of t, but depends on when the transitions occur between time t₀ and t. Predictions can then be made by simulation. The function sim.fmsm simulates trajectories from parametric semi-Markov models by repeatedly generating the time to the next transition until the individual reaches an absorbing state or a specified censoring time. This requires the presence of a function to generate random numbers from the underlying parametric distribution – and is fast for built-in distributions which use vectorized functions such as rweibull.

pmatrix.simfs calculates the transition probability matrix by using sim.fmsm to simulate state histories for a large number of individuals, by default 100000. Simulation-based confidence-intervals are also available in pmatrix.simfs, at an extra computational cost, and the expected total length of stay in each state is available from totlos.simfs.

R> pmatrix.simfs(crwei, trans = tmat, t = 5)
R> pmatrix.simfs(crwei, trans = tmat, t = 10)

Prediction via mstate

Alternatively, predictions can be made by supplying the cumulative transition-specific hazards, calculated with msfit.flexsurvreg, to functions in the mstate package.

For Markov models, the solution to the Kolmogorov equation (e.g., Aalen et al. 2008) is given by a product integral, which can be approximated as

$$P(t_0,t)={\displaystyle \prod _{i=0}^{m-1}\left\{I+Q(t_i)dt\right\}},$$

where a fine grid of times t₀, t₁, . . . , t_m = t is chosen to span the prediction interval, and Q(t_i)dt is the increment in the cumulative hazard matrix between times t_i and t_i+1. Q may also depend on other covariates, as long as these are known in advance. In mstate, these can be calculated with the probtrans function, applied to the cumulative hazards returned by msfit. For Cox models, the time grid is naturally defined by the observed survival times, giving the Aalen-Johansen estimator (Andersen, Borgan, Gill, and Keiding 1993). Here, the probability of remaining alive and free of BOS is estimated at 0.27 at 5 years and 0.17 at 10 years.

R> ptc <- probtrans(mfcox, predt = 0, direction = "forward")[[1]]
R> round(ptc[c(165, 193), ], 3)

     time  pstate1   pstate2  pstate3	se1	se2	se3
165 4.999    0.273     0.294	0.433 0.037   0.039   0.040
193 9.873    0.174     0.040    0.786 0.040   0.022   0.045

For parametric models, using a similar discrete-time approximation was suggested by Cook and Lawless (2014). This is achieved by passing the object returned by msfit.flexsurvreg to probtrans in mstate. It can be made arbitrarily accurate by choosing a finer resolution for the grid of times when calling msfit.flexsurvreg.

R> ptw <- probtrans(mfwei, predt = 0, direction = "forward")[[1]]
R> round(ptw[ptw$time %in% c(5, 10), ], 3)

   time   pstate1   pstate2   pstate3   se1   se2   se3
51    5     0.300     0.254     0.446 0.033 0.035 0.037
101  10     0.089     0.119     0.792 0.028 0.032 0.040

pstate1–pstate3 are close to the first rows of the matrices returned by pmatrix.fs. The discrepancy from the Cox model is more marked at 10 years when the data are more sparse (Figure 5). A finer time grid would be required to achieve a similar level of accuracy to pmatrix.fs for the point estimates, at the cost of a slower run time than pmatrix.fs. However, an advantage of probtrans is that standard errors are available more cheaply.

For semi-Markov models, mstate provides the function mssample to produce both simulated trajectories and transition probability matrices from semi-Markov models, given the estimated piecewise-constant cumulative hazards (Fiocco, Putter, and van Houwelingen 2008), produced by msfit or msfit.flexsurvreg, though this is generally less efficient than pmatrix.simfs. In this example, 1000 samples from mssample give estimates of transition probabilities that are accurate to within around 0.02. However with pmatrix.simfs, greater precision is achieved by simulating 100 times as many trajectories in a shorter time.

R> mssample(mrcox$Haz, trans = tmat, clock = "reset", M = 1000,
+    tvec = c(5, 10))
R> mssample(mrwei$Haz, trans = tmat, clock = "reset", M = 1000,
+    tvec = c(5, 10))

7. Potential extensions

More tools and documentation for multi-state modeling would be a useful addition to flexsurv. The msm package currently has a more accessible interface for fitting and summarizing multi-state models, but it was designed mainly for panel data rather than event time data, and therefore the event time distributions it fits are relatively inflexible.

Models where multiple survival times are assumed to be correlated within groups, sometimes called (shared) frailty models (Hougaard 1995), would also be a useful development. See, e.g., Crowther, Look, and Riley (2014) for a recent application based on parametric models. These might be implemented by exploiting tractability for specific distributions, such as gamma frailties, or by adjusting standard errors to account for clustering, as implemented in survreg. More complex random effects models would require numerical integration, for example, Crowther et al. (2014) provide Stata software based on Gauss-Hermite quadrature. Alternatively, a probabilistic modeling language such as Stan (Stan Team 2014) or BUGS (Lunn, Jackson, Best, Thomas, and Spiegelhalter 2012) would be naturally suited to complex extensions such as random effects on multiple parameters or multiple hierarchical levels.

Package flexsurv is intended as a platform for parametric survival modeling. Extensions of the software to deal with different models may be written by users themselves, through the facilities described in Sections 4 and 5.2. These might then be included in the package as builtin distributions, or at least demonstrated in the package’s other vignette flexsurv-examples. Each new class of models would ideally come with

• guidance on what situations the model is useful for, e.g., what shape of hazards it can represent;

• some intuitive interpretation of the model parameters, their plausible values in typical situations, and potential identifiability problems. This would also help with choosing initial values for numerical maximum likelihood estimation, ideally through an inits function in the custom distribution list (Section 4).

The examples in this paper were run using version 0.7.1 of flexsurv, available from the Comprehensive R Archive Network (CRAN) at https://CRAN.R-project.org/package=flexsurv. Development versions are available on https://github.com/chjackson/flexsurv-dev, and contributions are welcome.