The large mean body size of mammalian herbivores explains the productivity paradox during the last glacial maximum

Abstract

Large herbivores are a major agent in ecosystems, influencing vegetation structure and carbon and nutrient flows. During the last glacial period, the steppe-tundra ecosystem prevailed on the unglaciated northern lands, hosting a high diversity and density of megafaunal herbivores. The apparent discrepancy between abundant megafauna and the expected low vegetation productivity under a generally harsher climate with lower CO₂ concentration, termed productivity paradox, awaits large-scale quantitative analysis from process-based ecosystem models. Yet most of the current global dynamic vegetation models (DGVMs) lack explicit representation of large herbivores. Here we incorporated a grazing module in the ORCHIDEE-MICT DGVM based on physiological and demographic equations for wild large grazers, taking into account feedbacks of large grazers on vegetation. The model was applied globally for present-day and the last glacial maximum (LGM). The present-day results of potential grazer biomass, combined with an empirical land use map, infer a reduction of wild grazer biomass by 79-93% due to anthropogenic land replacement over natural grasslands. For the LGM, we find that the larger mean body size of mammalian herbivores than today is the crucial clue to explain the productivity paradox, due to a more efficient exploitation of grass production by grazers with a larger-body size.

Mammalian herbivores live in major terrestrial ecosystems on Earth¹. During the past decades, our understanding has increased about the important role of large mammalian herbivores (body mass >10 kg)² in controlling vegetation structure and carbon and nutrient flows within ecosystems. In herbivore-exclusion experiments, large herbivores have been shown to reduce woody cover^3,4, modify the traits and composition of herbaceous species^5,6, accelerate nutrient cycling rates^7,8, increase grassland primary production^9,10, and reduce fire occurrence¹¹. In paleo-ecological studies, the late Pleistocene megafaunal extinctions have been shown to result in cascading effects on vegetation structure and ecosystem function¹², including biome shifts from mixed open woodlands to more uniform, closed forests, and increased fire activities^13,14.

During the last glacial period from 110 to 14 ka BP (before present), the mammoth steppe ecosystem, also referred to as “steppe-tundra” or “tundra-steppe”¹⁵, prevailed in Eurasia and North America, covering vast areas that are occupied by boreal forests and tundra today^16–20. Characterized by a continental climate, intense aridity, and domination of herbaceous vegetation including graminoids, forbs and sedges, the mammoth steppe sustained a high diversity and probably a high density of megafaunal herbivores like woolly mammoth, muskox, horses, and bison^19,21–23. Yet the main driving force of the maintenance and disappearance of mammoth steppe remains controversial. Alternative to the climate hypothesis which attributes the end-Pleistocene vegetation transformation and mammalian extinctions to climate change, the “keystone herbivore” hypothesis argues that megaherbivores have maintained mammoth steppe through complex interactions with vegetation, soil and climate^18,24,25.

The apparent discrepancy between the late Pleistocene dry and cold climates and the abundant herbivorous fossil fauna found in the mammoth steppe biome has provoked long-standing debates, termed as “productivity paradox” by some paleontologists²⁶. Through the general relationship that larger animals require less food per unit body weight, Redmann²⁷ indicated that higher herbivore biomass densities could be maintained if large species dominate the ungulate community. Studies of modern analogous steppe communities in north-eastern Siberia emphasized the mosaic character of vegetation as a crucial factor in supporting herbivores, with various herbaceous plant types and landscape units of different productivities, depending on local heat and moisture supply affected by local topography^15,21. However, a large-scale quantitative analysis is missing about how local evidences for abundant megafauna^19,23 can be reconciled with low vegetation productivity under glacial climates and low atmospheric CO₂ concentrations²⁸, calling for the integration of interactions between large herbivores and terrestrial productivity within process-based ecosystem models.

Over the past 20 years, dynamic global vegetation models (DGVMs) have been developed and applied to simulate the global distribution of vegetation types, biogeochemical cycles, and responses of ecosystems to climate change²⁹. However, despite the non-negligible ecological impacts of large herbivores, most of the current DGVMs, or land surface models that include a dynamic vegetation module, lack explicit representation of large herbivores and their interactions with vegetation. One exception is the LPJ-GUESS which included a grazer module³⁰ and was applied to present-day Africa to study the potential impact of large grazers on African vegetation and fire³¹.

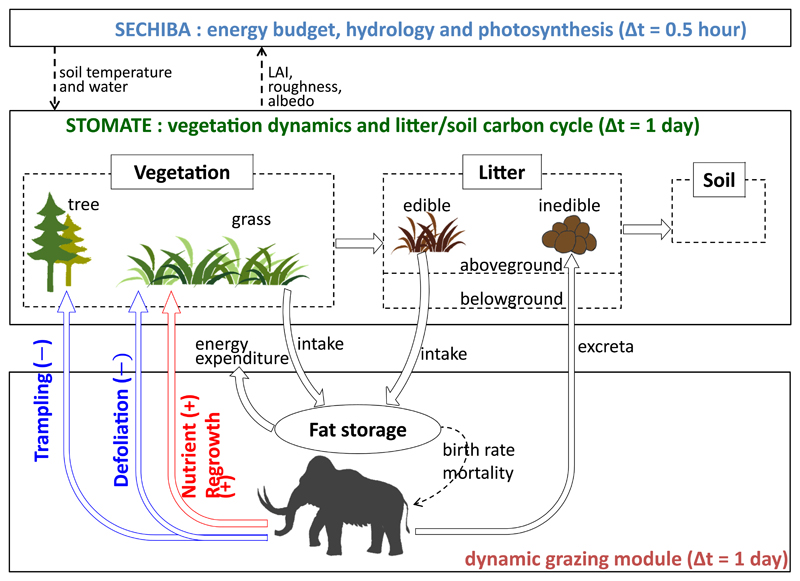
In this study, aiming to address the productivity paradox, we extended the modelling domain to the globe for two distinct periods, present-day and the last glacial maximum (LGM, ca. 21 ka BP), using the ORCHIDEE-MICT DGVM model^32,33. We incorporated the dynamics of large grazers within ORCHIDEE-MICT based on equations describing grass forage intake and metabolic rates dependent on body size, and demographic parameters describing the reproduction and mortality rates of large grazers^30,34 (Fig. 1). Feedbacks of large grazers on vegetation were simulated through simplified parameterizations for trampling of trees, grass biomass removal, and productivity enhancement by grazing calibrated from field experiments (Fig. 1, see detailed description in Methods section “Effects of grazers on vegetation”). Grazers were represented with a prescribed average body size, while browsers (i.e. herbivores feeding on woody plants) were not included, assuming herbaceous plants to dominate the diet of large herbivores^17,35,36. Simulated present-day grazer biomass were evaluated against field observations in protected areas across a wide range of ecosystems. For the LGM, we found that the larger mean body size of grazers than today is the key parameter that allows the model to reproduce a substantial density of large grazers on the cold steppe during the LGM.

Figure 1. Coupling between the ORCHIDEE-MICT dynamic vegetation model and the grazing module.

The grazing module, incorporated in this study, simulates wild grazer density supported by grassland production, and feedbacks (blue and red arrows) of grazers on vegetation (see Methods). The black arrows represent carbon fluxes among grass, grazer and litter.

Results

Present-day grazer biomass

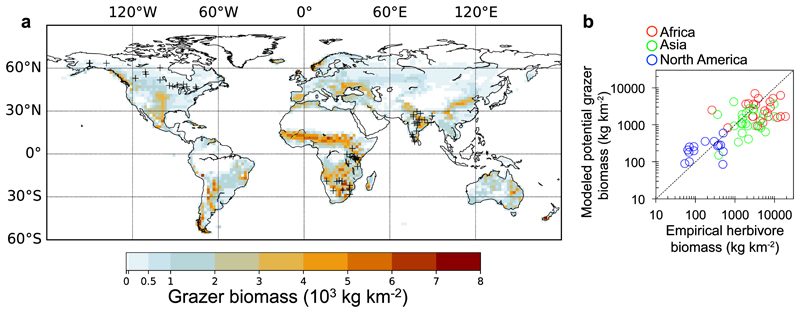
Simulated grazer biomass densities are shown in Fig. 2 for present-day (PD) climate conditions. They were in reasonable agreement with the herbivore densities observed in protected areas from Hatton et al.³⁷ (Fig. 2b). Model-data misfits may be due to simplifications of the grazing module (see Methods). First, the lack of browsing process underestimates food availability for herbivores. This leads to an underestimate for large herbivore populations not only because of missing browsers and underestimated mixed feeders, but also because of underestimated grazers, since conventional grazers can have some portion of woody plants as well in their diets, affected by available forage types^35,36. Second, the lack of explicit representation of predation, competition for resources like water and shelter, poaching in protected areas, outbreak of diseases³⁸, and hunting in the North American ecosystems³⁹, may lead to an overestimation of large grazer biomass compared to the Hatton et al.³⁷ data. In addition, bias of grass productivity in the model can also result in errors in the modelled grazer density. We verified that the simulated global pattern of grass gross primary productivity (GPP) generally matches an observation-driven dataset⁴⁰, yet with an overestimation in subarctic regions (Supplementary Fig. 1). This overestimation of grass GPP might be due to the high grass fractional cover produced by the vegetation dynamics module (Supplementary Fig. 1a) which does not represent shrubs, mosses and lichens³³.

Figure 2. Modelled potential large grazer biomass density for present-day (1960-2009 mean).

(a) Potential density without consideration of human land use, after subtracting the fractions of tropical rainforest (see Supplementary Note 1). The black crosses in (a) symbolize the locations of the empirical data from Hatton et al.³⁷, shown in (b) and listed in Supplementary Table 1. (b) Comparison between empirical herbivore biomass³⁷ and modelled potential grazer biomass (Pearson correlation coefficient r=0.55, n=63, p<0.01). The dashed line represents the 1-1 line.

Figure 2a shows the modelled global distribution of potential grazer biomass density for PD, after subtracting the fractions of tropical rainforest (see Supplementary Note 1). In order to estimate the reduction of wild large grazers due to human land use, we made use of the anthropogenic biome classification system from the Anthromes version 2 product⁴¹, which separated three major categories: Used, Seminatural, and Wild. We assumed the remnant habitat for large grazers to be the Wild category as a lower estimate, and the Seminatural and Wild categories as an upper estimate. The resulting spatial distributions are shown in Supplementary Fig. 2, and the regional total values are listed in Supplementary Table 2.

Simulated global potential biomass of large grazers for PD was slightly smaller than the pre-industrial (PI) value (Supplementary Table 2), mainly due to a slight decrease in modelled grassland area. This indicates that climate change and the increase of CO₂ by 100 ppm during the past century have had minor effects on potential grazer biomass. However, subtracting the used land by humans led to a 41-83% reduction of the potential biomass of wild grazers for PI, and an even greater reduction (79-93%) for PD due to the expansion of agricultural land use and settlements during the past century. Note that the estimated reduction here only considers the direct replacement of wildlife habitats by human land use, whereas other threats to wild grazers including hunting, competition with livestock, disease transmission from domestic to wild species, loss of genetic diversity, and the synergies among these threats⁴², are not included.

LGM grazer biomass

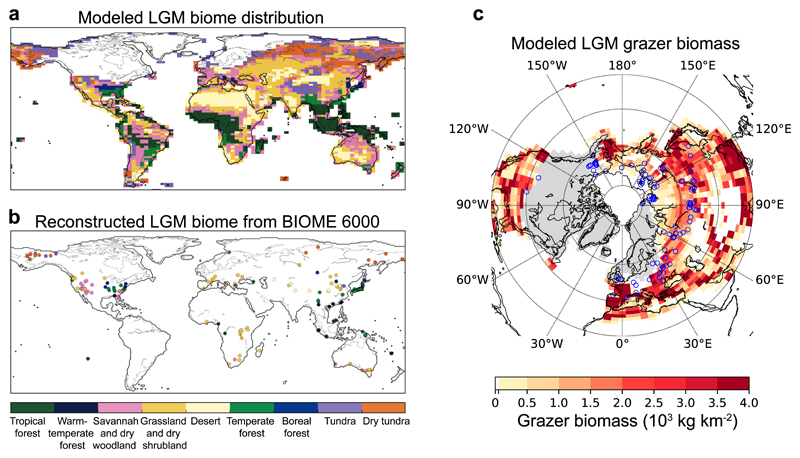
The biomass of large grazers at the LGM is closely related to the vegetation distribution and its productivity. In order to evaluate the simulated LGM vegetation, the plant functional types of the model were regrouped into the mega-biomes of the BIOME 6000 reconstruction based on pollen and plant macrofossil data^43,44 (Supplementary Note 2). The model can capture the retreat of forests in the northern middle and high latitudes during the LGM, largely replaced by grassland and tundra, in accordance with BIOME 6000 data (Fig. 3a and 3b). The scarcity of palaeoecological records, however, precludes a more quantitative evaluation of the modelled vegetation distribution.

Figure 3. Modelled LGM biome distribution and large grazer biomass density.

(a) Simulated biome distribution at the LGM, converted from the modelled plant functional types (PFTs) properties using the algorithm described in Supplementary Note 2, in comparison with reconstructions based on pollen and plant macrofossil records compiled by the BIOME 6000 project⁴³,⁴⁴ (b). (c) Simulated grazer biomass density at the LGM for Northern Hemisphere (north of 20°N). Blue circles on (c) indicate the dated megafauna fossil localities compiled by Lorenzen et al.²², corresponding to the time interval of 26-20 ka BP.

Figure 3c shows the simulated LGM grazer biomass density for the Northern Hemisphere. The spatial distribution can generally match the distribution of megafaunal fossil occurrences, with 60% of the locations where fossils have been found being in grid cells with a grazer density larger than 500 kg km^-2 (Fig. 3c). Compared with two reconstructions of large herbivore density of ca. 9 tonne km^-2 by Zimov et al.¹⁹ in northern Siberia and by Mann et al.²³ in arctic Alaska averaged for the period of 40-10 ka BP, our simulated grazer density was only ca. 1 tonne km^-2. This large underestimation is possibly due to: 1) a low bias of our model results using LGM climate, since the reported bone abundance is an average during 40-10 ka BP^19,23, a period during which LGM corresponds to the most severe climate, 2) uncertainties in the LGM climate used to force our DGVM model, considering limitations of climate models in capturing sub-continental patterns of temperature and precipitation for the LGM⁴⁵; and 3) the coarse resolution (ca. 30,000 km² for one pixel near 70°N) of our model results that do not capture local conditions of the areas from where densities were reconstructed (river banks and lowland sections of 10-80 kilometers^19,23). A simple sensitivity test was conducted for the two grid cells corresponding to the studies of Zimov et al.¹⁹ and Mann et al.²³, by setting temperature to be warmer by 1 or 2°C and annual rainfall to be higher by 50% or 100% (Supplementary Fig. 3). Grazer biomass density for both grid cells could increase to 4 tonne km^-2 in the case of +2°C warmer temperature and 100% higher rainfall, indicating a strong sensitivity of grazer biomass to the slightly milder climates in the context of very cold and dry conditions. This strong sensitivity is supported by the evidence of high variations in megafaunal populations during 45-10 ka BP, with peaks of bone abundance at warm interstadial periods⁴⁶.

Effects of temperature and body size on grazer biomass density

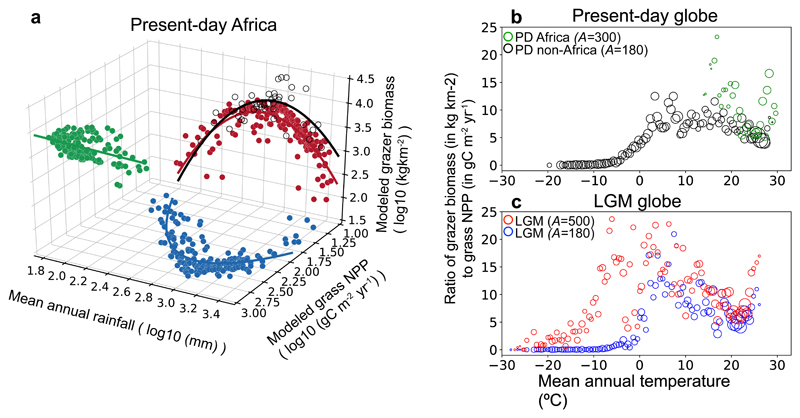
Climate conditions control large grazer densities through grass NPP supporting herbivores and the herbivore-ecosystem feedbacks (see Fig. 1). For present-day Africa, modelled relationship between potential grazer density and mean annual precipitation (MAP) was unimodal (Fig. 4a, red), close to the relationship found by ref47 based on observations (Fig. 4a, grey). The grazer density showed a peak at ca. 700 mm MAP, and gradually decreases under higher MAPs mainly due to grasslands being out-competed by trees, despite trampling by herbivores. This unimodal relationship mirrors the relationship between modelled grass NPP and MAP (Fig. 4a, blue), because of the roughly linear relationship between potential grazer density and grass NPP in Africa (Fig. 4a, green).

Figure 4. Relationship between modelled grazer biomass and grass NPP, affected by temperature and body size.

(a) Relationships between log-transformed grass NPP, grazer biomass and rainfall in present-day (PD) Africa. Points represent median values for 10 mm rainfall bins and are shown with regression lines using linear function for grazer biomass-grass NPP relationship (green) and quadratic function for grass NPP-rainfall (blue) and grazer biomass-rainfall (red) relationships. The grey open circles represent wild herbivore biomass data compiled by ref47 for 41 sites in Africa. A 2-D version of this figure is also shown in Supplementary Fig. 4. (b,c) Relationship between the grazer biomass-to-grass NPP ratio and mean annual temperature (MAT) for PD and LGM. Circles represent median values for 0.5 ºC MAT bins, with the size of each circle proportionate to the number of pixels in each bin. A indicates grazer body size (kg ind.^-1) prescribed in the model: for PD, 180 (except in Africa where A = 300) is used according to Hatton et al.³⁷; for LGM, 500 is used according to reconstructions by Mann et al.²³ and Zimov et al.¹⁹, and a sensitivity test with A=180 is conducted (see Methods).

For the globe, however, the relationship between grass NPP and potential grazer density was strongly affected by mean annual temperature (MAT) (Supplementary Fig. 5). In regions with MAT above ca. 0 °C, the grazer biomass-to-grass NPP ratio generally stayed in the range 5-10 (in kg live weight km^-2 : g C m^-2 yr^-1) (Fig. 4b); whereas in colder regions, the same grass productivity supported much less grazers, with barely any grazers when MAT is below -10 °C. This strong reduction of grazer biomass per unit of grass NPP under low MATs resulted from: 1) the energy expenditure which increases exponentially with decreasing temperature for mammals (Methods equation (3)), and 2) the growing season being shorter in high latitude regions compared to tropical and temperate regions, which leads to longer starvation period with low temperatures, acting to reduce fat reserves and birth rates and to increase starvation-induced mortality (Methods equations (6)-(8)).

Body size is a key parameter in the physiological equations in the model (see Methods). In the LGM run with body size (A) prescribed as 500 kg ind.^-1 (per individual), derived from the reconstructions by Mann et al.²³ and Zimov et al.¹⁹ based on the relative bone abundance of different taxa, the grazer biomass-to-grass NPP ratios were higher than in the PD run, especially for colder regions (Fig. 4c red). The strong reduction of this ratio occurred only below an MAT threshold of ca. -10 °C, instead of 0 °C in the PD run. We further conducted a sensitivity test for the same LGM run except that A was prescribed as 180 kg ind.^-1, the same as for PD in the northern hemisphere³⁷ (see Methods). The relationship between the grazer biomass-to-grass NPP ratio and MAT (Fig. 4c blue) was broadly similar to that in the PD run, despite larger variations than PD for MATs near 5 °C. Thus, Fig. 4c shows that a larger body size in the LGM effectively counteracted the effect of colder temperatures on grazer density. As denoted in Methods equations (1) and (3), when body size increases, the maximum forage intake rate increases faster than the energy expenditure, because the scaling exponent of intake in equation (1) (0.88 for grass living biomass and 0.84 for dead grass) is larger than that of energy expenditure (0.75). This leads to a more efficient exploitation of grass production by grazers with a larger-body size, thus a higher grazer density supported by the same level of grass production.

The spatial distribution of grazer biomass at the LGM in the sensitivity test with A equalling to 180 kg ind.^-1 is presented in Supplementary Fig. 6, showing that grazers could have barely existed in the mammoth steppe ecosystem in Eurasia and North America if they had a body mass as low as today’s northern herbivores. The global total grazer biomass would be only 235 million tonnes live weight, much less than that with A equalling to 500 kg ind.^-1 (319 million tonnes). This suggests that, during the LGM, the cold steppe in the middle and high latitudes was able to sustain substantial quantities of grazers mainly because the mean grazer body size was much bigger than today.

Impacts of grazing on land carbon cycle during the LGM

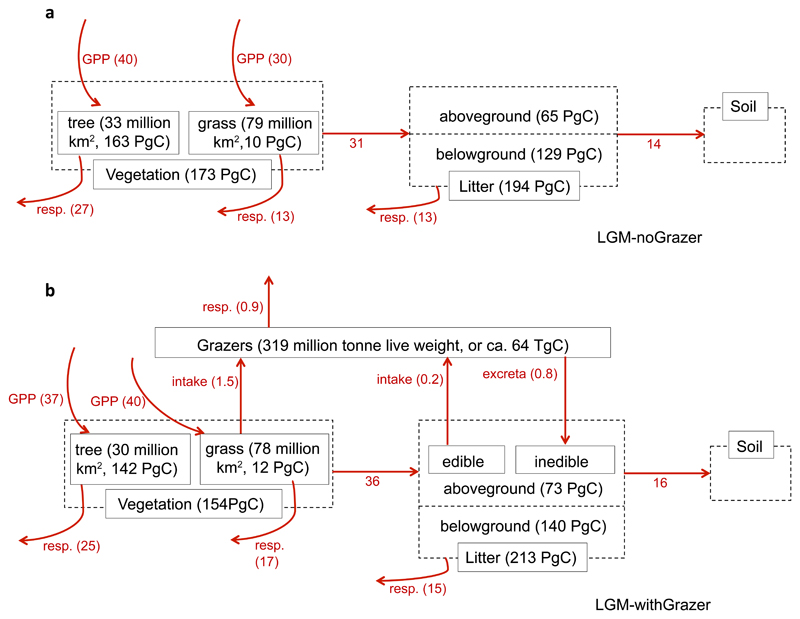
Due to the strong human intervention in today’s biosphere⁴⁸ and the human-caused collapse of large herbivore populations⁴², we focus on the LGM to analyse the impacts of grazing on vegetation distribution and the carbon cycle, by comparing the model results with and without grazers. Figure 6 presents the effect of grazers on the global land carbon fluxes during the LGM. Total NPP simulated with grazers was 35 Pg C yr^-1, 17% higher than without grazers. Turnover times of tree and grass biomass decreased from 12.5 and 0.57 years without grazers to 11.8 and 0.52 years with grazers. For trees, the additional trampling-induced mortality contributes to the faster turnover rate and lower equilibrium biomass than without grazers. For grasses, the continuous consumption by grazers removes aboveground biomass at a higher rate than by normal senescence in the simulation without grazers. For the total vegetation as a whole, turnover rate increased by 31%, not only because of faster cycling in grass and tree biomass, but also because of the smaller total forest area (30 vs. 33 Mkm²). More details on the effect of grazing on tree cover and carbon stocks and fluxes can be found in Supplementary Discussion.

Discussion

We implemented dynamic herbivores and their effects on vegetation types and the land carbon cycle in the ORCHIDEE-MICT DGVM model, based on physiological and demographic equations for large grazers. Evaluation against today’s empirical herbivore biomass data for protected areas across a wide range of ecosystems shows a reasonable model performance in simulating potential grazer biomass sustained by the grassland ecosystems. We then presented the global results of potential large grazer biomass for present-day and the LGM.

In the context of the so-called productivity paradox of the late Pleistocene mammoth steppe biome, our model shows that only if the prescribed average body size was much higher than today (500 vs. 180 kg ind.^-1) could high grazer densities be simulated under the harsh climate and low atmospheric CO₂ during the LGM. This property emerges from the different scaling of forage intake and energy expenditure with body size, namely, the allometric exponent of intake (0.88 for living grass and 0.84 for dead grass, Methods equation (1)) is higher than the exponent of expenditure (0.75, Methods equation (3)), the former from an animal model calibrated for cattle³⁴, and the latter conforming to the metabolic theory⁴⁹. A collection of body mass and dry matter intake across 46 large mammalian herbivores (body weight > 10 kg)⁵⁰ gives a value of 0.85 for the scaling exponent (Supplementary Fig. 7), which is indeed higher than the 3/4 power scaling of metabolic rates and production rates^37,51, and supports the high values used in our model. Note that the exponent of intake increases with forage digestibility (equation (1)), which are fixed values in the current model. In reality, digestibility varies at different phase of growth, with higher values in the early growing season, and decreases with the accumulating grass biomass⁵². Therefore, a potential positive feedback of large grazers on forage digestibility is missing in the model. Besides, the scaling exponent was reported to be different between ruminants (ca. 0.88) and hindgut fermenters (ca. 0.82)⁵³, thus the value for an “average grazer” may be lower than the values used in the current model, close to the regression coefficient of 0.85 by ref.50.

Evidences from fossil^54,55 and extant⁵⁶ mammal species have shown a long-term trend towards increasing body size in mammals throughout the Cenozoic, i.e. Cope’s rule in evolutionary biology⁵⁴. This indicates selective advantages of larger body sizes, such as larger guts of herbivores that allow microbes to break down low-quality plant materials, and higher tolerance to coldness and starvation⁵⁶. Our results show quantitatively the importance of body size to explain the productivity paradox, as a larger-body size enables grazers to live on the mammoth steppe in substantial densities during the LGM, despite colder temperatures and shorter growing seasons than today. After the end-Pleistocene extinction of large-body size species, to which the contributions of humans versus fast climate change remaining debated⁵⁷, the average body size of herbivores reduces, and the boreal and arctic grasslands today can only sustain a low biomass density of grazers (Figs. 2 and 4).

One limitation of our current model is a lack of separation among large herbivore species or types, in particular a specific representation of megaherbivores (body mass > 1000 kg). The keystone herbivore hypothesis is centred on the pivotal role of megaherbivores in creating and maintaining an open habitat dominated by fast-growing, more nutritious short grasses and woody plants, the habitat that is crucial for many smaller herbivores²⁴. This appears to be supported by observations in present-day Africa^58,59 that white rhino, not the smaller grazers, were able to maintain short grass communities, the loss of which led to declines in smaller grazers like impala and zebra. This interaction among plants, megaherbivores and smaller ones is, however, dependent on vegetation productivity along environmental gradients^58,60. Therefore, to expand the “average grazer” in our current model to a framework of herbivore functional types (HFTs, e.g. refs^31,61) is a future priority; and a mechanistically coupled HFTs and vegetation dynamics in DGVM models could be a promising tool to quantitatively investigate the ecological impacts of large herbivores.

For the ecological impacts of large grazers, our results show a general reduction of tree cover and an increase in grassland productivity with grazers (Fig. 5 and Supplementary Discussion). The current model, however, does not represent the composition changes of herbaceous species under grazing (which favours annual over perennial plants, short over tall plants, and high over low specific leaf area)^5,6, as well as competition between shrubs, mosses and grasses under grazing pressure^4,62. In a tundra ecosystem⁶², a heavy grazing has led to a transition from moss-rich heathland into graminoid-dominated steppe-like vegetation, and thus increased the aboveground primary production. Therefore, to better simulate the grazer-induced changes in biogeochemical cycle in DGVM models would require an explicit representation of mosses and shrubs, and their competition with grasses affected by grazers. It is worth noting that to disentangle the relative contribution of the factors, including species changes and increased nutrient availability, to the enhanced productivity is difficult in field grazer-exclusion experiments. The lack of a fully closed nutrient cycle in our model also limits its accuracy to estimate the full impact of grazers on ecosystems.

Figure 5. Modelled global carbon fluxes (red arrows, unit: Pg C yr^-1) among different reservoirs at the LGM.

(a) De-activating the grazing module; (b) activating the grazing module. The black numbers give the standing stocks of different pools at equilibrium, including tree and grass living biomass, litter, and grazers.

What adds more complexity to the ecological impacts of large grazers is a set of physical properties that are affected by grazing, especially in cold regions. As argued in refs^18,19,63, during summer, by removing the insulating moss carpet and litter layer, large grazers might increase soil temperature and deepen annual thaw depth and root penetration; during winter, by trampling snow in search for food, they might lower soil temperature in winter, meanwhile, quicken the spring melt of snow due to a lower albedo of dirty snow, and lengthen growing season. To test the magnitude of such effects requires parameterization of these biotic-abiotic interactions in future model developments. Large herbivores might have fundamentally modified Pleistocene ecosystems; to bring them into large-scale land surface models would help us better understand the intricate interactions among climate, plants and animals that shaped the biosphere.

Methods

ORCHIDEE-MICT model overview

ORCHIDEE (Organizing Carbon and Hydrology In Dynamic Ecosystems) is a process-based DGVM model designed for multi-scale applications³². It consists of two main modules: SECHIBA for energy and water exchanges and photosynthesis at half-hourly time-step, and STOMATE for vegetation dynamics and carbon cycle at daily time-step (Fig. 1). The model describes the land surface using a “tile” approach, i.e. each grid cell is occupied by a set of plant functional types (PFTs), with the fractional covers of all PFTs adding up to one. In the current model there are 13 PFTs, including 8 for trees, 2 for natural grasses (C3 and C4), 2 for crops, and bare land. PFTs go through the same suite of processes (photosynthesis, phenology, allocation of carbon assimilates to plant biomass compartments, carbon flow from living biomass to litter pools after senescence and/or mortality, and from litter to soil carbon pools, and heterotrophic respiration), but with PFT-specific parameter values, as detailed in ref32. Vegetation distribution, i.e. fractional covers of the PFTs, is simulated by the vegetation dynamics module through bioclimatic limits, competition between PFTs for space and light, and a series of mortality process³³. The soil thermal and hydrological dynamics are represented by a physically based multi-layer soil structure to simulate heat transfer and water movement between air and deeper soils^64,65. These physical processes interact with the vegetation and carbon processes mentioned above (Fig. 1).

Inputs required by ORCHIDEE include meteorological variables (surface air temperature, precipitation, air humidity, incoming short and long wave radiation, wind, and air pressure), atmospheric CO₂ concentration, and soil texture. For each simulation, the model needs to run at first a period of “spin-up”, namely, starting from zero carbon fluxes and pools, full cover of bare land, and default values for physical variables, the model gradually approaches an equilibrium state given the inputted climate and atmospheric CO₂ conditions. Then, transient simulations for the target time period can be conducted from the last year of spin-up. In ORCHIDEE, the spatial resolution of each simulation depends on the resolution of input climate forcing.

ORCHIDEE-MICT is an evolution of ORCHIDEE with additional high latitude processes, including a soil freezing scheme which simulates the liquid and solid water fractions in the soil and associated energy balance⁶⁶, a multi-layer snow scheme which improves the representation of snow thermal conductivity and soil temperature⁶⁷, and a vertically resolved litter and soil carbon module considering permafrost processes^68,69.

To incorporate grazing processes in ORCHIDEE-MICT, we firstly adapted the structure of the ORCHIDEE-GM version 2.1 (grassland management, ref70), originally designed to simulate the greenhouse gas balance of pastures, including forage consumption by grazing that decreases aboveground living biomass and keeps leaf age younger, excreta return that affects the decomposability of the litter pools, and animal respiration. We also revised two photosynthesis parameters for the grass PFTs, namely the maximum rate of Rubisco carboxylation (v_cmax) and the maximum specific leaf area (SLA_max), to be the same as those calibrated by Chang et al.⁷¹ based on literature analysis for modern grasslands. As in ORCHIDEE-GM, we simulate large grazers only, so biomass intake through browsing on woody plants is not included. The carbon mass simulated by ORCHIDEE-MICT is converted into dry matter mass used in the grazing module by dividing by 0.45. We further adapted the grazer population model of Illius and O’Connor³⁴ into ORCHIDEE-MICT, which calculates energy intake and expenditure, reproduction, and mortality using empirical relationships with body size. A major difference from the original equations proposed by Illius and O’Connor model is that we did not separate animals into age classes, thus there is only one type of “average grazer” with fixed mature body mass (denoted as A). Detailed implementations are described below.

The grazer population model

Daily intake and expenditure

For wild large grazers, the reduction in food resources during the non-growing season critically limits their density⁷². Unlike domestic livestock on pastures that can be fed on forage grass or crop products, wild herbivores resort to various ways to acquire energy during the non-growing season, such as migration and feeding on dead grasses⁷³. In the grazing module in ORCHIDEE-MICT, in order to sustain grazers throughout the year, especially for the high latitude regions with a short growing season, we divided the simulated aboveground litter pool of grass PFTs into two parts, an edible pool (L_edi, representing plant residues) and an inedible one (representing animal excreta) (Fig. 1). Grazers are allowed to eat L_edi when confronted with insufficient AGB (aboveground grass biomass of three tissues represented in ORCHIDEE, i.e. leaf, sapwood and fruit).

Maximum daily intake. The maximum forage intake in units of energy is related to grazers’ body size and forage digestibility (d), since a low digestibility diet decreases the rate of digestion of ungulates and thus limits the maximum intake^53,74, which is calculated as in Illius and O’Connor model³⁴:

$$I_{\text{max}}=0.034e^{3.57d}{A}^{\left(0.077e^d+0.73\right)}$$ (1)

where I_max (MJ d^-1 ind.^-1) is the maximum daily net energy intake per individual; A (kg live weight ind.^-1) the mean grazer body mass; d the forage digestibility, fixed at 0.7 for AGB and 0.4 for L_edi, following ref34.

The maximum intake in units of dry mass is converted from I_max by:

$$I_{DM,\text{max}}=\frac{I_{\text{max}}}{ME\times DE}$$ (2)

where I_DM,max (kgDM d^-1 ind.^-1) is the maximum daily dry matter intake; ME (MJ kgDM^-1) the metabolizable energy content, calculated as 15.6×d, following Pachzelt et al.³⁰; DE the digestible energy proportion in the forage not excreted in the faeces, fixed as 50%⁷⁵.

Daily energy expenditure. Energy expenditure in the original Illius and O’Connor model³⁴ applied to tropical grasslands was a function of body mass only, and did not account for environmental conditions. Ambient temperature has been shown to significantly affect energy expenditure for endotherms⁵¹. Since we aim to apply the model globally, we introduce the following equation to account for temperature dependent metabolic rate:

$$E=\frac{k_2}{e^{k_1\times T}}\times A^{0.75}$$ (3)

where E (MJ d^-1 ind.^-1) is the daily energy expenditure per individual; T (ºC) the long-term mean air temperature for each grid cell, calculated in the model using a linear relaxation method (see Eq. 3 in Krinner et al.³²) with the integration time equaling to 3 years; k₁ equals to 0.0079, derived from the regression model of Anderson and Jetz⁵¹; k₂ equals to 0.36, calibrated to yield a range close to the values in ref34. Note that this parameterization may overestimate energy expenditure for the large herbivores adapted to cold climates like woolly mammoth and muskox, which may spend less energy due to the insulating heavy hair coat and thick fat layer²⁶.

Conversion between energy and fat storage. Fat is the main energy reserve and affects the survival of grazers confronted with food shortages⁷⁴. The daily change in fat storage is calculated as:

$$\frac{dF}{dt}=\frac{I-E}{m}$$ (4)

where F (kg ind.^-1) is the fat mass per animal; I (MJ d^-1 ind.^-1) the actual daily net energy intake (described below); m (MJ kg^-1) the conversion coefficient between energy and fat, set at 39.3 if I<E (catabolism) or 54.6 if I>E (anabolism) (ref³⁴). Note that the body mass, A, is a fixed parameter in the model, neglecting the daily-changing F.

Actual daily intake. Actual daily intake depends on the amount of available forage. At each daily time step, the model determines whether grazers feed on AGB, L_edi, or nothing, by comparing the daily forage requirement, calculated as I_DM,max×P, given a population density P (ind. km^-2) calculated by the model (see below), with the amount of available AGB or L_edi. Grazers are assumed to feed in priority on i) AGB, if available AGB exceeds the AGB requirement; ii) L_edi, if condition i) is not met and L_edi exceeds the L_edi requirement; and iii) nothing, if neither conditions i) nor ii) are met. Note that I_DM,max for AGB is higher than for L_edi, i.e. the AGB requirement is always higher than the L_edi requirement, according to equation (1) and (2). A buffer time of five days is set to prevent grass from being grazed at the beginning of the growing season, i.e. the grazers are assumed to wait for five days to eat AGB after it first exceeds the forage requirement.

Actual intake also has a constraint so that a maximum fat storage cannot be exceeded, which is given by:

$$I=\{\begin{array}{ll}{I}_{\text{max}}\hfill & ifF+\frac{I-E}{m}\le F_{\text{max}}\hfill \\ m\times \left(F_{\text{max}}-F\right)+E\hfill & else\hfill \end{array}$$ (5)

where F_max (kg ind.^-1) is the maximum fat mass, set at 0.3×A (ref³⁴).

Note that the reduction factor of I_max with decreasing vegetation biomass density in the original Illius and O’Connor model³⁴ is not used here, assuming that the grazers have good access to the forage and can fulfil their daily demand whenever AGB or L_edi is higher than the forage requirement.

Grazer population dynamics

In ORCHIDEE-MICT, the grazer population density is updated at the end of each year, based on calculated annual mean birth and mortality rates, as described in the following.

Birth rate. Birth rate depends on body condition, represented by a function of the ratio of the fat storage to the maximum fat mass, following ref34:

$$B_{\text{max}}=\frac{0.8}{1+e^{-15\times (\frac{F}{F_{\text{max}}}-0.3)}}$$ (6)

where B_max (yr^-1) is the maximum birth rate, calculated at daily time-step and averaged over the year to be used in equation (7).

In this study, the actual birth rate is also constrained by fat storage, which implicitly considers the energy investment in breeding:

$$B=Minimum(B_{\text{max}},\frac{m\times F}{E\times 365})$$ (7)

where B (yr^-1) is the actual birth rate at the end of the year. Then the amount of energy $\frac{B\times E\times 365}{m}$ is subtracted from F to account for the energy transferred to newly added grazers.

Mortality rate. In the Illius and O’Connor model³⁴, mortality was caused by the exhaustion of fat storage during periods of food shortage. In ORCHIDEE-MICT, we define it as starvation-induced mortality (M_s), and calculate it using the same method as in Illius and O’Connor model: we assume the fat storage to be a normal distribution with a mean µ=F and a standard deviation σ = 0.125 × F_max; then the cumulative distribution function of fat storage returns the probability (defining the value for M_s) that fat mass is below a prescribed threshold F_thresh. The value of F_thresh was set at 0 in the original Illius and O’Connor model, but we set F_thresh at −0.2 × F_max, so that the grazers, especially those on temperate and boreal grasslands, could tolerate longer periods of starvation. The mortality rate M_s in the unit of yr^-1 is calculated at daily time-step and averaged over the year.

In addition to M_s, two other causes of mortality are taken into account: i) a background mortality rate (M_b) which is defined as the inverse of animal lifespan, fixed at 25 years³⁰; and ii) a density-dependent mortality rate (M_d=k_d×P) which represents the fact that a higher density leads to a more intensive competition between animals for limited resources (e.g. water and living space), and to more frequent epizootic diseases.

Therefore, the equation to calculate the dynamic annual evolution of grazer population density is:

$$\frac{dp}{dt}=B\times P-M_b\times P-M_s\times P-k_d\times P^2$$ (8)

where P (ind. km^-2) is the grazer population density, updated each year; P is initialized as P₀=0.001 ind. km^-2; whenever P is below P₀, P is reset to P₀ and F is reset to 0; k_d is the slope of the density-dependent mortality function, calibrated based on the property of equation (8) that the maximum P equals to $\frac{B-M_b}{k_d}$ given an infinite time under constant optimal condition (M_s =0, M_b =0.04, and B ≈ 0.6 according to Eqs. 6 and 7); the value of k_d is therefore set at $\frac{A}{3\times {10}^4},$ derived from observed maximum densities of 15~18×10³ kg km^-2 for large herbivore biomass observed in protected areas across Africa today (Hatton et al.³⁷; Supplementary Table 1).

Effects of grazers on vegetation

A direct negative impact of grazers on grass productivity is through biomass removal by grazing. This is included in the coupling between grazing and carbon cycle processes, as leaf area index (LAI) is updated every day in the model following the leaf mass reduction. Besides, a positive effect on grass productivity due to regrowth after defoliation is represented in the model by, first, the leaf age-related photosynthetic capacities, with younger leaves having a higher photosynthetic efficiency (see Eq. A12 in Krinner et al.³²), and second, the leaf age-related specific leaf area (SLA), with younger leaves having a higher SLA and subsequently a more rapid increase in LAI after a daily grazing event than if SLA was constant⁷⁰. Grazers could also positively affect grass productivity through accelerating nutrient turnover and modifying the traits and composition of herbaceous species^7,10,62, which may be more important than the regrowth effect. To explicitly represent these effects is difficult, partly because that our model lacks an explicit nutrient cycle and has limited herbaceous plant functional types (only two grass PFTs, C3 and C4, for natural non-woody plants) with fixed sets of traits, partly because that the observed enhancement of grass production by grazing in field experiments is a result of various effects mentioned above, making it difficult to be used for calibrating parameters for each individual pathway in a model. Therefore, we used a simple parameterization, i.e. a grazer density-related photosynthetic capacity, to coarsely approximate the positive effects of grazers associated with accelerated nutrient cycling and traits/composition changes, as detailed below.

Grazer density-related v_cmax and j_max

The enhancement of primary production by grazing has been observed in a wide range of ecosystems, such as African savannahs^76,77, North American grasslands⁹, and Arctic tundra^8,62, but few studies have reported measurements of both grazer density and its quantitative effect on grass productivity. A field study by Frank and McNaughton^9,78 in Yellowstone national park found a 11-85% higher aboveground net primary production (ANPP) for grazed than ungrazed vegetation, with 23-90% of the ANPP consumed by herds of elk and bison, from which a herbivore density of 2-18×10³ kg km^-2 was inferred.

We thus made a simple modification to the photosynthesis parameters of the maximum rate of Rubisco carboxylation (v_cmax) and electron transport (j_max) (the latter is dependent on v_cmax in the model) for the grass PFTs as a function of grazer density:

$$v_{\text{cmax}}=v_{\text{cmax}}^0\times \left[1+\left(k_a-e^{-k_b\times A\times P}\right)\right]$$ (9)

where k_a equals to 1, i.e. a maximum 2-fold increase from animal-induced nutrient availability, qualitatively in agreement with the results of grassland fertilization experiments compiled by Elser et al.⁷⁹ giving a response ratio of 1.7~2 (primary production in grassland manipulative experiments with nitrogen and phosphorus addition divided by the value in control treatments). The parameter k_b is set at 10^-4, calibrated based on the observed response of ANPP to herbivores by Frank and McNaughton^9,78 cited above.

Tree mortality caused by large grazers

The suppression of trees and shrubs by large mammalian herbivores, favouring grass species, has been observed in African national parks^80,81 and Arctic tundra^4,82. In their tree-population dynamics model developed for the Serengeti-Mara woodlands, Dublin et al.⁸³ proposed a tree mortality caused by elephants of 7% yr^-1 when the elephant biomass density was ca. 2000 kg km^-2, which accounted for 25% of the total herbivore biomass in that region³⁷. This grazer-induced tree mortality is higher than the simulated tree mortality in tropical forests by ORCHIDEE-MICT³³ of about 3% yr^-1.

Since the current version of ORCHIDEE-MICT lacks a specific shrub PFT, we introduced a grazer trampling-related mortality only for the tree PFTs, defined as a linear function of grazer population density:

$$M_{\text{tree},\text{tramp}}=k_{\text{tree},\text{tramp}}\times A\times P$$ (10)

where M_tree,tramp is the grazing-induced mortality rate of tree PFTs each day (d^-1); k_tree,tramp is set at 2.4×10^-8 d^-1, in order to match the observed elephant-induced tree mortality in Serengeti-Mara⁸³.

Evaluation data

Empirical present-day herbivore data

To evaluate the model, we compared the simulated present-day grazer density with the empirical data for large wild mammalian herbivores across various ecosystems (with low human footprints) compiled by Hatton et al.³⁷. Since Hatton et al.³⁷ focused on predator-prey relationships and excluded megaherbivores like elephant and rhinoceros, we re-calculated the total herbivore biomass density of each community, including all reported herbivore species from the raw data provided by Hatton et al.³⁷. Multi-year data for the same ecosystem were averaged, giving 23 protected areas in Africa, 25 in Asia, and 15 ecosystems in North America (Supplementary Table 1). Note that the 15 ecosystems in North America are not game reserves, and human hunting probably decreases animal densities below the local carrying capacities. The empirical herbivore biomass data in Hatton et al.³⁷ included both grazers and browsers, while our model could only simulate grazer densities. In the model-data comparison, it was thus assumed that grazers dominated the herbivore species³⁰, which may be ecosystem-specific.

Reconstruction data for paleo-megafauna

Few studies have investigated the megafaunal populations and biomass densities in the mammoth steppe during the late Pleistocene. By analysing ¹⁴C-dated animal bones accumulated in frozen loess in Siberia and Alaska, Zimov et al.¹⁹ estimated an average herbivore biomass of 10 tonne km^-2 over the period of 40-10 ka BP in northern Siberia, and Mann et al.²³ estimated a similar value of 9 tonne km^-2 for the same period in arctic Alaska. Although the bone abundance varies markedly with time, suggesting temporal instability of the mammoth steppe during the 30,000-year period⁴⁶, these estimates are the best available to date providing information on the magnitude of the biomass of large herbivores at the LGM for comparisons with the simulations.

The geographical ranges of ice-age megafaunal species are useful indicators of their presence in a grid-point of the model. Lorenzen et al.²² compiled a dataset of ca. 800 dated megafaunal fossil localities spanning the past 50,000 years. As a compromise between the number of localities and the period that could be considered coeval to the LGM, we selected the time interval of 26.5-20 ka BP⁸⁴ of these fossil localities (in total 215 localities) to compare with our results at the LGM. Note that debate still exists in the chronological definition of LGM (e.g. ref85), and that northern ice sheets peaked before 21 ka BP⁸⁴. Overlaying the fossil localities onto the simulated biomass density of large grazers enables a qualitative evaluation of the model results, knowing that the incomplete list of fossil localities may under-represent the megafauna’s actual distribution ranges²².

Model setup

Global runs with ORCHIDEE-MICT for present-day and LGM were conducted, as described below and summarized in Table 1.

Table 1.

Summary of the global runs with ORCHIDEE-MICT for present-day and LGM

	Spin-up		Transient simulation		Spatial resolution	Prescribed grazer body size (A, kg ind.-1)
	Climate forcing	Atmospheric CO2	Climate forcing	Atmospheric CO2
Present-day	CRU-NCEP 1901-1910 cycle	Pre-industrial level (285 ppm)	CRU-NCEP 1901-2010	Rising (ref87 after 1959, ref88 before 1959)	2°×2°	300 for Africa, 180 for the rest of the world
LGM	Outputs from IPSL-CM5A-LR, bias corrected	185 ppm86	Same as the spin-up		1.875°×3.75°	500
LGM (A=180)	The same as “LGM” except body size prescribed as 180 kg ind.-1
LGM-noGrazer	The same as “LGM” except de-activating the grazing module

Present-day

For the present-day run (hereafter “PD”), ORCHIDEE-MICT was forced by the 6-hourly CRU-NCEP gridded climate dataset at 2° spatial resolution (https://vesg.ipsl.upmc.fr/thredds/fileServer/store/p529viov/cruncep/readme.html). The model was first run for a 200-year spin-up to reach equilibrium for vegetation biomass and grazers for the pre-industrial period (PI), forced by repeating the CRU-NCEP 1901-1910 climate data (due to lack of gridded climate data for PI) and constant pre-industrial CO₂ concentration (285 ppm). Then a transient simulation for 1860-2010 was started from the last year of the spin-up, forced by CRU-NCEP reanalysis data from 1901 to 2010 (for 1860-1900, CRU-NCEP 1901-1910 climate were cycled) and by rising CO₂ concentrations. The model results for grazer biomass density averaged from 1960 to 2009 were used as PD, which roughly corresponded with the period for the data compiled by Hatton et al.³⁷. Since grazers in the model only appear on the grass fraction of the land, grazer biomass density for the entire grid cell was thus calculated using the following equation:

$$G{B}_i=P_{i,c3}\times A\times V_{i,c3}+P_{i,c4}\times A\times V_{i,c4}$$ (11)

where GB_i (kg km^-2) is the grazer biomass density for grid cell i; P_i,c3 and P_i,c4 (ind. km^-2) are the respective grazer population densities for the two types of grass PFTs, C3 and C4; and V_i,c3 and V_i,c4 are the fractional cover of the two grass PFTs.

The grazer body size, A, is a key parameter in the model. Note that the value of A, in the concept of “average grazer” in our current model, is the abundance-weighted average body size over different species, i.e. total animal biomass divided by total animal population. For PD, since ref37 provided the population of each herbivore species, a mean body size of ca. 300 kg across 23 ecosystems in Africa and of ca. 180 kg across the ecosystems in both Asia and North America was derived. Therefore, we prescribed A at 300 kg ind.^-1 for Africa and 180 kg ind.^-1 for the rest of the world in the PD run.

Only natural PFTs were simulated in all runs, excluding agricultural land cover. So the results represent a potential grazer biomass density without considering the replacement of wildlife habitats by human land use. The PD results can be compared locally with observations from Hatton et al.³⁷, which are from either protected areas or remote areas subject to minor human effects. For the modelled global distribution as shown in Fig. 2a, the fractional covers of tropical rainforest were subtracted from the direct output of potential grazer density (see Supplementary Note 1). Then, in order to estimate the reduction of wild grazers due to human land use, we applied the Anthromes version 2 map⁴¹, which separated three major categories: Used, Seminatural, and Wild (accounting for a total area of 71, 25, and 32 million km² respectively for the year 2000), to subtract the fraction of the Used category (or Used + Seminatural categories) in each 2° grid cell from the modelled potential grazer biomass, and calculated the relative reductions regionally and globally (Supplementary Table 2).

LGM

For the LGM (21 ka BP) runs, the climate forcing files were the same as those described in Zhu et al.⁶⁸, derived from the simulated LGM climate by the Earth System Model IPSL-CM5A-LR, with a 6-hourly time-step and a spatial resolution of 1.875°×3.75°, bias corrected using the differences between IPSL-CM5A-LR and observed climate in the historical period⁶⁸. Atmospheric CO₂ for the LGM was fixed at 185 ppm⁸⁶, and the land-sea mask was prescribed following the PMIP3 protocol (http://pmip3.lsce.ipsl.fr/). The model was run for 250 years; the first 200 years were discarded as spin-up, and the last 50 years were averaged and presented as the results.

For the LGM, the body size A was set at 500 kg ind.^-1, derived from the reconstructed population density and biomass for several large herbivore species based on their relative bone abundance by Mann et al.²³ and Zimov et al.¹⁹. We also tested the effect of body size by carrying out a similar LGM run except for setting A at 180 kg ind.^-1, the same as that used in the PD run for the northern hemisphere. To study the effects of grazing on vegetation, an LGM run in which the grazing module was deactivated was conducted (denoted as “LGM-noGrazer”).

Code availability

The grazing model used in this study is implemented in the ORCHIDEE-MICT global dynamic vegetation model, with its runtime environment developed at Le Laboratoire des Sciences du Climat et de l'Environnement (LSCE), France. The model, as well as the scripts to derive the results presented in this study from the model outputs, are available from the corresponding author upon request.

Data availability

The relevant model outputs (in NetCDF format) are deposited in the PANGAEA repository at https://doi.org/10.1594/PANGAEA.884853. The other data that support the findings of this study are available from the References or from the corresponding author (dan.zhu@lsce.ipsl.fr) on reasonable request.