Abstract
Purpose
The purpose of this study was to accelerate the acquisition and reconstruction time of 3D Magnetic Resonance Fingerprinting (MRF) scans.
Methods
A 3D MRF scan was accelerated by using a single shot spiral trajectory with an undersampling factor of 48 in the x-y plane, and an interleaved sampling pattern with an undersampling factor of 3 through plane. Further acceleration came from reducing the waiting time between neighboring partitions. The reconstruction time was accelerated by applying SVD compression in k-space. Finally, a 3D pre-measured B1 map was used to correct for the B1 inhomogeneity.
Results
The T1 and T2 values of the ISMRM/NIST MRI phantom showed a good agreement with the standard values, with an average concordance correlation coefficient of 0.99 and coefficient of variation of 7% in the repeatability scans. The results from in vivo scans also showed high image quality in both transverse and coronal views.
Conclusion
This study applied a fast acquisition scheme for a fully quantitative 3D MRF scan with a total acceleration factor of 144 as compared to the Nyquist rate, such that 3D T1, T2 and M0 maps can be acquired with whole brain coverage at clinical resolution in less than 5 minutes.
Keywords: MR Fingerprinting, 3D, T1, T2, Relaxometry
Introduction
Magnetic Resonance Fingerprinting (MRF)(1) is an acquisition and processing framework that utilizes a variable acquisition scheme to enable simultaneous quantification of multiple tissue properties, such as T1 and T2. Currently, most MRF implementations and in vivo applications utilize two dimensional (2D) (2–10) and multi-slice acquisitions(11–13). However, in order to achieve higher through plane resolution, and better tissue characterization, extension to a 3D acquisition is desirable.
In general, the two main concerns of a 3D MRF scan are 1) long acquisition time due to the increased number of excitations necessary to acquire the data and 2) signal intensity inhomogeneity across the 3D volume due to excitation profile imperfections and local changes in the B1 field. Since 3D acquisitions potentially allow a higher acceleration factor and more flexible undersampling schemes as compared to 2D acquisitions, several fast 3D methods have been proposed previously by using non-Cartesian trajectories(14–19), fast sampling schemes(20–22), and incorporating parallel imaging and compressed sensing methods(23–25). Any inhomogeneity in the flip angle can cause errors, which lead to inaccurate T1 and T2 results for many quantitative measurements including MRF scans(26–28). The two common ways to correct for the flip angle error are to premeasure the B1 or flip angle map(3,29,30), or to quantify B1 at the same time as tissue parameters(28,31,32).
The purpose of this study was to accelerate the 3D MRF scan and to correct for the flip angle error, in order to provide accurate T1 and T2 maps of a whole brain scan in a clinically acceptable time. Specifically, this study applied a simple accelerated acquisition scheme similar to k-t BLAST(21) for the 3D MRF scan to allow a total factor of 144 acceleration as compared to the Nyquist rate, so that 3D T1, T2 and proton density (M0) maps can be acquired from a whole brain with a resolution of 1.2×1.2×3 mm3 in less than 5 minutes. In addition, since the 3D MRF scan acquired over 1000 undersampled volumes, a singular value decomposition (SVD) compression(7) was applied in k-space prior to reconstruction to substantially reduce the computing memory and accelerate the post-processing time. To correct for the flip angle error, a 3D slab-selective RF pulse with an optimized excitation profile was used to minimize the excitation profile variation across partitions (or slices in a 3D volume) and a 3D B1 map that was premeasured using the Bloch-Siegert method(3,29) was used to measure the B1 inhomogeneity. The B1 values were then simulated into the dictionary to correct for inaccurate flip angles and improve the accuracy of the resulting T1 and T2 values.
Method
3D Acceleration Scheme
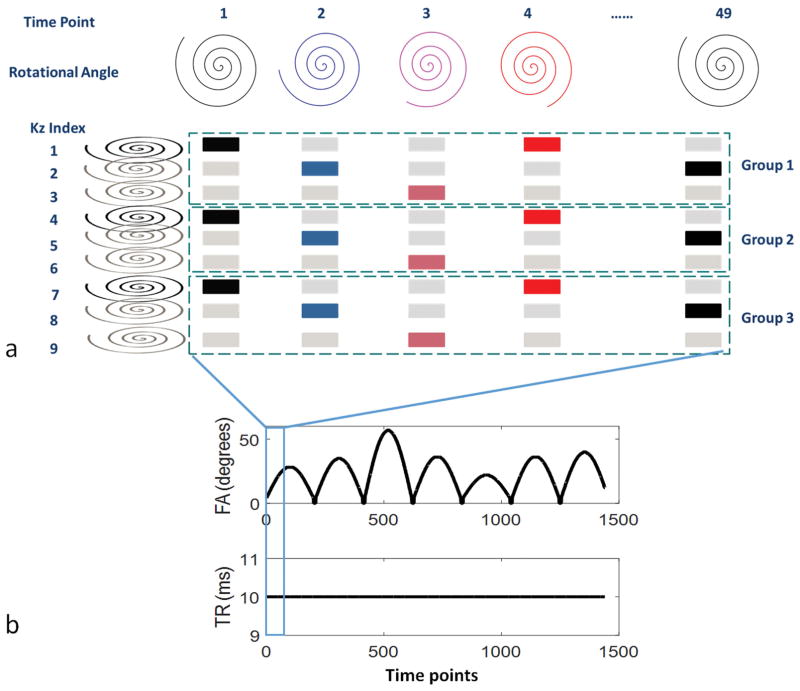
The 3D slab-selective MRF with the FISP-based readout(2) was implemented by adding phase encoding lines along kz direction from the 2D MRF. As a quick summary of the 2D MRF sequence(1,2), the MRF sequence was designed based on a TrueFISP or FISP sequence, but with randomized flip angles (FA) and repetition times (TR). To capture sufficient temporal information for multi-parametric quantification, 1000 to 3000 time points (or TRs) were acquired and one image was reconstructed at each time point. The resulting signal evolution in each pixel as a function of time was matched to a pre-defined dictionary to obtain multiple tissue properties (such as T1, T2 and proton density) simultaneously. In this study, the 3D acquisition acquired data along time points in the x-y plane first. After acquired all the time points at a certain phase encoding line in kz, the kz increased and the same acquisition pattern (FA, TR and spiral trajectories) was repeated. For each time point at each kz, a variable density spiral trajectory was used to sample the kx-ky data (note that spiral trajectory was designed to require 48 arms to fully sample the k-space) (2,33). After all sampling was complete, the spiral trajectory in kx-ky (in-plane) and Cartesian phase encoding in kz (through-plane) constitute a stack-of-spiral sampling pattern at each time point. However, in order to preserve the temporal fidelity of the rapidly changing MRF signals, the sampling order of this stack-of-spiral MRF acquisition is different from other time-resolved three-dimensional acquisitions that acquire all kz lines for a time point before proceeding to the next time point.
If this data were acquired at the Nyquist rate, the scan duration would be prohibitively long. As shown in previous MRF studies, individual time point can be greatly undersampled to reduce imaging times. Here, the acceleration scheme including both in-plane and through-plane acceleration is proposed. In-plane acceleration was achieved by using a single spiral arm in each time point (or TR) and for each kz. To improve spatial-temporal incoherence, a 7.5° (360/48) rotation of the trajectory was applied from one time point to the next, such that aliasing artifacts from neighboring time points are different. This yielded an in-plane acceleration factor of 48. Through-plane acceleration was achieved by uniformly undersamping the kz lines in an interleaved fashion by a factor of three.
An example of this undersampled 3D MRF acquisition is shown in Figure 1 for a scan using nine kz lines. These nine kz lines were divided into groups based on the through-plane acceleration factor (in this case there are three groups for the undersampling factor of three). Specifically, in the first repetition, the first kz line was acquired at the first time point, then the second kz line was acquired at the second time point, then the third kz line at third time point, followed by the first kz line at the fourth time point, and so on. Additionally, because the rotational angle of the spiral trajectory was repeated in every 48th time point, at the 49th time point, instead of acquiring the first kz line, the second kz line was acquired in group 1. Thus, in addition to shifting the kz line by one for each time point, the index of the kz line was shifted by one at each multiple of 48 time points. After the kz lines at all time points were acquired in the first group, a waiting time with no excitation was applied to allow for the signal recovery, followed by the acquisition of the second group of kz lines, starting with the first kz line at the first time point again. After all undersampled 3D MRF data were acquired, this resulted in an undersampled, interleaved, stack-of-spirals sampling. This sampling pattern is similar to k-t BLAST and k-t SENSE(21), which was used to shift the aliasing artifacts. The additional benefit of this sampling scheme was that the sampling density of each kz line as well as the sampling times of each rotational angle of the spiral trajectory were the same after the entire acquisition.
Figure 1.
Undersampling scheme (a), flip angle pattern and TR pattern (b) of the 3D MRF scan. In (a), the sampling scheme of a 3D MRF scan with nine partitions is illustrated. The acquisition starts with the time domain first. Along the time points, the rotational angles of the spiral trajectories are changed with a step of 7.5 degrees. With an acceleration factor of three, nine partitions are divided into three groups or repetitions. The colored kz lines are the ones that are acquired in the accelerated scan while the gray kz lines are the ones that are skipped.
The scan time is further reduced by shortening the waiting time between neighboring groups. Although traditional relaxometry methods require spins to be fully relaxed before sampling each kz, MRF can account for partial relaxation of the spins by simulating the known waiting time between neighboring kz lines in the dictionary. This property of MRF provides some inherent acceleration as it allows the minimization of the waiting time between neighboring groups.
Data Acquisition
All scans were performed in a 3T scanner system (Skyra, Siemens). For both phantom and in vivo studies, a field of view (FOV) of 300×300×144 mm3 with a matrix of 256×256×48 and an image resolution of 1.2×1.2×3 mm3 was acquired. Under an acceleration factor of three, 16 acquisition groups (or repetitions) were acquired. For each group, 1440 time points (30 repetitions of 48 rotation angles) were acquired with an acquisition time of 14 seconds, followed by a 3 second waiting time before the next group, in order to allow for relaxation and to improve signal to noise ratio (SNR). The flip angle and TR patterns are shown in Figure 1(b). An asymmetric 3D slab selective RF pulse with a duration of 2048 us was used for excitation. Adiabatic inversion pulses were added at the first and the 1201th time points at each repetition in order to improve sensitivity to T1. The total acquisition time was 4.6 minutes.
A 3D B1 map was acquired separately using the Bloch-Siegert method before each MRF scan(3,29). To accelerate the scan, a B1 map with a spatial resolution of 2.3×2.3×3 mm3 was first acquired. The B1 map in each partition was then interpolated to a spatial resolution of 1.2×1.2 mm2 to match the spatial resolution of the tissue maps. The total acquisition time was 1.6 minutes.
The accuracy and repeatability of the 3D MRF scan were first validated using the ISMRM/NIST MRI phantom which has T1 and T2 layers, each containing 14 spheres, with T1 values ranging from 20 ms to 2 seconds and T2 values ranging from 8 ms to 600 ms(34,35). The phantom was scanned in five consecutive days by both B1 and 3D MRF scans. The mean and standard deviations of the T1 values in the T1 layer as well as T2 values from the T2 layer were compared to those values measured by NMR experiment from the physical measurement laboratory at the National Institute of Standards and Technology(34).
The in vivo experiments were performed in five asymptomatic volunteers in an IRB-approved study, including written informed consent before each scan. B1 measurement and MRF scans were performed at the same 3D location. In the T1 and T2 maps from each volunteer, six regions including caudate nucleus, centrum semiovale, middle cerebellar pedencle, putamen, frontal white matter and parietal white matter were selected. The T1 and T2 values in each tissue type were first averaged for each volunteer, and then the mean and standard deviation of T1 and T2 values among five volunteers were calculated.
Dictionary Simulation
The dictionary used in the matching algorithm was simulated using the Bloch equations in MATLAB (MathWorks, Natick, MA) and was introduced previously(1). In each TR, signal evolutions due to RF excitation with nominal flip angles, relaxation during TE and TR times, and a 2π dephasing at the end of the TR from 200 isochromats was simulated. Since a 3D slab-selective RF pulse with an optimized excitation profile was applied, the RF profile was not simulated in the dictionary. In order to simulate the waiting time, the entire acquisition was simulated twice. At the end of first repetition, relaxation during the waiting time was simulated. The resulting magnetization became the starting magnetization of the second repetition, where the whole acquisition was simulated again. Based on the simulation from a wide range of T1 and T2 combinations, the starting magnetization was stable after the second repetition. Each isochromat was simulated independently for the whole sequence before summing over the voxel.
The B1 values were simulated as an additional dimension of the dictionary, with a range between 0.7 to 1.5 in steps of 0.02. The actual flip angles were calculated as nominal flip angles multiplied by B1. For each B1 value, a total of 12001 signal evolutions, each with 1440 time points, were simulated for a range of possible T1 values (2 to 100 ms in steps of 2, 120 to 2000 ms in steps of 20, and 2000 to 3000 ms in steps of 40ms) and T2 values (2 to 130 ms in steps of 2 ms, 140 to 200 ms in steps of 10 ms, 200 to 1000 ms in steps of 20 ms, and 1040 to 2000 in steps of 40 ms). The simulation time was 5.7 minutes for each B1 value and 3.4 hours for the whole dictionary on a standalone PC.
Accelerated Post-Processing
Since 1440 undersampled 3D volumes were acquired, which could lead to a large memory requirement and long computing time for both reconstruction and template matching, a singular value decomposition (SVD) compression method(7) was applied to the k-space data prior to the reconstruction. Specifically, the SVD of the full dictionary was first computed, which takes four minutes.
| [1] |
The first k=25 of the singular vectors were used to project the raw data and the full dictionary to the SVD space.
| [2] |
| [3] |
| [4] |
| [5] |
where in equation [2], Uk ∈ ℂt×Nk is the first Nk of the left singular vector of the dictionary, t is the number of TRs. In equation [3], Y ∈ ℂt×M is the sampled k-space data, where M = Ncoils × Nsamples_per_spiral × Nspirals × Nkz, and Yk ∈ ℂ Nk×M is the compressed k-space data in the SVD space. After projecting the raw data to the SVD space, instead of reconstructing 1440 undersampled 3D volumes, only 25 3D volumes with the compressed k-space data were reconstructed, which substantially reduced the computational effort. Each 3D volume was reconstructed using the GPU-NUFFT toolbox(36) with separately measured spiral trajectories(37). In equation [4], Xk is the reconstructed images, with the size of 25×256×256×48, and G is the NUFFT operator. To correct for B1 inhomogeneity, the same Uk as to compress the raw data was also used to project the full dictionary with different B1 values to the SVD space. In equation [5], D ∈ ℂt×Nt1t2×NB1 is the full dictionary and Dk ∈ ℂNk×Nt1t2×NB1 is the compressed dictionary. In this way, pattern recognition could be performed between Xk and Dk, which are much smaller than the original full matrix X and D. Based on the measured B1 map, the compressed signal evolution in each pixel was matched to those entries in the compressed dictionary that have the closest B1 values as measured. The maximum inner-product value from the match gave rise to T1, T2 and M0 values. The post-processing time of generating B1 corrected T1, T2 and M0 maps for a matrix size of 256×256×48 was 48 minutes in MATLAB (The MathWorks,Inc. Natick, MA).
Results
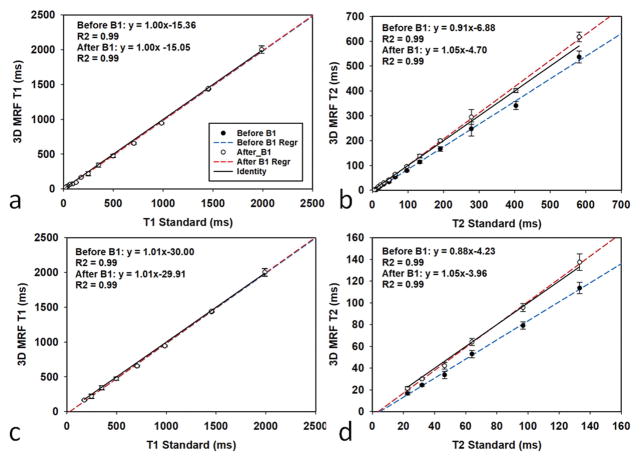
Figure 2 shows the accuracy and repeatability results of the 3D MRF scan before and after the B1 correction, with bi-directional error bars representing the standard deviation of five measurements. Figure 2(a, b) shows the results from all 14 spheres of each layer and Figure 2(c, d) shows the same results but with a reduced T1 range between 181 to 2038 ms and a reduced T2 range between 26 to 143 ms, which correspond to the main physiological range of the brain tissues. The linear regression and R2 of the results before and after the B1 correction are also listed in each plot. As shown in the figure, although the B1 correction has little impact on the T1 results, it greatly improves the accuracy of the T2 results. After the B1 correction, MRF results in general are in good agreement with the results from the reference values, with a concordance correlation coefficient (CCC)(38) of 0.99 for both T1 and T2. The MRF scans also demonstrate high repeatability, with an average coefficient of variation (CV) of 6.9% for T1 and 6.6% for T2.
Figure 2.
The accuracy and repeatability of the qMRI phantom scan. (a, b) T1 values and T2 values from 14 spheres from the ISMRM/NIST phantom are compared to the values from the spin echo (SE) measurement. (c, d) The same results but with a reduced T1 range between 181 to 2038 ms and a reduced T2 range between 26 to 143 ms. The blue line and red line in each plot are the linear regression results before and after B1 correction, respectively.
Figure 3 and 4 illustrate the T1 and T2 maps in the axial view and coronal view, respectively, from one of the volunteer scans. To illustrate the B1 effects, Figure 3 shows the B1 maps, as well as T1 and T2 maps before and after B1 correction. Similar to the phantom results, the B1 effects are more visible from T2 maps. Table 1 summarizes the T1 and T2 values from six regions of the brain maps. The T1 and T2 values along with the size of the regions of interest, as well as the mean±std of the T1 and T2 values among the five volunteers are listed. Based on Table 1, the T1 and T2 values from each region are relatively consistent among these five healthy volunteers.
Figure 3.

B1, T1 and T2 maps from a 3D in vivo scan in axial view.
Figure 4.
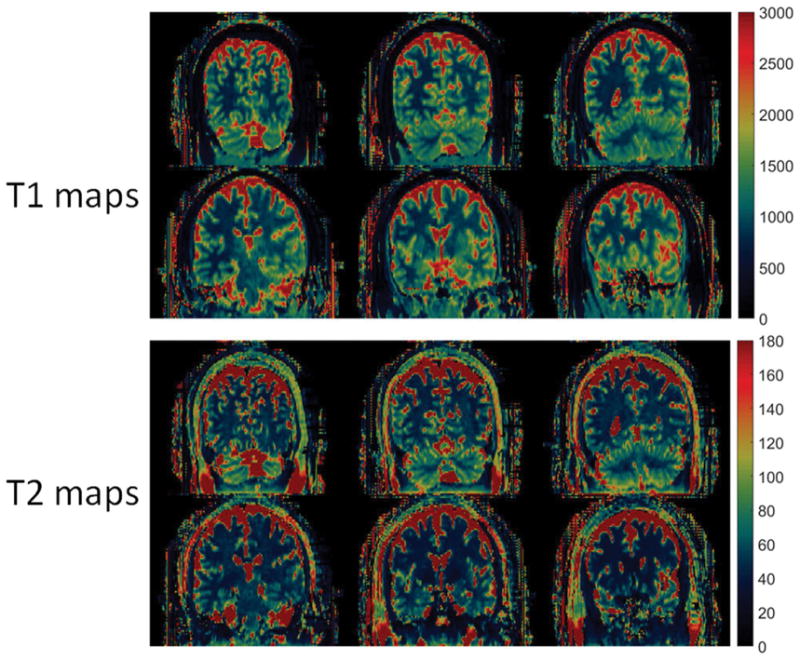
3D T1 (ms) and T2 (ms) maps from an in vivo scan in Coronal view.
Table 1.
In vivo T1 and T2 values along with the size of the regions of interest from five volunteers scanned from a 3T scanner. (units: ms)
| v1 | v2 | v3 | v4 | v5 | mean±std | ||
|---|---|---|---|---|---|---|---|
| Caudate Nucleus | T1 | 1397.2 | 1493.5 | 1293.5 | 1397.9 | 1368.9 | 1390.2±71.7 |
| T2 | 42.1 | 38.9 | 53.4 | 40.9 | 44.7 | 44.0±5.6 | |
| ROI | 38 | 27 | 17 | 23 | 24 | ||
| Centrum semiovale | T1 | 875.9 | 866.6 | 823.1 | 863.1 | 866.4 | 859.0±20.6 |
| T2 | 39.7 | 33.6 | 40.3 | 34.4 | 41.2 | 37.8±3.5 | |
| ROI | 108 | 102 | 145 | 149 | 207 | ||
| Middle Cerebellar Pedencle | T1 | 874.7 | 942.5 | 906.1 | 918.9 | 881.5 | 904.7±27.7 |
| T2 | 52.7 | 38.7 | 25.7 | 37.8 | 49.0 | 40.8 | |
| ROI | 72 | 54 | 47 | 75 | 87 | ||
| Putamen | T1 | 1285.9 | 1314.0 | 1169.5 | 1238.4 | 1234.3 | 1248.5±55.3 |
| T2 | 40.7 | 36.9 | 43.0 | 38.6 | 39.1 | 39.7±2.3 | |
| ROI | 37 | 52 | 24 | 32 | 55 | ||
| Frontal_wm | T1 | 843.1 | 854.3 | 794.8 | 809.1 | 818.1 | 823.9±24.5 |
| T2 | 30.8 | 29.1 | 42.6 | 35.1 | 35.6 | 34.6±5.3 | |
| ROI | 51 | 68 | 61 | 78 | 85 | ||
| Parietal_wm | T1 | 783.3 | 817.9 | 904.5 | 793.7 | 781.2 | 816.1±51.5 |
| T2 | 46.8 | 37.7 | 36,8 | 36.1 | 43,1 | 40.1±4.6 | |
| ROI | 79 | 85 | 45 | 31 | 100 |
Discussion
In this study, a fast acquisition scheme was applied for a fully quantitative 3D MRF scan in less than 5 minutes of acquisition time, demonstrating T1, T2 and M0 maps with 1.2×1.2×3 mm3 resolution and a whole brain coverage. A separate 1.6 minute B1 measurement scan was performed before the 3D scan. The resulting B1 map was used to correct for B1 inhomogeneity effects and improve the accuracy of T1 and T2 estimates. In fact, both B1 and 3D MRF scans can be further accelerated. A fast Bloch-Siegert scan has been proposed to measure the 3D B1 maps in only 32 seconds(39,40). By incorporating advanced reconstruction methods, substantial reduction of the scan time or/and further improvement of the spatial resolution can be achieved for 3D MRF scans. For example, by using low rank reconstruction methods(41,42), the scan time of the 3D MRF scan with the same spatial resolution and tissue coverage can be reduced to only 2.7 minutes(43). Optimization of the MRF scan could also lead to a reduction of the scan time(44,45). In addition, method has been proposed to simultaneously quantifying B1 as well as tissue properties without compromising the scan time(46).
The acceleration of the acquisition was achieved in 3 steps: intrinsic acceleration using short waiting times between neighboring phase encoding lines, in-plane acceleration factor of 48 and through-plane acceleration factor of 3. The in-plane acceleration has been demonstrated previously in 2D MRF scans, which took the advantage of the variable density spiral sampling pattern in order to generate incoherent aliasing artifacts both in each image and through time. The through-plane acceleration was achieved using a uniform undersampling pattern similar to the k-t sampling pattern. This pattern shifted the aliasing artifacts from one time point to the next, in order to create incoherent artifacts through time. This pattern also guaranteed that all 48 rotational angles of the spiral trajectory were used at the same rate (30 times for each spiral angle) and all kz lines were sampled at the same density. For this reason, no density compensation was needed along kz, although density compensation was still needed in the kx-ky plane for the image reconstruction.. In this study, all maps were generated by direct reconstruction and template matching. Advanced reconstruction methods that have been recently proposed for the 2D MRF could be applied in 3D MRF in order to further reduce the acquisition time or improve the image quality(47,48). Other sampling schemes such as variable density sampling can also be applied to the partition direction to potentially improve the sampling efficiency and increase the undersampling factor(49,50).
For a 3D scan with large volume coverage, B1 variation and its effect on the resulting T1 and T2 estimation are not negligible. In this study, the Bloch-Siegert B1 mapping method was performed separately before each MRF scan, and the resulting B1 map was used to correct for the B1 effect. Other approaches to correct for the B1 effect, such as quantifying B1 at the same time as T1 and T2, can also be applied(28,31). However, none of these methods has been effectively applied to 3D scans with such a high undersampling ratio. Although a separate scan to measure B1 takes an additional time, it reduces the sensitivity to potential tissue or system parameters, and thus reduces the amount of information and acquisition time required for the MRF scan. In addition, a prior knowledge of the B1 map reduces the dimensionality of the dictionary in pattern matching to estimate the tissue properties, which can lower the risk of mismatch and error propagation, especially in the present of strong aliasing artifacts and with low SNR from accelerated scans.
Based on the results obtained from the ISMRM/NIST MRI phantom, the 3D MRF scan shows high accuracy and repeatability as compared to the reference measurement. As described in our previous 2D study(51), we’ve consistently seen T2 difference between our results after B1 correction and literature reported values acquired using fast spin echo methods(2,52,53). Many groups have shown similar T2 reduction by correcting for stimulated echoes(54), slice profile(27,51), magnetization transfer(55) and finite RF pulse effects(56). The lower T2 values may also be related to tissue microstructure, intra voxel dephasing(57), and diffusion effect from the spoiling gradients used in the FISP sequence(58). These effects may also cause the T2 variation between frontal and parietal white matter regions as shown in Table 1. An exact analysis of this phenomenon is the subject of a future investigation.
In this study, a 3D MRF scheme with the FISP readout was used, which is less sensitive to the B0 inhomogeneity for large volume coverage. Therefore, this 3D MRF scheme has the potential to be used in other parts of the body. In addition, with a large flexibility on the MRF sequence design, navigation and magnetization preparation can be added to the sequence to make the 3D MRF scan robust to different applications.
Conclusions
A fast acquisition scheme for a 3D MRF scan with a whole brain coverage was presented. 3D T1, T2 and M0 maps with a spatial resolution of 1.2×1.2×3 mm3 can be generated in 4.6 minutes. An additional 1.6 minute B1 scan was used to reduce the system and subject related variations, and thus improve the accuracy of quantitative estimates. Given that this FISP-based sequence is also insensitive to the B0 inhomogeneity, the proposed MRF scan could have wide and robust clinical applications.
Acknowledgments
Support for this study was provided by NIH 1R01EB016728-01A1, NIH 5R01EB017219-02, NIH 1R01DK098503-01A1 and Siemens Healthcare. This work made use of the High Performance Computing Resource in the Core Facility for Advanced Research Computing at Case Western Reserve University.
References
- 1.Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, Griswold MA. Magnetic Resonance Fingerprinting. Nature. 2013;495:187–192. doi: 10.1038/nature11971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Jiang Y, Ma D, Seiberlich N, Gulani V, Griswold Ma. MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. Magn Reson Med. 2014 doi: 10.1002/mrm.25559. 0:n/a-n/a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chen Y, Jiang Y, Shivani Pahva, Ma D, Lu L, Tweig MD, Wright KL, Seiberlich N, Griswold MA, Gulani V. MR Fingerprinting for Rapid Quantitative Abdominal Imaging. Radiology. 2016;0:1–9. doi: 10.1148/radiol.2016152037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Badve C, Yu A, Rogers M, Ma D, Liu Y, Schluchter M, Sunshine J, Griswold M, Gulani V. Simultaneous T 1 and T 2 Brain Relaxometry in Asymptomatic Volunteers Using Magnetic Resonance Fingerprinting. Tomography. 2015:1. doi: 10.18383/j.tom.2015.00166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gao Y, Chen Y, Ma D, et al. Preclinical MR fingerprinting (MRF) at 7 T: effective quantitative imaging for rodent disease models. NMR Biomed. 2015;28:384–94. doi: 10.1002/nbm.3262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Christen T, Pannetier Na, Ni WW, Qiu D, Moseley ME, Schuff N, Zaharchuk G. MR Vascular Fingerprinting: A New Approach to Compute Cerebral Blood Volume, Mean Vessel Radius, and Oxygenation Maps in the Human Brain. Neuroimage. 2014;89:262–70. doi: 10.1016/j.neuroimage.2013.11.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.McGivney D, Pierre E, Ma D, Jiang Y, Saybasili H, Gulani V, Griswold MA. SVD Compression for Magnetic Resonance Fingerprinting in the Time Domain. IEEE Trans Med Imaging. 2014;62:1–13. doi: 10.1109/TMI.2014.2337321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cauley SF, Setsompop K, Ma D, Jiang Y, Ye H, Adalsteinsson E, Griswold Ma, Wald LL. Fast Group Matching for MR Fingerprinting Reconstruction. Magn Reson Med. 2014:0:1–6. doi: 10.1002/mrm.25439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jiang Y, Ma D, Renate J, Gulani V, Seiberlich N, Duerk JL, Griswold MA. MR Fingerprinting Using Spiral QUEST. Proceedings 21th Scientific Meeting, International Society for Magnetic Resonance in Medicine; 2013. p. 19. [Google Scholar]
- 10.Hamilton JI, Jiang Y, Chen Y, Ma D, Lo W-C, Griswold M, Seiberlich N. MR fingerprinting for rapid quantification of myocardial T1, T2, and proton spin density. Magn Reson Med. 2016 doi: 10.1002/mrm.26216. n/a-n/a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ye H, Ma D, Jiang Y, Cauley SF, Du Y, Wald LL, Griswold Ma, Setsompop K. Accelerating magnetic resonance fingerprinting (MRF) using t-blipped simultaneous multislice (SMS) acquisition. Magn Reson Med. 2015 doi: 10.1002/mrm.25799. n/a-n/a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ye H, Cauley SF, Gagoski B, Bilgic B, Ma D, Jiang Y, Du YP, Griswold MA, Wald LL, Setsompop K. Simultaneous multislice magnetic resonance fingerprinting (SMS-MRF) with direct-spiral slice-GRAPPA (ds-SG) reconstruction. Magn Reson Med. 2016 doi: 10.1002/mrm.26271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jiang Y, Ma D, Bhat H, Ye H, Cauley SF, Wald LL, Setsompop K, Griswold MA. Use of pattern recognition for unaliasing simultaneously acquired slices in simultaneous multislice MR fingerprinting. Magn Reson Med. 2016 doi: 10.1002/mrm.26572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lee GR, Griswold MA, Tkach JA. Rapid 3D radial multi-echo functional magnetic resonance imaging. Neuroimage. 2010;52:1428–1443. doi: 10.1016/j.neuroimage.2010.05.004. [DOI] [PubMed] [Google Scholar]
- 15.Stehning C, Börnert P, Nehrke K, Eggers H, Dössel O. Fast Isotropic Volumetric Coronary MR Angiography Using Free-Breathing 3D Radial Balanced FFE Acquisition. Magn Reson Med. 2004;52:197–203. doi: 10.1002/mrm.20128. [DOI] [PubMed] [Google Scholar]
- 16.Gurney PT, Hargreaves BA, Nishimura DG. Design and Analysis of a Practical 3D Cones Trajectory. Magn Reson Med. 2006;55:575–582. doi: 10.1002/mrm.20796. [DOI] [PubMed] [Google Scholar]
- 17.Pipe JG, Zwart NR, Aboussouan Ea, Robison RK, Devaraj A, Johnson KO. A New Design and Rationale for 3D Orthogonally Oversampled k-Space Trajectories. Magn Reson Med. 2011;66:1303–1311. doi: 10.1002/mrm.22918. [DOI] [PubMed] [Google Scholar]
- 18.Piccini D, Littmann A, Nielles-Vallespin S, Zenge MO. Spiral Phyllotaxis: The Natural Way to Construct a 3D Radial Trajectory in MRI. Magn Reson Med. 2011;66:1049–1056. doi: 10.1002/mrm.22898. [DOI] [PubMed] [Google Scholar]
- 19.Bilgic B, Gagoski BA, Cauley SF, Fan AP, Polimeni JR, Grant PE, Wald LL, Setsompop K. Wave-CAIPI for highly accelerated 3D imaging. Magn Reson Med. 2015;73:2152–2162. doi: 10.1002/mrm.25347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Breuer Fa, Blaimer M, Mueller MF, Seiberlich N, Heidemann RM, Griswold Ma, Jakob PM. Controlled Aliasing in Volumetric Parallel Imaging (2D CAIPIRINHA) Magn Reson Med. 2006;55:549–56. doi: 10.1002/mrm.20787. [DOI] [PubMed] [Google Scholar]
- 21.Tsao J, Boesiger P, Pruessmann KP. k-t BLAST and k-t SENSE: Dynamic MRI With High Frame Rate Exploiting Spatiotemporal Correlations. Magn Reson Med. 2003;50:1031–42. doi: 10.1002/mrm.10611. [DOI] [PubMed] [Google Scholar]
- 22.Tsao J, Kozerke S. MRI temporal acceleration techniques. J Magn Reson Imaging. 2012;36:543–60. doi: 10.1002/jmri.23640. [DOI] [PubMed] [Google Scholar]
- 23.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P, et al. SENSE: Sensitivity Encoding for Fast MRI. Magn Reson Med. 1999;42:952–962. [PubMed] [Google Scholar]
- 24.Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized Autocalibrating Partially Parallel Acquisitions (GRAPPA) Magn Reson Med. 2002;47:1202–10. doi: 10.1002/mrm.10171. [DOI] [PubMed] [Google Scholar]
- 25.Feng L, Axel L, Chandarana H, Block KT, Sodickson DK, Otazo R. XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magn Reson Med. 2016;75:775–788. doi: 10.1002/mrm.25665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mcrobbie DW, Lerski RA, Robinson EM, Hickey DS, Lerski RA, Bakker CJG, De Graaf CN, Van Dijk P. Slice Profile Effects and Their Calibration and Correction in Quantitative NMR NMR Imaging. Phys Med Biol. 1987;32:971–983. [Google Scholar]
- 27.Ehses P, Seiberlich N, Ma D, Breuer FA, Jakob PM, Griswold MA, Gulani V. IR TrueFISP with a golden-ratio-based radial readout: fast quantification of T1, T2, and proton density. Magn Reson Med. 2013;69:71–81. doi: 10.1002/mrm.24225. [DOI] [PubMed] [Google Scholar]
- 28.Buonincontri G, Sawiak SJ. MR fingerprinting with simultaneous B1 estimation. Magn Reson Med. 2015;0:1–9. doi: 10.1002/mrm.26009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sacolick LI, Wiesinger F, Hancu I, Vogel MW. B1 mapping by Bloch-Siegert Shift. Magn Reson Med. 2010;63:1315–1322. doi: 10.1002/mrm.22357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yarnykh VL. Actual Flip-Angle Imaging in the Pulsed Steady State: a Method for Rapid Three-Dimensional Mapping of the Transmitted Radiofrequency Field. Magn Reson Med. 2007;57:192–200. doi: 10.1002/mrm.21120. [DOI] [PubMed] [Google Scholar]
- 31.Cloos MA, Knoll F, Zhao T, Block K, Bruno M, Wiggins C, Sodickson D. Multiparametric imaging with heterogeneous radiofrequency field: Additional material. Nat Commun. 2016 doi: 10.1017/CBO9781107415324.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hurley Sa, Yarnykh VL, Johnson KM, Field AS, Alexander AL, Samsonov Aa. Simultaneous Variable Flip Angle-Actual Flip Angle Imaging Method for Improved Accuracy and Precision of Three-Dimensional T1 and B1 Measurements. Magn Reson Med. 2012;68:54–64. doi: 10.1002/mrm.23199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hargreaves BA. Minimum-Time Multi-Dimensional Gradient Waveform Design. [Google Scholar]
- 34.Keenan K, Boos M, Jackson EF, Kown S, Jennings D, Russek S. NIST/ISMRM MRI System Phantom T1 Measurements on Multiple MRI System. Proceedings 21th Scientific Meeting, International Society for Magnetic Resonance in Medicine; 2013. p. 4338. [Google Scholar]
- 35.Jiang Y, Ma D, Keenan KE, Stupic KF, Gulani V, Griswold MA. Repeatability of magnetic resonance fingerprinting T1 and T2 estimates assessed using the ISMRM/NIST MRI system phantom. Magn Reson Med. 2016;0:1–6. doi: 10.1002/mrm.26509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Knoll F, Schwarzl A, Diwoky C, Sodickson DK. gpuNUFFT-an open source GPU library for 3D regridding with direct MATLAB interface. Proc Intl Soc Mag Reson Med. 2014;22:4297. doi: 10.1002/mrm.24751. [DOI] [Google Scholar]
- 37.Duyn JH, Yang Y, Frank JA, van der Veen JW. Simple Correction Method for k-Space Trajectory Deviations in MRI. J Magn Reson. 1998;132:150–3. doi: 10.1006/jmre.1998.1396. [DOI] [PubMed] [Google Scholar]
- 38.Lin LI-K. A Concordance Correlation Coefficient to Evaluate Reproducibility. Biometrics. 1989;45:255–68. [PubMed] [Google Scholar]
- 39.Saranathan M, Khalighi MM, Kerr AB, Rutt B. Fast 3D B1+ Mapping using an Optimized, Asymmetric Bloch-Siegert Method. Proceedings 19th Scientific Meeting, International Society for Magnetic Resonance in Medicine; 2011. p. 577. [Google Scholar]
- 40.Saranathan M, Khalighi MM, Glover GH, Pandit P, Rutt BK. Efficient Bloch-Siegert B1 (+) Mapping Using Spiral and Echo-Planar Readouts. Magn Reson Med. 2013;0:1–5. doi: 10.1002/mrm.24599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zhao B, Setsompop K, Adalsteinsson E, Gagoski B, Ye H, Ma D, Jiang Y, Ellen Grant P, Griswold MA, Wald LL. Improved magnetic resonance fingerprinting reconstruction with low-rank and subspace modeling. Magn Reson Med. 2017;0:1–10. doi: 10.1002/mrm.26701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Assländer J, Cloos MA, Knoll F, Sodickson DK, Hennig J, Lattanzi R. Low rank alternating direction method of multipliers reconstruction for MR fingerprinting. Magn Reson Med. 2017 doi: 10.1002/mrm.26639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ma D, Pierre EY, McGivney DF, Mehta B, Chen Y, Jiang Y, Griswold MA. Applications of low rank modeling to fast 3D MRF. Proc Intl Soc Mag Reson Med. 2017;25:129. doi: 10.1002/mrm.25559.3. [DOI] [Google Scholar]
- 44.Zhao B, Haldar JP, Setsompop K, et al. Optimal experiment design for magnetic resonance fingerprinting. 38th Annu Int Conf IEEE Eng Med Biol Soc. 2016;2016:453–456. doi: 10.1109/EMBC.2016.7590737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Assländer J, Sodickson DK, Lattanzi R, Cloos MA. Relaxation in Polar Coordinates: Analysis and Optimization of MR-Fingerprinting. Proc Intl Soc Mag Reson Med. 2017;25:127. doi: 10.1038/ncomms12445. [DOI] [Google Scholar]
- 46.Buonincontri G, Schulte R, Cosottini M, Sawiak SJ, Tosetti M. Spiral MRF at 7T with simultaneous B1 estimation. Magn Reson Med. 2016:433. doi: 10.1002/mrm.26009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Zhao B, Setsompop K, Ye H, Cauley SF, Wald LL. Maximum Likelihood Reconstruction for Magnetic Resonance Fingerprinting. IEEE Trans Med Imaging. 2016;35:1812–1823. doi: 10.1038/nature11971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Doneva M, Amthor T, Koken P, Sommer K, Börnert P. Matrix completion-based reconstruction for undersampled magnetic resonance fingerprinting data. Magn Reson Imaging. 2016 doi: 10.1016/j.mri.2017.02.007. [DOI] [PubMed] [Google Scholar]
- 49.Otazo R, Kim D, Axel L, Sodickson DK. Combination of Compressed Sensing and Parallel Imaging for Highly Accelerated First-pass Cardiac Perfusion MRI. Magn Reson Med. 2010;64:767–776. doi: 10.1002/mrm.22463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Feng L, Srichai MB, Lim RP, Harrison A, King W, Adluru G, Dibella EVR, Sodickson DK, Otazo R, Kim D. Highly Accelerated Real-time Cardiac Cine MRI Using k-t SPARSE-SENSE. Magn Reson Med. 2013;70:64–74. doi: 10.1002/mrm.24440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Ma D, Coppo S, Chen Y, McGivney DF, Jiang Y, Pahwa S, Gulani V, Griswold MA. Slice profile and B1 corrections in 2D magnetic resonance fingerprinting. Magn Reson Med. 2017 doi: 10.1002/mrm.26580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wansapura JP, Holland SK, Dunn RS, Ball WS. NMR Relaxation Times in the Human Brain at 3. Tesla J Magn Reson Imaging. 1999;9:531–8. doi: 10.1002/(sici)1522-2586(199904)9:4<531::aid-jmri4>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]
- 53.Hasan KM, Walimuni IS, Kramer La, Narayana Pa. Human brain iron mapping using atlas-based T2 relaxometry. Magn Reson Med. 2012;67:731–9. doi: 10.1002/mrm.23054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ben-Eliezer N, Sodickson DK, Block KT. Rapid and accurate T2 mapping from multi-spin-echo data using bloch-simulation-based reconstruction. Magn Reson Med. 2015;73:809–817. doi: 10.1002/mrm.25156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Gloor M, Scheffler K, Bieri O. Quantitative Magnetization Transfer Imaging Using Balanced SSFP. Magn Reson Med. 2008;60:691–700. doi: 10.1002/mrm.21705. [DOI] [PubMed] [Google Scholar]
- 56.Crooijmans HJa, Scheffler K, Bieri O. Finite RF pulse correction on DESPOT2. Magn Reson Med. 2011;65:858–62. doi: 10.1002/mrm.22661. [DOI] [PubMed] [Google Scholar]
- 57.Assländer J, Glaser SJ, Hennig J. Pseudo Steady-State Free Precession for MR-Fingerprinting. Magn Reson Med. 2016;0:1–11. doi: 10.1002/mrm.26202. [DOI] [PubMed] [Google Scholar]
- 58.Terada Y, Kobayashi Y. Effect of diffusion weighting due to spoiler gradients in MR Fingerprinting. Proc Intl Soc Mag Reson Med. 2017;25:940. doi: 10.2463/mrms.tn.2018-0027. [DOI] [PMC free article] [PubMed] [Google Scholar]