Joint hierarchical Gaussian process model with application to personalized prediction in medical monitoring

Abstract

A two-level Gaussian process (GP) joint model is proposed to improve personalized prediction of medical monitoring data. The proposed model is applied to jointly analyze multiple longitudinal biomedical outcomes, including continuous measurements and binary outcomes, to achieve better prediction in disease progression. At the population level of the hierarchy, two independent GPs are used to capture the nonlinear trends in both the continuous biomedical marker and the binary outcome, respectively; at the individual level, a third GP, which is shared by the longitudinal measurement model and the longitudinal binary model, induces the correlation between these two model components and strengthens information borrowing across individuals. The proposed model is particularly advantageous in personalized prediction. It is applied to the motivating clinical data on cystic fibrosis disease progression, for which lung function measurements and onset of acute respiratory events are monitored jointly throughout each patient’s clinical course. The results from both the simulation studies and the cystic fibrosis data application suggest that the inclusion of the shared individual-level GPs under the joint model framework leads to important improvements in personalized disease progression prediction.

1 Introduction

In clinical care and research of chronic diseases, an important task is to monitor and predict disease progression based on data from multiple biomedical outcomes. Cystic fibrosis (CF), as a motivating example, is a lethal autosomal disease, marked by progressive loss of lung function over the lifespan. A variety of biomedical measures and outcomes are collected at each patient’s clinical visit, and these data are used to inform CF clinical studies. CF clinicians have great interest in prognostic models of monitoring and predicting disease progression. Particularly, there is an increasing emphasis on detection of severe CF disease at its early stage and prediction of its clinical course. Although the median age of survival has markedly improved, patients still continue to experience declining lung function and acute respiratory events during adolescence and early adulthood. Accurate prediction models could be used as a prognostic tool for more timely treatment of respiratory decline.

Despite the potential clinical utility of prediction models in biomedicine, it is widely known that patient-level extrapolation of disease progression is difficult. On one hand, the sparsity and irregularity of the data collection times pose great challenges in extracting sensible and flexible estimates with a reasonable level of confidence. On the other hand, the statistical models used in clinical practice are often based on unrealistic assumptions (such as a simple linear slope) and overlook or even violate many intrinsic properties inherent in the underlying progression of the disease (Szczesniak et al., 2016). Among these properties, nonlinearity and individual heterogeneity, which are pervasive challenges in modeling CF lung function decline (Szczesniak et al., 2017), are of particular importance for modeling the patient-level disease progression. Inspired by the developments in the field of joint modeling, we propose a two-level Gaussian process (GP) joint model for multiple longitudinal outcomes monitored by clinicians, both continuous and discrete. The goal is to address the nonlinear prediction needs in important biomedical outcomes on the personalized level.

Our key contributions focus on two aspects: one is for the data structure we study in the joint model and the other is for the model structure we propose in the joint model. The joint model conveniently accommodates the need to study multiple outcomes simultaneously. Particularly, for the CF data of interest, there are two important severity markers whose association has been evidenced in clinical practice. These two biomarkers are the forced expiratory volume in one second (hereafter, FEV₁) and the occurrence of acute respiratory events, known as pulmonary exacerbations (PEs). Details on both biomarkers and previous studies on them are discussed in Section 2. Both FEV₁ and PE are longitudinally collected (Figure 1). FEV₁ is a continuous measurement, and PE measurements are binary data on recurrent events. Though many longitudinal studies employ joint models to examine a single binary outcome and a number of longitudinal measurements (Horrocks and van Den Heuvel, 2009; Zhang et al., 2014; Li et al., 2015), they are not commonly used in studying longitudinal observations on both continuous and potentially recurring binary outcomes. Furthermore, we follow the shared parameter model approach to form the joint model (Taylor et al., 2013). The key innovation in our model structure is that we introduce the hierarchical GPs in the joint model, where not only the mean processes but also the shared parameters are modeled through GPs.

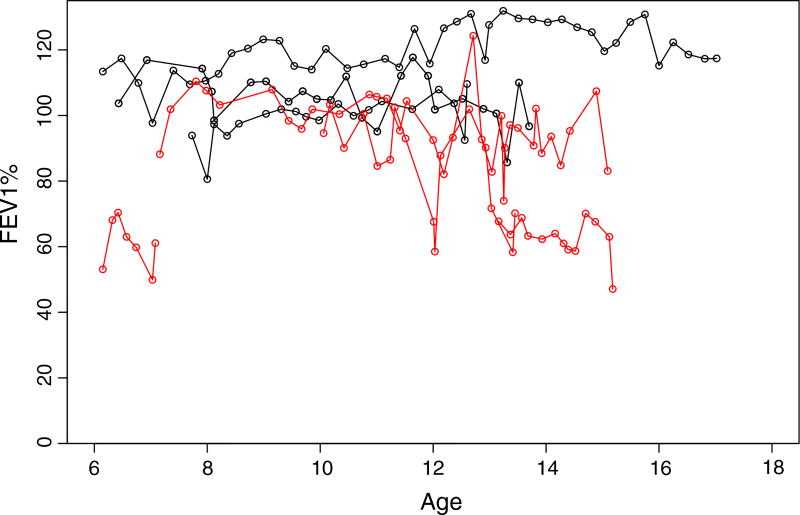
Figure 1.

Forced expiratory volume (FEV)₁ versus age (in years) from seven representative patients with data taken from the Cystic Fibrosis Foundation Patient Registry. Each set of points connected by a line represents observed FEV₁ over age for an individual patient. Trajectories in red represent individuals who had a pulmonary exacerbation, while trajectories in black represent individuals who were pulmonary exacerbation free during the observation period.

GP provides a useful paradigm for nonlinear interpolation and allows for borrowing strengths from data collected at all time points (Rasmussen & Williams, 2006). Compared to spline based methods, GP modeling does not require prior knowledge of important time points (knots). Its estimation is straightforward, and the predictive distribution is simple: the multivariate normal distribution associated with a GP model allows direct quantification of the uncertainty in the conditional variance. GPs have become particularly popular with the availability of fast estimation procedures such as the work by Banerjee et al. (2013). It has observed wide applications for many years in machine learning (Rasmussen & Williams, 2006) and spatial statistics (Cressie, 1988). However, its application has not been adequate in addressing the urgent demand for personalized prediction in biomedical settings.

In the proposed joint hierarchical Gaussian process model (JHGP), we adapt the GP to the inherently multilevel structure of the clinical data. On the population level, each of the two outcomes has its own nonlinear trend via GP modeling; on the individual level, each subject has a unique GP, which serves as the shared parameter to permit information borrowing across outcomes. Assuming the individual GPs are independently and identically distributed overcomes the challenges posed by the small sample size for a single subject and allow more stable estimates of the correlation parameter that characterizes the individual patterns. The model estimation is easy to be carried out through Hamiltonian Monte Carlo using Rstan (Stan Development Team, 2016). The direct goal of our proposed JHGP model is to address the nonlinear prediction needs in both FEV₁ and PE on the personalized level. The proposed model framework has wide applications in many other medical monitoring situations beyond the CF disease progression monitoring discussed here.

The remainder of the article is organized as follows. The motivating data set, including details of the clinical markers and previous research results, is described in Section 2. Section 3 presents the proposed JHGP model, including the personalized predictive distribution under the proposed model, prior distributions and posterior sampling. Section 4 shows the results from the simulation studies and assessments of the model prediction performance. Source code to reproduce these findings is included as Supporting Information. Section 5 shows results from applying the JHGP model to the CF clinical data set. Concluding remarks and discussion are presented in Section 6.

2 Motivating clinical data

2.1 Monitoring cystic fibrosis disease progression

Our JHGP model was motivated by medical monitoring data from the United States Cystic Fibrosis Foundation Patient Registry, which has provided epidemiologic surveillance on CF outcomes for more than 40 years. We obtained data on a sample of 38 patients with a total of 818 entries of observations. Data were analyzed from patients who had PE and FEV₁ data observed anytime from 6 to 18 years of age. This age range was selected for the following reasons. First, it was of interest to focus on data collected from childhood to adulthood, covering the most common interval in which there is a prolonged drop in lung function. Second, patients younger than 6 years of age were excluded due to potentially unreliable pulmonary function testing. We used the records from the calendar time January 1, 2003 to December 31, 2013. Encounter-level data available from 2003 onward were considered because PE events were consistently documented in the registry beginning in 2003. Data acquired after lung transplant were excluded. Quarterly ages were used as the time indices for the modeling.

2.2 Lung function measurement

As maintaining lung function is essential for survival in individuals with CF, lung function is routinely assessed in CF research and clinical practice. Lung function is monitored as forced expiratory volume in 1 second of percent predicted (denoted as FEV₁). FEV₁ is obtained as follows. Once a patient performs pulmonary function testing at a clinical encounter, a percent predicted value for his lung function is obtained based on his age, height, gender and race using standard reference equations (Wang et al., 1993; Hankinson et al., 1999). These computed values for each patient encounter are made available from the Cystic Fibrosis Foundation Patient Registry. The FEV₁ data in this sample range from 5% to 125% predicted.

As the most routine clinical measure of lung function in CF patients, FEV₁ data have motivated various longitudinal models, including recent development on individualized prediction (Taylor-Robinson et al., 2012) and nonlinear fitting of age-related FEV₁ progression (Szczesniak et al., 2013; Moss et al., 2016). Studies using CF registries have demonstrated that rapid changes in FEV₁ often occur during adolescence and adulthood (Vandenbranden et al., 2012) and that decline is nonlinear with age (Szczesniak et al., 2013). Previous statistical models being used in CF clinical practice for individualized prediction of such markers tend to feature simple functions (e.g., linear slope) or arbitrary rules (e.g., a decrease from maximum FEV₁ during the prior year of at least 10% predicted) (Szczesniak et al., 2016).

2.3 Pulmonary exacerbation event

Besides FEV₁, data on acute respiratory events, known as PEs, are also collected. Clinical diagnosis of a PE is often based on increased pulmonary symptoms, a loss of lung function, energy or weight and physical changes. It can occur multiple times in an individual CF patient. In our analysis, an event is defined as a PE event if it has a recorded treatment of PE with intravenous antibiotics in the registry.

Occurrence of PE has been associated with, among other adverse health outcomes, more rapid decline in FEV₁ (Konstan et al., 2007; Sanders et al., 2011). A converse association has been found, with PE occurrence being linked to a failure to recover to pre-PE or “baseline” FEV₁ (Sanders et al., 2010). Although PE onset is typically incorporated as a covariate in longitudinal modeling of FEV₁, it is a separate event process often clinically diagnosed by changes in lung function. Current joint modeling approaches used in monitoring CF disease progression have not yet incorporated data on PE. Therefore, it is desirable to construct a more informative, efficient approach to a simultaneous prediction of both occurrence of PE events and changes in FEV₁.

3 Model framework

3.1 Joint hierarchical Gaussian process model

Let {Y_it, R_it} be the observed outcomes for subject i at time t, where Y_it is the continuous longitudinal outcome and R_it is the binary longitudinal outcome. A shared parameter model is prescribed for these data:

$$Y_{\mathit{\text{it}}}~\mathrm{N}({\mu }_t^y+{\psi }_{\mathit{\text{it}}},{\sigma }^2),$$

$$R_{\mathit{\text{it}}}~\text{Bern}\{g({\mu }_t^R+c{\psi }_{\mathit{\text{it}}})\},$$

where N(a, b) represents a normal distribution with a mean a and a variance b, Bern(p) represents a Bernoulli distribution with the probability of success p, g(·) is the logistic link function g(λ_it) = {exp(λ_it)}/{1 + exp(λ_it)} with ${\mathit{\lambda }}_{\mathit{\text{it}}}={\mu }_t^R+c{\psi }_{\mathit{\text{it}}}$, and c is a scalar in [−1, 1]. Covariate effects can be easily added in both submodels, which are temporarily omitted here for focus on exploring the hierarchical GPs.

The uniqueness of this model is that ${\mu }_t^y$ and ${\mu }_t^R$ are parameters on the population level and, hence, are the same for all subjects; ψ_it is not only the individual deviation from the common trend but also acts as a shared parameter that induces correlation across the two outcomes.

Let μ^y and μ^R represent the two population mean processes $\{{\mu }_t^y\}$ and $\{{\mu }_t^R\}$, respectively, and ψ_i represents the individual heterogeneity, i = 1,…, n. Further denote λ_i = μ^R + c · ψ_i. To induce nonlinearity, GPs are used for both the population mean processes and the individual heterogeneities as

$${\mathit{\mu }}^y~\text{GP}(\mathbf{0},{\mathbf{\sum }}^y),$$

$${\mathit{\mu }}^R~\text{GP}(\mathbf{0},{\mathbf{\sum }}^R),$$

$${\mathit{\psi }}_i\stackrel{\mathit{\text{iid}}}{~}\text{GP}(\mathbf{0},\mathbf{\sum }),\text{for }i=1\dots n,$$

where X ~ GP(a, b) means that on any finite time point set {t₁,…t_k}, the joint distribution of X_k = {X(t₁), …, X(T_k)}′ is a k-variate normal distribution N(a_k, b_k) with the mean vector a_k = {a(t₁), …, a(t_k)}′ and covariance matrix b_k with the (ℓ,j)^th entry as b(t_ℓ, t_j), ℓ, j = 1,…, k.

This is a hierarchical GP since Y_i|μ^y ~ GP(μ^y, Σ +I·σ²) with I denoting the identify matrix and λ_i|μ^R ~ GP(μ^R, c²Σ) where the population mean processes μ^y and μ^R are each another GP. Jointly, the shared GP process induces the inter-outcome covariance: Cov(Y_i, λ_i) = cΣ.

The population mean processes is μ^y and μ^R are common to all subjects and, thus, can be estimated with high precision. A reliable estimation of the individual GP ψ_i, though, is challenging due to the limited amount of individual data. To maximize information borrowing across individuals and across outcomes, we allow the common Σ among the GP ψ_is’ and also include ψ_i’s as a shared component in the joint model. Both the simulation study and the real data application show that this model setup improves the flexibility and the precision in the personalized prediction.

3.2 Personalized predictive distribution

Let Z_it denote the joint vector of {Y_it, λ_it}′ and Z_i,T = {{Y_it}_t∈T, {λ_it}_t∈T}′, where T is a collection of time points. The key advantage of the hierarchical Gaussian process is the personalized predictive distribution: given the data t_i ≤ T, we predict Z_iti at T < t_i ≤ t_max, where t_max is the maximally observed time in the population. Let T₁ be the recorded set of time points in t_i ≤ T for subject i, and let T₂ be the time points of interest in T < t_i ≤ t_max. Using matrix notation, ${\mathbf{Z}}_{i,{\mathbf{T}}_2}|{\mathbf{Z}}_{i,{\mathbf{T}}_1}~\mathbf{N}\{{\mathit{\mu }}_{{\mathbf{T}}_2}+{\mathbf{K}}_{{\mathbf{T}}_2,{\mathbf{T}}_1}{\mathbf{W}}_{{\mathbf{T}}_1,{\mathbf{T}}_1}^{-1}({\mathbf{Z}}_{i,{\mathbf{T}}_1}-{\mathit{\mu }}_{T_1}),{\mathbf{W}}_{{\mathbf{T}}_2,{\mathbf{T}}_2}-{\mathbf{K}}_{{\mathbf{T}}_2,{\mathbf{T}}_1}{\mathbf{W}}_{{\mathbf{T}}_1,{\mathbf{T}}_1}^{-1}{\mathbf{K}}_{{\mathbf{T}}_1,{\mathbf{T}}_2}\}$, where μ_Tj is the joint vector of $({\mathit{\mu }}_{{\mathbf{T}}_j}^y,{\mathit{\mu }}_{{\mathbf{T}}_j}^R)\prime ,j=1,2,\mathbf{W}=\left[\begin{array}{cc}\hfill \mathbf{\sum }+\mathbf{V}\hfill & \hfill c\mathbf{\sum }\hfill \\ \hfill c\mathbf{\sum }\hfill & \mathbf{\sum }\end{array}\right],{\mathbf{K}}_{{\mathbf{T}}_2,{\mathbf{T}}_1}$ is the correlation matrix between mψ_iT2 and mψ_iT1 and V is a diagonal matrix σ² · I. Note that the prediction mean is the sum of two parts: (i) the nonlinear estimate μ_T2 obtained at the population level and (ii) the individual extrapolation based on its past deviation from the common trend (Z_i,T1 − μ_T1).

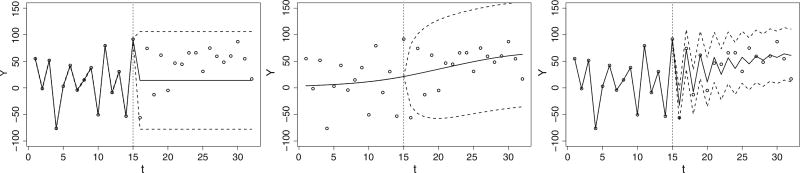
To illustrate the improvement in predictive accuracy with a two-level GP model, compared to a one-level GP model, extrapolation results taken from a simulated data set are presented in Figure 2. The three models shown are the model with only individual GPs, the model with the single population GP and the hierarchical GP model. The test samples include simulated data from n = 50 subjects, with the curve for each individual generated as the sum of a common random curve and an individual AR(1) process with ρ = −0.8. One subject was randomly selected, and the second half of the observed data points was removed. In the first test, an individual GP with the AR(1) (Figure 2, leftmost panel) is fitted to each subject. Although the fitted line shows that the model has adequate flexibility, it performs poorly in terms of extrapolation: the fitted line in the forecast range (t = 15 and forward) rapidly reverts to the constant mean due the underestimation of the autocorrelation. In the second test, all subjects are fitted with only the population GP with the squared exponential covariance; the prediction benefits from the similarity of trajectories and, hence, obtains some improvement (Figure 2, middle panel). In the last test, the hierarchical GP is used and leads to more gains, especially on the points near t = 15 (Figure 2, rightmost panel). Because the prediction is based on the individual level, the credible band is narrower than the population based GP when used alone.

Figure 2.

Illustration of the hierarchical Gaussian process (GP) in prediction based on simulated data. For a single subject, beginning with leftmost panel using autocorrelation of an individual GP; middle panel using the estimated μ from the population GP (with this subject excluded); ending with rightmost panel showing forecasting based on the estimated μ and the autocorrelation from the joint hierarchical Gaussian process model. In each panel, the vertical bar at t = 15 marks the beginning of the extrapolation.

3.3 Prior distributions and posterior sampling

A Bayesian method was employed to estimate the model parameters. Here, the squared exponential covariance ϕ exp(−ρ|t₁ − t₂|²) was used in Σ^y and Σ^R to induce smoothness on the population level. For Σ, Brownian motion ϕ min(t₁, t₂) or an autoregressive AR(1) structure with the (i, j)^th component as ϕρ^|t_j−t_i| was used to capture the fluctuation. Different covariance structures can be included based on the data structure. It is worth noting that ϕ and ρ are allowed to vary across the three processes defined in Section 3.1, but this notation has been suppressed for ease of exposition. Weakly informative proper priors were used for all the scale parameters, ϕ ~ C⁺(5), σ² ~ C⁺(5) or an inverse Gamma prior IG(2, 1) with a mean 1 and an infinite variance, ρ ~ C⁺(5) in Σ^y and Σ^R and ρ ~ Uniform(−1, 1) in Σ with AR(1), where C⁺(5) denotes a half Cauchy distribution with a scale of 5. The posterior sampling was carried out in Hamiltonian Monte Carlo via the software Rstan (Stan Development Team, 2016). The simulation file and source code are available as Supporting Information.

4 Simulation studies

4.1 Model estimation

To demonstrate estimation of the JHGP model, the following simulations were conducted. We simulated data sets with 50 subjects (i = 1, …, 50), each with observed Y_i and R_i at 25 time points (t = 1, …, 25) under three parameter settings, Sim 1 (ρ = −0.8, c = 0.9), Sim 2 (ρ = −0.5, c = −0.3) and Sim 3 (ρ = −0.1, c = 0.01), corresponding to three different levels of autocorrelation and inter-outcome association. Under each of the simulation settings, the data were simulated using the following framework:

$$\begin{array}{c}\mathbf{\text{Unobserved population and individual GPs}}:\hfill \\ {\mu }_t^y=50\text{ sin}\{(t-20)/100\}\text{ cos}\{-(t-10)/15\},t=1,\dots ,T,\hfill \\ {\mu }_t^R=4\text{ sin}\{(t-10)/5\}\text{ cos}\{t/10\},t=1,\dots ,T,\hfill \\ {\mathit{\psi }}_i\stackrel{\mathit{\text{indep}}}{~}\mathbf{N}(\mathbf{0},\mathbf{\sum }),\text{ where }\mathbf{\sum }\text{ is based on AR}(1)\text{with parameter }\rho ;\hfill \\ \mathbf{\text{Observed contionuous and binary longitudinal data}}:\hfill \\ {\mathbf{Y}}_i~\mathbf{N}({\mathit{\mu }}^y+{\mathit{\psi }}_i,0.01\mathbf{I}),\hfill \\ {\mathbf{R}}_i~\text{Bern}\{g({\mathit{\lambda }}_i)\},\text{ where }{\mathit{\lambda }}_i={\mathit{\mu }}^R+c{\mathit{\psi }}_i.\hfill \end{array}$$

The proposed JHGP model was fit to these three sets of data. The estimation of parameters is shown in Table 1; plots of estimated population processes (μ^y, μ^R) and a randomly selected individual processes (λ_i) for subject i are shown in Figure 3. The model correctly identified the values of autocorrelation ρ and the association parameter c. Moreover, the unobserved population processes (μ^y, μ^R) were accurately estimated. The estimates for λ_i, which are hidden behind the binary outcomes R_i, show high correlation with the true values.

Table 1.

Simulation with different values of the AR(1) parameter ρ and inter-outcome scalar c. The posterior means (with 95% credible intervals) show that these parameters are correctly recovered.

Sim No. (true values)	ρ	c
Sim 1 (ρ = −0.8, c = 0.9)	−0.77(−0.81,−0.74)	0.86 (0.69, 1.00)
Sim 2 (ρ= 0.5, c = −0.3)	−0.53(−0.48,−0.57)	−0.28(−0.44,−0.12)
Sim 3 (ρ = −0.1, c = 0.01)	−0.09(−0.14,−0.02)	0.03(−0.10, 0.18)

Figure 3.

Estimation of the unobserved nonlinear trends in simulation studies. The true (unknown) processes are shown in blue. The estimated values and corresponding 95% credible band are shown in red. The first two columns depict each of the longitudinal submodel results, while the last column shows the observed event occurrences against time for a randomly selected subject i.

4.2 Different covariance functions for individual deviation

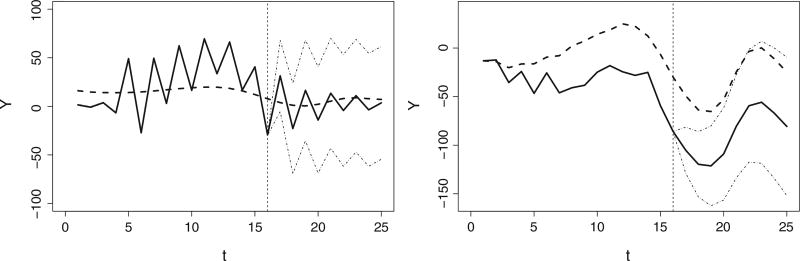
The choice of covariance function affects the behavior of extrapolation curves. A simple comparison between stationary (AR(1) process) and nonstationary (Brownian motion process) covariance functions was conducted. As shown in Figure 4, the stationary AR(1) process with a negative ρ tends to oscillate around the mean. This property is useful if the subject-specific trajectories tend to have similar progression while still accounting for the “saw-tooth” shape found in FEV₁ profiles in the CF data. On the other hand, Brownian motion as a martingale process always shows a constant difference from the mean process. This can reflect the notion that a loss or gain at a certain time is permanent for an individual.

Figure 4.

Simulated data illustrating different covariance functions in individual deviations (solid line) from the population mean (dashed line). Predictions with AR(1) (left) with negative ρ fluctuate around the common trend in the center; predictions with Brownian motion (right) tend to remain separate from the mean.

4.3 Robustness in association detection

In the joint model, the association between two responses is established by the shared individual GP, and its strength is measured by the association parameter c. We now assess its robustness under various levels of interference.

The same framework as in Section 4.1 was used to generate test samples with c = 0.5, except that an additional noise vector ${\mathit{\tau }}_i~\mathbf{N}(\mathbf{0},{\sigma }_{\tau }^2·\mathbf{I})$ was added into λ_i. We then gradually increase ${\sigma }_{\tau }^2$ in order to disturb the estimation of c. The noise-signal ratio is controlled by ${\sigma }_{\tau }^2/(c^2{\varphi }_{\psi })$, where ϕ_ψ is the scale parameter in the GP for ψ_i. The results are shown in Table 2. The numerical estimates only start to degrade around noise-signal ratio of 8.0, yet the association remains significant until the magnitude reaches 32.0. These findings suggest that the model is very robust in detecting the association between two responses in the presence of disturbance.

Table 2.

Association measures under different noise levels to assess model robustness.

Noise/Signal $({\sigma }_{\tau }^2/c^2{\varphi }_{\psi })$	c (true value: 0.50)
0.1	0.50 (0.34, 0.65)
0.5	0.46 (0.29, 0.58)
1.0	0.51 (0.37, 0.66)
2.0	0.44 (0.30, 0.58)
4.0	0.45 (0.30, 0.60)
8.0	0.25 (0.13, 0.37)
16.0	0.23 (0.11, 0.36)
32.0	0.09 (−0.03, 0.22)

4.4 Forecasting performance

We censored each subject in Sim1 data set (See Section 4.1) using random time C_i = min{t_max, t_c} where t_c ~ Uniform[0, 2t_max] and t_max is the largest recorded time. This mechanism results in censoring in about 50% of the subjects at random time points. Figure 5 plots the predicted values against the true values of Y and g(λ). The predicted values are highly correlated to the true values, with a Pearson correlation 0.86 for Y and 0.73 for g(λ).

Figure 5.

Prediction performance: predicted values versus true values in Sim1 data set for modeling the longitudinal process for Y (left) and the event process for g(λ) (right).

5 Application in cystic fibrosis medical monitoring

5.1 Analysis cohort selection

We applied the model to characterize the association between the longitudinal marker of lung function, FEV₁, and the occurrence of acute respiratory events, PEs, for patients with CF disease. The primary goal was to provide longitudinal predictions for each clinical marker. The analysis cohort and study variables are described in Section 2. Among the 38 patients included in the analysis cohort, 19 patients were randomly selected to assess prediction performance. For each patient in this sub-cohort, the more recent 50% of his or her observations (both FEV₁ and PE) were masked. Having this sub-cohort results in a training and testing split of about 75% and 25%, respectively. We use a random intercept for each patient (indexed by i) to offset the starting difference.

5.2 Parameter estimation

The JHGP model detects a strong autocorrelation (ρ = −0.82 ± 0.05) in the shared Gaussian process ψ_i, i = 1, …, 38; the variations of FEV₁ and the PE probability have a weak negative inter-outcome correlation (c = −0.29 ± 0.13). The fitted FEV₁ and PE probability are shown, along with corresponding 95% credible intervals, in Figure 6. The population mean processes and individual AR(1) processes appear to be reasonably estimated. Among which, the population-level estimate of age-related FEV₁ progression is consistent with what was found in previous CF studies using penalized splines (Szczesniak et al., 2013; Szczesniak et al., 2017). The mean evolution of lung function exhibits a gradual decline in earlier ages and subsequently becomes more progressive as patients enter adolescence and early adulthood. The risk of PE appears heightened around ages 10–11, which corresponds to the time preceding more progressive lung function decline. The overall PE risk has smooth estimates, yet it does not resemble any common parametric distribution. The stochasticity of individual variation in the PE risk is also captured by the model.

Figure 6.

Fitted longitudinal forced expiratory volume (FEV₁) (left) and pulmonary exacerbation event (right) data over age for representative cystic fibrosis patients using the joint hierarchical Gaussian process model. Each dot in the left panel represents observed FEV₁ for a patient at a given age, while each dot in the right panel indicates whether or not a given patient has experienced a pulmonary exacerbation. The smooth red line in each graph is the estimate of age-related progression at the population level. The individual blue lines are the fitted profiles representing personalized predictions based on the joint hierarchical Gaussian process.

5.3 Prediction performance

The predicted FEV₁ values are plotted against the corresponding observed yet masked values in Figure 7, which shows all points lie around the 45° reference line. We further evaluate the results and compare the effects of the hierarchical model with the nonhierarchical model using the median absolute deviation, root mean squared error and Pearson correlation. The three evaluation metrics median absolute deviation, root mean squared error and Pearson correlation are 6.43, 8.47 and 0.93, respectively, by the JHGP model, compared to 8.66, 10.63 and 0.89, respectively, by the single population GP model. Although the results from the population GP seem adequate for predicting the future trend, including the individual GPs apparently further improves the estimation accuracy.

Figure 7.

Prediction performance of the joint hierarchical Gaussian process longitudinal submodel for forced expiratory volume from the cystic fibrosis clinical data. The graph shows the predicted values from joint hierarchical Gaussian process against the observed values of forced expiratory volume with the 45° reference line.

5.4 Assessment of sensitivity and specificity

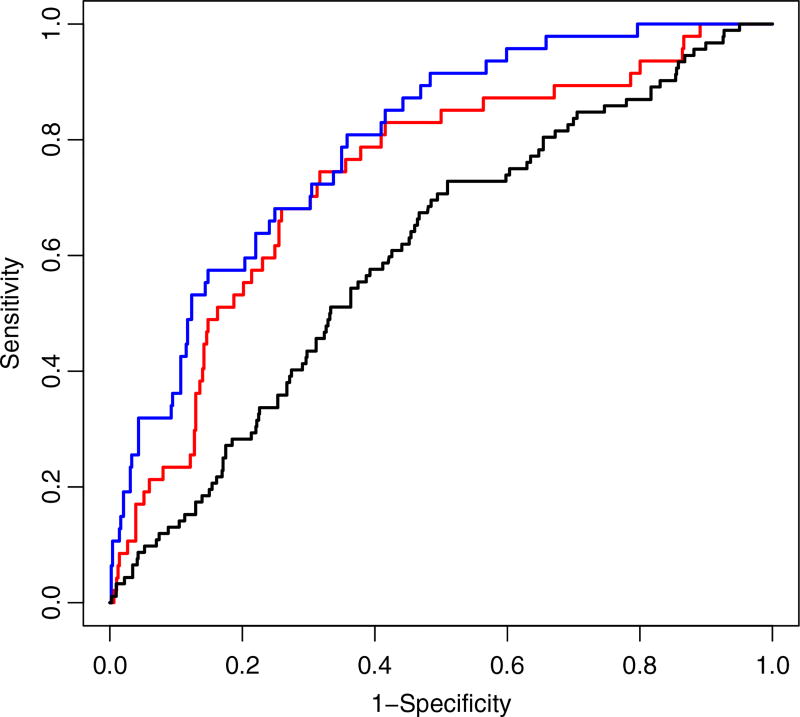
Sensitivity and specificity of the PE predictions using three different model settings were examined using Receiver Operating Characteristic curves (Figure 8). The models included the JHGP of FEV₁ and PE, a single logistic model that included a population-based GP to model PE events and a traditional linear-logistic model of PE events. In the later two single models, FEV₁ was included as a covariate. Both the JHGP and the single logistic GP models had higher AUC than the traditional linear-logistic model, indicating that the nonlinear attributes of the GP models improved predictive accuracy. The joint model with hierarchical GPs had better sensitivity, compared to the single GP model.

Figure 8.

Receiver Operating Characteristic curves of each model of the pulmonary exacerbation (PE) event data from the cystic fibrosis clinical data. From left to right, the joint hierarchical Gaussian process model (blue curve) shows highest AUC at 0.735, followed by the single logistic Gaussian process model of PE (red curve: 0.683) and lastly the traditional linear-logistic model of PE (black curve: 0.605).

6 Discussion

We have developed a joint model with hierarchical GPs in each submodel to accommodate the analysis and prediction of monitored clinical data. We consider a two-level design: the first (population) level describes the overall progression of the markers; the second stochastic (individual) level captures the finer, personalized variation in both continuous and binary outcomes. The hierarchical design is conceptually simple and allows information to be shared across individuals as well as different outcome types. This leads to an attractive form of the predictive distribution that joins population change and personal history.

Several extensions to this work can be made in the future. If the longitudinal data exhibit several distinct types of progression, then the population hierarchy can be replaced with a mixture of Gaussian processes as suggested in Shi et al. (2005). Additional levels could be incorporated in the model to accommodate a more refined hierarchical structure in the data; for example, different medical centers tend to have distinct practice patterns. Our JHGP application to the CF data suggests the presence of more heterogeneity between longitudinal FEV₁ trajectories, compared to PE hazard curves in Figure 6. This has not been previously characterized in the CF epidemiological literature, but additional work could be performed to standardize the processes and assess heterogeneity in this context. Findings on prediction performance for FEV₁ suggest the possibility of bimodality (Figure 7), but further assessments with additional covariate information, or perhaps an extension of the JHGP model to accommodate latent classes, would be needed to determine if results are indicative of subgroups. Also, the joint hierarchical GP modeling framework is general and can be extended to more than two outcomes. Although a pediatric cohort was examined in the current work, such an extension could accommodate censoring arising from death if studying the broader adult CF cohort or other data in which there is a potential for survivorship bias.

Often clinicians are interested in survival times of recurrent events. This would require, as in the motivating CF example, joint modeling of the longitudinal measurements on FEV₁ as well as the survival times of the recurrent PE events. The implementation of the proposed hierarchical GP model framework to this situation is currently under study. Furthermore, separate assessments of each component in the joint model help assess the goodness of fit for each component and is of clinical importance (Zhang et al., 2014; Zhang et al., 2017). It is of practical and theoretical interests to investigate how to achieve separate assessments in this JHGP model based on the work of Zhang et al. (2017) as a direct application of their criteria faces computational challenges due to the inclusion of the shared GPs component.