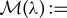Pulse dynamics in reaction–diffusion equations with strong spatially localized impurities

Abstract

In this article, a general geometric singular perturbation framework is developed to study the impact of strong, spatially localized, nonlinear impurities on the existence, stability and bifurcations of localized structures in systems of linear reaction–diffusion equations. By taking advantage of the multiple-scale nature of the problem, we derive algebraic conditions determining the existence and stability of pinned single- and multi-pulse solutions. Our methods enable us to explicitly control the spectrum associated with a (multi-)pulse solution. In the scalar case, we show how eigenvalues may move in and out of the essential spectrum and that Hopf bifurcations cannot occur. By contrast, even a pinned 1-pulse solution can undergo a Hopf bifurcation in a two-component system of linear reaction–diffusion equations with (only) one impurity.

This article is part of the theme issue ‘Stability of nonlinear waves and patterns and related topics’.

1. Introduction

The analysis of the impact of spatial defects on systems of partial differential equations has received a great deal of attention over the past few decades ([1–20], e.g.). A large part of this research centred around heterogeneous Schrödinger-type equations ([5,6,9,10,12,18], e.g.) and typical defects considered are Dirac delta-function-like defects ([5,10,12,14,18], e.g.) and step-function-like defects ([7,8], e.g.). It has, for instance, been shown that spatial defects are able to pin travelling waves in nonlinear wave equations [2,3,11].

In this manuscript, we are interested in the impact of large, spatially localized, nonlinear defects on the pattern formation process for linear systems of reaction–diffusion equations (RDEs). In particular, we are interested in strongly localized impurities that have the structure of Dirac delta-function-type perturbations in the singular limit ε→0,

1.1

where 0<ε≪1 is a sufficiently small parameter, 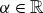is a parameter measuring the strength of the impurity and G is a sufficiently smooth nonlinear function (of the state variable U) that satisfies G(0)≠0. The Dirac delta-type impurity I is centred around ξ₀:=x₀/ε² and is assumed to decay exponentially fast. Without loss of generality, we furthermore assume that

1.2

A typical example of such a Dirac delta-type impurity is 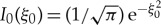. Hence, for 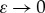, (1.1) is locally (near x₀) asymptotically large and effectively negligible otherwise.

We analyse the impact several of these strongly localized impurities of the form (1.1) can have on the existence, stability and bifurcations of stationary, or pinned, single- and multi-pulse solutions for systems of RDEs in one spatial dimension. More specifically, we study

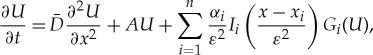1.3

where 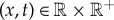, U(x,t): 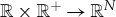are the state variables, 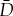is a diagonal diffusion N×N-matrix with positive entries, i.e. 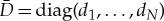with d_i>0. The constant N×N-matrix A is chosen such that the trivial state U≡0 of the unperturbed system

1.4

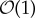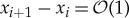is stable. Note that U≡0 is not a solution to the perturbed problem (1.3) since G_i(0)≠0 by assumption. In addition, 0<ε≪1 and all other parameters are assumed to be with respect to ε. The strongly localized impurities (α_i/ε²)I_i((x−x_i)/ε²)G_i(U) are all of the form (1.1) and they are centred around the well-separated locations x_i in the sense that for i=1,…,n−1. That is, and x_i+1−x_i≪1.

The unperturbed system (1.4) does not possess stationary pulse solutions since it is linear and the addition of strongly localized impurities (potentially) creates stationary/pinned—or even oscillatory—pulse solutions that asymptote to the background state U=0. This is similar to paradigmatic singularly perturbed slow-fast RDEs with linear slow flow, such as the Gray–Scott and Gierer–Meinhardt models, where a fast V -component can be interpreted as being added to the linear RDE for the slow U-component ([21–23], e.g.). In other words, adding the strongly localized impurities of the form (1.1) to (1.4) to create localized solutions can be seen as a simplifying alternative to adding fast components to (1.4). Adding strongly localized impurities to (1.4) is a very controllable way to make a linear system locally nonlinear and it is not unrealistic from an applied point of view as the linearity of the model breaks down under strong perturbations. Also, as we will show, (1.3) is very amendable for analysis while its localized structures exhibit rich and fully controlled behaviour. For instance, the leading order parts of the eigenvalues determining the stability of the pinned pulse solutions can be computed explicitly and the computations are drastically simpler than the technical Evans function computations for slow–fast RDEs ([24], e.g.). So, (1.3) could, for instance, easily be used as a starting point—and organizing centre—for understanding complex, or maybe even chaotic, pulse dynamics ([25,26], e.g.).

Remark 1.1. —

The present work distinguishes itself in two ways from the existing literature on the impact of strongly localized impurities on the dynamics of evolutionary PDEs ([5,10,12,14,18], e.g.). Firstly, our approach is developed in the setting of a general class of RDEs, while all the literature we are aware of is focused on specific models (see also the discussion in §4). Secondly, the present analysis is valid for ε>0 (but sufficiently small), i.e. for (more) realistic impurities of the type (1.1) that only become of Dirac delta-functions in the singular limit ε→0. In other words, the current analysis extends the singular limit approach—with Dirac delta-function-type impurities—of the large majority of the literature (see, however, also [17,18]). In fact, our approach may serve as a (geometric) framework by which results presented in the literature may be rigorously validated and extended beyond the Dirac delta-function limit to impurities of the type (1.1).

(a). Results and outlook

The strong localization of the nonlinearities in (1.3) allows us to develop a general geometrical singular perturbation framework to study the existence, stability and bifurcations of these pinned pulse solutions supported by (1.3). More specifically, (1.3) is to leading order linear away from the impurities and it can thus be solved—to leading order—explicitly in these slow regions. The nonlinearities G_i of the strongly localized impurities are then used to construct pinned pulse solutions by appropriately concatenating the different slow parts over the fast regions. Also, by the linearity of the slow problem (i.e. (1.4)) it directly follows that n impurities are needed to be able to construct a pinned n-pulse solution. Observe that the construction of the pinned pulse solutions is similar to—but algebraically simpler than—the construction of pulse solutions in, for example, the Gray–Scott and Gierer–Meinhardt models with linear slow components ([21–23], e.g.).

To determine the spectral—and nonlinear [27]—stability of such a constructed pinned pulse solution, we linearize (1.3) around the pinned pulse solution. The spectrum of the linearized stability problem naturally falls into two parts: the essential spectrum σ_ess and the point spectrum σ_pt containing the associated eigenvalues ([27], e.g.). The former deals with instabilities arising from , while the latter deals with instabilities arising near the pulses, or interfaces, of the associated pinned pulse solution. By the particulars of the model, the essential spectrum of a pinned pulse solution supported by (1.3) coincides, to leading order, with the spectrum of the trivial state U≡0 of the unperturbed problem (1.4). Since we require the latter to be stable, the essential spectrum of a pinned pulse solution is—by assumption—always fully contained in the open left-half plane and thus does not yield instabilities. Consequently, the stability of a pinned pulse solution supported by (1.3) is fully determined by the location of its eigenvalues. In sharp contrast to typical RDEs, it is relatively straightforward to determine the leading order parts of these eigenvalues as we can directly relate the associated linear stability problem to the existence problem in the different slow and fast regions. However, see also remark 1.4. Hence, we have explicit control over the eigenvalues—and thus the stability—of the pinned pulse solutions supported by (1.3). This allows us, for example, to directly search for Hopf, and other types of more complex, bifurcations.

For the scalar case, the diffusion matrix 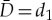can be scaled to one, and the requirement that the trivial state U≡0 of the unperturbed problem (1.4) is stable implies that A (which is a scalar in this case) is negative. Therefore, we define μ:=−A and we prove the following result.

Theorem 1.2. —

Fix N=1,d₁=1 and 0>A:=−μ and let ε be small enough. Then, (1.3) with n impurities supports pinned n-pulse solutions (with the ith pulse centred at x_i) if there exist non-degenerate solving the system of equations

1.5

The amplitude of the ith pulse of such a pinned n-pulse solution is to leading order given by .

All eigenvalues λ of such a pinned n-pulse solution are real-valued and the n-pulse solution is stable if all λ>−μ for which the matrix

1.6

is non-invertible, necessarily have ℜ(λ)<0—see also remark 1.5.

See figure 1 for an example of a numerically obtained stable pinned 1-pulse solution supported by the scalar version of (1.3). The fact that all eigenvalues of a pinned n-pulse solution of the scalar version of (1.3) are real-valued stems from the fact that the associated stability problem is a Sturm–Liouville problem ([27], e.g.). A direct consequence is that, unlike their counterparts in two-component slow-fast RDEs ([24], e.g.), pinned n-pulse solutions of the scalar version of (1.3) cannot undergo Hopf bifurcations. A straightforward computation also shows that the matrix 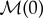(1.6) is non-invertible if and only if 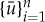is a degenerate solution of (1.5). So, upon changing a system parameter, a stable pinned n-pulse solution and unstable pinned n-pulse solution generically merge and disappear in a saddle-node bifurcation when λ=0 is an eigenvalue (of both pinned 1-pulse solutions), see, for example, §2a(i) and figure 1. Or, alternatively, a stable pinned n-pulse solution and unstable pinned n-pulse solution merge and exchange stability via a transcritical bifurcation when λ=0 is an eigenvalue. In §2, we first introduce the geometrical singular perturbation framework to study the existence and stability of pulse solutions supported by (1.3) for N=1 and n=1. As it turns out, the linearity of (1.3) away from the localized impurities significantly simplifies the stability analysis and the stability condition follows, in essence, directly from the existence analysis. However, see also remark 1.4. Next, we use this general framework to prove theorem 1.2.

Figure 1.

(a) Numerically obtained stable pinned 1-pulse solution U⁺_p supported by the scalar version of (1.3) with one impurity located at the origin. In particular, n=1 and x₁=0 in (1.3). In addition, 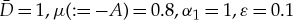, and G₁(U)=−U²+4U−1. (b) Close-up of (a) around the impurity. The dots indicate the numerically obtained pinned 1-pulse solution, while the solid curve represents the asymptotically constructed leading order pinned 1-pulse solution. (c) The leading order magnitude 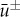of the pinned 1-pulse solutions supported by the model as function of the system parameter μ obtained from the existence condition (1.5) of theorem 1.2. The solid curve represents stable pulse solutions U⁺_p as obtained from the stability condition related to (1.6) of theorem 1.2. The dashed curve represents unstable pulse solutions U⁻_p also supported by the model. The dot on the stable curve at 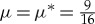indicates the emergence/disappearance of a point eigenvalue out of/into the essential spectrum, see remark 2.1 and §2a(i) for more details.

In contrast to the scalar case, pinned pulse solutions can undergo a Hopf bifurcation for systems of RDEs with strongly localized impurities—even when there is only one impurity. To show this, we study the simplest system of RDEs of the form (1.3) in §3. That is, we study (1.3) with N=2 and n=1. However, see also remark 1.6. Without loss of generality, we can assume that the impurity is located at the origin and that the diffusion coefficient of the U₁-component is scaled to 1, i.e. d₁=1. That is, we study

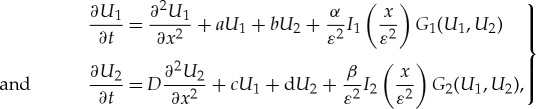1.7

with G₁(0,0)≠0≠G₂(0,0) to ensure that U≡0 is not a solution to (1.7). The requirement that the trivial state U≡0 of the unperturbed problem (1.4) is stable implies that a+d<0,ad−bc>0 and a+d/D<0—which is the standard condition that prevents Turing instabilities ([28], e.g.). We prove the following result by generalizing the geometric singular perturbation framework for the scalar case.

Theorem 1.3. —

Let a,b,c,d,D be such that a+d<0,a+d/D<0 and ad−bc>0 and let ε be small enough. Then, (1.7) supports pinned 1-pulse solutions (U_1,p,U_2,p) centred around 0 if there exist non-degenerate solving

1.8

Here, and are explicitly known quantities depending on the system parameters and the particulars of the impurity. The amplitudes of the (U₁,U₂)-coordinates of a pinned 1-pulse solution are to leading order given by .

A pinned 1-pulse solution (U_1,p,U_2,p) is stable if all solving

1.9

have ℜ(λ)<0. Here, σ_ess and are explicitly known and depend on the system parameters and the impurities.

We refer to §3 for the details regarding 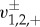, 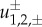and the matrix 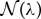. Observe that, as for the scalar case, λ=0 being an eigenvalue is again related to the solution 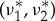of (1.8) being degenerate. It is now straightforward to derive conditions on the system parameters and impurities such that a pinned pulse solution of (1.7) can undergo a Hopf bifurcation, see §3b(i).

We end the manuscript with a discussion and outlook of future projects related to systems with strong localized impurities.

Remark 1.4. —

In principle, we could have used an Evans function framework ([29], e.g.) to obtain the stability results of theorems 1.2 and 1.3. In fact, (1.6) and (1.9) can be directly related to a condition of the form , where is a—remarkably simple and very explicit—Evans-function associated with the spectral stability problem. We decided not to pursue this direction for the brevity and readability of the manuscript.

Remark 1.5. —

In this manuscript, we use the convention that for .

Remark 1.6. —

While theorem 1.3 only entails pinned 1-pulse solutions of (1.7) (i.e. (1.3) with N=2 and n=1), the geometrical singular perturbation framework presented in this manuscript can also be used to study linear systems of RDEs of arbitrary size and with an arbitrary number of impurities, i.e. (1.3) for arbitrary N and n. However, for algebraic simplicity and brevity, we decided to focus on only the scalar case (i.e. N=1) and the two-component case with one impurity (i.e. N=2 and n=1) in this manuscript.

2. Scalar linear reaction–diffusion equations with impurities

We start by analysing the scalar version of (1.3)

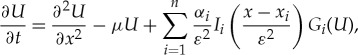2.1

with 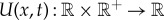and where, without loss of generality, the diffusion constant 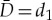has been scaled to 1, −A:=μ>0—to ensure that trivial state U≡0 of the unperturbed problem (1.4) is stable—and the impurities are as described in (1.1).

(a). Pulse solutions with one impurity

To introduce the methodology, we first focus on the impact of one impurity, i.e. we take n=1. Without loss of generality, we centre this impurity at the origin, i.e. we set x₁=0. Hence, pinned pulse solutions correspond to homoclinic solutions governed by the following second-order ordinary differential equation (ODE)

2.2

The strong spatial localization of the impurity imposes two different spatial scales, x versus ξ:=x/ε², on (2.2). Consequently, we can study (2.2) using geometric singular perturbation theory (GPST) [30,31]. More specifically, we split our spatial domain into three regions 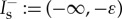, I_f:=[−ε,ε] and 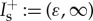, and we use the two different spatial scales to study (2.2) in the different regions. Note that the boundaries ±ε of these regions are asymptotically small compared to x, while they are asymptotically large compared with ξ. In the slow regions I^±_s, the impurity is exponentially small and the slow flow of (2.2) is approximated by the following system of first-order ODEs

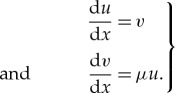2.3

The origin is a saddle point with stable manifold 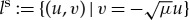and unstable manifold 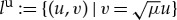. So, for a fixed u, the distance between the stable manifold and unstable manifold is .

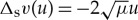In the fast, or defect, region I_f near the origin, the impurity is dominating the dynamics of (2.2) and to describe this fast flow we use the fast spatial time scale ξ:=x/ε². This transforms (2.2) to

2.4

Note that (2.2) and (2.4) are equivalent as long as ε≠0. To leading order, the flow of (2.4) is governed by d²u/dξ²+ε²αI(ξ)G(u)=0, which we equivalently write as

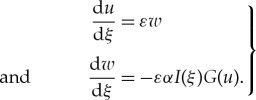2.5

Note that w=εv=εu_x and that since 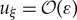in (2.5), u is to leading order constant in the fast region I_f. In other words 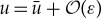in I_f. Consequently, the accumulated change of w during a passage through the fast region I_f is

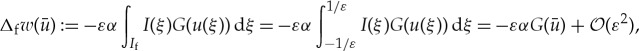2.6

since we assumed that .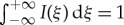

In the singular limit ε→0, a homoclinic solution to (u,v)=(0,0) to (2.2) should follow l^u of (2.3), take off from l^u following the fast dynamics of (2.5) and touch down again on l^s, and then follow l^s of (2.3) back to the origin ([22], e.g). Thus, 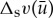and 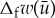should be the same up to a factor ε (since w=εv) and we get that 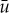—the leading order component of u over the fast field—is determined by the solutions 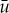of the nonlinear algebraic expression

2.7

In addition, a homoclinic solution to (2.2) is in the singular limit ε→0 given by

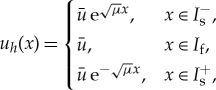2.8

where 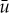solves (2.7) and observes that the magnitude of the homoclinic solution u_h is given by 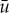. This homoclinic solution u_h corresponds to a pinned 1-pulse solution U_p(x) of (2.1) with one impurity (i.e. n=1). As long as the solution 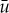to (2.7) is non-degenerate, i.e. as long as the curves of (2.7) intersect transversally, then this pinned 1-pulse solution persists, and is to leading order given by (2.8), for ε≠0 small [30,31]. Note that this in essence establishes the existence part of theorem 1.2 for n=1, for more details see the proof of theorem 1.2 below.

To determine the spectral (and nonlinear) stability of a pinned 1-pulse solution U_p(x), which is to leading order given by (2.8), we linearize (2.1) around U_p(x). As alluded to in the Introduction, the linearized operator has no essential spectrum [27] in the right-half plane. Hence, we focus on the point spectrum of the linearized operator. The associated eigenvalue problem determining the point spectrum σ_pt is obtained by substituting the ansatz U(x,t)=U_p(x)+e^−λtp(x), w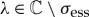ith with 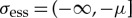, into (2.1) and linearizing the resulting expression. This gives

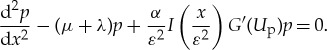2.9

The spatial localization of the impurity and the fact that U_p is to leading order constant in the fast field I_f allows us to treat (2.9) in a similar fashion as (2.2). In fact, in the slow regions I^±_s the impurity is exponentially small and the slow flow of (2.9) is approximated by

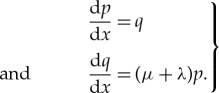2.10

Hence, the leading order slow flow of (2.9) in the slow regions can be obtained from the leading order slow flow of (2.3) by replacing μ with μ+λ. In particular, 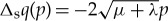. In the fast region near the origin, the impurity is dominating the dynamics of (2.9). Moreover, since 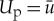to leading order in the fast field, the fast flow of (2.9) is approximated by

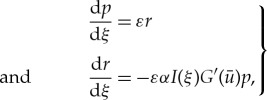2.11

with 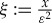. We can directly relate (2.11) to (2.5) by replacing 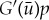with G(u). Hence, p is to leading order constant in I_f and 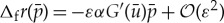. Consequently, the eigenvalue of a non-trivial eigenfunction p related to a pinned 1-pulse solution U_p is, to leading order, determined by the solution of

2.12

see also (2.7).

Since 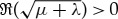, (2.12) has no solutions for . Consequently, a pinned 1-pulse solution U_p for which 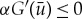only has essential spectrum and is thus stable. For 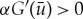, the eigenvalue of a pinned 1-pulse solution U_p can be determined explicitly from (2.12) and is given by

2.13

Hence, for 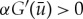, the pinned 1-pulse solution U_p is stable if 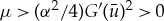and unstable if .

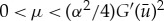Remark 2.1. —

At μ=μ* such that , an eigenvalue disappears into the essential spectrum to form a resonance pole ([27], e.g.). Note that this provides a remarkably simple explicit example of an eigenvalue moving into the essential spectrum σ_ess. See also figure 1c.

Remark 2.2. —

While the trivial state U≡0 of the scalar RDE without impurities, i.e. (1.4), looses stability as μ becomes negative, a pinned 1-pulse solution U_p(x) of the scalar RDE with one impurity ceases to exist or looses stability at . That is, a pinned 1-pulse solution U_p(x) of the heterogeneous system becomes unstable before the trivial solution U≡0 of the associated homogeneous system becomes unstable. This can be interpreted as that the impurity generates an instability within the defect region for , but that the equation wants to remain near its trivial state in the slow regions away from the impurity. Hence, for we expect that the solution blows-up in the defect region or evolves to another stable pinned 1-pulse solution. This is confirmed by numerical simulations.

(i). Example 1: scalar pinned 1-pulse solutions

To further illustrate the theoretical results discussed above, we consider the following scalar linear RDE with one impurity

2.14

where ε>0 is small enough, μ>0 and 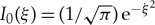. The existence criterion (2.7) implies that, for ε small enough, (2.14) supports a pinned 1-pulse solution with leading order magnitude 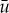if 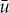solves 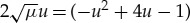. This gives

2.15

Hence, (2.14) has two positive pinned 1-pulse solutions U^±_p with leading order magnitude 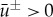(2.15) for 0<μ<1. These two solutions merge and disappear in a saddle-node bifurcation for μ=1. Note that (2.14) also has two negative 1-pinned pulse solutions for μ>9, we will not consider these solutions here.

The eigenvalue expression (2.12) is only well defined for , and while 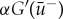is always positive for 0<μ<1, 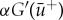is only positive for 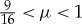. In other words, the eigenvalue of 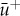disappears into the essential spectrum 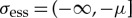upon decreasing μ (from 1) to 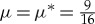, see also remark 2.1. For 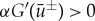, the eigenvalue expression (2.13) for (2.14) reduces to

2.16

So, λ⁻>0 for 0<μ<1, while λ⁺<0 for 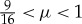. Consequently, the pinned 1-pulse solution U⁻_p is unstable for 0<μ<1, while the pinned 1-pulse solution U⁺_p is stable for 0<μ<1. See also figure 1.

(b). Proof of theorem 1.2.

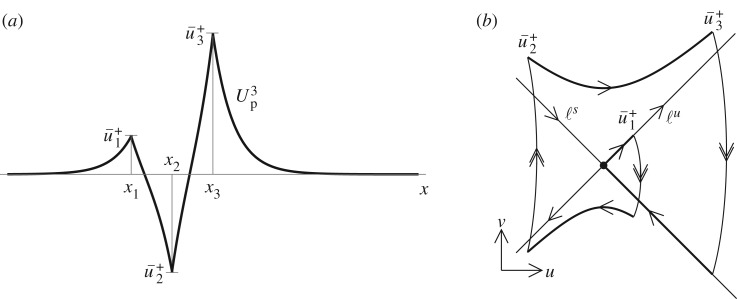
In this section, we study the impact of n impurities on the scalar RDE (2.1) and we prove theorem 1.2. A pinned n-pulse solution Uⁿ_p(x), see figure 2 for a typical sketch of a pinned 3-pulse solution U³_p(x), corresponds to a homoclinic solution of

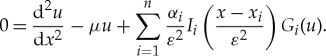2.17

We proceed as in §2a to construct these pinned n-pulse solutions, but now we split the spatial domain in n+1 slow regions away from the impurities and n fast regions around the impurities. That is, 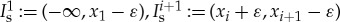, for i=1,…,n−1, and Iⁱ_f:=[x_i−ε,x_i+ε], for i=1,…,n. All the impurities are exponentially small in the n+1 slow regions since the centres of the impurities are by assumption well-separated. Hence, the slow flow of (2.17) in the slow regions is still to leading order given by the linear equation (2.3), and

2.18

where A_n+1=B₁=0 to ensure that the n-pulse solution approaches the background state U=0 as , while the other remaining 2n integration constants A_i and B_i still need to be determined.

Figure 2.

(a) Sketch of a pinned 3-pulse solution U³_p(x). (b) The associated phase portrait in the slow (u,v)-coordinates. The transitions through the three fast fields induced by the three impurities centred around x_1,2,3 are indicated by the double arrows.

In the ith fast region Iⁱ_f, the ith impurity is dominating the dynamics of (2.17). Therefore, we introduce n new fast variables ξ_i:=(x−x_i)/ε² for i=1,…,n, and the flow of (2.17) in the ith fast region Iⁱ_f is to leading order governed by

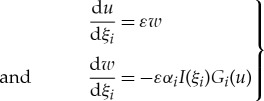2.19

for i=1,…,n, see also (2.5). Equivalently to (2.6), we get that the u-component is to leading order constant, say 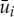, in the ith fast region Iⁱ_f for i=1,…,n. By contrast, the accumulated change of w during a passage through the ith fast region 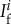is, to leading order, given by

2.20

Combining (2.18) and (2.20), with the observation that u is to leading order constant over the fast fields, allows us—after a tedious, but straightforward, algebraic computation—to determine the remaining 2n unknown integration constants. They are given by

2.21

where we adapted the convention that an empty sum is zero, i.e. B₁=A_n+1=0. By (2.18) evaluated at x_i—so that 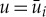—it follows that the 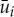s are indeed determined by the existence condition (1.5). The constructed homoclinic solution corresponds to a pinned n-pulse solution of (2.1) in the singular limit ε→0. It follows from a direct application of GPST [30,31] that such a pinned n-pulse solution persists—and is to leading order given by (2.18) and (3.10)—for 0<ε≪1, as long as the solution set of (1.5) is non-degenerate. This proves the first part of theorem 1.2.

To determine the stability of a pinned n-pulse solution Uⁿ_p(x), we linearize (2.17) around Uⁿ_p(x). Again, by construction, the resulting linearized operator has no essential spectrum in the right-half plane and we can focus on the point spectrum. The associated eigenvalue problem is given by

2.22

where we recall that 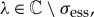with 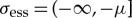. All eigenvalues λ of (2.22) are real-valued since (2.22) is a Sturm–Liouville problem ([27], e.g.). In a similar fashion as for the stability problem for the scalar equation with one impurity (2.9), we can relate (2.22) to (2.17) to explicitly determine the leading order parts of the eigenvalues. In particular, the leading order slow flow of (2.22) in the slow fields can be obtained from the leading order slow flow of (2.17) in the slow fields by replacing μ with μ+λ. In addition, the leading order fast flow of (2.22) in the fast field Iⁱ_f can be obtained from the leading order fast flow of (2.17) in the fast field Iⁱ_f, i.e. (2.19), by replacing G_i(u) with G_i′(Uⁿ_p)p. Since both the pinned n-pulse solution Uⁿ_p and the eigenfunction p are to leading order constant in the fast field Iⁱ_f, we get that the eigenvalues of a non-trivial eigenfunction are determined by the solutions of

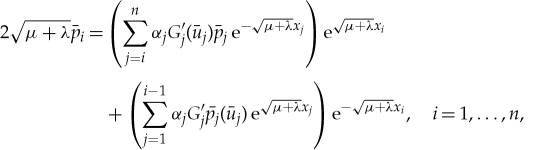2.23

where 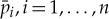, is the leading order constant value of the eigenfunction p in the ith fast field Iⁱ_f. Since (2.23) is equivalent to 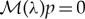, with 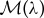as in (1.6), (2.23) has non-trivial solutions if and only if 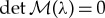. This completes the second part of theorem 1.2.

(i). Example 2: scalar pinned 3-pulse solutions

As an example, we further study the existence condition (1.5) and stability condition (2.23) for pinned 3-pulse solutions in the scalar linear RDE (2.1) with three impurities. See figure 2 for a typical sketch of a pinned 3-pulse solution and its associated slow phase portait. For n=3, the existence condition (1.5), respectively, stability condition (2.22), reduces to

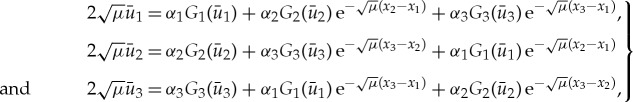2.24

respectively,

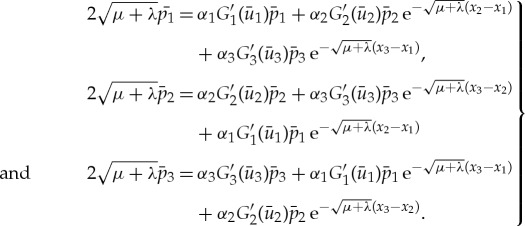2.25

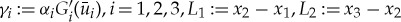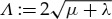Upon introducing the short-hand notation and (with ℜ(Λ)>0), (2.25) can be rewritten as

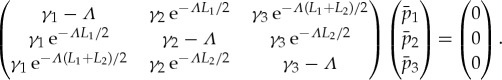2.26

For the determinant of the above matrix to be zero we get

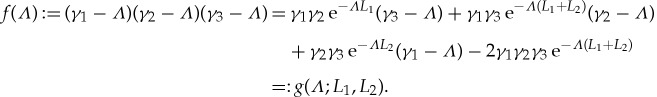2.27

Since the stability problem from which (2.22) originated is a Sturm–Liouville problem, we know—surprisingly—that the above equation (2.27) cannot have any complex-valued roots with ℜ(Λ)>0. Hence, upon changing the system parameters, roots of (2.27) can only emerge from or enter into the essential spectrum at Λ=0, see also remark 2.1.

For example, for 0<γ₁<γ₂<γ₃ a direct computation shows that f(0)=g(0;L₁,L₂)=γ₁γ₂γ₃>0 and f′(0)=g′(0;L₁,L₂)=−γ₁γ₂−γ₁γ₃−γ₂γ₃<0. By contrast, f′′(0)=2(γ₁+γ₂+γ₃)>0 and g′′(0;L₁,L₂)=2L₁γ₁(γ₂+γ₃)+2L₂γ₃(γ₁+γ₂)−2L₁L₂γ₁γ₂γ₃. For large L_1,2, g′′(0;L₁,L₂)≪−1. Furthermore, for Λ≠0, g(Λ;L₁,L₂)→0 for L_1,2 large, while g(Λ;L₁,L₂)→g₀(Λ):=γ₁γ₂γ₃−Λ(γ₁γ₂+γ₁γ₃+γ₂γ₃) for L_1,2 small. In other words, (2.27) has three real-valued solutions, one near each γ_i, for L_1,2 large, while (2.27) has only one real-valued solution, near γ₁+γ₂+γ₃, for L_1,2 small, see also (a) and (c) of figure 3. Upon decreasing L_1,2 the real-valued roots near γ_1,2 move sequentially towards zero and enter into the essential spectrum. For example, in figure 3b one of the roots of (2.27) for L_1,2 large already disappeared into the essential spectrum and (2.27) has only two real-valued roots left. This sequentially (dis)appearing of the solutions of (2.27) from the essential spectrum can be determined explicitly by comparing the relative magnitudes of f′′(0) and g′′(0;L₁,L₂) as function of L₁ and L₂, see figure 3d. Similar results can be obtained for γ_1,2,3 with different parities.

Figure 3.

(a–c): Typical sketches of f(Λ) and g(Λ;L₁,L₂) for 0<γ₁<γ₂<γ₃ with both L_1,2 respectively, small, intermediate and large. Equation (2.27) has, respectively, one, two and three positive solutions. (d): The first, respectively second, root of f(Λ)=g(Λ;L₁,L₂) emerges from the essential spectrum at Λ=0 (for increasing L_1,2) at the curves ω_1,2(L₁,L₂) where g(0;L₁,L₂)=f′′(0). In other words, g(0;L₁,L₂)<f′′(0) in the grey areas and (2.27) has one, respectively, three, positive solutions, while g(0;L₁,L₂)>f′′(0) in the intermediate white area and (2.27) has two positive solutions.

3. Linear two-component reaction–diffusion equations with one localized impurity

While pinned pulse solutions to the scalar version of (1.3) cannot undergo Hopf bifurcations, pinned pulse solutions supported by a system of linear RDEs of the form (1.3) can potentially undergo Hopf bifurcations. To show this we study the simplest system of linear RDEs of the form (1.3), that is, a linear two-component system of RDEs with one localized impurity (1.7), i.e. (1.3) with N=2 and n=1. However, see also remark 1.6.

(a). Proof of theorem 1.3.

We prove theorem 1.3 by deriving the conditions for the existence and stability of pinned 1-pulse solutions in system (1.7). Pinned 1-pulse solutions of (1.7) correspond to homoclinic solutions of

3.1

Recall that we assumed that G₁(0,0)≠0≠G₂(0,0) and—since we want the background state (0,0) of the unperturbed problem (1.4) (i.e. (1.7) with α=β=0) to be stable—we require that a+d<0,a+d/D<0 and ad−bc>0.

As before, we split our spatial domain into three regions 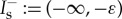, I_f:=[−ε,ε] and 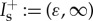. In the slow regions 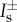away from x=0, the impurity is exponentially small and the slow flow of (3.1) can be approximated by

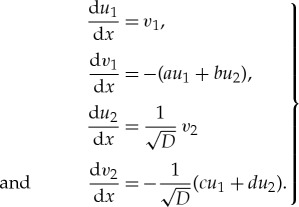3.2

The characteristic equation of (3.2) associated with the equilibrium point at the origin (0,0,0,0) is λ⁴+λ²(a+d/D)+(ad−bc)/D=0. This gives 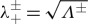and , with

3.3

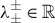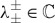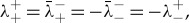By assumption Λ⁺Λ⁻=(ad−bc)/D>0 and Λ⁺+Λ⁻=−(a+d/D)>0. Consequently, ℜ(Λ^±)>0 and, for Δ≥0, and λ⁺₋≤λ⁻₋<0<λ⁻₊≤λ⁺₊ with λ^±₋=−λ^±₊, while and with ℜ(λ⁺₊)>0 and ℑ(λ⁺₊)>0, for Δ<0. So, in all cases we get that the origin has a two-dimensional unstable manifold W^u spanned by the eigenvectors V ^±₊ associated with λ^±₊ and a two-dimensional stable manifold W^s spanned by eigenvectors V ^±₋ associated with λ^±₋. For Δ≥0 the origin is of (degenerate) saddle-type, while trajectories are spiralling for Δ<0. In the remaining part of this proof we, for simplicity and brevity, assume that Δ>0. The proof in the other two cases goes in exactly the same fashion and will be omitted. The eigenvectors 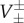are given by 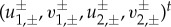such that 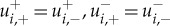and 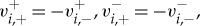for i=1,2. In particular,

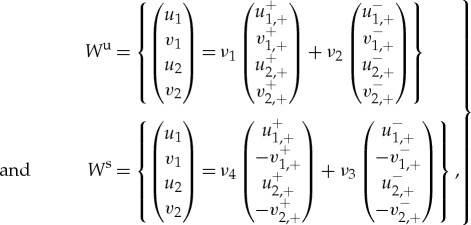3.4

with 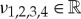. Consequently, the distance between a point on the stable manifold and another point on the unstable manifold is

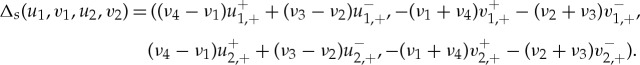In the fast region I_f near x=0, the impurity is dominating the dynamics of (3.1). Therefore, we write (3.1) in its equivalent fast form in the fast variable ξ=x/ε²

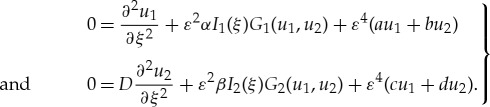3.5

The fast flow of (3.5) can to leading order be approximated by

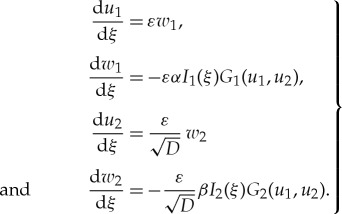3.6

As for the scalar problem, this implies that the u-components are only slowly varying near the fast field I_f. Consequently, they are to leading order constant in I_f, that is 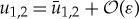in I_f. As a result, the accumulated change of w₁ during a passage through the fast region I_f is to leading order given by 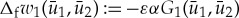and similarly .

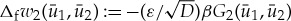The fact that the u-components are to leading order constant over the fast field I_f implies that the u-components of the stable manifold W^s and unstable manifold W^u (3.4) need to match at x=0. This gives ν₁=ν₄ and ν₂=ν₃ and consequently 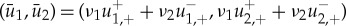. In addition, to account for the change of w_1,2, or v_1,2, over the fast region I_f, we get

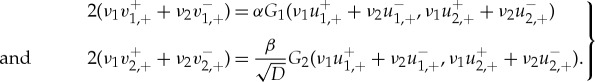3.7

Each equation determines a (collection of) curve(s) in the (ν₁,ν₂)-plane that, typically, intersect (transversally) several times, say at 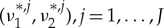. In the singular limit ε→0, this yields J homoclinic solutions corresponding to J pinned 1-pulse solutions 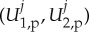of (1.7) with leading order amplitude 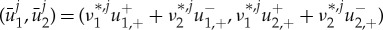. For 0<ε≪1, standard GPST arguments show that these pinned 1-pulse solution 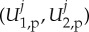persist as long as its corresponding solution 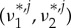of (3.7) is non-degenerate [30,31]. This completes the first part of the proof of theorem 1.3.

To determine the stability of such a pinned 1-pulse solution (U_1,p,U_2,p) (where we dropped the superscript j), we linearize (1.7) around (U_1,p,U_2,p). Again, by assumption, the resulting linearized operator has no essential spectrum in the right-half plane and we can focus on the point spectrum. The associated eigenvalue problem for 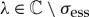is given by

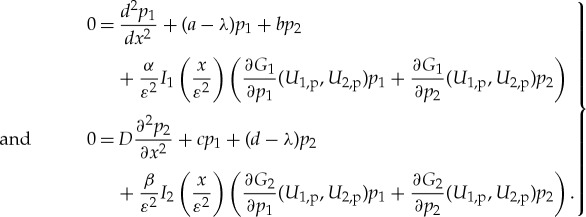3.8

As for the scalar equations studied in the previous section, we can relate the stability problem (3.8) to the existence problem (3.1). Specifically, the leading order slow flow of (3.8) in the slow fields can be obtained from the leading order slow flow of (3.1) in the slow fields by replacing (a,d) in (3.1) with (a−λ,d−λ). In addition, the leading order fast flow of (3.8) in the fast field I_f can be obtained from the leading order fast flow of (3.1) in the fast field I_f by replacing G_1,2(u₁,u₂) in (3.1) with (∂G_1,2/∂p₁)(U_1,p,U_2,p)p₁+(∂G_1,2/∂p₂)(U_1,p,U_2,p)p₂. Since both (U_1,p,U_2,p) and (p₁,p₂) are to leading order constant in the fast field I_f, we get that the eigenvalues of a non-trivial eigenfunction (p₁,p₂) are to leading order determined by the (ω₁,ω₂)-solutions of

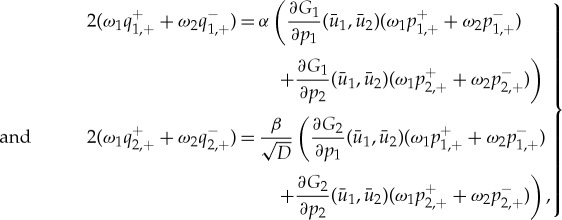3.9

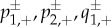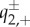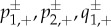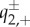where and are related to the stable and unstable manifolds of the slow flow of (3.8) in a similar fashion as (3.4) of the existence problem. In particular, and depend on the system parameters, and thus on a−λ and d−λ. The system of equations (3.9) is linear in (ω₁,ω₂) and is non-trivially solvable if (1.9), with the entries of the matrix 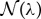(1.9) given by

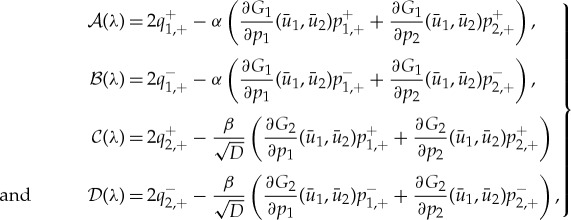3.10

and where we suppressed the explicit dependence of 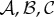and 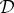on the system parameters and 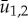. From (1.9) with (3.10) we get

3.11

In other words, the solutions of (3.11) determine the leading order parts of the eigenvalues, and hence the stability, of a pinned 1-pulse solution (U_1,p,U_2,p) supported by (1.7). This completes the second part of the proof of theorem 1.3.

(b). A Hopf bifurcation

We further analyse the existence condition (3.7) and stability condition (3.11) to confirm that a pinned pulse solution of theorem 1.3 can indeed undergo a Hopf bifurcation. To make the analysis manageable, we further simplify (1.7) by assuming that b=0,G₁(U₁,U₂)=G₁(U₂) and G₂(U₁,U₂)=G₂(U₁). Since b=0, we require that both a and d are negative to ensure that the background state (0,0) of the unperturbed problem (1.4) is stable. Therefore, we set μ₁:=−a and μ₂:=−d and assume that both μ₁ and μ₂ are positive. So, we study

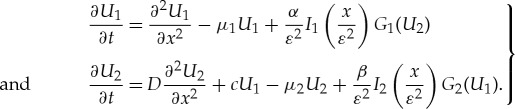3.12

Since Δ>0 (3.3) for b=0, the characteristic equation related to the slow flow has two real-valued negative roots and two real-valued positive roots. More precisely, 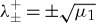and 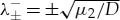. So, if we in addition assume that μ₁≠μ₂/D, then these roots do not coincide. A straightforward computation shows that the associated stable manifold W^s and unstable manifold W^u are given by (3.4) with 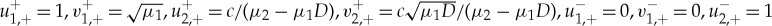and 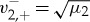. Since the u-components are to leading order constant in the fast field I_f, we—as before—have that ν₁=ν₄ and ν₂=ν₃ in (3.4) and the existence condition (3.7) becomes

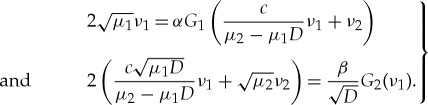3.13

So, as long as (3.13) has a non-degenerate real-valued solution (ν₁,ν₂), (3.12) supports a pinned 1-pulse solution (U_1,p,U_2,p) with leading order amplitudes 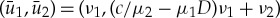for ε small enough.

To determine the stability of such a pinned pulse solution (U_1,p,U_2,p), we have to explicitly compute 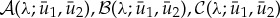and 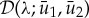(3.10) and solve (3.11). Therefore, we analyse the eigenvalue problem associated with (3.12)

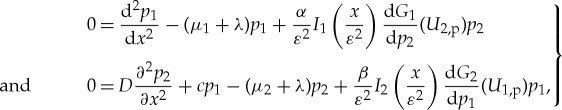3.14

with 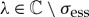where 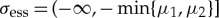. The associated stable and unstable manifold associated with (3.14) can directly be obtained from the stable and unstable manifold of the existence problem by replacing μ_1,2 by μ_1,2+λ. In the end, the stability condition (3.9) becomes

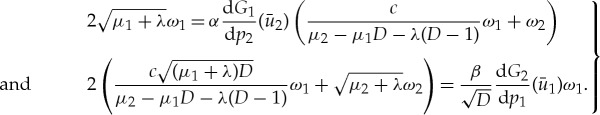This system has non-trivial (ω₁,ω₂)-solutions if

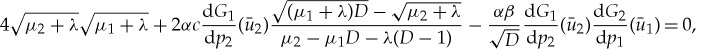3.15

which is the stability condition (3.11) for a pinned 1-pulse solution (U_1,p,U_2,p) of (3.12).

(i). Example 3: pinned 1-pulse solutions in a system of reaction–diffusion equations with a Hopf bifurcation

To further simplify the existence condition (3.13) and stability condition (3.15), we assume that μ₁=μ₂=μ>0 (and we thus also assume that D≠1). The two conditions reduce to

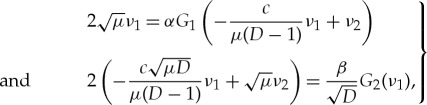3.16

respectively,

3.17

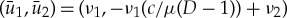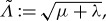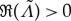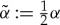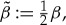
If we assume that (3.16) has a non-degenerate solution (ν₁,ν₂), then (3.12) with μ₁=μ₂=μ>0 supports a pinned 1-pulse solution (U_1,p,U_2,p) with leading order amplitudes for ε small enough. Upon defining with to ensure that λ∉σ_ess, , 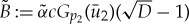and 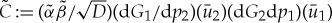, we rewrite the stability condition (3.17) as

3.18

For 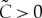, this cubic polynomial 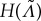has a minimum 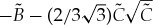at 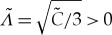. If, in addition, 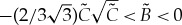, then (3.18) has two real-valued positive solutions. These two real-valued solutions merge and become complex-valued at 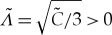for 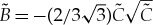. Thus, there exist system parameters and impurities such that (3.18) has complex-valued solutions 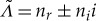, with n_r>0. This gives 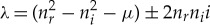, and we can tune μ such that ℜ(λ)=0, i.e. set 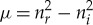. Hence, pinned 1-pulse solutions supported by (3.12) with μ₁=μ₂=μ can undergo a Hopf bifurcation.

For instance, for (3.12) with 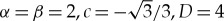, G₁(U₂)=U₂+1 and G₂(U₁)=U₁+2, we have that the existence condition, respectively, stability condition, is given by

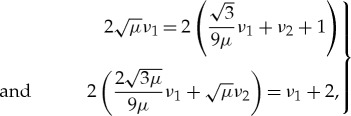3.19

respectively,

3.20

The existence condition is solved by

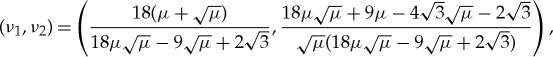and hence there exist a unique pinned 1-pulse solution for the given system parameters and impurity. By the linearity of G₁ and G₂, the stability condition (3.20) is independent of the profile of this pinned 1-pulse solution. Moreover, (3.20) can be solved explicitly and the roots with positive real-valued part are given by

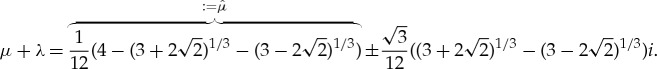3.21

Hence, setting 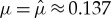(3.21) yields a pair of purely imaginary eigenvalues 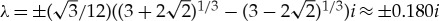. Note that for 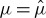, the solution to the existence condition (3.19) becomes (ν₁,ν₂)≈(8.73,−10.0) and 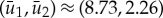. Hence, a Hopf bifurcation is expected for the given system parameters and impurity upon decreasing μ through 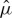. See also figures 4 and 5.

Figure 4.

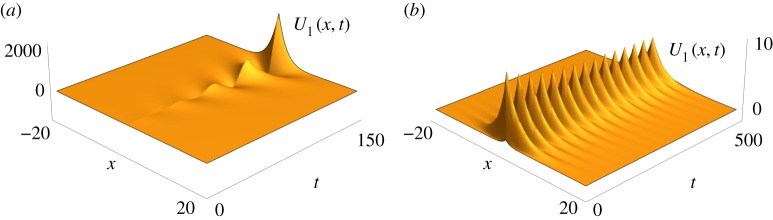
(a) Numerically obtained evolution of the U₁-component to a stable pinned 1-pulse solution for (3.12) with the system parameters as in Example 3, that is, 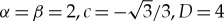, G₁(U₂)=U₂+1, G₂(U₁)=U₁+2, 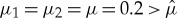(3.21) and ε=0.1. (b) We observe excellent agreement between the numerical obtained profiles of both the U₁-component and the U₂-component at t=100 (solid black curved) and the predicted asymptotic profiles (coloured dotted curves). (Online version in colour.)

Figure 5.

(a) Numerically obtained evolution of the U₁-component of (3.12) with 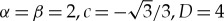, G₁(U₂)=U₂+1, G₂(U₁)=U₁+2, 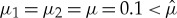(3.21) and ε=0.1. We observe that the profile—as expected since 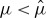—blows-up, see also remark 2.2. (b) Numerically obtained evolution of the U₁-component for the same system and with the same initial condition, except that 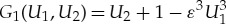. The added small nonlinearity 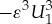to G₁ prevents the profile from blowing-up (while it does not alter the leading order asymptotic results) and we observe the evolution of the profile to a breathing pinned 1-pulse solution. (Online version in colour.)

4. Results and outlook

The class of N-component systems of RDEs (1.3) proposed in this paper provides a very promising combination of tractable analysis, complex dynamics and applied relevance. The systems are linear, except for asymptotically small regions in space in which the system experiences asymptotically strong nonlinear impurities (and these are the only sources of nonlinearities). We have shown that these systems typically exhibit (multi) pulse-type solutions that are localized around the impurities. Owing to the asymptotic nature of the heterogeneities, the existence of these patterns can be established by the methods of GPST in a manner that is very similar to the construction of pulse-type patterns in singularly perturbed slow-fast RDEs ([21,23], e.g) (where the fast component plays the role of the impurities in the present systems). In recent years, the stability analysis of pulse-patterns in these singularly perturbed slow-fast RDEs (on unbounded domains) has evolved into an established approach, based on Evans function theory [29] and NLEP (non-local eigenvalue problem) methods [24,32], see [33] and references therein. Although the spectral stability thus is largely under control, the technical effort is—in general—formidable. As a consequence, the analysis of the bifurcations of these patterns is strongly limited [25], since the necessary centre manifold analysis is largely based on explicit calculations on (inverting) the spectral operator [34,35]. The systems introduced here do not suffer from this obstruction: we have shown—again by the methods of GPST—that the spectral stability problem associated with an impurity-induced pulse pattern reduces to linear algebra and it is based on solving linear constant coefficient equations, see our main theorems 1.2 and 1.3 and their proofs. Moreover, due to the spatial heterogeneities, the trivial translational eigenvalue λ=0 is removed from the system, which also strongly simplifies the centre manifold analysis [25,34]. Thus, the systems presented here are ideal candidates to enter deeper into the realm of bifurcations of localized pulse patterns in singularly perturbed RDEs on unbounded domains. The three explicit examples worked out in the text show that it is relatively simple to cook up explicit spectral configurations. Hence, we indeed may use systems of the type (1.3) to perform a centre manifold analysis near spectral configurations of co-dimension one and higher. Natural next analytical steps may be a detailed unfolding of a Bogdanov–Takens bifurcation [35] of a localized pinned pulse solution in (1.3), or a hunt for controllable chaotic pulse dynamics by unfolding a (specific) co-dimension three bifurcation [36]. In turn, this may serve as a first analytical step towards understanding the (numerical) observations in [26].

Another fundamental aspect of pulse dynamics in RDEs that is significantly limited by the technical effort it takes to control the spectral problem, is that of the interactions of pulses, or, more general, of localized structures, beyond the weak interaction limit [37]. Especially, the impact of essential spectrum near the imaginary axis on these interactions is yet not at all understood [38,39]. The literature on localized patterns with oscillating tails is very limited—see however [40,41]—while it is natural to expect that especially in these situations the impact of marginally stable essential spectrum on the interaction dynamics will be significant. As shown here, these types of patterns can be constructed along the very same lines as the more classical pulse solutions with monotonic tails, see the proof of theorem 1.3 (and note the sign of Δ (3.3) does not impact the approach). Therefore, fundamental novel insights can be expected by studying (1.3) with two or more impurities for parameter combinations that make the essential spectrum approach the unstable right-half plane, especially for pulse patterns that have oscillating tails.

Finally, it should be remarked that the systems considered here are of a slowly linear nature according to the terminology introduced in [23,26] for two-component singularly perturbed slow-fast RDEs (which was generalized to N≥2-component models in [33]). The extended class of singularly perturbed slowly nonlinear RDEs introduced in these papers corresponds to allowing the U-equation outside the impurities, i.e. (1.4), to be nonlinear. At present, it is not clear how strong the traditional restriction to slowly linear systems effects the dynamics of the system (note that all paradigmatic models considered in the literature—FitzHugh–Nagumo, Gierer–Meinhardt, Gray–Scott, Schnakenberg, etc.—are of this slowly linear type). Once again, simplified models of type (1.3), but now with a general nonlinear structure outside the impurities, may help to understand this distinction: even if the unperturbed model (1.4) is nonlinear, the analysis of the class of models introduced here is drastically more simple than that of the corresponding singularly perturbed model.

Data accessibility

This article has no additional data.

Authors' contributions

All three authors contributed equally and gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

P.v.H. acknowledge support under the Australian Research Council’s Discovery Early Career Researcher Award funding scheme DE140100741. J.S. acknowledges support of the Science Foundations of China and the Fujian Province (11771082,2015J01004) and the Nonlinear Analysis Innovation Team of FJNU (IRTL 1206).