Abstract
Due to its cooperative nature, magnetic ordering involves a complex interplay between spin, charge, and lattice degrees of freedom, which can lead to strong competition between magnetic states. Binary Fe3Ga4 is one such material that exhibits competing orders having a ferromagnetic (FM) ground state, an antiferromagnetic (AFM) behavior at intermediate temperatures, and a conspicuous re-entrance of the FM state at high temperature. Through a combination of neutron diffraction experiments and simulations, we have discovered that the AFM state is an incommensurate spin-density wave (ISDW) ordering generated by nesting in the spin polarized Fermi surface. These two magnetic states, FM and ISDW, are seldom observed in the same material without application of a polarizing magnetic field. To date, this unusual mechanism has never been observed and its elemental origins could have far reaching implications in many other magnetic systems that contain strong competition between these types of magnetic order. Furthermore, the competition between magnetic states results in a susceptibility to external perturbations allowing the magnetic transitions in Fe3Ga4 to be controlled via temperature, magnetic field, disorder, and pressure. Thus, Fe3Ga4 has potential for application in novel magnetic memory devices, such as the magnetic components of tunneling magnetoresistance spintronics devices.
Introduction
Incommensurate spin-density wave (ISDW) phases have long been known to be generated from paramagnetic (PM) metals either through a Fermi surface (FS) instability known as nesting or through the coupling of local magnetic moments via the Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction1,2. Interestingly, no ISDW phase stemming from an instability in the spin polarized FS of a FM metal has been previously identified. We have discovered such a material in the transition metal binary compound Fe3Ga4 that hosts both FM and ISDW phases at zero applied field. Here, both of these phases are stable over wide temperature (T) ranges with the FM phase evident at temperatures above and below the T range of stability of the ISDW phase. Furthermore, we have discovered the mechanism for the formation of the ISDW state in Fe3Ga4, which is distinct from any previously identified and that makes clear the connection between the FM and ISDW states. This mechanism, indicated by our data and simulations, is likely not limited to Fe3Ga4, suggesting that ISDW order or spin fluctuations stemming from spin-polarized FS instabilities should be investigated in a wide range of complex magnetic materials.
ISDW phases caused by FS instabilities are common in d-electron systems such as the prototypical ISDW system Cr3,4, while the local moment picture is usually associated with magnetism in rare earth materials where the magnetic moments derive from well localized f-electrons5–9. ISDW phases are commonly associated with antiferromagnetic (AFM) interactions, as opposed to incommensurate helical states which are more aptly described as being derived from FM states. In fact, transitions between ISDW and FM states in zero applied field are extraordinarily rare in contrast to helical magnets where transitions to FM ground states are more common10,11. There are only a handful of FM materials that display ISDW phases over narrow T ranges with distinct, fairly restrictive mechanisms. These include: ferromagnets which seemingly avoid quantum criticality via a transition to a small ordered moment ISDW, Nb1−yFe2+y, YbRh2Si2, and PrPtAl12–15; a frustrated magnetic insulator described as a Kagomé staircase system that undergoes transitions between several magnetic states, Co3V2O816; and a very small number of Ce and U compounds which display ISDW states over a very narrow T range just above their FM transitions and where the mechanism is unclear, CeRu2Al2B and UCu2Si217–19. The paucity of examples that we are able to find in the literature stemming from decades of intense investigation of magnetic materials is surprising.
In this article, we focus on the investigation of the magnetic and electronic structure of Fe3Ga4 because previous magnetization, M, measurements indicated that there may be an interesting and unusual re-entrant FM phase surrounding an AFM phase at both low and high T20. Neither the magnetic structure, nor the character of the magnetic phases had been identified. The transitions between FM and AFM phases in Fe3Ga4 can be tuned via T, magnetic field, and pressure20–23. We discover through neutron scattering measurements that Fe3Ga4 adopts an ISDW ordering between T1 = 60 and T2 = 360 K where the magnetic moments are oriented nearly transverse to the incommensurate wavevector. This magnetic structure is locally FM with neighboring magnetic moments being aligned but having a sinusoidal amplitude modulation occurring over several crystalline unit cells. In addition, we confirm that this material appears to display a thermodynamically odd re-entrant ferromagnetism above T220. A clue as to the cause for this unusual behavior comes from simulations of the electronic structure. In the non-magnetic case, our calculations do not indicate regions of FS nesting. However, we discovered significant nesting in the FM majority-spin FS with a nesting vector that is in excellent agreement with the measured ISDW wavevector, q = (0 0 0.29). The FS instability along with anomalies in the charge transport support an itinerant mechanism for the magnetism in Fe3Ga4. This indicates that the ISDW emerges from an unstable FS in the FM phase so that a return to ferromagnetism is required prior to reaching the high T PM phase above T3 = 420 K. This mechanism, a FS instability in the majority band of a ferromagnet that drives a transition to an ISDW, has, to our knowledge, not been previously considered.
Results
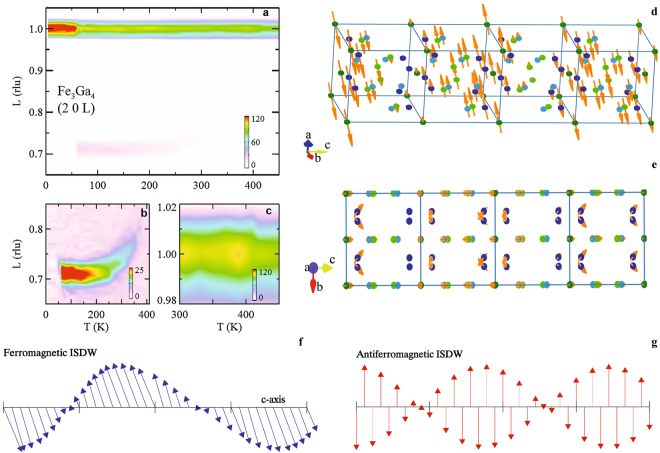
Fe3Ga4 forms in a monoclinic (C2/m) crystal structure with no evidence of a structural change associated with the magnetic phase transitions20,22–25. The description of the crystal structure is available in the Supplementary Information. A summary of our neutron scattering data is presented in Fig. 1a, which displays the intensity map for the scattering in the (2 0 L) reciprocal lattice direction. Three features of this plot represent our main experimental findings. First, the large increase in the scattering cross section at the (2 0 1) Bragg peak position below ~60 K (T1) demonstrates FM ordering consistent with the magnetic susceptibility, χ, (Fig. 2a) and previous measurements of M20,22,23,26,27. Second, for T just above T1, the reduced scattering at the Bragg peak position is accompanied by an increase in scattering centered at (2 0 0.71) indicating the existence of an incommensurate magnetic phase. The T and q dependence of this scattering contribution can be better viewed in Fig. 1b and in Fig. 2b,c where an abrupt loss of scattering is evident below T1 while a more continuous change is seen above 300 K. At these higher temperatures, the scattering moves to somewhat larger q before this signal is reduced below the background at T > 360 K (T2). Third, in this same T range, the scattering at the (2 0 1) Bragg peak position increases (Figs 1a,c and 2a) before decreasing at T > 420 K. This is consistent with the paramagnetism found in χ and M above T3 = 420 K20. Thus, our data indicate a FM ordered state below T1 transitioning to an incommensurate magnetic state for T1 < T < T2 along with a re-emergence of ferromagnetism between T2 and T3.
Figure 1.
Neutron Diffraction. Temperature, T, dependence of the neutron scattering intensity along the (2 0 L) direction. Scans were performed in increments in L of 0.005 reciprocal lattice units (rlu) for K in increments of 5 K. Color-bars indicate the scattering intensity in counts/s. Intensity plots displaying scattering (a) over the full q and T range of the data, (b) near the incommensurate wave-vector (2 0 1-δ) for K, and (c) in proximity to (2 0 1) for K. (d) Magnetic structure at 100 K over a four unit cell length along the c-axis depicting the ISDW state. Solid circles represent the 4 different Fe sites within the Fe3Ga4 unit cell. Structural data can be found in Supplementary Table S1. (e) Magnetic structure at 100 K viewed along the a-axis highlighting the non-collinear magnetic structure determined from the refinement of the neutron diffraction data. (f) Schematic of a modulated ferromagnetic ordering similar to the ISDW state in Fe3Ga4. The lattice constant is indicated by the tick marks and the tilting of the magnetic moments along the modulation direction (c-axis) is representative of the ISDW state determined for Fe3Ga4. (g) Schematic of the more common ISDW state found in antiferromagnets such as Cr.
Figure 2.
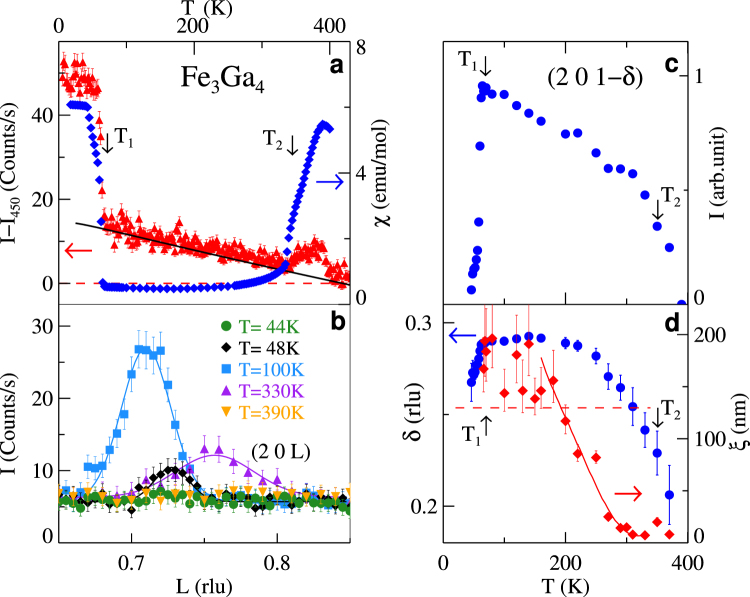
Temperature dependent magnetic scattering and magnetic susceptibility. (a) Neutron scattering intensity at the (201) Bragg peak position, I − I450, (red triangles) and magnetic susceptibility, χ, at 100 Oe (blue diamonds) vs. T. I − I450 is the intensity, I, measured after subtraction of the intensity at 450 K, I450. Solid line is a fit of the Debye model43 to the data between 90 and 300 K with ΘD = 125 K20. (b) Scattering along the (2 0 L) direction at several representative temperatures demonstrating the incommensurate order. (c) Integrated intensity of the scattering at (2 0 1−δ) vs. T. (d) T dependence of δ (blue bullets) and the correlation length of the incommensurate scattering, ξ, (red diamonds) vs. T. Solid line is a guide to the eye. Dashed line is the instrumental resolution. Transition temperatures T1 and T2 are indicated in frames a, c, and d.
Surveys of a large number of reciprocal lattice positions have allowed a full refinement of the magnetic structure. The details of the refinement are presented in the Supplementary Information along with the results presented in Supplementary Table S2 for the low T FM state (T < T1) and Supplementary Table S3 for the incommensurate magnetic order at 100 K. In Supplementary Table S2, we report the size of the magnetic moment on each of the Fe sites refined with the magnetic moment constrained to lie along the crystallographic c-axis. These are in good agreement with the average magnetic moment determined from M20,23,26. When the constraint is removed a small contribution along the a and b directions is found that is smaller than the error in the refinement (~0.3 μB). In Fig. 2a we present a comparison of the scattering intensity, after subtraction of the Bragg scattering in the paramagnetic state at 450 K, to χ, measured on the same crystal. The two regions in T where χ is large correspond well with the increased scattering at (201).
The result of the refinement of the magnetic scattering at 100 K (incommensurate phase) is significantly more complex with the best fit to our data consisting of a structure that closely resembles that of an ISDW having a propagation vector of q = (0 0 0.29). After establishing the ISDW character of the magnetic state, we have further constrained the model such that crystallographically equivalent sites were required to have the same magnetic moment amplitude. The results of this refinement are displayed in Fig. 1d,e. In Supplementary Table S3 the magnitude of the magnetic moments in one particular unit cell is presented, but we note that the incommensurate nature of the ordering results in moments that vary from cell to cell accordingly. The refinement places the magnetic moments mostly along the a-axis with a maximum magnitude of 2.31(6) μB. However, there is also a considerable contribution along the c-axis of amplitude of as well as along the b-axis for one of the four crystallographically unique Fe sites (see Supplementary Table S3). Thus, there is a significant non-collinear and non-coplanar magnetic moment indicated by our data. Previously, we had speculated about such a non-coplanar magnetic moment based upon a large topological Hall effect in the range of temperatures and fields where the AFM is stable20 and the data presented here confirm this interpretation. The ISDW magnetic structure indicated by our refinement of the neutron diffraction data is consistent with the anisotropy in M presented in Fig. 3a. Here, significant differences in M, including the field induced metamagnetic transition, measured with fields along the 3 principle crystal axes rule out any simple helimagnetic structures.
Figure 3.
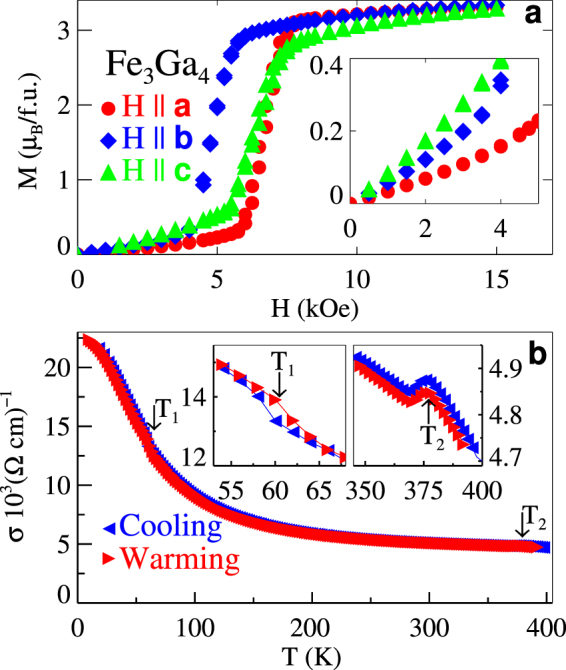
Magnetization Anisotropy and Electrical Conductivity. (a) Magnetization, M, vs. magnetic field, H, along the 3 principle crystal axes, a, b, and c, within the incommensurate spin density wave phase at 100 K. (b) Temperature, T, dependence of the electrical conductivity conductivity, σ, measured with current along the c-axis. Insets: changes to σ at the magnetic phase transitions. Transition temperatures T1 and T2 are indicated.
The magnetic state at 100 K represented in Fig. 1d retains a FM orientation of neighboring magnetic moments with an amplitude that is modulated by the wave vector δ = 0.29 in reciprocal lattice units. This is distinct from the simpler ISDW materials, such as Cr3, where neighboring sites are antiferromagnetically aligned. Thus, the ISDW state appears to be a long wavelength modulation of a FM state as demonstrated schematically in Fig. 1f and compared to the ISDW state associated with antiferromagnetism (Fig. 1g). The average size of the magnetic moments in the ISDW state are within error of those in the FM state indicating a conservation of total moment magnitude at T1. However, there is a significant change in the direction of the magnetic moments in the FM and ISDW structures. The complexity of the ISDW phase and the significant differences in the two competing magnetic phases highlight the question of the mechanism driving the ISDW ordering and its instability at low T.
The evolution of δ and the correlation length for the magnetic scattering, ξ, with T can lend insight into the character of the magnetic state and the competing interactions which are of clear importance in Fe3Ga4. In Figs 1b and 2b,d, the T evolution of δ is displayed. This T dependence is usually associated with the competition between the electronic degrees of freedom responsible for the incommensurate nature of the wavevector and the lattice degrees of freedom which prefer a commensurate density wave28. Here, we observe a decrease in δ as the FM phases are approached either by warming or cooling with a large decrease in δ apparent above 250 K. Preceding this decrease in δ is a precipitous reduction in ξ as determined from the widths of the (2 0 1−δ) scattering peak for T > 200 K (Fig. 2b,d). Above 300 K, ξ has decreased such that it is equivalent to several wavelengths of the ISDW phase (2π/δ). Thus, there is an extended T range where only short range ordering exists.
Independent of the mechanism responsible, most ISDW phases are accompanied by a discontinuous decrease in conductivity, σ, and an increase in the Hall constant as the result of a partial FS gapping. This is a consequence of either FS nesting2 or simply the additional periodicity associated with the ISDW phase. Fe3Ga4 does not disappoint in this regard as we identify both a decreased σ(T) at T1 and a somewhat smaller increase at T2 (Fig. 3b) indicating a significant change to the FS20,23. Note that there is some sample-to-sample variation in T2 for our crystals likely caused by small differences in the density of antisite defects20 so that T2 = 375 K in Fig. 3b. Furthermore, the ordinary Hall coefficient is observed to undergo large changes at both T1 and T220 also consistent with a significant change to the FS at these temperatures.
To establish the itinerant nature of the magnetism, the electronic structure of Fe3Ga4 was calculated in the nonmagnetic and spin polarized phases employing the full potential linearized augmented plane wave method29. The resulting Fermi Surfaces were examined for possible nesting along the c-axis. Although we find no such nesting condition in the non-magnetic FS, the majority spin-band FS in the FM state contains a FS sheet with a substantial region that is flat and perpendicular to the c* direction (see Fig. 4). Here, the nesting across the Brillouin zone boundary is demonstrated indicating the likely formation of density wave ordering. The nesting wavevector shown in this figure, qnest = (0 0 0.276), is in very good agreement with the experimentally observed ISDW providing compelling evidence that the FM state is unstable to the formation of a density wave.
Figure 4.
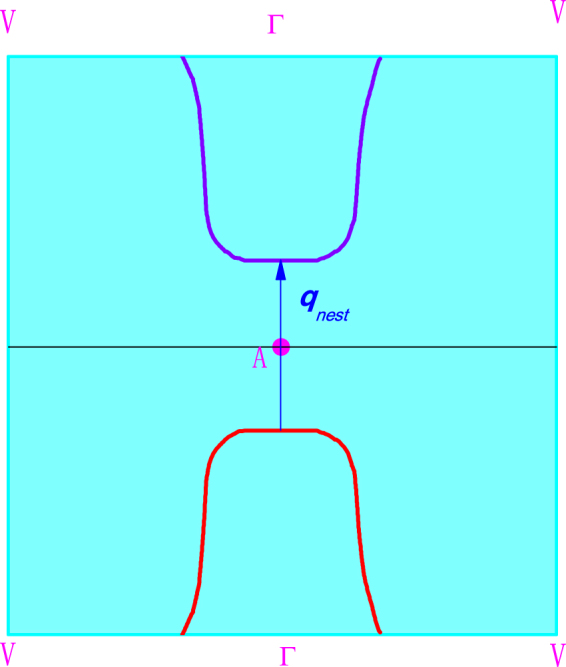
Electronic Structure. Calculated Fermi surface of Fe3Ga4 on a (010) plane through Γ with the proposed nesting illustrated. Here Γ = (0 0 0), A = (0 0 1/2) and V = (1/2 0 0). Red and violet are sheets of Fermi surface belonging to adjacent Brillouin zones.
Discussion
We have carried out an extensive neutron diffraction investigation of Fe3Ga4 solving, for the first time, the magnetic structure of what had been reported to be an AFM state finding, instead, an ISDW phase. The ground state is confirmed as a robust FM state and the re-emergence of this ferromagnetism is also confirmed for K. Although the magnetic contribution to the neutron scattering signal is small and data too sparse above 360 K to make a convincing comparison between the low and high T FM states, our χ(T) and M(H,T) data display identical anisotropy as well as similar moment magnitudes and field dependencies indicating that these FM states are likely identical20. Furthermore, electronic structure calculations reveal a FS sheet in the majority band of the FM state that is unstable towards density wave formation with a nesting vector that matches the neutron data both in direction and magnitude. Interestingly, the ISDW state likely results from a FS instability in only one of the spin-polarized bands of Fe3Ga4, a mechanism that, thus far, has not been considered or identified in other materials. The details of how the transition between itinerant FM and ISDW states takes place are not yet clear since a residual magnetic moment may be expected for a simple FS reconstruction in conflict with our M(H)20 and neutron diffraction data.
These conclusions place Fe3Ga4 as a unique compound among the large number of FM materials reported in the literature such that identifying materials that are more than tangentially related is difficult. UCu2Si2 and CeRu2Al2B, where the Fermi surfaces are likely to be involved in the mechanism creating ISDW phases, are the closest comparisons that we have been able to find17–19. Extending the conversation to examples of FM materials with consequential FS nesting in their PM states broadens the number of comparisons slightly as this is only somewhat rare. Most of these are associated with competing orders and none, that we are aware of, report ISDW states resulting from nesting. Competing orders occur, for example, in SmNiC2 which has a charge density wave (CDW) phase that exists only above its Curie T30. In addition, nesting of the PM FS is common in the heavy rare earth elemental metals which tend to have FM ground states10,11. This nesting leads to transitions from PM into helimagnetic, rather than ISDW, states. More interesting is the idea that triplet superconductivity in FM UGe2 is related to coupled CDW-ISDW fluctuations that emerge with pressure within the FM phase31. Because the unusual transition between ISDW and FM states in Fe3Ga4 occurs just above room temperature, it has been suggested as a possible material for a magnetic tunneling junction device32. This suggestion takes advantage of the ability to drive a phase transition between the ISDW and spin-polarized phases with moderately sized magnetic fields and the ability to tune the phase transition temperature via pressure and disorder. Our findings here support the idea of Fe3Ga4 as a possible material for phase transition tunneling anisotropic magnetoresistance (PT-TAMR) devices since our simulations suggest a large difference in the electronic density of states at the Fermi level between the ISDW and FM (spin polarized) states.
We are left with two important unanswered questions about the mechanism we discovered for the transitions between FM and ISDW states in Fe3Ga4. The first is the character of the magnetism and its relationship to the conducting charge carriers. Somewhat in contrast to an itinerant magnetism in Fe3Ga4 are the large magnetic moments evident in M, simulation, and the neutron scattering cross-sections suggesting magnetic moments may be more localized to the Fe sites. This would indicate an important coupling mechanism between the charge carriers and the more localized electrons responsible for the magnetic moments. A similar cooperative mechanism has been proposed for GdSi where both RKKY and FS nesting are thought to play a role in creating an ISDW state33 and for the Fe-based superconducting families where this coupling is responsible for the various AFM structures34–36. The second related question is the cause of the FM ground state. We speculate that the re-emergence of FM ground state at low T may be a result of a loss of RKKY coupling with the establishment of partial energy gaps in the FS of the ISDW state, as has been suggested for the helimagnetic rare earth elemental metals, such as Dy and Tb10,11,37,38. In these materials an abrupt transition from FM-to-helimagnetic ordering results from superzone gaps in the FS of the incommensurate phase along with considerations of spin-orbit coupling10. As such, the incommensurate phase appears to be self limiting as the ordering creates a partial energy gap that removes carriers responsible for the RKKY coupling. Additionally, there is a complex and interesting variation of the magnetic wavevector and metamagnetic fields that is in many ways similar to what we observe in Fe3Ga4. Despite these remaining issues, our data and computational results indicate that Fe3Ga4 is the first material that has been discovered to evolve from a FM FS to an ISDW, a discovery that suggests that there is likely a rich and mostly unrecognized competition between magnetic states caused by FS instabilities of spin polarized bands.
Methods
Single crystals of Fe3Ga4 with masses up to 100 mg were grown from high purity Fe powder and gallium pieces that were melted in a RF furnace prior to employing floating zone techniques. The resulting crystals were sealed in quartz tubes under vacuum and annealed at 550 °C for 48 hours.
The structure of the crystals was determined by single crystal X-ray diffraction using a Bruker D8 Quest Kappa single-crystal diffractometer (Mo Kα IμS microfocus source, Å) operating at 50 kV and 1 mA, a HELIOS optics monochromator, and a CMOS detector. These measurements confirmed a base-centered monoclinic structure having the space group C2/m24,25 for K. Single crystal X-ray diffraction data were collected at 100, 300, 328, 350, and 380 K. Crystals were cut to an appropriate size and mounted onto a glass fiber using epoxy. The Bruker program SADABS was used to correct the collected data for absorption39. The intrinsic phasing method in SHELXT40 was used to obtain starting crystallographic models and SHELXL201441 was used to refine atomic sites. The crystallographic parameters and atomic positions for Fe3Ga4 at 300 K are provided in Table S1 to serve as a representative of all the data collected. No evidence for an incommensurate scattering contribution at 100, 300, and 380 K that would indicate a possible strain wave associated with the incommensurate magnetic ordering was apparent in precession images.
We have also performed powder X-ray diffraction on ground crystals for K and found no crystallographic changes beyond the expected thermal expansion and a small decrease in the angle β. This included temperature-dependent powder X-ray diffraction data collected at 300, 328, 350, 380, 450, and 670 K using a Bruker D8 Advance powder X-ray diffractometer operating at 40 kV and 30 mA with Cu K α radiation ( Å) equipped with a temperature stage and a LYNXEYE XE detector. Data were collected in the 2θ range of 10–80° with a step size of 0.01°. Rietveld refinements were performed using the TOPAS5 software package. The scale factor, background (Chebyshev function with eight terms), and unit cell were independently refined.
Magnetic measurements carried out in a SQUID magnetometer revealed behavior indistinguishable from previously grown vapor transport crystals20. A single crystal with a mass of 24 mg was chosen for magnetic structure determination via neutron scattering using the HB-3A four-circle diffractometer at the High Flux Isotope Reactor of Oak Ridge National Laboratory employing a wavelength of 1.546 Å. The sample was placed in a closed-cycle refrigerator allowing exploration for K. We established the FM order parameter by scanning the (111) and (201) Bragg reflections over the 5 to 450 K range. Wave-vector scans along the (2 0 L) direction with were collected at a large number of temperatures to characterize the magnetic phase diagram. In addition, a large region of reciprocal space was scanned that included all of the accessible nuclear reflections as well as a large number of peaks associated with the ISDW ordering. Altogether, 94 peaks were used for a full refinement of the FM state at 5 K and 154 q-scans taken at 100 K were employed in determining the ISDW state. Refinement of both the nuclear and magnetic structures was performed using the FULLPROF Suite42. The correlation length for the magnetic scattering in the incommensurate spin density wave phase (ξ) was determined via a fit of the data by a Lorentzian function convoluted with the instrumental resolution.
Electrical transport measurements were made on rectangular shaped single crystals polished with emery paper. Four Epotek silver epoxy contacts with an average spacing between voltage probes of 0.3 mm were formed on the surface of the crystals to make electrical contact to thin Pt wires. Conductivity measurements were were performed at 19 Hz using standard lock-in techniques in a gas flow cryostat.
Data availability
The authors declare that the main data supporting the findings of this study are available within this article and its Supplementary Information. Extra data are available from the corresponding author upon reasonable request. See author contributions for specific data sets.
Electronic supplementary material
Acknowledgements
We thank W. Xie and X. Gui for technical assistance. This work was supported by the U.S. Department of Energy (DOE) under EPSCoR Grant No. DE-SC0012432 with additional support from the Louisiana Board of Regents. The X-ray diffraction experiments were supported by the National Science Foundation under grant number DMR-1360863 (JYC). The work at ORNL’s High Flux Isotope Reactor was sponsored by the Scientific User Facilities Division, Office of Science, Basic Energy Sciences, U.S. DOE.
Author Contributions
Single crystals for this experiment were synthesized by G.C., Y.W. and R.J. X-ray characterization was carried out by K.A.B., G.T.M. and J.Y.C. Electrical conductivity, magnetic susceptibility, and magnetization measurements were performed by Y.W., S.K. and J.F.D. Neutron diffraction experiments were carried out by Y.W., H.B.C. and J.F.D. Electronic structure calculations were performed by Z.N. and W.A.S. All authors contributed to the data analysis, scientific discussions, and the preparation of the manuscript. This project was supervised by J.F.D.
Competing Interests
The authors declare no competing interests.
Footnotes
Electronic supplementary material
Supplementary information accompanies this paper at 10.1038/s41598-018-23555-4.
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Overhauser AW, Arrott A. Mechanism of antiferromagnetism in chromium. Phys. Rev. Lett. 1960;4:226–227. doi: 10.1103/PhysRevLett.4.226. [DOI] [Google Scholar]
- 2.Overhauser AW. Spin density waves in an electron gas. Phys. Rev. 1962;128:1437–1452. doi: 10.1103/PhysRev.128.1437. [DOI] [Google Scholar]
- 3.Fawcett E. Spin-density-wave antiferromagnetism in chromium. Rev. Mod. Phys. 1988;60:209–283. doi: 10.1103/RevModPhys.60.209. [DOI] [Google Scholar]
- 4.Fawcett E, Alberts HL, Galkin VY, Noakes DR, Yakhmi JV. Spin-density-wave antiferromagnetism in chromium alloys. Rev. Mod. Phys. 1994;66:25–127. doi: 10.1103/RevModPhys.66.25. [DOI] [Google Scholar]
- 5.Barandiaran JM, Gignoux D, Schmitt D, Gomez Sal JC. Magnetic properties of PrNi2Si2. Sol. St. Commun. 1986;57:941–945. doi: 10.1016/0038-1098(86)90929-4. [DOI] [Google Scholar]
- 6.Islam, Z. et al. Effects of band filling on magnetic structures: the case of RNi2Ge2. Phys. Rev. Lett.83, 2817–2820 (1999).
- 7.Bud’ko, S. L. et al. Anisotropy and metamagnetism in the RNi2Ge2 (R = Y, La-Nd, Sm-Lu) series. J. Magn. Magn. Mat.205, 53–78 (1999).
- 8.Good W, et al. Magnetic structure of GdCo2Ge2. Phys. Rev. B. 2005;71:224427. doi: 10.1103/PhysRevB.71.224427. [DOI] [Google Scholar]
- 9.Lynn, J. W. et al. Magnetic order and crystal structure in the superconducting RNi2B2C materials. Phys. Rev. B55, 6584–6598 (1997).
- 10.del Moral A, Lee EW. Exchange force explanation for the antiferromagnet-ferromagnet transition in dysprosium. J. Phys. C: Solid State Phys. 1975;8:3881–3886. doi: 10.1088/0022-3719/8/22/027. [DOI] [Google Scholar]
- 11.Mendive-Tapia E, Staunton JB. Theory of magnetic ordering in the heavy rare earths: Ab initio electronic origin of pair- and four-spin interactions. Phys. Rev. Lett. 2017;118:197202. doi: 10.1103/PhysRevLett.118.197202. [DOI] [PubMed] [Google Scholar]
- 12.Rauch D, et al. Spectroscopic study of metallic magnetism in single-crystalline Nb1-yFe2+y. Phys. Rev. B. 2015;91:174404. doi: 10.1103/PhysRevB.91.174404. [DOI] [Google Scholar]
- 13.Niklowitz, P. G. et al. Ultra-small moment incommensurate spin density wave order masking a ferromagnetic quantum critical point in NbFe2. Preprint available at https://arxiv.org/abs/1704.08379 (2017). [DOI] [PubMed]
- 14.Lausberg S, et al. Doped YbRh2Si2: Not only ferromagnetic correlations but ferromagnetic order. Phys. Rev. Lett. 2013;110:256402. doi: 10.1103/PhysRevLett.110.256402. [DOI] [PubMed] [Google Scholar]
- 15.Abdul-Jabbar G, et al. Modulated magnetism in PrPtAl. Nat. Phys. 2015;11:321–327. doi: 10.1038/nphys3238. [DOI] [Google Scholar]
- 16.Chen Y, et al. Complex magnetic order in Kagomé staircase compound Co3V2O8. Phys. Rev. B. 2006;74:014430. doi: 10.1103/PhysRevB.74.014430. [DOI] [Google Scholar]
- 17.Bhattacharyya A, et al. Incommensurate spin-density-wave antiferromagnetism in CeRu2Al2B. Phys. Rev. B. 2016;93:060410. doi: 10.1103/PhysRevB.93.060410. [DOI] [Google Scholar]
- 18.Honda F, Metoki N, Matsuda TD, Haga Y, Onuki Y. Long-period, longitudinal spin density modulation in an itinerant 5f magnetic compound UCu2Si2. J. Phys.: Condens. Matter. 2006;18:479–492. [Google Scholar]
- 19.Troć, R., Samsel-Czekała, M., Stępien-Damm, J. & Coqblin, B. Interplay between ferromagnetism, SDW order, and underscreened Kondo lattice in UCu2Si2. Phys. Rev. B85, 224434 (2012).
- 20.Mendez JH, et al. Competing magnetic states, disorder, and the magnetic character of Fe3Ga4. Phys. Rev. B. 2015;91:144409. doi: 10.1103/PhysRevB.91.144409. [DOI] [Google Scholar]
- 21.Wagini H. Magnetische elektrische und thermische eigenschaften von FeGa1.3. Z. Naturforsch. 1966;21A:528–530. [Google Scholar]
- 22.Duijn HGM, et al. Pressure dependence of the ferromagnetic to antiferromagnetic transition in Fe3(Ga1-xAlx)4 with x = 0.0 and 0.1. J. Appl. Phys. 1999;85:4738–4740. doi: 10.1063/1.370465. [DOI] [Google Scholar]
- 23.Duijn, H. Magnetotransport and magnetocaloric effects in intermetallic compounds. Ph.D thesis, Universiteit van Amsterdam (2000).
- 24.Philippe M, Malaman B, Roques B. Preparation and study of intermetallic iron-gallium compounds in single-crystal state. Comptes Rendus Hebdomadaires Des Seances De L Academie Des Sciences Serie C. 1974;278:1093–1095. [Google Scholar]
- 25.Philippe M, Malaman B, Roques B, Courtois A, Protas J. Crystal-structures of phases Fe3Ga4 and Cr3Ga4. Acta Crystallographica Section B-Structural Science. 1975;31:477–482. doi: 10.1107/S0567740875003068. [DOI] [Google Scholar]
- 26.Kawamiya N, Adachi K. Magnetic and Mössbauer studies of metamagnetic Fe3Ga4. J. Phys. Soc. Jpn. 1986;55:634–640. doi: 10.1143/JPSJ.55.634. [DOI] [Google Scholar]
- 27.Kawamiya N, Adachi K. Magnetic phase changes in Fe3Ga4. J. Magn. Magn. Mat. 1986;54–57:941–942. doi: 10.1016/0304-8853(86)90324-0. [DOI] [Google Scholar]
- 28.Feng Y, et al. Itinerant density wave instabilities and classical quantum critical points. Nature Physics. 2015;11:865–872. doi: 10.1038/nphys3416. [DOI] [Google Scholar]
- 29.http://elk.sourceforge.net/. The Elk FP-LAPW Code.
- 30.Lei H, Wang K, Petrovic C. Magnetic-field-tuned charge density wave in SmNiC2 and NdNiC2. J. Physics: Condensed Matter. 2016;29:075602. doi: 10.1088/1361-648X/aa520e. [DOI] [PubMed] [Google Scholar]
- 31.Watanabe, S. & Kazumasa, M. A scenario for superconductivity of UGe2 due to coupled charge and spin fluctuations. J. Phys. Chem. Solids63, 1465 (2002).
- 32.Chen XZ, et al. Tunneling anisotropic magnetoresistance driven by magnetic phase transition. Nature Comm. 2017;8:449. doi: 10.1038/s41467-017-00290-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Feng Y, et al. Incommensurate antiferromagnetism in a pure spin system via cooperative organization of local and itinerant moments. PNAS. 2013;110:3287–3292. doi: 10.1073/pnas.1217292110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hosono H. Layered iron pnictide superconductors: discovery and current status. J. Phys. Soc. Jpn. 2008;77:1–8. doi: 10.1143/JPSJS.77SC.1. [DOI] [Google Scholar]
- 35.Paglione J, Greene RL. High-temperature superconductivity in iron-based materials. Nature Physics. 2010;6:645. doi: 10.1038/nphys1759. [DOI] [Google Scholar]
- 36.Stewart GR. Superconductivity in iron compounds. Rev. Mod. Phys. 2011;83:1589. doi: 10.1103/RevModPhys.83.1589. [DOI] [Google Scholar]
- 37.McEwen, K. A. Magnetic and transport properties of the Rare Earths, chap. 6, 411–488. Handbook on the Physics and Chemistry of Rare Earths (North-Holland Publishing Company, 1978).
- 38.Jensen, J. & Mackintosh, A. R. Rare Earth Magnetism, Structures and Excitations (Clarendon Press, Oxford, 1991).
- 39.Krause L, Herbst-Irmer R, Sheldrick GM, Stalke D. Comparison of silver and molybdenum microfocus X-ray sources for single-crystal structure determination. J. Appl. Crystallogr. 2015;48:3–10. doi: 10.1107/S1600576714022985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Sheldrick GM. SHELXT - integrated space-group and crystal-structure determination. Acta Crystallogr. Sect. A: Found. Adv. 2015;71:3–8. doi: 10.1107/S2053273314026370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sheldrick GM. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C: Struct. Chem. 2015;71:3–8. doi: 10.1107/S2053229614024218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Rodriguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Physica B192, 55 (1993) For a more recent version see Rodriguez-Carvajal, J. Recent Developments of the Program FULLPROF, in Commission on Powder Diffraction (IUCr) Newsletter, 26, 12–19 (2001).
- 43.Sirdeshmukh, D. B., Sirdeshmukh, L. & Subhadra, K. G. Micro- and Macro-Properties of Solids, vol. 80 of Materials Science, chap. 3, 77–133 (Springer Berlin Heidelberg, 2006).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The authors declare that the main data supporting the findings of this study are available within this article and its Supplementary Information. Extra data are available from the corresponding author upon reasonable request. See author contributions for specific data sets.