Potts Hamiltonian models of protein co-variation, free energy landscapes, and evolutionary fitness

Abstract

Potts Hamiltonian models of protein sequence co-variation are statistical models constructed from the pair correlations observed in a multiple sequence alignment (MSA) of a protein family. These models are powerful because they capture higher order correlations induced by mutations evolving under constraints and help quantify the connections between protein sequence, structure, and function maintained through evolution. We review recent work with Potts models to predict protein structure and sequence-dependent conformational free energy landscapes, to survey protein fitness landscapes and to explore the effects of epistasis on fitness. We also comment on the numerical methods used to infer these models for each application.

Introduction

There is a long history of the use of coevolutionary information in the form of protein sequence variation to probe the relationship between protein structure, function, and fitness, to understand how allosteric interactions are transmitted through proteins, and to predict protein structure from sequence. Reviews of this history can be found in [1–4]. More recently, powerful inverse inference statistical approaches have been developed to study these relationships, which encode sequence variation extracted from multiple sequence alignments (MSAs) into spin-glass Hamiltonian models of the sequence space. The Hamiltonians take the form

$$H(S)=\sum _{i=1}^L{h}_i(s_i)+\sum _{i=1}^L\sum _{i<j}^L{J}_{ij}(s_i,s_j)$$ (1)

where the sequence S is a string of letters corresponding to the amino acid types {s} at each of L positions, encoded in an alphabet of q letters, and h_i(s_i) (‘fields’) and J_ij(s_i, s_j) (‘couplings’) are single-site and pair-site parameters [5,6]. For some problems it is sufficient to use a q = 2 binary alphabet {0, 1} at each position, where 0 corresponds to the wildtype or consensus amino acid type and 1 corresponds to a mutant; this Hamiltonian is referred to as an Ising model by analogy with the Hamiltonian which describes magnetic spin systems in condensed matter physics. To describe the 20 amino acid types (plus a gap character) at each position the generalized model is referred to as a Potts Hamiltonian model, describing spin glasses. As with spin glasses, this Hamiltonian can describe complex landscapes with multiple local minima. The model is based on the maximum entropy principle that seeks to construct the minimally biased sequence probability distribution that reproduces the one-site 〈s_i〉 and two site 〈s_is_j〉 mutational probabilities (or marginal probabilities) of a protein MSA, giving a distribution P(S)/_expH(S). Its parameters can be determined by maximum likelihood inference given data, by methods reviewed below.

This area of research is a rapidly developing field of computational biology at the intersection with structural biology, biological physics, and branches of biology concerned with evolutionary protein fitness. The fast paced developments in sequencing, including the sequencing of large numbers of whole genomes for many species, and the development of deep sequencing techniques [7–9], has provided a rich source of data for the construction of correlated mutation models of protein structure, energetics, and evolution. The purpose of this article is to review the most recent developments using Ising/Potts models in computational biology with a particular focus on: firstly protein structure and the mapping of (free) energy landscapes; secondly modeling of fitness landscapes as proteins evolve under selective pressure, and finally a review of the most recent numerical methods for solving the inverse inference problem, and how well they perform in the context of the kinds of problems reviewed in the following sections.

Protein structure and free energy landscapes

Evolutionary sequence patterns contain information about protein structure, which can complement experimental data such as crystallographic and NMR structures. Before the introduction of Ising/Potts spin models of protein sequence variation, covariance matrices evaluated from MSAs were used in this way for protein structure modeling [10–12]. Covariance occurs because interacting residues are constrained by physical proximity effects and their mutations are therefore correlated. But correlations are induced by both direct and indirect effective interactions between residues that need not be close in space. For example, allosteric effects often involve long range interactions mediated by networks of interacting residues. One of the prime motivations for developing Potts models of protein sequence space has been to disentangle the direct from the indirect correlations as part of a procedure known as ‘direct coupling analysis’ (DCA), which improves on traditional covariance methods by providing a mapping between strongly directly interacting residues inferred from the model and contacts in 3D protein structure [13].

For contact prediction, the Potts model parameters are not used directly but an ‘interaction score’ summarizing the q² residue-dependent coupling parameters J_ij(s_i, s_j) is computed for each position-pair i, j, and the top-ranking position-pairs are interpreted as predicted contacts for the family as a whole. These contacts can then be used as input in further computations to study protein structures and conformational landscapes, for example for abinitio structure prediction of the native (folded) conformation using NMR (distance geometry) structure determination algorithms [14,15], or using the contacts to bias or constrain molecular dynamics simulations and Go-models using a homologous crystal structure as a starting point [16–18]. Progressively more detailed aspects of the conformational-energy landscapes of proteins have been explored with this strategy. The inferred contact constraints have been used to predict alternate (experimentally unobserved) intermediate conformations [19^•], to sample conformational space along a conformational transition, predict conformational flexibility of parts of a protein and simulate the folding transition [20^•], and to predict conformations of dimers, multimers, and repeat proteins [21–24]. Other studies investigate ways of combining the predicted contacts with additional structural data [25–27].

Recent studies have begun to mine the residue-specific parameters of the Potts model to map out sequence-dependent conformational free energy landscapes. These applications implicitly relate the coupling parameters J_ij(s_i, s_j) of the Potts model to pairwise physical interaction strengths or free energy contributions. In one approach the sequence-specific coupling strengths J_ij(s_i, s_j) are used as interaction strengths (biases) in coarse grained molecular simulations [28]. By examining the residue-dependent coupling parameters for sequences in a common family, it is possible to detect which interaction pairs contribute to the stability of particular conformations (not necessarily the native conformation) and the sequence dependence of these conformational preferences (see Figure 1) [29^•].

Figure 1.

The Potts model can be used to predict sequence-dependent conformational landscapes. (Left) Coevolutionary (Potts) interaction score map (upper triangle), and crystal structure contact frequency map (lower triangle, 6 Å cutoff) for the kinase family, showing high correspondence [29^•]. Interactions predicted to be relevant to a conformational transition in kinases between a ‘DFG-out’ (cyan) and a ‘DFG-in’ (magenta) conformation are highlighted. (Right) Crystal structure of the two conformations (pdb-id 1IEP and 2GQG) illustrating the change in the activation loop (colored red/blue), showing C-α to C-α contacts relevant to the transition predicted by the Potts model (cyan/magenta, as in the contact map). The Potts model gives a sequence-dependent score J_ij(s_i, s_j) for each interaction.

The correspondence between the Potts Hamiltonian and free energy landscapes has been made even more explicit in other studies, which compare H(S) to the free energy of folding of a protein sequence in its native fold ΔG(S), motivated by the idea that the folding process is a major determinant of protein fitness and therefore prevalence of sequences in the MSA. Experimental evidence supports this relationship. A number of studies have shown that for single and double mutants to a sequence, the change in the sequence’s statistical Potts score ΔH is linearly related to the experimental change in free energy of folding upon mutation ΔΔG [30^••,31^••,32]. The Potts energy H(S) of entire sequences has also been found to be correlated to protein melting temperature [33,34]. The distribution of free energies of folding predicted by the Potts model can be interpreted using the energy landscape theory of protein folding [35,36], and it has been shown that the Potts model gives results consistent with energy landscapes predicted from physiochemical considerations [31^••]. Other studies have sought to better understand the physical origin of individual Potts model parameters. The value of certain coupling parameters can be rationalized from charge–charge interactions modulated by distance [37], and using lattice models the relationship between the coupling terms {J} and pairwise interaction strengths in the native folded state has been shown to be modulated by the effect of competing non-native (decoy) folds and interactions [38].

Epistasis and fitness

The relationship between conformational free energy and H(S) is mediated by effects related to protein (and organismal) fitness, and fitness may be affected by other protein properties such as enzyme efficiency and the specificity for interactions with other proteins in signaling networks [39]. This motivates another avenue of research using Potts models in which the Potts Hamiltonian is used to probe protein fitness.

The Potts Hamiltonian is a mapping of sequences to statistical scores in which sequences with lower Potts statistical energy are more probable, generating a landscape termed the ‘prevalence landscape’ [40,41,42^••, 43^••]. Recent studies have demonstrated that experimental measurements of fitness differences are empirically well correlated with the change in Potts statistical energy ΔH for sequences from large protein families [30^••,34]. Potts models have also been used to interrogate the fitness landscapes of viral systems, most notably HIV proteins escaping immune pressure [40,41,42^••,44] or HIV enzymes evolving under drug pressure [45^•]. These studies have demonstrated linear relationships between Potts energy and experimental measurements of viral fitness, and these combined with the previously mentioned studies provide strong evidence that there exists a correspondence between the Potts prevalence landscape and the protein fitness landscape.

Interpreting the meaning of individual Potts model parameters in terms of evolutionary quantities is complicated by the nontrivial differences between the evolution of viruses and protein families to which the Potts model has been applied, such as the strength of selection, mutation rate, effective population size and population dynamics [46,47]. A systematic comparison of the implications of these features on model building is lacking. For proteins evolving nearly neutrally the suggestive relationship between the evolutionary fitness landscape and the prevalence landscape described by statistical physics (with several caveats) [48] reinforces the observed correlations between large experimental fitness datasets and Potts statistical energies in studies of protein families [30^••,34]. In viral systems the Potts model parameters have been related to parameters in viral evolution models, such as Eigen’s model of quasispecies, showing that there exist complex mappings from Potts prevalence landscape parameters to those of the fitness function [41,40]. Other work has incorporated the Potts Hamiltonian as a fitness function in population genetics simulations; a recent study has demonstrated that the relationship between in vivo fitness of HIV proteins targeted by the immune system and Potts equilibrium predictions of fitness can be improved by creating a dynamical model combining the Potts Hamiltonian with Wright-Fisher evolutionary simulations [43^••]

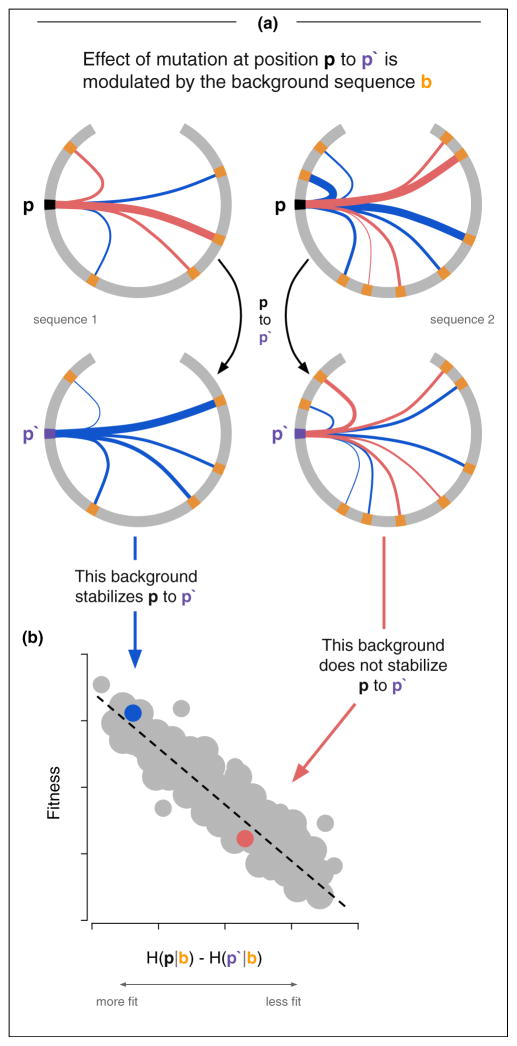
A key aspect of the Potts model in this application is its ability to model epistasis, the intuitively understandable phenomenon that the effect of a mutation is modulated by the background sequence in which it is acquired, because of the collective effects of pairwise couplings. Experimental technologies like deep mutational scanning [49–52] have allowed for the full mapping of the genotype space located one or two mutations from the native sequence to the phenotype space, yielding insights into the local fitness landscape around the native sequence. However, the size of the sequence space increases exponentially as the number of sites included in high throughput mutagenesis increases, and thus only a tiny portion of the mutational landscape and the associated epistatic effects can be sampled. Organizing principles discovered through statistical modeling are needed to interpret the massive amounts of data becoming available (see Figure 2).

Figure 2.

The effect of a mutation depends on the background in which it’s acquired. Shown in (a) are two sequences (gray annulus) with a focal residue p (black), and different background mutations (orange). Stabilizing (blue, J < 0) and destabilizing (red, J > 0) couplings between the focal residue and the background mutations are shown. The effect of mutation at the focal residue (p to p′, black to purple) is dependent on the couplings between the mutation and the background sequence. Certain backgrounds are more accommodating than others of this particular mutation, which leads to higher observed fitness (b). Potts statistical energy H is well correlated with experimentally observed fitness measurements.

A central premise of Potts spin glass models applied to biological systems is the assumption that modeling pair correlations is both necessary and sufficient to describe higher order correlation patterns beyond pairs [53]. For Potts models of protein sequence variation, this includes mutation patterns up to and including whole sequences, including those with many simultaneous mutations and those not observed in the multiple sequence alignment. This makes the Potts model a capable probe for exploring the regional mutational landscape around the native sequence, pushing the size of the surveyable sequence space to much larger landscapes than are currently accessible experimentally. A vivid illustration of the predictive power of spin models of protein sequence variation is the successful prediction of the occurrence of HIV protease sequences in a second curated database which were not present in the one used to parameterize the Ising model [37]. Another study has recently demonstrated that deleterious mutations in HIV-1 protease needed to escape drug pressure become advantageous in the context of specific sequence backgrounds that are observed when a sufficient number of mutations have accumulated [45^•] and become more advantageous (or entrenched [54–56]) as additional mutations accumulate in the presence of these formerly deleterious mutations. Fit variants with multiple resistance mutations are less likely to revert to wildtype in infected individuals not undergoing antiretroviral therapy, and thus pose a significant risk to transmit resistance.

The use of (a properly parameterized) Potts model to survey the prevalence landscape far from the native sequence is justifiable given the model’s ability to capture higher order correlations in the input dataset. While the model is trained on pair correlations, studies have demonstrated the model’s ability to reproduce marginal probability distributions higher than 2nd order, typically showing the preservation of 3-body or 4-body correlation statistics [20^•,37,38,42^••,43^••,57]. These studies have also demonstrated that the distribution of observed hamming distances from a reference sequence can be accurately modeled by the Potts Hamiltonian, and studies demonstrating the accurate prediction of higher order marginal distributions are forthcoming [45^•]. Further, these results indicate that models without pair couplings, often termed independent models because they model the effect on fitness of each site individually, are poor predictors of these experimental quantities, meaning the incorporation of pairwise epistatic terms are necessary to accurately model a mutation’s impact on fitness [30^••,34,37,45^•]. Potts models provide an unprecedented glimpse into the fitness landscape around naturally observed protein sequences which is not yet achievable with current mutagenesis experiments.

Inverse inference methods

Inferring the maximum likelihood set of parameters of the Potts model J_ij(s_i, s_j) given the MSA statistics 〈s_is_j〉 is a significant computational challenge, and a variety of methods have been developed to solve it including message passing [13,37], mean field approximations [17,58], pseudolikelihood methods (PLM) [59,60], Monte Carlo methods [6,20^•,29^•,42^••], and adaptive cluster expansion (ACE) [57]. These have each been implemented with particular applications in mind, generally either contact prediction or fitness mapping (prediction of statistical energies), potentially at the expense of other uses.

Many inference techniques were developed for protein contact prediction. The accuracy of the Potts model’s estimate of probabilities P(S) and 〈s_is_j〉, and the value of the individual residue-dependent parameters J_ij(s_i, s_j) are not directly relevant in this application, and relaxing the requirements on their accuracy allows stronger approximations to be made. Message passing, used in some of the earliest studies, assumes the interaction network is mostly ‘loop-free’, making the computation of 〈s_is_j〉 given trial {J} computationally efficient so that the maximum likelihood values {J} may be solved for iteratively. This method has been superseded by mean-field methods, which using the weak-coupling limit relate the J_ij(s_i, s_j) and the correlation coefficients C_ij(s_i, s_j) = 〈s_is_j〉 – 〈s_i〉〈s_j〉 by a simple and efficient matrix inversion [61]. This method has proven particularly popular because of its speed. Pseudolikelihood methods, which approximate the likelihood function and maximize likelihood by gradient descent, have been shown to give more accurate contact prediction at moderately higher computational cost [62]. While these methods reliably distinguish the most strongly interacting position-pairs from the rest, they generally do not correctly model sequence statistics, including the univariate and bivariate statistics the model is based on [57]. A benchmarking study comparing statistics of an input MSA to MSAs generated from models inferred from the input by different methods shows that mean-field methods underestimate the amount of sequence diversity and generate overly fit sequences, while PLM tends to generate models giving less stable sequences than in the original dataset [38].

In evolutionary applications other methods are favored which more faithfully model the dataset sequence statistics, including Monte Carlo methods, which solve for 〈s_is_j〉 given trial {J} by Monte Carlo sampling of sequences from the model and solve for the optimal {J} iteratively, as well as Cluster Expansion techniques which recursively solve sub-networks of the full problem, allowing uncorrelated sub-networks to be left out of the computation. These methods are much more computationally intensive than mean-field and pseudolikelihood methods, but can accurately model the bivariate (and higher) statistics of the dataset and the distribution of sequence probabilities of the MSA as described in the previous section, though the ACE method may generate models with sequences with slightly higher statistical energies than the original data-set [38]. Studies using Monte Carlo methods have also shown that low-dimensional (Principal Component) representations of the inferred Potts model landscape match those of the dataset [20^•,41]. Monte Carlo methods have been used for the purpose of contact prediction, as well [20^•,29^•,33].

In addition to the Potts model inference itself, data preprocessing steps can have a significant influence on the inferred model. The Potts model is an equilibrium model assuming each sequence in the dataset is generated by an independent process according to the distribution P(S), however in practice MSAs are constructed from datasets with experimental and phylogenetic structure [20^•]. For MSAs constructed from large cross-species alignments a correction should be applied for over-counting of sequences or organisms which received more experimental focus or which are phylogenetically related. Current methods to account for this are rudimentary, involving simple sequence similarity cutoffs, and it has been suggested that a more rigorous approach is desirable [20^•,63]. In HIV datasets, in contrast, corrections are applied to sequences originating from the same individual but otherwise such phylogenetic filtering is not performed, because evidence suggests HIV data is not distorted by phylogenetic effects [9,43^••,64].

Extensions to the Potts Hamiltonian have also been proposed, such as inclusion of higher order terms [32,65,66], inclusion of population-genetics terms [67] to account for phylogenetic structure. Other studies examine how to combine data from multiple data sources or inference methods [68,69].

Concluding remarks

Potts statistical models of protein sequence variation are being used to map the conformational energy and fitness landscapes of proteins with impressive results, but the full potential of this modeling is just beginning to be tapped. Through constraints imposed by evolution so as to maintain the fitness of the organism, pair and higher order correlations are induced in the sequence patterns that are captured by the models, even though the Potts Hamiltonian only includes pair interaction energy terms. Potts modeling can be used to interrogate epistatic effects whereby the probability of observing a particular mutation in a protein sequence depends strongly on the background. There are many opportunities and challenges to pursue; they include establishing closer synergies between protein conformational free energy landscapes and Potts model evolutionary landscapes, clarifying the relationship between Potts model parameters and physical free energy terms, and incorporating population genetics concepts into preprocessing steps which are performed on MSAs, as well as the interpretation of the model itself.