Systematic identification of feature combinations for predicting drug response with Bayesian multi-view multi-task linear regression

Abstract

Motivation

A prime challenge in precision cancer medicine is to identify genomic and molecular features that are predictive of drug treatment responses in cancer cells. Although there are several computational models for accurate drug response prediction, these often lack the ability to infer which feature combinations are the most predictive, particularly for high-dimensional molecular datasets. As increasing amounts of diverse genome-wide data sources are becoming available, there is a need to build new computational models that can effectively combine these data sources and identify maximally predictive feature combinations.

Results

We present a novel approach that leverages on systematic integration of data sources to identify response predictive features of multiple drugs. To solve the modeling task we implement a Bayesian linear regression method. To further improve the usefulness of the proposed model, we exploit the known human cancer kinome for identifying biologically relevant feature combinations. In case studies with a synthetic dataset and two publicly available cancer cell line datasets, we demonstrate the improved accuracy of our method compared to the widely used approaches in drug response analysis. As key examples, our model identifies meaningful combinations of features for the well known EGFR, ALK, PLK and PDGFR inhibitors.

Availability and Implementation

The source code of the method is available at https://github.com/suleimank/mvlr.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Identifying the genomic and molecular features predictive of drug response in cancer cells is one of the prime aims of computational precision medicine. The identified features may help the clinician to choose therapies tailored to an individual cancer patient and may also reveal mechanisms of drug actions. Recent large scale high-throughput screening experiments have opened new opportunities to build computational models of drug response predictions, by providing genomic and molecular profiles and drug response measurements on several hundreds of human cancer cell lines (Barretina et al., 2012; Basu et al., 2013; Garnett et al., 2012; Iorio et al., 2016). Furthermore, the potential of genomic and molecular features to predict drug responses in cell lines has been demonstrated in many recent studies (Costello et al., 2014; Cortés-Ciriano et al., 2015; De Niz et al., 2016; Jang et al., 2014; Zhang et al., 2015). However, the small sample size in most of drug response studies poses a challenging prediction task with a limited statistical strength resulting into uncertain predictions.

A promising direction is to help the learning process by formulating the problem as integrating multiple data sources, which are either readily available from high-throughput experiments or extracted from external sources as known prior knowledge. The underlying assumption is that some or all of the data sources may exhibit a signal (set of features) predictive of the response variable. For example, the expression patterns in only a small subset of the pathways may be linked to drug response, or a mutated gene present in one data source may show up- or down-regulation of its expression in the other data source. Modeling the combination of shared signals from multiple sources may reveal hidden statistical relationships which may not be obvious from the data itself and are relevant for the drug response prediction task. There is a need to develop computational methods, commonly referred to as multi-view learning, that can effectively infer these signals from the data sources. Here, a key methodological challenge involves determining what is the ‘useful signal’ (combination of predictive features) to extract.

Another, closely-related problem of multi-task allows learning a task from other related tasks. For example, predicting one drug response alone can be considered as an individual task, whereas two drugs whose responses are highly correlated can provide statistical boost when learned together. This is especially beneficial when the number of samples are small, or when the samples come from a diverse collection such as in the pan-cancer scenario.

A naive approach comprises of combining the different data sources into one data source and the use of a discriminative model to learn a set of potentially predictive features by explicitly optimizing a cost function. However, such a discriminative model may result in too simple approach requiring strong regularization to eliminate the false positives, and it may be difficult to fully exploit the multi-view nature of the data to extract the relevant signal. Kernel-based multi-view and multi-task predictive models have shown to provide effective learning among distinct data sources and drug classes (Ammad-ud din et al., 2016, 2014; Cichonska et al., 2015; Costello et al., 2014). Although these models can result in highly accurate response predictions, they are less powerful in their capability to identify the most predictive features (e.g. genes or mutations), making their practical usefulness quite limited for translational applications. While modeling the non-linear interactions of the signaling network in an interpretable fashion is an ongoing challenge, a simple formulation would be to model the linear combination of features and their networks that are relevant for drug response prediction.

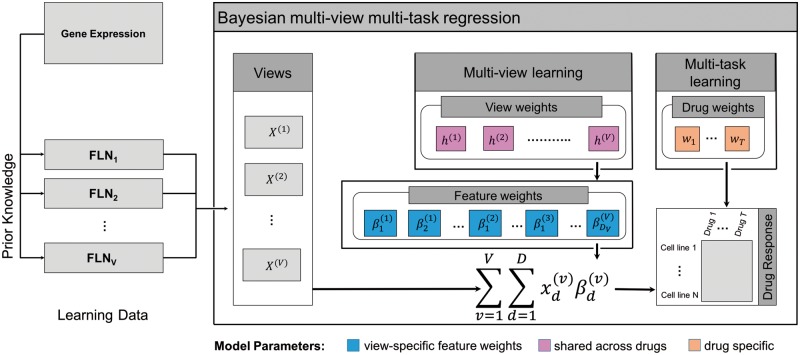
In this study, we present a Bayesian multi-view multi-task sparse linear regression model for cellular drug response prediction (illustrated in Fig. 1). The method solves the prediction problem by learning a model from multiple input data sources (here groups of molecular features) and output variables (here groups of drug responses). The model additionally identifies feature combinations from the relevant data sources by assuming structured sparsity. The proposed formulation assumes that only a few of the input data sources and features are predictive of a particular group of drugs, which share highly correlated response patterns. Hence addressing the small sample size and high-dimensionality problem in drug response prediction.

Fig. 1.

Flow chart of the Bayesian multi-view multi-task linear regression approach. Left: The learning data consists of multiple data sources (here FLNs) extracted using prior knowledge and denoted by ${\mathbf{X}}^{(1)}\mathrm{..}{\mathbf{X}}^{(V)}$. Right: The model combines multi-view and multi-task learning to systematically identify feature combinations (${\beta }_1^{(1)},{\beta }_2^{(1)},{\beta }_1^{(2)},{\beta }_1^{(3)},{\beta }_{D_v}^{(v)}$) predictive of drug responses. The view-weights h^(v) control the view-specific feature weights ${\mathit{\beta }}^{(v)}$ which are predictive of the drug responses and are shared across all the drugs. This structured formulation allows identification of predictive views as well as features. The responses of multiple drugs are modeled by drug specific weights w_t

To capitalize on the proposed assumption, multiple input data sources are generated based on prior biological knowledge; here we extracted Functional-Linked-Networks of genes (FLNs) of the recently studied human cancer protein kinomes (Fleuren et al., 2016).

1.1 Contributions

Specifically, our contributions are 2-fold:

1. We propose a novel formulation of Bayesian multi-view multi-task linear regression. The method is simple to use and it provides straightforward means to identify feature combinations that are most predictive of drug responses.

2. We introduce a way for incorporating prior biological knowledge, in the form of Functional-Linked-Networks (FLNs) for drug response modeling. Instead of using a single data source comprising the genome-wide features, we treat FLN-based groups of features as multiple input data sources. Here the key assumption is that biologically meaningful grouping of the features introduces additional structure that is valuable for prediction of drug responses.

We first demonstrate the model’s predictive power on a synthetic dataset. We then show the significantly better performance of our approach on predicting drug responses in two publicly available cancer datasets. Finally, we examine the inferred relationships between drug responses, FLNs and molecular features in the larger dataset, elucidating drug action mechanisms.

2 Computational models in drug response prediction

The main idea of the computational models is very simple: given genome-wide features of the cell lines as input (also known as independent variables or covariates) and drug responses as target (output or dependent variables), learn a regression model of the drug sensitivity. The regression model can predict responses to new cell lines and can help interpreting features relevant to the response prediction task.

Nonlinear regression models such as kernel methods, support vector regression, neural networks and random forests have been well-studied for drug response prediction on new cancer cell lines (Ammad-ud din et al., 2014; Ammad-ud din et al., 2016; Cichonska et al., 2015; Costello et al., 2014; Dong et al., 2015; Menden et al., 2013; Ospina et al., 2014; Riddick et al., 2011; Zhang et al., 2015). Kernel-based methods have shown better predictive accuracy but lacks the ability to infer what genes are predictive of drug responses. Similarly, the random forest regression is built on the ensemble approach and is expected to provide high prediction accuracy, however its interpretability at the level of FLNs is currently limited. Although the method can handle a large number of features, the number of regression trees needed would also be very high raising potential complexity issues.

On the contrary, in most translational applications, the objective is to identify features and networks that are relevant to the drug response prediction, linear models become a natural choice. A convenient aspect of the linear models is that they are easier to interpret and provide a straightforward analysis on the relationship between the genomic and molecular features and drug responses.

2.1 Linear regression

Consider $\mathbf{X}\in {ℝ}^{N\times D}$ a matrix of genome-wide features and $\vec{y}\in {ℝ}^{N\times 1}$, the vector of drug responses. Here N denotes the number of samples (cell lines) and D represents the number of features (genes). Linear regression models the drug responses $\vec{y}$ as a linear combination of unknown weight vector $\beta \in {ℝ}^{1\times D}$ and the features X as

$$\vec{y}\sim \mathbf{X}{\beta }^T$$

The machine learning goal is then to learn the optimal $\beta$ to gain insights into important features. In genomic and molecular data, since the number of features is often much higher than the number of samples, the inference becomes ill-posed and suffers from over-fitting. A frequent solution is to introduce regularization that penalizes the complexity of the model. The widely used elastic net regularization by Zou and Hastie (2005), is represented as:

$$\widehat{\beta }=\underset{\beta }{\arg \min }\left|\right|\mathbf{Y}-\mathbf{X}\beta |{|}_2^{\mathrm{2}}+(\alpha \left|\right|\beta |{|}_1+\frac{(1-\alpha )}{2}|\left|\beta \right|{|}_2^{\mathrm{2}})\times \lambda$$

Here λ > 0 is the penalty parameter that controls the amount of regularization and shrinking of the weight vector $\beta$. The penalty reduces to the ridge regression (Hoerl and Kennard, 1988) when α = 0, and the lasso regression (Tibshirani, 1996) when α = 1. For all $\alpha \in (0,1)$, it is the combination of the ridge and lasso regression.

To identify genomic and molecular features predictive of drug responses in cancer cell lines, linear regression models employing ridge, lasso and elastic net regularizations have been used in numerous benchmark experimental studies (Barretina et al., 2012; Basu et al., 2013; Garnett et al., 2012; Iorio et al., 2016) and they have served as popular comparison models in the context of drug response prediction in various applications (Chen et al., 2015; Cortés-Ciriano et al., 2015; Costello et al., 2014; De Niz et al., 2016; Jang et al., 2014), as well as in this paper.

Additionally, several extensions of linear models have also been studied for modeling drug responses including sparse partial least squares (sPLS) and sparse group lasso (SGL). In particular, sPLS is used for simultaneous dimension reduction and feature selection (Chun and Keleş, 2010), while SGL extends lasso regression to groups of features (Chun and Keleş, 2010). For drug response datasets of higher order, joint tensor models can be useful to analyse feature relationships (Khan and Kaski, 2014; Khan et al., 2016).

3 Materials and methods

3.1 Bayesian multi-view multi-task linear regression

We formulate the multi-view multi-task linear regression (MVLR) problem for a collection of v = 1,…, V input matrices (views or data sources) ${\mathbf{X}}^{(v)}\in {ℝ}^{N\times D_v}$ and outcome matrix $\mathbf{Y}\in {ℝ}^{N\times T}$, as a joint regression that learns each views contribution to the multiple regression task while pruning out any excessive views. This is achieved by incorporating two characteristics, i) controlling each view’s (${\mathbf{X}}^{(v)}$) activation through a view-specific parameter for multi-view learning; ii) performing simultaneous regression sharing information from multiple tasks (T) in $\mathbf{Y}$. Here, a view is said to be active when (at least) some of its features are predictive of the outcome.

Figure 1 illustrates MVLR model for the joint regression problem from the multiple views ${\mathbf{X}}^{(v)}\in {ℝ}^{N\times D_v}$, each representing an FLN of genes. More formally, the ${\beta }^{(v)}$ are feature-level coefficients that regress each of the corresponding views. Here, the view-specific weights $h^{(v)}$ controls the activation at the view-level, effectively limiting the search space to the predictive views (FLNs). The regression for multiple tasks is modeled through the ${\mathbf{w}}_t$ weights that span across the set of drugs. The subscripts v, t and i index views, tasks, and training samples, while the total numbers of input views, tasks, and training samples are denoted by V, T and N, respectively.

We next formulate a Bayesian treatment of the MVLR by complementing it with priors for model parameters. The distributional assumptions for multi-view learning combined with multiple task learning for $\mathbf{Y}$ are as follows,

$$\begin{array}{l}{y}_t\sim \mathcal{N}\left(\sum _{v=1}^V({\mathbf{X}}^{(v)}{\beta }^{(v)}){\mathbf{w}}_t,{\tau }_t\right)\\ {\beta }_{d_v}^{(v)}\sim Cauchy(0,{\lambda }_{d_v}^{(v)}{h}^{(v)})\\ h^{(v)}\sim Dir({\alpha }^h)\\ {\lambda }_{d_v}^{(v)}\sim Cauch{y}_{+}(0,b^{\lambda })\\ {\mathbf{w}}_t\sim Dir({\alpha }^{\mathbf{w}})\\ {\tau }_t\sim Cauch{y}_{+}(0,b^{\tau })\hspace{0.17em},\end{array}$$

where Cauchy(a, b) is the Cauchy distribution parameterized by location a, scale b, and Dir is a Dirichlet prior with concentration parameter α. The ${\beta }^{(v)}$ coefficients are modeled using a Cauchy prior centered at zero to induce regularization. The multi-view learning is achieved through the view-level parameters $h^{(v)}$, which control the variance for all coefficients ${\beta }^{(v)}$ in the corresponding view. As $h^{(v)}\sim 0$, all ${\beta }^{(v)}$ for the view v approach zero, while as $h^{(v)}$ increases each ${\beta }_{d_v}^{(v)}$ is then controlled primarily by the corresponding feature-level variance ${\lambda }_{d_v}^{(v)}$. This structured-sparsity formulation allows the model to identify the relevant views as well as the predictive features, while pruning out the excessive views. The $h^{(v)}$ are modeled using a Dirichlet prior to induce view-level regularization, which matches our application assumption that only a subset of the views are relevant for the task. The multi-task parameters ${\mathbf{w}}_t$ model the regression for multiple joint tasks.

On the distributional choices, the Cauchy is a long tailed prior that concentrates most of the mass around the area where values are expected, though also leaves a considerable mass in the tails. It’s usefulness has been demonstrated previously in regression settings (Gelman et al., 2008). Our Dirichlet-Cauchy formulation, may also be seen as an extension of a global-local shrinkage construction, where the local shrinkage is enforced by the Cauchy while Dirichlet controls the view-level shrinkage. For single input, global-local shrinkage priors have shown robust performance when the features are sparse, with the normal-Cauchy based horseshoe prior outperforming the laplace (Carvalho et al., 2010). For the variance parameter τ_t we use the half-Cauchy prior of Gelman et al. (2006). Our formulation can also be seen as an extension of the sparse group regularizer (Simon et al., 2013) in a Bayesian hierarchical formulation with joint multi-task learning. The model is implemented in STAN (Carpenter et al., 2017) and inference is performed via variational approximation.

3.2 Publicly available datasets and preprocessing

In this study, we used two publicly available cancer datasets to analyze cellular drug response predictions.

3.3 Genomics of drug sensitivity in cancer

The first drug response data originated from Genomics of Drug Sensitivity in Cancer (GDSC) project by Wellcome Trust Sanger Institute (Yang et al., 2013). For our analysis, we used data from 124 human cancer cell lines and 47 anti-cancer drugs (belonging to the class of kinase inhibitors), for which complete measurements were available, and the drug response range was consistent with earlier publications (Garnett et al., 2012; Menden et al., 2013). Drug response measurements were summarized as log IC₅₀ values, denoting the concentration of a drug required to inhibit the cell line’s growth by half. Additional information about drugs were also available, for instance, their primary therapeutic targets.

The drugs were grouped into 16 classes based on their primary target, sample size and batch information. Specifically, drugs belonging to each target class and batch effect were considered an independent group. For example, two EGFR inhibitors, Erlotinib and Lapatinib were profiled in a single batch and show comparable response, while other two Gefitinib and BIBW2992 were profiled in the second batch showing correlated response; and were therefore considered as independent groups for the modeling. Supplementary Material Information section on "Cancer Data Sets" describes the batch identification procedures and the groups in detail.

3.4 Triple negative breast cancer

The second data contained responses of 301 approved and investigational anti-cancer drugs measured on 19 triple negative breast cancer (TNBC) cell lines at Institute for Molecular Medicine Finland FIMM (Gautam et al., 2016). The response data were summarized with a drug sensitivity score (DSS) (Yadav et al., 2014). For our case study, we focused on the set of 14 drugs belonging to the class of kinase inhibitors and 17 cell lines whose gene expression measurements were available from the GDSC project (Iorio et al., 2016). The drugs were grouped into 6 classes based on their primary target information (Supplementary Material Section on "Cancer Data Sets").

In this article, we used gene expression profiles to represent the cell lines. Several studies including the benchmark drug sensitivity prediction challenge showed that the gene expression was the most predictive "omic" data source amongst others (Costello et al., 2014).

3.5 Functional-linked-networks

To incorporate prior biological knowledge, we extracted FLNs of known human cancer protein kinases. This was done as a three-step process. First, we obtained the set of 45 kinase families represented by 91 driver kinases in human cancers from (Fleuren et al., 2016). Fleuren et al. (2016) demonstrated that members of these kinase families are commonly dysregulated in cancer.

In the second step, we exploited the knowledge of kinase families in a biologically meaningful way to build functional linked networks. Specifically, for each of the 45 families, we used genes corresponding to the set of driver proteins to extract FLNs from the GeneMANIA prediction server (Warde-Farley et al., 2010). GeneMANIA takes in the list of genes and returns an extended list of genes, that are predicted to be functionally related using a large set of association data, such as protein and genetic interactions, pathways, co-expression, co-localization and protein domain similarity. The recommended default settings of the GeneMANIA server were used to extract the FLNs.

Finally, we take the genes participating in the FLNs as features and split the gene expression data into ‘views’, as shown in Figure 1. More specifically, a view comprises expression profiles of the genes that belong to an FLN, and thereby represent a kinase family. As an example, the EGFR kinase family contains EGFR, ERBB2, ERBB3 and ERBB4 driver kinases, and is represented by an FLN of 24 genes. The total number of genes in the 45 FLNs are listed in Table 1, while the description of FLNs along with the number of genes in each FLN, and the drug groups are provided in the Supplementary Material Information.

Table 1.

Multi-view data used in the drug response predictions

Datasets	Cell lines	Drugs	All genes	FLNs (genes)
GDSC	124	47	13321	45 (816)
FIMM	17	14	17420	45 (935)

Note: In parenthesis, the number of genes found in FLNs.

3.6 Experimental setup

We compared the performance of our multi-view model with the most widely used linear regression models in drug response prediction problems over a grid of modeling choices, as shown in Table 2. Particularly, we learned regression models by varying the amount of input data (i.e. AllGenes, FLNsGenes, L1000Genes) and regularization parameters (i.e. ridge, elastic net and lasso). FLNsGenes denotes the setting when the linear regression is learned using the non-redundant set of genes derived from FLNs. We also used the set of 1000 genes (L1000Genes) provided by the LINCS project as a benchmark, denoting a common set of genes that are widely expressed in diverse cellular processes and are representative of the genome.

Table 2.

Computational models of drug response predictions

Method	Regularization	Data	Abbreviation
Bayesian multi-view	Structured priors	FLNs	MVLR
Multi-task
Linear regression	Ridge	All genes	R:AllGenes
		FLNs genes	R:FLNsGenes
		L1000 genes	R:L1000Genes
	Elastic Net	All genes	EN:AllGenes
		FLNs genes	EN:FLNsGenes
		L1000 genes	EN:L1000Genes
	Lasso	All genes	L:AllGenes
		FLNs genes	L:FLNsGenes
		L1000 genes	L:L1000Genes

We performed a leave-one-out cross validation (LOOCV) procedure, where in each fold one cell line is completely held-out (as a test cell line) and models were trained on the remaining cell lines (training data). The gene expression and drug response measurements were normalized to have zero mean and unit variance. An independent model was learned for each of the drug groups.

We used sparse linear regression model implemented in the glmnet R-package (Friedman et al., 2010). The sparse linear regression has two parameters to be optimized: α (elastic net mixing parameter) and λ (the penalty parameter), as discussed in section 2. For elastic net predictions, we performed a nested 10-fold cross validation procedure on the training data, to choose optimal values for $\alpha \in [0.1,0.9]$ with an increment of 0.1 and λ (from 100 values). We finally selected a combination of α and λ values that gave minimum average error over the internal 10 fold cross-validation on training data. To obtain the ridge and lasso predictions on the test cell line, we fixed α = 0 and α = 1 and choose λ analogously.

With MVLR, we can encode our prior belief through a stronger feature-level sparsity when the number of views are small (${\alpha }^h,{\alpha }^{\mathbf{w}},b^{\lambda },b^{\tau }$ set to 1,1,0.1,1) in the synthetic data case, and stronger view-level sparsity when the number of views is large in the two drug response applications (${\alpha }^h,{\alpha }^{\mathbf{w}},b^{\lambda },b^{\tau }$ set to 0.1,0.1,1,1). However, in the absence of prior belief’s the hyper-parameters can also be learned using cross-validation. We evaluated the predictive performance of the methods in the unnormalized space using correlations (Spearman and Pearson) and root-mean-squarred error (RMSE) averaged over all the drugs in each drug-group. The RMSE was normalized to compute NRMSE such that the baseline (mean prediction) NRMSE is 1. The run time of MVLR and elastic net algorithms were less than 60 seconds for one cross-validation fold on the larger dataset (GDSC) using a Mac Book Pro (2.9Ghz, Intel Core i7, 16 GB RAM; MVLR: 43 sec, Elastic Net: 11 sec).

4 Results and discussion

4.1 Synthetic dataset

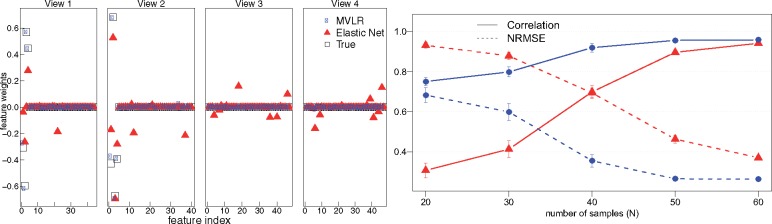
We first demonstrate in a simulated example the model’s ability to correctly prune out the excessive views, as well as precisely identify the sparse feature weights. We plot the behaviour of elastic net regression simultaneously, for illustration purpose.

To demonstrate the ability of our method in a multi-view example case, four views were generated ${\mathbf{X}}^{(v)}\in {ℝ}^{N\times D_v}$, for v = 1: 4, N = 40 and D_v = 45 ± 5 dimensions in each view v, such that the first two views were embedded with 10% features whose combinations were predictive of the response variables ($\mathbf{Y}\in {ℝ}^{N\times T}$, T = 6), while the remaining two views were composed of random features. Figure 2, left shows the loadings used to create the response variables in all the four views, and the corresponding estimates of the model parameters by our method. Our model correctly segregates the views relevant for the predictions from the excessive ones, as well as correctly identifies the feature weights for the predictive features. The feature weights learned by the elastic net by concatenation of the features from multiple views is also plotted. While the embedded features are correctly identified by both methods, deviations in the excessive views were pruned out only by the multi-view formulation.

Fig. 2.

Performance of the method on synthetic dataset. Left: The figure demonstrates the models functionality by effectively shutting down excessive views to prune the search space, and its ability to identify the features weights correctly. The true weights corresponding to the four views are shown along with the weights learned by our model and elastic net regression. The view-sparsity in MVLR shuts down the irrelevant views. Right: Prediction performance of our model and the comparison approach when the number of sample size is varied. Each point represents the average prediction performance over 50 experiments with error bars indicating one standard error over the mean. The structured sparsity assumptions of our model are especially beneficial when the sample sizes are small in comparison to the number of dimensions

We next evaluate the models performance over the spectrum of small sample and high-dimensional settings (Fig. 2, right). Specifically, we generate data analogous to the above settings $v=1:4,\hspace{0.17em}{D}_v=45\pm 5$ while varying the number of samples on x-axis. We repeat each experiment 50 times with noise varying between 1-25% of the variation of data, to obtain robust estimates; and plot the average LOOCV performance, using correlation and NRMSE. Our multi-view regression performs consistently well, and is especially beneficial when the sample sizes are small.

We also validate our model on single-view datasets, confirming that it performs comparably to the existing methods in identifying analogous and correct set of features in the synthetic data (Supplementary Fig. S1).

4.2 Cancer datasets

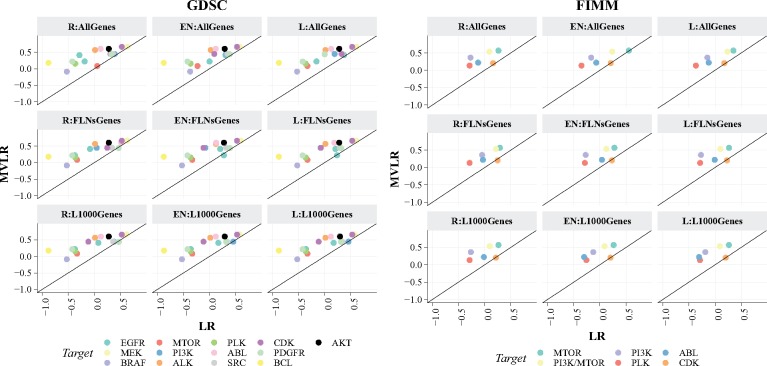
We next compare the MVLR method with the alternatives on two case studies GDSC (pan-cancer) and FIMM (TNBC), and report their predictive performances in the LOOCV procedure for the different drug groups. Figure 3 shows the predictive performances of all the methods on the GDSC (left) and FIMM (right) datasets. MVLR outperformed its competitor in both case studies. The predictive performance obtained by MVLR was found to be significantly higher than the others (p <0.01; one-sided paired Wilcoxon signed-rank test, corrected for multiple testing, Supplementary Table S5) in GDSC dataset. Also in the smaller FIMM dataset, the predictive performance obtained by MVLR was also found to be significantly higher than the others (P <0.05; one-sided paired Wilcoxon signed-rank test, corrected for multiple testing, Supplementary Table S9).

Fig. 3.

Spearman correlations on individual drug groups colored according to their primary target, computed across cell lines. Left: GDSC dataset, Right: FIMM dataset. Table 2 explains the method abbreviations. The predictive performance obtained by MVLR (shown on y-axis) for both datasets is found to be significantly higher than the others shown on x-axis (P <0.05; one-sided paired Wilcoxon signed-rank test corrected for multiple testing). Here, negative correlations correspond to poor performance as the baseline performance is –1, which is obtained using the mean of the training drug response data as predictions for the test sample

Figure 3 demonstrates the predictive performances over the drugs groups for each method. As the key observation, multi-view regression combined with prior biological knowledge improves the drug response predictions. MVLR supplemented with FLNs outperformed ridge, elastic net and lasso regressions either supplemented with or without FLNs/L1000 information. This result confirms that standard linear regression model does not seem to greatly benefit from the prior knowledge mainly due to the lack of systematic multi-view modeling approach. When using FLNs information, the performance was not better than using the full set of genes (i.e. AllGenes), except for the R:FLNsGenes scenario in FIMM dataset. Moreover, we also observed in our feasibility tests that the prediction performance did not improve even if the linear regression was applied in a heuristic multi-view setting (for instance concatenating the FLNs with duplicates to make one big input data matrix X). Secondly, the biological knowledge (FLNs) and the molecular features showed response predictive signal, outperforming the baseline performance. The baseline prediction for the test sample is obtained as the mean of the training drug response data. Notably, the mean prediction of uncentered data yields a correlation of –1, when using LOOCV (See Empirical evidence of mean prediction correlation’ in the Supplementary Material Information); implying that negative correlations in Figure 3 represent lower prediction performances that are closer to the baseline.

In GDSC dataset, when predicting responses to EGFR inhibitors (Erlotinib and Lapatinib, see methods for drug groups), MVLR demonstrated better performance then linear regression. Whereas EN:FLNsGenes (Spearman correlation = 0.272), L:FLNsGenes (0.233), EN:FLNs (0.272) and L:FLNs (0.233) gave slightly better predictions than MVLR (0.218) for the Gefitinib and BIBW2992 (EGFR inhibitors). As expected, MEK inhibitors were predicted with high accuracy with all the methods. Most of the drug groups were consistently predicted better by MVLR than with any variant of the standard linear regression. While predicting GW843682 and BI-2536 (PLK inhibitors), Sunitinib and Sorafenib (PDGFRA, PDGFRB, KDR, KIT, FLT3 inhibitors) and TW-37 and Obatoclax-Mesylate (BCL inhibitors) MVLR gave correlation values of 0.151, 0.214 and 0.173 compared to –0.367, –0.425 and –0.881, respectively. Similar trends in predictive performances can be observed in Pearson correlation and NRMSE from the Supplementary Material Information (Supplementary Fig. S8 and S2–S4).

Likewise, in FIMM (TNBC) dataset, MVLR shows robust predictions for PI3K, PLK and ABL inhibitors, compared to other methods. Linear regression also performs well in predicting responses to MTOR and PI3K/MTOR inhibitors, nevertheless does not outperform the MVLR method. On the other hand, in case of CDK inhibitors, linear regression gave slightly improved predictions with EN:AllGenes (0.206), R:FLNsGenes (0.246), EN:FLNsGenes (0.227) and L:FLNsGenes (0.227) compared to MVLR (0.202). Supplementary Material Information (Supplementary Fig. S9 and Tables S6–S8) demonstrates the comparison results in the form of Pearson correlation and NRMSE.

In the case of a single cancer subtype when the number of samples is often quite limited, evaluating the predictions becomes a challenging task. We therefore investigate the reproducibility of the predictions on FIMM TNBC dataset (n = 17), and compute the variance of the performance scores across ten model runs. The results show that the prediction performance of our model is similar with standard deviations between 0.05 and 0.12 for different drug groups (Supplementary Table S10).

In addition to the widely used linear approaches in drug response modeling, we also investigate MVLR in comparison to other computational methods. Specifically, we compare the model’s performance to sparse partial least squares (sPLS; Chun and Keleş, 2010), sparse group lasso (SGL; Simon et al., 2013), random forest (RF; Ishwaran et al., 2008) and support vector machine (SVM; Tuia et al., 2011), using comparable multi-task variants where available. Table 3 shows the prediction correlation averaged over all the drug groups, while individual performances can be found in Supplementary Tables S11–S13. MVLR demonstrates better mean prediction correlation in comparison to all the methods (except SVM in FIMM dataset); and significantly outperforms linear methods sPLS and SGL with p¡0.05, one-sided paired Wilcoxon signed-rank test in the GDSC dataset. Notably, our method provides mechanistic interpretations at the level of both, FLNs and genes, in contrast to SVM and RF.

Table 3.

Prediction performance measured as the Spearman correlation averaged over the drug groups

	MVLR	sPLS	SGL	RF	SVM
GDSC	0.375	0.330	0.338	0.359	0.363
FIMM	0.336	0.273	0.300	0.295	0.349

4.3 Inferring gene-FLNs-drug response relationships

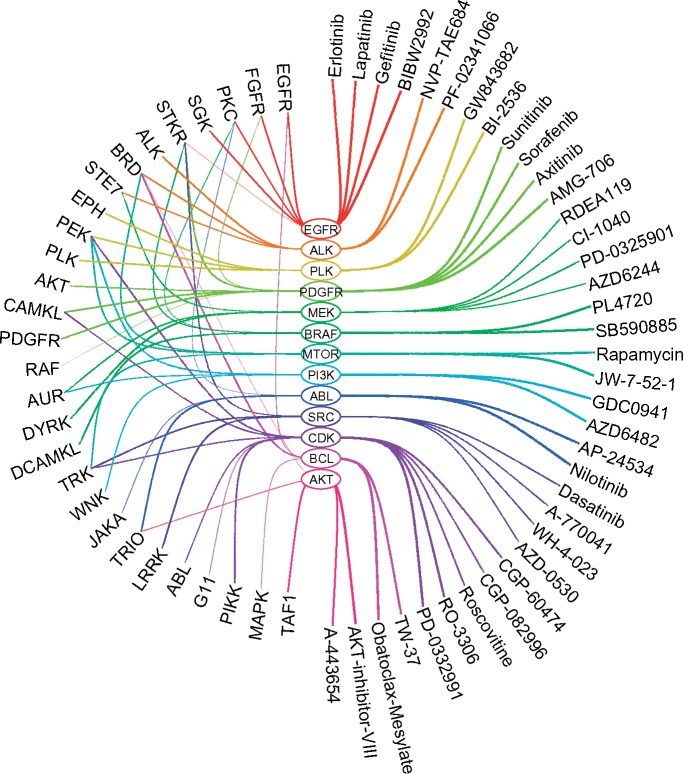
The use of multi-view data and model not only improves the prediction performance, but also helps to infer gene-FLNs-drug response relationships. We further analyze the FLNs-drug response relationship in the GDSC dataset, followed by the subsequent analysis for the well known EGFR, ALK, PLK and PDGFRA, PDGFRB, KDR, KIT, FLT3 inhibitors. To focus on the most predictive FLNs we consider the top-3 FLNs identified by the model for each drug group, in the subsequent analysis.

Figure 4 illustrates the FLNs-drug response relationships in the form of an eye diagram. A striking characteristic of the model is evident from the findings. In the case of four different inhibitor classes, MVLR identifies top predictive FLNs correctly. For the remaining classes either the direct FLN is not available or MVLR has identified a downstream FLN which may require further lab validation (for instance MAPK for BCL inhibitors, PEK for CDK, PI3K, MTOR and PLK target groups). Nevertheless, the identified FLNs already serve as proof-of-concept positive controls for the validation of the model. These FLNs include EGFR, FGFR, PKC, SGK and STKR predictive of EGFR inhibitors (erlotinib, lapatinib, gefitinib and BIBW2992), ALK, BRD and STK7 predict ALK inhibitors (NVP-TAE684 and PF-02341066), PLK, PEK and EPH are found predictive of PLK inhibitors (GW843682X and BI-2536) and PDGFR, CAMKL and AKT predict PDGFRA, PDGFRB, KDR, KIT, FLT3 inhibitors (sunitinib and sorafenib) respectively. It is biologically meaningful that the inhibitors are related to these FLNs, making it possible to inhibit the corresponding gene activities in the respective FLNs.

Fig. 4.

FLNs-drug response relationships in the GDSC dataset, visualized as an "eye diagram". For each primary target group (middle) and their corresponding drugs (right), and the top three predictive FLNs (left) are shown. (a) EGFR Inhibitors (Erlotinib and Lapatinib). (b) EGFR Inhibitors (Gefitinib and BIBW2992). (c) ALK Inhibitors. (d) PLK Inhibitors. (e) PDGFRA, PDGFRB, KDR, KIT and FLT3 Inhibitors

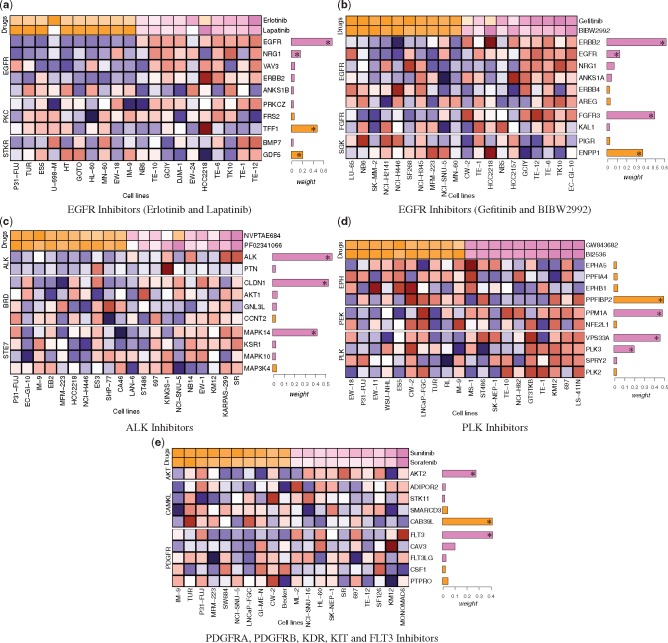
We next analyze the combination of features from these FLNs and the drug responses, visualized as heatmaps (drawn using the Complexheatmap package in R programming language (Gu et al., 2016)).

4.4 EGFR inhibitors

Figure 5a and b illustrates multiple known features as top predictors of responses to EFGR inhibitors. For example EGFR, ERBB2 and NRG1 were among the top predictive features identified by the MVLR method. The over expression of these genes links to the response of EGFR inhbitors. As a sanity check, we also validated these results from the findings reported in the benchmark study that published the original data (Garnett et al., 2012). Our results were consistent with their findings. ERBB2 (also known as HER2) over expression was associated with sensitivity to EGFR-family inhibitors including lapatinib and BIBW2992. Interestingly, the second most predictive feature predicting responses to gefitinib and BIBW2992 is FGFR3 which is a part of FGFR FLN. The role of FGFR signaling pathway in cancer is highly studied, however its downstream effects on the EGFR signaling for all types of cancers is not fully understood (Turner and Grose, 2010). Early studies have reported that over expression of FGFR2 and FGFR3 can mediate resistance to EGFR inhibitor therapy in lung cancer (Ware et al., 2010) and resistance to HER2 inhibitors in HER-positive breast cancer (Koziczak et al., 2004). In Figure 5b, the identification of FGFR3 may generate novel hypothesis on the effect of FGFR3 gene on the EGFR/ERBB2 gene family in oesophagus, stomach and kidney cancers (cell line names TE-6, TE-12, EC-GI-10, GCIY, TK10). These findings either suggests that FGFR3 is involved in EGFR/ERBB2 signaling or it can feed the same type of oncogenic signals as EGFR. For these cancers, especially FGFR3 may play a kind of co-factor role with EGFR and may be investigated to design therapeutically targetted drugs in future.

Fig. 5.

Heatmaps of feature combinations predictive of drug responses (log IC₅₀) for the 10 most sensitive (shown in violet) and resistant (shown in orange) cancer cell lines from the GDSC dataset. For each cell line, gene expression features are shown (blue corresponds to lower expression, red to higher expression). On the right side of each feature is a bar indicating the absolute value of the weight (β of the MVLR model). Bars in violet are negative weights, indicating features associated with sensitivity, and bars in orange are positive weight, indicating features associated with resistance. For clarity, only the top ten features having largest weights from the top three FLNs are shown. Feature weights marked with an asterisk (*) are statistically significant (p¡0.05, permutation test). The gene expression features are grouped based on the FLNs information, denoted on the left of the heatmaps

4.5 ALK inhibitors

Figure 5c shows the predicted features associated with sensitivity to ALK inhibitors. Among others ALK, CLDN1 and MAPK14 as the most predictive features identified by MVLR. ALK inhibitors connected to the high expression of ALK gene is biologically plausible.

4.6 PLK inhibitors

Figure 5d represents the top features predictive of responses to PLK inhibitors. For example PPM1A, VPS33A and PLK3 were among the top predictors identified by the MVLR method. High expression of PLK3 and VPS33A genes are positively associated with the sensitivity to PLK inhibitors.

4.7 PDGFRA, PDGFRB, KDR, KIT, FLT3 inhibitors

Figure 5e illustrates the top predictors of responses to sunitinib and sorafenib, which are essentially the multi-target inhibitors (PDGFRA, PDGFRB, KDR, KIT, FLT3). MVLR found FLT3 from the PDGFR FLN as one of the features postively associated with their responses in blood cell line (MONOMAC6). It is also known that PDGFR inhibition leads to AKT activation (Zhang et al., 2007), supporting the identification of the AKT-related FLN in the analysis.

The analysis demonstrated that gene-FLNs-drug response relationships provide biologically meaningful insights. These are well-studied examples serving as proof-of-concept positive controls, for the proposed MVLR method. As demonstrated, MVLR was successfully able to identify predictive feature combinations within a single FLN and from across multiple FLNs. This systematic identification of feature combinations is made possible with a multi-view learning approach defined with structured sparse priors. The priors allowed MVLR to choose first the correct FLNs and secondly identify the feature combinations maximally predictive of drug responses, from the chosen FLNs.

5 Conclusion

We presented a new Bayesian multi-view multi-task linear regression model for identifying features predictive of drug responses in cancer cells. In experiments with a synthetic as well as two publicly available cancer datasets, the proposed method showed improved predictive accuracy compared to state of the art linear regression model in drug response prediction. We also demonstrated the usefulness of our model, combined with prior knowledge for inferring the relationships between FLNs and drug responses. The results showed that the proposed model identified robust and biologically meaningful feature combinations for predicting sensitivity to the well known EGFR, ALK, PLK and PDGFR inhibitors. This way of identifying predictive feature combinations using groups of genes (encoded in the form of FLNs) may enhance our understanding of the action mechanism of drugs and can potentially be used to identify novel combination of predictive biomarkers for designing personalized therapies for cancer patients.

Funding

This work was financially supported by the Academy of Finland (grants 296516 to S.A.K.; grants 272577, 277293 to K.W.; grants 269862, 272437, 279163, 292611 and 295504 to T.A.), Cancer Society of Finland (T.A. and K.W.) and the Sigrid Jusélius Foundation (K.W.). The authors wish to acknowledge Aalto Science-IT project and CSC-IT Center for Science, Finland, for computational resources.

Conflict of Interest: none declared.