Abstract
Motivation
The interpretation of transcriptional dynamics in single-cell data, especially pseudotime estimation, could help understand the transition of gene expression profiles. The recovery of pseudotime increases the temporal resolution of single-cell transcriptional data, but is challenging due to the high variability in gene expression between individual cells. Here, we introduce HopLand, a pseudotime recovery method using continuous Hopfield network to map cells to a Waddington’s epigenetic landscape. It reveals from the single-cell data the combinatorial regulatory interactions among genes that control the dynamic progression through successive cell states.
Results
We applied HopLand to different types of single-cell transcriptomic data. It achieved high accuracies of pseudotime prediction compared with existing methods. Moreover, a kinetic model can be extracted from each dataset. Through the analysis of such a model, we identified key genes and regulatory interactions driving the transition of cell states. Therefore, our method has the potential to generate fundamental insights into cell fate regulation.
Availability and implementation
The MATLAB implementation of HopLand is available at https://github.com/NetLand-NTU/HopLand.
1 Introduction
The traditional time-series gene expression data analyses of a large population of cells, e.g. microarray data, overlook the high variability among individual cells. However, the heterogeneity among single cells contributes to the transcriptional dynamics of a temporal process such as cell differentiation. From the bulk data, it is difficult to separate cells from different developmental stages or identify rare sub-populations of cells. On the contrary, high-throughput single-cell technologies are new and promising to give insights into the heterogeneous distribution and dynamics of individual cells (Buganim et al., 2012).
The ‘pseudotime’ is a quantitative measure of progress through a biological process along which cells are arranged based on their expression profiles. The recovery of pseudotime is made possible by taking advantage of single-cell technologies which provide unprecedented access to the underlying processes and intrinsic functional relationships among cells, and thereby reveals the mechanisms of complex biological systems. For example, using the estimated pseudotimes of single cells from cell differentiation in embryonic development, crucial regulators can be identified by comparing the expression profiles around the branching time points. The recovery of pseudotime can also facilitate cancer studies, such as revealing the progression from normal tissues to malignant lesions.
The intrinsic signals of cell-to-cell variability in the extracted gene expression profiles are often corrupted with technical noises (Stegle et al., 2015), such as distortion caused by overdispersion, outliers and dropout events, which makes the interpretation of biological meaning highly challenging. Although several methods have been developed to recover pseudotimes from single-cell data, there is still room for improvement in the analysis. In these methods, individual cells are projected onto the constructed trajectories or landscape estimated from the transcriptional data. The pseudotime of a cell in the differentiation process is measured by the distance from its projected position on the time line to the given starting point, based on the assumption that cells with similar expression profiles should be gathered together.
Given the prior knowledge of marker genes, the Wanderlust method (Bendall et al., 2014) uses a graph-based trajectory detection algorithm that maps cells onto a 1D developmental trajectory assuming that there is no branch. The pseudotime of a cell is defined by its coordinate on the path. However, Wanderlust fails to report the divergent time points when there are branching processes, and it relies on the prior knowledge of marker genes. Wishbone (Setty et al., 2016) overcomes the defects of Wanderlust by aligning single cells into bifurcating branches. It identifies the bifurcation points and recovers the pseudo-temporal ordering of cells. SCUBA (Marco et al., 2014) uses the temporal information to perform bifurcation analysis of single-cell data to recover the cell lineages. In applications where the time information is not available, it fits a smooth curve passing through the reduced data using the principal curve analysis. The pseudotime of each cell is determined by its mapped position along the principal curve.
Several other methods, e.g. diffusion map (Haghverdi et al., 2015), Monocle (Trapnell et al., 2014) and Topslam (Zwiessele and Lawrence, 2016), which do not require the prior knowledge of marker genes or temporal information, are capable of simulating differentiation processes with multiple lineages. The differentiation path or landscape is visualized by mapping from the high-dimensional space of single-cell gene expression profiles to a lower dimensional space using linear or non-linear dimensionality reduction techniques, such as diffusion map (Coifman et al., 2005), independent component analysis (ICA) (Hyvärinen and Oja, 2000) and Bayesian Gaussian process latent variable model (Bayesian GP-LVM) (Lawrence, 2003; Titsias and Lawrence, 2010).
The diffusion map for single-cell analysis uses diffusion distances to simulate cell differentiation and order cells along the differentiation path while preserving the non-linear structure of data. Monocle builds a minimum spanning tree (MST) to connect cells and the longest path in the MST serves as the main pseudotime axis. One pitfall of Monocle is the use of ICA, a linear dimensionality reduction method, which may not be able to accurately capture the nonlinearity in the biological system. Topslam estimates the pseudotime by mapping the individual cells to the surface of a Waddington’s epigenetic landscape (Waddington, 1957) using the probabilistic dimensionality reduction technique of Bayesian GP-LVM. Following the topography of the probabilistic landscape, the locations of cells reflect their degrees of maturity during the differentiation.
Although the above state-of-the-art methods show promising performance for pseudotime estimation, there are a few concerns. For example, most of the current methods project the high-dimensional data into two or three latent components, and the distances in the latent space are interpreted as biological cell-to-cell variability. This assumption might cause misleading results as the dimensionality reduction methods could be sensitive to noise in gene expression data. Instead of using the distance in the 2D latent space, Topslam has used the topography of the landscape to refine the distance, but the definition of the landscape therein lacks biological meaning. Furthermore, although some of the existing data-driven methods could reveal the dynamics of a specific process, they are confined to the identification of key regulators without the involvement of the system dynamics driven by molecular interactions, e.g. reactions among transcription factors, genes and epigenetic modifiers.
To address these issues, we propose HopLand, a method for pseudotime recovery from single-cell gene expression data by mapping cells to the Waddington’s epigenetic landscape. By inferring the gene–gene interactions from single-cell transcriptional data, we construct a kinetic model, using the continuous Hopfield network (CHN) which is a type of recurrent neural network proposed by John Hopfield in 1984 (Hopfield, 1984). Waddington’s epigenetic landscape can be seen as a non-linear map which visualizes the branching process driven by the interactions among genes in the cells. The performance of HopLand running on single-cell qPCR and RNA-seq datasets was superior to most of the existing methods in most cases. Moreover, a list of key regulators and interactions were identified. This method can be applied broadly to understanding various cellular processes, including embryonic development, stem cell reprogramming and cancer cell proliferation.
2 Materials and methods
We adopted the concept of Waddington’s epigenetic landscape to analyze and visualize the dynamics of the biological processes from a global point of view. The virtual individual cells modeled based on the single-cell gene expression data are to be placed on the surface regions corresponding to their developmental stages. To plot such a landscape, we constructed a kinetic model from transcriptional data, using the CHN to describe the transcriptional regulation. For each target gene, the model associates its change rate with the adaptation of the neurons. Then, the pseudotime can be estimated by calculating the geodesic distance between every two cells in the landscape. Based on the above framework, the HopLand algorithm is designed as follows:
Step 1. Normalize the gene expression data and select differentially expressed genes (by filtering out genes with low variances).
Step 2. Construct the kinetic model by neural network inference from data.
Step 3. Construct the Waddington’s epigenetic landscape based on the kinetic model.
Step 4. Calculate geodesic distances to estimate the pseudotimes of the input single cells.
Algorithm 1 illustrates the steps of HopLand which are further elaborated in the following subsections.
Algorithm 1.
HopLand algorithm
INPUT: Single-cell gene expression data where S is the number of cells and N is the number of genes, and temporal information cellStages (which is not compulsory)
OUTPUT: Kinetic model of Waddington’s epigenetic landscape landModel, and pseudotimes of cells PT
1: ifcellStages is available then
2: Set startPoints as the earliest samples in cellStages;
3: randomInitials = generateRandomInitialStates(startPoints);
4: realTraj = generateTrajectory(D, cellStages);
5: gmmModels = fitMixtureGaussian(D);
6: θ = ParameterOptimization(D, cellStages, randomInitials, realTraj, gmmModels); // Algorithm 2
7: else
8: θ = initializeParam(D);
9: end if
10: landModel = LandscapeConstruct(D, θ); // Algorithm 3
11: PT = PseudotimeRecovery(landModel); // Algorithm 4
12: returnlandModel, PT.
2.1 Data-driven kinetic modeling
2.1.1 Network formulation
CHN consists of a set of N interconnected neurons which update their activation values synchronously or asynchronously. Compared with the original two-state HN proposed by Hopfield himself in 1982 (Hopfield, 1982), CHN uses continuous variables and predicts continuous responses. The discrete Hopfield network has been used to study biological systems with each neuron representing a gene (Lang et al., 2014; Maetschke and Ragan, 2014; Taherian Fard et al., 2016). Gene expression values tend to have continuous input–output relations which cannot be fully characterized by the simplified discrete states of neurons in the two-state HN. Thus we adopted the framework of CHN to model the system dynamics with each neuron corresponding to an individual gene whose adaptation indicates the change of gene expression value.
In the framework of CHN, the gene expression of a cell is characterized by the outputs of the neurons , where N is the number of genes. The inputs to each neuron come from two sources, i.e. the background noise and signals from other neurons. The time evolution of the system is represented by ordinary differential equations (ODEs). The change rate of neuron i is modeled by
| (1) |
| (2) |
where Wij is an entry of the weight matrix of CHN representing the interconnection weight coefficient from neuron j to neuron i, and Ci is an amplifier on the synaptic connections. The external input Ii represents a combination of propagation delays, regulations by other genes not in our model, and noise in transcriptional regulation. δi denotes the degradation rate of gene i. The activation function represents the input–output relationship of a nonlinear amplifier with negligible response time. The activation function is required to be a monotonically increasing function to make the system stable (Zhang et al., 2014). In our model, a sigmoid activation function is used (Equation (3)) which has been used in (Ay and Arnosti, 2011; Chen et al., 2005) to describe the regulatory function of a gene:
| (3) |
In Equation (3), and are the mean and standard deviation of the expression levels of the jth gene in all cells, respectively.
2.1.2 Parameter estimation
There are several parameters in the ODE model of kinetics in Equation (1). To infer these parameters from the data, we propose an optimization method (Algorithm 2), which fits the simulated and observed single-cell data, based on the premise that a realistic model should be able to generate simulated data consistent with the real data.
The consistency between experimental data and simulated data is measured in two aspects. First, the gene expression values where T is the number of time points (or cell stages) in the single-cell data should follow a similar distribution. Normally, it is believed to follow the Gaussian mixture distribution with the mean values of components as the representative gene expression values in different lineages (Kalmar et al., 2009; Rais et al., 2013). The second aspect of consistency lies in the change of a single gene, e.g. down-regulated or up-regulated, along the time evolution of cell states. Thus the objective functions are defined as follows:
| (4) |
| (5) |
where and are the density functions for the observed and simulated expression levels of the ith gene, respectively. σit is the standard deviation of the expression values of gene i at the time point (or cell developmental stage) t. is an average trajectory derived from the simulated trajectories with m time points by simulating the CHN of Equation (1) using the generated initial states.
The gradient descent learning algorithm (Baldi, 1995) is used to optimize the parameters in the CHN. The update of a parameter value at the kth iteration is defined as
| (6) |
| (7) |
where η is the learning rate between 0 and 1, which controls the rate of parameter adjustment. We also iteratively adapt the learning rate according to the Bold Driver technique (Ruder, 2016). The weight matrix is initialized as the Pearson correlation coefficients between samples. To simulate the dynamic trajectories, we use the Euler’s method (the first-order Runge–Kutta) to solve the ODEs with the initial states generated near the given starting points. In each iteration of the gradient descent learning, we calculate the value of the objective function in Equation (4) using the current parameters. At the end, the optimized parameters are selected with the minimum sum of the two objective functions in Equations (4) and (5).
Algorithm 2.
Parameter optimization
INPUT: Single-cell gene expression data D, temporal information cellStages, observed trajectories realTraj, coefficient matrix σ, and Gaussian mixture models gmmModels
OUTPUT: Optimized parameters
Initialization: Set , Ii = 0, Ci = 1, , maxIts = 2000.
1: fordo
2: ;
3: ;
4: ifthen
5: ;
6: else
7: ;
8: end if
9: end for
10: ;
11: return.
2.2 Construction of Waddington’s epigenetic landscape
2.2.1 Energy function
Under certain conditions, the activation values of the units in a CHN undergo a relaxation process such that the network will converge to a stable state in which these activation values will not change anymore. These conditions include that the weight matrix has to be symmetric, and the activation functions must be continuous, bounded, and strictly monotonically increasing, such as a sigmoid function (Equation (3)). The behavior of a CHN system can be described with an energy function (Equation (8)) which is a Lyapunov function:
| (8) |
Based on the essential idea of Waddington’s epigenetic landscape, the differentiation processes follow the paths of losing potential energy determined by the topography of the landscape. Compared with the entry point, the valleys possess relatively lower potentials representing states that are more stable. Here we use the network energy in Equation (8) to quantify the altitude of the landscape, similar to previous works (Lang et al., 2014; Maetschke and Ragan, 2014; Taherian Fard et al., 2016).
2.2.2 Visualizing the landscape
To visualize the cellular dynamics in a landscape whose shape is determined by the energy function in Equation (8), we project the high-dimensional data to a 2D latent space as the xy-plane in the landscape. The non-linear dimensionality reduction method, named Gaussian process latent variable model (GP-LVM), is used to generate the mapping between the original space and the latent space (Lawrence, 2003; Wang et al., 2008). GP-LVM is a probabilistic approach to modeling high-dimensional data in a low-dimensional latent space with a probabilistic model. It has been used for computer vision, biological data analysis, etc. We have recently used this method to process simulated gene expression time-series data in the visualization of landscape (Guo et al., 2017).
Using GP-LVM to reduce the dimensions of the observed data to two dimensions, we create a mapping from the original space to the latent space. Then we generate a 2D grid in the reduced space covering all the cells in order to plot a continuous surface. Since the energy is calculated in the high-dimensional space, we project the grid points back into their original space. The landscape is plotted on the grid data. The pseudocode of the landscape construction method is shown in Algorithm 3.
Algorithm 3.
Landscape construction
INPUT: Single-cell gene expression data D with S samples and N genes, parameter vector θ from Algorithm 2
OUTPUT: A landscape model landModel
1: Generate mapping , where latent variables are encoded in matrix ;
2: Define a 2D grid , where and are the first and second components of samples, and ε is a small positive constant which determines the size of margins around the observed data in the latent space;
3: Perform inverse dimensionality reduction , where , and SGrid is the number of points in Grid;
4: Calculate the energy according to Equation (8);
5: ;
6: returnlandModel.
2.3 Pseudotime estimation
In Waddington’s epigenetic landscape, a single cell with specific gene expression pattern is simplified as a point, hence the time evolution of cell states is defined as the state-transition movement on the landscape which is determined by the topography of the landscape surface. Thus the geodesic distance between two cells can be calculated from the coordinates of the cells on the landscape.
We used the fast marching algorithm (Sethian, 1999) to perform geodesic extraction on a triangulated mesh generated from the single-cell data. Then, using the extracted geodesic distances as the weights of edges connecting the cells, an MST is constructed with the given starting point as the root. The geodesic distances to the starting point are considered proportional to the pseudotimes, setting the pseudotime of the starting point to zero. As such, the pseudotime of the ith cell is estimated as the length of path from the corresponding tree node to the starting point in the MST.
The pseudocode of the pseudotime estimation is shown in Algorithm 4.
Algorithm 4.
Pseudotime recovery
INPUT:landModel, StartPoint
OUTPUT: pseudotimes of cells PT
1: ;
2: ;
3: ;
4: ;
5: ;
6: returnPT.
3 Results
In this section, we evaluate the performance of HopLand by comparing it with 6 state-of-the-art methods, i.e. Monocle, Topslam, Wanderlust, Wishbone, SCUBA and Diffusion map, on 11 testing datasets including a qPCR dataset GUO2010 (Guo et al., 2010), 5 synthetic datasets and 5 scRNA-seq datasets, i.e. DENG2014 using Smart-seq2 (Deng et al., 2014), YAN2013 (Yan et al., 2013) using scRNA-seq method demonstrated in (Tang et al., 2009), ES_MEF using STRT (Islam et al., 2011), LPS (Amit et al., 2009) and HSMM (Trapnell et al., 2014).
3.1 Pseudotimes inferred from synthetic data
We tested HopLand on five synthetic datasets generated by simulating the early development of mouse embryos. Each dataset contains a randomly generated differentiation pattern by angled linear splits in two dimensions (Zwiessele and Lawrence, 2016). We extracted the pseudotimes of the cells using the HopLand algorithm and compared it with other methods (Table 1). An example of synthetic data is shown in a contour plot (Fig. 1), which contains two diverging events splitting cells into four lineages. We mapped the cells onto the landscape surface according to the extracted pseudotimes. The cells at early developmental stages (dark red dots) are located in the bottom middle region of the landscape with high energy, while the four lineages (white or light red dots) rest in valleys. The movement directions of the cells following the shape of the landscape can reflect the irreversible transitions of cell states during the differentiation in the embryonic development.
Table 1.
Accuracies of pseudotime recovery on 5 synthetic datasets and 6 experimental datasets using different pseudotime recovery methods. Pearson correlation coefficient between the predicted and observed times is used to evaluate the result. We compared HopLand with 6 other methods, i.e. Monocle, Wanderlust, Topslam, SCUBA, Wishbone and Diffusion map
| Method | Dataset | HopLand | Wanderlust | Monocle | Topslam | SCUBA | Wishbone | Diffusion map |
|---|---|---|---|---|---|---|---|---|
| Synthetic data (Zwiessele and Lawrence, 2016) | Synthetic data 1 | 0.8997 | 0.9224 | 0.8158 | 0.8872 | 0.9069 | 0.2534 | 0.8441 |
| Synthetic data 2 | 0.9578 | 0.9627 | 0.8202 | 0.9693 | 0.9396 | 0.5089 | 0.9420 | |
| Synthetic data 3 | 0.9159 | 0.7527 | 0.8322 | 0.8840 | 0.7947 | 0.4704 | 0.8365 | |
| Synthetic data 4 | 0.9111 | 0.8988 | 0.9095 | 0.9236 | 0.8772 | 0.2249 | 0.7849 | |
| Synthetic data 5 | 0.9261 | 0.9100 | 0.8988 | 0.9488 | 0.9205 | 0.4498 | 0.9390 | |
| qPCR | GUO2010 (Guo et al., 2010) | 0.9230 | 0.8121 | 0.5796 | 0.9297 | 0.9401 | 0.5476 | 0.4949 |
| scRNA-Seq | DENG2014 (Deng et al., 2014) | 0.8198 | 0.8879 | 0.9177 | 0.9269 | 0.9655 | 0.5115 | 0.8395 |
| YAN2013 (Yan et al., 2013) | 0.9129 | 0.8426 | 0.9421 | 0.9380 | 0.9776 | 0.2876 | 0.8893 | |
| LPS (Amit et al., 2009) | 0.6712 | 0.7902 | 0.8899 | 0.7117 | 0.5307 | 0.6064 | 0.5783 | |
| HSMM (Trapnell et al., 2014) | 0.5716 | 0.2810 | 0.4560 | 0.1890 | 0.0397 | 0.4850 | 0.1386 | |
| ES_MEF (Islam et al., 2011) | 0.8712 | 0.8919 | 0.5166 | 0.9035 | 0.8518 | 0.3952 | 0.8343 | |
| Average of scores | 0.8527 | 0.8138 | 0.7799 | 0.8374 | 0.7885 | 0.4310 | 0.7383 | |
| SD of scores | 0.1216 | 0.1874 | 0.1756 | 0.2256 | 0.2990 | 0.1256 | 0.2432 |
Note: The top three scores in each dataset are in bold.
Fig. 1.
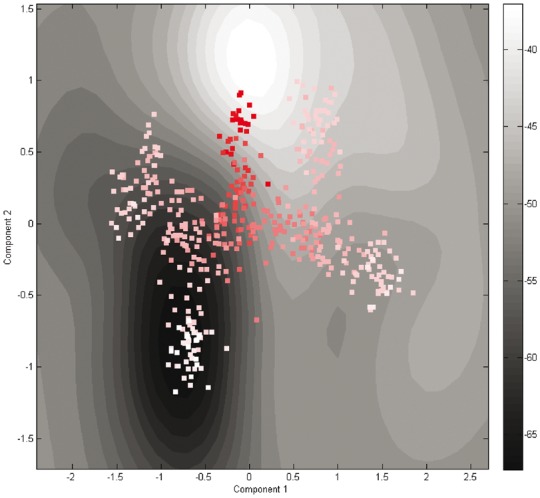
The contour plot of the constructed Waddington’s epigenetic landscape using the third synthetic dataset. The contour lines represent heights in the landscape. The dark areas indicate low energy, and the light regions have high energy. The cells from early stages to late stages are colored from dark red to white
3.2 Single-cell pseudotimes in mouse embryonic development
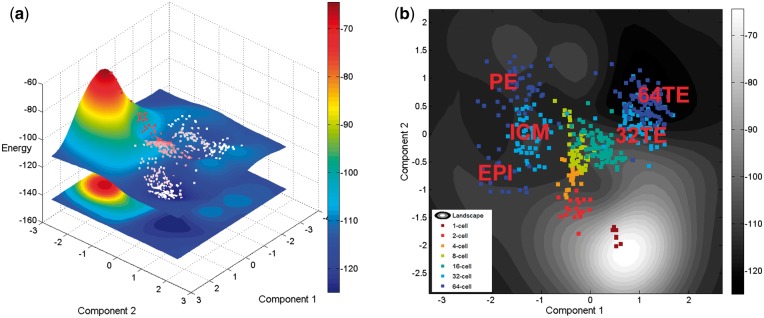
The single-cell dataset of mouse pre-implantation development contains the expression profiles of 438 cells with 48 genes per cell covering the developmental stage from the 1-cell to 64-cell stages (Guo et al., 2010). Two distinct cell lineages, i.e. trophectoderm (TE) and inner cell mass (ICM), emerge from the 16- to 32-cell stages. During the transitions from the 32- to 64-cell stages, another two cell lineages, i.e. primitive endoderm (PE) and epiblast (EPI), are split from ICM. We applied the HopLand algorithm on this dataset and recovered the pseudotimes of the cells.
Analyzing the expression profiles of individual genes, we found that the expression of marker genes follows a mixture of Gaussian distributions (data not shown). The mean values in different components indicate differential expression in separate lineages. We inferred the moments of the Gaussian distributions from the data. The cells from the 1-cell stage were used to generate the training data as the initial states for the simulation of Hopfield network in order to calibrate the model. Then we learned a dynamical model to capture the kinetics in the cell differentiation process of early mouse embryonic development.
After projecting the high-dimensional data into a 2D latent space using GP-LVM, we calculated the energy values according to Equation (8) which are used for the z-axis of the landscape (Fig. 2a). In the contour plot of the landscape (Fig. 2b), two bifurcations are shown corresponding to the cell fate decisions made at the 16- to 32-cell stages (cyan dots to light blue dots) and the 32- to 64-cell stages (light blue dots to dark blue dots). Then, we mapped the expression values of marker genes into the landscape to trace the differentiation process (Fig. 3). The expression profiles of the cells in different branches are separated using the marker genes for different cell lineages (e.g. ICM, TE, PE, and EPI). The result shows that cells belonging to the same stage are located together in the landscape and they follow the developmental orders. In the landscape, the change of the network energy shows a decreasing trend along the differentiation process which confirms our premise that cell differentiation is a process with decreasing energy.
Fig. 2.
(a) Waddington’s epigenetic landscape recovered using HopLand. (b) The contour plot of the constructed Waddington’s epigenetic landscape. The dots are colored according to the developmental stages of the represented cells
Fig. 3.
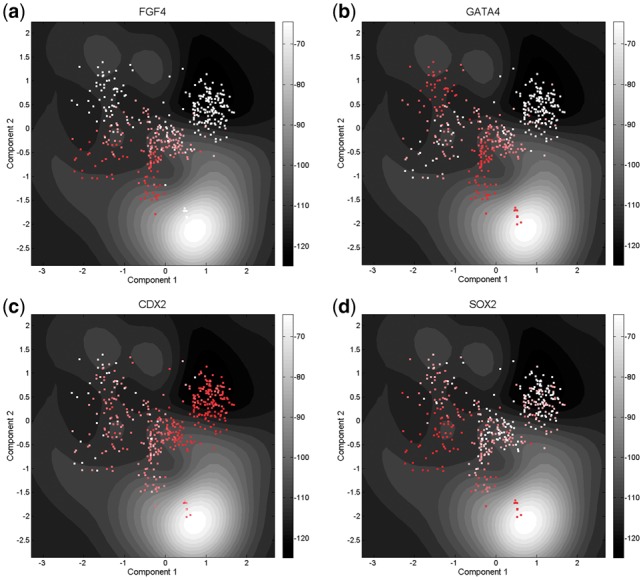
Mapping gene expression values to Waddington’s epigenetic landscape using (a) FGF4, (b) GATA4, (c) CDX2 and (d) SOX2. The value decreases from dark red to white
Using the topography of Waddington’s epigenetic landscape as a correction, we extracted the pseudotime information. The cells were connected in an MST (or a forest of multiple trees) which contains the estimated pseudotimes revealing the transitions of cell states (Fig. 4). We identified a small group of cells (in dark red) isolated from others. It contains cells from the 1-cell stage due to the sparsity of data during the early mouse embryonic development. We also compared HopLand with other methods. The accuracies of pseudotime recovery measured by correlation coefficient between the predicted and observed pseudotimes are listed in Table 1. For each method, we calculated the average and standard deviation of scores in the 11 testing datasets. It shows that HopLand achieves the best performance among all the methods.
Fig. 4.
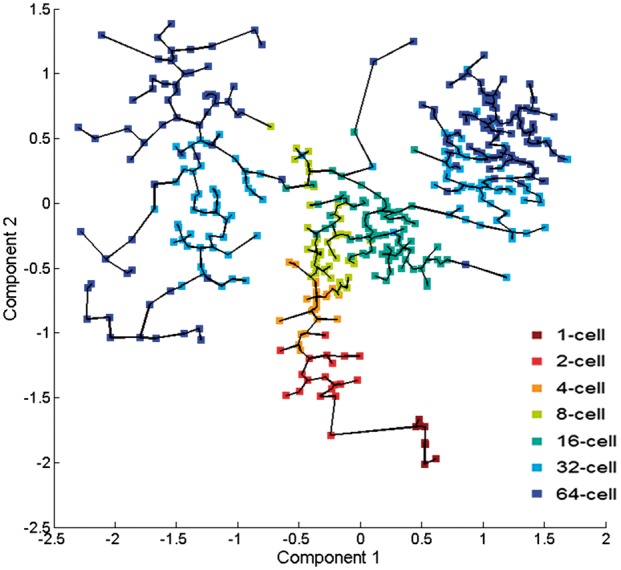
The minimum spanning tree constructed from Waddington’s epigenetic landscape. The dots are colored according to the developmental stages of the cells in the dataset of GUO2010
The weight matrix in the CHN inferred from the dataset of GUO2010 (Fig. 5) contains information about the interactions between genes which can help us find the key regulatory relations and reveal the dynamics of gene expression during cell differentiation. The top 10 significant interactions in the learned weight matrix of the mouse pre-implantation data are listed in Table 2. Seven of the top 10 gene pairs are confirmed. Some of them have direct interactions, e.g. transcriptional regulation. Although we have not yet found evidence for the rest of interactions, some genes from these interactions, e.g. DPPA1, HAND1, are known to be involved in mouse embryonic development. For example, HAND1 is a transcription factor expressed in extra-embryonic mesoderm and trophoblast, and DPPA1 is associated with developmental pluripotency.
Fig. 5.
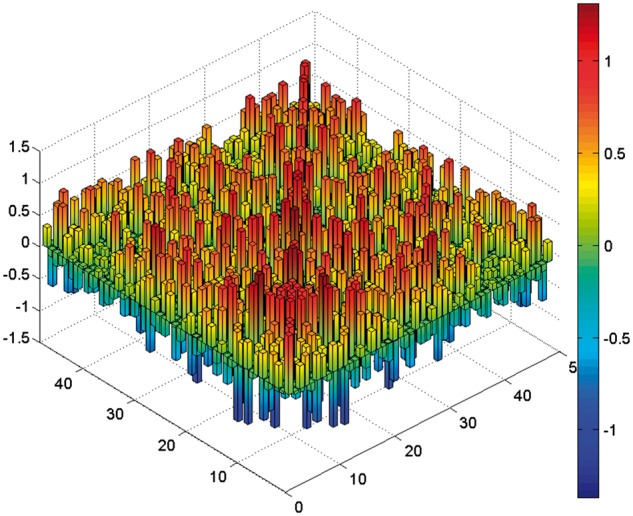
The weight matrix contains N × N interactions of CHN learned from the mouse embryonic early development dataset. N is the number of genes
Table 2.
Top 10 key interactions identified from the weight matrix ranked by the absolute value of the weight in CHN
| Rank | Gene 1 | Gene 2 | References (PMID) |
|---|---|---|---|
| 1 | GATA4 | LCP1 | 18555785, 22083510, 16153702, 14990861 |
| 2 | GATA4 | GATA4 | 15987774 |
| 3 | ATP12A | DPPA1 | – |
| 4 | ESRRB | ESRRB | 16767105, 19136965 |
| 5 | AQP3 | DPPA1 | – |
| 6 | AQP3 | LCP1 | 18700969, 19884255 |
| 7 | HNF4A | LCP1 | 21852396, 15159395 |
| 8 | GRHL1 | HAND1 | – |
| 9 | ESRRB | FGF4 | 26206133 |
| 10 | KLF4 | KLF4 | 18264089, 18358816, 19030024, 18555785 |
From the weight matrix, we also ranked genes by the sum of weights of incident edges and identified a few essential regulators, e.g. FGF4, OCT4, GATA4 and ESRRB, which have been experimentally tested to be essential for early embryonic development (Guo et al., 2010; Li et al., 2005; Martello et al., 2012; Kehat et al., 2001; Sozen et al., 2014). These key factors play important roles in the regulation of embryonic development, cell proliferation, and cell differentiation.
3.3 Testing results on single-cell RNA-seq data of mouse embryonic development
We also compared the HopLand algorithm with other methods on monoallelic mouse pre-implantation embryo RNA-Seq data (Deng et al., 2014). This single-cell RNA-seq dataset comprises transcriptome profiles of 317 cells from zygote to blastocyst and two mature cell types including 11 stages. The constructed landscape is shown in Figure 6. Splitting occurs in both 8- and 16-cell stages. The two developed cell types, fibroblast and adult liver, are separated from the early embryonic developmental lineages. The blastocyst cells (colored in green, cyan and light blue) are clustered together with lower energy than cells of the early lineages. Early blastocyst cells (colored in green) and middle blastocyst cells (colored in cyan) are mixed together but separated from the late-stage cells (colored in light blue) indicating a closer developmental relations. The mature cells (colored in dark blue) located in a valley have low-energy values.
Fig. 6.
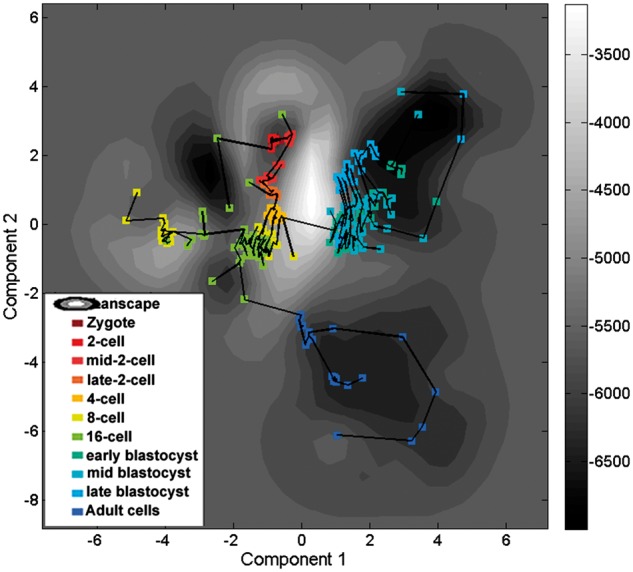
The contour plot of the landscape constructed from the dataset of DENG2014. The cells are connected in a minimum spanning tree
The result of comparing the accuracies of different methods in estimating pseudotimes are shown in Table 1. HopLand is not as good as most other methods for this dataset, partly due to the dearth of time information from the early blastocyst stage to the late blastocyst stage. In addition, due to the lack of specific temporal information between the late blastocyst samples and mature cells, HopLand cannot accurately recover the trajectories from the pre-implantation development to the mature cells. Nevertheless, HopLand can successfully reconstruct the progress from zygote to blastocyst (Fig. 6) achieving a correlation coefficient of 0.91 with real data.
4 Discussion
In this paper, we proposed a novel method, named HopLand, to recover the pseudotimes from single-cell data using CHN-based modeling of Waddington’s epigenetic landscape. The order of cells is determined by the geodesic distances in the landscape. Waddington’s epigenetic landscape constructed from the neural network model serves as a stage on which the progression of cell fate decision is simulated. In addition, our method models the dynamics of gene regulation using the framework of CHN which generates simulation results consistent with the observed data. The constructed model has allowed us to make novel, experimentally testable hypotheses about transcriptional mechanisms that control the cell fate conversions.
Applied to real single-cell gene expression data from different types of biological experiments and compared against other methods, HopLand outperformed most of the other methods in most cases. In addition, our method could also be used to identify key regulators and interactions, which is helpful for the understanding of underlying mechanisms.
The simulation and analysis results have shown that HopLand has some advantages, whereas the other methods fail in certain circumstances. First, our method does not rely on any priori knowledge of key marker genes. Secondly, the non-linear dimensionality reduction method used in HopLand generates a non-linear mapping between the landscape and the phenotype space respecting the non-linear structures of biological systems. Thirdly, HopLand constructs the landscape based on biological interactions between genes that allows to simulate real biological processes.
HopLand is a pseudotime estimation algorithm using dynamical systems modeling. It still needs to address several issues. First, the mathematical modeling approach makes use of several types of information, e.g. the physical time points within the single-cell data, which is not required by some other methods. Nevertheless, our method tries to recover the underlying regulatory mechanisms from the data using the extracted information. The physical time points provide the consecutive updates during the process that is useful for the modeling, but for a dataset without temporal information, HopLand can skip the training process and directly predict the pseudotimes based on a landscape constructed using an initial settings of parameters. Secondly, HopLand is computationally costly compared with other methods. The parameter learning process is time-consuming partially due to the repeated numerical solution of ODEs. Moreover, our method was implemented in MATLAB which is not suitable for intensive computation. In the future, we will implement our method in C/C ++ to speed it up. Thirdly, our algorithm was proposed under the premise that the single-cell transcriptional data cover the critical stages along a biological process. If that is not the case, however, the predicted model might give misleading results. Fourthly, HopLand makes use of GP-LVM to extract a 2D latent space from a high-dimensional space which may suffer from the high technical noise in the single-cell data. Although the recovery of pseudotime relies on not only the reduced components, but also a third value, i.e. network energy, which can alleviate the influence from the noise, we still recommend users to preprocess their data using some single-cell analysis techniques, e.g. PAGODA (Fan et al., 2016), scLVM (Buettner et al., 2015).
The result of HopLand on the qPCR dataset is better than those on the scRNA-seq data. It is probably because the protocols of qPCR make data less prone to the dropout effect (Kalisky and Quake, 2011). Among the 5 RNA-seq datasets, HopLand has unstable performances, which may be partly caused by the different scRNA-seq protocols used in generating the data (Ziegenhain et al., 2016). In the future, We will try to analyze HopLand in different sequencing datasets and make it satisfy specific needs of different types of sequencing technologies.
Funding
This work has been supported by the MOE AcRF Tier 1 grant (RG120/15, 2015-T1-002-094), Ministry of Education, Singapore, and the PhD scholarship from NTU Provost office for the SCE-BII joint PhD program.
References
- Amit I. et al. (2009) Unbiased reconstruction of a mammalian transcriptional network mediating pathogen responses. Science, 326, 257–263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ay A., Arnosti D.N. (2011) Mathematical modeling of gene expression: a guide for the perplexed biologist. Crit. Rev. Biochem. Mol. Biol., 46, 137–151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baldi P. (1995) Gradient descent learning algorithm overview: a general dynamical systems perspective. IEEE Trans. Neural Netw., 6, 182–195. [DOI] [PubMed] [Google Scholar]
- Bendall S.C. et al. (2014) Single-cell trajectory detection uncovers progression and regulatory coordination in human b cell development. Cell, 157, 714–725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buettner F. et al. (2015) Computational analysis of cell-to-cell heterogeneity in single-cell RNA-sequencing data reveals hidden subpopulations of cells. Nat. Biotechnol., 33, 155–160. [DOI] [PubMed] [Google Scholar]
- Buganim Y. et al. (2012) Single-cell expression analyses during cellular reprogramming reveal an early stochastic and a late hierarchic phase. Cell, 150, 1209–1222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen K.C. et al. (2005) A stochastic differential equation model for quantifying transcriptional regulatory network in Saccharomyces cerevisiae. Bioinformatics, 21, 2883–2890. [DOI] [PubMed] [Google Scholar]
- Coifman R.R. et al. (2005) Geometric diffusions as a tool for harmonic analysis and structure definition of data: diffusion maps. Proc. Natl. Acad. Sci. USA, 102, 7426–7431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng Q. et al. (2014) Single-cell RNA-Seq reveals dynamic, random monoallelic gene expression in mammalian cells. Science, 343, 193–196. [DOI] [PubMed] [Google Scholar]
- Fan J. et al. (2016) Characterizing transcriptional heterogeneity through pathway and gene set overdispersion analysis. Nat. Methods, 13, 241–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo G. et al. (2010) Resolution of cell fate decisions revealed by single-cell gene expression analysis from zygote to blastocyst. Dev. Cell, 18, 675–685. [DOI] [PubMed] [Google Scholar]
- Guo J. et al. (2017) NetLand: quantitative modeling and visualiza-tion of Waddington’s epigenetic landscape using probabilistic potential. Bioinformatics, DOI: 10.1093/bioinformatics/btx022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haghverdi L. et al. (2015) Diffusion maps for high-dimensional single-cell analysis of differentiation data. Bioinformatics, 31, 2989–2998. [DOI] [PubMed] [Google Scholar]
- Hopfield J.J. (1982) Neural networks and physical systems with emergent collective computational abilities. Proc. Natl Acad. Sci. USA, 79, 2554–2558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hopfield J.J. (1984) Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. USA, 81, 3088–3092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyvärinen A., Oja E. (2000) Independent component analysis: algorithms and applications. Neural Netw., 13, 411–430. [DOI] [PubMed] [Google Scholar]
- Islam S. et al. (2011) Characterization of the single-cell transcriptional landscape by highly multiplex rna-seq. Genome Res., 21, 1160–1167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalisky T., Quake S.R. (2011) Single-cell genomics. Nat. Methods, 8, 311–314. [DOI] [PubMed] [Google Scholar]
- Kalmar T. et al. (2009) Regulated fluctuations in nanog expression mediate cell fate decisions in embryonic stem cells. PLoS Biol., 7, e1000149.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kehat I. et al. (2001) Human embryonic stem cells can differentiate into myocytes with structural and functional properties of cardiomyocytes. J. Clin. Invest,, 108, 407–414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lang A.H. et al. (2014) Epigenetic landscapes explain partially reprogrammed cells and identify key reprogramming genes. PLoS Comput. Biol., 10, e1003734.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawrence N.D. (2003) Gaussian process latent variable models for visualisation of high dimensional data. Proc. Advances in Neural Information Processing Systems (NIPS), 329–336. [Google Scholar]
- Li Y. et al. (2005) Murine embryonic stem cell differentiation is promoted by socs-3 and inhibited by the zinc finger transcription factor klf4. Blood, 105, 635–637. [DOI] [PubMed] [Google Scholar]
- Maetschke S.R., Ragan M.A. (2014) Characterizing cancer subtypes as attractors of Hopfield networks. Bioinformatics, 30, 1273–1279. [DOI] [PubMed] [Google Scholar]
- Marco E. et al. (2014) Bifurcation analysis of single-cell gene expression data reveals epigenetic landscape. Proc. Natl. Acad. Sci., 111, E5643–E5650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martello G. et al. (2012) Esrrb is a pivotal target of the gsk3/tcf3 axis regulating embryonic stem cell self-renewal. Cell Stem Cell, 11, 491–504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rais Y. et al. (2013) Deterministic direct reprogramming of somatic cells to pluripotency. Nature, 502, 65–70. [DOI] [PubMed] [Google Scholar]
- Ruder S. (2016). An overview of gradient descent optimization algorithms. Web Page, .1–12.
- Sethian J. (1999) Fast marching methods. SIAM Rev., 41, 199–235. [Google Scholar]
- Setty M. et al. (2016) Wishbone identifies bifurcating developmental trajectories from single-cell data. Nat. Biotechnol., 34, 637–645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sozen B. et al. (2014) Cell fate regulation during preimplantation development: a view of adhesion-linked molecular interactions. Dev. Biol., 395, 73–83. [DOI] [PubMed] [Google Scholar]
- Stegle O. et al. (2015) Computational and analytical challenges in single-cell transcriptomics. Nat. Rev. Genet., 16, 133–145. [DOI] [PubMed] [Google Scholar]
- Taherian Fard A. et al. (2016) Not just a colourful metaphor: modelling the landscape of cellular development using Hopfield networks. npj Syst. Biol. Appl., 2, 16001.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang F. et al. (2009) mRNA-Seq whole-transcriptome analysis of a single cell. Nat. Methods, 6, 377–382. [DOI] [PubMed] [Google Scholar]
- Titsias M.K., Lawrence N.D. (2010) Bayesian gaussian process latent variable model. AISTATS, 9, 844–851. [Google Scholar]
- Trapnell C. et al. (2014) The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol., 32, 381–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waddington C.H. (1957). The strategy of the genes: a discussion of some aspects of theoretical biology. With an appendix by H. Kacser. Allens & Unwin: London, UK. [Google Scholar]
- Wang J.M. et al. (2008) Gaussian process dynamical models for human motion. IEEE Trans. Pattern Anal. Mach. Intell., 30, 283–298. [DOI] [PubMed] [Google Scholar]
- Yan L. et al. (2013) Single-cell RNA-seq profiling of human preimplantation embryos and embryonic stem cells. Nat. Struct. Mol. Biol., 20, 1131–1139. [DOI] [PubMed] [Google Scholar]
- Zhang H. et al. (2014) A comprehensive review of stability analysis of continuous-time recurrent neural networks. IEEE Trans. Neural Netw. Learn. Syst., 25, 1229–1262. [Google Scholar]
- Ziegenhain C. et al. (2017). Comparative analysis of single-cell RNA sequencing methods. Molecular Cell, 65, 631–643. [DOI] [PubMed]
- Zwiessele M., Lawrence N.D. (2016). Topslam: Waddington landscape recovery for single cell experiments. bioRxiv, p. 057778.