Removal of batch effects using distribution-matching residual networks

Abstract

Motivation

Sources of variability in experimentally derived data include measurement error in addition to the physical phenomena of interest. This measurement error is a combination of systematic components, originating from the measuring instrument and random measurement errors. Several novel biological technologies, such as mass cytometry and single-cell RNA-seq (scRNA-seq), are plagued with systematic errors that may severely affect statistical analysis if the data are not properly calibrated.

Results

We propose a novel deep learning approach for removing systematic batch effects. Our method is based on a residual neural network, trained to minimize the Maximum Mean Discrepancy between the multivariate distributions of two replicates, measured in different batches. We apply our method to mass cytometry and scRNA-seq datasets, and demonstrate that it effectively attenuates batch effects.

Availability and Implementation

our codes and data are publicly available at https://github.com/ushaham/BatchEffectRemoval.git

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Biological data are affected by the conditions of the measuring instruments. For example, two distributions of multidimensional molecular data generated from two identical blood drops of the same person (technical replicates) in two experimental batches, may deviate from each other due to variation in conditions between batches. The term batch effects, often used in the biological community, describes a situation where subsets (batches) of the measurements significantly differ in distribution, due to irrelevant instrument-related factors (Leek et al., 2010). Batch effects introduce systematic error, which may cause statistical analysis to produce spurious results and/or obfuscate the signal of interest. Typically, the systematic effect of varying instrument conditions on the measurements depends on many unknown factors, whose impact on the difference between the observed and underlying true signal cannot be modeled.

For example, CyTOF, a mass cytometry technique for measuring multiple protein levels in many cells of a biological specimen, is known to incur batch effects. When replicate blood specimens from the same patient are measured on a CyTOF machine in different batches (e.g. different days), they might differ noticeably in the distribution of cells in the multivariate protein space. In order to run a valid and effective statistical analysis on the data, a calibration process has to be carried out, to account for the effect of the difference in instrument conditions on the measurements.

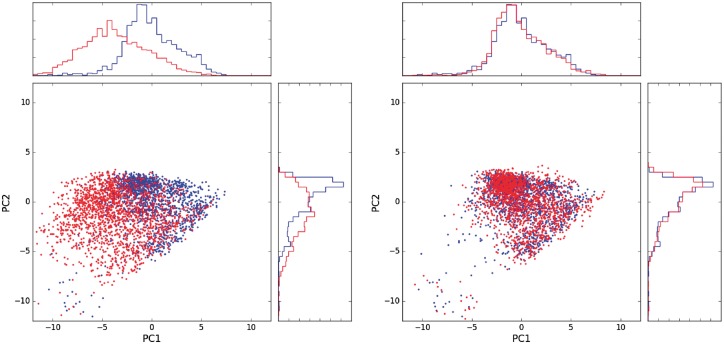
In this article, we consider cases where replicates differ in distribution, due to batch effects. By designating one replicate to be the source sample and the other to be the target sample, we propose a deep learning approach to learn a map that calibrates the distribution of the source sample to match that of the target (The term sample is used with different meanings in the biological and statistical communities. Both meanings are used in this article, however, usage should be clear from context.). Our proposed approach is designed for data where the difference between these source and target distributions is moderate, so that the map that calibrates them is close to the identity map; such an assumption is fairly realistic in many situations. An example of the problem and the output of our proposed method is depicted in Figure 1. A short demo movie is available at https://www.youtube.com/watch?v = Lqya9WDkZ60. To evaluate the effectiveness of our proposed approach, we employ it to analyze mass cytometry (CyTOF) and single-cell RNA-seq (scRNA-seq), and demonstrate that it strongly attenuates the batch effect. We also demonstrate that it outperforms other popular approaches for batch effect removal. To the best of our knowledge, prior to this work, neural nets have never been applied to batch effect removal.

Fig. 1.

Calibration of CyTOF data. Projection of the source (red) and target (blue) samples on the first two principal components of the target data. Left: before calibration. Right: after calibration

The remainder of this article is organized as follows: in Section 2, we give a brief review of Maximum Mean Discrepancy (MMD) and Residual Nets, on which our approach is based. The calibration learning problem is defined in Section 3, where we also describe our proposed approach. Experimental results on CyTOF and scRNA-seq measurements are reported in Section 4. In Section 5, we review some related works. Section 6 concludes the manuscript. Additional experimental results and discussion appear in the Appendix.

2 Materials and methods

2.1 Maximum mean discrepancy

MMD (Gretton et al., 2006, 2012) is a measure for distance between two probability distributions p, q. It is defined with respect to a function class $\mathcal{F}$ by

$$\text{MMD}(\mathcal{F},p,q)\equiv \underset{f\in \mathcal{F}}{\sup }({\mathbb{E}}_{x\sim p}f(x)-{\mathbb{E}}_{x\sim q}f(x)).$$

When $\mathcal{F}$ is a reproducing kernel Hilbert space with kernel k, the $\text{MMD}$ can be written as the distance between the mean embeddings of p and q

$${\text{MMD}}^2(\mathcal{F},p,q)=\left|\right|{\mu }_p-{\mu }_q|{|}_{\mathcal{F}}^2,$$ (1)

where ${\mu }_p(t)={\mathbb{E}}_{x\sim p}k(x,t)$. Equation (1) can be written as

$${\text{MMD}}^2(\mathcal{F},p,q)={\mathbb{E}}_{x,x\prime \sim p}k(x,x\prime )-2{\mathbb{E}}_{x\sim p,y \sim q}k(x,y)+{\mathbb{E}}_{y,y\prime \sim q}k(y,y\prime ),$$ (2)

where x and $x\prime$ are independent, and so are y and $y\prime$. Importantly, if k is a universal kernel, then $\text{MMD}(\mathcal{F},p,q)=0$ iff p = q. In practice, the distributions p, q are unknown, and instead we are given observations $X=\{x_1,\dots x_n\},Y=\{y_1,\dots y_m\}$, so that the (biased) sample version of (2) becomes

$${\text{MMD}}^2(\mathcal{F},X,Y)=\frac{1}{n^2}{\sum }_{x_i,x_j\in X}k(x_i,x_j)$$

$$-\frac{2}{nm}{\sum }_{x_i\in X,y_j\in Y}k(x_i,y_j)$$

$$+\frac{1}{m^2}{\sum }_{y_i,y_j\in Y}k(y_i,y_j).$$

MMD was originally proposed as a non-parametric two sample test, and has since been widely used in various applications. Li et al. (2015) and Dziugaite et al. (2015), use it as a loss function for neural net; here we adopt this direction to tackle the calibration problem, as discussed in Section 3.

2.2 Residual nets

Residual neural networks (ResNets), proposed by He et al. (2016a) and improved in (He et al., 2016b), is a recently introduced class of very deep neural nets, mostly used for image recognition tasks. ResNets are typically formed by concatenation of many blocks, where each block receives an input x (the output of the previous block) and computes output $y=x+\delta (x)$, where $\delta (x)$ is the output of a small neural net, which usually consists of two sequences of batch normalization (Ioffe and Szegedy, 2015), weight layers and non-linearity activations, as depicted in Figure 2.

Fig. 2.

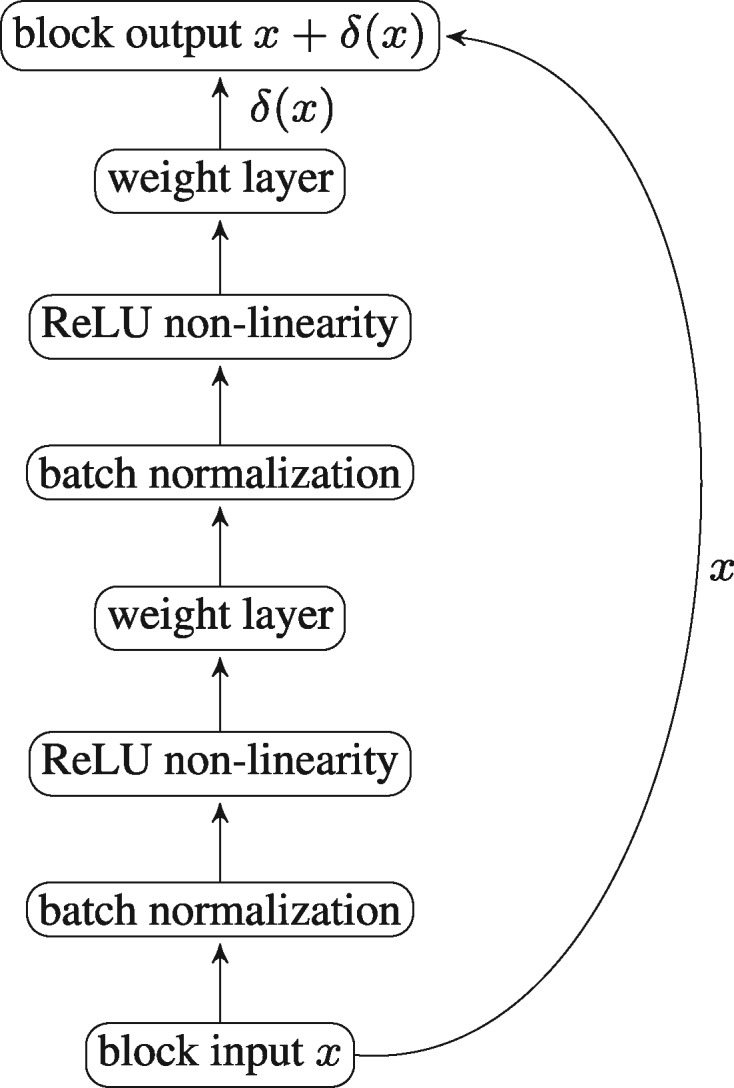
A typical ResNet block

It was empirically shown by He et al. (2016a) that the performance of very deep convolutional nets without shortcut connections deteriorates beyond some depth, while ResNets can grow very deep with increasing performance. In a subsequent work, He et al. (2016b) showed that the gradient backpropagation in ResNets is improved, by avoiding exploding or vanishing gradients, comparing to networks without shortcut connections; this allows for more successful optimization, regardless of the depth. Li et al. (2016) showed that ResNets with shortcut connections of depth 2 are easy to train, while deeper shortcut connections make the loss surface more flat. In addition, they argue that initializing ResNets with weights close to zero performs better than other standard initialization techniques.

Since a ResNet block consists of a residual term and an identity term, it can easily learn functions close to the identity function, when the weights are initialized close to zero, which is shown to be a valuable property for deep neural nets (Hardt and Ma, 2016). In our case, the ability to efficiently learn functions which are close to the identity is appealing from an additional reason: we are interested in performing calibration between replicate samples whose multivariate distributions are close to each other; to calibrate the samples, we are therefore interested in learning a map which is close to the identity map. A ResNet structure is hence a convenient tool to learn such a map.

3 Approach

Formally, we consider the following learning problem: let ${\mathcal{D}}_1,{\mathcal{D}}_2$ be two distributions on ${\mathbb{ℝ}}^{\mathrm{d}}$, such that there exists a continuous map $\psi :{\mathbb{ℝ}}^{\mathrm{d}}\to {\mathbb{ℝ}}^{\mathrm{d}}$ so that if $X\sim {\mathcal{D}}_1$ then $\psi (X)\sim {\mathcal{D}}_2$. We also assume that ψ is a small perturbation of the identity map.

We are given two finite samples $\{x_1,\dots ,x_n\},\{y_1,\dots ,y_m\}$ from ${\mathcal{D}}_1,{\mathcal{D}}_2$, respectively. The goal is to learn a map $\widehat{\psi }:{ℝ}^{\mathrm{d}}\to {ℝ}^{\mathrm{d}}$ so that $\{\widehat{\psi }(x_1),\dots ,\widehat{\psi }(x_n)\}$ is likely to be a sample from ${\mathcal{D}}_2$.

Since we assume that ψ is close to the identity, it is convenient to express it as $\psi (x)=x+\delta (x)$, where $\delta (x)$ is small, so that the connection to ResNets blocks becomes apparent.

Our proposed solution, which we term MMD-ResNet is therefore a ResNet. The input to the net is a sample $\{x_1,\dots x_n\}$ of points in ${ℝ}^{\mathrm{d}}$, to which we refer as the source sample; the net is trained to learn a map of the source sample, to make it similar in distribution to a target sample $\{y_1,\dots ,y_m\}$, also in ${ℝ}^{\mathrm{d}}$. Specifically, we train the net with the following loss function

$$L(w)=\sqrt{{\text{MMD}}^2(\{\widehat{\psi }(x_1),\dots \widehat{\psi }(x_n)\},\{y_1,\dots y_m\})},$$

where $\widehat{\psi }$ is the map computed by the network, and depends on the network parameters w. We train the net in a stochastic mode, so that in fact the MMD is computed only on mini-batches from both samples, and not on the entire samples.

4 Results

In this section, we report experimental results on biological data obtained using two types of high-throughput technologies: CyTOF and scRNA-seq. CyTOF is a mass cytometry technology that allows simultaneous measurements of multiple protein markers in each cell of a specimen (e.g. a blood sample), consisting of ${10}^3-{10}^6$ cells (Spitzer and Nolan, 2016). scRNA-seq is a sequencing technology that allows to simultaneously measure mRNA expression levels of all genes in thousands of single cells.

4.1 Technical details

All MMD-ResNets were trained using RMSprop (Tieleman and Hinton, 2012), using the Keras default hyper-parameter setting; a penalty of 0.01 on the ${\ell }_2$ norm of the network weights was added to the loss for regularization. We used mini-batches of size 1000 from both the source and target samples. A subset 10% of the training data was held out for validation, to determine when to stop the training.

Any fixed scale makes a Gaussian kernel sensitive to similarities in a certain range; to increase the sensitivity of our kernel to a wider range, the kernel we used is a sum of three Gaussian kernels with different scales

$$k(x,y)={\sum }_i\hspace{0.17em}\text{exp}\hspace{0.17em}\left(\frac{\left|\right|x-y|{|}^2}{{\sigma }_i^2}\right).$$

We chose the σ_is to be $\frac{m}{2},m,2m$, where m is the median of the average distance between a point in the target sample to its nearest 25 neighbors, a popular practice in kernel-based methods.

4.2 Calibration of CyTOF data

Mass cytometry uses a set of antibodies, each of which is conjugated to a unique heavy ion and binds to a different cellular protein. Cells are then individually nebulized and subjected to mass spectrometry. Protein abundance is indirectly observed from the signal intensity at each protein’s associated ions’ mass to charge ratio. Multiple specimens can be measured in the same batch by using barcoding with additional ions to record the origin of each specimen (Spitzer and Nolan, 2016). A CyTOF batch contains measurements of numerous cells from a few specimens, and each batch is affected by systematic errors (Finck et al., 2013).

4.2.1. Data

Our calibration experiments were performed on data collected at Yale New Haven Hospital; Peripheral Blood Mononuclear Cells (PBMCs) were collected from two MS patients at baseline and 90 days after Gilenya treatment and cryopreserved. At the end of the study, PBMC were thawed in two batches (on two different days) and incubated with or without PMA + ionomycin (using a robotic platform). PMA/ionomycin stimulated and unstimulated samples were barcoded using Cell-ID (Fluidigm), then pooled and labeled for different markers with mass cytometry antibodies and analyzed on CyTOF III Helios. Here we analyzed a subset of eight unstimulated samples: 2 patients × 2 conditions × 2 days. From this collection, we assembled four source-target pairs, where for each patient and biological condition, the sample from day 1 was considered as source and the one from day 2 as target. All samples were of dimension d = 25 and contained 1800–5000 cells. A full specification of the markers is given in Supplementary Section S1

4.2.2. Pre-processing

All samples were manually filtered by a human expert to remove debris and dead cells. Log transformation, a standard practice for CyTOF, was applied to the data. In addition, a bead-normalization procedure was applied to the data; this is a current practice for normalizing CyTOF data (Finck et al., 2013). Yet, our results demonstrate that the samples clearly differ in distribution, despite the fact that they were normalized.

A typical CyTOF sample contains large proportions of zero values (up to 40% sometimes) which occur due to instabilities of the CyTOF instrument and usually do not reflect biological phenomenon. As leaving the zero values in place might incur difficulties to calibrate the data, a cleaning procedure has to be carried out. In our experiments, we collected the cells with non or very few zero values and used them to train a denoising autoencoder (DAE; Vincent et al., 2008). Specifically, the DAE was trained to reconstruct clean cells x from noisy inputs $\tilde{x}$, where $\tilde{x}$ was obtained from x by multiplying each entry of x by an independent Bernoulli random variable with parameter = 0.8. The DAE contained two hidden layers, each of 25 ReLU units; the output units were linear. As with the MMD-ResNets, the DAEs were also trained using RMSprop, and ${\ell }_2$ penalization of the weights was added to their loss. Once the DAE was trained, we passed the source and target samples through it, and used their reconstructions, which did not contain zeros, for the calibration. In all our CyTOF experiments, source and target refer to the denoised version of these samples. Lastly, as a standard practice, in each of the experiments the input to the net (i.e. the source sample) was standardized to have zero mean and unit variance in each dimension. The parameters of the standardization were then also applied to the target sample.

4.2.3. CyTOF calibration

We trained a MMD-ResNet on each of the four source-target pairs. All nets had identical architecture, consisting of three blocks, where each block is as in Figure 2. Each of the weight matrices was of size 25 × 25. The net weights were initialized by sampling from a $\mathcal{N}(0,{10}^{-4})$ distribution. The projection of the target and source data onto the first two PCs of the target sample in a representative source-target pair is shown in Figure 1. The plots of the remaining three pairs are presented in Supplementary Figure S7. In the left plot, it is apparent that before calibration, the source sample (red) differs in distribution from the target sample (blue). After calibration (right plot), the gap between the source and the target distributions decreases significantly. The MMD between the source and target before and after calibration in each of the four pairs is shown in Table 1. In addition, we also report the MMD obtained using a multi-layer perceptron (MLP) MMD-net with a similar architecture to the ResNet, except without shortcut connections. The MLP was initialized in a standard fashion (Glorot and Bengio, 2010). A corresponding table, where the samples from day 2 are used as source and from day 1 as target is provided in Supplementary Section S2. As can be seen, the calibrated data are significantly closer to the target data than the original source data. The ResNet achieves similar performance to the MLP on two pairs and outperforms the MLP on the other two. In Section 4.2.4, we will show that ResNet architecture is in fact a crucial element in our approach, for a more important reason.

Table 1.

CyTOF calibration experiment: MMD values between random batches of size 1000 from the source and target samples, before and after calibration on each of the four source-target pairs (patient1-baseline, patient2-baseline, patient1-treatment, patient2-treatment)

Method\pair	pa.1 base.	pa.2 base.	pa.1 treat.	pa.2 treat.
no calibration	0.62	0.56	0.59	0.65
MLP calibration	0.20	0.16	0.28	0.22
ResNet calibration	0.19	0.15	0.20	0.18
MMD(target,target)	0.12	0.12	0.12	0.13

Note: The MMD between two random batches of the target sample is provided as reference in the bottom row. The calibrated data is significantly closer in MMD to the target sample. The presented values are averages, based on sampling of five random subsets of size 1000; all standard deviations were at most 0.01.

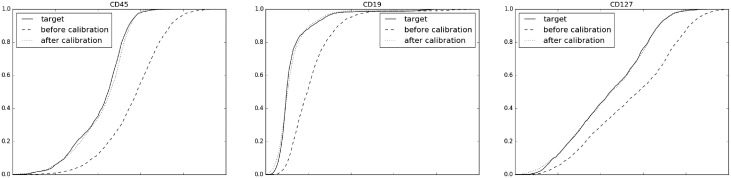
On a per-marker level, Figure 3 shows the empirical cumulative distribution functions of the first three markers in the source sample before and after the calibration, in comparison to the target sample. The plots for the next three markers are shown in Supplementary Figure S8. In all cases, as well as on the remaining markers that are not shown here, the calibrated source curves are substantially closer to the target than the curves before calibration.

Fig. 3.

Quality of calibration in terms of the marginal distribution of each marker. Empirical cumulative distribution functions of the first three markers in the CyTOF calibration experiment. In each plot the full, dashed and dotted curves corresponds to the target, source and calibrated source samples, respectively. In each marker the full and dotted curves are substantially closer than the full and dashed curves

4.2.4. Biological validation and the importance of shortcut connections

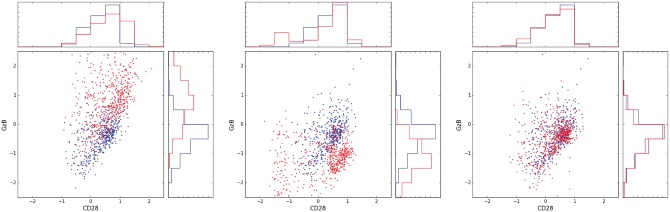
To biologically assess the quality of the calibration and further justify our choice of ResNet architecture, we inspect the effect of calibration not only at a global level across all types of cell sub-populations, but also zoom in to a specific cell sub-population. Specifically, we focus here on CD8 + T-cells, also known as Killer T-cells, in the 2D space of the markers CD28 and GzB. In each sample, we identified the CD8 + T-cells sub-population based on manual gating, performed by a human expert. Figure 4 shows the CD8 + T-cells of the source and target samples from the baseline samples of patient 2 (pa.2 base.), before calibration, after calibration using a ResNet and after calibration using a similar net without shortcut connections (MLP) (The plots for the remaining three source-target pairs are shown in Supplementary Fig. S9.). As can be seen, when the calibration is performed by a net without shortcut connections, the CD8 + T-cells sub-population is not mapped to the same region as its target sample counterpart. However, with ResNet it is mapped appropriately.

Fig. 4.

Calibration of CyTOF data: CD8 + T-cells cells (red) and target (blue) samples in the (CD28, GzB) plane. Left: before calibration. Center: calibration using MLP. Right, calibration using ResNet

Observe that in Table 1, for this patient, the MMD score between the target sample and the ResNet-calibrated source sample of this patient is very similar to the MMD score between the target sample and the MLP-calibrated source sample. We therefore see that in order to achieve good calibration, it does not suffice that the calibrated source sample will be close in MMD to the target sample. It is also crucial that the calibration map will be close to the identity. Nets without shortcut connections can clearly compute maps which are close to the identity. However, when trained to minimize MMD, the resulting map is not necessarily close to the identity, as there might be different maps that yield low MMD, despite being far from the identity, and are easier to reach from random initialization by optimization. Therefore, to obtain a map that is close to the identity, ResNet is a more appropriate tool, if not crucial, comparing to nets without shortcut connections.

4.2.5. Comparison to linear methods

In this section, we compare the quality of calibration of our MMD-ResNet to three popular techniques for removal of batch effects. The simplest and most common (Nygaard et al., 2016) adjustment is zero centering, i.e. substracting from any value the global mean of its batch; see, for example the batchadjust command in the R package PAMR (Hastie et al., 2015). The first linear method that we consider here is calibration by matching each markerng mean and variance in the source sample to the corresponding values in target sample. The second common practice is to obtain the principal components of the data, and remove the components that are most correlated with the batch index (Liu and Markatou, 2016). The third technique is Combat (Johnson et al., 2007), a standard tool for batch effect removal, mostly in gene expression data. Combat performs linear adjustments, where the corrections are based on Bayesian estimation. We used the Combat implementation of the R package SVA (Leek et al., 2012).

Table 2 compares the performances of our approach and the three approaches mentioned earlier in terms of MMD scores. As can be seen, the MMD-ResNet achieves better MMD than the ones obtained by the other methods.

Table 2.

CyTOF calibration: comparison of calibration using (i) matching mean and variance of each marker, (ii) PCA, (iii) Combat and (iv) MMD-ResNet

Method\pair	pa.1 base.	pa.2 base.	pa.1 treat.	pa.2 treat.
mean, variance	0.27 ± 0.02	0.26 ± 0.01	0.29 ± 0.01	0.29 ± 0.02
PCA	0.40 ± 0.02	0.40 ± 0.01	0.36 ± 0.01	0.36 ± 0.01
Combat	0.27 ± 0.01	0.25 ± 0.01	0.29 ± 0.01	0.29 ± 0.01
MMD-ResNet	0.19 ± 0.01	0.15 ± 0.01	0.20 ± 0.01	0.18 ± 0.01

Note: The table entries are average MMD between the target sample and the calibrated source sample, based on five random subsets of size 1000.

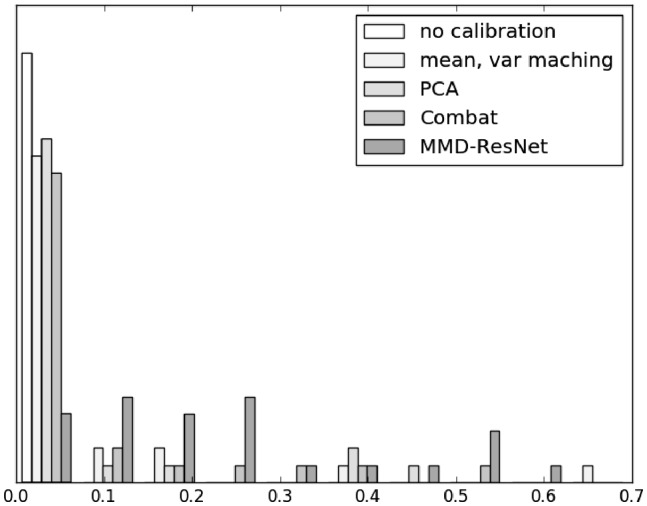
In addition, we also compared the methods using Kolmogorov-Smirnov test for the marginal distribution of each marker. Figure 5 shows histograms of the 25 p-values of the test on the treatment samples of patient 2 (pa.2 treat), comparing the calibrated data of each method to the corresponding target distribution. The greater P-values of the MMD-ResNet relative to the other calibration methods indicate a superiority in removing batch effects.

Fig. 5.

Histograms of the 25 P-values of Kolmogorov-Smirnov tests, comparing the distributions of the calibrated data with the target distribution of each of the 25 markers

4.3 Calibration of scRNA-seq data

Drop-seq (Macosko et al., 2015) is a novel technique for simultaneous measurement of single-cell mRNA expression levels of all genes of numerous individual cells. Unlike traditional single cell sequencing methods, which can only sequence up to hundreds or a few thousands of cells (Picelli et al., 2013), (Jaitin et al., 2014), Drop-seq enables researchers to analyze many thousands of cells in parallel, thus offers a better understanding of complex cell types of cellular states.

However, even with several thousands of cells (∼5000) in each run, only less than half of the cells typically contain enough transcribed genes, that can be used for statistical analysis. As the number of cells in a single run is not sufficient for studying very complicated tissues, one needs to perform multiple runs, in several batches, so that the cumulative number of cells is a good representation of the distribution of cell populations. This process may create batch effects, which need to be removed.

In Shekhar et al. (2016), seven replicates from two batches were sequenced to study bipolar cells of mouse retina. Applying their approach to clean and filter the data, we obtained a dataset of 13 166 genes, each expressed in more than 30 cells and has a total transcript count of more than 60, and 27 499 cells, each of which has more than 500 expressed genes. Data were then normalized such that counts in each cell sum to 10 000, followed by a $\text{log}\hspace{0.17em}$ transform of (count + 1). Shekhar et al. (2016) estimated that most of the signal is captured by the leading 37 principal components and used them for downstream analysis. We therefore projected the 13 166 dimensional data onto the subspace of the leading 37 principal components and used this reduced data for our calibration experiment.

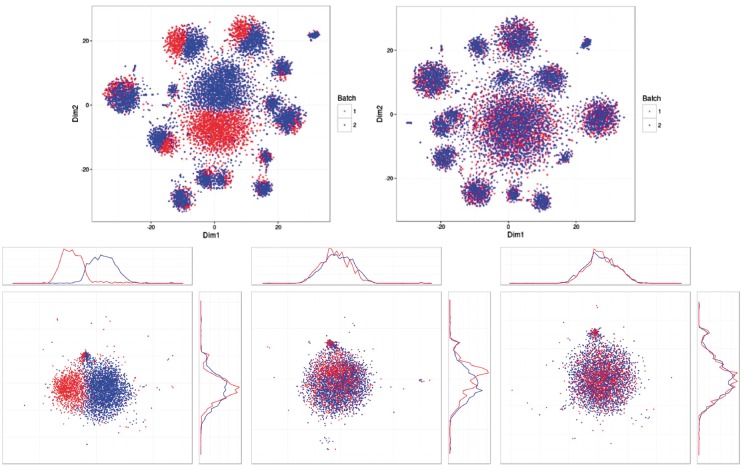
We arbitrarily chose batch 1 to be the target and the one from batch 2 to be the source, and used them to train a MMD-ResNet. The net had three blocks, where each block is as in Figure 2. In each block, the lower weight matrix was of size 37 × 50 and the upper one was of size 50 × 37. The net weights were initialized by sampling from a $\mathcal{N}(0,{10}^{-4})$ distribution. t-SNE plots of the data before and after calibration are presented in the top part of Figure 6, which shows that after calibration, clusters from the source batches are mapped onto their target batch counterparts.

Fig. 6.

Calibration of scRNA-seq. Top: t-SNE plots before (left) and after (right) calibration using MMD-ResNet. Bottom: Calibration of cells with high expression of Prkca. t-SNE plots before calibration (left), after calibration using Combat (middle) and MMD-ResNet (right)

Table 3 shows the MMD distance between the target and the source, calibrated by MMD-ResNet, as well as the MMD distances between the target and the source, calibrated by each of the three linear calibration methods mentioned in Section 4.2.5. Combat and the mean-variance matching were applied on the full set of 13 166 genes, after normalization as in (Shekhar et al., 2016), rather than on the projection of the data onto the leading 37 principal components, which was the input to the MMD-ResNet on this dataset. As can be seen, MMD-ResNet outperforms all other methods in terms of MMD.

Table 3.

RNA calibration: comparison of calibration using (i) matching mean and variance of each gene, (ii) PCA, (iii) Combat and (iv) MMD-ResNet

Before calib.	Mean, variance	PCA	Combat	ResNet	Target–target
0.43	0.25	0.21	0.15	0.12	0.11

Note: The table entrees are MMD between the target sample and the calibrated source sample, based on five random subsets of size 1000. The MMD between two random batches of the target sample is provided as reference in the rightmost column.

To further assess the quality of calibration, and explore how well our approach preserves the underlying biological patterns in the data, we examine the sub-population of cells with high log-transformed expression values (≥3) of the Prkca marker (which characterizes the cell sub-population of the large cluster in the top part of Fig. 6). The bottom part of Fig. 6) shows this sub-population before and after calibration, as well as after calibration using Combat. Visually, in this example, MMD-ResNet performs better calibration than Combat.

5 Related work

Leek et al. (2010) thoroughly discuss the importance of tackling batch effects and review several existing approaches for doing so.

Bead normalization (Finck et al., 2013) is a specific normalization procedure for CyTOF. As we observed in Section 4, two CyTOF samples may significantly differ in distribution even after Bead normalization. Warping (Hahne et al., 2010) is an approach for calibration of cytometry data where for each marker, the peaks of the marginal distribution in the source sample are (possibly non-linearly) shifted to match the peaks of the corresponding marginal distribution in the target sample. We argue that warping can perhaps be performed by training MMD-ResNet for each single marker. The advantage of MMD-ResNet over a warping is that the former is multivariate, and can take into account dependencies, while the latter assumes that the joint distributions are products of their marginals.

Surrogate variable Analysis (Leek and Storey, 2007) is a popular approach for batch effect adjustment, primarily in gene expression data. However, it is designed for supervised scenarios where labels representing the phenotype of each gene expression profile are provided hence it is not directly applicable to our case, which is purely unsupervised.

MMD was used as a loss criterion for artificial neural networks in (Dziugaite et al., 2015; Li et al., 2015), where the goal was to learn a generative model that can transform standard input distributions (e.g. white noise) to a target distribution. To the best of our knowledge, MMD nets have not been applied to the problem of removal of batch effects, which is considered here.

6 Conclusions and future research

We presented a novel deep learning approach for non-linear removal of batch effects, based on residual networks, to match the distributions of source and target samples. Our approach is general and can be applied to various data modalities. We applied our approach to CyTOF and scRNA-seq and demonstrated impressive performance. To the best of our knowledge, such a performance on CyTOF data was never reported. To justify our choice of residual nets, we showed that equivalent nets that lack the shortcut connections may distort the biological conditions manifested in the samples, while residual nets preserve them.

We are currently developing applications of MMD-ResNets to perform calibration in scenarios where multiple batches are present, each batch contains multiple samples and all batches contain a reference sample. The idea is to perform calibration of all samples by training MMD-ResNets only on the reference samples. We note that a reference sample should be a pool from a representative population similarly to control in Genome Wide Association Studies. Success in such a task will imply that the MMD-ResNets overcome the batch effects (i.e. the machine-dependent variation), without distorting the biological properties of each sample. To the best of our knowledge, such application is not performed elsewhere. It is based on an appealing property of using neural nets for calibration, which is the fact that the nets define a map that can be later applied to new data.

Last, an intensively growing number of general deep learning techniques, operating on raw data, outperform traditional algorithms tailored for specific data types and involving domain knowledge and massive pre-processing. In the same way, we find our proposed approach and experimental results very promising and hope that they open new directions for removing batch effects in biological datasets. For example, recent proposed experimental approaches to standardization (Kleinsteuber et al., 2016), should provide an excellent source for application of MMD-ResNet for calibration.

Funding

This research was partially funded by NIH grant 1R01HG008383-01A1 (Y.K.).

Conflict of Interest: none declared.