Molecular signatures that can be transferred across different omics platforms

Abstract

Motivation

Molecular signatures for treatment recommendations are well researched. Still it is challenging to apply them to data generated by different protocols or technical platforms.

Results

We analyzed paired data for the same tumors (Burkitt lymphoma, diffuse large B-cell lymphoma) and features that had been generated by different experimental protocols and analytical platforms including the nanoString nCounter and Affymetrix Gene Chip transcriptomics as well as the SWATH and SRM proteomics platforms. A statistical model that assumes independent sample and feature effects accounted for 69–94% of technical variability. We analyzed how variability is propagated through linear signatures possibly affecting predictions and treatment recommendations. Linear signatures with feature weights adding to zero were substantially more robust than unbalanced signatures. They yielded consistent predictions across data from different platforms, both for transcriptomics and proteomics data. Similarly stable were their predictions across data from fresh frozen and matching formalin-fixed paraffin-embedded human tumor tissue.

Availability and Implementation

The R-package ‘zeroSum’ can be downloaded at https://github.com/rehbergT/zeroSum. Complete data and R codes necessary to reproduce all our results can be received from the authors upon request.

1 Introduction

Today, molecular data describing blood, urine, stool or tissue specimens is high-content data. Machine learning methods extract biomarker signatures from molecular data that can be used for therapy recommendations. Among the best established methods are penalized linear regression models such as the LASSO (Tibshirani, 1996) and the elastic net (Zou and Hastie, 2005). A more recent method is zero-sum regression (Altenbuchinger et al., 2017; Lin et al., 2014). These algorithms select features and endow them with weights forming predictive linear signatures.

Data sharing is critical to advance precision medicine. Molecular high-content data of patient specimens together with matching diagnostic, histologic and clinical data across many studies are made easily accessible, comparable and jointly analyzable (Quackenbush, 2014). Projects like DECIPHER (Firth et al., 2009), the NCI Genomic Data Commons (NCI Center for Cancer Genomics (CCG), 2016), or the Australian Genomics Health Alliance are on the forefront of buildung such digital medicine resources. But data ambiguity and data dissonance still present major obstacles in the sharing of data (Grossman et al., 2016; Quackenbush, 2014).

Current data resources are not harmonized. Protocols for retrieval of biological specimens, extraction and measurement of molecules of interest, and data processing may vary considerably among datasets. Differences in data generation leave traces in the datasets rendering their joint analysis difficult. Cross platform analysis is particularly essential in case of signatures developed on omics high-content platforms to be later applied to targeted platforms that generate data only for the selected features. Similarly, signatures developed for fresh frozen material need to be transferred to formalin-fixed paraffin-embedded (FFPE) material, which is more readily available (Masqué-Soler et al., 2013; Scott et al., 2014).

To identify requirements for data harmonization, we need a better understanding of inter-technical variability: the systematic discrepancies in data generated by different protocols. Moreover, we need to better understand how these dissonances propagate through subsequent analysis steps. From the precision medicine perspective, there are two types of data problems: those that can affect treatment decisions and those that cannot. Vice versa, there are two types of predictive signatures, those that are sensitive to specific data dissonances and those that are not.

Here we study and model systematic discrepancies in transcriptome and proteome data generated by various protocols and platforms. Based on the model we study which properties of linear signatures enhance or reduce the effect that data dissonance has on treatment recommendations and give advice on choosing proper regression models.

2 Results

2.1 Modelling inter-technical variability

Let x and z be two datasets covering the same features for the same patients but generated with different protocols. Both x_ij and z_ij are matrices with i = 1, …, N denoting samples and j = 1, …, p denoting features. We further assume that both data matrices are normalized using a state of the art protocol and are log-transformed.

Data generated by different technical platforms for the same sample is quantitatively and qualitatively different even after normalization. In Figure 1 row (1), the heatmaps (a) and (b) contrast Affymetrix gene expression data of fresh frozen material of 40 non-Hodgkin lymphomas from (Klapper et al., 2012) to matching nCounter data of FFPE material (Masqué-Soler et al., 2013). The plots in row (2) show proteomics data for 23 of the lymphomas using (a) sequential window acquisition of all theoretical fragment ion spectra (SWATH) (Gillet et al., 2012) and (b) targeted selected reaction monitoring (SRM) (Faktor et al., 2016). For measurement details we refer to the methods section. Finally, the third row shows (a) microarray mRNA and (b) RNA-Seq profiles from Zhao et al. (2014) for the 12 most variable genes in 12 activated T cell samples. For details on data preprocessing, see the methods section.

Fig. 1.

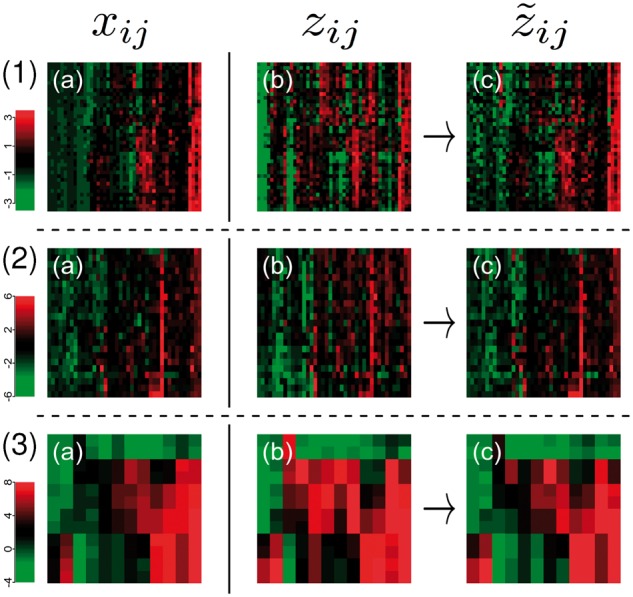
Comparison and adjustment of omics data of the same samples profiled with different technologies and protocols. The first two columns contrast state of the art normalized datasets. Row (1) shows paired gene expression data of the same non-Hodgkin lymphomas using the Affymetrix GeneChip (a) and NanoString nCounter (b) technology. Row (2) shows paired protein expression data acquired by SWATH (a) and SRM (b), for a subset of the non-Hodgkin lymphomas. And Row (3) shows paired expression levels of activated T cells for microarray (a) and RNA-Seq data (b). Column (c) shows heatmaps for the datasets (b) adjusted to match the datasets (a) using our model. Columns always correspond to molecular features (mRNA or protein) and rows to samples

To model the discrepancies we assume that they result from two independent biases: (i) sample effects θ_i that systematically affect all features of a sample i in the same way. (ii) feature effects ω_j that systematically affect feature j in all samples in the same way. We model technical variability Δ using these two effects by:

$${\Delta }_{ij}=z_{ij}-x_{ij}={\theta }_i+{\omega }_j+r_{ij},$$ (1)

where r_ij is the residue of the model. Tukey’s median polish algorithm (Tukey, 1977) estimates θ_i and ω_j. The plots in column (c) of Figure 1 show

$${\tilde{z}}_{ij}=z_{ij}-{\theta }_i-{\omega }_j.$$ (2)

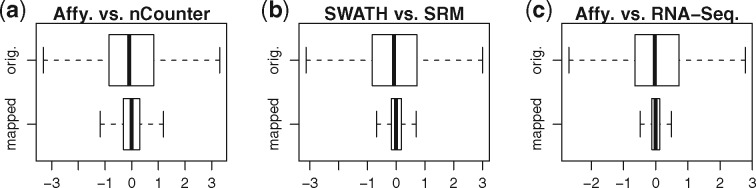
This is the data of technology (b) adjusted to the systematic sample and feature effects. The adjusted data of the technology (b) is visually closer to the data of technology (a), and also quantitatively: Figure 2 shows for each of the three paired datasets box plots of the differences between the two original datasets (top) and between the original first versus the adjusted second dataset (bottom). The two independent biases accounted for 69%, 79% and 94% of the inter-technology variability ${\Delta }_{ij}^2$, respectively.

Fig. 2.

Most of the inter-technical variability can be explained by our independent effects model. Figures (a) to (c) show box plots of the differences between data generated by different technologies. The plots on top show the original non-adjusted but individually normalized data, while those below compare adjusted datasets. 69%-94% of inter-technical variability could be explained by our model

By minimizing Δ_ij in Equation (1) we adjust data from different technologies. However, this is not our primary aim here. Instead we strive for signatures that can be used on non-harmonized data directly. The model will guide us to these signatures.

2.2 Propagation of inter-technical variability

Here we analyze how technical variability that can be modeled by (2) propagates in linear signatures of the form

$$y_i={\beta }_0+\sum _{j\in C}{\beta }_j{x}_{ij}\hspace{0.17em},$$ (3)

where the β_j are feature weights, and y_i is a response variable like the response of patient i to a certain treatment. C contains all indices of non-zero regression weights. Assume that the signature features are covered by both datasets x and z but that the signature was only trained on x. What happens if we apply the signature unchanged to dataset z from a different platform?

2.2.1 An instructive simulation

We used Affymetrix GeneChip data from 281 diffuse large B-cell lymphomas (DLBCL) (Hummel et al., 2006; Klapper et al., 2008; Salaverria et al., 2011). 122 DLBCL are of the ABC and 159 of the GCB subtype. We first restricted the dataset to 47 genes, which were also covered by nanoString nCounter data of 40 DLBCL (Masqué-Soler et al., 2013). Next, we divided the data for which we only had Affymetrix data into a training set of 51 ABC and 87 GCB and a validation set of 71 ABC and 72 GCB. Using the LASSO logistic regression algorithm implemented in the R package glmnet (Friedman et al., 2010), we trained 1000 linear GCB/ABC classifiers each on a different random subset of 40 genes and evaluated them on the validation cohort. While the gene weights varied strongly across signatures, all signatures reached almost perfect performance (Fig. 3a).

Fig. 3.

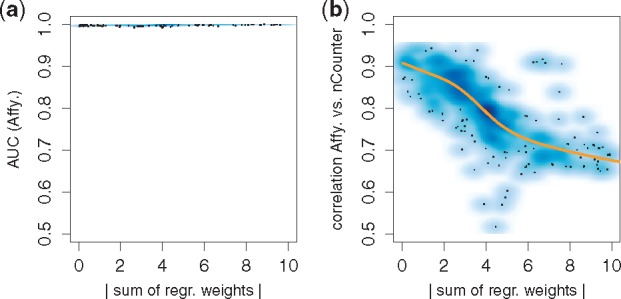
Comparing classifications across technologies: Plot (a) shows the absolute sum of regression weights for 1000 signatures trained on re-sampled data from technology 1 (Affymetrix) plotted against their classification performances (area under the receiver operating characteristic curve (AUC)) on independent data of the same technology. All signatures perform excellent independent of their strongly varying weights. The y-axis of Figure (b) shows the correlation (agreement) of classification scores for data of technology 1 (Affymetrix) and 2 (nanoString). Predictions from signatures with balanced weights (x-axis near zero) agree well across technologies, while unbalanced signatures produce conflicting predictions on the second technology

We next applied these signatures unchanged to 40 DLBCL for which nanoString data were available and which were not part of the training set. For signatures with regression weights that sum up close to zero the linear predictive scores

$$\sum _{j\in C}{\beta }_j{x}_{ij}$$

for the Affymetrix data and the nanoString data showed correlation around 0.9, while for signatures with unbalanced weights this was reduced to 0.75 on average and fell for some signatures below 0.6 (Fig. 3b). Balanced signatures worked equally well on data from both technologies while unbalanced signatures did not.

This observation can be explained by model (1). Plugging equation (1) into equation (3), assuming that the residues r_ij are small, yields

$$y_i={\beta }_0+\sum _{j\in C}{\beta }_j{x}_{ij}={\beta }_0+\sum _{j\in C}{\beta }_j(z_{ij}-{\theta }_i-{\omega }_j)\hspace{0.17em}.$$ (4)

If the regression weights β_j add up to zero this simplifies to

$$y_i={\tilde{\beta }}_0+\sum _{j\in C}{\beta }_j{z}_{ij}\hspace{0.17em},$$ (5)

where ${\tilde{\beta }}_0={\beta }_0-\sum _{j\in C}{\beta }_j{\omega }_j$. Hence if the weights β_j sum up to zero, the sample effects θ_i cancel, while the feature effects ω_j absorb into the intercept ${\tilde{\beta }}_0$. Thus, the same model can be applied to x and z. In this case θ_i and ω_j which account for the majority of technology related discrepancies in the data do not affect the predictions except maybe for a constant shift across all samples. The same argument also holds for generalized and penalized linear models like the LASSO logistic regression used above.

2.2.2 Zero-sum regression reduces cross platform adjustments to the calibration of a single parameter

The LASSO can yield signatures with a small sum of regression weights but it does not guarantee it (Fig. 3). However, balanced weights can be enforced. Zero-sum regression is an instance of constrained LASSO regression (Tibshirani, 1996). It was originally developed for compositional data only (Lin et al., 2014), but its spectrum of applications is broader (Altenbuchinger et al., 2017).

Here we argue that zero-sum regression is a method of choice for cross technology data analysis. The method adopts the penalized LASSO log-likelihood but additionally enforces the sum of the regression weights to zero:

$$\begin{array}{c}({\widehat{\beta }}_0,\widehat{\mathit{\beta }})=\underset{{\beta }_0,\mathit{\beta }}{\text{argmin}}\{\frac{1}{2N}\sum _{i=1}^N{\left(y_i-{\beta }_0-\sum _{j=1}^p{\beta }_j{x}_{ij}\right)}^2\\ +\lambda \left|\right|\mathit{\beta }\left|{|}_1\right\}\hspace{0.17em},\hspace{1em}\text{subject} \text{to}\sum _{j=1}^p{\beta }_j=0\hspace{0.17em}.\end{array}$$ (6)

Above we showed in three examples that platform differences can be mostly explained by two independent effects: a sample effect θ_i and an independent feature effect ω_j. Zero-sum signatures yield the same prediction for shifted data $x_{ij}+{\theta }_i$ and non-shifted data x_ij. Moreover, unlike the standard LASSO, zero-sum learns the same signature if applied to x_ij or $x_{ij}+{\theta }_i$ (Altenbuchinger et al., 2017), and, up to an arbitrary offset β₀, also on $x_{ij}+{\theta }_i+{\omega }_j$. If we use the LASSO, we must adjust all regression weights when moving from data of one technology to the next. For data where our model explains 100% of the inter-technology variability, zero-sum signatures will only need an adjustment of the off-set β₀. Below we will show that on real data, where the model explains only some 80% of the inter-technology variability, zero-sum signatures, nevertheless, yield consistent predictions across datasets.

2.3 Simulation studies

Here we further substantiate the benefits of zero-sum signatures in cross technology data analysis in simulation studies. We simulated paired data representing two technologies linked by Equation (1), and quantitatively study how the simulated inter-technology variability propagates from feature data to predictions.

Omics data can be either continuous intensity or discrete count data. NanoString nCounter, RNA-seq, and many other quantitative next-generation sequencing based methods yield discrete data. We thus simulated counts from a negative binomial distribution, $\text{NB}({\mu }_j,{\varphi }_j)$, where μ_j is the mean count of feature j and ${\varphi }_j$ its dispersion, which is directly related to its variance via $\text{var}({\mathbf{X}}_j)={\mu }_j+{\varphi }_j{\mu }_j^2$. To obtain realistic values for both μ_j and ${\varphi }_j$ we estimated 1000 pairs $({\mu }_j,{\varphi }_j)$ by a maximum likelihood estimate using the 1000 most abundant genes from the RNA-seq data (doi:10.1371/journal.pone.0078644.s008) of Zhao et al. (2014).

For each simulation run, we randomly drew 100 mean-dispersion pairs and simulated counts from the corresponding negative binomial distributions. In total, we simulated 150 samples, of which 50 served as training set and 100 as test set. Taking logarithms yielded simulated screening data matrices. For the two weight vectors $\mathbf{\beta }$ shown in Table 1 we calculated response variables to which we added the random Gaussian errors ${\mathrm{ϵ}}_i\sim \mathrm{N}(\mu =0,\sigma =1)$ resulting in a vector of responses (y_i). Experimentally, no calibrated data is available. Thus, we normalized the raw count data, X, by its sample-wise means. After taking the logarithms, we ended up with the normalized predictor data x = (x_ij), where i = 1, …, 150 and j = 1, …, 100.

Table 1.

Data generating weights for the two simulation scenarios

Simulation	β1	β2	β3	β4	β5	β6	β7	β8	β9	β10	β11	…	β100
A	1	2	3	4	5	−1	−2	−3	−4	−5	0	…	0
B	1	2	3	4	5	1	2	3	4	5	0	…	0

In scenario A the weights are balanced, while in B they are all non-negative.

We trained linear models on (y, x) using (i) zero-sum regression, (ii) the standard LASSO and (iii) and ordinary least square regression (OLS) combined with feature filtering. The latter method, first screens for the top k features with highest absolute correlation to y and fits a standard linear model on the selected features using OLS. k is calibrated in cross validation on the training data and so is the tuning parameter λ of both LASSO and zero-sum regression. While by definition the sum of coefficients is zero for all zero-sum signatures, it ranges from −10.7 to 11.1 (−0.1 to 21.1) in the LASSO signatures and from −16.5 to 10.7 (−12.6 to 18.9) in the f-OLS signatures for simulation scenario A (B), respectively, showing that the three methods produce different signatures. Figure 4a and d shows violin plots of the correlations $r_1=\text{cor}({\widehat{y}}_1,y)$ between observed and predicted responses calculated on the test cohort, where ${\widehat{y}}_1$ are the predictions, for scenario A and B, respectively. For both zero-sum and LASSO signatures we observe that the median correlation over all simulation runs, shown as a grey dot, is roughly the same indicating that the zero-sum constraint is not compromising predictive performance on the screening data. This is not surprising for signature A where the data generating coefficients $\mathit{\beta }$ sum up to zero. But also for signature B with only positive coefficients the predictive performance of zero-sum regression was not compromised. f-OLS combined with feature filtering performed significantly worse in scenario A.

Fig. 4.

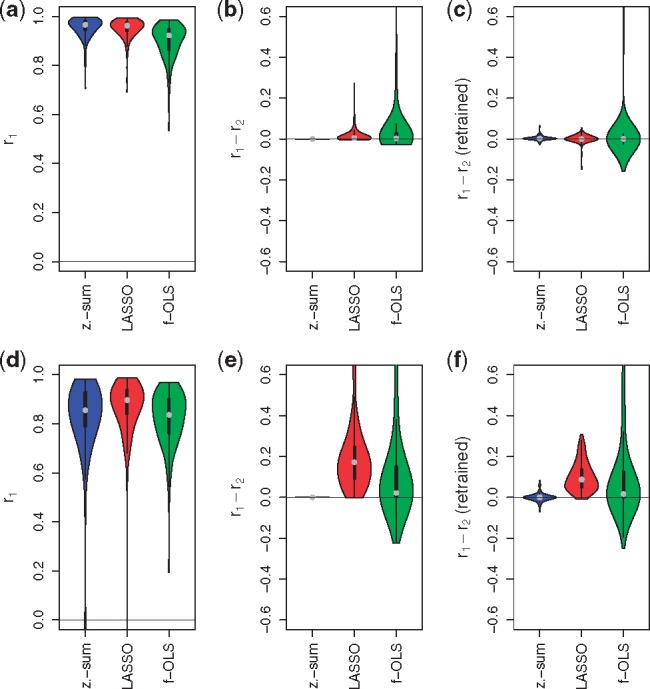
Simulation results: Correlations between predicted and true responses for simulation scenario A (top) and B (bottom) summarized in Table 1. Models were trained using zero-sum regression (z.-sum), LASSO and OLS with feature filtering (abbreviated as f-OLS). Plots (a) and (d) show correlations between true and predicted responses for simulated technology 1 data, $r_1=\text{cor}({\widehat{y}}_1,y)$, for scenario A and B, respectively. Zero-sum regression can compete with the standard LASSO and out competes f-OLS on consistent data from the same technology. Plots (b) and (e) show correlation differences for simulated technology 1 and technology 2 data. The signatures were trained on simulated technology 1 data and applied unchanged to simulated technology 2 data. For the simulation with balanced weights (top) both zero-sum and LASSO show good agreement across datasets, while for unbalanced weights (bottom) the LASSO and f-OLS show systematic reduced agreement across datasets. Plots (c) and (f) also show correlation differences for simulated technology 1 and technology 2 data, but this time the signatures were retrained on simulated technology 2 data. Retraining did not improve the agreement of predictions across technologies

Next we simulated a matching second dataset representing a second technological platform. Technological platforms typically do not cover the exact set of features. Nevertheless, we here assume that at least all signature features are covered. We thus perturbed x by $x_{ij}\to x_{ij}+{\theta }_i+{\omega }_j$, cut out the features selected by a signature s and normalized this data by the same strategy as x, but now on the signature features s only. This yielded a data matrix z(s).

2.3.1 Only zero-sum signatures apply on both technology 1 and 2 data

We first describe the performance of signatures, for which only the offset β₀ was adjusted. For these signatures we obtained predictions ${\widehat{y}}_1$ on the first dataset and ${\widehat{y}}_2$ on the second. Figure 4b and e shows $r_1-r_2=\text{cor}({\widehat{y}}_1,y)-\text{cor}({\widehat{y}}_2,y)$ calculated for the 100 test samples for signature A and B, respectively. As expected, the performance of zero-sum signatures applied to z(s) is not compromised at all while those of LASSO and f-OLS models frequently is. For signature A this effect was less pronounced than for signature B. LASSO estimates coefficients close to those used for data generation. In A these coefficients correctly summed to a small number, thus LASSO signatures approximate zero-sum signatures. In contrast f-OLS predictions were off target. In B the LASSO correctly estimated predominantly positive coefficients yielding signatures far away from a zero-sum. In simulation A LASSO signatures lost precision on the second dataset, in simulation B they broke down. f-OLS signatures performed poorly in both simulations.

2.3.2 Unchanged zero-sum signatures were more reliable than retrained signatures

The most common approach to moving signatures from one technology to the next, is to keep the selected features from the first study and retrain all feature weights on a training dataset generated with the second technology. In this simulation study, we compared retraining to learning a zero-sum signature and leaving it unchanged. Thus, using the simulated data we predicted the response y by (i) using the original signatures and adjusting only the offset β₀ and (ii) by retraining all coefficients β₀ and $\mathit{\beta }\in s$ on (y,z(s)).

Again we had test data predictions ${\widehat{y}}_1$ and ${\widehat{y}}_2$. Figure 4c and f compare the performances of zero-sum, the LASSO and f-OLS for simulations A and B, respectively. All three methods did not profit from retraining. Unchanged zero-sum signatures guaranteed equal performance on targeted data, while a retrained signature was a lottery that yielded very good performance but even more frequently a strongly reduced performance. In summary, the unchanged zero-sum signatures appeared to be the safest choice.

2.4 Classifications using different proteomics platforms

DLBCL are a heterogeneous group of lymphomas comprising distinct molecular subtypes: the activated B-cell like (ABC) and the germinal center B-cell like (GCB) lymphomas (Alizadeh et al., 2000; Rosenwald et al., 2002). Differential diagnosis becomes increasingly important as drugs are under investigation that appear to be effective for only one of the subtypes (Wilson et al., 2015).

We frame ABC/GCB diagnosis as a regression problem. The ABC and GCB subtypes are themselves heterogeneous groups. They are not sharply separated. Instead, there is a continuous spectrum on how ‘GCB-like’ a DLBCL can be. We have lymphomas that are either clear GCBs or ABCs, but many are in between these prototypic cases. Such lymphomas are labelled ‘unclassified’ (Rosenwald et al., 2002). Masqué-Soler et al. (2013) have accounted for the continuous transition between GCB and ABC by using a GCB score instead of just the three classes GCB, unclassified and ABC. The score is positive for GCB, negative for ABC and near zero for unclassified lymphomas. We follow this strategy. In more statistical words, we frame this diagnostic problem as a regression problem and not as a classification problem. The gold standard for DLBCL subtyping is a gene expression signature generated by the Affymetrix GeneChip technology applied to fresh frozen material. On FFPE material, the diagnosis can be performed using either the nanoString nCounter transcriptomics platform (Masqué-Soler et al., 2013; Scott et al., 2014) or a shotgun proteomics approach employing a stable-isotope tagged reference proteome (Deeb et al., 2012). To complement these methods, we here attempted diagnosis with low cost proteomics data from (a) the SWATH and (b) the SRM platform, again using FFPE material.

The ABC/GCB subtype is a property of a lymphoma. Its diagnosis must not depend on the technology used nor should it depend on whether the tissue was frozen or FFPE. Here, we aimed for a single set of regression coefficients that can be used with both SWATH and SRM data.

2.4.1 Data and results

The data comprised 23 DLBCL of which 12 were GCBs, 7 were ABCs and the remaining 4 were unclassified. FFPE biopsy specimens of this cohort were subjected to SWATH proteomics, which yielded expression levels for 235 proteins that were supported by at least 6 detected peptides in all samples. We trained zero-sum signatures using the SWATH proteomics data to predict the gold standard ABC/GCB scores y_i using zero-sum regression. This was done in a leave-one-out cross validation across platforms. Figure 5a shows predicted scores (SWATH proteomics) plotted against gold standard scores (Affymetrix transcriptomics). The scores correlate well (r = 0.93) and GCB samples (blue circles) are clearly separated from ABC samples (red triangles). The dashed lines are classification boundaries for ABC, unclassified and GCB, derived from the gold-standard ABC/GCB scores. The heatmap below the plot contrasts the corresponding classifications showing an excellent agreement between the proteomics predictions and the gold standard classifications.

Fig. 5.

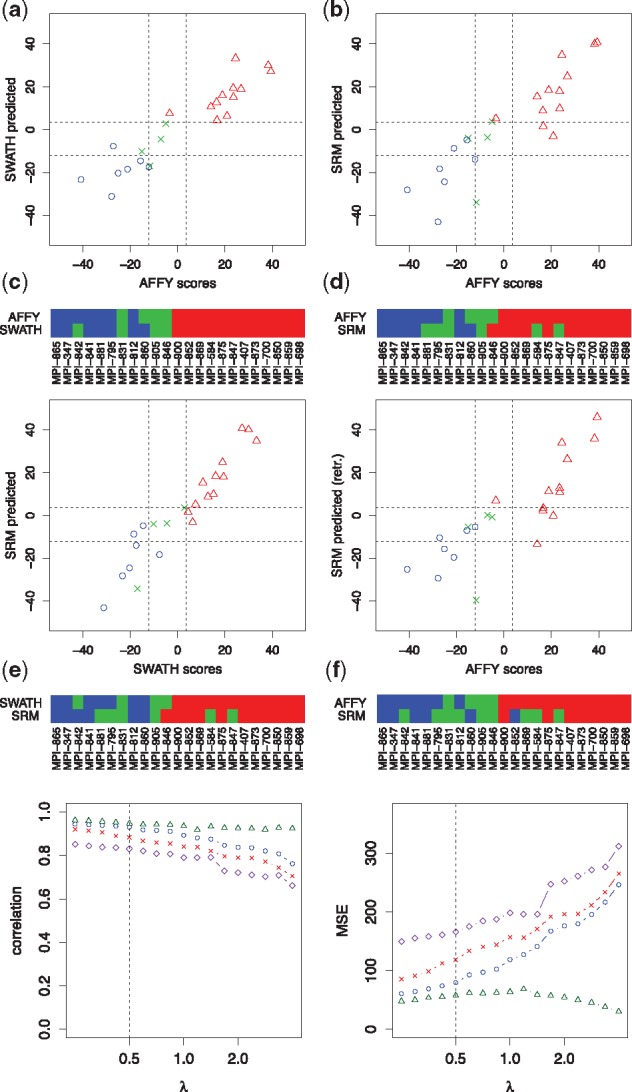
DLBCL subtyping using different technological platforms and different biopsy conservation protocols. Plot (a) shows the ABC/GCB gold-standard scores (Affymetrix gene expression) versus zero-sum scores predicted in a leave-one-out cross validation on SWATH proteomics data. The scores from both technologies agree well. The dashed lines are classification boundaries for ABC, unclassified and GCB, derived from the gold-standard scores. The color bars below the plot contrast the resulting classifications showing an excellent agreement between the proteomics predictions and the gold standard classifications. Similarly, Plot (b), shows gold-standard scores versus scores predicted on SRM data. Here, the original SWATH signature was applied on the SRM data directly, where only the offset β₀ was retrained. The SWATH signature carried over well to SRM data. Plot (c) shows SWATH versus SRM predictions with excellent agreement. Plot (d) shows scores predicted on SRM versus the gold standard scores, where this time the signature was completely retrained on SRM data. The retrained signature was inferior to the SWATH trained zero-sum signature in (b). All signatures were trained for the penalizing parameter λ = 0.5. In all four figures, (a–d), GCBs are indicated in red (triangles), ABCs in blue (circles) and unclassified cases in green (crosses). The dependence of correlations and mean squared errors of Figure (a) to (d) on λ is shown in Figure (e) and (f). Comparison (a) corresponds to the blue circles, (b) to the red crosses, (c) to the green triangles and (d) to the purple diamonds

Next we applied this signature unchanged to SRM data generated for FFPE material from the same lymphomas. As expected by theory, the resulting ABC/GCB scores correlated well with both the gold standard (r = 0.88) and the SWATH based scores (r = 0.95) (Fig. 5b and c). As an alternative strategy to zero-sum signatures we tested re-training a signature on the SRM data, which ended in notably more discrepancies to the gold standard than the zero-sum signature (Fig. 5d).

To ensure comparability of results we kept the regularization parameter λ fixed at 0.5 in all results from Figure 5a thru 5d. Figure 5e and f illustrate how the results depend on λ. The circles correspond to scenario (a), the crosses to (b), the triangles to (c) and the diamonds to (d). Interestingly, the SWATH signature remains remarkably predictive between λ = 0.25 and λ = 2, also on the SRM data. Furthermore, SWATH and SRM predictions are highly concordant for all values of λ.

In summary, zero-sum proteomics signatures accurately reproduced the transcriptomics based gold standard ABC/GCB classification. Zero-sum signatures did not break down when switching from SWATH to SRM based proteomics. Moreover, when applied to SRM data, unchanged zero-sum SWATH signatures were more faithful to the classification than a retrained signature that was specifically adapted to SRM data.

2.5 Classifications using different transcriptomics platforms and different tissue preservation protocols

Most proteomics platforms work well for both fresh frozen and FFPE material. The situation is different for transcriptomics, as RNA degradation in FFPE material will affect quantification.

We used gene expression data of molecular Burkitt lymphomas (mBL) and DLBCL (non-mBL) that were assessed on fresh frozen material using Affymetrix Gene Chips (Hummel et al., 2006). Furthermore, FFPE data of a separate set of lymphomas was available from (Masqué-Soler et al., 2013) using the nanoString nCounter platform. The differential diagnosis between mBL and non-mBL can be challenging using standard histopathological assessment (Hummel et al., 2006), but is nevertheless important because the entities are generally treated differently (Dave et al., 2006). As for the ABC/GCB sub-typing we use a continuous mBL-score, with the label intermediate between mBL and non-mBL cases, and frame the diagnostic challenge as a regression problem.

We applied zero-sum regression to the training cohort from Hummel et al. (2006), consisting of 23 mBL, 26 intermediate cases and 62 DLBCL, available on Affymetrix Gene Chips. Two samples were removed from the training cohort, because they were also part of the data from (Masqué-Soler et al., 2013). The predictor variables were restricted to features that were also covered by the nCounter platform. The signature was then applied to a validation set of 9 mBL, 8 intermediate and 23 DLBCL, for which nCounter data was available (Masqué-Soler et al., 2013). All regression weights were used as they were, except the offset β₀, which was readjusted in a leave-one-out cross validation.

The results are summarized in Figure 6. The nCounter data reproduced the gold standard scores well in line with (Masqué-Soler et al., 2013). The zero-sum signatures did not break down when switching the platform from Affymetrix Gene Chips to nanoString nCounter and the tissue preservation protocol from freezing to FFPE, and again the transferred signature out-competed retraining.

Fig. 6.

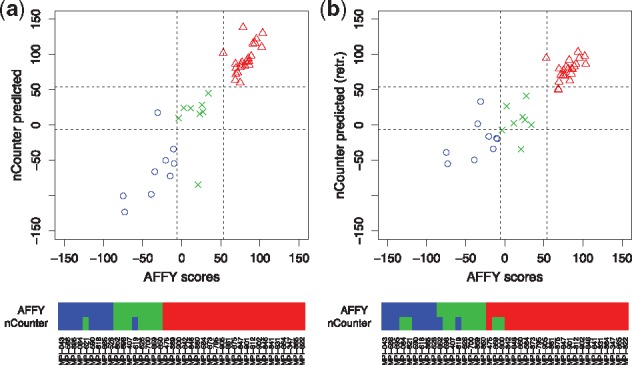
Differential diagnosis of mBL and DLBCL. Figure (a) shows mBL scores predicted on FFPE data (nanoString) versus the gold standard scores from fresh frozen material (Affymetrix). The signature was trained by zero-sum regression on GeneChip data and was directly applied to the FFPE data, where only the offset β₀ was readjusted in cross validation. The color bars below the plot contrast the resulting classifications showing an excellent agreement between the FFPE predictions and the gold standard classifications. In Figure (b) the FFPE nCounter scores were obtained by a leave-one-out cross validation, where the signature was retrained on the nCounter data. Retraining did not yield any advantages over the original zero-sum signature. In both figures, DLBCLs are indicated in red (triangles), mBLs in blue (circles) and intermediate cases in green (crosses)

3 Discussion

This is the first systematic analysis of how data dissonance caused by varying experimental protocols propagates in downstream analysis from signature learning to predictions and possible treatment recommendations. We have observed that data dissonance can be mostly modeled by independent sample and feature effects. As a consequence we showed that in zero-sum signatures the sample effects fully vanish while feature effects can be absorbed in a single parameter that can be easily adjusted. For these signatures data dissonance appears under control. This is in contrast to signatures with predominantly positive or negative regression weights, where data dissonance strongly compromises predictions.

Independent sample and feature effects together accounted for 69 to 94% of data dissonance. This still leaves considerable disagreements. Clearly, non-linear effects cannot be compensated nor can systematic difference in noise, like for lowly expressed genes in continuous microarray versus discrete RNA-Seq and nCounter data. One remedy might be to learn signatures and select features not only on a single platform but on joint dissonant data. In such a case lowly expressed features and features that display non-linear discrepancies across platforms might not be selected simply because other features out-compete them.

To date, the most frequently used strategy to transfer signatures across platforms was a two step procedure: first learn a sparse signature on high-content data. Then transfer the features to a second targeted analytical platform. On the second platform keep the features but discard the weights of this signature. New platform adjusted weights can be learned in a training phase on the data of the new platform (Masqué-Soler et al., 2013; Scott et al., 2014, 2013; Sha et al., 2015). Surprisingly, in our studies this strategy was inferior to simply keeping the weights of a zero-sum regression signature learned on high-content data. While this observation might not hold up for all data types, we nevertheless believe that zero-sum signatures are a method of choice when working with large but diverse data collections from digital medicine initiatives. With data from numerous labs with different underlying experimental protocols it might not be practical to readjust the parameters of prediction algorithms for all of them.

Advancing a culture of data sharing and harmonized data generation is key to treatment decisions that build on all scientific evidence available at any point of time. Maybe our results make data harmonization a little less tedious. We observed that with the right algorithms treatment recommendations remained stable even if the data were not yet perfectly harmonized, supporting the prospect that data sharing and integration can improve patient care immediately.

4 Materials and methods

4.1 Data preprocessing

The Affymetrix GeneChip data of Figure 1.1a, Sections 2.2 and 2.5 was preprocessed as in Hummel et al. (2006). Corresponding GCB/ABC diagnosis scores, which served as responses throughout Sections 2.4 and 2.5, were provided by the Molecular Mechanisms in Malignant Lymphoma (MMML) consortium.

NanoString nCounter data from (Masqué-Soler et al., 2013) were preprocessed by, first, scaling sample-wise to an equal number of endogenous gene counts (to the total average over the raw counts of endogenous genes), second, a pseudocount of 1 was added and, finally, the data was transformed by the natural logarithm. Here, the natural logarithm is necessary to ensure that the data is comparable to the GeneChip data.

The protein expression data shown in Figure 1.2a, 1.2b, and used in Section 2.4, were first normalized sample-wise by their total intensity, then scaled by a factor of 1000 and finally log₂ transformed.

The data shown in Figure 1.3a and 1.3b were taken from (Zhao et al., 2014). RMA normalized microarray data for 12 samples were downloaded from doi:10.1371/journal.pone.0078644.s006. Probe sets were annotated with gene names using the annotation file doi:10.1371/journal.pone.0078644.s004 and redundant genes were summarized by mean averaging. Corresponding RPKM normalized RNA-seq data was downloaded from doi:10.1371/journal.pone.0078644.s009. After summing up RPKM-normalized counts of redundant genes, a pseudocount of 1 was added and the data was log₂ transformed. Finally, both datasets were restricted to common genes, as provided in doi:10.1371/journal.pone.0078644.s005.

For all comparisons in Figure 1, the datasets were additionally brought to the same scale by subtracting the mean over all features and samples available on both platforms.

4.2 SWATH/SRM signature transfer: computational and measurement details

4.2.1 Protein profiling using SWATH^TM acquisition

Two 10 µm sections of each FFPE-specimen were extracted according to Ostasiewicz et al. (2010) and the proteins were subjected to tryptic digestion using the GASP-protocol (Fischer and Kessler, 2015). An aliquot of 1 µL of the digest was used for SWATH-measurements using a 3 h binary gradient and variable SWATH-windows (Reinders et al., 2016; Simbürger et al., 2016; Zhang et al., 2015). Targeted data extraction was conducted with the SWATH Acquisition MicroApp 2.0 within the PeakView 2.2 software (Sciex, Darmstadt, Germany).

4.2.2 Targeted protein profiling using SRM

The two most intensive, proteotypic peptide signals for each of the respective proteins were used for scheduled SRM measurements using 10 min retention time windows on a 73 min binary gradient with an accumulation time of 120 ms per precursor (Limm et al., 2016). Quantification of the signals was done with the Skyline software (version 3.6) (MacLean et al., 2010) using at least 4 transitions.

4.2.3 Model training and cross validation across platforms

In each cross-validation step, we performed the following steps on the training data. First, we fix λ to a specific value. Here, we focused on the interval λ = 0.25 to 4. This restriction was necessary, because each feature selected on SWATH needed to be remeasured on SRM. For this reason, smaller λ values, i.e. less sparse signatures could not be studied using SRM, due to drastically increasing experimental effort. Next, we trained a signature consisting of features $j\in C$ with coefficients unequal zero. Of these selected proteins, we removed those that acquired coefficients $\left|{\beta }_j\right|<0.5$, leaving a protein set $C\prime$ (this cutoff was included to enforce additional sparseness of models). Then, a zero-sum model was retrained on the proteins $C\prime$, yielding the final signature. The selected proteins were measured in a targeted SRM measurement (this measurement was done once and covered all proteins selected in all cross-validations). The offset β₀ was adjusted on the SRM training data, and finally we predicted a score for the left-out test sample, measured on SRM.