deBGR: an efficient and near-exact representation of the weighted de Bruijn graph

Abstract

Motivation

Almost all de novo short-read genome and transcriptome assemblers start by building a representation of the de Bruijn Graph of the reads they are given as input. Even when other approaches are used for subsequent assembly (e.g. when one is using ‘long read’ technologies like those offered by PacBio or Oxford Nanopore), efficient k-mer processing is still crucial for accurate assembly, and state-of-the-art long-read error-correction methods use de Bruijn Graphs. Because of the centrality of de Bruijn Graphs, researchers have proposed numerous methods for representing de Bruijn Graphs compactly. Some of these proposals sacrifice accuracy to save space. Further, none of these methods store abundance information, i.e. the number of times that each k-mer occurs, which is key in transcriptome assemblers.

Results

We present a method for compactly representing the weighted de Bruijn Graph (i.e. with abundance information) with essentially no errors. Our representation yields zero errors while increasing the space requirements by less than 18–28% compared to the approximate de Bruijn graph representation in Squeakr. Our technique is based on a simple invariant that all weighted de Bruijn Graphs must satisfy, and hence is likely to be of general interest and applicable in most weighted de Bruijn Graph-based systems.

Availability and implementation

https://github.com/splatlab/debgr.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction and related work

The de Bruijn Graph has become a fundamental tool in genomics (Compeau et al., 2011) and the de Bruijn Graph underlies almost all short-read genome and transcriptome assemblers—(Chang et al., 2015; Grabherr et al., 2011; Kannan et al., 2016; Liu et al., 2016; Pevzner et al., 2001; Simpson et al., 2009; Schulz et al., 2012; Zerbino and Birney, 2008)—among others. De Bruijn graphs, and k-mer-based processing in general, have also proven useful, even for long read sequence analysis (Carvalho et al., 2016; Koren et al., 2017; Salmela et al., 2016).

Despite the computational benefits that the de Bruijn Graph provides above the overlap-layout-consensus paradigm, the graph still tends to require a substantial amount of memory for large datasets. This has motivated researchers to derive memory-efficient de Bruijn Graph representations. Many of these representations build upon approximate membership query (AMQ) data structures (such as Bloom filters) to achieve an economy of space.

Approximate membership query data structures are set (or multiset) representations that achieve small space requirements by allowing queries, occasionally, to return false positive results. The Bloom filter (Bloom, 1970) is the archetypal example of an AMQ. Bloom filters began to gain notoriety in bioinformatics when Melsted and Pritchard (2011) showed how they can be coupled with traditional hash tables to vastly reduce the memory required for k-mer counting. By inserting k-mers into a Bloom filter the first time they are observed, and adding them to the higher-overhead exact hash table only upon subsequent observations. Later, Zhang et al. (2014) demonstrated that the count-min sketch (Cormode and Muthukrishnan, 2005) (a frequency estimation data structure) can be used to approximately answer k-mer presence and abundance queries when one requires only approximate counts of k-mers in the input. Such approaches can yield order-of-magnitude improvements in memory usage over competing methods.

These ideas were soon applied to the construction and representation of the de Bruijn Graph. For example, Pell et al. (2012) introduce a completely probabilistic representation of the de Bruijn Graph using a Bloom filter to represent the underlying set of k-mers. Though this representation admits false positives in the edge set, they observe that this has little effect on the large-scale structure of the graph until the false positive rate becomes very high (i.e. $\ge 0.15$).

Building upon this probabilistic representation, Chikhi and Rizk (2013) introduce an exact de Bruijn Graph representation that couples a Bloom-filter-based approximate de Bruijn Graph with an exact table storing critical false positive edges. Chikhi and Rizk’s de Bruijn Graph representation exploits the fact that, in the de Bruijn Graph, there are very few edges connecting true-positive k-mers to false-positive k-mers of the Bloom filter representation of the k-mer set. Such edges are called critical false positives. Further, they observe that eliminating these critical false positives is sufficient to provide an exact (navigational) representation of the de Bruijn Graph. This compact representation allows large de Bruijn Graphs to be held in RAM, which enables relatively efficient assembly of even large and complex genomes.

Subsequently, the representation of Chikhi and Rizk was refined by Salikhov et al. (2013), who improved the memory requirements even further by replacing the exact table with a cascading Bloom filter. The cascading Bloom filter stores an approximate set using a combination of an approximate (i.e. Bloom filter-based) representation of the set and a smaller table to record the relevant false-positives. This construction can be applied recursively to substantially reduce the amount of memory required to represent the original set. Salikhov et al. (2013) provide a representation that requires as little as $8-9$ bits per k-mer, yet remains exact from a navigational perspective. Even more memory-efficient exact representations of the unweighted de Bruijn Graph are possible. For example, Bowe et al. (2012) introduced the succinct de Bruijn Graph (often referred to as the BOSS representation), which provides an exact navigational representation of the de Bruijn Graph that uses < 5 bits per k-mer, which compares favorably to the lower bound of $\approx 3.24$ bits per k-mer on navigational representations (Chikhi et al., 2014).

While the above approaches used auxiliary data structures to correct errors in an approximate representation of the de Bruijn Graph, Pellow et al. (2016) showed how to exploit redundancy in the de Bruijn Graph itself to correct errors. Essentially, they observed that true k-mers are not independent—each true k-mer will have a k–1-base overlap with another true k-mer. If a Bloom filter representation of the de Bruijn Graph indicates that a particular k-mer x exists, but that no k-mer overlapping x exists, then x is likely to be a false positive. Thus, by checking for the existence of all overlapping k-mers, they can dramatically reduce the false-positive rate of a Bloom-filter-based de Bruijn Graph representation. Our representation of the weighted de Bruijn Graph can be viewed as an extension and generalization of this basic idea. See Sections 2.3 and 3 for details.

However, the Bloom filter omits critical information—the frequency of each k-mer—that is necessary when performing assembly of a transcriptome. Thus, ‘topology-only’ representations are inadequate in the case where knowing the abundance of each transcript, and by extension, each k-mer in the de Bruijn Graph that is part of this transcript, is essential. In the transcriptomic context, then, one is interested primarily in the weighted de Bruijn Graph (see Definition 2). The weighted de Bruijn Graph associates with each k-mer its abundance in the underlying dataset upon which the de Bruijn Graph was constructed. Unlike the case of genomic assembly, we expect the counts in the weighted de Bruijn Graph for transcriptomic data to have a very large dynamic range, and maintaining exact or near-exact counts for each k-mer can be important for accurately identifying transcripts.

In this paper, we introduce a memory-efficient and essentially exact representation of the weighted de Bruijn Graph. Our representation is based upon a recently-introduced counting filter data structure Pandey et al. (2017a) which, itself, provides an approximate representation of the weighted de Bruijn Graph. Observing certain abundance-related invariants that hold in an exact weighted de Bruijn Graph, we devise an algorithm that uses this approximate data representation to iteratively self-correct approximation errors in the structure. The result is a data structure that takes 18–28% more space than the approximate representation and has zero errors. This makes our new representation, which we call deBGR, essentially an exact representation of the weighted de Bruijn Graph. In datasets with billions of distinct k-mers, deBGR typically exhibits zero topological errors. Further, our algorithm corrects not only the topology of the approximate representation, but also misestimates of abundance that result from collisions in the underlying counting filter.

Additionally, while existing space-efficient representations of the de Bruijn Graph, are static, i.e. k-mers cannot easily be deleted from the graph; our representation supports removal of edges from the de Bruijn Graph. This capability is enabled by the counting quotient filter’s ability to delete items (which cannot be done reliably in Bloom filters). Since aggressive simplification of the de Bruijn Graph (e.g. to remove spurious topology like bubbles and tips) is typically done prior to assembly, this deletion capability is important. Previous approaches avoided the standard simplification step by instead adopting more complicated traversal algorithms (Chikhi and Rizk, 2013). By removing this limitation of the Bloom filter, our representation benefits both from simpler traversal algorithms which allow the in-memory creation of a more manageable simplified weighted de Bruijn Graph. Recently, Belazzougui et al. (2016) have introduced a dynamic representation of the unweighted de Bruijn Graph based on perfect hashing, and it will be interesting to explore the ability of this approach to represent the weighted de Bruijn Graph. However, to the best of our knowledge, this representation has not yet been implemented.

We believe that our representation of the weighted de Bruijn Graph can be successfully applied to considerably reduce the computational requirements for de Bruijn Graph-based transcriptome assembly (Chang et al., 2015; Grabherr et al., 2011; Kannan et al., 2016; Liu et al., 2016). One of the major benefits of our approach is that weighted de Bruijn Graph construction should require considerably less memory than the approaches taken by these other tools. This will allow for the assembly of larger and more complicated transcriptomes on smaller and less expensive computers. Further, since our compact representation of the de Bruijn Graph can be kept completely in memory, even for relatively large transcriptomes, we can avoid the ad hoc and potentially complicated step of partitioning the de Bruijn Graph for further processing (Kannan et al., 2016; Pell et al., 2012).

2 Background

deBGR is built on our prototype k-mer counter Squeakr (Pandey et al., 2017b), which is in turn built on our counting quotient filter data structure (Pandey et al., 2017a). We explain the key features of these systems that are needed to understand deBGR. We then review prior work on exploiting redundancy in de Bruijn Graphs to correct errors in approximate de Bruijn Graph representations. We also note that, throughout the paper, we assume a DNA (i.e. 4 character) alphabet.

2.1 The counting quotient filter

The counting quotient filter (CQF) supports functionality similar to a counting Bloom filter, but offers much better performance and uses far less space (Pandey et al., 2017a) than a counting Bloom filter. The CQF is essentially an approximate multiset: items can be inserted and deleted, and queries return the number of instances of an item that are currently in the multiset. Queries may return an incorrect count with probability $\epsilon$. Like the counting Bloom filter, errors are one-sided—the count returned by the CQF is never smaller than the true count.

The CQF stores an approximation of a multiset $S\subseteq \mathcal{U}$ by storing a compact, lossless representation of the multiset h(S), where $h:\mathcal{U}\to \{0,\dots ,2^p-1\}$ is a hash function. To handle a multiset of up to n distinct items while maintaining a false positive rate of at most $\epsilon$, the CQF sets $p={\text{log}}_2\frac{n}{\epsilon }$ (see the original quotient filter paper for the analysis (Bender et al., 2012)).

The counting quotient filter divides h(x) into its first q bits, quotient$h_0(x)$, and its remaining r bits, remainder$h_1(x)$. The counting quotient filter maintains an array Q of $2^q$r-bit slots, each of which can hold a single remainder. When an element x is inserted, the counting quotient filter attempts to store the remainder $h_1(x)$ at index $h_0(x)$ in Q (which we call x’s home slot). If that slot is already in use, then the counting quotient filter uses a variant of linear probing, to find an unused slot where it can store $h_1(x)$. The CQF also maintains a small amount of additional metadata in order to determine (1) which slots are in use and (2) the home slot of each each remainder stored in Q. The CQF metadata adds 2.125 bits of overhead per slot. See the CQF paper for details (Pandey et al., 2017a). In order to maintain good performance, the array of slots cannot be filled beyond 95%.

Table 1 summarizes the per-element space required in a Bloom filter, Cuckoo filter (Fan et al., 2014) and CQF, assuming no duplicates (we can’t compare a Bloom filters or Cuckoo filter to a CQF on multisets, since Bloom and Cuckoo filters do not support tracking the number of instances of each item). The CQF is always more space efficient than the Cuckoo filter and more space-efficient than the Bloom filter for any false positive rate less than 1/64.

Table 1.

Space usage of several AMQs, as a function of $\epsilon$, the false positive rate, and α, the load factor

Filter	Bits per element	Max α
Bloom	$\frac{\hspace{0.17em}{\text{log}}_{2}1/\epsilon }{\ln 2}$	N/A
Cuckoo	$\frac{3+{\text{log}}_{2}1/\epsilon }{\alpha }$	0.95
CQF	$\frac{2.125+{\text{log}}_{2}1/\epsilon }{\alpha }$	0.95

Note: The CQF is more space efficient than the cuckoo filter for all false positive rates and more space efficient than the Bloom filter for false positive rates less than 1/64. The Cuckoo filter and CQF offer good performance until 95% load factor. A Cuckoo filter or CQF offers good performance up to a load factor of 0.95.

The CQF is an exact representation of h(S)—all false positives are due to collisions in h. Thus, by choosing h to be an invertible hash function, we can use a CQF to store S losslessly. We use both lossy and lossless CQFs in deBGR.

Instead of storing multiple copies of the same item to count, like a quotient filter, the counting quotient filter employs an encoding scheme to count the multiplicity of items. The encoding scheme enables the counting quotient filter to maintain variable-sized counters. This is achieved by using slots originally reserved to store the remainders to, instead, store count information. The metadata bits maintained by the counting quotient filter allow this dynamic reuse of remainder slots for large counters while still ensuring the correctness of all counting quotient filter operations. See the CQF paper for details (Pandey et al., 2017a).

The variable-sized counters in the counting quotient filter enable the data structure to handle highly skewed datasets efficiently. By reusing the allocated space, the counting quotient filter avoids wasting extra space on counters and naturally and dynamically adapts to the frequency distribution of the input data. The counting quotient filter never takes more space than a quotient filter for storing the same multiset. For highly skewed distributions, like those observed in HTS-based datasets, it occupies only a small fraction of the space that would be required by a comparable (in terms of false-positive rate) quotient filter.

In summary, the features of the CQF that we take advantage of in deBGR are:

• CQFs support insertions of items and queries for the number of instances of an item,

• queries to a CQF always return a count that is at least as large as the true count,

• CQFs can be either lossy or lossless,

• when used to represent a set losslessly, they support enumerating the elements of that set, and

• CQFs are space efficient, even for skewed input distributions.

2.2 Squeakr

Squeakr is a k-mer-counter built on CQFs. Essentially, Squeakr reads and parses input files containing reads, and inserts the k-mers into a CQF. It can then write the CQF to disk for later querying.

Squeakr supports two modes: approximate and exact. In exact mode, Squeakr inserts k-mers using an invertible 2k-bit hash function, and hence has no false positives. In approximate mode, Squeakr uses a p-bit hash function, where p is chosen as described above to maintain the desired error rate while handling the expected number of input k-mers.

Squeakr is competitive or outperforms state-of-the-art k-mer counters. In exact mode, Squeakr use about half the memory of KMC2 and roughly the same amount of memory as Jellyfish2 (both of which are exact k-mer counters). For approximate counts, Squeakr uses considerably less memory (1.5X–4.3X) than Jellyfish2 and KMC2. Squeakr offers counting performance similar to that of KMC2 and faster than Jellyfish2. However, Squeakr offers an order-of-magnitude improvement in query performance. Squeakr offers very fast query performance for both random queries and de Bruijn Graph traversal workloads.

Fast queries turn out to be helpful in downstream data analyses, such as de Bruijn Graph traversals (Chikhi and Rizk, 2013), inner-product computations (Murray et al., 2016; Vinga and Almeida, 2003), and searches (Solomon and Kingsford, 2016).

2.3 Prior approximate de Bruijn graph representations

deBGR extends and generalizes an idea first suggested by Pellow et al. (2016), for correcting errors in approximate de Bruijn Graph representations.

The Bloom filter false-positive rate is calculated assuming all the items inserted in the Bloom filter are independent. However, when we use a Bloom filter to represent a de Bruijn Graph, the items (or k-mers in this case) are not independent. Each k-mer has a k–1-base overlap with adjacent k-mers in the sequence.

Pellow et al. (2016) use this redundancy to detect false positives in a Bloom filter representation of the de Bruijn Graph. Whenever they want to determine whether a k-mer x is present in the de Bruijn Graph, they first query the Bloom filter for x. If the Bloom filter indicates that x is not present, then they know that x is not in the de Bruijn Graph. If, however, the Bloom filter indicates that x might be in the de Bruijn Graph, they then query the Bloom filter for every possible k-mer that overlaps x in k–1 bases. If the Bloom filter indicates that none of these k-mers is part of the de Bruijn Graph, then x is very likely to be a false positive. If the Bloom filter returns true for at least one of the k-mers overlapping with x, then they conclude that x is very likely to be in the de Bruijn Graph.

Pellow et al. (2016) present two versions of the k-mer Bloom filter, a one-sided k-mer Bloom filter and a two-sided k-mer Bloom filter. The one-sided k-mer Bloom filter only looks for the presence of a single overlapping neighbor out of the eight possible neighbors (four on each side) of a k-mer x. The one-sided k-mer Bloom filter achieves a smaller false-positive rate than a standard Bloom filter using the same space.

The two-sided k-mer Bloom filter achieves an even lower false-positive rate by requiring that there is an overlapping k-mer present on either side of x. However, this approach can result in false-negative results for k-mers that are at the edges of reads, since the k-mers at the edges might not have neighbors on both sides.

The two-sided k-mer Bloom filter deals with the k-mers at the edges of reads (i.e. start and end k-mers) specially. It maintains a separate list that contains all the k-mers that occur at the beginning or end of a read. While constructing the k-mer Bloom filter, the first and last k-mer of each read are stored in separate lists. During a query for x, if it finds a neighboring k-mer on only one side of x, then it checks whether x is in the list of edge k-mers. If yes, then it returns positive; else it returns negative.

2.4 Lower bounds on weighted de Bruijn graph representation

In the experiments, we perform in Section 4, we find that deBGR is practically exact from a navigational perspective (i.e. it yields zero errors in terms of topology or abundance). It is useful, therefore, to keep in mind some lower bounds for what is achievable in representing the weighted de Bruijn Graph exactly from a navigational perspective. We know that a navigational structure for the unweighted de Bruijn Graph requires at least 3.24 bits per kmer (Chikhi et al., 2014), and that exactly representing the counts requires at least $F=\sum _{k\in K}\lceil \hspace{0.17em}{\text{log}}_2(f_k)\rceil$ bits where K is the set of k-mers in a dataset and f_k is the frequency of k-mer k, so that a reasonable lower bound would be $3.24+\frac{F}{\left|K\right|}$ bits per k-mer. To make such a representation efficient would likely require more space (e.g. a fast way to index the encoded, variable-size frequency data).

We consider what this bound implies for the dataset GSM984609 in Section 4. Here, we have 1 146 347 598 distinct k-mers and $F=$ 1 119 742 769, yielding a lower bound of $\approx 4.217$ bits per k-mer for an exact navigational representation of this weighted de Bruijn Graph. Approaching such a bound closely, is, of course, a challenge. For example, the cosmo¹https://github.com/cosmo-team/cosmo implementation of the BOSS data structure requires $\approx 5.995$ bits per k-mer on this dataset, but does not encode the weight of each edge. If we couple this with an array of fixed-size counters large enough to represent the frequency distribution losslessly (for this dataset, 23 bits per k-mer), it yields a representation requiring $\approx 28.995$ bits per k-mer. deBGR, on the other hand, requires 26.52 bits per k-mer. Thus, this example shows that there is still a considerable gap between what existing approaches achieve and the absolute theoretical lower bound for an exact navigational representation of a weighted de Bruijn Graph. However, deBGR is dynamic, supports membership queries, and provides efficient access (expected $O(1)$) to k-mer abundances.

3 Materials and methods

We begin by first presenting an invariant of de Bruijn Graphs that we exploit in our compact de Bruijn Graph representation. We then describe how we use this invariant to extend Squeakr (Pandey et al., 2017b) to create a near-exact representation of the weighted de Bruijn Graph.

3.1 A weighted de Bruijn graph invariant

This section explains the structure of weighted de Bruijn Graphs that we exploit to correct errors in approximate weighted de Bruijn Graph representations, such as that provided by Squeakr.

Definition 1. For a k-mer x, we will denote its reverse complement as $x^{-1}$. The canonical form of a k-mer x, denoted $\widehat{x}$, is the lexicographically smaller of x and $x^{-1}$. For two k-mers x and y, we write $x\simeq y$ if $\widehat{x}=\widehat{y}$.

A read is a string of bases over the DNA alphabet A, C, T, and G.

Definition 2. The weighted de Bruijn Graph G of k-mers for a set of reads R has a node $\widehat{n}$ for each $(k-1)$-mer n that occurs in R. For each k-mer $b_{1}x{b}_2$ in R, where b₁ and b₂ are bases and x is a $(k-2)$-mer, there is an edge $\widehat{b_{1}x{b}_2}$ connecting the nodes $\widehat{b_{1}x}$ and $\widehat{x{b}_2}$. The abundance of an edge $\widehat{e}$, denoted $a(\widehat{e})$, is the number of times that $\widehat{e}$ (i.e. e or $e^{-1}$) occurs in R.

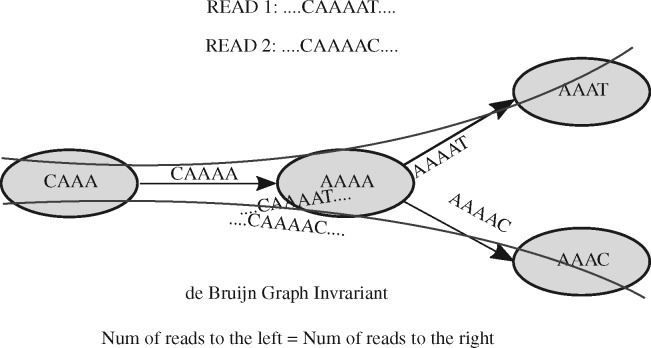
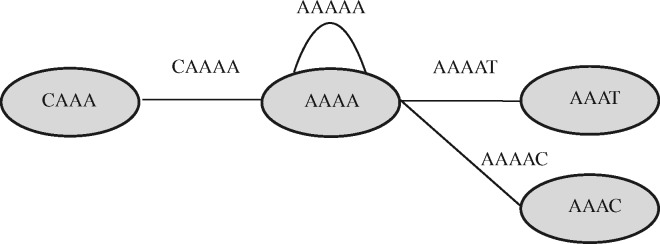
In this formalization, a read of length $\ell$ corresponds to a walk of length $\ell -k$ edges in the de Bruijn graph. Figure 1 shows two reads in the de Bruijn graph before canonicalization, and Figure 2 shows the edges induced by those reads after canonicalization.

Fig. 1.

Weighted de Bruijn Graph invariant. The nodes are 4-mers and edges are 5-mers. The nodes and edges are drawn from Read1 and Read2 mentioned in the figure. The solid curve shows the read path. The nodes/edges are not canonicalized

Fig. 2.

Types of edges in a de Bruijn Graph. The nodes are 4-mers and edges are 5-mers. For node AAAA, CAAAA is a left edge and AAAAT, AAAAC are right edges. We introduced another edge AAAAA in order to show a duplex edge. All the nodes/edges are canonicalized and the graph is bi-directional

Definition 3. For a node $\widehat{n}$ and edge $\widehat{e}$ , we say that $\widehat{e}$ is a duplex edge of $\widehat{\text{n}}$ if there exist bases b and $b\prime$ (and possibly $b=b\prime$ ) such that $\widehat{e}\simeq b\widehat{n}$ and $\widehat{e}\simeq \widehat{n}b\prime$ . We say that $\widehat{e}$ is a left edge of $\widehat{\text{n}}$ if $\widehat{e}$ is not a duplex edge of $\widehat{n}$ and there exists a base b such that $\widehat{e}\simeq b\widehat{n}$ . Similarly, $\widehat{e}$is aright edge of$\widehat{\text{n}}$if$\widehat{e}$is not a duplex edge of$\widehat{n}$and there exists a base b such that$\widehat{e}\simeq \widehat{n}b$.

There are several subtleties to this definition. Left, right, and duplex are defined relative to a node $\widehat{n}$. An edge $\widehat{e}$ connecting nodes $\widehat{n_1}$ and $\widehat{n_2}$ may be a left edge of $\widehat{n_1}$ and a right edge of $\widehat{n_2}$, or a left edge of both $\widehat{n_1}$ and $\widehat{n_2}$, or any other combination. Note also that left, right, and duplex are mutually exclusive—every edge of $\widehat{n}$ is exactly one of left, right, or duplex, with respect to $\widehat{n}$.

Our compact representation of the de Bruijn graph is based on the following observation:

Observation 1. Let $\widehat{e_1},\widehat{e_2},\dots ,\widehat{e_{\ell }}$ be the sequence of edges in a walk corresponding to a read, and $\widehat{n_0},\dots ,\widehat{n_{\ell }}$ the corresponding sequence of nodes in the walk. Then for $i=1,\dots ,\ell -1,\hspace{0.17em}\widehat{e_i}$ and $\widehat{e_{i+1}}$ cannot both be left edges of $\widehat{n_i}$ , nor can they both be right edges of $\widehat{n_i}$.

In other words, whenever a read arrives at a node $\widehat{n}$ via a left edge of $\widehat{n}$, it must depart via a right or duplex edge of $\widehat{n}$, and whenever it arrives via a right edge of $\widehat{n}$, it must depart via a left or duplex edge of $\widehat{n}$. (When a walk arrives via a duplex edge, it may leave via any kind of edge.) This is because two successive edges of the walk correspond to a substring $b_{1}n{b}_2$ of the read, where b₁ and b₂ are bases and n is a $(k-1)$-mer. If $\widehat{n}=n$, then $\widehat{b_{1}n}$ is a left (or duplex) edge of $\widehat{n}$ and $\widehat{n{b}_2}$ is a right (or duplex) edge of $\widehat{n}$. If $\widehat{n}=n^{-1}$, then $\widehat{b_{1}n}\simeq \widehat{n}{b}_1^{-1}$ is a right (or duplex) edge of $\widehat{n}$, and $\widehat{n{b}_2}\simeq b_2^{-1}\widehat{n}$ is a left (or duplex) edge of $\widehat{n}$.

The following lemma implies that duplex edges are rare, since only nodes of a special form can have duplex edges.

Lemma 1. If a node $\widehat{n}$ has a duplex edge, then either (1) $n=n^{-1}$ or (2) $\widehat{n}$ is equal to either $A^{k-1}$ or $C^{k-1}$ , where A and C are the DNA bases.

Proof. Suppose node $\widehat{n}$ has a duplex edge $\widehat{e}$. Without loss of generality, we can assume $\widehat{n}=n$ (by replacing n with $n^{-1}$ if necessary). Then there exist (possibly equal) bases b and $b\prime$ such that $bn\simeq \widehat{e}\simeq nb\prime$, i.e., $bn\simeq nb\prime$. Let $n=n_1\cdots n_{k-1}$, i.e., n_i are the bases constituting n. Then there are two cases:

• $bn=nb\prime$. In this case, $b=n_1=n_2=\cdots =n_{k-1}=b\prime$, i.e. n is a string of equal bases. Thus, n is equivalent to $A^{k-1}$ or $C^{k-1}$.

• $bn=b{\prime }^{-1}{n}^{-1}$. Thus, $n=n^{-1}$.

We call nodes that can have duplex edges duplex nodes, for example see Figure 2.

We say that a walk, path, or cycle is left-right-alternating if, for every successive pair of edges $\widehat{e}$ and $\widehat{e\prime }$ in the path, walk, or cycle, one is a left edge of $\widehat{n}$ and one is a right edge of $\widehat{n}$, where $\widehat{n}$ is the node common to $\widehat{e}$ and $\widehat{e\prime }$. We say that nodes $\widehat{n}$ and $\widehat{n\prime }$ have left-right-alternating distance d if the shortest left-right-alternating path from $\widehat{n}$ to $\widehat{n\prime }$ has length d.

We now explain the main invariant used in our compact weighted de Bruijn Graph representation, as illustrated in Figure 1.

This observation leads to the following invariant.

Theorem 1 (The weighted de Bruijn Graph invariant). Let$\mathcal{R}$be a set of reads that does not include any duplex edges. Let$a(\widehat{e})$be the number of occurrences of the edge$\widehat{e}$in a set of reads. Let$\ell (\widehat{n})$be the number of reads that begin or end with a left edge of$\widehat{n}$, and$r(\widehat{n})$the number of reads that begin or end with a right edge of$\widehat{n}$. Let$s(\widehat{e})$be 1 if$\widehat{e}$is a self-loop, and 0 otherwise. Let$\widehat{n}$be a node and assume, WLOG, that$\widehat{n}=n$. Then

$$\left({\displaystyle \sum _{{}_{\begin{array}{c}b\in \{A,C,\\ G,T\}\end{array}}}{2}^{s(\widehat{bn})}a(\widehat{bn})}\right)-\ell (\widehat{n})=\left({\displaystyle \sum _{{}_{\begin{array}{c}b\in \{A,C,\\ G,T\}\end{array}}}{2}^{s(\widehat{nb})}a(\widehat{nb})}\right)-r(\widehat{n}).$$

Proof. We argue the invariant for a single read. The overall invariant is established by summing over all the reads.

Let W be a read. Since W contains no duplex edges, it corresponds to a left-right alternating walk in the de Bruijn Graph. Thus, every time W visits $\widehat{n}$, it must arrive via a right edge of $\widehat{n}$ and depart via a left edge of $\widehat{n}$ (or vice versa), unless W starts or ends at $\widehat{n}$. We call an arrival at or departure from $\widehat{n}$ a threshold. Each occurrence of $\widehat{n}$ in W corresponds to two thresholds (except with the possible exception of occurrences of $\widehat{n}$ at the beginning or end of W). We call an arrival at or departure from $\widehat{n}$ via a left edge of $\widehat{n}$ a left threshold of $\widehat{n}$, and define right thresholds similarly.

Thus, ignoring occurrences of $\widehat{n}$ at the beginning or end of W, the number of left thresholds of $\widehat{n}$ must equal the number of right thresholds of $\widehat{n}$. Let $L_W(\widehat{n})$ and $R_W(\widehat{n})$ be the number of left and right thresholds, respectively, of $\widehat{n}$ in W. Let ${\ell }_W(\widehat{n})$ be the number of left thresholds of occurrences of $\widehat{n}$ at the beginning or end of W, and define $r_W(\widehat{n})$ analogously for right thresholds of $\widehat{n}$. Thus we have the equality

$$L_W(\widehat{n})-{\ell }_W(\widehat{n})=R_W(\widehat{n})-r_W(\widehat{n}).$$

Each occurrence of a left edge $\widehat{e}$ of $\widehat{n}$ in W corresponds to a single threshold of $\widehat{n}$, unless $\widehat{e}$ is a loop connecting $\widehat{n}$ to itself, in which case each occurrence of $\widehat{e}$ corresponds to two thresholds. Note that, since by assumption $\widehat{e}$ is not a duplex edge, if it is a loop, it corresponds to two left thresholds or two right thresholds of $\widehat{n}$ (i.e. it does not correspond to one left and one right threshold of $\widehat{n}$). Let $a_W(\widehat{e})$ be the number of occurrences of $\widehat{e}$ in W. Then

$$L_W(\widehat{n})={\displaystyle \sum _{\begin{array}{c}b\in \{A,C,\\ G,T\}\end{array}}{2}^{s(\widehat{bn})}{a}_W(\widehat{bn})}$$

and

$$R_W(\widehat{n})=\sum _{\begin{array}{c}b\in \{A,C,\\ G,T\}\end{array}}{2}^{s(\widehat{nb})}{a}_W(\widehat{nb}).$$

Thus

$$\sum _{\begin{array}{c}b\in \{A,C,\\ G,T\}\end{array}}{2}^{s(\widehat{bn})}{a}_W(\widehat{bn})-{\ell }_W(\widehat{n})=\sum _{\begin{array}{c}b\in \{A,C,\\ G,T\}\end{array}}{2}^{s(\widehat{nb})}{a}_W(\widehat{nb})-r_W(\widehat{n}).$$

The final result is obtained by summing over all reads $W\in \mathcal{R}$. □

3.2 deBGR: a compact de Bruijn graph representation

We now describe our compact weighted de Bruijn Graph representation. Given a set R of reads, we build counting quotient filters representing the functions a, $\ell$, and r. For $\ell$ and r, we use exact CQFs, so these tables will have no errors. Since $\ell$ and r have roughly one entry for each read, these tables will be relatively small (see Section 3.6). For a, we build a space-efficient approximate CQF, which we call $a_{\text{CQF}}$. Since we build exact representations of $\ell$ and r, we will use $\ell$ and r to refer to both the actual functions and our tables representing these functions. The CQF guarantees that, for every edge $\widehat{e},\hspace{0.17em}{a}_{\text{CQF}}[h(\widehat{e})]\ge a(\widehat{e})$. We then compute a table c of corrections to $a_{\text{CQF}}$ (we explain how to compute c below). After computing c, a query for the abundance of an edge $\widehat{e}$ returns $g(\widehat{e})$, where g is defined to be $g(\widehat{e})=a_{\text{CQF}}[h(\widehat{e})]-c[\widehat{e}]$. Thus, since c is initially 0, we initially have that $g(\widehat{e})\ge a(\widehat{e})$ for all $\widehat{e}$.

Definition 4. We say that g satisfies the weighted de Bruijn Graph invariant for $\widehat{\text{n}}$ if

$$\left({\displaystyle \sum _{{}_{\begin{array}{c}b\in \{A,C,\\ G,T\}\end{array}}}{2}^{s(\widehat{bn})}g(\widehat{bn})}\right)-\ell [\widehat{n}]=\left({\displaystyle \sum _{{}_{\begin{array}{c}b\in \{A,C,\\ G,T\}\end{array}}}{2}^{s(\widehat{nb})}g(\widehat{nb})}\right)-r[\widehat{n}].$$

3.3 Local error-correction rules

We first describe our local algorithm for correcting errors in g. This algorithm can be used to answer arbitrary k-mer membership queries by correcting errors on the fly. Thus this algorithm can be used to perform queries on a dynamic weighted de Bruijn Graph.

The process for computing c maintains the invariant that $g(\widehat{e})\ge a(\widehat{e})$ for every edge $\widehat{e}$ in the weighted de Bruijn Graph, while using the following three rules to correct errors in g.

1. If we know that g is correct for all but one edge of some node $\widehat{n}$, then we can use the weighted de Bruijn Graph invariant to solve for the true abundance of the remaining edge.

2. Since $g(\widehat{e})\ge a(\widehat{e})$ for all $\widehat{e}$, if (1) g satisfies the weighted de Bruijn Graph invariant for some node $\widehat{n}$ and, (2) we know that g is correct for all of $\widehat{n}$’s left edges, then we can conclude that g is correct for all of $\widehat{n}$’s right edges, as well (and vice versa for ‘left’ and ‘right’).

3. If $\sum _{b\in \{A,C,G,T\}}{2}^{s(\widehat{bn})}g(\widehat{bn})=\ell [\widehat{n}]$ and $r[\widehat{n}]=0$, then the abundance of all of $\widehat{n}$’s right edges must be 0 (and vice versa for ‘right’ and ‘left’).

Given an initial set C of edges for which we know g is correct, we can use the above rules to correct errors in g and to expand C. But how can we get the initial set of edges C that is required to bootstrap the process? Our algorithm uses two approaches.

First, whenever $g(\widehat{e})=0$, it must be correct. This is because g can never be smaller than a. Thus, the above rules always apply to leaves of the approximate weighted de Bruijn Graph and, more generally, to any nodes that have only left or only right edges.

Leaves and nodes with only right or only left edges are not sufficient to bootstrap the error correction process, however, because weighted de Bruijn Graphs can contain cycles in which each node has both left and right edges that are part of the cycle. Starting only from leaves and one-sided nodes, the above rules are not sufficient to infer that g is correct on any edge in such a cycle, because each node in the cycle will always have a left and right edge for which g is not known to be correct.

We can overcome this problem by exploiting the random nature of errors in the CQF to infer that g is correct, with very high probability, on almost all edges of the approximate weighted de Bruijn Graph, including many edges that are part of cycles.

Theorem 2. Suppose that errors in g are independent and random with probability $\epsilon$. Suppose $\widehat{n}$ is not part of a left-right-alternating cycle of size less than d. Suppose also that g satisfies the weighted de Bruijn Graph invariant at every node within a left-right-alternating distance of $\lceil d/2\rceil$ from $\widehat{n}$. Then the probability that g is incorrect for any edge attached to $\widehat{n}$ is less than ${(4\epsilon )}^d$.

Proof. Since g is never smaller than a, if g is incorrect for a left edge of some node $\widehat{n}$ and g satisfies the weighted de Bruijn Graph invariant at $\widehat{n}$, then g must be incorrect for at least one right edge of $\widehat{n}$. (And symmetrically for right/left). Thus, if g is incorrect for some edge attached to $\widehat{n}$, then since g satisfies the weighted de Bruijn Graph invariant for all nodes within a radius $d/2$ of $\widehat{n}$, it must be the case that g is incorrect for every edge along some left-right-alternating path of length at least d edges. Since $\widehat{n}$ is not part of a cycle of length less than d, all the edges in this path must be distinct. Since errors in g are independent and have probability $\epsilon$, the probability of this occurring along any single path is at most ${\epsilon }^d$.

Since each node of the weighted de Bruijn Graph has at most 4 left and 4 right edges, the total number of left-right-alternating paths of length d centered on node $\widehat{n}$ is at most $4^d$. Hence, by a union bound, the probability that such a path exists is at most ${(4\epsilon )}^d$. □

We can use this theorem to infer, with high probability, that g is correct for many edges in the graph. We can choose larger or smaller d to control the probability that we incorrectly infer that g is correct on an edge. By choosing $d\ge \text{log}\hspace{0.17em}n/\hspace{0.17em}\text{log}\hspace{0.17em}(1/4\epsilon )$, where n is the number of edges in the approximate weighted de Bruijn Graph, we can make the expected number of such edges less than 1.

On the other hand, we expect many nodes from actual weighted de Bruijn Graphs to meet the criteria of Theorem 2. The vast majority of nodes in a weighted de Bruijn Graph are simple, i.e., they have exactly 1 left edge and 1 right edge. Therefore, for most nodes, there are only O(d) nodes within left-right-alternating distance $\lceil d/2\rceil$. Thus, for most nodes, the probability that they fail to meet the criteria is $O(d\epsilon )$. When $d=\text{log}\hspace{0.17em}n/\hspace{0.17em}\text{log}\hspace{0.17em}(1/4\epsilon )$, this becomes $O(\epsilon \hspace{0.17em}\text{log}\hspace{0.17em}n/\hspace{0.17em}\text{log}\hspace{0.17em}(1/4\epsilon ))$. This means that for most values of n and $\epsilon$ that arise in practice, the vast majority of nodes will meet the criteria of Theorem 2. For example, when $n\le 2^{40}$ and $\epsilon \le 2^{-8}$, the fraction of nodes expected to fail the criteria of Theorem 2 is less than 3%.

The above analysis suggests that large cycles (i.e. cycled of length at least $\text{log}\hspace{0.17em}n/\hspace{0.17em}\text{log}\hspace{0.17em}(1/4\epsilon )$) in the weighted de Bruijn Graph will have at least a few nodes that meet the criteria of Theorem 2, so the correction process can bootstrap from those nodes to correct any other incorrect edges in the cycle. Small cycles (i.e. of size less than $\text{log}\hspace{0.17em}n/\hspace{0.17em}\text{log}\hspace{0.17em}(1/4\epsilon )$), however, still pose a problem, since Theorem 2 explicitly forbids nodes in small cycles.

We can handle small cycles as follows. Any kmer that is part of a cycle of length q < k must be periodic with periodicity q, i.e. it must be a substring of a string of the form $x^{\lceil k/q\rceil }$, where x is a string of length q. Thus, small cycles are quite rare. We can detect k-mers that might be involved in a cycle of length less than d during the process of building $a_{\text{CQF}}$ and record their abundance in a separate, exact CQF. Since periodic k-mers are rare, this exact CQF will not consume much space. Later, during the correction phase, we can add all the edges corresponding to these k-mers to the set C.

As mentioned before, the weighted de Bruijn Graph invariant only applies to nodes without duplex edges. Our weighted de Bruijn Graph representation handles duplex edges as follows. Suppose a read corresponds to a walk visiting the sequence of nodes $\widehat{n_1},\widehat{n_2},\dots ,\widehat{n_q}$. We treat every time the read visits a duplex node as the end of one read and the beginning of a new read. By breaking up reads whenever they visit a duplex node, we ensure that whenever a walk arrives at a node via a left or right edge, it either ends or departs via a left or right edge. Thus we can use the weighted de Bruijn Graph invariant to correct errors in $a_{\text{CQF}}$ as described above.

3.4 Global, CQF-specific error-correction rules

So far, our error-correction algorithm uses only local information about discprencies in the weighted de Bruijn Graph invariant to correct errors. It also uses the CQF in a black-box fashion—the same algorithm could work with, for example, a counting Bloom filter approximation of a.

We now describe an extension to our error-correction algorithm that, in our experiments, enables it to correct all errors in the approximate weighted de Bruijn Graph. This extension exploits the fact that the CQF represents a multiset S by storing, exactly, the multiset h(S), where h is a hash function. It also performs a global analysis of the graph in order to detect more errors than can be detected by the local algorithm. Thus, this algorithm is appropriate for applications that need a static, navigational weighted de Bruijn Graph representation.

Note that applications can mix-and-match the two error correction algorithms. Both the local and global algorithms can be run repeatedly, in any order, and even intermixed with intervening modifications to the weighted de Bruijn Graph (e.g. after inserting additional k-mers).

For a read set R, let K be the set of distinct k-mers occurring in R. During the k-mer counting phase, every time we see a k-mer e, we increment the counter associated with $h(\widehat{e})$ in $a_{\text{CQF}}$. Thus, after counting is completed, for any edge $\widehat{e}$,

$$a_{\text{CQF}}[h(\widehat{e})]=\sum _{\widehat{x}\in K\cap h^{-1}(\widehat{e})}a(\widehat{x})$$

where $h^{-1}(\widehat{e})=\left\{\widehat{x}\right|h(\widehat{x})=h(\widehat{e})\}$.

The above equation enables us to use knowledge about the abundance of an edge $\widehat{e}$ to infer information about the abundance of other edges that collide with $\widehat{e}$ under the hash function h. For example, if we know that we have inferred the true abundance for all but one edge in some set $h^{-1}(\widehat{e})$, then we can use this equation to infer the abundance of the one remaining edge.

Our algorithm implements this idea as follows. Recall that, with high probability, whenever an edge $\widehat{x}\in C$, then $g(\widehat{x})=a(\widehat{x})$. Thus we can rewrite the above equation as:

$$a_{\text{CQF}}[h(\widehat{e})]-\sum _{\widehat{x}\in C\cap h^{-1}(\widehat{e})}g(\widehat{x})=\sum _{\widehat{x}\in \overline{C}\cap h^{-1}(\widehat{e})}a(\widehat{x}),$$

where $\overline{C}=K\mathrm{\setminus }C$. For convenience, write $z(\widehat{e})=a_{\text{CQF}}[h(\widehat{e})]-\sum _{\widehat{x}\in C\cap h^{-1}(\widehat{e})}g(\widehat{x})$. Note that z factors through h, i.e., if $h(\widehat{x})=h(\widehat{y})$, then $z(\widehat{x})=z(\widehat{y})$, and hence $z(\widehat{x})$ is the same for all $\widehat{x}$ in some set $h^{-1}(\widehat{e})$.

The above equation implies two invariants that our algorithm can use to infer additional information about edge abundances:

• For all $\widehat{e},\hspace{0.17em}a(\widehat{e})\le z(\widehat{e})$. This is because, by definition, $a(\widehat{e})\ge 0$. Thus, if the algorithm ever finds an edge $\widehat{e}$ such that $g(\widehat{e})>z(\widehat{e})$, then it can update $c[\widehat{e}]$ so that $g(\widehat{e})=z(\widehat{e})$.

• If, for some $\widehat{e}$, $\sum _{\widehat{x}\in \overline{C}\cap h^{-1}(\widehat{e})}g(\widehat{x})=z(\widehat{e})$, then $g(\widehat{x})=a(\widehat{x})$ for all $x\in \overline{C}\cap h^{-1}(\widehat{e})$. This is because $0\le a(\widehat{x})\le g(\widehat{x})$ for all $\widehat{x}$. Thus, in this case, the algorithm can add all the elements of $x\in \overline{C}\cap h^{-1}(\widehat{e})$ to C.

3.5 An algorithm for computing abundance corrections

Algorithm 1 in the Supplementary Material shows our algorithm for computing c based on these observations. The algorithm is a standard work queue algorithm—it creates a work queue of edges that might have abundance errors and then pulls items off the worklist, looking for opportunities to apply the above rules. To save RAM, the algorithm computes the complement M of C, since for typical error rates C would contain almost all the edges in the weighted de Bruijn Graph.

The worst-case running time of the algorithm is $O(n^{1+1/\hspace{0.17em}\text{log}\hspace{0.17em}(1/4\epsilon )})$ but, for real weighted de Bruijn Graphs, the algorithm runs in $O(n\hspace{0.17em}\text{log}\hspace{0.17em}n/\hspace{0.17em}\text{log}\hspace{0.17em}(1/4\epsilon ))$ time. The running time is dominated by initializing M, which requires traversing the graph and and finding any nodes within distance $\text{log}\hspace{0.17em}n/\hspace{0.17em}\text{log}\hspace{0.17em}(1/4\epsilon$) of a weighted de Bruijn Graph invariant discrepancy. Since real weighted de Bruijn Graphs have nodes mostly of degree 2, there will usually be $O(d)=O(\text{log}\hspace{0.17em}n/\hspace{0.17em}\text{log}\hspace{0.17em}(1/4\epsilon ))$ such nodes, giving a total running time of $O(n\hspace{0.17em}\text{log}\hspace{0.17em}n/\hspace{0.17em}\text{log}\hspace{0.17em}(1/4\epsilon ))$.

When used to perform a local correction as part of an abundance query, we use the same algorithm, but restrict it to examine the region of the weighted de Bruijn Graph within O(d) hops of the edge being queried. In the worst case, this could require examining the entire graph, resulting in the same complexity as above. In the common case, however, the number of nodes within distance d of the queried edge is O(d), so the running time of a local correction is $O(\text{log}\hspace{0.17em}n/\hspace{0.17em}\text{log}\hspace{0.17em}(1/4\epsilon ))$.

The space for deBGR can be analyzed as follows. To represent a multiset S with false positive rate $\epsilon$, the CQF takes $O(|S|\hspace{0.17em}{\text{log}}_{2}1/\epsilon +C(S))$, where C(S) is the sum of the logs of the counts of the items in S. To represent S exactly, assuming that each element of S is a b-bit string, takes $O(|S|\hspace{0.17em}{\text{log}}_{2}b/|S|+C(S))$. So let K be the multiset of k-mers, and let $E\subseteq K$ be the multiset of k-mer instances in K that occur at the beginning or end of a read or visit a duplex node. Then the space required to represent $a_{\text{CQF}}$ is $O(|K|\hspace{0.17em}\text{log}\hspace{0.17em}1/\epsilon +C(K))$. The space required for $\ell$ and r is $O(|E|\hspace{0.17em}\text{log}\hspace{0.17em}{4}^k/|E|+C(E))$. Note that since $E\subseteq K$, $C(E)\le C(K)$. The space required to represent c is $O(\epsilon |K|\hspace{0.17em}\text{log}\hspace{0.17em}{4}^k/\epsilon |K|+C(K))$. Thus the total space required for deBGR is

$$O(|K|\hspace{0.17em}\text{log}\hspace{0.17em}\frac{1}{\epsilon }+|E|\hspace{0.17em}\text{log}\hspace{0.17em}\frac{4^k}{\left|E\right|}+\epsilon |K|\hspace{0.17em}\text{log}\hspace{0.17em}\frac{4^k}{\epsilon \left|K\right|}+C(K)).$$

3.6 Implementation

We extended Squeakr to construct the exact CQFs $\ell$ and r as described above, in addition to the approximate CQF $a_{\text{CQF}}$ that it already built. We then wrote a second tool to compute c from $a_{\text{CQF}},\hspace{0.17em}\ell$, and r. Our prototype handles duplex nodes and small cycles as described. Our current prototype uses a standard hash table to store M and standard set to store Q. Also, we use a standard hash table to store c. An exact CQF would be more space efficient, but c is small enough in our experiments that it doesn’t matter.

3.7 Size of the first and last tables

We explore, through simulation, how the sizes of the first and last tables $\ell$ and r grow with the coverage of the underlying data. Here, for simplicity, we focus on genomic (rather than transcriptomic) data, as coverage is a well-defined notion. We simulated reads generated from the Escheria coli (E. coli) (strain E1728) reference genome at varying levels of coverage, and recorded the number of total distinct k-mers, as well as the number of distinct k-mers in $\ell$ and r (Fig. 3). Reads were simulated using the Art Huang et al. (2012) read simulator, using the error profiles 125 bp, paired-end reads sequences on an Illumina HiSeq 2500. As expected, the number of distinct k-mers in all of the tables grows with the coverage (due to sequencing error), Yet, even at 80x coverage, the $\ell$ and r tables, together, contain fewer than 25% of total distinct k-mers. On the experimental data examined in Section 4, the $\ell$ and r tables, together, require between than 18–28% of the total space required by the deBGR structure.

Fig. 3.

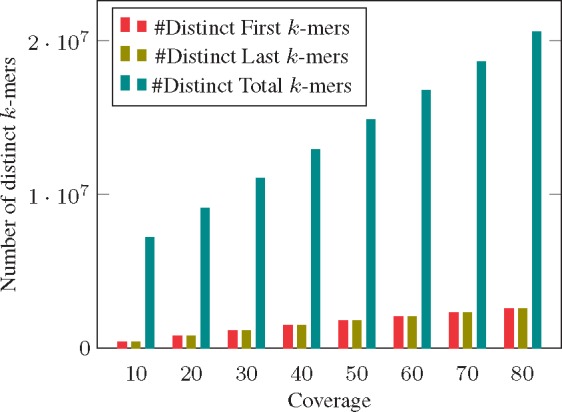
Total number of distinct k-mers in First QF, Last QF, and Main QF with increasing coverage of the same dataset. We generate dataset simulations using Huang et al. (2012)

4 Evaluation

In this section, we evaluate deBGR, as described in Section 3.

We evaluate deBGR in terms of space and accuracy. The space is the size of the data structure(s) needed to represent the weighted de Bruijn Graph. The accuracy is the measure of how close the weighted de Bruijn Graph representation is to the actual weighted de Bruijn Graph. We also report the time taken by deBGR to construct the weighted de Bruijn Graph representation, perform global abundance correction, and perform local abundance correction for an edge.

As described in Section 3.6, deBGR uses two exact counting quotient filters ($\ell$ and r) in addition to the approximate counting quotient filter that stores the number of occurrences for each k-mer. The error-correction algorithm then computes a table c of corrections. In our evaluation we report the total size of all these data structures, i.e. $a_{\text{CQF}},\hspace{0.17em}\ell$, r, and c.

We measure the accuracy of systems in terms of errors in the weighted de Bruijn Graph representation. There are two kind of errors in the weighted de Bruijn Graph, abundance errors and topological errors. An abundance error is an error when the weighted de Bruijn Graph representation returns an over-count for the query k-mer (deBGR never resulted in an undercount in any of our experiments). Topological errors are abundance error for edges whose true abundance is 0. Topological errors are also known as false-positives.

In both cases, we report the number of reachable errors. Let G be the true weighted de Bruijn Graph and $G\prime$ our approximation. Since g is never smaller than a, the set of edges in $G\prime$ is a superset of the set of edges in G. An error on edge $\widehat{e}$ of $G\prime$ is reachable if there exists a path in $G\prime$ from $\widehat{e}$ to an edge that is also in G. Note that reachable false positives are not the same as Chikhi et al.’s notion of critical false positives (Chikhi and Rizk, 2013). Critical false positives are false positives that are false positive edges that share a node with a true positive edge. Reachable false positives, on the other hand, may be multiple hops away from a true edge of the weighted de Bruijn Graph.

We compare deBGR to Squeakr in both its approximate and exact configurations. Recall that the exact version of Squeakr stores k-mers in a CQF using a 2k-bit invertible hash function, so that it has no false positives. We use the exact version of Squeakr as the reference weighted de Bruijn Graph for computing the number of reachable errors in Squeakr and deBGR.

We do not compare deBGR against other Bloom filter based de Bruijn Graph representations (Chikhi and Rizk, 2013; Salikhov et al., 2013) because Bloom filter based de Bruijn Graph representations do not have abundance information.

4.1 Experimental setup

All experiments use 28-mers. In all our experiments, the counting quotient filter was configured with a maximum allowable false-positive rate of 1/256.

All the experiments are performed in-memory. We use several datasets for our experiments, which are listed in Table 2. All the experiments were performed on an Intel(R) Xeon(R) CPU (E5-2699 v4 @ 2.20GHz with 44 cores and 56MB L3 cache) with 512GB RAM and a 4TB TOSHIBA MG03ACA4 ATA HDD.

Table 2.

Datasets used in our experiments

Dataset	File size	#Files	#k-mer instances	#Distinct k-mers
GSM984609	26	12	19662773 330	1146347598
GSM981256	22	12	16470774825	1118090824
GSM981244	43	4	37897872977	1404643983
SRR1284895	33	2	26235129875	2079889717

Note: The file size is in GB. All the datasets are compressed with gzip compression.

4.2 Space versus accuracy trade-off

In Table 3, we show the space needed and the accuracy (in terms of navigational errors) offered in representing the weighted de Bruijn Graph by deBGR and the exact and approximate versions of Squeakr. For deBGR, Table 3 gives the final space usage (i.e. $a_{\text{CQF}},\hspace{0.17em}\ell$, r, and c). deBGR offers 100% accuracy and takes 48–52% less space than the exact version of Squeakr that also offers 100% accuracy. deBGR takes 18–28% more space than the approximate version but the appropriate version has millions of navigational errors.

Table 3.

Space versus Accuracy trade-off in Squeakr and deBGR

System	Dataset	Space	Navigational errors
		(bits/k-mer)	Topological	Abundance
Squeakr	GSM984609	18.9	14263577	16655318
Squeakr (exact)		50.8	0	0
deBGR		26.5	0	0
Squeakr	GSM981256	19.4	13591254	15864754
Squeakr (exact)		52.1	0	0
deBGR		27.1	0	0
Squeakr	GSM981244	30.9	10462963	12257261
Squeakr (exact)		79.8	0	0
deBGR		37.0	0	0
Squeakr	SRR1284895	20.9	23272114	27200821
Squeakr (exact)		53.95	0	0
deBGR		25.38	0	0

Note: Topological errors are false-positive k-mers. Abundance errors are k-mers with an over count.

The space required by deBGR in Table 3 is the total space of all data structures ($a_{\text{CQF}},\hspace{0.17em}\ell$, r, and c). In Table 4, we report the maximum number of items stored in auxiliary data structures (see Algorithm 1) while performing abundance correction. This gives an upper bound on the amount of space needed by deBGR to perform abundance correction.

Table 4.

The maximum number of items present in auxiliary data structures, edges (k-mers) in MBI and nodes ($(k-1)$-mers) in work queue as described in the Algorithm 1, during abundance correction

Dataset	#Edges in M	#Edges in work queue (Q)
GSM984609	30815799	76178634
GSM981256	29359913	72606572
GSM981244	22674515	56309858
SRR1284895	50320986	124558299

4.3 Performance

In Table 5, we report the time taken by deBGR to construct the weighted de Bruijn Graph representation and perform global abundance correction. The time information for construction and global abundance correction is averaged over two runs.

Table 5.

Time to construct the weighted de Bruijn Graph, correct abundances globally in the weighted de Bruijn Graph, and perform local correction per edge in the weighted de Bruijn Graph (averaged over 1M local corrections)

Dataset	Construction	Global correction	Local correction
	(seconds)	(seconds)	(microseconds)
GSM984609	6605.65	14857.68	12.93
GSM981256	5470.83	15390.56	18.25
GSM981244	13373.78	22266.86	16.50
SRR1284895	8429.17	41218.85	16.62

We also report the time taken to perform local abundance correction for an edge. The time for local abundance correction per edge is averaged over 1M local abundance corrections. After performing abundance correction, computing $g(\widehat{e})=a_{\text{CQF}}[h(\widehat{e})]-c[\widehat{e}]$ takes 3.45 microseconds on average.

5 Conclusion

We argue that Squeakr, a space-efficient and approximate representation of the weighted de Bruijn Graph can be extended to build a near-exact representation of weighted de Bruijn Graph with almost no space cost. We demonstrate that abundance information in an approximate weighted de Bruijn Graph representation can be used to correct almost all the errors in that representation.

Our representation is based on a simple invariant that all weighted de Bruijn Graphs must satisfy, so we believe this technique is likely to be of use in other weighted de Bruijn Graph applications.

We believe precise abundance information can have a real impact on transcriptome assembly. For example, without error correction, low-abundance transcripts may collide with high-abundance transcripts, causing the low-abundance transcripts to become lost in the noise. Accurate abundance information can enable applications to detect such faint signals and possibly recover such transcripts.

Funding

We gratefully acknowledge support from National Science Foundation grants BBSRC-NSF/BIO-1564917, IIS-1247726, IIS-1251137, CNS-1408695, CCF-1439084, and CCF-1617618, and from Sandia National Laboratories.

Conflict of Interest: none declared.