JDINAC: joint density-based non-parametric differential interaction network analysis and classification using high-dimensional sparse omics data

Abstract

Motivation

A complex disease is usually driven by a number of genes interwoven into networks, rather than a single gene product. Network comparison or differential network analysis has become an important means of revealing the underlying mechanism of pathogenesis and identifying clinical biomarkers for disease classification. Most studies, however, are limited to network correlations that mainly capture the linear relationship among genes, or rely on the assumption of a parametric probability distribution of gene measurements. They are restrictive in real application.

Results

We propose a new Joint density based non-parametric Differential Interaction Network Analysis and Classification (JDINAC) method to identify differential interaction patterns of network activation between two groups. At the same time, JDINAC uses the network biomarkers to build a classification model. The novelty of JDINAC lies in its potential to capture non-linear relations between molecular interactions using high-dimensional sparse data as well as to adjust confounding factors, without the need of the assumption of a parametric probability distribution of gene measurements. Simulation studies demonstrate that JDINAC provides more accurate differential network estimation and lower classification error than that achieved by other state-of-the-art methods. We apply JDINAC to a Breast Invasive Carcinoma dataset, which includes 114 patients who have both tumor and matched normal samples. The hub genes and differential interaction patterns identified were consistent with existing experimental studies. Furthermore, JDINAC discriminated the tumor and normal sample with high accuracy by virtue of the identified biomarkers. JDINAC provides a general framework for feature selection and classification using high-dimensional sparse omics data.

Availability and implementation

R scripts available at https://github.com/jijiadong/JDINAC

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

It is well known that a complex biological process, such as the development and progression of cancer, is seldom attributed to a single molecule. Numerous cellular constituents, such as proteins, DNA, RNA and small molecules do not function in isolation, but rather interact with one another to fulfill particular biological functionality. In the view of network biology (Yoshimura et al., 1998; Zhou et al., 2011), a cellular function is a contextual attribute of quantifiable patterns of interactions between myriad of cellular constituents. Such interactions are not static processes, instead they are dynamic in response to changing genetic, epigenetic and environmental factors (Bandyopadhyay et al., 2010; Califano, 2011). The molecular interactions can be effectively abstracted as a network. In the biological networks, the nodes represent biomolecules (e.g. genes), and the edges represent functional, causal, or physical interactions between the nodes. Differential network analysis aims to identify the difference between the networks under two conditions. Each of the edges in the differential network indicates a change in the connection between two nodes across the two conditions. Thus, differential network analysis becomes an important tool to understand the roles of different modules in complex biological processes, and draws tremendous attention. Typically, differential genetic interactions are a reflection of which cellular processes are differentially important under the studied condition (de la Fuente A, 2010; Ideker and Krogan, 2012).

In the past decade, many methods have been proposed to detect the differential network connection patterns between two condition-specific groups (e.g. patients and health controls). Gambardella et al. (2013) introduced DINA procedure to identify whether a known pathway is differentially co-regulated between different conditions. Yates and Mukhopadhyay (2013) provided a dissimilarity measure that incorporates nearby neighborhood information for biological network hypothesis tests. Recently, Ruan et al. (2015) developed the dGHD algorithm for detecting differential interaction patterns in two-network comparisons. All of the aforementioned methods endeavor to identify whether the global network topology changed significantly between two groups. However, it will be of benefit to reveal critical pairwise molecular or genetic interactions that are responsible for the different physiological or pathological states of an organism in many applications. The identification of such interactions may help us to illuminate the underlying genetic mechanisms of complex diseases (e.g. cancer), to predict drug off-target effects (Evangelidis and Xie, 2014), to develop multi-target anti-cancer therapy (Xie and Bourne, 2015), and to discover clinical biomarkers for disease classification.

To this end, the primary focus in this article is to identify pairwise differential interactions among genes that are most closely related to a certain disease status. Most of such studies first require to divide the data into two separate groups according to the factor of interest. Besides, a specific correlations matrix is often involved to represent the strength of pairwise interaction between nodes in the network. The existing methods mainly fall into two categories. The first category is to compare topological characteristics, such as degree, clustering coefficient of vertices within the network, of the constructed sparse network on grouping specific data (Reverter et al., 2006; Zhang et al., 2009). The main challenge of this approach lies in how to select appropriate threshold for constructing sparse network, although there have been miscellaneous methods proposed to address this challenge (Carter et al., 2004; Elo et al., 2007). To the best of our knowledge, no commonly feasible approach has been available yet. Approaches in the second category normally handle weighted group-specific network to further construct the differential network. In one manner such approach can only concentrate on edge-level to construct edge-difference based differential network (Hudson et al., 2009; Liu et al., 2010; Tesson et al., 2010). On the other hand, it could focus more on finding gene sets and identify correlation pattern's difference between groups. For example, the CoXpress (Watson, 2006) first performs hierarchical clustering with correlation matrix obtained from normal samples (or disease sample), then applies statistical test to determine whether the average correlation within one cluster is higher (or lower) than expected by chance and thus finally identifies the differentially co-expressed gene groups. Similarly, DiffCorr (Fukushima, 2013) identifies the first principal component based ‘eigen-molecules’ in the correlation matrices constructed from the grouped dataset, then performs Fisher z-test between the two groups to discover differential correlation. In addition, Zhao et al. (2014) proposed a direct estimation method (DEDN), which models each condition-specific network using the precision matrix under Gaussian assumption. However, most of the methods mentioned earlier are based on marginal or partial correlation. It can only capture the linear relationship among genes, which could be restrictive in real applications. It is often the case that non-linear relationships exist between genes. Another critical but inadequately addressed issue is how to adjust the confounding factors in the differential network analysis. For instance, the condition-specific label is the length of the survival time of cancer patients, one group are patients with longer survival time and the other group are those with short survival time. Then the age of the patients is a potential confounding factor which needs to be adjusted. If the patients’ ages are different between two groups, it’s hard to know whether the identified differential network is associated with the survival time or the age. Furthermore, how to use the identified network biomarkers to achieve classification still poses great challenge in discriminant analysis especially in high-dimensional settings (He et al, 2016).

To address the challenges in differential network analysis and classification mentioned above using high-dimensional sparse omics data, we propose a Joint density based non-parametric Differential Interaction Network Analysis and Classification (JDINAC) method to identify differential patterns of network activation between condition-specific groups (e.g. patients and health controls). The contribution of our work lies in that we can not only deal with the non-linear relationship between the genes but also adjust the confounding factors in the differential network analysis. Furthermore, JDINAC is free of the assumption of a parametric probability distribution of gene measurements. We compare the ability of identifying differential network of our methods with DiffCorr (Fukushima, 2013), DEDN (Zhao et al., 2014) and Lasso based method. By integrating the logistic regression into our method, our method is capable of accurate classification using high-dimensional sparse data. We also compared the classification performance of our method with Random Forest (RF) (Breiman, 2001), Naive Bayes (NB) and Lasso based methods in both simulation studies and real data example.

2 Materials and methods

Network differential analysis and classification using high-dimensional sparse omics data face several challenges. First, the number of data points n is often much smaller than the number of features p, e.g. p ≫ n problem. Second, the relationship between two biological variables is often non-linear. Third, confounding factors often need to be adjusted in the differential network analysis and classification. Finally, the underlying distribution of biological variable may not follow Gaussian or other probability distribution on which many algorithms are based. JDINAC is proposed to address these problems.

JDINAC assumes that the network-level difference between two biological states comes from the collective effect of differential pairwise gene–gene interactions that can be characterized by conditional joint density of two genes. Formally, assume that we have observed gene-level activities (such as mRNA, methylation or copy number) for p genes measured over individuals. For individual l (l = 1, 2, ⋯, n), the binary response variable is denoted as $Y_l=\{\begin{array}{c}0\hspace{0.17em}\hspace{0.17em}l\in class0\\ 1\hspace{0.17em}\hspace{0.17em}l\in class\hspace{0.17em}1\end{array}$ and the expression level of ith gene is denoted as $x_{li}$. Let $\mathbf{Y}={(Y_1,Y_2,\dots ,Y_n)}^T$ and $\mathbf{X}={(X_1,X_2,\dots ,X_n)}^T$, $X_l={(x_{l1},x_{l2},\dots ,x_{lp})}^T$, (l = 1, 2,⋯, n). $\mathbf{X}$ is a $n\times p$ matrix, p is the total number of genes, and $X_l$ denotes the gene features for individual l. Let P denotes the probability Pr(Y = 1), i.e. P = Pr(Y = 1), and $G_i$ is the ith gene. The JDINAC approach based on the logistic regression model can be constructed as,

$$\text{logit}(P)={\alpha }_0+{\sum }_{k=1}^K{\alpha }_k{Z}_k+{\sum }_{i=1}^p{\sum }_{j>1}^p{\beta }_{ij}\ln \frac{f_{ij}(G_i,G_j)}{g_{ij}(G_i,G_j)},{\sum }_{i=1}^p{\sum }_{j>1}^p\left|{\beta }_{ij}\right|\le c,\hspace{0.17em}c>0,$$

where $Z_k$ ($k=1,\dots ,K$) denote the covariates (e.g. age and gender). $f_{ij}$ and g_ij denote the class conditional joint density of $G_i$ and $G_j$ for class 1 and class 0, respectively, i.e., $((G_i,G_j)|Y=1)\sim f_{ij}$ and $((G_i,G_j)|Y=0)\sim g_{ij}$. The conditional joint densities $f_{ij}(G_i,G_j)$ can indicate the strength of association between $G_i$ and $G_j$ in class 1. Since the number of pairs $(G_i,G_j)$ can be larger than the sample size, the $L_1$ penalty (Tibshirani, 1996) was adopted in this high-dimensional setting. Note that the above formulation can be viewed as an extension of the FANS approach (Fan et al., 2016). Parameters ${\beta }_{ij}\ne 0$ indicate differential dependency patterns between condition-specific groups.

$L_1$ regularized estimate for $\mathit{\beta }$:

$$\begin{array}{c}\widehat{\mathit{\beta }}=\underset{\lambda }{\arg \min }\{{{\sum }_{l=1}^n}_{((1-Y_l)({\mathit{\alpha }}^T{\mathbf{Z}}_l+{\mathit{\beta }}^T{\mathbf{\Gamma }}_l)}\\ \hspace{0.17em}{+\ln (1+\text{exp}\hspace{0.17em}(-{\mathit{\alpha }}^T{\mathbf{Z}}_l\mathit{-}{\mathit{\beta }}^T{\mathbf{\Gamma }}_{\mathit{l}})))+\lambda \Vert \mathit{\beta }\Vert }_1\}\end{array}$$

where $\mathit{\alpha }={({\alpha }_0,{\alpha }_1,\dots ,{\alpha }_K)}^T$, ${\mathbf{Z}}_l={(1,Z_1,\dots ,Z_K)}^T$, $\mathit{\beta }=\text{vec}{({\beta }_{ij})}_{j>i}$, ${\mathbf{\Gamma }}_l=\text{vec}{\left(\ln \frac{f_{ij}(x_{li},x_{lj})}{g_{ij}(x_{li},x_{lj})}\right)}_{j>i}$. ${\Vert \Vert }_1$ denotes $L_1$ norm and the operator $\text{vec}{(A)}_{j>i}$ stacks the columns of the upper triangular position of matrix A excluding the diagonal elements to a vector (e.g. $A={(a_{ij})}_{4\times 4}$ is a matrix with four rows and four columns, $\mathrm{v}\mathrm{e}\mathrm{c}{(a_{ij})}_{j>i}={(a_{12},a_{13},a_{23},a_{14},a_{24},a_{34})}^T$).

The advantages of the JDINAC approach over existing methods lie in the following aspects: (i) it can achieve differential network analysis and classification simultaneously; (ii) it can adjust confounding factors in the differential network analysis, for example, if the samples are from cancer patients with different length of survival time, then the age of the patient is a potential confounding factor which needs to be adjusted. (iii) it is a non-parametric approach and can identify the non-linear relationship among variables. Besides, it does not require any conditions on the distribution of the data, which makes it more robust.

JDINAC can be implemented as follows with its workflow shown in Figure 1.

Fig. 1.

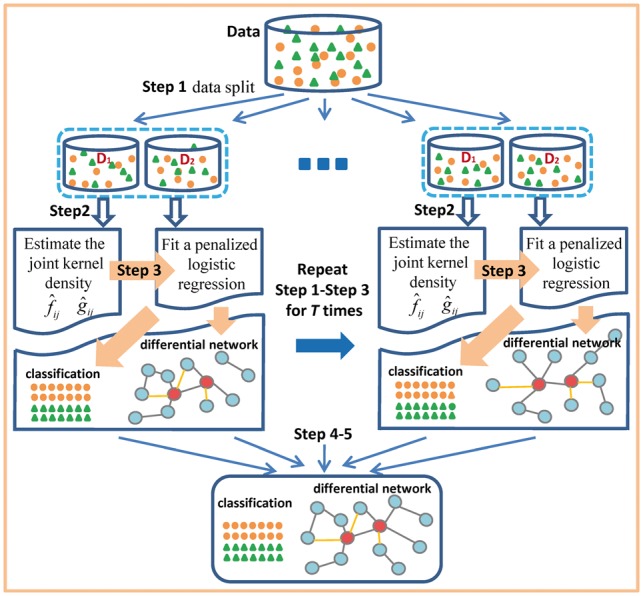
Workflow of JDINAC

Step 1. Given the data of n observations $D=\{(Y_l,X_l),l=1,\dots ,n\}$. Randomly split the data into two parts: $D=(D_1,D_2)$.

Step 2. On part $D_1$, estimate the joint kernel density functions ${\widehat{f}}_{ij}$ and ${\widehat{g}}_{ij}$, $i,j=1,\dots ,p$, $j>i$.

Step 3. On part $D_2$, fit an $L_1$ penalized logistic regression $\text{logit}(P)={\alpha }_0+{\sum }_{k=1}^K{\alpha }_k{Z}_k+{\sum }_{i=1}^p{\sum }_{j>1}^p{\beta }_{ij}\ln ({\widehat{f}}_{ij}(G_i,G_j)/{\widehat{g}}_{ij}(G_i,G_j))$, using cross validation to get the best penalty parameter.

Step 4. Repeat Steps 1– 3 T times, on tth repetition obtain predicted probability ${\widehat{P}}_t$ and coefficient ${\widehat{\beta }}_{ij,t}$, $t=1,2,\dots ,T$.

Step 5. Calculate the average prediction $\widehat{P}=T^{-1}{\sum }_{t=1}^T{\widehat{P}}_t$ as the final prediction for classification. Calculate the differential dependency weight of each pair $(G_i,G_j)$ between two groups, $w_{ij}={\sum }_{t=1}^{T}I({\widehat{\beta }}_{ij,t}\ne 0)$, $i,j=1,\dots ,p$, $j>i$; where $I(\hspace{0.17em})$ is the indicator function. A differential network is inferred by connecting the pairs with high differential dependency weights through their shared genes.

2.1 Simulation studies

Four simulation scenarios were designed for assessing the performances of differential network analysis and classification accuracy. In scenarios 1 and 2, the difference of association strength between pairs of genes in a network is caused by the different correlation (Fig. 2a and b). In scenario 3, the differential pairs have the same correlation structure between condition-specific groups but different joint density (Fig. 2c). In scenario 4, the differential strength of association between pairs of genes in a network is caused by the non-linear dependence (Fig. 2d). The differential networks of four simulation scenarios are shown in the Supplementary Figures S1–S4. For scenarios 1–3, we generated 100 pairs of datasets, each representing the case (class 1) and the control (class 0) conditions. Each dataset contains 300 observations with p variables drawn from the multivariate normal distribution with mean 0 and covariance matrix $\mathbf{\Sigma }$, that is, $\mathbf{X}\sim N_p(0,\mathbf{\Sigma })$. $\mathbf{\Sigma }$ consists of 3 blocks along the diagonal, $\mathbf{\Sigma }=diag({\Sigma }_1,{\Sigma }_2,{\Sigma }_3)$, ${\Sigma }_1={({\sigma }_{ij})}_{m\times m}$, for $i,j=1,\dots ,m$; $m=80$; ${\Sigma }_2={\Sigma }_3={({\sigma }_{ij}^{\ast })}_{10\times 10}$.

Fig. 2.

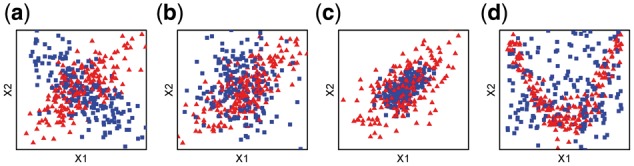
The scenarios of simulation studies. The blue square and red triangle represents the scatter plots for the two variables in class 0 and class 1 respectively, (a) scenario 1, the two variables is negatively correlated in class 0 and positively correlated in class 1, (b) scenario 2, the two variables are correlated in one group and are independent in the other, (c) scenario 3, the two variables are equally correlated but with different density in the two groups, (d) scenario 4, the two variables are independent in one group and have non-linear relationship in the other group

Scenario 1: In class 0, $p=100$, $\rho =0.5$, ${\sigma }_{ii}^{\ast }=1$ for $i=1,\dots ,10$, ${\sigma }_{ij}^{\ast }={(-1)}^{\left|i-j\right|}\times 0.5$ for $i\ne j$; in class 1, $p=100$, $\rho =0.5$, ${\sigma }_{ii}^{\ast }=1$ for $i=1,\dots ,10$, ${\sigma }_{ij}^{\ast }=0.5$ for $i\ne j$.

Scenario 2: In class 0, $p=100$, $\rho =0.5$, ${\sigma }_{ii}^{\ast }=1$ for $i=1,\dots ,10$, ${\sigma }_{ij}^{\ast }=0$ for $i\ne j$; in class 1, $p=100$, $\rho =0.5$, ${\sigma }_{ii}^{\ast }=1$ for $i=1,\dots ,10$, ${\sigma }_{ij}^{\ast }=0.7$ for $i\ne j$.

Scenario 3: In class 0, $p=100$, $\rho =0.5$, ${\sigma }_{ii}^{\ast }=1$ for $i=1,\dots ,10$, ${\sigma }_{ij}^{\ast }=0.6$ for $i\ne j$; in class 1, $p=100$, $\rho =0.5$, ${\sigma }_{ii}^{\ast }=5$ for $i=1,\dots ,10$, ${\sigma }_{ij}^{\ast }=3$ for $i\ne j$.

Scenario 4: In class 0, generate data $X^{(0)}=(X_1^{(0)},\dots ,X_p^{(0)})$, where $X_j^{(0)}=u_j^2+v_j$, $j=1,\dots ,p/2$, $u_j\sim Unif(-2,2)$ and $v_j\sim N(-4/3,1/4)$; $X_j^{(0)}=u_j$, $j=p/2+1,\dots ,p$, $p=100$. In class 1, generate data $X^{(1)}=(X_1^{(1)},\dots ,X_p^{(1)})$, where $X_j^{(1)}=u_{j+p/2}^2+v_j$, $j=1,\dots ,p/2$, $u_j\sim Unif(-2,2)$ and $v_j\sim N(-4/3,1/4)$; $X_j^{(1)}=u_j$, $j=p/2+1,\dots ,p$, $p=100$.

We compared JDINAC with several existing state-of-the-art methods under the aforementioned four scenarios in differential network analysis and classification. Additional simulation studies are detailed in Supplementary Methods.

2.2 Differential network analysis

We compare the performance of JDINAC in terms of differential network estimation with DiffCorr (Fukushima, 2013), DEDN (Zhao et al., 2014) and cross-product penalized logistic regression (cPLR). The cPLR is defined as

$$\text{logit}(P)={\beta }_0+{\sum }_{i=1}^p{\sum }_{j>1}^p{\beta }_{ij}{G}_i{G}_j.$$

The $L_1$ penalty function was used to optimize the parameters, which is the same for JDINAC. Parameters ${\beta }_{ij}\ne 0$ indicate differential dependency patterns between two groups.

True discovery rate (TDR; Precision), true positive rate (TPR; Recall) and true negative rate (TNR) are used to evaluate the performance of different methods. TDR, TPR, and TNR are defined as follows,

$$TDR=\frac{TP}{{\sum }_{i\ne j}I({\widehat{\delta }}_{ij}\ne 0)},\hspace{0.17em}TPR=\frac{TP}{{\sum }_{i\ne j}I({\delta }_{ij}\ne 0)},\hspace{0.17em}TNR=\frac{TN}{{\sum }_{i\ne j}I({\delta }_{ij}=0)},$$

where TP and TN are the numbers of true positives and true negatives respectively, which are defined as $TP={\sum }_{i\ne j}I({\delta }_{ij}{\widehat{\delta }}_{ij}\ne 0)$, $TN={\sum }_{i\ne j}\{I({\delta }_{ij}=0)I({\widehat{\delta }}_{ij}=0)\}$ respectively. ${({\delta }_{ij})}_{p\times p}$ is the differential adjacency matrix, ${\delta }_{ij}\ne 0$ indicate the pair $(G_i,G_j)$ are differential dependency between two groups; ${({\widehat{\delta }}_{ij})}_{p\times p}$ is the estimated differential adjacency matrix.

2.3 Classification and evaluation

We compare the classification performance of JDINAC with RF, NB, cPLR and original penalized logistic regression (oPLR). The oPLR is defined as

$$\text{logit}(P)={\beta }_0+{\beta }_1{G}_1+\cdots +{\beta }_p{G}_p.$$

Similarly, the $L_1$ penalty function was used to optimize the parameters for high-dimensional data. Both cPLR and oPLR are Lasso based methods.

Receiver operating characteristic (ROC) curve and classification error are used to assess the accuracy of four methods.

2.4 Evaluation of computational complexity

We carried out additional simulations to estimate the computing time under various numbers of genes with sample size 100 for each group, using a single core node with 2.00 GHz Intel(R) Xeon(R) CPU E5-2430L.

2.5 Application

Breast Invasive Carcinoma (BRCA) is the most common type of breast cancer. This subtype of breast cancer is able to spread to other parts of the body through the lymphatic system and bloodstream, which makes BRCA potentially a highly lethal killer. Most of the genome-wide studies for BRCA focus on identifying differentially expressed genes. However, BRCA is largely determined by a number of genes that interact in a complex network, rather than a single gene perturbed (gene mutation, expression and methylation etc.). A key but inadequately addressed issue is how to identify the underlying molecular interaction mechanisms. The TCGA BRCA study include 1098 patients, along with their matched mRNA, copy number, methylation and microRNA data. The RNASeq Version 2 expression data and clinical data were downloaded from TCGA through TCGA-Assembler (Zhu et al., 2014). In this study, we select 114 patients who have both tumor and matched normal samples as our training subjects. The proposed method was applied to identify differential patterns of network activation between the tumor group and the control group. We focus on the 397 genes listed in the cancer pathway (hsa05200) of KEGG as our candidate gene sets. After filtering those genes which include >30% of zero gene expression values in the training data, we have 373 genes as our final candidate genes. To evaluate the performances of classification, we randomly choose 50 of 114 individuals in each group as our test data set. More detailed data description and processing are provided in Supplementary Methods.

3 Results

3.1 Simulation

We calculate the TDR, TPR and TNR of identifying the differential network that corresponds to a given threshold by varying thresholds from 1 to 20 (number of random split was set to be 20 in the Step 4). We average those measures over 100 datasets in each of the four scenarios.

Table 1 presents the TPR, TNR and TDR of the JDINAC, DiffCorr, DEDN and cPLR under different scenarios. It shows that JDINAC significantly outperforms all the other three methods. Although DiffCorr was set to control the false discovery rate (FDR) < 0.1, the FDR tended to be significantly inflated. In particular, JDINAC performs quite well in scenario 4. The TDR, TPR and TNR of JDINAC are close to 1, but the TDR and TPR of the other three methods are close to 0. It indicates that JDINAC can indeed capture the perturbation of non-linear dependence in the network.

Table 1.

The TPR, TNR and TDR of different methods

Scenario	JDINACa			DiffCorrb			DEDN			cPLR
	TDR	TPR	TNR	TDR	TPR	TNR	TDR	TPR	TNR	TDR	TPR	TNR
1	93.7	81.6	99.9	81.3	100	99.8	33.5	96.7	99	19.8	64.9	97.3
2	95.6	74.5	99.9	85	100	99.7	16.5	89.1	94.3	25.6	49.8	97.1
3	88.3	69.5	99.3	7.5	0.2	99.8	2.1	10.1	81.6	53.6	23.6	98.1
4	99.9	99.8	100	3.8	0.4	99.9	5.0	0.2	100	0.7	0.3	99.8

Average of 100 replications, %, the best performance is highlighted in bold.

^aPair $(G_i,G_j)$ was taken as differential edge in the network for JDINAC, when the differential dependency weight $w_{ij}\ge 4$.

^bSet to control the FDR = 0.1.

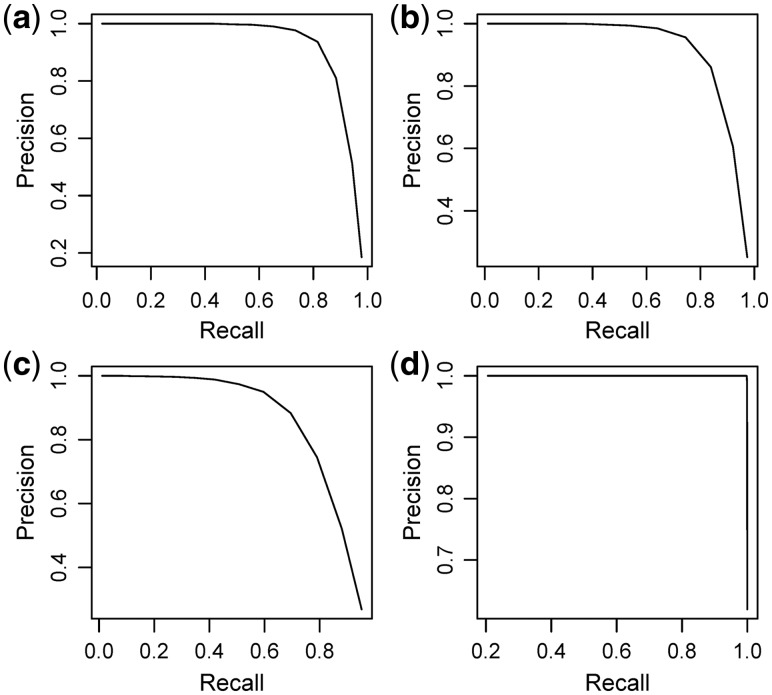
By using repeated procedure, JDINAC allows us to assign a weight to each selected pair of genes, which is the frequency as a pair of genes is selected. Thus we can use the precision-recall curve (PRC) to evaluate the performance of JDINAC under various weight cutoff, and to obtain the differential network by controlling the trade-off of precision and recall. Figure 3 illustrates the PRC of JDINAC under different scenarios. The JDINAC has high PRC in all scenarios. The PRC is not included for DiffCorr, DEDN and cPLR, because they cannot report the same weights as JDINAC.

Fig. 3.

PRC for JDINAC for differential network analysis under scenario1 (a), scenario 2 (b), scenario 3 (c), scenario 4 (d). The differential dependency weights $w_{ij}$ were used as the differential adjacency matrix, ${({\widehat{\delta }}_{ij})}_{p\times p}=I(w_{ij}\ge t)$, $t=1,\dots ,20$

The average ROC curves over 100 replications for the classification using five methods under different scenarios (Fig. 4) show that JDINAC performs the best among the five methods. The fractions of votes were used as the continuous predictions for RF models. After getting the continuous prediction, we used 0.5 as the cutoff of prediction to obtain the classification errors (Table 2). JDINAC is much more accurate than other methods.

Fig. 4.

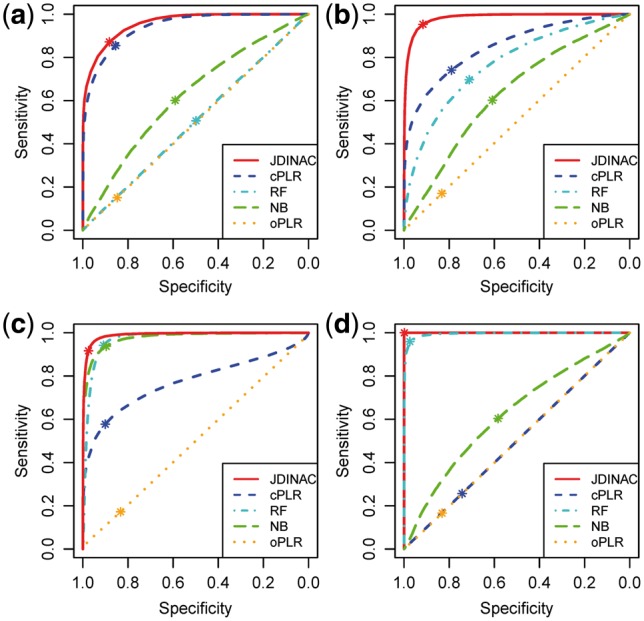
ROC curves of 5 methods for the classification under scenario 1 (a), scenario 2 (b), scenario 3 (c) and scenario 4 (d). The asterisk indicates the location where the cutoff of prediction was set to 0.5

Table 2.

Average classification errors (%)

Scenario	JDINAC	RF	NB	cPLR	oPLR
1	12.3 (1.4)	49.7 (1.9)	40.4 (2.2)	14.5 (1.6)	50.1 (1.0)
2	6.5 (1.2)	29.6 (2.8)	39.5 (2.1)	23.4 (2.0)	49.9 (1.4)
3	7.0 (1.0)	6.6 (1.1)	8.3 (1.2)	26.1 (1.6)	49.8 (1.5)
4	0.1 (0.1)	3.4 (1.3)	40.7 (2.1)	50.0 (1.4)	50.1 (1.3)

Standard errors are in the parentheses. The best performance is highlighted as bold.

To further evaluate the performance of JDINAC, we have simulated other non-linear relationship pattern. The two variables are independent in one group and have exponential relationship in the other group (see Supplementary Fig. S5). Supplementary Figure S6 illustrates the ROC curves in this non-linear scenario. JDINAC still performs the best among the five methods.

We also evaluate how the variance of data distribution affects the performance of JDINAC. As shown in Supplementary Figure S7, the ROC of all five methods goes down when the variance increases. Again, the proposed method JDINAC still has more robust performance than the other four.

Furthermore, we conducted the simulation study for the case with multidimensional outliers. Five percent variables in one group are randomly chosen to be missed. Then for each missing variable 5% samples are randomly chosen to be missed (see Supplementary Methods S2). The results of classification are shown in Supplementary Figure S8. It indicates that the proposed JDINAC has the best performance. Supplementary Table S1 presents the TPR, TNR and TDR of the JDINAC, DiffCorr, DEDN and cPLR. It shows that JDINAC has the highest TDR and TPR, and acceptable TPR. The results indicate that JDINAC indeed performs well in the case with multidimensional outliers.

As we have balanced number of cases and controls in this study, we used 0.5 as the cutoff of prediction to assign two classes in the classification. However, the optimal cutoff value may depend on ratio of case/control in the training data and application. We conducted another simulation study in imbalanced case/control setting (see Supplementary Fig. S9 and Table S2). The sample size was designed to be 100 for class 0 and 500 for class 1, another scenario is 200 for class 0 and 400 for class 1. The maximum value of Youden index (also called Youden’s J statistic, J = Sensitivity + Specificity −1) was used as a criterion for selecting the optimum cutoff value. Supplementary Table S2 shows the optimal cutoff point for all methods, as expected, 0.5 is not the optimal cutoff point. Different criteria can lead to different optimal cut off in real world scenario, Youden index puts equal weights to the sensitivity and specificity. In some special diagnostic tests, sensitivity is more important than specificity, or vice versa. Larger weight should be given to sensitivity or specificity.

Table 3 presents the measured computing time in a single core machine. The time complexity of JDINAC is sub-linear. It is slower than DiffCorr but much faster than DEDN for the differential network analysis. The bottleneck of JDINAC mainly comes from the estimation of the pairwise kernel density and the resampling procedure. As these computations can be easily divided into independent processes, parallel computation with multiple cores and nodes can be employed when the datasets become relatively large.

Table 3.

Average computing time (seconds) of different methods with p genes

p	JDINAC	RF	NB	oPLR	DiffCorr	DEDN	cPLR
40	30.1	2.1	1.3	0.1	0.002	29.7	0.7
60	65.7	4.7	2.9	0.2	0.003	297.6	1.1
80	114.2	8.2	5.2	0.6	0.003	2138.5	1.7
100	176.8	12.7	8.2	1.7	0.004	9519.5	2.5

RF, NB, cPLR are based on $p\times p$ features.

3.2 Application

Figure 5 depicts the BRCA differential network estimated by JDINAC, DiffCorr, DEDN and cPLR. Only genes connected with at least one other gene were included in the figure. The top 10 differential dependency pairs identified by JDINAC ordered by weight are shown in Table 4. Figure 6 presents the Venn diagram for the edges in the differential networks identified by different methods JDINAC, DiffCorr, cPLR, and DEDN. There are few overlaps of predicted differential interactions (edges in the network) among these methods. Thus, JDINAC may identify complementary information to the existing methods. The overlapped edges between JDINAC and DiffCorr, JDINAC and cPLR and DiffCorr and cPLR are shown in Supplementary Table S3.

Fig. 5.

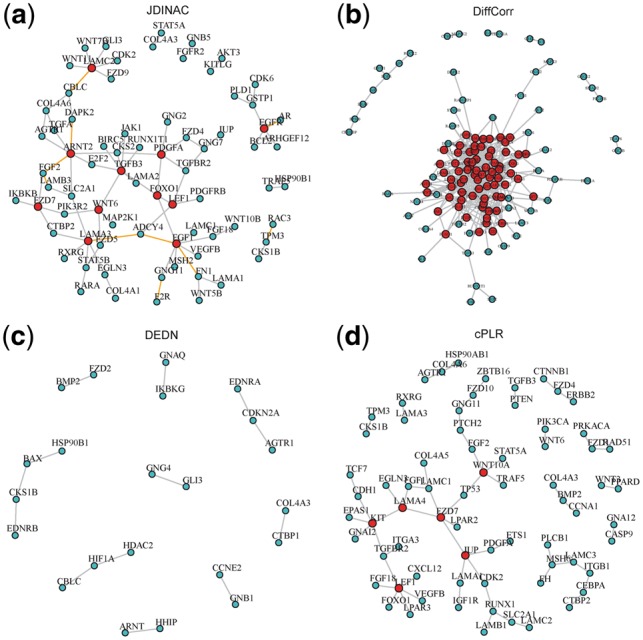
The differential network of cancer pathway between BRCA tumor samples and controls. An edge presented in the differential network means the dependency of corresponding pair genes is different between two condition-specific groups. The red nodes stand for hub genes. (a) Differential network estimated by JDINAC; The orange edges indicate the top 10 differential dependency pairs. (b) Differential network estimated by DiffCorr; (c) Differential network estimated by DEDN; (d) Differential network estimated by cPLR

Table 4.

Top 10 differential dependency pairs identified by JDINAC

Gene 1	Gene 2	$w_{1,2}$	Gene 1	Gene 2	$w_{1,2}$
GNG11	F2R (PAR1)	18	LAMA3	ADCY4	12
FN1	FGF1	17	EGFR	AR	10
LAMB3	FGF2	17	DAPK2	ARNT2	10
TPM3	RAC3	17	FGF2	ARNT2	10
FGF1	ADCY4	13	LAMC2	CBLC	10

Fig. 6.

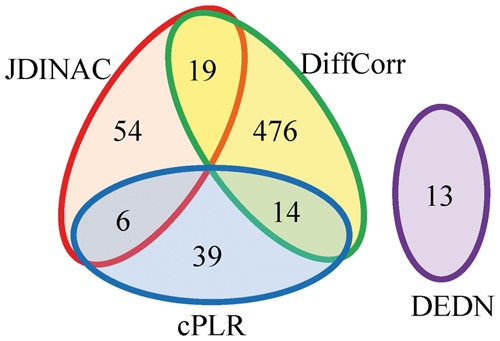
Summary of the number of edges in the differential networks for the four methods

Although there are no common edges shared by all of these methods, several common Gene Ontology (Ashburner et al., 2000) terms and a KEGG pathway (Kanehisa and Goto, 2000) are enriched by JDINAC, DiffCorr, and cPLR, as identified by R package ‘clusterProfiler’ (Yu et al., 2012) when inspecting the differential network as a whole (Supplementary Table S4). The common biological process and pathway suggest that the change of hemidesmosome assembly and ECM-receptor interaction are important in the etiology of invasive breast cancer. These predictions are supported by the literatures (Bergstraesser et al., 1995; Oskarsson, 2013); both of these processes are the hallmark of invasive breast cancer. It is noted that DEDN does not have enriched terms in the pathway enrichment analysis. Although common individual gene pairs could be missed by different methods due to the multigenic nature of complex diseases such as BRCA, and stochastic process of underlying algorithms, our result suggests that a differential network view may provide more robust biological meaningful signals.

No gold standard is available for evaluating differential network analysis in the real dataset since the true underlying dependence relationships are unknown. We found there are experimental supports for the top ranked pairs by JDINAC. For example, F2R (PAR1) is a G-protein coupled receptor that binds and regulates G-protein. It contributes to tumor progression and metastasis in breast cancer (Shi et al., 2004). Meanwhile, GNG11 is a G-protein, plays a role in the transmembrane signaling system. It implies that the molecular role of F2R in the breast cancer progression and metastasis origins from the altered F2R-GNG11 interaction. In other cases, dysregulated pairs may not have direct physical interactions, but strong functional associations. The matrix form of fibronectin (FN1) is believed to support cell adhesion, tumor growth, and inflammation. Fibroblast growth factors (FGF1, FGF2) are important factors regulating expression of FN1 and LAMB3 (Kashpur et al., 2013; Tang et al., 2007). RAC3 is a GTPase which is related to the cell growth and the activation of protein kinases. Rac GTPase activity and paxillin phosphorylation are elevated in cells from the TPM3 tropomyosin gene deleted mice (Lees et al., 2013).

Supplementary Table S5 presents the hub genes and the corresponding number of neighbor genes identified by JDINAC. The hub genes are the ones that have at least three neighbor genes in the differential networks. FGF1 and TGFB3 have the largest number of neighbor genes in the differential networks of BRCA data. FGF1 plays an important role in a variety of biological processes involved in embryonic development, cell growth and differentiation, morphogenesis, tumor growth and invasion (Zhou et al., 2011). The expression of FGF1 is dysregulated in breast cancer and contributes to the proliferation of breast cancer cells (Yoshimura et al., 1998; Zhou et al., 2011). Laverty et al. (Ghellal et al., 2000) reviewed numerous literatures and reported TGFB3 is associated with the progression of breast cancer. PDGFA is confirmed to be one of the progesterone target genes on breast cancer cells (Soares et al., 2007). FOXO1 contributes to multiple physiological and pathological processes including cancer, and targeting of FOXO1 by microRNAs may promote the transformation or maintenance of an oncogenic state in breast cancer cells (Fu and Tindall, 2008; Guttilla and White, 2009). Moreover, FOXO1 is regulated by AKT (Tzivion et al., 2011), and PDGFA is the upstream gene of AKT. Indeed, we identified an edge between PDGFA and FOXO1 (Fig. 5a). Wendt et al. (2015) demonstrated that EGFR is a critical gene in primary breast cancer initiation, growth and dissemination. FZD7 plays a critical role in cell proliferation in triple negative breast cancer (TNBC) via Wnt signaling pathway and was considered to be a potential therapeutic target for TNBC (Yang et al., 2011). An edge between FZD7 and CTBR2 was identified by JDINAC (Fig. 5a). Actually, CTBP2 is a key gene in Wnt pathway. The identified differential network provides new insight into the underlying genetic mechanisms of BRCA, and testable hypothesis for further experimental validations. The differential interaction patterns and hub genes may serve as biomarkers for early diagnosis or drug targets.

It is quite difficult to quantify the non-linear relationship in real world scenario. We randomly selected 10 genes from the BRCA data, and described the pairwise scatterplot matrix (Supplementary Fig. S10). Overall, there are clear non-linear relationships among these genes. Thus it is necessary to develop methods that can capture the non-linear relationship in the differential network analysis as exampled by JDINAC.

Next, we study the classification performances of methods JDINAC, RF, NB, cPLR and oPLR. The classification errors are shown in Table 5. The classification accuracy of JDINAC is the same with oPLR that uses single genes as features, but better than RF, NB and cPLR, all of which use the pair of genes for the classification. The low error rate of JDINAC implies that the identified differential network could be biological meaningful to distinguish the disease state with the normal one.

Table 5.

Classification errors on application test data set (%)

Dataset	JDINAC	RF	NB	cPLR	oPLR
BRCA	1	19	2	17	1

To further verify the predictive ability of JDINAC, we carried out Y-randomization experiments. Firstly, 20% of the data as the hold-out test set was randomly select, and the left 80% as training data. Secondly, response variable Y with the training data was randomly permuted 1000 times; a JDINAC model was trained using each permutated data set; and the performance of the trained model over the hold-out data was measured. Finally, the statistical significance of performance measure of JDINAC from the non-permutated data was determined based on the distribution of performance measures from permutated models. As shown in Supplementary Figure S11, JDINAC predictive model performs significantly better than the randomized model, with estimated P-values of 3.47 × 10⁻³, 2.89 × 10⁻³ and 5.31 × 10⁻³ for AUROC (Area Under the ROC curve), AUPR (Area Under Precision-Recall curve) and accuracy, respectively.

4 Discussion

A complex disease phenotype (e.g. cancer) is rarely a consequence of an abnormality in a single gene, but reflects various pathobiological processes that interact in a network (Barabasi et al., 2011). Network comparison or differential network analysis has become an important means of revealing the underlying mechanism of pathogenesis. The identified differential interaction patterns between two group-specific biological networks can be taken as candidate biomarkers, and have extensive biomedical and clinical applications (Ji et al., 2015, 2016; Laenen et al., 2013; Yang et al., 2013). Although numerous differential network analysis methods (Fukushima, 2013; Ha et al., 2015; Watson, 2006; Yates and Mukhopadhyay, 2013; Zhao et al., 2014) have been proposed, most of the methods rely on marginal or partial correlation to measure the strength of connection between pairs of nodes in a network. They usually cannot capture the non-linear relationship among genes, which could be ubiquitous in real applications.

We propose a joint kernel density based method, JDINAC, for identifying differential interaction patterns of networks between condition-specific groups and conducting discriminant analysis simultaneously. A multiple splitting and prediction averaging procedure were employed in the algorithm of JDINAC. It can not only make the approach more robust and accurate, but also make more efficient use of limited data (Fan et al., 2016). Moreover, the non-parametric kernel method was used to estimate the joint density, which does not require any conditions on the distribution of the data; this also makes JDINAC more robust and has the ability to capture the non-linear relationship among genes. Extensive simulations were conducted to assess the performances of differential network analysis and classification accuracy. It indicated that JDINAC has high reliability (Fig. 3) and significantly outperforms other state-of-the-art methods, DiffCorr, DEDN and cPLR, especially in scenarios 3 and 4 for the differential network analysis (Table 1). One advantage for JDINAC is that it can achieve classification simultaneously, making it more attractive in practical applications. Figure 4 and Table 2 further highlighted that JDINAC is much more accurate in classification than other methods.

Although JDINAC can in principle be applied to genome-wide data sets, such application may be limited due to high computational costs. In this study, we focus on identifying the differential interaction patterns between genes in a given pathway (or a candidate gene set). JDINAC can be directly used in most cases, since >95% pathways from KEGG database contain <150 genes. Under the scenario when the pathway is too large or in the case of genome-wide study, prior knowledge or screening method can be used to shrink the candidate gene pair numbers before applying JDINAC. Although the proposed JDINAC method was applied to gene network differential network analysis in this article, it can be used to incorporate other biological networks, such as metabolic network and brain functional connectivity network. It can also be generalized to identify of between pathway interactions.

The freely available JDINAC software is available as R script at https://github.com/jijiadong/JDINAC.