Advances in Time Estimation Methods for Molecular Data

Abstract

Molecular dating has become central to placing a temporal dimension on the tree of life. Methods for estimating divergence times have been developed for over 50 years, beginning with the proposal of molecular clock in 1962. We categorize the chronological development of these methods into four generations based on the timing of their origin. In the first generation approaches (1960s–1980s), a strict molecular clock was assumed to date divergences. In the second generation approaches (1990s), the equality of evolutionary rates between species was first tested and then a strict molecular clock applied to estimate divergence times. The third generation approaches (since ∼2000) account for differences in evolutionary rates across the tree by using a statistical model, obviating the need to assume a clock or to test the equality of evolutionary rates among species. Bayesian methods in the third generation require a specific or uniform prior on the speciation-process and enable the inclusion of uncertainty in clock calibrations. The fourth generation approaches (since 2012) allow rates to vary from branch to branch, but do not need prior selection of a statistical model to describe the rate variation or the specification of speciation model. With high accuracy, comparable to Bayesian approaches, and speeds that are orders of magnitude faster, fourth generation methods are able to produce reliable timetrees of thousands of species using genome scale data. We found that early time estimates from second generation studies are similar to those of third and fourth generation studies, indicating that methodological advances have not fundamentally altered the timetree of life, but rather have facilitated time estimation by enabling the inclusion of more species. Nonetheless, we feel an urgent need for testing the accuracy and precision of third and fourth generation methods, including their robustness to misspecification of priors in the analysis of large phylogenies and data sets.

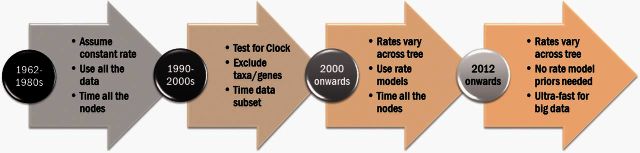
Molecular phylogenies scaled to time (timetrees) are fundamental to understanding the evolution of organisms. For example, they aid in deciphering micro- and macroevolutionary processes, including the role of geologic history in shaping the evolution of life, temporal patterns of diversification, the expansion of genomes through duplication events, and the coevolution of hosts and pathogens. In this review, we outline four generations of methods for dating evolutionary divergences using molecular data (fig. 1). We highlight differences among methods, advances they provide, and challenges associated with their use. A detailed early historical development of molecular clock methods is found in Kumar (2005) and extensive methodological descriptions are found in other recent reviews (Ho and Duchene 2014; Bell 2015; Biek et al. 2015; O'Reilly et al. 2015; dos Reis et al. 2016).

Fig. 1.

Four generations of molecular dating methods. Generations of methods are delineated based on their statistical properties and chronological order of origin. Importantly, innovative approaches continue to be developed in the third and fourth generation categories.

First Generation Approaches

The first approaches applied a strict molecular clock, where protein sequence differences were assumed to accumulate linearly over time. Zuckerkandl and Pauling (1962) were the first to apply this method to date the divergence of two duplicated genes (alpha and beta globins) and two species (human and gorilla), where a fossil-based divergence time between human and horse was used. A linear regression through the origin was used to derive the clock calibration, which is the slope of the regression line, to convert distances into time. A strong correlation between the level of sequence similarity and fossil-based divergence times supported the use of first generation methods (Margoliash 1963; Doolittle and Blombaeck 1964; Fitch 1976a, 1976b; Fitch and Langley 1976). In those early days, researchers applied the molecular clock concept to date the divergence of humans and chimpanzees (Sarich and Wilson 1967, 1973), protostomes and deuterostomes (Brown et al. 1972), and many eukaryotic and prokaryotic groups (Hori and Osawa 1979). However, molecular clocks were extensively debated (Jukes and Holmquist 1972; Easteal et al. 1995). In the following decade, there were no major methodological developments in molecular dating techniques, because the rate of sequence data generation was slow due to laborious and time-consuming technologies available at that time.

Second Generation Methods

With advances in sequencing technologies, DNA and amino acid sequence data began to accumulate in substantial volumes, albeit modest by today’s standards. Their analyses showed that the equality of evolutionary rates was frequently violated, which led to the development of relative-rate tests (Fitch 1976b; Felsenstein 1981; Wu and Li 1985; Muse and Weir 1992; Tajima 1993; Takezaki et al. 1995). These new tests, and the growing availability of sequence data, prompted the practice of eliminating genes and species that did not pass the rate equality tests. Then, a molecular clock was assumed to date divergences within the reduced data set. This protocol was an advancement over the first generation approaches and enabled many large protein-clock analyses to construct timescales for the evolution of mammals, vertebrates, metazoans, and eukaryotes (Doolittle et al. 1996; Hedges et al. 1996; Wray et al. 1996; Feng et al. 1997; Kumar and Hedges 1998).

During this time, it also became clear that the relative-rate tests lacked power. They do not reject the null hypothesis of rate equality when the sequences are short or when the evolutionary rate is slow (Tajima 1993). Such concerns prompted the use of more stringent rate tests in order to exclude genes and species showing even small rate differences (Kumar and Hedges 1998; Hedges and Kumar 2003; Hedges and Shah 2003). Despite extensive debates about the precision and usefulness of molecular dating (e.g., Graur and Martin 2004; Hedges and Kumar 2004), excitement about the use of molecular data to time species divergences grew during the 1990s (fig. 2). During this period, the idea of applying different evolutionary rates to different parts of the tree (local clocks) was also proposed (Hasegawa et al. 1989; Takezaki et al. 1995; Sanderson 1997; Yoder and Yang 2000).

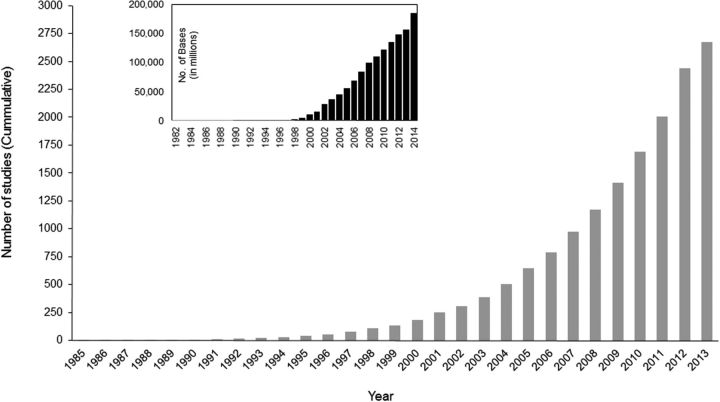
Fig. 2.

Cumulative number of publications reporting the use of molecular data to estimate species divergence times; redrawn from Hedges et al. (2015). This graph is a representative trend for the growth of the corpus of peer-reviewed literature available. Inset shows the growth of sequence databanks since 1982. Number of bases in each release of GenBank are shown (data from http://ftp://ftp.ncbi.nih.gov/genbank/gbrel.txt).

Third Generation Methods

Seeds for the development of this generation of approaches were planted by Gillespie (1984), who proposed correlated evolutionary rates between ancestral and descendant branches of a tree. This predicted a greater similarity of evolutionary rates between closely related species than between clades (see also Hasegawa et al. 1989; Kishino and Hasegawa 1990; Sanderson 1997). Sanderson (2002) developed a penalized-likelihood method using this concept and made a practical tool that automatically determined shifts in evolutionary rates in different lineages (Sanderson 2003). In this method, rates are assigned to branches such that differences between ancestor–descendant pairs are minimized (correlated rates). This procedure leads to smoothing of rates locally in a tree (see also Sanderson 1997; Britton et al. 2002, 2007) and the relaxation of the molecular-clock assumption. Penalized likelihood methods continued to be extended by allowing for rates to vary independently among branches and by using least squares (Xia and Yang 2011; Smith and O'Meara 2012; Paradis 2013).

In 1998, a Bayesian framework was developed for dating species divergences under a correlated rates model (Thorne et al. 1998). In the following years, new methods were proposed to statistically model the distribution of rates in different branches of the tree, many of which did not require rates across the tree to be correlated (Drummond et al. 2006; Lepage et al. 2007; Rannala and Yang 2007). This includes lognormal and exponential distributions, which have been widely used (see reviews in Ho and Duchene 2014; O'Reilly et al. 2015; dos Reis et al. 2016). Overall, a method belongs to the category of third generation approach if it requires that a statistical model or correlation be used to specify rate variation in the tree globally or locally.

In the Bayesian framework, one may choose a model for the speciation process (e.g., birth-and-death or birth-only process) and it allows for the incorporation of prior information on calibration times, including their minimum and maximum boundaries and the distribution of their uncertainties (Thorne et al. 1998; Kishino et al. 2001; Ho and Phillips 2009). This has been very useful in integrating greater amounts of biological information in dating analysis. However, the use of such information can be challenging, because the correct statistical distributions of calibration uncertainty are rarely known, and even the determination of minimum and maximum time bounds is not straightforward due to ambiguous phylogenetic affinities of fossils (Heath et al. 2014; dos Reis et al. 2016).

Theoretically, it is well established that the prior distribution of calibration densities assigned to interior nodes will dictate the final (posterior) times produced by Bayesian methods (Rannala and Yang 2007; dos Reis et al. 2016). This effect has been observed in practice, because one or a few calibration priors may have a large influence on the resulting timetrees and produce biased inference (e.g., Battistuzzi et al. 2015; Duchene et al. 2015). For these reasons, a number of methods have been proposed to identify potentially problematic calibrations (Near and Sanderson 2004; Near et al. 2005; Dornburg et al. 2011; Battistuzzi et al. 2015). As an alternative to specifying calibration constraints and associated probability distributions, a new method has been proposed to directly incorporate all available fossil data in a Bayesian framework through a fossilized birth–death process (Heath et al. 2014). However, this method assumes that the speciation and extinction rates are constant, and will likely work best when the fossil recovery rate and proportion of sampled living species can be specified reliably.

In addition to calibrations, the choice of the models used to describe the speciation process and rate variation across the tree are also expected to influence the posteriors (time estimates) in Bayesian methods. In particular, the choice of rate-model prior can have a significant impact on the divergence time estimates and the credible intervals (see discussion later). For this reason, methods to select the best model have been proposed (Lepage et al. 2007; Duchene et al. 2014). Ultimately, the rate model itself is expected to vary in a large phylogeny spanning diverse species, with closely related species showing greater similarity (autocorrelation) of rates and distantly related groups showing greater rate independence (Drummond et al. 2006; Ho 2009). Therefore, no one rate model may fit a comprehensive data matrix.

By eliminating the need to remove genes and species that did not evolve with a constant rate, third generation approaches have allowed for the inclusion of increasing number of species in data sets along with all the genes available. These efforts have been impeded by the rather large computational time needs of these methods, which have been a major bottleneck in their application (Akerborg et al. 2008; Battistuzzi et al. 2011; Tamura et al. 2012; Ho 2014). This is particularly problematic, because progress in sequencing technology has been a boon for molecular systematics and biodiversity research, leading to a two-dimensional expansion of data sets (sites and species) and, thus, to dating studies employing genome data sets (e.g., Jarvis et al. 2014; Misof et al. 2014; Zeng et al. 2014). For this reason, faster Bayesian implementations are being developed (Akerborg et al. 2008; Lartillot et al. 2013). In general, slower speeds of popular implementations of Bayesian methods have afforded rather limited computer simulation-based testing of their accuracy and precision. Many of these tests have been for a few species, but they have indicated that slower and faster implementations of Bayesian methods produce similarly accurate results (Akerborg et al. 2008; Battistuzzi et al. 2010, 2011). At present, we see an urgent need to examine the performance of Bayesian methods for larger data sets.

Third versus Second Generation Methods

More than 2,000 studies have reported new estimates of species divergence times in the peer-reviewed literature (Hedges et al. 2015). A vast majority of these publications have appeared in the last decade, which is coincident with the availability of software tools that implement third generation methods. Therefore, it is instructive to examine whether time estimates from the second generation approaches, generally published prior to year 2000, are significantly different from those reported in studies published in recent years. If so, it would indicate that third generation approaches fundamentally altered the estimated timescale of life that emerged from earlier studies in the 1980s and 1990s.

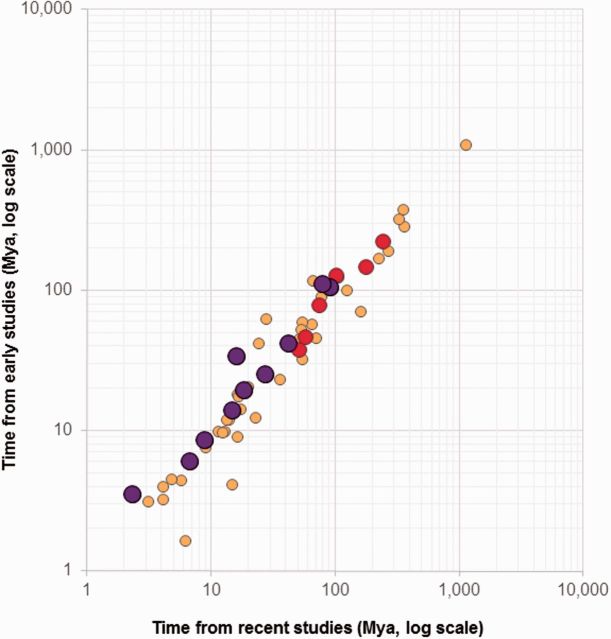
A comparison of ages of corresponding nodes in studies published prior to the year 2000 with those published most recently (2010–2015) shows a linear relationship (fig. 3). Although some time estimates differ between early and recent studies, we observe extensive consistency in multistudy averages (correlation  =  0.98, slope  =  0.97). A similar pattern is observed when all studies since year 2,000 are included in the comparison (results not shown). This means that the time estimates obtained using second generation methods, which removed genes and species exhibiting significant rate differences and used one or a few calibrations, are validated by using third and fourth generation methods and larger data sets. This result does not agree with the claims that the new analyses using genome-scale data and third generation approaches have revised the timescale for life on Earth (dos Reis et al. 2016). In fact, node ages estimated using even third generation methods applied to large genome-scale data sets, with a multitude of calibrations, are being contested vigorously in recently published studies (e.g., Erwin et al. 2011; Jarvis et al. 2014; Misof et al. 2014; Battistuzzi et al. 2015; Cracraft et al. 2015; Kjer et al. 2015; Mitchell et al. 2015; Tong et al. 2015). This dialog and other evidence now suggests that timing differences between any two studies occur due to the use of different numbers or densities of calibrations, different size of the sequence data set, different phylogenies used for timing, and different modelling of rate variation. Therefore, an important future research direction is to evaluate relative contributions of various assumptions and, especially, calibrations that strongly influence posterior time estimates.

Fig. 3.

A comparison of divergence times published before year 2000 (second generation, early studies) and since year 2010 (third generation, recent studies). Divergence times in Hedges et al. (2015) were scanned to identify timetree nodes where at least two studies published before year 2,000 were available. Average divergence times from these studies are plotted on the y-axis (log-scale), and those reported in studies recently (≥2010) are on the y-axis (log scale). Regression analysis through the origin shows a linear trend with a slope of 0.997 for all points (r  =  0.98). Average times from two (small yellow circles), three (medium red circles), and more (large purple circles) studies published before year 2000 are compared with those published more recently (≥2010) for the same nodes in the Hedges et al. (2015) timetree.

New Classes of Third Generation Approaches

In recent years, Bayesian approaches have also been developed for data sets in which the molecular sequences come from biological samples acquired at different times in the past, including those from pathogens or ancient DNA (Rambaut 2000; Shapiro et al. 2011; Stadler and Yang 2013). That is, the tips of the evolutionary tree are not contemporaneous. Like other third generation methods, they require prior specification of a rate-model and, sometimes, speciation process (reviewed in Biek et al. 2015; dos Reis et al. 2016). These methods have been very useful in tracking microbial and viral evolution, particularly the origin and spread of fast-evolving pathogens (e.g., Biek et al. 2015). In further developments, tip-dating methods are now incorporating uncertainties in affiliations of fossils, where fossil species are connected into the molecular phylogenies and their evolution is modelled by incorporating morphological and other nonmolecular characters (Ronquist, Klopfstein, et al. 2012). This total-evidence dating approach may not be successful, because the quantity, quality, and unambiguity of molecular data far surpasses information from morphological and fossil character data (O'Reilly et al. 2015; dos Reis et al. 2016). Nonmolecular data are also likely to show much greater variation in evolutionary rates than molecular data, and many studies using these methods are currently producing surprisingly ancient dates for different clades (dos Reis et al. 2016).

Fourth Generation Approaches

Elimination of the need to specify a statistical distribution to model rates, while accounting for rate variation from branch to branch, is a new conceptual advance in dating divergences. It seemed have begun with the RelTime method (Tamura et al. 2012), which decomposes the divergence time estimation into two steps. In the first step, relative node ages are obtained by using the sequence data along with a model of nucleotide or amino acid substitution to estimate branch lengths reliably in a maximum likelihood or ordinary least squares framework. In the second step, one uses reliable calibration anchors (with maximum and minimum bounds) to scale relative node ages into absolute dates (Tamura et al. 2012, 2013). Bayesian methods can also be used for estimating relative node ages; however, they require specification of rate model. To et al. (2016) have proposed a fourth-generation least-squares dating (LSD) method for timing divergences for serially sampled data, which also does not require a prior specification of speciation process or rate model.

The ability to produce “relative” node ages without using a specific rate-model, speciation-model, or calibration priors has many benefits (Tamura et al. 2012). First, it yields a distribution of estimated (relative) rates for the tree, which would enable one to examine rate-models that best fit the patterns observed locally and globally in the tree. Second, the estimates of relative rates are directly useable to identify lineages with significantly slower or faster evolutionary rates, because the standard errors of the relative rate estimates are available. Third, the estimates of relative node ages enable a direct comparison of (relative) times from molecular data and those from nonmolecular data (e.g., fossil record). This is important because the current use of calibration priors and densities causes circularity in tests of fossil-derived hypotheses using node dates from molecular data. Fourth, relative node ages help identify calibration constraints with the greatest influence on the final time estimates in Bayesian methods (Battistuzzi et al. 2015). Ultimately, one can determine the relative ordering and spacing of divergence events in the tree based on relative ages, with reliable calibration anchors (with maximum and minimum bounds) useable to scale relative node ages into absolute dates and rates (Tamura et al. 2013).

The accuracy of RelTime and LSD methods has been tested by computer simulations and empirical data analysis. They show excellent performance for small and large data sets, where lineages have evolved with auto-correlated rates (Tamura et al. 2012; Filipski et al. 2014) and where the rates have varied independently among branches (Tamura et al. 2012; Filipski et al. 2014; To et al. 2016). They have also performed well in empirical data analysis and produced results comparable to those obtained using the Bayesian methods where many priors and calibrations were used (Tamura et al. 2012; To et al. 2016). Both third and fourth generation methods have been found to perform well even when the sequence alignments are missing a substantial portion of the data (Filipski et al. 2014; Zheng and Wiens 2015).

In addition to the accuracy of the fourth generation approaches, their computational speed makes them attractive in practical data analysis. They scale well with increasing numbers of sequences and sites in the data sets, while allowing for rates to vary throughout the tree. This overcomes a major computational limitation of third-generation Bayesian methods, and makes dating practical for large, genome-scale data sets.

Measuring the Precision of Time Estimates

In biological interpretations, the measurement of the precision of time estimates is important to test hypotheses and establish evolutionary and ecological patterns reliably. Standard errors and confidence intervals are important measures of precision and are reported in most studies. Early on, in the first generation approaches, standard errors of the evolutionary distance estimate were used directly to generate standard errors of time estimates (e.g., Hori and Osawa 1979). In the second generation approaches, standard errors of the mean time estimate derived from multiple genes were reported in some studies (Hedges et al. 1996; Kumar and Hedges 1998) and the time–distance regression or bootstrap variance was used in some others (Wray et al. 1996; Feng et al. 1997). All of these methods produce overly optimistic estimates of precision. By simultaneously incorporating a rate-model and calibration probability densities, the advent of Bayesian approaches finally enabled the estimation of credibility intervals that are more appropriate for biological hypothesis testing.

Analysis of computer simulated data shows that Bayesian credibility intervals have an average failure rate close to 5% when all the priors used are correct (Battistuzzi et al. 2010). That is, the 95% credibility interval contains the true time with a probability equal to 0.95. However, the failure rates may become large if incorrect rate model priors are used (Battistuzzi et al. 2010). This led to the suggestion that composite credibility intervals, derived from individual credibility intervals generated under different assumptions, be used in biological hypothesis testing (Battistuzzi et al. 2010). Also, the credibility intervals of time estimates are found to become large when an incorrect rate model is used (Rannala and Yang 2007; Battistuzzi et al. 2010). The use of incorrect and overly strict calibration constraints is known to produce overly precise and erroneous time credibility intervals, so soft minimum and maximum constraints have been advocated (Rannala and Yang 2007), although in practice, soft constraints used are maxima. This practice will remedy some problems caused by incorrect hard bounds, but the degree of softness is subjective and it has been argued that soft maximum constraints are often underestimates of the true divergence (Hedges and Kumar 2009). Unfortunately, soft constraints continue to be widely used despite that potential bias.

In contrast, the estimation of confidence intervals in the fourth generation methods is in its infancy. The bootstrap site-resampling methods will yield overly narrow confidence intervals, because they only capture errors associated with the estimation of branch lengths in the tree. The sampling variance is a function of the size of the data set and overall sequence divergence, and diminishes with increasing amount of data (Rannala and Yang 2007). But, the bootstrap method cannot provide the variance contributed by the existence of actual rate differences across the tree. For all data sets, error contributed by rate differences would generally be rather large. Tamura et al. (2013) proposed one simple method to generate a confidence interval encompassing the error due to rate variation for the RelTime method, but this method produces rather wide confidence intervals and would result in low-powered statistical tests. Therefore, urgent need exists to develop better approaches to estimate reliable confidence intervals for the fourth generation methods and to evaluate the failure rates of credibility/confidence intervals of third and fourth generation approaches for larger data sets.

Conclusions

Continued innovation and increasing sophistication of molecular dating techniques are responsible for their expanding use in diverse biological research. Clearly, the development of third generation approaches has been instrumental in broader use of molecular dating, including studies of pathogen evolution, timing of gene duplications, and building the timetree of life. Previous and new third generation methods have enabled the use of extensive biological information, and the new fourth generation methods show promise as accurate alternatives when the prior information is limited. All of these methods are expected to become important tools to keep up with the larger and more complex genome-scale data sets employed in modern timetree research. They are available in several software packages (Ronquist, Teslenko, et al. 2012; Tamura et al. 2013; Ho and Duchene 2014; To et al. 2016).