A Bayesian group sparse multi-task regression model for imaging genetics

Abstract

Motivation

Recent advances in technology for brain imaging and high-throughput genotyping have motivated studies examining the influence of genetic variation on brain structure. Wang et al. have developed an approach for the analysis of imaging genomic studies using penalized multi-task regression with regularization based on a novel group $l_{2,1}$-norm penalty which encourages structured sparsity at both the gene level and SNP level. While incorporating a number of useful features, the proposed method only furnishes a point estimate of the regression coefficients; techniques for conducting statistical inference are not provided. A new Bayesian method is proposed here to overcome this limitation.

Results

We develop a Bayesian hierarchical modeling formulation where the posterior mode corresponds to the estimator proposed by Wang et al. and an approach that allows for full posterior inference including the construction of interval estimates for the regression parameters. We show that the proposed hierarchical model can be expressed as a three-level Gaussian scale mixture and this representation facilitates the use of a Gibbs sampling algorithm for posterior simulation. Simulation studies demonstrate that the interval estimates obtained using our approach achieve adequate coverage probabilities that outperform those obtained from the nonparametric bootstrap. Our proposed methodology is applied to the analysis of neuroimaging and genetic data collected as part of the Alzheimer’s Disease Neuroimaging Initiative (ADNI), and this analysis of the ADNI cohort demonstrates clearly the value added of incorporating interval estimation beyond only point estimation when relating SNPs to brain imaging endophenotypes.

Availability and Implementation

Software and sample data is available as an R package ‘bgsmtr’ that can be downloaded from The Comprehensive R Archive Network (CRAN).

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Imaging genetics involves the use of structural or functional neuroimaging data to study subjects carrying genetic risk variants that may relate to neurological disorders such as Alzheimer’s disease (AD). In such studies the primary interest lies with examining associations between genetic variations and neuroimaging measures which represent quantitative traits. Compared to studies examining more traditional phenotypes such as case-control status, the endophenotypes derived through neuroimaging are in some cases considered closer to the underlying etiology of the disease being studied, and this may lead to easier identification of the important genetic variations. A number of settings for statistical analysis in imaging genetics have been studied involving different combinations of gene versus genome-wide and region of interest (ROI) versus image-wide analysis, all of which have different advantages and limitations as discussed in Ge et al. (2013).

The earliest methods developed for imaging genomics data analysis are either based on significant reductions to both data types or they employ full brain-wide genome-wide scans based on a massive number of pairwise univariate analyses (e.g. Stein et al., 2010). While these approaches are convenient in terms of their implementation they ignore potential multi-collinearity arising from variants within the same linkage disequilibrium (LD) block, and they also ignore the potential relationship between the different neuroimaging endophenotypes. Ignoring these relationships precludes the borrowing of information about the genetic associations across components of the response vector. Hibar et al. (2011) use gene-based multivariate statistics and avoid having collinearity of SNP vectors by using dimensionality reduction. Vounou et al. (2010) develop a sparse reduced-rank regression approach for studies involving high-dimensional neuroimaging phenotypes, while Ge et al. (2012) develop a flexible multi-locus approach based on least squares kernel machines. In the latter case, the authors employ permutation testing procedures and take advantage of the spatial information inherent in brain images by using random field theory as an inferential tool (Worsley, 2002). More recently, Stingo et al. (2013) develop a Bayesian hierarchical mixture model for relating brain connectivity to genetic information for studies involving functional magnetic resonance imaging (fMRI) data. The mixture components of the proposed model correspond to the classification of the study subjects into subgroups, and the allocation of subjects to these mixture components is linked to genetic covariates with regression parameters assigned spike-and-slab priors. The proposed model is used to examine the relationship between functional brain connectivity based on fMRI data and genetic variation.

In contrast, the focus of our work concerns the development of methodology for studies where the neuroimaging phenotypes consist of volumetric and cortical thickness measures derived from MRI which summarize the structure (as opposed to the function) of the brain over a relatively moderate number (e.g. up to 100) ROI’s, and we are interested in relating brain structure to genetics.

We develop a Bayesian approach based on a continuous shrinkage prior that encourages sparsity and induces dependence in the regression coefficients corresponding to SNPs within the same gene, and across different components of the imaging phenotypes. Our approach is related to the Bayesian group lasso (Kyung et al., 2010; Park and Casella, 2008) but it is adapted to accommodate multivariate phenotypes and it is extended to allow for grouping penalties both at the gene and SNP level. Our work is primarily motivated by the recent work of Wang et al. (2012) who propose an estimator based on group sparse regularization applied to multivariate regression where SNPs are grouped by genes or LD blocks. In what follows we will assume for specificity that the groups correspond to genes; however, this assumption is not necessary and any approach for grouping the SNPs (e.g. LD blocks) may be used. Let ${\mathbf{y}}_{\ell }={(y_{\ell 1},\dots ,y_{\ell c})}^{\mathrm{T}}$ denote the imaging phenotype summarizing the structure of the brain over c ROIs for subject $\ell ,\hspace{0.17em}\ell =1,\dots ,n$. The corresponding genetic data are denoted by ${\mathbf{x}}_{\ell }={(x_{\ell 1},\dots ,x_{\ell d})}^{\mathrm{T}},\ell =1,\dots ,n$, where we have information on d SNPs, and $x_{\ell j}\in \{0,1,2\}$ is the number of minor alleles for the jth SNP. We further assume that the set of SNPs can be partitioned into K groups, for example K genes, and we let ${\pi }_k,k=1,2,\dots ,K$, denote the set containing the SNP indices corresponding to the kth group and $m_k=\left|{\pi }_k\right|$. We assume that $E({\mathbf{y}}_{\ell })={\mathbf{W}}^{\mathrm{T}}{\mathbf{x}}_{\ell },\ell =1,\dots ,n$, where W is a d × c matrix, with each row characterizing the association between a given SNP and the brain summary measures across all ROIs. The estimator proposed by Wang et al. (2012) takes the form

$$\widehat{\mathbf{W}}=\underset{\mathbf{W}}{\text{arg}\hspace{0.17em}\text{min}}{\sum }_{\ell =1}^n\left|\right|{\mathbf{W}}^{\mathrm{T}}{\mathbf{x}}_{\ell }-{\mathbf{y}}_{\ell }|{|}_2^2+{\gamma }_1|\left|\mathbf{W}\right|{|}_{G_{2,1}}+{\gamma }_2\left|\right|\mathbf{W}|{|}_{l_{2,1}}$$ (1)

where γ₁ and γ₂ are regularization parameters weighting a $G_{2,1}$-norm penalty $\left|\right|\mathbf{W}|{|}_{G_{2,1}}={\sum }_{k=1}^K\sqrt{{\sum }_{i\in {\pi }_k}{\sum }_{j=1}^c{w}_{ij}^2}$ and an ${\ell }_{2,1}$-norm penalty $\left|\right|\mathbf{W}|{|}_{l_{2,1}}={\sum }_{i=1}^d\sqrt{{\sum }_{j=1}^c{w}_{ij}^2}$ respectively. The $G_{2,1}$-norm addresses group-wise association between SNPs and encourages sparsity at the gene level. This regularization differs from group lasso (Yuan and Lin, 2006) as it penalizes regression coefficients for a group of SNPs across all imaging phenotypes jointly. As an important gene/group may contain irrelevant individual SNPs, or a less important group may contain individually significant SNPs, the second penalty, an ${\ell }_{2,1}$-norm (Evgeniou and Pontil, 2007), is added to allow for additional structured sparsity.

The estimator (1) provides a novel approach for assessing associations between neuroimaging phenotypes and genetic variations as it accounts for several interrelated structures within genotyping and imaging data. The incorporation of biological group structure in regression analysis with genetic data has been developed in a variety of contexts (see e.g. Rockova et al., 2014; Stingo et al., 2011; Wen, 2014; Zhu et al., 2014). Wang et al. (2012) show that such an approach when applied to imaging genetics is able to achieve enhanced predictive performance and improved SNP selection compared with a number of alternative approaches in certain settings. Notwithstanding these advantages, a limitation of the proposed methodology is that it only furnishes a point estimate $\widehat{\mathbf{W}}$ and techniques for obtaining valid standard errors or interval estimates are not provided. The primary contribution of this article is to provide an approach for doing this.

Resampling methods such as the bootstrap are a natural starting point for this problem; however, as discussed in Kyung et al. (2010) the bootstrap estimates of the standard error for the lasso or lasso variations such as the estimator (1) might be unstable and not perform well. An alternative way forward is to exploit the connection between penalized regression methods and hierarchical modeling formulations. Following the ideas of Park and Casella (2008) and Kyung et al. (2010) we develop a hierarchical Bayesian model that allows for full posterior inference. The spread of the posterior distribution then provides valid measures of posterior variability along with credible intervals for each regression parameter. Along similar lines, Bae and Mallick (2004) develop a two-level hierarchical model for gene selection that incorporates the univariate Laplace distribution as a prior that favors sparsity and employ the representation of the Laplace distribution as a Gaussian scale mixture in their model hierarchy. In our work, we use a multivariate prior based on a Gaussian scale mixture representation which is assigned independently to the set of coefficients corresponding to each gene. The prior is chosen so that the corresponding posterior mode is exactly the Wang et al. (2012) estimator. To our knowledge this specific form of multivariate shrinkage prior has not been considered previously, though the formulation is related to the general ideas developed in Kyung et al. (2010).

The remainder of the article proceeds as follows. In section 2, we specify the hierarchical model and its motivation based on the estimator (1). The scale mixture representation is specified and a Gibbs sampling algorithm for computing the posterior distribution is presented. Section 3 presents a study of computation time and scaling, while simulation studies are presented in section 4. Section 5 applies our methodology to a dataset obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database, where we relate MRI based structural brain summaries at 56 ROIs to 486 SNPs belonging to 33 genes. The final section concludes with a discussion of potential model extensions.

2 Materials and methods

Let ${\mathbf{W}}^{(k)}={(w_{ij})}_{i\in {\pi }_k}$ denote the $m_k\times c$ submatrix of W containing the rows corresponding to the kth gene, $k=1,\dots ,K$. The hierarchical model corresponding to the estimator (1) takes the form

$$y_{\ell }|W,{\sigma }^2\stackrel{\text{ind}}{\sim }\stackrel{}{\text{M}}{\text{VN}}_c(W^{\text{T}}{x}_{\ell },{\sigma }^2{I}_c)\ell =1,\dots ,n,$$ (2)

with the coefficients corresponding to different genes assumed conditionally independent

$$W^{(k)}|{\lambda }_1^2,{\lambda }_2^2,{\sigma }^2\stackrel{\text{ind}}{\sim }\stackrel{}{p}(W^{(k)}|{\lambda }_1^2,{\lambda }_2^2,{\sigma }^2)k=1,\dots ,K,$$ (3)

and with the prior distribution for each ${\mathbf{W}}^{(k)}$ having a density function given by

$$\begin{array}{c}p({\mathbf{W}}^{(k)}|{\lambda }_1^2,{\lambda }_2^2,{\sigma }^2)\propto \hspace{0.17em}\text{exp}\hspace{0.17em}\left\{-\frac{{\lambda }_1}{\sigma }\sqrt{{\sum }_{i\in {\pi }_k}{\sum }_{j=1}^c{w}_{ij}^2}\right\}\hfill \\ \times \prod _{i\in {\pi }_k}\hspace{0.17em}\text{exp}\hspace{0.17em}\left\{-\frac{{\lambda }_2}{\sigma }\sqrt{{\sum }_{j=1}^c{w}_{ij}^2}\right\}.\hfill \end{array}$$ (4)

The shrinkage prior (4) is not a multivariate Laplace distribution; however, each term of the product on the right-hand side of (4) is the kernel of a form of the multivariate Laplace distribution discussed in Kotz et al. (2012), and so we refer to this prior as the product multivariate Laplace distribution. The prior is specified conditional on σ and the dependence of the prior density on σ follows the parameterization of the univariate Laplace distribution considered in Park and Casella (2008) who show that this parameterization guarantees a unimodal posterior for the Bayesian lasso. By construction, the posterior mode, conditional on ${\lambda }_1^2,{\lambda }_2^2,{\sigma }^2$, corresponding to the model hierarchy (2)–(4) is exactly the estimator (1) proposed by Wang et al. (2012) with ${\gamma }_1=2\sigma {\lambda }_1$ and ${\gamma }_2=2\sigma {\lambda }_2$. This equivalence between the posterior mode and the estimator of Wang et al. (2012) is the motivation for our model; however, we note that generalizations that allow for a more flexible covariance structure in (2) could also be considered. For the current model each component of ${\mathbf{y}}_{\ell }$ is scaled to have unit variance across subjects, making the assumption of a single variance component ${\sigma }^2$ tenable. We also note that while (2) assumes conditional independence across imaging phenotypes, the prior distribution (4) induces dependence in the regression coefficients across the imaging phenotypes for coefficients corresponding to the same gene (group).

Proposition 1. (Prior Propriety)

The prior for $\mathit{W}$ based on (3) and (4) is proper.

Proof

For each $k\in \{1,\dots ,K\}$ we define I_k as

$$\begin{array}{cc}\hfill & I_k=\int \hspace{0.17em}\text{exp}\hspace{0.17em}\left\{-\frac{{\lambda }_1}{\sigma }\sqrt{{\sum }_{i\in {\pi }_k}{\sum }_{j=1}^c{w}_{ij}^2}\right\}\hfill \\ \hfill & \times \prod _{i\in {\pi }_k}\hspace{0.17em}\text{exp}\hspace{0.17em}\left\{-\frac{{\lambda }_2}{\sigma }\sqrt{{\sum }_{j=1}^c{w}_{ij}^2}\right\}d{\mathbf{W}}^{(k)}.\hfill \end{array}$$

It is sufficient to show that ${\prod }_{k=1}^K{I}_k$ is finite. We note that

$$I_k\le \int \hspace{0.17em}\text{exp}\hspace{0.17em}\left\{-\frac{{\lambda }_1}{\sigma }\sqrt{{\sum }_{i\in {\pi }_k}{\sum }_{j=1}^c{w}_{ij}^2}\right\}d{\mathbf{W}}^{(k)}$$ (5)

since $\text{exp}\hspace{0.17em}(-x)\le 1$ for $x\ge 0$. The integrand on the right-hand side of (5) is proportional to the probability density function of a particular form of the multivariate Laplace distribution discussed in Kotz et al. (2012). Given this form, the integral can be evaluated as

$$\begin{array}{cc}\hfill & \int \hspace{0.17em}\text{exp}\hspace{0.17em}\left\{-\frac{{\lambda }_1}{\sigma }\sqrt{{\sum }_{i\in {\pi }_k}{\sum }_{j=1}^c{w}_{ij}^2} \right\}d{\mathbf{W}}^{(k)}={\pi }^{(m_{k}c-1)/2}\hfill \\ \hfill & \times \Gamma ((m_{k}c+1)/2)2^{m_{k}c}{({\lambda }_1^2/{\sigma }^2)}^{-m_{k}c/2}<\infty ,\hfill \end{array}$$

so that $I_k<\infty$ and therefore ${\prod }_{k=1}^K{I}_k<\infty$ as required. □

If the hyper-parameters ${\sigma }^2$, λ₁ and λ₂ are fixed or assigned proper priors then Proposition 1 is sufficient to ensure that the posterior distribution is proper. The following proposition provides a stochastic representation of the prior based on a Gaussian scale mixture. This representation is important as it facilitates computation of the posterior distribution using a simple Gibbs sampling algorithm.

Proposition 2. (Scale mixture representation)

For each $i\in \{1,\dots ,d\}$ let $k(i)\in \{1,\dots ,K\}$ denote the gene associated with the ith SNP. The prior (4) can be obtained through the following scale mixture representation:

$$w_{ij}\hspace{0.17em}|\hspace{0.17em}{\sigma }^2,\hspace{0.17em}{\mathit{\tau }}^2,\hspace{0.17em}{\mathit{\omega }}^2\hspace{0.17em}\stackrel{\text{ind}}{\sim }N\left(0,\hspace{0.17em}{\sigma }^2{\left(\frac{1}{{\tau }_{k(i)}^2}+\frac{1}{{\omega }_i^2}\right)}^{-1} \right),$$ (6)

with continuous scale mixing variables${\mathit{\tau }}^2=({\tau }_1^2,\dots ,{\tau }_K^2)\prime$and${\mathit{\omega }}^2=({\omega }_1^2,\dots ,{\omega }_d^2)\prime$distributed according to the density

$$\begin{array}{cc}\hfill & p({\mathit{\tau }}^2,{\mathit{\omega }}^2|{\lambda }_1^2,{\lambda }_2^2)\hfill \\ \hfill & \propto {\prod }_{k=1}^K{\left(\frac{{\lambda }_1^2}{2}\right)}^{\left(\frac{m_{k}c+1}{2}\right)}{\left({\tau }_k^2\right)}^{\left(\frac{m_{k}c+1}{2}\right)-1}\hspace{0.17em}\text{exp}\hspace{0.17em}\left\{-\left(\frac{{\lambda }_1^2}{2}\right){\tau }_k^2\right\}\hfill \\ \hfill & \times {\prod }_{i\in {\pi }_k}{\left(\frac{{\lambda }_2^2}{2}\right)}^{\left(\frac{c+1}{2}\right)}{\left({\omega }_i^2\right)}^{\left(\frac{c+1}{2}\right)-1}\hspace{0.17em}\text{exp}\hspace{0.17em}\left\{-\left(\frac{{\lambda }_2^2}{2}\right){\omega }_i^2\right\}\hfill \\ \hfill & \times {({\tau }_k^2+{\omega }_i^2)}^{-\frac{c}{2}}.\hfill \end{array}$$ (7)

Proof.

From Kyung et al. (2010) we have the following:

$$\begin{array}{cc}\hfill & \hspace{0.17em}\text{exp}\hspace{0.17em}\left\{-\frac{{\lambda }_1}{\sigma }\left|\right|{\mathit{W}}^{(k)}|{|}_2\right\}\propto {\int }_0^{\infty }{\left(\frac{1}{2\pi {\sigma }^2{\tau }_k^2}\right)}^{\frac{m_{k}c}{2}}\hfill \\ \hfill & \times \text{exp}\hspace{0.17em}\left\{-\frac{\left|\right|{\mathit{W}}^{(k)}|{|}_2^2}{2{\sigma }^2{\tau }_k^2}\right\}\hspace{0.17em}\frac{{\left(\frac{{\lambda }_1^2}{2}\right)}^{\left(\frac{m_{k}c+1}{2}\right)}}{\Gamma \left(\frac{m_{k}c+1}{2}\right)}{({\tau }_k^2)}^{\left(\frac{m_{k}c+1}{2}\right)-1}\hspace{0.17em}\hfill \\ \hfill & \times \text{exp}\hspace{0.17em}\left\{-\left(\frac{{\lambda }_1^2}{2}\right){\tau }_k^2\right\}d{\tau }_k^2,\hfill \end{array}$$ (8)

and

$$\begin{array}{cc}\hfill & \hspace{0.17em}\text{exp}\hspace{0.17em}\left\{-\frac{{\lambda }_2}{\sigma }\left|\right|{\mathit{w}}^i|{|}_2\right\}\propto \hspace{0.17em}{\int }_0^{\infty }{\left(\frac{1}{2\pi {\sigma }^2{\omega }_i^2}\right)}^{\frac{c}{2}}\hspace{0.17em}\text{exp}\hspace{0.17em}\left\{-\frac{\left|\right|{\mathit{w}}^i|{|}_2^2}{2{\sigma }^2{\omega }_i^2}\right\}\hfill \\ \hfill & \times \frac{{\left(\frac{{\lambda }_2^2}{2}\right)}^{\left(\frac{c+1}{2}\right)}}{\Gamma \left(\frac{c+1}{2}\right)}{({\omega }_i^2)}^{\left(\frac{c+1}{2}\right)-1}\hspace{0.17em}\hspace{0.17em}\text{exp}\hspace{0.17em}\left\{-\left(\frac{{\lambda }_2^2}{2}\right){\omega }_i^2\right\}d{\omega }_i^2,\hfill \end{array}$$ (9)

where ${\mathit{w}}^i$ denotes the ith row of $\mathit{W}$. Beginning with (4) we substitute (8) and (9), apply some algebra, and simplify to obtain $p({\mathbf{W}}^{(k)}|{\lambda }_1^2,{\lambda }_2^2,{\sigma }^2)$

$$\propto {\int }_0^{\infty }\cdots {\int }_0^{\infty } \prod _{i\in {\pi }_k}\left[{\left({\sigma }^2{\left(\frac{1}{{\tau }_k^2} + \frac{1}{{\omega }_i^2}\right)}^{-1}\right)}^{-\frac{c}{2}}\right]\times \text{exp}\hspace{0.17em}\left\{-\sum _{i\in {\pi }_k}\left(\frac{{\sum }_{j=1}^c{w}_{ij}^2}{2{\sigma }^2{\left(\frac{1}{{\tau }_k^2}+\frac{1}{{\omega }_i^2}\right)}^{-1}}\right)\right\}\hspace{0.17em}\text{exp}\hspace{0.17em}\left\{-\frac{{\lambda }_1^2}{2}{\tau }_k^2\right\}\times \left[\prod _{i\in {\pi }_k}{\left({\sigma }^2{\left(\frac{1}{{\tau }_k^2} + \frac{1}{{\omega }_i^2}\right)}^{-1}\right)}^{\frac{c}{2}}\right]\times {\left(\frac{{\lambda }_1^2}{2}\right)}^{\left(\frac{m_{k}c+1}{2}\right)}{({\tau }_k^2)}^{-\frac{1}{2}}\times \left[\prod _{i\in {\pi }_k}{\left(\frac{{\lambda }_2^2}{2}\right)}^{\left(\frac{c+1}{2}\right)}{({\omega }_i^2)}^{-\frac{1}{2}}\hspace{0.17em}\text{exp}\hspace{0.17em}\left\{-\frac{{\lambda }_2^2}{2}{\omega }_i^2\right\}d{\omega }_i^2\right]d{\tau }_k^2$$

From (3), we are able to take the product of the expression above over $k\in \{1,\dots ,K\}$, and after simplification we obtain $p\left(\mathbf{W}\right|{\lambda }_1^2,{\lambda }_2^2,{\sigma }^2)$

$$\begin{array}{cc}\hfill & \propto {\int }_0^{\infty }\cdots {\int }_0^{\infty }\prod _{k=1}^K\prod _{i\in {\pi }_k}N(w_{ij};0,{\sigma }^2{\left(\frac{1}{{\tau }_k^2}+\frac{1}{{\omega }_i^2}\right)}^{-1})\hfill \\ \hfill & \times \prod _{k=1}^K{\left(\frac{{\lambda }_1^2}{2}\right)}^{\left(\frac{m_{k}c+1}{2}\right)}{\left({\tau }_k^2\right)}^{\frac{m_{k}c+1}{2}-1}\hspace{0.17em}\text{exp}\hspace{0.17em}\left\{-\frac{{\lambda }_1^2}{2}{\tau }_k^2\right\}\hfill \\ \hfill & \times \left[\prod _{i\in {\pi }_k}{\left(\frac{{\lambda }_2^2}{2}\right)}^{\left(\frac{c+1}{2}\right)}{\left({\omega }_i^2\right)}^{\frac{c+1}{2}-1}\hspace{0.17em}\text{exp}\hspace{0.17em}\left\{-\frac{{\lambda }_2^2}{2}{\omega }_i^2\right\}\right]\hfill \\ \hfill & \times \left[\prod _{i\in {\pi }_k}{({\tau }_k^2+{\omega }_i^2)}^{-\frac{c}{2}}d{\omega }_i^2\right]d{\tau }_k^2,\hfill \end{array}$$ (10)

where $N(x;\mu ,{\sigma }^2)$ denotes the density of a normal distribution with mean μ, variance ${\sigma }^2$ evaluated at x. The first line of the integrand in (10) corresponds to (6), while the remaining lines of (10) correspond to (7), and the integration is over the scale mixing variables ${\mathit{\tau }}^2$ and ${\mathit{\omega }}^2$. It follows that (3) and (4) can be represented through the Gaussian scale mixture (6) and (7). □

This hierarchical representation of the shrinkage prior (7) introduces gene specific latent variables ${\tau }_1^2,\dots ,{\tau }_K^2$ as well as SNP specific latent variables ${\omega }_1^2,\dots ,{\omega }_d^2$ that modulate the conditional variance of each regression coefficient in (6). Unlike other formulations for Bayesian lassos the scale mixing variables are not assumed independent. The dependence in the joint distribution arises from the term ${({\tau }_k^2+{\omega }_i^2)}^{-\frac{c}{2}}$ in (7) and this is required to ensure that the resulting marginal distribution for $\mathit{W}$ has the required form (4). The parameter ${\sigma }^2$ is assigned a proper inverse-Gamma prior

$${\sigma }^2\hspace{0.17em}\sim \hspace{0.17em}\text{Inv}-\text{Gamma}(a_{\sigma },b_{\sigma }),$$ (11)

and the hierarchical model (2), (6), (7) and (11) has a conjugacy structure that facilitates posterior simulation using a Gibbs sampling algorithm. As the normalizing constant associated with (7) is not known and may not exist, we work with the unnormalized form which yields proper full conditional distributions having standard form. Our focus of inference does not lie with the scale mixing variables themselves, rather, the use of the scale mixture representation is a computational device that leads to a fairly straightforward Gibbs sampling algorithm which enables us to draw from the marginal posterior of $\mathit{W}$. By Proposition 1 and the fact that (11) is proper we are assured that this posterior distribution is always proper. The Gibbs sampler is presented in Algorithm 1 while the corresponding derivations are presented in the Supplementary Material. Starting values for the algorithm can be obtained in part by first computing the estimator (1) and using these to initialize the Markov chain Monte Carlo (MCMC) sampler.

Algorithm 1.

Gibbs Sampling Algorithm

(i) Set tuning parameters ${\lambda }_1^2$ and ${\lambda }_2^2$.

(ii) Initialize $\mathit{W},\hspace{0.17em}{\mathit{\tau }}^2,\hspace{0.17em}{\mathit{\omega }}^2$ and repeat steps (3)–(6) below to obtain the desired Monte Carlo sample size after burn-in.

(iii) Update ${\sigma }^2\sim \hspace{0.17em}\text{Inv}-\text{Gamma}\hspace{0.17em}(a_{\sigma }^{*},b_{\sigma }^{*})$, $a_{\sigma }^{*}=\frac{c}{2}(n+d)+a_{\sigma }$

$$\begin{array}{cc}\hfill & b_{\sigma }^{*}=\frac{1}{2}{\sum }_{l=1}^n\left|\right|{\mathbf{y}}_{\ell }-{\mathbf{W}}^T{\mathbf{x}}_{\ell }|{|}_2^2\hfill \\ \hfill & +\frac{1}{2}{\sum }_{i=1}^d\left(\frac{1}{{\tau }_{k\left(i\right)}^2}+\frac{1}{{\omega }_i^2}\right){\sum }_{j=1}^c{w}_{ij}^2+b_{\sigma }.\hfill \end{array}$$

(iv) For $k=1,\dots ,K$ update ${\tau }_k^2$, through

$$1/{\tau }_k^2\sim \hspace{0.17em}\text{Inverse}-\text{Gaussian}\hspace{0.17em}(\sqrt{\frac{{\lambda }_1^2{\sigma }^2}{\left|\right|{\mathbf{W}}^{\left(k\right)}|{|}_{\mathrm{F}}^2}},{\lambda }_1^2).$$

(v) For $i=1,\dots ,d$ update ${\omega }_i^2$, through

$$1/{\omega }_i^2\sim \hspace{0.17em}\text{Inverse}-\text{Gaussian}\hspace{0.17em}\left(\sqrt{\frac{{\lambda }_2^2{\sigma }^2}{{\sum }_{j=1}^c{w}_{ij}^2}},{\lambda }_2^2\right).$$

(vi) For $k=1,\dots ,K$ update ${\mathbf{W}}^{\left(k\right)}$, based on

$\hspace{0.17em}\text{vec}\hspace{0.17em}\left({\mathbf{W}}^{\left(k\right)\prime }\right)\sim {\text{MVN}}_{m_{k}c}({\mathit{\mu }}_k,{\Sigma }_k)$ where

$$\begin{array}{cc}\hfill & {\mathit{\mu }}_k=-{\mathit{A}}_k^{-1}{\sum }_{l=1}^n({\mathit{x}}_{\ell }^{\left(k\right)}\otimes {\mathit{I}}_c)({\mathit{x}}_{\ell }^{(-k)\prime }\otimes {\mathit{I}}_c)\hspace{0.17em}\text{vec}\hspace{0.17em}\left({\mathbf{W}}^{(-k)\prime }\right)\hfill \\ \hfill & +{\mathit{A}}_k^{-1}{\sum }_{l=1}^n({\mathit{x}}_{\ell }^{\left(k\right)}\otimes {\mathit{I}}_c){\mathbf{y}}_{\ell },\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\Sigma }_k={\sigma }^2{\mathit{A}}_k^{-1},\hspace{0.17em}{\mathit{A}}_k=\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \sum _{l=1}^n({\mathit{x}}_{\ell }^{\left(k\right)}\otimes {\mathit{I}}_c)({\mathit{x}}_{\ell }^{\left(k\right)\prime }\otimes {\mathit{I}}_c)+\text{Diag}\hspace{0.17em}{\left\{\frac{1}{{\tau }_k^2}+\frac{1}{{\omega }_i^2}\right\}}_{i\in {\pi }_k}\otimes {\mathit{I}}_c\hfill \end{array}$$

and where ${\mathbf{W}}^{(-k)}={\left(w_{ij}\right)}_{i\cancel{\in }{\pi }_k,j},\hspace{0.17em}{\mathit{x}}_{\ell }^{\left(k\right)}={\left(x_{\ell j}\right)}_{j\in {\pi }_k}$, and ${\mathit{x}}_{\ell }^{(-k)}={\left(x_{\ell j}\right)}_{j\cancel{\in }{\pi }_k}$.

The tuning parameters γ₁, γ₂ in (1) and ${\lambda }_1^2,\hspace{0.17em}{\lambda }_2^2$ in the hierarchical model (2), (6), (7) and (11) control the strength of the regularization terms and thus the structure of the penalty that governs the bias-variance tradeoff associated with the estimator of W. Wang et al. (2012) suggest the use of 5-fold cross-validation (CV) over a discrete 2D grid ${\{{10}^{-5},{10}^{-4},\dots ,{10}^4,{10}^5\}}^2$ of possible values. A problem with the use of CV when MCMC runs are required to fit the model is that an extremely large number of parallel runs are needed to cover all points on the grid for each possible split of the data. To avoid some of this computational burden we approximate leave-one-subject-out CV using the Watanabe-Akaike information criterion (WAIC) (Gelman et al., 2014; Watanabe, 2010)

$$\text{WAIC}=-2\sum _{l=1}^n\hspace{0.17em}\text{log}\hspace{0.17em}{E}_{\mathbf{W},{\sigma }^2}[p({\mathbf{y}}_{\ell }|\mathbf{W},{\sigma }^2)|{\mathbf{y}}_1,\dots ,{\mathbf{y}}_n]+2\sum _{l=1}^{n}VA{R}_{\mathbf{W},{\sigma }^2}[\text{log}\hspace{0.17em}p({\mathbf{y}}_{\ell }|\mathbf{W},{\sigma }^2)|{\mathbf{y}}_1,\dots ,{\mathbf{y}}_n]$$

where $p({\mathbf{y}}_{\ell }|\mathbf{W},{\sigma }^2)$ is the probability density function associated with (2) and the required posterior means and variances are approximated based on the output of the MCMC sampler at each point of the grid. These samplers are run in parallel using a high performance computing cluster. The values of ${\lambda }_1^2$ and ${\lambda }_2^2$ are then chosen as those values that minimize the WAIC across the grid and no data-splitting is required. We note that alternative approaches based on either empirical Bayes (EB) or hierarchical Bayes (HB) could also be used to choose the tuning parameters; however, for the model under consideration we have found (Nathoo et al., 2016) that using both EB and HB to select the tuning parameters can lead to severe over-shrinkage of the posterior mean of the regression coefficients when d > n or when the genetic effects are weak.

3 Computation time and scaling

In this section, we report on computation times and scaling as the number of subjects n, the dimension of the phenotype c, and the number of SNPs d changes. Three experiments are performed with each examining how the computation time scales with one of the three input dimensions. The computation times reported here are based on a total of 10 000 MCMC iterations (5000 iterations was a sufficient burn-in in all cases considered) with each run employing 49 cores (each 2.66-GHz Xeon x5650) on a computing cluster with 20 GB of RAM requested for each job. To be clear on the parallel aspect of the computing, each core is simply used to run the Gibbs sampler with a different value of $({\lambda }_1^2,{\lambda }_2^2)$ and the value minimizing the WAIC is used for inference in each case. The computational algorithm itself runs on a single core. The use of multiple cores and MCMC chains along with the WAIC is the recommended approach for choosing the model tuning parameters based on the investigations of Nathoo et al. (2016). When multiple cores are not available, our R package ‘bgsmtr’ provides an alternative ad hoc approach for choosing the tuning parameters with the computations requiring only a single core. This approach is based on applying the original estimator of Wang et al. (2012) and choosing the tuning parameters for that estimator, γ₁ and γ₂, using 5-fold CV. Given the values obtained for γ₁ and γ₂, we use the relationship between these parameters and the tuning parameters of our model, namely, ${\gamma }_1=2\sigma {\lambda }_1$ and ${\gamma }_2=2\sigma {\lambda }_2$ to obtain the values of λ₁ and λ₂ for each sampled value of σ.

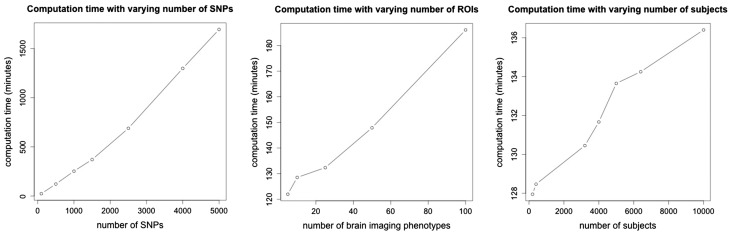
We choose baseline values of c = 12, d = 500, n = 600, and in each of the three experiments the data are simulated from the model with one dimension varying while the other two are fixed at the baseline values. The results from the three experiments are displayed in Figure 1. In each case the computation time scales approximately linearly with the given input when the other two inputs are fixed, and overall, the computation time scales as O(ndc). For a fully Bayesian approach with implementation based on MCMC, the computation time is not extensive even for the most extreme values (d = 5000, c = 100, n = 10 000) and larger values can be considered if more memory is available, or alternatively, thinning can be applied to the MCMC chains to reduce the memory requirements.

Fig. 1.

Computation time in minutes (y-axis) as a function of the number of SNPs d (c = 12, n = 600), the number of phenotypes c (d = 500, n = 600), and the number of subjects n (c = 12, d = 500). In each case, the computation time reported is based on 10 000 MCMC iterations (5000 iterations was a sufficient burn-in in all cases considered) with each run employing 49 cores (each 2.66-GHz Xeon x5650) on a computing cluster with 20 GB of RAM requested for each job. Each core is used to run the MCMC algorithm with a unique setting for the tuning parameters and a total of 49 settings are considered. Increasing or decreasing the number of settings, and hence the number of cores used, has no impact on the reported computation times

4 Simulation studies

We conduct four simulation studies in which our proposed methodology is evaluated with the primary objective of evaluating the coverage probabilities of the 95% equal-tail credible intervals for the regression coefficients $\mathit{W}.$ We focus on evaluating coverage probabilities as the ability to quantify uncertainty through interval estimation is the primary value-added of our methodology over and above the estimator proposed by Wang et al. (2012). We also compare our approach to a more standard approach, the nonparametric bootstrap applied to the estimator (1).

The application of the non-parametric bootstrap involves resampling the data with replacement and recomputing the estimator (1) for each bootstrap sample. The bootstrap distribution of the resulting estimators over a large number B = 1000 bootstrap samples is then used to construct ∼95% CIs. In this case the bootstrap resampling is done at the level of subjects. The tuning parameters γ₁ and γ₂ are recomputed for each simulated dataset in the simulation study but they are fixed across all bootstrap replicates corresponding to a single simulated dataset. The selection for these tuning parameters is based on 5-fold CV.

The simulation studies are based on genetic data obtained from the ADNI database. The data comprise information on d = 486 SNPs belonging to K = 33 genes obtained from a total n = 632 subjects [179 cognitively normal (CN), 144 AD, 309 late mild cognitive impairment (LMCI) stage]. The genes for which we have information along with the number of SNPs included for each gene are depicted in Supplementary Figure S1.

We include all 486 SNPs and simulate imaging data from c = 12 ROIs, with Study I having n = 632 subjects, and Study II having n = 250 (83 CN, 83 AD, 84 LMCI) subjects. Study II differs from Study I in that we move to a high-dimensional setting by reducing the value of n so that n < d. In each case we set the true values as ${\lambda }_1^2={\lambda }_2^2={\sigma }^2=2$, and set the true values for $\mathit{W}$ by first simulating ${\tau }_k^2\hspace{0.17em}|\hspace{0.17em}{\lambda }_1^2\hspace{0.17em}\stackrel{\text{ind}}{\sim }\hspace{0.17em}\text{Gamma}\left(\frac{m_{k}c+1}{2}\hspace{0.17em},\hspace{0.17em}\frac{{\lambda }_1^2}{2}\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}k=1,\dots ,K,$ and ${\omega }_i^2\hspace{0.17em}|\hspace{0.17em}{\lambda }_2^2\hspace{0.17em}\stackrel{\text{ind}}{\sim }\hspace{0.17em}\text{Gamma}\left(\frac{c+1}{2}\hspace{0.17em},\hspace{0.17em}\frac{{\lambda }_2^2}{2}\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,d,$ and then simulating the regression coefficients from (6), and finally, the true values for $\mathit{W}$ are obtained by setting the entries of all but 50 rows of $\mathit{W}$ to zero. This adds additional sparsity to the SNP effects and makes the simulation setup more realistic. We note that the simulation of ${\mathit{\tau }}^2$ and ${\mathit{\omega }}^2$ from Gamma distributions is not based on our assumed model and the additional sparsity added after simulation from (6) does not correspond to the prior from our model, so that we are not assuming that the model is correctly specified. The non-zero rows correspond to 5 genes containing exactly 14, 10, 6, 4 and 1 SNP(s) respectively (for a total of 35 SNPs), along with an additional 15 rows corresponding to additional SNPs. The imaging data are simulated from (2) and we note that the model assumption (2) is common to both of the approaches being compared, so neither has an advantage.

To further investigate the robustness of our approach relative to the bootstrap in settings where the model assumptions do not match the model from which the data have been generated we conduct two additional simulation studies, labelled Studies III and IV, which have the same settings as Studies I and II, respectively, with the exception that the regression errors are drawn from a heavy-tailed multivariate t₄ distribution.

For each of 100 simulation replicates we compute the bootstrap 95% CI based on the estimator (1) and the posterior distribution from our Bayesian model using the Gibbs sampling algorithm. In total each simulation study involves $d\times c=5832$ regression parameters and we use the 100 simulation replicates to estimate the coverage probability of the 95% equal-tail confidence/credible intervals for each parameter. The results are presented in Table 1.

Table 1.

Simulation studies—interval estimation

Study I
Method	MCP (overall)	MCP ($w_{ij}\ne 0$)
Bayesian model	0.95	0.83
Non-parametric bootstrap	0.85	0.45
Study II
Method	MCP (overall)	MCP ($w_{ij}\ne 0$)
Bayesian Model	0.94	0.72
Non-parametric bootstrap	0.85	0.42
Study III
Method	MCP (overall)	MCP ($w_{ij}\ne 0$)
Bayesian model	0.97	0.77
Non-parametric bootstrap	0.86	0.49
Study IV
Method	MCP (overall)	MCP ($w_{ij}\ne 0$)
Bayesian model	0.95	0.73
Non-parametric bootstrap	0.84	0.41

The coverage probability of each ∼95% credible/confidence interval is estimated based on 100 simulation replicates and then averaged (mean coverage probability, MCP) overall and also separately over the parameters that correspond to active SNPs.

In Study I we find that the mean (over all 5832 parameters) coverage probability is 95% for intervals constructed based on our approach, while that for the nonparametric bootstrap applied to the estimator of Wang et al. (2012) is 85%, below the nominal level. Considering only those 600 parameters with non-zero effects the mean coverage probability for our approach drops to 83%, while that for the nonparametric bootstrap drops to an unreasonable 45%. In Study II (n < d) we find that the mean (over all 5, 832 parameters) coverage probability is 94% for our approach while that obtained for intervals constructed using the nonparametric bootstrap is 85%. Considering only those parameters with non-zero true values the mean coverage probabilities associated with both approaches drops as in Study I, to 72% for our approach and to 42% for the nonparametric bootstrap. The results for Studies III and IV generally indicate the same patterns as those seen in Studies I and II, demonstrating that our comparisons exhibit some robustness to model misspecification.

We find that the Bayesian approach is clearly outperforming the estimator of Wang et al. (2012) combined with the non-parametric bootstrap in all cases. In all four studies the mean coverage probability for both methods drops when considering only active SNPs. This is expected since both approaches are based on estimators that shrink to zero, and for active SNPs this implies shrinkage away from the true value. In this case the values obtained from the nonparametric bootstrap are unreasonably low while those obtained from our approach are still somewhat reasonable.

5 Application to ADNI data

We illustrate our methodology by applying it to a dataset obtained from the ADNI-1 database. This dataset includes both genetic and structural MRI data and is similar to a dataset analyzed by Wang et al. (2012); however, we use a larger number of regions of interest in our analysis leading to 56 imaging phenotypes rather than the 12 imaging phenotypes analyzed by Wang et al. (2012). The imaging phenotypes used in our analysis are listed in Table 2.

Table 2.

Imaging phenotypes defined as volumetric or cortical thickness measures of 28 × 2 = 56 ROIs from automated Freesurfer parcellations

ID	Measurement	ROI
AmygVol	Volume	Amygdala
CerebCtx	Volume	Cerebral cortex
CerebWM	Volume	Cerebral white matter
HippVol	Volume	Hippocampus
InfLatVent	Volume	Inferior lateral ventricle
LatVent	Volume	Lateral ventricle
EntCtx	Thickness	Entorhinal cortex
Fusiform	Thickness	Fusiform gyrus
InfParietal	Thickness	Inferior parietal gyrus
InfTemporal	Thickness	Inferior temporal gyrus
MidTemporal	Thickness	Middle temporal gyrus
Parahipp	Thickness	Parahippocampal gyrus
PostCing	Thickness	Posterior cingulate
Postcentral	Thickness	Postcentral gyrus
Precentral	Thickness	Precentral gyurs
Precuneus	Thickness	Precuneus
SupFrontal	Thickness	Superior frontal gyrus
SupParietal	Thickness	Superior parietal gyrus
SupTemporal	Thickness	Superior temporal gyrus
Supramarg	Thickness	Supramarginal gyrus
TemporalPole	Thickness	Temporal pole
MeanCing	Mean thickness	Caudal anterior cingulate, isthmus cingulate, posterior cingulate, rostral anterior cingulate
MeanFront	Mean thickness	Caudal midfrontal, rostral midfrontal, superior frontal, lateral orbitofrontal, and medial orbitofrontal gyri, frontal pole
MeanLatTemp	Mean thickness	Inferior temporal, middle temporal, and superior temporal gyri
MeanMedTemp	Mean thickness	Fusiform, parahippocampal, and lingual gyri, temporal pole and transverse temporal pole
MeanPar	Mean thickness	Inferior and superior parietal gyri, supramarginal gyrus, and precuneus
MeanSensMotor	Mean thickness	Precentral and postcentral gyri
MeanTemp	Mean thickness	Inferior temporal, middle temporal, superior temporal, fusiform, parahippocampal, lingual gyri, temporal pole, transverse temporal pole

Each of the phenotypes in the table corresponds to two phenotypes in the data: one for the left hemisphere and the other for the right hemisphere.

Registered ADNI investigators may obtain the preprocessed data used in this analysis by contacting the corresponding author. These data can be used in conjunction with our R package ‘bgsmtr’ implementing our methodology to reproduce the results presented here.

The data are available for n = 632 subjects (179 CN, 144 AD, 309 LMCI), and among all possible SNPs we include only those SNPs belonging to the top 40 AD candidate genes listed on the AlzGene database as of June 10, 2010. The data presented here are queried from the most recent genome build as of December 2014, from the ADNI-1 data.

After quality control and imputation steps, the genetic data used for this study includes 486 SNPs from 33 genes and these genes along with the distribution of the number of SNPs within each gene is depicted in Supplementary Figure S1. The freely available software package PLINK (Purcell et al., 2007) was used for genomic quality control. Thresholds used for SNP and subject exclusion were the same as in Wang et al. (2012), with the following exceptions. For SNPs, we required a more conservative genotyping call rate of at least 95% (Ge et al. 2012).

For subjects, we required at least one baseline and one follow-up MRI scan and excluded multivariate outliers. Sporadically missing genotypes at SNPs in the HapMap3 reference panel (Gibbs et al., 2003) were imputed into the data using IMPUTE2 (Howie et al., 2009). Further details of the quality control and imputation procedure can be found in Szefer (2014). The MRI data from the ADNI-1 database are preprocessed using the FreeSurfer V4 software which conducts automated parcellation to define volumetric and cortical thickness values from the c = 56 brain regions of interest that are detailed in Table 2. Each of the response variables are adjusted for age, gender, education, handedness, and baseline total intracranial volume (ICV) based on regression weights from healthy controls and are then scaled and centered to have zero-sample-mean and unit-sample-variance.

We fit our model, which for the current dataset has 27 216 regression parameters, by running a total of 49 Gibbs sampling chains in parallel on a computing cluster with each chain corresponding to a different value of $({\lambda }_1^2,{\lambda }_2^2)$. The WAIC is applied to select which of the 49 chains to use for posterior inference. The Wang et al. (2012) estimator is also computed with tuning parameters γ₁ and γ₂ in (1) based on ${\gamma }_1=2\sigma {\lambda }_1$ and ${\gamma }_2=2\sigma {\lambda }_2$, with the values of λ₁ and λ₂ chosen using WAIC and the posterior mean for σ from the Gibbs sampler are used.

To select potentially important SNPs we evaluate the 95% equal-tail credible interval for each regression coefficient and select those SNPs where at least one of the associated credible intervals excludes 0. In total there are 45 SNPs and 152 regression coefficients for which this occurs. Table 1 in the supplementary material lists each of the 152 SNP–ROI associations along with the corresponding point and interval estimates.

The 45 selected SNPs and the corresponding phenotypes at which we see a potential association based on the 95% credible interval are listed in Table 3. Three SNPs, rs4311 from the ACE gene, rs405509 from the APOE gene, and rs10787010 from the SORCS1 gene stand out as being potentially associated with the largest number of ROIs. The 95% credible intervals for the coefficients relating rs4311 to each of the c = 56 imaging measures are depicted in Figure 2, while similar figures for rs405509 and rs10787010 are presented in Supplementary Figures S2 and S3. In the original methodology of Wang et al. (2012) the authors suggest ranking and selecting SNPs by constructing a SNP weight based on the point estimate $\widehat{\mathit{W}}$ and a sum of the absolute values of the estimated coefficients of each single SNP over all of the tasks. Doing so, the top 45 highest ranked SNPs contain 21 of the SNPs chosen using our approach and these 21 SNPs are highlighted in Table 3. The number 1 ranked (highest priority) SNP using this approach is SNP rs3026841 from gene ECE1. In Figure 3 we display the corresponding point estimates along with the 95% credible intervals (obtained via our Gibbs sampler) relating this SNP to each of the c = 56 imaging measures. We note that all 56 of the corresponding 95% credible intervals include the value 0. This result demonstrates clearly the importance of accounting for posterior uncertainty beyond the point estimate and illustrates the potential problems that may arise when estimation uncertainty is ignored. It thus serves to illustrate the practical value of our proposed methodology.

Table 3.

The 45 SNPs selected from the Bayesian model along with corresponding phenotypes where (L), (R) and (L,R) denote that the phenotypes are on the left, right and both hemispheres, respectively

SNP	Gene	Phenotype ID (hemisphere)
rs4305	ACE	LatVent (R)
rs4311	ACE	InfParietal (L,R), MeanPar (L,R), Precuneus (L,R), SupParietal (L), SupTemporal (L), CerebCtx (R),MeanFront (R),
		MeanSensMotor (R), MeanTemp (R), Postcentral (R), PostCing (R), Precentral (R), SupFrontal (R), SupParietal (R)
rs405509	APOE	AmygVol (L), CerebWM (L), Fusiform (L), HippVol (L), InfParietal (L,R),SupFrontal (L,R), Supramarg (L,R),
		InfTemporal (L), MeanFront (L,R), MeanLatTemp (L,R), MeanMedTemp (L,R), MeanPar (L,R),
		MeanSensMotor (L,R), MeanTemp (L,R), MidTemporal (L,R), Postcentral (L,R), Precuneus (L,R)
		SupTemporal (L,R), Precentral (R), SupParietal (R)
rs11191692	CALHM1	EntCtx (L)
rs3811450	CHRNB2	Precuneus (R)
rs9314349	CLU	Parahipp (L)
rs2025935	CR1	CerebWM (R), Fusiform (R), InfLatVent (R)
rs11141918	DAPK1	CerebCtx (R)
rs1473180	DAPK1	CerebCtx (L,R),EntCtx (L), Fusiform (L), MeanMedTemp (L), MeanTemp (L), PostCing (L)
rs17399090	DAPK1	MeanCing (R), PostCing (R)
rs3095747	DAPK1	InfLatVent (R)
rs3118846	DAPK1	InfParietal (R)
rs3124237	DAPK1	PostCing (R), Precuneus (R), SupFrontal (R)
rs4878117	DAPK1	MeanSensMotor (R), Postcentral (R)
rs212539	ECE1	PostCing (R)
rs6584307	ENTPD7	Parahipp (L)
rs11601726	GAB2	CerebWM (L), LatVent (L)
rs16924159	IL33	MeanCing (L), PostCing (L), CerebWM (R)
rs928413	IL33	InfLatVent (R)
rs1433099	LDLR	CerebCtx.adj (L), Precuneus (L,R)
rs2569537	LDLR	CerebWM (L,R)
rs12209631	NEDD9	CerebCtx (L), HippVol (L,R)
rs1475345	NEDD9	Parahipp (L)
rs17496723	NEDD9	Supramarg (L)
rs2327389	NEDD9	AmygVol (L)
rs744970	NEDD9	MeanFront (L), SupFrontal (L)
rs7938033	PICALM	EntCtx (R), HippVol (R)
rs2756271	PRNP	EntCtx (L), HippVol (L,R), InfTemporal (L), Parahipp (L)
rs6107516	PRNP	MidTemporal (L,R)
rs1023024	SORCS1	MeanSensMotor (L), Precentral (L)
rs10787010	SORCS1	AmygVol (L), EntCtx (L,R), Fusiform (L), HippVol (L,R), InfLatVent (L), InfTemporal (L), MeanFront (L),
		MeanMedTemp (L,R), MeanTemp (L), Precentral (L), TemporalPole (R)
rs10787011	SORCS1	EntCtx (L,R), HippVol(R)
rs12248379	SORCS1	PostCing (R)
rs1269918	SORCS1	CerebCtx (L), CerebWM (L), InfLatVent (L)
rs1556758	SORCS1	SupParietal (L)
rs2149196	SORCS1	MeanSensMotor (L), Postcentral (L,R)
rs2418811	SORCS1	CerebWM (L,R), InfLatVent.adj (L)
rs10502262	SORL1	MeanCing (L), InfTemporal (R), Supramarg (R)
rs1699102	SORL1	MeanMedTemp (R), MeanTemp (R)
rs1699105	SORL1	MeanCing (L), Precuneus (L)
rs4935774	SORL1	CerebWM (L,R)
rs666004	SORL1	InfTemporal (L)
rs1568400	THRA	Precentral (L), TemporalPole (R)
rs3744805	THRA	MeanSensMotor (R), Postcentral (R), Precentral (R)
rs7219773	TNK1	MeanSensMotor (L), Precentral (L), Postcentral (R)

SNPs also ranked among the top 45 using the Wang et al. (2012) estimate are listed in bold.

Fig. 2.

The 95% equal-tail credible intervals relating the SNP rs4311 from ACE to each of the c = 56 imaging phenotypes. Each imaging phenotype is represented on the x-axis with a tick mark and these are ordered in the same order as the phenotypes are listed in the rows of Table 2, first for the left hemisphere and then followed by the same phenotypes for the right hemisphere

Fig. 3.

The 95% equal-tail credible intervals relating the SNP rs3026841 from ECE1 to each of the c = 56 imaging phenotypes. Each imaging phenotype is represented on the x-axis with a tick mark and these are ordered in the same order as the phenotypes are listed in the rows of Table 2, first for the left hemisphere and then followed by the same phenotypes for the right hemisphere

6 Conclusion

We have proposed a framework for the analysis of data arising in studies of imaging genomics that extends a previously developed regularization approach in order to allow for the quantification of estimation (posterior) uncertainty in multi-task regression with a $G_{2,1}-\text{norm}$ penalty. The value added of our approach has been demonstrated using both simulation studies as well as the analysis of a real dataset from the ADNI database. We have compared our approach to the nonparametric bootstrap applied to (1) and have demonstrated that our methodology clearly outperforms the latter in terms of mean coverage probability, for the settings considered. We note that our implementation of the bootstrap estimates the tuning parameters from the dataset using CV and subsequently these parameters are fixed across all bootstrap replicates. To keep the computational burden down, it is routine to fix tuning parameters when bootstrapping; however, fixing these parameters does ignore the uncertainty associated with the estimated tuning parameters and this may be contributing to the bias towards below-nominal coverage in the bootstrap intervals. Re-estimating the tuning parameters for each bootstrap replicate is computationally infeasible without massively parallel computers.

It should be noted that we have not addressed statistical adjustments for multiplicity; however, our contribution is a step forward in moving from point estimation to posterior distributions for this regression model. Bayesian false discovery rate procedures (Morris et al., 2008) can be used to adjust for multiplicity in the selection of SNPs based on the output of the Gibbs sampler and this will be considered in future work.

We are currently investigating an extension of the model that allows for a more flexible covariance structure in the specification (2), and alternative shrinkage prior formulations such as the horseshoe prior (Carvalho et al., 2010) that could potentially be further developed for the type of bi-level penalization we have considered here. An alternative approach that is potentially of interest in allowing for increased scalability of the proposed model is the use of a low-rank approximation to the regression coefficient matrix $\mathit{W}$ as considered in Marttinen et al. (2014), though this would require an appropriate choice for the rank of the regression model. This potential improvement to scalability is an important direction for future work as the run times reported in Section 3 for a model with 5000 SNPs would make our approach difficult to apply to genome-wide analyses without applying some screening to reduce the number of SNPs first. The sparsity structure we propose in this article could then be incorporated into such an approximation as an extension to the current approach. In addition, extending our model to accommodate potential hidden confounding factors through a joint modelling approach as considered in Fusi et al. (2012), and the incorporation of terms allowing for gene–gene interactions are interesting avenues for future work.