RNAscClust: clustering RNA sequences using structure conservation and graph based motifs

Abstract

Motivation

Clustering RNA sequences with common secondary structure is an essential step towards studying RNA function. Whereas structural RNA alignment strategies typically identify common structure for orthologous structured RNAs, clustering seeks to group paralogous RNAs based on structural similarities. However, existing approaches for clustering paralogous RNAs, do not take the compensatory base pair changes obtained from structure conservation in orthologous sequences into account.

Results

Here, we present RNAscClust, the implementation of a new algorithm to cluster a set of structured RNAs taking their respective structural conservation into account. For a set of multiple structural alignments of RNA sequences, each containing a paralog sequence included in a structural alignment of its orthologs, RNAscClust computes minimum free-energy structures for each sequence using conserved base pairs as prior information for the folding. The paralogs are then clustered using a graph kernel-based strategy, which identifies common structural features. We show that the clustering accuracy clearly benefits from an increasing degree of compensatory base pair changes in the alignments.

Availability and Implementation

RNAscClust is available at http://www.bioinf.uni-freiburg.de/Software/RNAscClust.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The structure of an RNA molecule or non-coding RNA (ncRNA) is often crucial to its function. A main characteristic is that evolutionary changes in the primary sequence are often compensatory such that, e.g. an A-U base pair in human may correspond to a G-C base pair in mouse, thus preserving a functional RNA structure while (partly) erasing sequence similarity.

In silico genome-wide screens for structured RNAs have therefore focused on finding RNAs with evolutionarily conserved secondary structure (see Backofen and Hess, 2010; Gorodkin et al., 2010; for reviews). A main reason is that it is not feasible to search for structured RNAs on single sequences only, as their secondary structure is not significantly more stable compared to that of random sequences (Rivas and Eddy, 2000). Although all screens take outset in corresponding or syntenic sequences, two lines of strategies have been employed, one searching for structured RNAs in sequence based alignments and one conducting structural alignments. Whereas the former has the advantage of faster screenings, the latter is able to handle sequence identities below about 60 to 70%. In this identity range sequence based alignments are no longer accurate enough to represent RNA structure conservation (Gardner and Giegerich, 2004; Washietl and Hofacker, 2004). Examples of methods working on sequence based alignments include RNAz (Gruber et al., 2010) and EvoFold (Pedersen et al., 2006). Programs for structural alignment applied to genomic screens includes Foldalign, Dynalign, LocaRNA and CMfinder (Havgaard et al., 2007; Fu et al., 2014; Will et al., 2013a; Yao et al., 2006). Corresponding screens for structure RNAs range from prokaryotes (Uzilov et al., 2006; Weinberg et al., 2010) to fly (Will et al., 2013b) to vertebrates (Smith et al., 2013; Torarinsson et al., 2006, 2008).

The output of each screen for conserved RNA secondary structures is a set of multiple alignments containing orthologous RNAs predicted to adapt a common secondary structure. These sets are largely unannotated and the road to obtain functional evidence for these putative ncRNAs is tedious. One of the most promising annotation strategies would be to detect paralogs in form of RNA families or classes. Whereas members of RNA families originate from a common ancestor, members of an RNA class share the same functional structure without evolutionary relationship (Stadler, 2014). A prominent example for such an RNA class are microRNAs.

An attractive strategy to detect RNA families and classes in computational ncRNA screens is to cluster the RNA candidates based on sequence and structure. Early approaches directly clustered RNA sequences based on their sequence-structure alignment scores (Havgaard et al., 2007; Will et al., 2007), despite the high complexity of at least $O(n^4)$ for aligning two sequences. Albeit recent sequence-structure alignment tools are able to compute the alignment in time quadratic in sequence length (Otto et al., 2014; Will et al., 2015), the overall approach still does not scale to large datasets since it remains quadratic in the number of sequences clustered. For this reason, alignment-free RNA clustering approaches have been introduced (Heyne et al., 2012; Middleton and Kim, 2014).

In this paper, we boost the alignment-free clustering pipeline GraphClust (Heyne et al., 2012) by employing information about covariation contained in the alignments. The GraphClust pipeline works on single sequences and clusters paralogs. Work extending over single sequence clustering has been introduced by EvoFam to cluster EvoFold predictions (Parker et al., 2011). However, these predictions are grounded in sequence based alignments with limited degree of sequence variation. Here, we are interested in uncovering the full potential to search for paralogs including less sequentially conserved structured RNAs that may only be found through the structural alignment strategy. Thus, in contrast to previous work, we here focus on measuring the clustering performance as a function of the degree of compensatory base changes, or equivalently the degree of sequence similarity, in the structural alignments.

We develop RNAscClust, which clusters sequences from an organism of interest that are aligned to their orthologs found in different species. Firstly, RNAscClust represents the sequence stemming from the species of interest in each input alignment as a secondary structure that is obtained by constraining highly conserved base pairs. The pipeline then compares these structures using a graph kernel (Costa and De Grave, 2010). The graph kernel decomposes each structure into several substructures and can be regarded as an extension of k-mer decompositions from sequences to graphs. Comparing these substructures finally induces a similarity measure used to cluster the structures. The usage of locality sensitive hashing techniques (Broder, 1997) enables a complexity linear in the size of the dataset, considerably lower than the quadratic time performance of clustering approaches relying on all-vs-all comparisons.

We compare the performance of RNAscClust to GraphClust using benchmark datasets derived from the Rfam database (Nawrocki et al., 2014). RNAscClust is benchmarked with sets of RNA sequence alignments restricted to specific ranges of sequence identity. Each RNAscClust clustering is compared to a corresponding GraphClust result obtained by clustering human sequences contained in each alignment.

We demonstrate a considerable positive effect of incorporating structure conservation in alignments of orthologous sequences when clustering paralogous RNA sequences from an organism of interest. This results in a beneficial accuracy compared to clustering of single sequences alone, especially for datasets with low to medium sequence identity.

2 Materials and methods

2.1 Clustering approach

This section describes the RNAscClust pipeline and analyzes its computational complexity. RNAscClust accepts a set of multiple alignments as input where each alignment contains a sequence from the organism of interest structurally aligned to its orthologs. Our approach first predicts the secondary structure for the sequence from the organism of interest in each alignment using information about conserved base pairs. The secondary structure is then encoded as a sparse feature vector. Candidate clusters are iteratively selected in linear time and refined in a final post-processing step. Figure 1 compares this structure conservation-aware clustering to single sequence clustering. We furthermore introduce classification and clustering performance measures used in this work.

Fig. 1.

Hypothetical example to illustrate the difference between single sequence clustering and clustering using conserved structure. Assume the indicated G-U base pair between the first and last nucleotide in the left-most blue human sequence is part of its correct secondary structure. While single sequence structure prediction (a) fails to predict the G-U pair, information about covariation contained in the alignment (b) yields the correct secondary structure for the human sequence and allows to emphasize covarying base pairs. Taking covariation and conserved structures into account may thus yield an improved clustering

2.1.1 Representing a multiple sequence alignment as an RNA secondary structure

Let M be the set of structural alignments of RNA sequences to be clustered by RNAscClust. In the first step, we predict the consensus structure S_m of each alignment $m\in M$ to identify conserved base pairs. We chose PETfold (Seemann et al., 2008) in this step as it is shown to perform well for predicting the consensus structure from a set of aligned sequences (Puton et al., 2013). PETfold predicts a consensus structure by taking evolutionary and thermodynamic information into account and assigns a reliability $r\in [0,1]$ to each base pair. For a given alignment m and reliability threshold τ, a base pair (i, j) is considered conserved if its reliability $r_{ij}\ge \tau$. Conserved base pairs are used as constraints for predicting the secondary structure of the sequence from the species of interest using RNAfold (Lorenz et al., 2011). This allows to project conserved base pairs from the alignments onto the sequence, while tolerating variations in less structurally conserved alignment columns.

Additionally, we use the recently proposed R-scape (Rivas et al., 2016) to identify base pairs with statistically significant (E-value < 0.05) covariation. R-scape assesses the statistical significance of the observed covariation by simulating alignments under the null hypothesis that nucleotide substitutions appear independently in each column under a phylogenetic model. This allows to put further emphasis on covarying base pairs, independent of sequence information, in the clustering process by adding decorated graphs (see Section 2.1.2) whenever at least 20% of the base pairs are supported by covariation. The outcome of this first step, illustrated in Figure 2a, is a secondary structure representing the alignment m in the remaining part of the RNAscClust pipeline.

Fig. 2.

Representing the constrained folded secondary structure as a graph and feature extraction. (a) Base pairs with a reliability greater than t are set as structure constraints (blue boxes) derived from the alignment consensus structure. A constrained secondary structure prediction is performed for the human sequence, the organism of interest in this example. Plain and, if enough covarying base pairs are found, decorated secondary structure are represented as graphs. (b) Auxiliary vertices (gray) are added to the secondary structure graph to emphasize stacked base pairs. The secondary structure is decomposed into substructures using a graph kernel. Here, only neighborhood subgraphs for $N_1^v$ and $v=1,\dots ,6$ are shown and d = 0 which results in the extraction of single root vertices instead of root vertex pairs. The hashing function H encodes each subgraph as an integer which in turn becomes the index of the subgraph in the sparse feature vector counting subgraph occurrences. Since , the feature is counted twice while the other neighborhood subgraphs are unique. The feature extraction for N-N decorated structures is implemented the same way (Color version of this figure is available at Bioinformatics online.)

2.1.2 Efficient encoding of the RNA secondary structure

RNAscClust follows the approach implemented by Heyne et al. (2012) and represents each secondary structure as a graph where nucleotides are encoded as vertices with discrete labels A, C, G, U while the backbone and the base pair relations are encoded as edges. Auxiliary vertices adjacent to four nucleotides forming stacked base pairs are added (see Fig. 2b, top) to emphasize base pair stacks. We define the graph G^m as the secondary structure graph associated with the alignment $m\in M$. Our framework allows to add path graphs to G^m to include sequence information. Path graphs are graphs that only contain the backbone (i.e. the ribose-phosphate bond) as edges. Adding a path graph to G^m allows to consider sequence similarities in addition to similarities at the secondary structure level. Decorated graphs, according to R-scape, are created by representing significantly covarying base pairs as generic N-N pairs. Thus sequence information for these base pairs is removed allowing to match corresponding features between alignments without requiring the exact base pairs to be matched.

In RNAscClust sparse feature vectors are extracted from G^m using the Neighborhood Subgraph Pairwise Distance Kernel (NSPDK) (Costa and De Grave, 2010), a convolutional graph kernel. A graph kernel allows to compute the similarity of two graphs using the dot product in the induced feature space. While graph kernels commonly define a feature space only implicitly and compute directly the resulting dot product, NSPDK explicitly enumerates the features and stores them in a sparse feature vector that remains of manageable size. More precisely, the NSPDK defines as feature all small subgraph-pairs at short distance from each other as defined in the following.

NSPDK considers neighborhood subgraphs: a neighborhood subgraph $N_r^v(G^m)$ is defined as the subgraph induced by all vertices that are reachable from a given root vertex v in not more than r hops along the edges of G^m. The distance d between a pair of neighborhood subgraphs is defined as the distance between the respective root vertices. Finally, a feature in NSPDK is a pair $N_r^u(G^m)$ and $N_r^v(G^m)$ with root vertices u, v that are at distance d. The complete feature set is generated by considering all possible pairs of neighborhood subgraphs for all values of the parameters r and d such that $r\in \{0,\dots ,r_{max}\}$ and $d\in \{0,\dots ,d_{max}\}$. Each pair of neighborhood subgraphs is then encoded as an integer using a fast hashing procedure (see Fig. 2b;Costa and De Grave, 2010 for details) that yields a low number of hash collisions. One crucial advantage of NSPDK is that given a graph $G=(V,E)$ with vertex set V and edge set E, the size of the associated sparse feature vector (i.e. number of non-zero features) is bounded to a factor of $\left|V\right|$, allowing fast computations in subsequent steps. While other graph kernels commonly yield a number of features (i.e. subgraphs) that is exponential in the size of V, NSPDK generates a number of subgraphs that is linear in $\left|V\right|$ (Costa and De Grave, 2010).

2.1.3 Similarity notion between RNA alignments

The similarity between two alignments is defined as the dot product of the corresponding sparse feature vectors. As larger values of radius r and distance d tend to generate a larger number of highly specific features, the feature vectors are normalized such that each combination of r and d contributes equally to the final vector encoding. That is, each feature vector ${\varphi }_{r,d}(G)$, generated by neighborhood subgraph pairs of radius r at distance d, is normalized to unit length: ${\widehat{\varphi }}_{r,d}(G)={\varphi }_{r,d}(G)/\left|\right|{\varphi }_{r,d}(G)\left|\right|$ and then assembled into the final feature vector $\varphi (G)=\sum _{r\in R,d\in D}{\widehat{\varphi }}_{r,d}(G).$

2.1.4 Clustering secondary structures

To avoid the quadratic complexity arising from an all-vs-all comparisons of all secondary structures, RNAscClust performs approximate nearest neighbor queries to identify candidate clusters. More precisely, we build an inverse index based on a compact signature (obtained using the min-hash approach (Broder, 1997)) of the feature vectors which can be used to retrieve similar instances with a lookup operation in constant time. See Heyne et al. (2012) for further details. Running the approximate nearest neighbor query on each instance yields candidate clusters each consisting of a set of sequences. All candidate clusters are ranked by their mean pairwise similarity and are accepted or rejected, in rank order, using a greedy procedure. The procedure discards a cluster if it does not contain at least fraction ρ of unseen sequences, i.e. if the candidate cluster overlaps too much with the union of all previously accepted clusters. To further improve the consistency of the retrieved clusters, we post-process each cluster by computing the sequence-structure alignment tree of the clustered sequences using LocARNA (Will et al., 2007, 2012). Sequences belonging to the subtree with the highest average pairwise alignment score are then used to fit a covariance model using Infernal (Nawrocki and Eddy, 2013). The covariance model ultimately decides cluster membership by scanning the entire dataset and populating the cluster with all the instances that score above a bit-score threshold.

2.1.5 Runtime complexity of RNAscClust

For the input set of alignments M of size $N=\left|M\right|$, let L denote the maximum sequence length in the alignments, let $S=\underset{m\in M}{max}(|m|)$ denote an upper bound on the number of sequences per alignment. The initial consensus structure prediction using PETfold and constrained folding using RNAfold have complexity $\mathcal{O}(S·L^3)$ per alignment therefore $\mathcal{O}(N·S·L^3)$ for the complete dataset.

Let m be an alignment with the maximal number of vertices and edges. Generating its encoded graph $G^m=(V_m,E_m)$ has complexity $\mathcal{O}(|V_m|+|E_m|)$ and complexity $\mathcal{O}(N·(\left|V_m\right|+\left|E_m\right|))$ for the whole dataset. As outlined in Section 2.1.2, generating the sparse feature vectors from G^m has complexity $\mathcal{O}(|V_m|),\mathcal{O}(N·|V_m|)$ for the whole dataset M, by hashing feature vectors to integer codes. Finally, both clustering steps using approximate nearest neighbors queries and post-processing have complexity $\mathcal{O}(N)$ (see Costa and De Grave, 2010; Heyne et al., 2012 for further details). Since in realistic scenarios $N\gg L$ and $N\gg S$, the overall runtime of RNAscClust is $\mathcal{O}(N)$. The runtime of RNAscClust is thus linear in the number of input alignments. Figure 3 depicts the complete RNAscClust pipeline and indicates pipeline steps that are executed in parallel.

Fig. 3.

An overview of RNAscClust with steps executed in parallel shown as stacks. The sequence of interest in each alignment is constraint folded to generate a conservation aware secondary structure (steps 1 & 2). The resulting secondary structure graph is transformed into a feature vector in step 3. Using local sensitivity hashing (step 4), candidate clusters are extracted in the fifth step. Then a series of post-processing steps as implemented in GraphClust are invoked (steps 6–8): sequences of each cluster are aligned using LocARNA and only well aligning sequences are retained. A covariance model is generated with Infernal to extend clusters with sequences matching the model. Steps 6–8 are repeated until all candidate clusters are processed

2.2 Evaluation metrics

Classification: Consider a binary classification problem. A true positive (TP) is an object correctly classified as positive, a false positive (FP) is an object wrongly classified as positive. Similarly, we define true and false negatives (TN and FN). We use the following measures to assess the performance of a binary classifier:

Precision (also known as positive predictive value) is the fraction of correctly classified positives out of all objects classified as positive, i.e. TP∕(TP + FP).

Recall (also known as sensitivity) is the fraction of correctly classified positives out of all positives, i.e. TP∕(TP + FN). Finally, F1-Score (van Rijsbergen, 1979) is the harmonic mean of Precision and Recall:

$$\text{F1-Score}=2·\frac{\hspace{0.17em}\text{Precision}\hspace{0.17em}·\hspace{0.17em}\text{Recall}\hspace{0.17em}}{\hspace{0.17em}\text{Precision}+\text{Recall}\hspace{0.17em}}$$

In a multi-class scenario, as presented below, the F1-Score is the mean of the class-wise F1-Score weighted by the class size.

Clustering: The Rand Index (Rand, 1971) measures the fraction of object pairs that are grouped in the same way in a predicted clustering and the true class assignment. Let a be the number of object pairs that are in the same class and in the same cluster and let b be the number of pairs that are in different classes and in different clusters, then the Rand Index is defined as (a + b)∕(|M|⋅ (|M|- 1)∕2). The Adjusted Rand Index (Hubert and Arabie, 1985), a version of the Rand Index adjusted for chance, is defined as:

$$\hspace{0.17em}\text{Adjusted}\hspace{0.17em}\text{Rand}\hspace{0.17em}\text{Index}=\frac{\hspace{0.17em}\text{Rand}\hspace{0.17em}\text{Index}-E[\hspace{0.17em}\text{Rand}\hspace{0.17em}\text{Index}\hspace{0.17em}]}{1-E[\hspace{0.17em}\text{Rand}\hspace{0.17em}\text{Index}\hspace{0.17em}]}$$

Here, the $E[\hspace{0.17em}\text{Rand}\hspace{0.17em}\text{Index}\hspace{0.17em}]$ is the expected Rand Index. The Adjusted Rand Index has an upper bound of 1 and higher values indicate a better agreement between the clustering and the true class assignment.

2.3 Materials

To the best of our knowledge no dataset is available that can be directly used to benchmark RNAscClust. We thus created benchmark datasets following two different approaches to assess the performance of RNAscClust. These benchmarks are named the Rfam-ome and Rfam-cliques datasets. All benchmark sets were derived from the Rfam database (Nawrocki et al., 2014). The central design idea is to split each Rfam family seed alignment into subalignments and assess how well the clustering pipeline retrieves the Rfam families. Here a subalignment is considered to be a subset of an Rfam seed alignment. Human is the organism of interest in our benchmark. Each subalignment must hence contain a human sequence. The quality of a cluster assignment is measured by rating how well it agrees with the true Rfam family assignment.

2.3.1 Rfam-ome benchmark dataset

The Rfam-ome dataset was designed to collect orthologs of a particular human RNA in one subalignment. On the other hand, human paralogs of the same Rfam family are assigned to different subalignments. The Rfam-ome benchmark is generated by processing each Rfam family individually. In the first step, human sequences are extracted from the family seed alignment. The genomic locations of these human sequences are then identified by a sequence search against the human genome using BLAST (Altschul et al., 1997) while only accepting exact sequence matches. To extend these genomic locations to their genomic neighborhood, context of the same length as the hit is appended in up- and downstream of each hit. Regions syntenic to these extended hits are identified in 26 other species using LiftOver (Kent et al., 2003). For each species other than human, exact matches of the organism’s sequences contained in the input Rfam seed alignment are searched in the regions orthologous to the human neighborhood. This step yields sequences trusted to be orthologous to the original human sequence hit. Finally a subalignment containing each human (paralog) sequence along with its orthologous sequences is built.

Collecting the subalignments for all Rfam families yields the complete dataset named Rfam-ome. Note that all alignments in the Rfam-ome benchmark set are created by extracting the respective rows from Rfam seed alignments, while LiftOver is solely used to assign orthologous sequences to each human paralog. All genomes as well as chain files used by LiftOver were downloaded from the UCSC genome browser (Rosenbloom et al., 2015). Information about the genomes used are listed in the Supplementary Section S1 along with further details about the Rfam-ome pipeline.

2.3.2 Rfam-cliques benchmark datasets

The Rfam-ome dataset contains only few alignments with mean pairwise sequence identity (PSI) below 70% (Supplementary Section S1.2). Using constraints on the PSI of sequences added to the same alignment, the Rfam-cliques sets control the mean PSI and hence the amount of covariation captured in each alignment.

To generate the Rfam-cliques benchmark dataset, each Rfam family seed alignment is processed separately and depicted as a graph. Each sequence in the alignment is a vertex. Two vertices are connected by an edge if they originate from different species. More precisely, for an Rfam family F an undirected graph G is defined such that

$$G=(V,E),$$

$$V=\left\{s_i\right|s_i\hspace{0.17em}\text{is}\hspace{0.17em}\mathrm{a}\hspace{0.17em}\text{sequence}\hspace{0.17em}\text{in}\hspace{0.17em}\text{the}\hspace{0.17em}\text{seed}\hspace{0.17em}\text{alignment}\hspace{0.17em}\text{of}\hspace{0.17em}F\},$$

$$E=\left\{\right\{s_i,s_j\left\}\right|s_i\hspace{0.17em}\text{and}\hspace{0.17em}{s}_j\hspace{0.17em}\text{belong}\hspace{0.17em}\text{to}\hspace{0.17em}\text{different}\hspace{0.17em}\text{species}\hspace{0.17em}\}.$$

We then generate subgraphs of G where vertices are connected only if their PSI is in a specific range. For PSI thresholds $l\in [0,1]$ and $h\in [0,1]$ such that l < h, we define $G_l^h$, a subgraph of G:

$$G_l^h=(V,E_l^h),$$

$$E_l^h=\left\{\right\{s_i,s_j\left\}\right|\{s_i,s_j\}\in E \text{and} l<\text{PSI}\hspace{0.17em}(s_i,s_j)\le h\},$$

where PSI(s_i, s_j) is the PSI of the sequences s_i and s_j. $G_l^h$ contains the same vertices as G but only those edges whose corresponding pairs of sequences have a PSI in the range $[l,h]$.

The Algorithm generating the Rfam-cliques set for an individual family is outlined below. Subalignments are selected to be maximal cliques with maximum mean PSI in each iteration. A clique is a subset of the vertices of a graph in which each pair of vertices is connected by an edge. A clique is maximal if it is not a subset of a larger clique. Extracted cliques must have at least five vertices/sequences, one of human origin.

The Algorithm considers different PSI ranges in descending order. It starts with a graph containing vertices in V and the edge set $E_{0.9}^{0.95}$. After extracting subalignments as maximal cliques, additional edge sets

$$\Gamma =\{E_{0.8}^{0.9},E_{0.7}^{0.8},\dots ,E_{0.4}^{0.5}\}$$

are added iteratively to G and additional subalignments extracted. This iterative approach extracts cliques with homogeneous similarities first and allows remaining edges to form cliques in subsequent iterations thus yielding a broader PSI distribution in the alignments. Note that Γ contains non-overlapping edge sets selected according to the PSI of the adjacent sequences. The described procedure is performed for each Rfam family separately and the resulting subalignments are combined to create the dataset named Rfam-cliques High. Further details about the dataset generation can be found in Supplementary Section S2.

Algorithm generating the Rfam-cliques benchmark set for a single family.

1: $G=(V,E)=(V,\varnothing )$

2: $Rfam‐cliques=\varnothing$

3: for$(h,l)\in \{(0.95,0.9),(0.9,0.8),\dots ,(0.5,0.4)\}$ do

4: $E=E\cup E_l^h$

5:whileG has a maximal clique of size$\ge 5$that contains a human sequencedo:

6:    $C={\displaystyle \underset{\begin{array}{c}c\in \text{maximal}‐\text{cliques}(G),\\ c\hspace{0.17em}\text{has}\hspace{0.17em}\text{human}\hspace{0.17em}\text{sequence}\hspace{0.17em},\\ \mathrm{\Vert }c\mathrm{\Vert }\ge 5\end{array}}{\arg \max }}\text{meanPSI}(c)$

7: $Rfam‐cliques=Rfam‐cliques\cup C$

8: $V=V\mathrm{\setminus }C$   ▹ remove vertices in C from G

9: end while

10: end for

11: returnRfam-cliques

2.3.3 Rfam-cliques variants

Besides the Rfam-cliques High set, we generated two additional variants of the Rfam-cliques dataset. The Rfam-cliques Medium benchmark set was generated by modifying Line 3 of the Algorithm as follows:

$$(h,l)\in \{(0.8,0.7),\dots ,(0.5,0.4)\}$$

The Rfam-cliques Low benchmark was generated by setting Line 3 as:

$$(h,l)\in \{(0.7,0.6),\dots ,(0.5,0.4)\}$$

This means that each pair of sequences assigned to one subalignment of the Rfam-cliques Medium dataset has a PSI of at most 0.80 while each sequence pair contained in a subalignment of the Rfam-cliques Low dataset has a PSI of at most 0.70.

Our motivation for creating the Rfam-cliques Medium and Rfam-cliques Low datasets in addition to the Rfam-cliques High benchmark was to test RNAscClust on benchmark sets with varying degrees of mean PSI of the alignments. This in turn allows us to assess the clustering performance of RNAscClust for different amounts of covariation (see Supplementary Section S3.3 for an R-scape covariation analysis). Table 1 lists the mean of the subalignment-wise mean PSI, referred to as mean PSI from here on, in each dataset together with the respective number of subalignments and Rfam families. All families comprising less than three alignments were removed from the datasets prior to benchmarking.

Table 1.

Benchmark dataset statistics: Mean of the subalignment-wise mean PSI (mean PSI), number of subalignments and Rfam families in the benchmark datasets. Only Rfam families with at least three subalignments are counted

Dataset	Mean PSI	Subalignments	Families
Rfam-ome	0.78	118	28
Rfam-cliques High	0.73	234	48
Rfam-cliques Medium	0.63	166	26
Rfam-cliques Low	0.50	92	10

2.3.4 Single-sequence datasets

By design, each subalignment in the Rfam-ome and Rfam-cliques benchmarks contains a human sequence. This enables the comparison of RNAscClust and GraphClust by measuring the degree to which Rfam families are reconstructed using human sequences alone and comparing the outcome to an RNAscClust result harnessing covariance information contained in the structural alignments.

3 Results

3.1 Similarity metric evaluation through classification

First, we assess the quality of the similarity metric, based on dot products of sparse feature vectors, induced by RNAscClust without performing a clustering. An established approach (Videm et al., 2014) is to test the performance of a classifier only depending on the pairwise similarities of all objects in the dataset. Here, pairwise similarities based on RNAscClust sparse feature vectors are compared to those similarities generated by GraphClust using a k-Nearest-Neighbor (k-NN) classifier. RNAscClust default parameters are used in all subsequent analyses (RNAscClust’s pipeline default values are: $\tau =0.9$ (see Supplementary Section S3.4), $r_{max}=d_{max}=3,\hspace{0.17em}\rho =50\%,\hspace{0.17em}\varphi =20$ bits and the size of the feature space is 2³⁰. GraphClust was run with default parameters except that no sequence windowing was performed to obtain a clustering of full-length sequences. Up to 15 rounds of iterative clustering was performed for both tools.).

The evaluation was performed by computing sparse feature vectors for the Rfam-ome and Rfam-cliques benchmark datasets. The similarity of each pair of alignments was then computed as detailed in Section 2.1.3. A k-Nearest Neighbor classifier combined with 3-fold stratified cross-validation was used to rate the accuracy of the pairwise similarities for the benchmark sets. Stratified cross-validation ensures that each fold contains roughly the same distribution of class labels as the entire dataset. The classifier’s parameter k was fixed to 1 and cross-validation was solely used to measure the classification performance. Precision, recall and F1-Score obtained by the k-NN classifier after cross-validation are depicted in Table 2 for k = 1. The k-NN classifier based on RNAscClust similarities outperformed the classifier based on GraphClust similarities under all metrics and benchmarks considered. This indicates that the structure conservation-based similarities generated by RNAscClust reflect the Rfam family structure in the Rfam-ome and Rfam-cliques datasets more accurately than sequence-based similarities produced by GraphClust. We obtained similar results for the 3-NN classifier of both RNAscClust and GraphClust (Supplementary Table S1).

Table 2.

1-Nearest-Neighbor classification performance based on pairwise similarities computed by RNAscClust and GraphClust

Dataset	Precision		Recall		F1-Score
	RNAscClust	GraphClust	RNAscClust	GraphClust	RNAscClust	GraphClust
Rfam-cliques Low	0.93 ± 0.04	0.79 ± 0.06	0.95 ± 0.01	0.78 ± 0.09	0.93 ± 0.03	0.76 ± 0.09
Rfam-cliques Medium	0.92 ± 0.03	0.83 ± 0.02	0.93 ± 0.01	0.85 ± 0.01	0.92 ± 0.02	0.83 ± 0.02
Rfam-cliques High	0.92 ± 0.01	0.88 ± 0.02	0.91 ± 0.00	0.87 ± 0.00	0.90 ± 0.00	0.86 ± 0.00
Rfam-ome	0.96 ± 0.03	0.88 ± 0.03	0.97 ± 0.02	0.92 ± 0.02	0.96 ± 0.03	0.90 ± 0.03

Mean ± standard deviation of Recall, Precision and F1-Score for 3-fold stratified cross validation are depicted.

Note that both RNAscClust and GraphClust use sparse feature vectors to iteratively extract clusters from the dataset. These clustering and post-processing steps were not taken into account in the above evaluation and are thus considered next.

3.2 Clustering evaluation

We compared the clustering accuracy of RNAscClust and GraphClust for all benchmark datasets. Both RNAscClust and GraphClust use an iterative clustering procedure, however RNAscClust has the advantage of generating more accurate feature vectors as demonstrated in the previous section. We hence addressed the question to which extent these more accurate feature vectors translate into beneficial clusterings. All RNAscClust and GraphClust clusterings were compared to the Rfam family labels of each benchmark dataset serving as the ground truth clustering. Instances that were not assigned to a cluster by GraphClust or RNAscClust were assigned to singleton clusters.

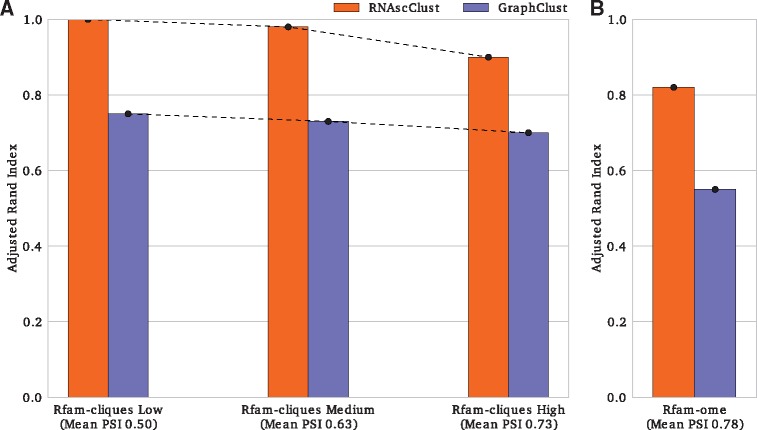
Figure 4A depicts the Adjusted Rand Index of RNAscClust and GraphClust for the Rfam-cliques datasets, Figure 4B shows clustering results for Rfam-ome set. The Rand Index is depicted in Supplementary Figure S1. Three alternative configurations of the graph encoder are also proposed in Supplementary Section S3 with an overall evaluation depicted in Supplementary Figure S8. These experiments confirmed that RNAscClust yields better clustering results than GraphClust for all benchmarks. Furthermore, RNAscClust performed best for the Rfam-cliques Low set while the performance decreased for Rfam-cliques Medium and Rfam-cliques High sets. Recall that the mean PSI of the Rfam-cliques Low dataset is lower than the mean PSI in the Rfam-cliques Medium set while the Rfam-cliques High has the highest mean PSI. We hypothesize that the performance increase achieved by RNAscClust is a result of the larger covariation captured in the Rfam-cliques Medium and, even larger, in the Rfam-cliques Low set, when compared to the Rfam-cliques High set. Additional covariation may yield more accurate structure predictions in each alignment and hence an improved clustering performance.

Fig. 4.

RNAscClust and GraphClust clustering performances, measured by the Adjusted Rand Index, depending on the mean of the alignment-wise mean pairwise sequence identity (mean PSI) of the Rfam-cliques Low, Medium and High (A) as well as Rfam-ome (B) benchmark sets

An example for the largely improved performance of RNAscClust compared to GraphClust is the SECIS-1 (RF00031) Rfam family in the Rfam-cliques Medium set with a mean PSI of 39%. RNAscClust correctly clusters all seven human sequences into one cluster consisting only of SECIS-1 sequences; GraphClust wrongly places them into multiple clusters mixed with sequences from other families. The same difference is observed in the Rfam-cliques High set. For the Rfam-cliques Low set, RNAscClust outperforms GraphClust by, for example, predicting more homogeneous and complete clusters for the well-known structurally conserved tRNA family (RF00005) with a mean PSI of 43%.

4 Discussion

We presented RNAscClust, a pipeline for clustering a set of multiple alignments of structured RNAs each containing a sequence from an organism of interest that is aligned to orthologous sequences. RNAscClust is geared towards clustering RNA structures by taking structural conservation into account. RNAscClust harnesses evolutionarily conserved secondary structure in the clustering process by maintaining conserved base pairs in a constrained folding. This emphasizes the core secondary structure of each alignment while allowing flexibility in the structure arising due to insertions, deletions and non-compensatory mutations. RNA structures are encoded as graphs and a graph kernel is used to generate sparse feature vectors inducing a pairwise similarity notion. RNAscClust has a runtime linear in the number of input alignments making it amenable to cluster large datasets.

Employing structure conservation yielded a more accurate pairwise similarity measure and improved the clustering performance. The largest improvements in clustering accuracy were observed for benchmark datasets with low to medium sequence identities. We hypothesize this happens for two reasons: Firstly, evolutionary information contained in the alignments can yield better secondary structure predictions than single sequence folding, explaining the increased clustering performance. Secondly, since RNAscClust focuses on evolutionarily conserved base pairs when comparing secondary structures between alignments, identifying these conserved base pairs enables a better estimation of the ncRNA transcript boundaries within the alignment. This helps further improving the secondary structure prediction accuracy in comparison with single sequence clustering.

RNAscClust could be extended by an improved post-processing step. For instance, a novel post-processing step based on CMcompare (Höner zu Siederdissen and Hofacker, 2010) could be used to improve the clustering performance. The approach would be based on covariance models trained for each alignment which are afterwards compared using the Link score as computed by CMcompare. The graph kernel could be extended to allow for vectors of real numbers as node and edge labels. This way, both nucleotide and base pair distributions in the input alignments could be encoded after defining an appropriate similarity function for subgraphs.

RNAscClust produces accurate clusterings while running in linear time. This will facilitate the interpretation of currently available and future large scale genomic screens for structured RNAs potentially containing millions of instances to be clustered (e.g. Smith et al., 2013).

Pipeline availability: RNAscClust is available as source code and as a Docker container (Merkel, 2014) making it possible to run the pipeline without the need to install individual dependencies. Furthermore the container allows to reproduce all Figures and Tables shown in Section 3.