Abstract
Motivation
Over the past decade, there has been a remarkable improvement in our understanding of the role of genetic variation in complex human diseases, especially via genome-wide association studies. However, the underlying molecular mechanisms are still poorly characterized, impending the development of therapeutic interventions. Identifying genetic variants that influence the expression level of a gene, i.e. expression quantitative trait loci (eQTLs), can help us understand how genetic variants influence traits at the molecular level. While most eQTL studies focus on identifying mean effects on gene expression using linear regression, evidence suggests that genetic variation can impact the entire distribution of the expression level. Motivated by the potential higher order associations, several studies investigated variance eQTLs.
Results
In this paper, we develop a Quantile Rank-score based test (QRank), which provides an easy way to identify eQTLs that are associated with the conditional quantile functions of gene expression. We have applied the proposed QRank to the Genotype-Tissue Expression project, an international tissue bank for studying the relationship between genetic variation and gene expression in human tissues, and found that the proposed QRank complements the existing methods, and identifies new eQTLs with heterogeneous effects across different quantile levels. Notably, we show that the eQTLs identified by QRank but missed by linear regression are associated with greater enrichment in genome-wide significant SNPs from the GWAS catalog, and are also more likely to be tissue specific than eQTLs identified by linear regression.
Availability and Implementation
An R package is available on R CRAN at https://cran.r-project.org/web/packages/QRank.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Genome-wide association studies (GWAS) have led to remarkable progress in our understanding of the role of genetic variation in complex human diseases, resulting in the identification of thousands of common genetic variants affecting human diseases and other complex traits. Most genetic variants discovered through GWAS are non-coding, and therefore may play a role in regulating gene expression levels. Identifying genetic variants that influence the expression level of a gene, i.e. expression quantitative trait loci (eQTLs), is essential to interpreting the GWAS loci and understanding how genetic variants influence traits at the molecular level. In addition, eQTL discovery by itself is an important area, since it helps understand how genetic variants influence gene regulation and discover complex gene regulatory networks. An important resource for eQTL discovery is the Genotype-Tissue Expression (GTEx) project, a major international project designed to establish a comprehensive data resource on genetic variation, gene expression and other molecular phenotypes across multiple human tissues (Aguet et al., 2016).
Most of the existing eQTL studies focus on identifying mean effects, or associations between genotype and the mean value of the expression level of a gene. However, the entire distribution of gene expression may be regulated by genetic variants. For instance, Wei et al. (2014) identified a set of single nucleotide polymorphisms (SNPs) that are associated with the variance of gene expression, and also found that these SNPs are more likely to exhibit interactions with environment and other SNPs than SNPs that are identified by mean-based methods. Their findings suggest that higher order genetic associations are meaningful, and hence have great potential for new eQTL discoveries.
Along this direction, several methods have been proposed to identify variance eQTLs by testing heteroscedasticity, including (i) Levene’s test (Schultz, 1985), (ii) Brown-Forsythe test (Brown and Forsythe, 1974) and (iii) correlation least squared (CLS) test (Brown et al., 2014). Both Levene and Brown-Forsythe tests test the marginal variance differences between two and more groups. While beneficial for experimental studies, their inability to account for continuous covariates such as imputed SNPs and principal components of population stratification largely limits their application to genetic studies in human populations. The CLS method is more flexible in accommodating covariates with an assumption of a linear location-scale model. It is a two-step regression-based test. The first step is to regress gene expression levels on genotypes and covariates, and the second step exploits Spearman rank correlation tests to assess whether the residual squares are correlated with genotypes. The covariate effect is only considered in the regression step, but not in the correlation test step. More recently, a Bayesian test (Dumitrascu et al., 2015) has been proposed to relax the linear assumption at the expense of increased computational cost, which could be undesirable for genome-wide identification of eQTLs that involves hundreds of millions of tests.
Mean and variance only partially reveal the distributional heterogeneity. In this paper, we exploit quantile regressions (Koenker and Bassett Jr, 1978) to systematically investigate how genotypes and covariates affect the entire distribution of a gene expression. In particular, we consider a series of quantile levels and use a rank-score approach (Gutenbrunner et al., 1993) to identify eQTLs with impact on the distribution of each gene expression. The resulting quantile test, which we call Quantile Rank-score based test (QRank) throughout the paper, enjoys the following advantages: (i) it is computationally efficient, requiring only about 1.75 times the computing time of linear regressions in simulations; (ii) it can easily accommodate various types of covariates, continuous or discrete; (iii) it accommodates a wide range of distributions without assuming an a priori parametric likelihood for the gene expressions; (iv) it is robust against outliers in the data; (v) it simplifies the preprocessing normalization procedure; and (vi) it controls the type I error under various simulation settings.
We applied the proposed QRank tool to the Genotype-Tissue Expression (GTEx) project v6 data (dbGaP accession number phs000424.v6.p; project website at www.gtexportal.org), and compared the eQTL discoveries with those identified by linear regressions (Aguet et al., 2016) and CLS. We found that the eQTLs identified by QRank or CLS are more likely to be tissue specific, and have higher enrichment in the GWAS SNP set (Welter et al., 2014), than those identified by linear regressions. It may suggest that the eQTLs with higher order effects on gene expressions are more likely to be disease-related. In addition, QRank has higher power and identifies many more new eQTLs than CLS.
2 Systems and methods
2.1 Notations and settings
Suppose the data consists of n subjects who have their gene expression measured on a total of K genes, and are genotyped for a total of M SNPs. We then denote Y as a n × K gene expression matrix, where is the gene expression level of the ith subject on the kth gene, Gk. We denote X as a n × M genotype matrix, where is the ith subject’s genotype on the jth SNP. We finally denote as the vector of covariates of the ith subject, including the intercept. Throughout the paper, we denote as the τth conditional quantile of Y given X.
Let Λk be the subset of SNPs that are within the pre-defined distance of the the transcriptional start site (TSS) of gene Gk, such as ±1 MB, then for each SNP–gene pair (j, k) where and , we build the following linear quantile model
| (1) |
where is the random error whose τth conditional quantile , and is the quantile level of interest. Under Model (1), the conditional quantile of is a linear function of and , i.e. . In this model, is the primary parameter of interest, which characterizes the association between the genotype and the gene expression level of Gk. The goal of the analysis is to identify the (j, k) pairs whose for any given .
2.2 Quantile rank-score based test at a fixed quantile
At a fixed quantile level, the existing inference tools for quantile regression can be generally classified into three categories: Wald-type inference, rank-score method and resampling methods (Kocherginsky et al., 2012). The Wald-type inference requires the direct estimation of the asymptotic variance-covariance matrix. That, however, is computationally difficult, since the limiting variance-covariance matrix contains the density of the error at the τth quantile. In the framework of quantile regression, the error distribution is non-i.i.d. and completely unspecified. As a result, the limiting variance-covariance matrix contains n nuisance parameters. Without a parametric likelihood, it is hard to estimate those local densities. Several kernel based approaches have been proposed in this context, but their estimates are often unreliable at extreme quantiles or with relatively small sample sizes. In our preliminary analyses, we also found that direct Wald type inference with kernel estimated densities has inflated type I errors at very small significance level (e.g. ). Alternatively, resampling based inference such as bootstrap does not require density estimation; however it is computationally intensive, and hence undesirable in gene expression applications where one needs to repeat the analysis for hundreds of millions of SNP–gene pairs for each tissue.
We hence propose to extend the rank-score test (Gutenbrunner et al., 1993) for eQTL discovery. For any fixed quantile τ, the rank score function in quantile regression can be written as
| (2) |
where is an asymmetric sign function, and is the estimated coefficient under the null . Define as the residual vector of projected on the column space of (the design matrix under the null), then in (2) is the ith element of ; the projection is done to achieve the asymptotic independence between and . Hence the test statistics measures the quantile association between and that is accounted for the co-linearity between and . Since the function essentially measures the signs of the residuals, and is in the form of Hájek’s rank generating function (Hájek, 1965), is hence called rank score statistic.
Note that is the quantile regression estimating function that is associated with . When u is the residual under the null hypothesis, is close to zero if and only if the null hypothesis is true. Any deviation from the null model will push away from zero. Consequently, one could construct a test statistics to test whether by
| (3) |
where is the variance of such that 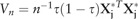 . According to the rank-score inference (Gutenbrunner et al., 1993),
. According to the rank-score inference (Gutenbrunner et al., 1993),
| (4) |
under the null hypothesis . Similar construction in maximum likelihood estimation (MLE) can be found in Fisher’s score test (Nelder and Baker, 2004), or generalized likelihood ratio statistics (Fan et al., 2001).
The asymptotic distribution of Equation (3) was established under the assumption of i.i.d. errors. Although this assumption is often unrealistic for quantile regressions, many studies (Wang, 2009; Wei et al., 2006) have consistently found that the rank score test is very robust with non-i.i.d. errors. A generalized rank score test with non-i.i.d. densities could be found in Wang (2009). However, it requires the estimation of the nuisance parameters ’s. Even though it is theoretically appealing, such generalized rank score test is much harder to implement, and may bring extra uncertainty to the estimates. For this reason, we will investigate the performance of the simple rank score test (2) in the setting of eQTL discovery. The quantile regression rank-score test enjoys the following advantages. (1) It is a distribution-free statistic. The asymptotic distribution of the test statistics is independent of distribution of the gene expressions. Hence it can be applied to any gene expression data without requiring a pre-transformation to achieve normality. (2) The construction of the test statistics is simple and avoids the estimation of local densities. (3) It is computationally fast. To construct rank-score test statistics, we only need to estimate the null model where once, which greatly reduces the computation cost from M × K pair-wise regressions for each SNP–gene pair to K regressions.
2.3 Composite rank-score test
Instead of individual quantile level P-values, it would be desirable to have a single P-value for a SNP–gene pair from a composite test across multiple quantile levels. Suppose we consider quantile levels of , then define as the vector of rank score test statistics at the corresponding quantile levels. We can show that, under the null hypothesis, asymptotically follows a multivariate normal distribution,
| (5) |
where is the variance-covariance matrix. The diagonal elements of are 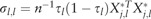 for , and the off-diagonal elements of are
for , and the off-diagonal elements of are 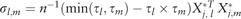 for and .
for and .
A natural composite rank score test statistic can be constructed by the following quadratic form in :
| (6) |
To select the quantile levels, one could either choose evenly spaced quantile levels, or go with the commonly used quantile levels, such as 0.1, 0.25, 0.5, 0.75 and 0.9. Depending on the nature of the application, one may also select quantile levels in a specific interval of interest. For example, if we were only interested in identifying eQTLs that are associated with extreme values of gene expression, we could select only quantiles at the upper tail.
The composite rank score combines the quantile associations over multiple quantiles, regardless of the directions of the quantile associations. To some extent, one can view the mean effect as 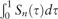 , an integrated quantile effect. When the quantile association is homogeneous at all the quantiles in terms of both direction and magnitude, then testing the composite quantile association at evenly spaced quantile levels is equivalent to testing the mean effect. When the association is heterogeneous across quantile levels, especially when the association is ‘crossing’ over quantile levels, i.e. is positive for certain quantiles but negative for others, or the association only manifests at extreme quantiles, the linear regression could underestimate, or even completely miss the underlying SNP–gene link. The composite quantile test hence has better chance to discover such heterogeneous associations. As we report below in the Results section, the eQTLs associated with heterogeneous associations are more likely to be associated with complex traits, which underscores the potential of quantile analysis in eQTL discovery.
, an integrated quantile effect. When the quantile association is homogeneous at all the quantiles in terms of both direction and magnitude, then testing the composite quantile association at evenly spaced quantile levels is equivalent to testing the mean effect. When the association is heterogeneous across quantile levels, especially when the association is ‘crossing’ over quantile levels, i.e. is positive for certain quantiles but negative for others, or the association only manifests at extreme quantiles, the linear regression could underestimate, or even completely miss the underlying SNP–gene link. The composite quantile test hence has better chance to discover such heterogeneous associations. As we report below in the Results section, the eQTLs associated with heterogeneous associations are more likely to be associated with complex traits, which underscores the potential of quantile analysis in eQTL discovery.
3 Results and discussion
3.1 Overview of GTEx data
We applied the QRank tool to the GTEx data to illustrate the potential value of the quantile based gene expression test. We analyzed the GTEx midpoint v6 data, which comprises RNA sequencing (RNA-seq) data from 7051 samples of 449 individuals representing 44 tissues (dbGaP accession number phs000424.v6.p1). We used data from 4 tissues with sufficient sample sizes (n > 275) including: muscle-skeletal (n = 361), whole blood (n = 338), lung (n = 278) and thyroid (n = 278) for the identification of eQTLs. Because of the relatively small sample sizes, we focused on identifying eQTLs within ±1 MB of TSS of each gene.
In this paper, we focus on the protein coding genes defined in the GENCODE version 19 (Harrow et al., 2012). The genotype and gene expression data underwent the same quality control procedures as in the previous GTEx study (Aguet et al., 2016). In particular, the gene expression values are transformed via the inverse quantile normalization. We remark, however, that QRank makes no distributional assumption of gene expressions. The use of the normalized gene expression data is merely out of consideration for fair comparison between different methods. In addition, we remove genes with more than 10% zero read count, as in such a case the Gaussian assumption in linear regression is violated and our preliminary analyses also found that the existing variance eQTL method CLS (Brown et al., 2014) had largely inflated type I error. We also adjust for 40 known and inferred technical covariates in order to control for potential confounding factors including gender, genotyping array platform (Illumina’s OMNI 5m or 2.5M array), 3 principal components of SNPs and 35 PEER factors (Stegle et al., 2012) of the top 10 000 expressed genes in each tissue in the analysis. More information about the data processing and analyses can be found in the supplementary materials.
3.2 Comparison methods
We compare the proposed QRank tool with two existing methods: (i) linear regression (LR) following the GTEx analysis protocol, and (ii) the CLS test for variance eQTLs. In particular, LR measures the genetic effects of the mean levels of gene experiences; CLS measures the genetic effects on variances of gene expressions; QRank measures the genetic effects on the entire distribution of gene expressions. When implementing the proposed QRank test, we consider 5 quantile levels at , and combine their rank score functions to test whether genetic variants have effect on the entire distribution of gene expression levels.
The LR assumes that the gene expression level after quantile-normalization follows a linear model
| (7) |
where is the quantile-normalization function, and is the random error with mean zero. Here, measures the effect of the variant on the mean of the normalized .
The CLS test (Brown et al., 2014) takes the residuals from the LR Equation (7), and then calculates the Spearman correlation between the genotype and the residuals squares . If the resulting correlation is significant, it claims that SNP j is associated with the variance of the normalized gene expression level .
3.3 Simulations
3.3.1. Type I error estimate and power
In this section, we evaluated the type I error and power of the QRank test in various simulated settings, and compared the results with those from LR and CLS. Specifically, we considered a simple scenario where a gene expression is associated with a single SNP with minor allele frequency (MAF) 0.3 and a single covariate, and investigated various joint distributions of (Y, X, Z).
We first considered a ‘homogeneous’ model
where e is the random error. In this setting, the association of X and Y is constant across different quantile levels with the common slope β. We then considered the ‘location-scale’ model
where e is i.i.d. with cumulative density distribution (CDF) Fe. Under this model, the effect of X on Y is , and as τ increases, the true effect increases. Finally, we considered a ‘local’ model, where quantile effect only exists on a small interval of . We assume that the quantile function of Y follows
, where
Y is not associated with X when quantile levels are greater than 0.3, but negatively associated with X when quantile levels are less than 0.3. In each of the model settings, we considered 4 error distributions. (1) , the standard normal distribution, (2) 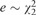 , a skewed distribution, (3) , a symmetric and heavy-tailed distribution, and (4) Cauchy distribution, an extremely heavy-tailed distribution with unbounded variance. Since the gene expression levels are matched to normal distribution in preprocessing procedure of the GTEx data, the error distributions are most likely to be close to be normally distributed. However, this simulation aims to provide a comprehensive investigation of the validity of QRank (as well as LR and CLS approach), as it is proposed to apply for studies with no distributional assumption of gene expressions. For example, it can be directly used to read counts or RPKM (Reads Per Kilobase of transcript per Million mapped reads) gene expression data.
, a skewed distribution, (3) , a symmetric and heavy-tailed distribution, and (4) Cauchy distribution, an extremely heavy-tailed distribution with unbounded variance. Since the gene expression levels are matched to normal distribution in preprocessing procedure of the GTEx data, the error distributions are most likely to be close to be normally distributed. However, this simulation aims to provide a comprehensive investigation of the validity of QRank (as well as LR and CLS approach), as it is proposed to apply for studies with no distributional assumption of gene expressions. For example, it can be directly used to read counts or RPKM (Reads Per Kilobase of transcript per Million mapped reads) gene expression data.
Finally, the regression coefficient β represents the genetic association of interest. Here we consider three scenarios of corresponding to no effect, small effect and large effect, respectively. In particular, when β = 0, Y is not associated with X. Any discovery would be a false positive. To mimic the GTEx data, we simulated 300 samples in each setting. We used five pre-selected quantile levels of in QRank for estimation.
Table 1 presents the type I errors and powers estimated from 5000 Monte-Carlo replicates. Both LR and QRank have well-controlled type I errors in all scenarios. QRank is slightly more conservative than LR. Under the homogeneous setting, the combined quantile effect is similar to the mean effect. As expected LR is more powerful than QRank when the error distribution is normal. However, when the error distribution is t3, their performances are comparable, and when the error distribution is skewed (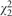 ) or extremely heavy-tailed (Cauchy), QRank is more powerful than LR. When the genetic associations are heterogeneous across quantile levels (e.g. under the location-scale setting and the local setting), QRank is more powerful than LR in detecting such higher order heterogenous associations.
) or extremely heavy-tailed (Cauchy), QRank is more powerful than LR. When the genetic associations are heterogeneous across quantile levels (e.g. under the location-scale setting and the local setting), QRank is more powerful than LR in detecting such higher order heterogenous associations.
Table 1.
The comparison of LR, CLS and QRank in terms of the Type I error (when β = 0) and power (when ) under different simulation settings
| β | Homogeneous |
Location-scale |
Local |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LR | CLS | QRank | LR | CLS | QRank | LR | CLS | QRank | ||
| 0 | 0.050 | 0.053 | 0.042 | 0.055 | 0.083 | 0.047 | 0.047 | 0.049 | 0.045 | |
| N(0, 1) | 0.2 | 0.596 | 0.049 | 0.315 | 0.484 | 0.730 | 0.527 | 0.111 | 0.155 | 0.322 |
| 0.4 | 0.994 | 0.052 | 0.914 | 0.899 | 0.986 | 0.977 | 0.315 | 0.498 | 0.934 | |
| 0 | 0.048 | 0.159 | 0.046 | 0.051 | 0.260 | 0.050 | 0.048 | 0.252 | 0.045 | |
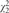 |
0.2 | 0.191 | 0.252 | 0.513 | 0.810 | 0.761 | 0.769 | 0.065 | 0.326 | 0.895 |
| 0.4 | 0.592 | 0.242 | 0.977 | 0.998 | 0.968 | 0.999 | 0.111 | 0.427 | 1.000 | |
| 0 | 0.049 | 0.057 | 0.048 | 0.054 | 0.074 | 0.049 | 0.048 | 0.050 | 0.046 | |
| t3 | 0.2 | 0.272 | 0.055 | 0.213 | 0.233 | 0.590 | 0.381 | 0.069 | 0.091 | 0.133 |
| 0.4 | 0.740 | 0.051 | 0.738 | 0.534 | 0.942 | 0.892 | 0.132 | 0.234 | 0.556 | |
| 0 | 0.050 | 0.579 | 0.046 | 0.057 | 0.587 | 0.052 | 0.057 | 0.585 | 0.045 | |
| Cauchy | 0.2 | 0.055 | 0.580 | 0.153 | 0.066 | 0.647 | 0.223 | 0.050 | 0.587 | 0.064 |
| 0.4 | 0.065 | 0.585 | 0.536 | 0.075 | 0.727 | 0.666 | 0.046 | 0.606 | 0.111 | |
Interestingly, we observed that CLS has inflated type I errors in many scenarios. As described in the introduction, the covariate effect is only considered in the regression step, but not in the correlation test step in CLS. As the confounding effect of Z is not adjusted in the second step of CLS, it leads to the inflation. In addition, when the error distribution is skewed or extremely heavy-tailed, CLS may also encounter inflated type I errors.
In addition to the simulated models above, we also investigated the type I error based on the real GTEx data, whose gene expressions are matched to normal distribution. We generate each Monte Carlo sample by randomly selecting a gene Gk from all the genes in each tissue who have non-zero expressions in at least 90% of the subjects, and then randomly select a SNP j from all the genotyped and imputed SNPs. We consider all 40 covariates as in real data analysis. Since the expected association between a random SNP and a random gene from genome-wide data is close to zero, we assume that such a generated random sample follows the null model, and hence we expect the false discovery rate to be close to its nominal level. We repeat this random sampling a million times per tissue, and for each random sample, we apply all the three approaches to test the conditional association between and (.
The estimated type I errors from all the Monte-Carlo replicates (4 million in total) are presented in Table 2 at multiple significance levels ranging from 0.05 to . Same as in the simulated models, both LR and QRank have well-controlled type I errors. We do observe a slightly inflated type I error in CLS. Due to the observed inflation pattern in the simulated data, we evaluated canonical correlations between the 40 covariates and the variance of gene expressions, which we denote as R2. We then repeat the procedure to re-estimate the type I errors restricting to the genes whose . The resulting type I errors are presented in the second half of Table 2. As expected, we observed even larger type I errors in the CLS method. Luckily, in GTEx, only less than 1% of the genes have .
Table 2.
The Type I errors for LR, CLS and QRank at different nominal levels, based on the GTEx data
| Nominal P-value | LR | CLS | Qrank | |
|---|---|---|---|---|
| 5E-02 | 5.01E-02 | 5.40E-02 | 3.08E-02 | |
| All genes | 1E-02 | 1.02E-02 | 1.13E-02 | 5.14E-03 |
| 1E-03 | 1.06E-03 | 1.21E-03 | 4.47E-04 | |
| 1E-04 | 1.15E-04 | 1.38E-04 | 4.51E-05 | |
| 5E-02 | 5.04E-02 | 6.66E-02 | 3.38E-02 | |
| Genes with | 1E-02 | 1.04E-02 | 1.74E-02 | 5.79E-03 |
| 1E-03 | 1.17E-03 | 3.19E-03 | 5.24E-04 | |
| 1E-04 | 1.66E-04 | 8.22E-04 | 6.07E-05 |
3.4 GTEx data analysis
3.4.1. eQTLs identified in four tissues
Supplemental Table S1 provides information for each of the four tissues we analyzed (muscle-skeletal, whole blood, lung and thyroid), including the sample size, the number of genes with zeros, the number of SNPs genotyped or imputed within the ±1 MB neighborhood of the genes and the number of SNP–gene pairs.
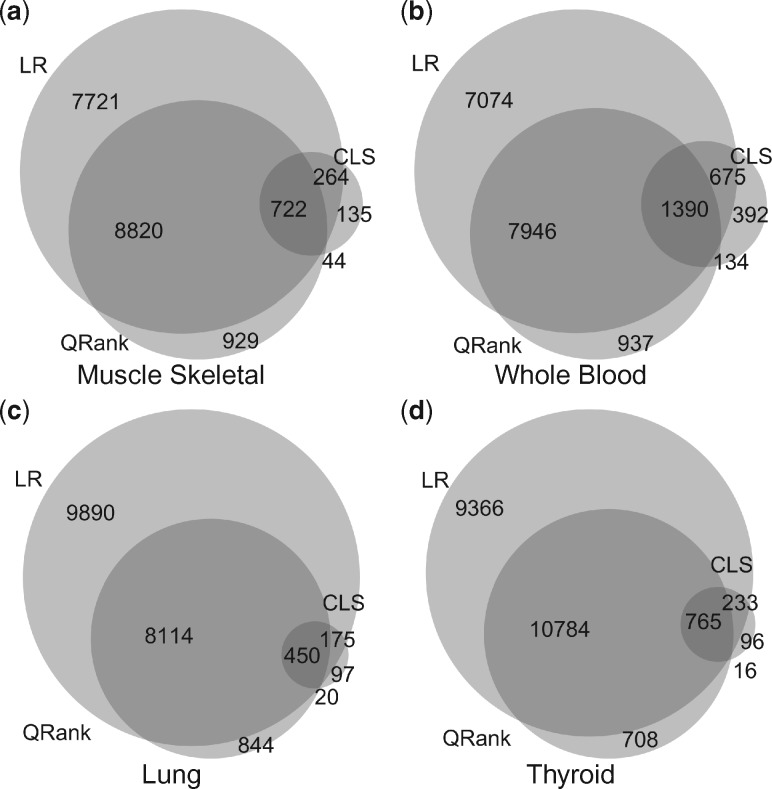
Stratified by the type of tissues, the Venn diagrams in Figure 1 displays the numbers of identified genes from different methods at the false discovery rate (FDR) level of 5%, and how they overlap with each other. (The Venn diagrams at the SNP–gene pair level are available in Supplementary Fig. S1). Each gene may correspond to multiple eQTLs due to linkage disequilibrium (LD) among SNPs. We observed similar patterns across the four tissues. In particular, LR identified the most significant genes/eQTLs, CLS identified the least, and QRank in between. This suggests that linear regression remains a powerful tool to identify eQTLs, while the CLS test may have limited power in eQTL discoveries. Most of the genes/eQTLs identified by QRank are also identified by LR, however, there are a fairly substantive number of new genes/eQTLs that were uniquely identified by QRank.
Fig. 1.
Venn diagrams depicting the overlap among genes identified by LR, CLS and QRank controlling FDR at
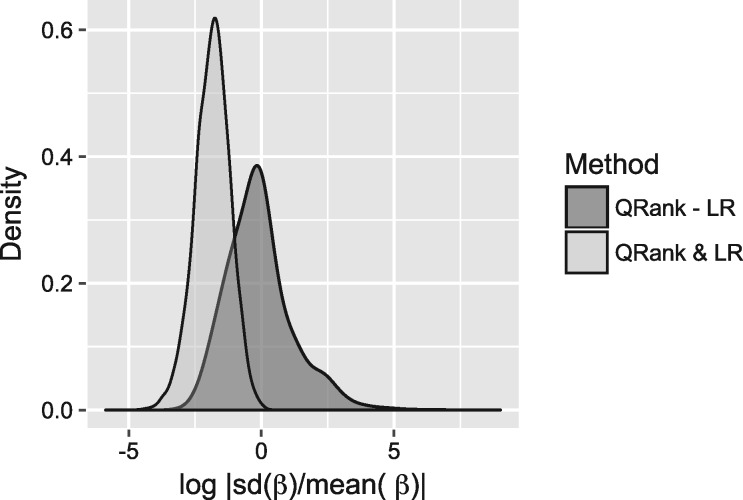
We carefully examined the quantile specific effects of those eQTLs that were identified by QRank. It reveals that most of the overlapping eQTLs with LR have homogenous effects across the quantile levels. In contrast, the eQTLs that are uniquely identified by QRank often exhibit substantial heterogeneity across the quantiles, and consequently are missed by LR (similar to what was shown in our simulation study). To illustrate the differences between the two sets of eQTLs, we quantify the degree of heterogeneity for each SNP–gene pair by the log transformed ratio between the standard deviation and the absolute mean of their 5 estimated quantile coefficients s. The higher the number, the more heterogeneity in the quantile effects. In Figure 2, we overlaid densities from the resulting heterogeneity indexes between the two sets of eQTLs at 5% FDR in four tissues. In Figure 2, the density in dark gray is estimated from the heterogeneity indexes from the SNP–gene pairs uniquely identified by QRank (QRank-LR), and the light gray one is that from the SNP–gene pairs identified by both approaches (QRank & LR). Clearly, as shown, the QRank-LR eQTLs presented more heterogeneous effects compared to those identified by QRank & LR. Such results are not surprising, since when the quantile effects are homogenous, they are equivalent to the mean effect. Consequently, LR is expected to be more powerful than QRank, as the LR is the most powerful test for mean effects with normalized outcomes. For the same reason, a large number of homogenous eQTLs were identified by LR but missed by QRank.
Fig. 2.
Densities of the log transformed value of the ratio between the standard deviation and the absolute mean of their 5 estimated quantile coefficients s for eQTLs identified at 5% FDR in four tissues. In legend, QRank-LR stands for the SNP–gene pairs that were identified by QRank but missed by LR, and QRank & LR stands for the SNP–gene pairs identified by both approaches. The QRank-LR eQTLs are more heterogeneous than the QRank & LR eQTLs
3.4.2. Explore the eQTL association patterns using quantile specific QRank
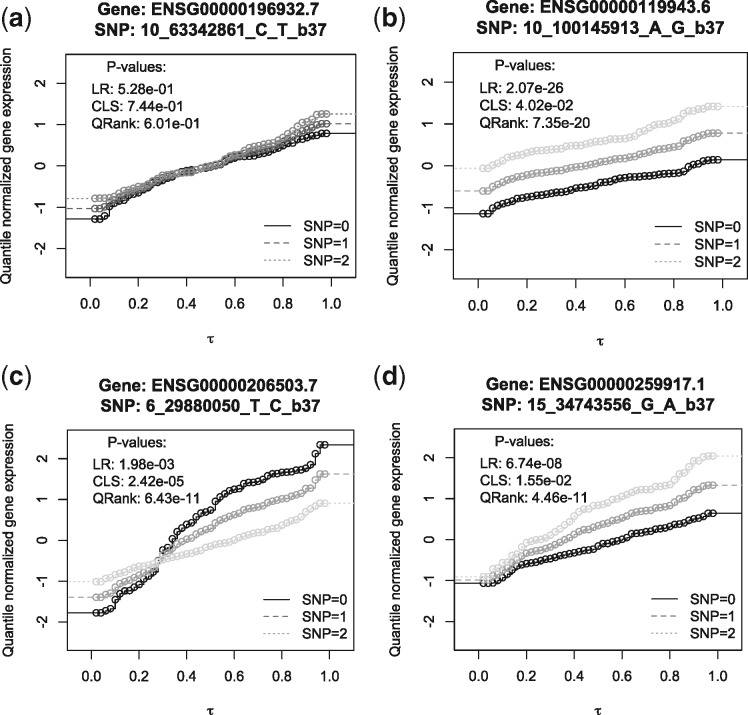
One advantage of quantile based approach is to investigate how the eQTLs impact the entire distribution of the gene expression. To do that, we estimate the quantile coefficients on a fine grid of quantile levels (we used 49 evenly spaced quantile levels ranging from 0.02 to 0.98). The estimated conditional quantile of Y given X and Z is then . One can then exam how changes with a genotype X. It provides a comprehensive picture on gene-SNP association.
To get a better understanding on why different methods identify different eQTLs, we applied this approach to a set of eQTLs identified (or not identified) by different methods to evaluate their quantile association patterns. The resulting conditional distribution functions of 4 representative gene-SNP pairs in thyroid tissue are plotted in Figure 3. Specifically, the black solid curve is the estimated quantile function with reference SNP values, while the dark grey and light grey dot curves are the estimated quantile functions with one or two alternative alleles assuming additive genetic models. Each sub-figure represents a distinctive association pattern. Figure 3(a) presents a SNP–gene pair that is not identified by any of the approaches. As shown, the three curves are nearly identical at all the quantile levels, which suggest that the SNP genotype has little impact on the gene expression level. Figure 3(b) presents a SNP–gene pair that is identified by both LR and QRank, but missed by CLS. In this case, the effect of the SNP on gene expression is homogeneous in both the direction and magnitude across all quantile levels. In this case, LR is more efficient than QRank with smaller P-value. Figure 3(c) presents a SNP–gene pair with a ‘crossing’ heterogeneous effect such that the SNP is positively associated with the gene expression at lower quantiles, and negatively associated with the gene expression at upper quantiles. Such eQTLs would be missed by LR as their effect at lower and upper quantiles cancels out at the mean level; in contrast, the proposed QRank is not affected by such crossing effect because the test statistics accumulates the squared estimating functions. As shown in their P-values, the CLS test detects such an association pattern with limited power. Finally, Figure 3(d) presents another heterogeneous effect pattern, in which case the SNP has an effect that is mostly evident at upper quantile levels. In this case, LR is less powerful than QRank as it misses the local effect while QRank captures it.
Fig. 3.
The estimated conditional distribution functions of gene expression levels for a few SNP–gene pairs in thyroid tissue. The x-axis is the grid of quantile levels , and the y-axis is the estimated conditional distribution functions for each quantile level given three SNP values and averaged covariates. This figure presents how the entire distribution of gene expression differs by SNP values for 4 SNP–gene pairs
These examples illustrate the advantage of QRank in identifying SNP–gene pairs with heterogeneous effects, and in providing a more comprehensive association picture for eQTL discoveries.
3.4.3. Tissue-specific effects in the four tissues
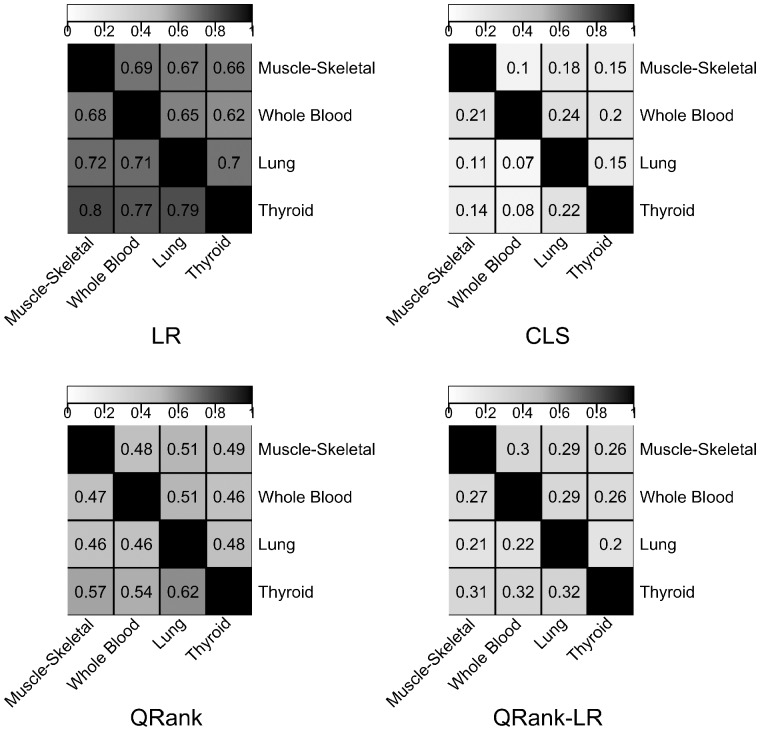
We also investigated the sharing patterns of eQTLs across tissues, for each method separately. As complex traits may be influenced by regulatory elements that act in a tissue-specific manner, tissue-specific eQTLs are more likely to be linked with disease risk than cross-tissue eQTLs (Torres et al., 2014). To understand the eQTLs sharing patterns for each method, we compute a pairwise eQTL sharing coefficient (eQTL a gene with eQTL(s) in tissue i a gene with eQTL(s) in tissue j). In Figure 4, we show the pairwise sharing coefficients at the gene-level for different approaches. The pairwise sharing at the SNP level is provided in Supplementary Figure S2. As QRank-LR corresponds to genes/eQTLs identified by QRank but missed by LR in the same tissue, the pairwise sharing of QRank-LR corresponds to those genes/eQTLs also identified by QRank in other tissues. As shown, genes/eQTLs that are identified by CLS or QRank-LR tend to be less shared than those identified by LR and QRank. At gene level, the CLS identified eQTLs are the least shared among all approaches, and at SNP–gene pair level, the QRank-LR identified eQTLs are the least shared.
Fig. 4.
Cross-tissue sharing of genes. The entry in row i and column j is an estimate of (gene with eQTL(s) in tissue i a gene with eQTL(s) in tissue j)
In Table 3 we show the relative risk (RR) of being tissue-specific genes for genes identified by each approach at 5% FDR in comparison with LR. About 20.7% LR-identified genes are tissue specific. Statistical tests on RR show that CLS, QRank, QRank-LR are all significantly more likely to detect tissue-specific eQTLs than LR. Out of the 3631 unique genes identified by QRank-LR, 42% are tissue specific. In the next section, we validate these QRank-LR tissue-specific associations using the enrichment in GWAS catalog.
Table 3.
The tissue-specificity of genes identified by different approaches
| LR | QRank | CLS | QRank-LR | |
|---|---|---|---|---|
| No. of identified genes | 28066 | 21726 | 4788 | 3631 |
| % of tissue-specific genes | 20.7% | 43.6% | 87.5% | 42.0% |
| RR | Ref | 2.111 | 4.235 | 2.034 |
| 95% CI | Ref | (2.05, 2.17) | (4.13,4.34) | (1.95, 2.13) |
| P-value | Ref | < 2.2e-16 | < 2.2e-16 | < 2.2e-16 |
Note: The relative risk (RR) is calculated as the probability of being tissue-specific genes for genes identified by each approach in comparison with LR.
3.4.4. Enrichment of GWAS SNPs among the eQTLs identified in the four tissues
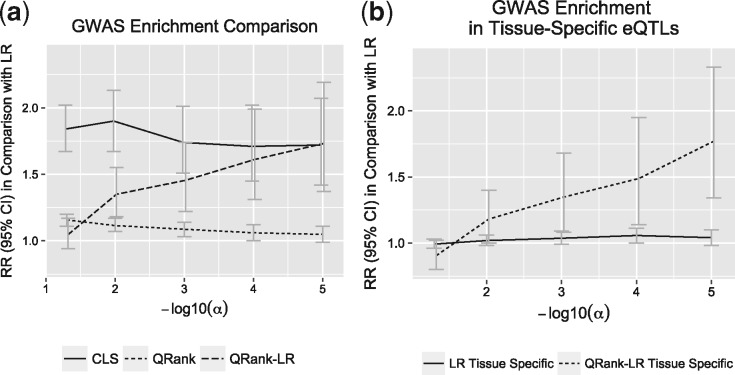
We studied the enrichment of GWAS SNPs ((Welter et al., 2014); version June 2016) by matching exactly the eQTLs identified by different methods to the SNPs in the GWAS catalog. The catalog is a quality controlled collection of all published GWAS assaying at least 100 000 SNPs and all SNP–trait associations with P-values . Figure 5(a) presents the enrichment results at FDR range from 0.05 to . The RR of GWAS enrichment is calculated with reference to LR. Figure 5(a) shows that both CLS and QRank-LR are significantly enriched in GWAS catalog SNPs in comparison with LR. As the significance criteria become more stringent, the enrichment of QRank-LR in the GWAS catalog becomes larger. The eQTLs identified by CLS show the largest enrichment in the GWAS catalog across different levels.
Fig. 5.
The comparison of GWAS enrichment for eQTLs identified by different approaches with FDR ranging from 0.05 to . (a) The relative risk (RR) of GWAS enrichment for CLS, QRank and QRank-LR identified eQTLs in comparison with LR identified eQTLs. (b) The RR of GWAS enrichment for LR and QRank-LR identified tissue-specific eQTLs in comparison with LR identified eQTLs (tissue-specific and non-tissue-specific)
Figure 5(b) serves to validate the QRank-LR tissue-specific eQTLs, by comparing the enrichment of LR and QRank-LR tissue-specific eQTLs relative to LR identified eQTLs (tissue-specific and non-tissue-specific) at FDR ranging from 0.05 to . Figure 5(b) shows that the LR tissue-specific eQTLs are not enriched in GWAS catalog, while the QRank-LR tissue-specific eQTLs are significantly enriched, supporting the validity of QRank-LR tissue-specific eQTLs. A replication study to an independent data could be considered in the future to further validate the identified tissue-specific eQTLs.
4 Conclusion
In this paper, we develop a new quantile regression based association test. The method is widely applicable to a range of problems, including the genome-wide identification of eQTLs and allele specific expression analysis. Unlike linear models which focus on the effect of SNPs on mean expression levels, quantile regressions characterize a comprehensive picture of how genetic variants affect gene expressions at different quantiles. Test statistics are derived from the rank score function in quantile regressions. In particular, for the fixed quantile test, the test statistic is a quadratic form of the rank score at a fixed quantile. For the composite quantile test, we combine rank scores across a set of quantiles. The test statistics have explicit asymptotic distributions under the null, and thus the hypothesis testings are computationally efficient. The computation time of QRank is about 1.75 times the time of LR for a SNP–gene pair. When multiple SNPs are considered per gene, its computation time is further reduced as it only needs to estimate the sign function once. The proposed method can easily accommodate continuous or discrete covariates, and is robust against non-i.i.d. error terms. In the simulation study, we show that the method controls the type I error and is more powerful than LR in the detection of heterogenous effects. In the GTEx v6 data analysis, the proposed method not only identifies eQTLs with significant mean effect differences, but also makes many unique discoveries not obtainable from linear models. We further investigate the additional discoveries and obtain interesting patterns of how genetic variants regulate gene expressions with heterogeneity in effect across different quantiles. The GWAS enrichment analysis shows that the additional eQTLs are highly enriched in the SNPs in the GWAS catalog. The tissue-specific analysis shows that the additional eQTLs are more likely to be tissue-specific than linear regression identified eQTLs. Therefore those eQTLs detected by QRank but missed by LR might be interesting in understanding the existing GWAS findings. Overall, the proposed method provides an alternative approach for eQTL detection, and the results complement the existing knowledge by understanding the differential expression across the entire distribution.
The proposed QRank approach provides a flexible framework for selecting single or multiple quantile levels to understand eQTLs. When the regression model is corrected specified, the type I error is well-controlled (not too liberal or conservative), no matter how many quantile levels we combine, while the power of the approach may be affected. When the number of quantiles is large, adding one more quantile for estimation won’t contribute much information, but increases one degree of freedom in hypothesis tests. When the regression model is mis-specified such as a number of covariates included in the models are unrelated, it also induces the conservativeness into the type I errors for large number of quantile levels. This is because it creates additional noises into the estimation. For this reason, we only observe the conservativeness in the real data based simulation, where the principal component scores of the genes and SNPs are included into the model to adjust for potential confounding factors. Additional simulations and explanation are provided in Supplementary Table S3 for readers interested in this topic. A recommended number of quantile levels for eQTL discovery is 3–5.
There are several interesting directions for future work. One is to better accommodate zero inflation in gene expression data. So far, we have focused on genes with fewer than 10% zero read count. In practice, many genes have excessive zero read counts due to various experimental and biological reasons. The abundance of zeros may be problematic with the lower quantiles and leads to numerical instability of the proposed method. New methods are needed to deal with the zero inflation problem. For example, one may add small perturbations to the zero values to break the ties. Conceptually this will not affect the estimation very much but will greatly improve the computational performance of the method. Another idea is to introduce an additional latent variable to indicate the presence of zeros (Muthén, 2004), and model zeros separately. A second direction is to build joint models for eQTL analysis in multiple tissues simultaneously. It is well known that most eQTLs are shared across tissues, while some are highly tissue specific (The GTEx Consortium, 2015). Analyzing gene expression data from multiple tissues simultaneously will increase the power of eQTL detection by borrowing strength across tissues, and will also facilitate the assessment of tissue specificity (Flutre et al., 2013; Li et al., 2013). However, how to extend the quantile regression method to multiple tissues is not trivial. A SNP may regulate the expression level of a gene at different quantiles in different tissues. Furthermore, the computational burden will be more severe in multi-tissue analysis. This calls for further investigation. A third direction is to use functional effect predictions for genetic variants, non-tissue specific such as GERP (Davydov et al., 2010) and Eigen (Ionita-Laza et al., 2016), or tissue-specific (Backenroth et al., 2016) as priors to improve power to identify eQTLs, especially in trans-eQTL mapping studies.
Software implementing the proposed QRank is available on R CRAN at https://cran.r-project.org/web/packages/QRank, the data containing eQTLs with P-value in at least one of the three approaches (LR, CLS and QRank) is available on Github at https://github.com/songxiaoyu/QRank and the interactive website of search engine and summary statistics is available at https://XiaoyuSong.shinyapps.io/QRank.
Supplementary Material
Acknowledgements
We would also like to thank the GTEx Project, which is supported by the Common Fund of the Office of the National Institutes of Health with additional funds provided by the NCI, NHGRI, NHLBI, NIDA, NIMH and NINDS.
Funding
This work has been supported by National Institute of Health grant R01HG008980 to XS, GL, IIL and YW; by National Institute of Health grant R03HG007443 to XS and YW; by National Institute of Mental Health grant MH106910 to IIL.
References
- Aguet F. et al. (2016) Local genetic effects on gene expression across 44 human tissues. bioRxiv.
- Backenroth D. et al. (2016) Tissue-specific functional effect prediction of genetic variation and applications to complex trait genetics. bioRxiv.
- Brown A.A. et al. (2014) Genetic interactions affecting human gene expression identified by variance association mapping. Elife, 3, e01381.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown M.B., Forsythe A.B. (1974) Robust tests for the equality of variances. J. Am. Stat. Assoc., 69, 364–367. [Google Scholar]
- Davydov E.V. et al. (2010) Identifying a high fraction of the human genome to be under selective constraint using GERP ++. PLoS Comput. Biol., 6, e1001025.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumitrascu B. et al. (2015). A bayesian test to identify variance effects. arXiv preprint arXiv:151201616.
- Fan J. et al. (2001) Generalized likelihood ratio statistics and Wilks phenomenon. Ann. Stat., 29, 153–193. [Google Scholar]
- Flutre T. et al. (2013) A statistical framework for joint eQTL analysis in multiple tissues. PLoS Genet., 9, e1003486.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutenbrunner C. et al. (1993) Tests of linear hypotheses based on regression rank scores. J. Nonparametric Stat., 2, 307–331. [Google Scholar]
- Hájek J. (1965) Extension of the kolmogorov-smirnov test to regression alternatives In: Bernoulli 1713 Bayes 1763 Laplace 1813, pp. 45–60. Springer. [Google Scholar]
- Harrow J. et al. (2012) GENCODE: the reference human genome annotation for The ENCODE Project. Genome Res., 22, 1760–1774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ionita-Laza I. et al. (2016) A spectral approach integrating functional genomic annotations for coding and noncoding variants. Nat. Genet., 48, 214–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kocherginsky M. et al. (2012) Practical confidence intervals for regression quantiles. J. Comput. Graph. Stat. [Google Scholar]
- Koenker R., Bassett G. Jr (1978) Regression quantiles. Econometrica J. Econometric Soc., 46, 33–50. [Google Scholar]
- Li G. et al. (2013) An empirical Bayes approach for multiple tissue eQTL analysis. arXiv preprint arXiv:13112948. [DOI] [PMC free article] [PubMed]
- Muthén B. (2004) Latent variable analysis The Sage Handbook of Quantitative Methodology for the Social Sciences. pp. 345–68. Sage Publications, Thousand Oaks, CA. [Google Scholar]
- Nelder J.A., Baker R.J. (2004) Generalized linear models. Encyclopedia of Statistical Sciences. John Wiley & Sons, Inc., Hoboken, NJ. [Google Scholar]
- Schultz B.B. (1985) Levene’s test for relative variation. Syst. Biol., 34, 449–456. [Google Scholar]
- Stegle O. et al. (2012) Using probabilistic estimation of expression residuals (PEER) to obtain increased power and interpretability of gene expression analyses. Nat. Protoc., 7, 500–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The GTEx Consortium (2015) The genotype-tissue expression (GTEx) pilot analysis: multitissue gene regulation in humans. Science, 348, 648–660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torres J.M. et al. (2014) Cross-tissue and tissue-specific eQTLs: partitioning the heritability of a complex trait. Am. J. Hum. Genet., 95, 521–534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H.J. (2009) Inference on quantile regression for heteroscedastic mixed models. Stat. Sin., 19, 1247–1261. [Google Scholar]
- Wei W.-H. et al. (2014) Detecting epistasis in human complex traits. Nat. Rev. Genet., 15, 722–733. [DOI] [PubMed] [Google Scholar]
- Wei Y. et al. (2006) Quantile regression methods for reference growth charts. Stat. Med., 25, 1369–1382. [DOI] [PubMed] [Google Scholar]
- Welter D. et al. (2014) The NHGRI GWAS Catalog, a curated resource of SNP–trait associations. Nucleic Acids Res., 42, D1001–D1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.