Structure-function relationships during segregated and integrated network states of human brain functional connectivity

Abstract

Structural white matter connections are thought to facilitate integration of neural information across functionally segregated systems. Recent studies have demonstrated that changes in the balance between segregation and integration in brain networks can be tracked by time-resolved functional connectivity derived from resting-state functional magnetic resonance imaging (rs-fMRI) data and that fluctuations between segregated and integrated network states are related to human behavior. However, how these network states relate to structural connectivity is largely unknown. To obtain a better understanding of structural substrates for these network states, we investigated how the relationship between structural connectivity, derived from diffusion tractography, and functional connectivity, as measured by rs-fMRI, changes with fluctuations between segregated and integrated states in the human brain. We found that the similarity of edge weights between structural and functional connectivity was greater in the integrated state, especially at edges connecting the default mode and the dorsal attention networks. We also demonstrated that the similarity of network partitions, evaluated between structural and functional connectivity, increased and the density of direct structural connections within modules in functional networks was elevated during the integrated state. These results suggest that, when functional connectivity exhibited an integrated network topology, structural connectivity and functional connectivity were more closely linked to each other and direct structural connections mediated a larger proportion of neural communication within functional modules. Our findings point out the possibility of significant contributions of structural connections to integrative neural processes underlying human behavior.

Introduction

The increasing availability of network data on the structure and function of neural systems motivates the growing interest in brain networks that consist of neurons, neuronal populations or brain regions as nodes, and structural or functional connections between them as edges (Sporns 2013b; Bassett and Sporns 2017). Structural connectivity refers to a pattern of direct anatomical links between neural elements (Bullmore and Sporns 2009; Sporns 2011) and underlies the emergence of coherent neural activity, which gives rise to patterns of statistical dependence among remote neural elements, termed functional connectivity (Friston 1994; Fox et al. 2005). Structural networks promote segregation and integration of neural information through their network communities and hubs (Sporns 2013a), where segregation is indicated by strong and weak functional connectivity within and between network communities, respectively, and integration is indicated by globally strong functional connectivity mediated through network hubs. Maintaining the balance between segregation and integration is thought to be crucial for the operation of distributed networks underpinning cognitive function (Tononi et al. 1994; Fox and Friston 2012). There is an emerging focus on changes in the balance between segregation and integration over time, which manifest in continuously changing global patterns of brain functional connectivity (Sporns 2013a; Deco et al. 2015).

Recently, it has been reported that the balance between segregated and integrated network architecture of functional connectivity, as measured by resting-state functional magnetic resonance imaging (rs-fMRI), fluctuates on a time scale of tens of seconds (Shine et al. 2016a). Shine and colleagues defined states of network segregation and integration in the human brain based on fluctuations in the patterns of within-module degree and participation coefficient (Guimerà and Nunes Amaral 2005), computed from short-timescale time-resolved functional connectivity (Chang and Glover 2010; Hutchison et al. 2013; Zalesky et al. 2014). Fluctuations between these segregated and integrated network states have been associated with cognitive function and the activity of neuromodulatory systems; the participation coefficient averaged over nodes (a network attribute for integration) was correlated with measures for effective cognitive performance as well as with pupil dilation as a surrogate measure for arousal (Shine et al. 2016a). In addition, greater network integration has been shown to be related to heightened attention and less fatigue using longitudinal rs-fMRI datasets (Shine et al. 2016b). Temporal changes in global connectivity patterns, which are similar to fluctuations between the segregated and integrated states, were also associated with spontaneous eyelid closures (Wang et al. 2016) and decoding accuracy of visual stimuli (Cocchi et al. 2017). These previous findings indicate that temporal changes in the balance between segregation and integration, as tracked by time-resolved functional connectivity, are linked to human cognition and behavior.

While segregated and integrated network states of functional connectivity have been shown to be associated with several functional aspects of the brain as mentioned above, it remains largely unexplored how these two network states are related to structural connectivity. There are a number of studies demonstrating that the strength of functional connectivity is partially predicted by the strength of structural connectivity (Hagmann et al. 2008; Skudlarski et al. 2008; Honey et al. 2009; Shen et al. 2012; for a review, see Damoiseaux and Greicius 2009). Importantly, the goodness of this prediction, or the similarity between structural and functional connectivity, has been shown to change in different conditions. The similarity of connectivity has been reported to change depending on sleep stages in humans (Tagliazucchi et al. 2016; Haimovici et al. 2017) as well as states of consciousness (levels of sedation) in primates (Barttfeld et al. 2015) and rodents (Ma et al. 2017). Moreover, the similarity between human structural and functional connectivity has also been shown to continuously change during rest (Liégeois et al. 2016). These previous findings naturally raise the question of how the relationship between structural and functional connectivity changes with fluctuations between segregated and integrated states of functional connectivity.

In this study we investigated how structure-function relationships in brain connectivity change with fluctuations between the segregated and integrated network states in the resting human brain. Drawing on structural connectivity derived from diffusion MRI tractography and functional connectivity as measured by rs-fMRI, we examined between-state differences in structure-function relationships, both in terms of network edge weights and network partitions into communities (modules). We first compared the similarity of structural and functional edge weights between the segregated and integrated states and demonstrated that functional connectivity is more closely related to structural connectivity during the integrated state. The edge weight similarity was evaluated over the whole cortex as well as at each pair of intrinsic connectivity networks (Yeo et al. 2011) to determine which functional network components exhibit greater between-state differences. We then compared the similarity of structural and functional network partitions between the segregated and integrated states to establish the consistency of between-state differences over the edge weight similarity and the partition similarity. An intuitive understanding of between-state differences in network partitions was obtained by further comparing the density of structural connections within modules in functional networks, which has not been examined in previous studies on structure-function relationships. This comparison suggests that a larger amount of neural communication within functional modules is supported by and mediated through direct structural connections in the integrated as compared to the segregated state.

Materials and methods

Dataset

The primary data source for this study was the Washington University-University of Minnesota consortium of the Human Connectome Project (HCP; http://www.humanconnectome.org). Reproducibility of results was assessed using an independent set of data from the enhanced Nathan Kline Institute (NKI)-Rockland Sample (http://fcon_1000.projects.nitrc.org/indi/enhanced), which we used in a previous study (Betzel et al. 2016). We describe details of the HCP dataset in the following, while the NKI dataset is described in the Supplementary methods.

Subject cohort

The HCP consortium recruited participants and they provided written informed consent (Van Essen et al. 2013). Since the detection of communities in time-resolved functional network is computationally demanding, we focused on the data coming from the sample labeled 100 Unrelated Subjects in ConnectomeDB (https://db.humanconnectome.org). This sample set has been used in a previous study investigating segregated and integrated states of time-resolved functional connectivity (Shine et al. 2016a). We eliminated 15 participants from this sample due to large head movements during rs-fMRI scans. These participants were excluded because their motion estimates in at least one of the rs-fMRI runs met either 1) maximum translation > 3 mm, 2) maximum rotation > 3° or 3) mean framewise displacement (FD) > 0.2 mm (Xu et al. 2015), where the FD was derived from the l2 norm of the six translation and rotation parameter differences in the motion estimates. We further discarded one participant aged ≥ 36 years and obtained a quality-controlled sample of healthy young adults aged ≥ 22 years and < 36 years, consisting of 84 subjects (40 males and 44 females).

Image acquisition

Multimodal MRI data were acquired using a 32-channel head coil on a modified 3T Siemens Skyra scanner. Scanning parameters of rs-fMRI data were: repetition time (TR) = 720 ms, echo time (TE) = 33.1 ms, flip angle = 52°, field of view (FOV) = 208 × 180 mm², 72 slices and voxel size = 2 mm isotropic. The resting data were collected in four runs of around 14 min (1,200 time samples) each with an eyes open condition. Two runs were included in a session on day 1 and the other two runs were included in a session on day 2, where the data in each session were recorded with the left-to-right (LR) phase encoding direction in one run and the right-to-left (RL) direction in the other run. In this study, each of the four runs (1LR, 1RL, 2LR and 2RL) was analyzed independently. Diffusion-weighted images (DWI) were acquired with 270 gradient directions, three shells (b-value = 1,000, 2,000, 3,000 s/mm²), two repeats, and in a total of 36 b0 scans (scanning parameters: TR = 5,520 ms, TE = 89.5 ms, flip angle = 78°, FOV = 210 × 180 mm², 111 slices and voxel size = 1.25 mm isotropic). A T1-weighted structural image was acquired with the following parameters: TR = 2,400 ms, TE = 2.14 ms, flip angle = 8°, FOV = 224 × 224 mm², 320 slices and voxel size = 0.7 mm isotropic.

Preprocessing

From the ConnectomeDB, we downloaded images preprocessed with the HCP minimal preprocessing pipelines (Glasser et al. 2013) as in a previous study (Shine et al. 2016a). The preprocessing pipelines for rs-fMRI data included gradient distortion correction, motion correction, bias field removal, spatial distortion correction, transformation to Montreal Neurological Institute (MNI) space and intensity normalization; and those for DWI data included intensity normalization, susceptibility distortion correction, eddy current distortion and motion correction, gradient nonlinearly correction, and transformation to MNI space.

The minimally preprocessed rs-fMRI data were further processed by performing 1) exclusion of volumes during the first 10 s, 2) outlier volume removal and interpolation (the percentage of interpolated volumes was 3.6 ± 0.1% in runs 1LR, 1RL and 2LR, and 3.7 ± 0.2% in run 2RL [mean ± SD]), 3) nuisance regression using the Friston-24 motion time series (Friston et al. 1996) and global, white matter and cerebrospinal fluid (CSF) mean signals 4) band-pass filtering and 5) linear and quadratic detrending. The outlier removal in step 2) is essentially similar to the motion scrubbing (Power et al. 2012) and censoring (Power et al. 2014), but instead of eliminating affected time points, we replaced outlier volumes with interpolated ones to preserve the number of time points in a sliding window for estimation of time-resolved functional connectivity. We performed the outlier detection and interpolation using an AFNI function 3dDespike (Cox 2012) as in Allen et al. (2014). The cutoff frequencies of the band-pass filtering in step 4) were 1/(66 TRs) = 0.021 Hz (low) and 0.1 Hz (high), where the low-cut frequency was specified as the reciprocal of the width of the sliding window to exclude spurious connectivity fluctuations (Leonardi and Van De Ville 2015; Zalesky and Breakspear 2015).

From the minimally preprocessed DWI data, white matter fibers were reconstructed using generalized q-sampling imaging (Yeh et al. 2010), allowing for the reconstruction of complex fiber structures, and deterministic streamline tractography. Tractography procedures are detailed in de Reus and van den Heuvel (2014) and van den Heuvel et al. (2015, 2016).

Parcellation

Structural connectivity and time-resolved functional connectivity were assessed within the cerebral cortex in a region-wise manner. Nodes of structural and functional networks in the HCP dataset were specified as 114 distinct cortical regions produced by a subdivision of the Desikan-Killiany atlas (Cammoun et al. 2012) (see Fig. S1). This cortical parcellation was derived from the atlas files myatlas_60_lh.gcs and myatlas_60_rh.gcs in Connectome Mapper (https://github.com/LTS5/cmp). By evaluating the area of overlap, we associated every parcel with one of the 7 intrinsic connectivity networks defined based on functional connectivity profiles of 1,000 subjects (Yeo et al. 2011); namely, the control network (CON), the default mode network (DMN), the dorsal attention network (DAN), the limbic system (LIM), the saliency/ventral attention network (VAN), the somatomotor network (SMN) and the visual network (VIS).

Structural connectivity

Structural connectivity was quantified based on the number of streamlines between cortical regions. Since the size of regions has an effect on the number of streamlines (Hagmann et al. 2008), we used the streamline count between regions divided by the geometric mean of the surface area of regions, as a measure of edge weight in structural networks.

In addition to individual-level structural connectivity, we also employed group-level structural connectivity robust to outliers (see Sensitivity analysis). The group-level structural connectivity matrix was constructed by averaging non-zero edge weights across subjects. When averaging non-zero edge weights, we set to zero all those edges for which no streamlines were found in more than half of the subjects. The choice of this group threshold is based on a guideline to derive group-level connectivity from deterministic tractography in de Reus and van den Heuvel (2013).

Time-resolved functional connectivity

Time-resolved functional connectivity was estimated using a tapered sliding window approach (Hutchison et al. 2013; Preti et al. 2016), where the Fisher z-transformed Pearson correlation coefficient of regional rs-fMRI time courses was used as a metric of functional connectivity (for presentation of connectivity matrices in figures, the raw correlation coefficient was used instead). We determined the shape of tapered sliding window and the between-window duration in a similar manner as in Allen et al. (2014). Specifically, we made tapered sliding windows by convolving a rectangle (width, 66 TRs = 47.52 s) with a Gaussian kernel (kernel size, σ = 9 TRs = 6.48 s) and moved them in steps of 3 TRs = 2.16 s, resulting in the total number of windows = 369.

Community detection

Communities (modules) in structural networks and in time-resolved functional networks were detected by maximization of a modularity quality function (Newman and Girvan 2004) using the Louvain algorithm (Blondel et al. 2008). Since functional networks may contain negative edge weights, we maximized a modularity quality function generalized for networks with positive and negative edge weights (Rubinov and Sporns 2011):

$$Q=\frac{1}{{\nu }^{+}}{\displaystyle \sum _{i,j}\left(w_{i,j}^{+}-e_{i,j}^{+}\right)}{\delta }_{M_i,M_j}-\frac{1}{{\nu }^{+}+{\nu }^{-}}{\displaystyle \sum _{i,j}\left(w_{i,j}^{-}-e_{i,j}^{-}\right)}{\delta }_{M_i,M_j},$$ (1)

where $w_{i,j}^{+}$ is equal to the edge weight w_i,j between nodes i and j if w_i,j is positive and $w_{i,j}^{+}$ is equal to zero otherwise. Likewise, $w_{i,j}^{-}$ is equal to −w_i,j if w_i,j is negative and $w_{i,j}^{-}$ is equal to zero otherwise. The term $e_{i,j}^{\pm }=s_i^{\pm }{s}_j^{\pm }/{\nu }^{\pm }$, where $s_i^{\pm }={\sum }_j{w}_{i,j}^{\pm }$ and ${\nu }^{\pm }={\sum }_{i,j}{w}_{i,j}^{\pm }$, refers to the expected density of positive or negative weights given a random null model preserving the nodal strengths. The term δ_Mi,Mj is equal to one when nodes i and j are within the same module and is equal to zero otherwise.

Both for structural networks and time-resolved functional networks, community detection was performed by maximizing Q using the function community_louvain.m in the Brain Connectivity Toolbox (http://www.brain-connectivity-toolbox.net) with the default resolution parameter, set to one. We ran this function 100 times per each adjacency matrix of structural and time-resolved functional networks and chose the community assignment with the maximum Q over the trials for later analysis of modules and network partitions.

Estimation of segregated and integrated states

In keeping with Shine et al. (2016a), we estimated segregated and integrated network states of functional connectivity based on the patterns of within-module degree z-score and participation coefficient (Guimerà and Nunes Amaral 2005), computed from time-resolved functional networks and their communities detected by modularity maximization.

For each node in a time-resolved network at each time window, the within-module degree z-score was computed using the BCT function module_degree_zscore.m. The within-module degree z-score in this study quantifies the extent to which a node is functionally coupled with the other nodes in its (functional) module, relative to the within-module strength of the other nodes in the module, and is given by

$$z_{i,t}=\frac{{\kappa }_{i,t}-{\overline{\kappa }}_{s_i,t}}{{\sigma }_{{\kappa }_{s_i,t}}},$$ (2)

where κ_i,t is the strength of node i to the other nodes in its module s_i at time t, and ${\overline{\kappa }}_{s_i,t}$ and ${\sigma }_{{\kappa }_{s_i,t}}$ are the mean and SD of the strengths over all nodes in module s_i at time t. High (respectively, low) values of the within-module degree z-score indicate strong (respectively, weak) intramodular connectivity of a node.

The participation coefficient for each node within each time window was computed using the BCT function participation_coef_sign.m. The participation coefficient in this study expresses the level at which a node is diversely coupled with other nodes across all modules and is described as

$$P_{i,t}=1-\sum _{s=1}^{N_M}{\left(\frac{{\kappa }_{is,t}}{k_{i,t}}\right)}^2,$$ (3)

where κ_is,t is the strength of the positive edge weights of node i to nodes in module s at time t, k_i,t is the strength of the positive edge weights of node i to all the other nodes at time t, and N_M is the number of modules. High values of the participation coefficient indicate that a node is coupled with other nodes in a large proportion of modules in a network, and low values of the participation coefficient indicate that a node is coupled only with other nodes in a single or a small number of modules. High mean participation coefficients over nodes can therefore be associated with the existence of highly integrative processes across the whole network.

It should be mentioned that a node with a high (low) value of the participation coefficient does not necessarily have a low (high) value of the within-module degree z-score. For example, if a node functionally coupled with many other nodes both within and between modules, such a node has high values of these two measures. The within-module degree z-score and the participation coefficient capture complementary characteristics of the role of nodes in networks; the former measure can be used for determining whether a node is a hub or not and the latter measure for whether a node is a connector or not (Guimerà and Nunes Amaral 2005).

Fluctuations between segregated and integrated network topology were tracked with a joint histogram of the within-module degree z-score z_t and the participation coefficient P_t across nodes in each time window (Shine et al. 2016a) (see Fig. 1a). The states of network segregation and integration were estimated by classifying the joint histogram of each time window using the k-means clustering algorithm (k = 2) (Shine et al. 2016a). Each time window was assigned to one of two clusters (Fig. 1a) and the cluster with higher participation coefficients on average was regarded as the cluster of the integrated state. The k-means clustering was performed individually and repeated with 500 random initial conditions per subject (Shine et al. 2016a).

Fig. 1.

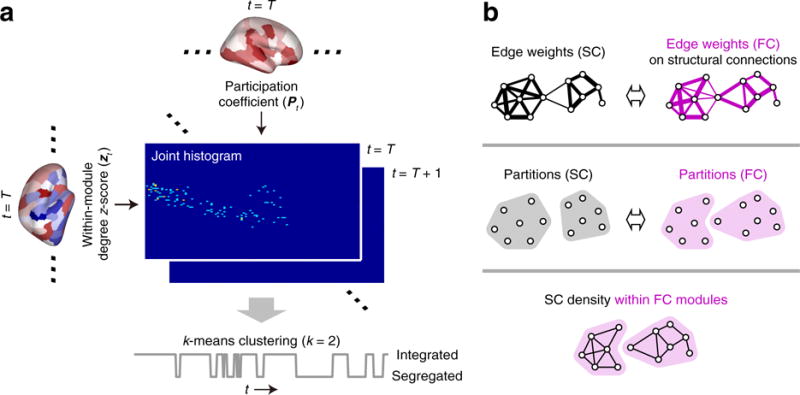
a Workflow diagram describing the procedure for estimating the segregated and integrated network states. The joint histogram of each time window was created by summing the instances of each value of z_t and P_t within 100 equally defined bins along each axis (Shine et al. 2016b). b Illustrations for the assessment of the relationship between structural connectivity (SC) and functional connectivity (FC). Top: computing the similarity of edge weights between structural and functional networks. Middle: computing the similarity of partitions between structural and functional networks. Bottom: computing the density of structural connections within functional connectivity modules. The similarities (top and middle) and the density (bottom) were compared between the segregated and integrated states

We chose two clusters for the k-means analysis because the work by Shine et al. (2016a) previously suggested that this choice was reflective of the broader patterns in the data compared across multiple values of k. To ensure that this was also the case in our data, we compared the clusters (joint histograms) obtained from k = 2 to those acquired with k = 3 and 4.

Assessment of structure-function relationships

We investigated structure-function relationships during the segregated and integrated states using structural connectivity and the median of individual time-resolved functional connectivity over time windows of each state (i.e., the centroid of a cluster in, e.g., Allen et al. 2014 and Barttfeld et al. 2015). The relationship between structural and functional networks was examined both in terms of edge weights and partitions (community detection was also applied to the individual centroids), and was compared between the segregated and integrated states as follows.

Edge weights

Edge-level structure-function relationships were evaluated using the similarity of edge weights between structural and functional networks (see Fig. 1b top). The edge weight similarity was quantified by the Pearson correlation coefficient, computed between structural and functional edge weights at only pairs of nodes with non-zero structural edge weights. Between-state differences in the edge weight similarity were assessed over the whole cortex as well as at each pair of the 7 intrinsic connectivity networks in Yeo et al. (2011) to find out which network components exhibit a greater between-state difference in the edge weight similarity. The Pearson correlation coefficient between structural and functional edge weights was z-transformed prior to statistical analysis.

Partitions

Based on the communities detected by modularity maximization, structure-function relationships at the level of network partitions were investigated in two ways. First, we evaluated partition-level structure-function relationships using the similarity of partitions between structural and functional networks (see Fig. 1b middle), to confirm the consistency of between-state differences over the edge weight similarity and the partition similarity. The similarity of partitions was quantified by the normalized mutual information using the BCT function partition_distance.m and was compared between the segregated and integrated states over all subjects. Between-state differences in the partition similarity were also assessed on a subset of subjects, whose numbers of detected functional modules in both states equaled the number of modules most frequently observed across the two states.

Second, to gain insight into the structural underpinnings of between-state differences in network partitions, we further compared the density of direct structural connections within functional connectivity modules (see Fig. 1b bottom) between the segregated and integrated states. Through this analysis, we aimed to discover how neural communication within functional modules was differentially supported by direct structural connections in the two different network states. In addition to the direct structural connections, we also examined the density of indirect structural connections within functional modules. The density was separately computed for indirect connections with respective shortest path lengths L = 2 and 3 (indirect connections with L ≥ 4 were not assessed because their proportion over the entire network was very small [0.042 in group-level structural connectivity]).

Sensitivity analysis

To confirm the robustness of between-state differences in the structure-function relationships, we also examined between-state differences in the relationship between structural and functional networks for both edge weights and partitions under the following alternative conditions:

• Use of group-level structural connectivity. Instead of individual-level structural connectivity, group-level structural connectivity was used for the assessment of structure-function relationships.

• Same number of time windows in the network states. The numbers of time windows in the segregated and integrated states were equalized in each individual when computing the centroid of a state from time-resolved functional connectivity. The numbers of time windows were matched by randomly removing time windows in the integrated state (the number of time windows was larger in the integrated state in all subjects). We examined the robustness of results using 100 sets of time window data with random removal.

When between-state differences in the structure-function relationships were examined for edge weights, we also assessed the relationships with the following other conditions of structural and functional edge weights:

• Resampled edge weights in structural networks. The structural edge weights were set to values resampled from a Gaussian distribution with a mean of 0.5 and an SD of 0.1 to correct its skewed distribution (Honey et al. 2009), maintaining the rank order of edge weights across the raw and resampled values.

• Removal of negative edge weights in functional networks. To exclude effects derived from negative functional connectivity, all of the negative functional edge weights were regarded as zero when the similarity score was computed.

Effects of equalizing the number of time windows across the states and removing negative functional connectivity were also examined when differences in centroid edge weights were explored between the segregated and integrated states.

Results

The results presented in Figs. 2–5 in this section are from run 2LR of rs-fMRI data in the HCP dataset. Reproducibility of results across runs and datasets was examined using the other three runs of the HCP dataset as well as a single run of the NKI dataset in Supplementary results. We selected Run 2LR because a measure of network integration in this run was least affected by the head movement artifacts. The correlation coefficient across individuals between the mean participation coefficient and the FD, both of which were averaged over time, was 0.20 in run 1LR, 0.057 in run 1RL, −0.015 in run 2LR and 0.21 in run 2RL (all p > 0.05). This correlation was also found to be small in the single run of the NKI dataset (r = 0.13; p > 0.05). The relationship between the mean participation coefficient and the FD is investigated in more detail in Supplementary results.

Properties of segregated and integrated states

We first investigated basic characteristics of the segregated and integrated states of functional connectivity to confirm previous findings reported in Shine et al. (2016a). Figure 2a shows the time series of the mean participation coefficient and a sequence of state transitions in a representative subject. As seen in Shine et al. (2016a), transitions between segregated and integrated states were well represented by fluctuations in the mean participation coefficient. Joint distributions of the within-module degree z-score and the participation coefficient shown in Fig. 2b exhibited patterns similar to those observed in Shine et al. (2016a), with the peaks of distributions in the segregated and integrated states located near 0 and 0.5, respectively, along the axis of the participation coefficient. Distributions of the within-module degree z-score overlapped across the states, while the peaks in the 2D space were separated along its axis (segregated, 1.25; integrated, −0.65).

Fig. 2.

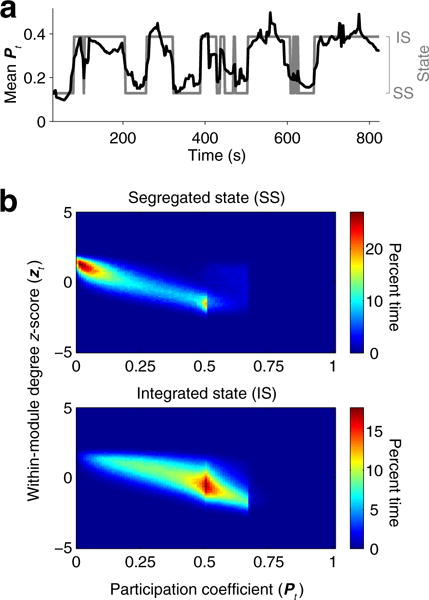
a Time series of the mean participation coefficient and state transitions in a representative subject. b Joint distributions of the within-module degree z-score and the participation coefficient over time across all subjects (upper, the segregated state; lower, the integrated state)

Similar patterns in the joint histograms were also observed at higher values of k (Fig. S2). Patterns in the joint histogram of the segregated state (k = 2) were similar to those observed in a cluster with the lowest mean participation coefficient (k = 3 and 4); and patterns in the integrated state (k = 2) were similar to those of the other clusters (k = 3 and 4). This result indicates that the clustering into the segregated or the integrated state is maintained across larger numbers of clusters.

Figure 3a shows the centroid of each network state within individuals in representative subjects. Although there were some variations in spatial connectivity patterns across individuals, connectivity patterns associated with the segregated state can be characterized by a pronounced segregation of the task-negative DMN from the task-positive attention (DAN/VAN) and sensory (SMN/VIS) networks, while this modular organization was weakened in connectivity patterns in the integrated state. Consistent with Shine et al. (2016a), time windows associated with the segregated state had greater modularity Q compared to the integrated state (Q_SS = 0.55 ± 0.04 [mean ± SD]; Q_IS = 0.50 ± 0.04; Cohen’s d = 1.4). During the integrated state, edge weights within the DMN and within the task-positive networks (DAN, VAN, SMN and VIS) decreased on average (Fig. 3b; a pronounced decrease within/between the SMN and VIS was less noticeable in the NKI dataset than in the HCP dataset [see Supplementary results for details]) while edge weights between the DMN and the task-positive networks increased. Similar patterns of edge-weight differences between the states were also found with the same number of time windows across the states (see Fig. S3 left for one representative random sample of time-window removal; the minimum correlation coefficient of the edge-weight differences among all 100 random samples > 0.988). When negative functional connectivity weights were removed by setting them to zero, between-state differences in centroid edge weights were localized within either task-negative or task-positive systems (see Fig. S3 right), indicating that increased functional connectivity between these two systems during the integrated state was associated with decreased strength of negative correlation between their regional activities.

Fig. 3.

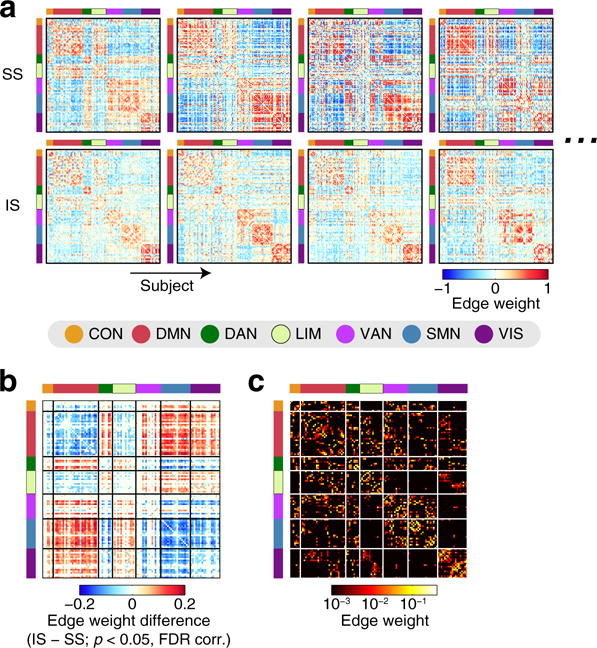
a The centroids of the segregated (upper) and the integrated (lower) states in four representative subjects. Cortical nodes in each connectivity matrix are associated with the 7 network components in Yeo et al. (2011). b Between-state differences in centroid edge weights (integrated − segregated), averaged over subjects. The differences in edge weights were shown only for edges with significant between-state differences (p < 0.05, FDR corrected). c Group-level structural connectivity

Between-state differences in structure-function relationships

Next, we examined differences in structure-function relationships between the segregated and integrated states. We evaluated the between-state differences both in terms of edge weights and partitions of structural and functional networks, using individual-level or group-level structural connectivity (Fig. 3c) and the centroid of each state within individuals (Fig. 3a).

Edge weights

We found that the similarity between structural and functional edge weights over the whole cortex was greater in the integrated state than in the segregated state (see Fig. 4a). Elevated edge weight similarity in the integrated state was also observed when the similarity was evaluated at the level of network components. The edge weight similarity was greater in the integrated state at a large proportion of network component pairs in which significant between-state differences were found (see Fig. 4b, left). In particular, greater similarity in the integrated state was consistently found in edges connected to the DMN as presented in Fig. 4b, showing a predominance of the DMN in shaping the between-state differences in the similarity of structural and functional edge weights. Figure 4c shows network component pairs in which between-state differences in the edge weight similarity were greater than those evaluated over the whole cortex. While between-state differences in several pairs of components were greater than the global between-state differences in the run that we focused on in this section (run 2LR of the HCP dataset), the DMN–DAN was the only pair of components for which greater differences were consistently observed across all runs and datasets (see Supplementary results).

Fig. 4.

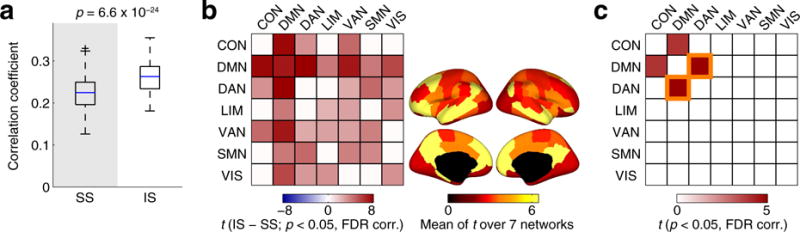
a Similarity of edge weights between structural connectivity and the centroid of the segregated (left) or the integrated (right) state. b Left: between-state differences in the edge weight similarity (integrated − segregated), evaluated at each pair of the 7 network components in Yeo et al. (2011). The between-state differences were shown as t-scores and were presented only for pairs of network components with significant differences (p < 0.05, FDR corrected). Right: the mean of the t-scores in each network component, overlaid on the cortical surfaces. c Pairs of network components in which between-state differences in the edge weight similarity were greater than those evaluated over the whole cortex (p < 0.05, FDR corrected). The t-score of the DMN–DAN in this comparison is highlighted since it was significant across all runs and datasets (see Supplementary results)

We confirmed that these between-state differences in the edge weight similarity were highly robust against the use of alternative conditions for connectivity data setup (see Sensitivity analysis for descriptions of these conditions). Elevated similarity in the integrated state (Fig. 4a), a predominance of the DMN in the pair-wise between-state differences (Fig. 4b) and greater between-state differences in the DMN–DAN than those evaluated over the whole cortex (Fig. 4c) were also observed when the structure-function relationships were assessed with group-level structural connectivity, the same number of time windows across the states (in all 100 realizations of random time window removal), the resampled structural connectivity and the removal of negative functional connectivity (see Fig. S4; results for the same number of time windows were shown for one representative random sample).

Partitions

Consistent with the edge weight similarity, the partition similarity between structural and functional networks was greater in the integrated state than in the segregated state (Fig. 5a). Here the median and mode of the number of detected modules in structural networks were seven, and those in individual functional networks (centroids) were three in both of the states. Greater similarity in the integrated state was not merely a result of between-state differences in the number of functional modules in individuals, because this greater similarity was confirmed even when the partition similarity was assessed with a subset of subjects, exhibiting exactly three functional modules in both of the states (n = 39; t = 4.2; p = 1.6 × 10⁻⁴).

Fig. 5.

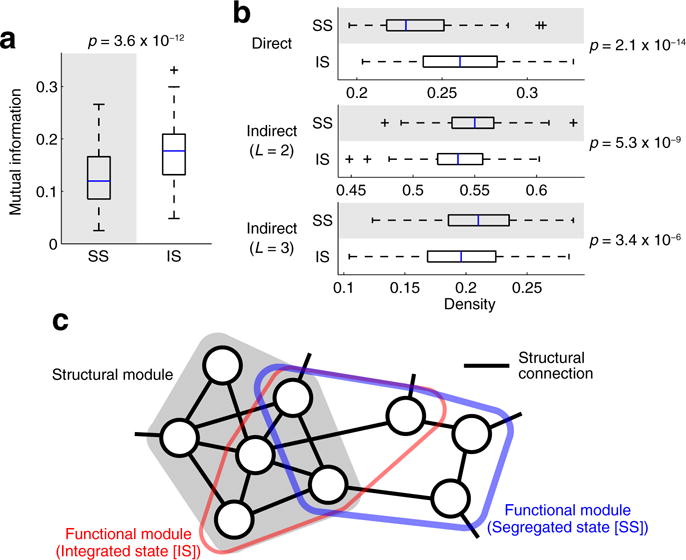
a Similarity of network partitions between structural connectivity and the centroid of the segregated (left) or the integrated (right) state. b Density of structural connections within functional modules. The density is shown for direct structural connections (top) and for indirect structural connections with the shortest path lengths L = 2 (middle) and L = 3 (bottom). c A schematic view of the relationship among a single structural module and an overlapping functional module captured during segregated and integrated states. Nodes represent brain regions, and the thickness of the blue or red line indicting boundaries of the functional module represents the strength of within-module functional connectivity. In the segregated state, the functional module is more coherent than in the integrated state, while also deviating more strongly from the underlying structural module

Between-state differences in network partitions were further examined by comparing the density of structural connections within functional modules between the segregated and integrated states. Our comparison of the density demonstrated that direct structural connections within functional modules were denser in the integrated state than in the segregated state (Fig. 5b top), suggesting that within-module functional couplings were more strongly shaped by the underlying structural connectivity during network integration. In contrast to the case with direct structural connections, indirect structural connections within functional modules were denser in the segregated state than in the integrated state (Fig. 5b middle and bottom; significant between-state differences were found for the shortest path length L = 3 across all runs and datasets, see Supplementary results).

The observed between-state differences in the partition similarity and the within-functional-module density of structural connections are illustrated by a schematic shown in Fig. 5c. While the segregated state was associated with greater modularity of functional connectivity Q_SS as mentioned before, its functional modules (shown in blue in Fig. 5c) were less similar to structural modules and direct structural connections were less dense within its functional modules. On the other hand, in the integrated state, functional modularity Q_IS was weaker than Q_SS but its functional modules (shown in red in Fig. 5c) shifted toward structural modules and the density of direct structural connections was elevated within its functional modules. These findings suggest that, when functional connectivity exhibited a greater level of integrative network topology, activity of nodes within functional modules was less coherent while functional interactions among such nodes were more strongly supported by direct structural connections.

Greater similarity of network partitions in the integrated state was confirmed with group-level structural connectivity and with the same number of time windows across the states (in all 100 realizations of random time window removal) (see Fig. S5a; results for the same number of time windows were shown for one representative random sample). Elevated within-functional-module density of direct and indirect structural connections in the integrated and segregated states, respectively, was also found with these alternative conditions for connectivity data setup (Fig. S5b).

Discussion

While recent studies have demonstrated that fluctuations between segregated and integrated network architecture of functional connectivity are related to human behavior, how such fluctuations are linked to the underlying structural connectivity has remained poorly understood. To reveal the changes in the relation to structural connectivity associated with these state fluctuations, we investigated between-state differences in the relationship between structural connectivity and the segregated and integrated states of functional connectivity, both in terms of edge weights and partitions of connectivity networks. We showed that the similarity of structural and functional edge weights, assessed over the whole cortex, was greater in the integrated state. Analysis of similarity at the level of network components demonstrated that greater similarity in the integrated state was mainly observed on edges linking the DMN with other network components, especially the DAN. Moreover, we found that the similarity of partitions between structural and functional networks increased during the integrated state and so did the density of direct structural connections within modules in functional networks. The observed between-state differences in structure-function relationships of network partitions suggest that neural communication within functional modules was more strongly supported by direct structural connections during the integrated state.

The between-state differences in structure-function relationships were robust against the use of multiple conditions for connectivity data setup and were also reproducible across multiple runs of rs-fMRI data and imaging datasets. Our findings were observed with either individual-level or group-level structural connectivity, and either with or without a correction of the skewed distribution of structural edge weights by a resampling method (Honey et al. 2009). Increased similarity in the integrated state was observed even when negative functional edge weights were removed by setting them to zero, which suggests that the between-state differences are not mainly attributable to negative functional connectivity that could emerge as an artifact of global signal regression (Murphy et al. 2009; but see also Fox et al. 2009). Greater similarity in the integrated state was also observed when the centroid of a state was computed from the equalized numbers of time samples across segregated and integrated states, demonstrating that the between-state differences are not due to the dependency of the similarity of structural and functional connectivity on the timescale of functional connectivity (Honey et al. 2007; Shen et al. 2015). Results were reproducible across all runs of rs-fMRI data in the HCP dataset, as well as in another independent dataset (the NKI dataset) that we used in a previous study (Betzel et al. 2016).

Our finding of a closer link to structural connectivity during the integrated state supports recent findings on the association between integrated network topology of functional connectivity and integrative neural processes underlying human behavior and cognition (Shine et al. 2016a, b). Reconfiguration of functional connectivity in the integrated state, where its edge weights and partitions become closer to those in structural networks with decreasing modularity of functional connectivity and increasing density of direct structural connections within functional modules, can be thought to reflect integrative neural communication across the whole brain. During the segregated state, by contrast, the density of indirect structural connections increases within functional modules, suggesting that direct communication between nodes within functional modules is less evident in this state despite the higher modularity of functional connectivity. Instead, this may indicate coherent but parallel neural processing at the level of subsets of nodes in a functional module. Results of parallel processing may be globally broadcast during the integrated state by changing the pattern of functional coupling, which enables global communication between nodes through direct structural connections within loosen functional modules. The transition from parallel processing to broadcasting is reminiscent of the ’connective core hypothesis’ (Shanahan 2012), where it is hypothesized that interconnected hub regions that are topologically central to the whole network support a distinctive blend of parallel and serial processing that promotes the availability of the full repertoire of process combinations in the brain. This raises a question: how is the connective core, or the structural rich club (van den Heuvel and Sporns 2011, 2013), associated with the segregated and integrated states of functional connectivity? Future studies are needed to clarify the relationship of such topological features between structural connectivity and time-resolved functional connectivity.

A predominance of between-state differences in the similarity of structure and function at edges connecting the DMN with other network components, particularly the DAN, suggests characteristic changes in the pattern of functional interaction on structural connections that link task-negative and task-positive systems. It is known that the variance of time-resolved functional connectivity is greater at connections associated with heteromodal association regions (Allen et al. 2014; Gonzalez-Castillo et al. 2014), which partially include the DMN and the DAN. Regions in the DMN have also been shown to most significantly change their community co-assignments with other regions, especially those in task-positive networks, when global functional connectivity changes occur (Betzel et al. 2016). Similarly, a recent study has demonstrated that changes in functional interaction between task-negative and task-positive systems are a major contributing factor in fluctuations in functional connectivity (Fukushima et al. 2017). The finding in this study that between-state differences in the similarity of structure and function are strongly expressed at connections linking the DMN and the DAN is in line with these previous results demonstrating large variance of fluctuations in the interaction between task-negative and task-positive systems. Our current finding provides a potential structural explanation, by raising the possibility that the phenomenon originates from large fluctuations in the frequency of neural communication along the structural connections between these two functional systems.

In contrast, between-state differences in the similarity of structural and functional edge weights were small within task-positive networks, in which functional edge weights (especially within/between the SMN and VIS in the HCP dataset) were stronger during the segregated than the integrated state. This result suggests that between-state differences in the relationship of structural and functional connectivity were not simply accounted for by changes in the overall magnitude of functional connectivity, but rather derived from fluctuations in specific functional connectivity patterns.

We showed that the centroid of the integrated state, which exhibited greater similarity to structural connectivity, was characterized by weaker segregation of the DMN from the task-positive networks. This observation supports previous findings of fluctuations in the relationship between structural and functional connectivity. Liégeois et al. (2016) tracked temporal changes in the similarity between structural connectivity and time-resolved functional connectivity in the resting state. Consistent with our observation, they demonstrated that a segregation of the DMN from primary sensory networks is less clear in time-resolved functional connectivity when it exhibits a greater similarity to structure connectivity and that the level of segregation increased when the similarity to the structure becomes low. However, they associated durations of greater segregation of the DMN from primary sensory networks with low modularity whereas Shine et al. (2016a) and the present study associated the segregated state with high modularity—this inconsistency likely results from the use of absolute functional connectivity for computing the modularity Q in Liégeois et al. (2016), which underestimates modularity when two large network components are strongly anti-correlated. Barttfeld et al. (2015) investigated how the similarity of resting-state functional connectivity to structural connectivity changes depending on vigilance conditions in awake and anesthetized monkeys. They demonstrated that a functional connectivity pattern appearing most frequently during deep sedation exhibited the greatest similarity to structural connectivity and that modules in the centroid of this state were most unclear, which are also in line with our finding that segregation of functional networks becomes weak during the state of high similarity to structural connectivity.

While fluctuations between segregated and integrated network architecture in functional connectivity have been shown to be associated with arousal and attention necessary for effective cognitive processing (Shine et al. 2016a), several studies reported that similar changes in global functional connectivity patterns were related to changes in sleep stages (Tagliazucchi et al. 2016; Haimovici et al. 2017) and sedation (Barttfeld et al. 2015; Ma et al. 2017). Future research is needed to clarify whether fluctuations between segregated and integrated network states and their relationship to structural connectivity are more reflective of changes in wakefulness and sleep, or in arousal and attention, by examining their relations to other neural or physiological signals simultaneously measured with rs-fMRI acquisition. Potential relations to wakefulness and sleep can be assessed using electroencephalography (EEG) which is well suited for determining sleep stages (Berry et al. 2015). While EEG was not measured in the datasets employed in this study, a respiratory signal, which is also related to sleep (Snyder et al. 1964), was simultaneously measured with rs-fMRI in the HCP dataset. We confirmed that this signal did not have any consistent relationship to fluctuations between segregated and integrated states of functional connectivity (see Supplementary Results). For examination of relations to arousal and attention, pupil diameter can be used because it is known to be correlated with neuromodulatory activity reflecting neural gain (Aston-Jones and Cohen 2005). Pupil dilation has been shown to be associated with arousal and task engagement (McGinley et al. 2015) as well as a greater level of network integration (Shine et al. 2016a). The relationship of pupil dilation to fluctuations in the similarity between structural and functional connectivity remains to be explored.

Methodological considerations

The results from the present study are subject to several methodological limitations. First, although computational tractography based on DWI is the leading technique for reconstructing human structural connectivity, it has also been shown to be prone to inaccuracies (Jones et al. 2013; Thomas et al. 2014), especially when estimating interhemispheric structural connections (Messé et al. 2014). However, we confirmed that the similarity between structural and functional edge weights was also greater in the integrated state even when the similarity was assessed only within each hemisphere (left, t = 14, p = 1.9 × 10⁻²³; right, t = 12, p = 2.8 × 10⁻²⁰). This observation indicates that at least between-state differences in structure-function relationships, which we focused on in this study, were not a consequence of an underestimation of inter-hemispheric structural connections.

Second, there is an ongoing debate on the detectability of fluctuations in neural synchronization across brain areas from rs-fMRI data (Laumann et al. 2016; Liégeois et al. 2017; Miller et al. 2017; Abrol et al. 2017). Fluctuations in functional connectivity with rs-fMRI have been shown to be induced by potential confounds, especially head movements during image acquisition (Laumann et al. 2016). Therefore, employing appropriate methods to remove movement-related artifacts and confirming the absence of clear relationships to head movements are essential for all studies focusing on fluctuations in functional connectivity. In this study we applied extensive artifact reduction methods to the datasets by excluding high motion subjects, censoring and interpolating artifactual time points in the rs-fMRI data, and regressing out motion estimates and the global, white matter and CSF mean signals, to minimize the influence of motion on the estimates of fluctuations between segregated and integrated network architecture. We confirmed that the influence of head movements on the mean participation coefficient (a measure of integration) was weak in all rs-fMRI runs of the HCP and NKI datasets. Moreover, our findings presented in Results were all derived from the run least affected by head movements and in this run no consistent relationship was found between the mean participation coefficient and the framewise displacement (a measure of head movements) both at the single-subject level and the group level (see Supplementary results). These observations suggest that the reliability of our findings should not be compromised by head motion.

Related to the above issue, potential relationships among head movements, respiration and the spatial mean of rs-fMRI signals across the whole brain (the global rs-fMRI signal) have been recently pointed out (Power et al. 2017). In Supplementary results, we demonstrated that the mean participation coefficient and state transitions in our data were not related to respiratory belt traces or the strength or variance of the global rs-fMRI signal. These results indicate that neither changes in respiratory patterns nor changes in the overall signal to noise ratio of rs-fMRI data can explain the fluctuations in network integration reported in this study.

Third, different data processing pipelines were applied to the HCP and NKI datasets independently (see Supplementary methods) and one cannot specify which factor was most responsible for several minor differences found in the results between the datasets. Multiple ways of data processing must be equally applied to both of the datasets if the effect of the choice of datasets and data processing steps on the results needs to be precisely examined. Nevertheless, the main results from which our conclusions were drawn were also reproducible across the HCP and NKI datasets (see Supplementary results) reinforcing the reliability of our findings.

Future directions

While the present study has focused on describing the relationship between structural connectivity and the segregated and integrated states of functional connectivity, future research is needed to clarify how the underlying structural connectivity contributes to the emergence of fluctuations between segregated and integrated states. A promising approach to accomplish this goal is to reproduce the fluctuations of functional connectivity using dynamic models of neural populations linked by structural white matter pathways (Hansen et al. 2015; Ponce-Alvarez et al. 2015). Such computational models can be used to uncover structural determinants of fluctuations between network segregation and integration through manipulation of local and global properties of structural connectivity and examination of its effects on the simulated network dynamics. Contributions of structural connectivity to fluctuating patterns of functional connectivity have only begun to be explored in modeling studies (Messé et al. 2014; Gollo et al. 2015). We believe that modeling approaches will reveal a precise role of structural connectivity on fluctuations in the balance between network segregation and integration, and we plan to pursue this avenue in future work.