Shared and distinct rupture discriminants of small and large intracranial aneurysms

Abstract

Background and Purpose

Many ruptured intracranial aneurysms (IAs) are small. Clinical presentations suggest that small and large IAs could have different phenotypes. It is unknown if small and large IAs have different characteristics that discriminate rupture.

Methods

We analyzed morphologic, hemodynamic, and clinical parameters of 413 retrospectively collected IAs (training cohort; 102 ruptured IAs). Hierarchal cluster analysis was performed to determine a size cutoff to dichotomize the IA population into small and large IAs. We applied multivariate logistic regression to build rupture discrimination models for small IAs, large IAs, and an aggregation of all IAs. We validated the ability of these 3 models to predict rupture status in a second, independently collected cohort of 129 IAs (testing cohort; 14 ruptured IAs).

Results

Hierarchal cluster analysis in the training cohort confirmed that small and large IAs are best separated at 5mm based on morphologic and hemodynamic features (area under the curve [AUC]=0.81). For small IAs (<5mm), the resulting rupture discrimination model included undulation index, oscillatory shear index, previous subarachnoid hemorrhage (SAH), and absence of multiple IAs (AUC=0.84, 95% confidence interval[CI] 0.78-0.88); whereas for large IAs (≥5mm), the model included undulation index, low wall shear stress, previous SAH, and IA location (AUC=0.87, 95% CI 0.82-0.93). The model for the aggregated training cohort retained all the parameters in the size-dichotomized models. Results in the testing cohort showed that the size-dichotomized rupture discrimination model had higher sensitivity (64% vs. 29%) and accuracy (77% vs. 74%), marginally higher AUC (0.75, 95% CI 0.61-0.88 vs. 0.67, 95% CI 0.52-0.82), and similar specificity (78% vs. 80%) compared to the aggregate-based model.

Conclusions

Small (<5mm) and large (≥5mm) IAs have different hemodynamic and clinical, but not morphologic, rupture discriminants. Size-dichotomized rupture discrimination models performed better than the aggregate model.

Introduction

The most widely used surrogate for assessing intracranial aneurysm (IA) rupture risk is aneurysm size.^1–3 This metric was adopted from longitudinal prospective studies, which found that larger aneurysms are more likely to rupture.^{1, 3, 4} However, studies have shown that 13-75% of ruptured aneurysms are small.^5–8 This poses a dilemma for treatment decisions of small IAs. Furthermore, there is no consensus on the definition of “small” and “large” IAs:⁷ 5mm,^{9, 10} 7mm,^{1, 3, 4} and 10mm² have all been used as cutoffs.

Clinical evidence suggests that small and large IAs tend to have different pathophysiological presentations.^11–14 Intraoperative observations show that smaller IAs (<4mm) typically have thin, translucent walls, whereas larger IAs (>10mm) tend to have thick, irregular, and whitish walls.¹¹ Histological studies of ruptured and unruptured IAs have found that small aneurysms (<10mm) are characterized by thin, hypocellular walls, whereas large IAs (>10mm) have thick atherosclerotic walls with the presence of inflammatory cells.^{11, 12} These differences in the IA wall anatomy suggest that small and large IAs may need to be analyzed separately.

On the other hand, because size may not adequately reflect the risk of IA rupture,^15–17 alternative rupture characteristics have been investigated for rupture discrimination models.^{17, 18} However, these models were built without establishing a cutoff measure to distinguish small and large aneurysms. We hypothesized that small and large IAs could have different morphologic, hemodynamic, and clinical characteristics associated with rupture, and such differences may affect image–based rupture discrimination models.

In this study, we investigated whether building rupture classification models separately for small and large IAs could better discriminate IA rupture status. We performed a cross sectional analysis of morphologic, hemodynamic, and clinical rupture characteristics of both small and large IAs in an existing dataset. To define small and large aneurysms objectively, we used unsupervised hierarchal cluster analysis to determine an inherent size cutoff that would dichotomize the IA population. Multivariate logistic regression was used to build rupture discrimination models based on small and large IAs separately as well as in combination (aggregate model). Lastly, we validated the 3 new models and determined the performance of the model predictions in an independent testing cohort.

Materials and Methods

Patient Cohorts

The data that support the findings of this study are available from the corresponding author upon reasonable request. The University at Buffalo Institutional Review Board approved the protocol for this study, which waived the need for patient consent. All patients were from Gates Vascular Institute. The inclusion criteria included: patients who had 3D digital subtraction or computed tomographic angiography, a confirmed ruptured or unruptured IA, and sufficient image quality for segmentation with no noticeable artifacts to accurately represent the IA and surrounding vasculature. The accurate geometry is necessary for computational fluid dynamics (CFD). Two cohorts of patients with IAs were retrospectively collected: 1) the training cohort, consisting of patients evaluated between May 2006 and May 2013 (n=413), and 2) the testing cohort, consisting of patients evaluated between June 2015 and May 2016 (n=129). The IAs in the training cohort were comprehensively analyzed for morphologic, hemodynamic, and clinical features, and were used in building rupture discrimination models. The testing cohort was used for model validation.

Analyses of Morphologic, Hemodynamic, and Clinical Features

We computed 3D morphologic and hemodynamic features from segmented images (Table 1; analyses and features defined in the Supplemental Material and Supplemental Table I). Image segmentation and CFD methods were described previously.^{15, 17, 19–21} To gain further insight into the flow dynamics of IAs, the inflow was classified as either Jet Breakdown Mode or Continuous Jet Mode.²² We also collected and analyzed clinical features, including previous subarachnoid hemorrhage (SAH), hypertension, and IA location (Table 2).

Table 1.

Comparison of morphologic and hemodynamic features of ruptured and unruptured small and large IAs.

	Small IAs (≤5mm)			Large IAs (>5mm)
	Unruptured n=206 Mean±SD	Ruptured n=63 Mean±SD	p-value	Unruptured n=105 Mean±SD	Ruptured n=39 Mean±SD	p-value
Patient Feature
Age(yrs)	59±29	59±16	0.595	62±26	57±11	0.039
Morphologic Features
Size(mm)	3.11±1.70	3.29±1.22	0.256	8.10±4.79	7.54±2.06	0.682
Neck(mm)	3.64±1.20	4.49±7.72	0.369	5.39±2.23	4.61±1.30	0.078
SR	1.35±0.86	2.02±0.99	<0.001	3.13±2.38	3.88±1.57	0.001
AR	0.90±0.50	1.00±0.44	0.069	1.63±0.93	1.72±0.50	0.166
UI	0.06±0.06	0.09±0.07	0.001	0.07±0.06	0.11±0.06	0.001
EI	0.10±0.06	0.13±0.06	0.001	0.17±0.08	0.19±0.043	0.006
NSI	0.12±0.07	0.16±0.08	<0.001	0.19±0.10	0.23±0.057	0.003
An	0.84±0.49	1.24±0.660	<0.001	1.07±0.52	1.19±0.53	0.171
Hemodynamic Features
WSS	0.69±0.51	0.54±0.42	0.014	0.49±0.35	0.32±0.25	0.003
OSI	0.004±0.007	0.017±0.034	<0.001	0.007±0.011	0.016±0.026	0.001
WSSG	−49±162	−27±215	0.547	−68±312	−40±57	0.539
RRT	2.44±2.83	5.04±6.99	0.006	4.53±5.72	7.03±8.37	0.003
LSA	0.10±0.17	0.27±0.32	<0.001	0.23±0.27	0.39±0.30	0.001
MWSS	3.97±2.48	4.09±3.24	0.286	4.88±3.89	3.73±2.82	0.019
PLc	6.07±16.82	5.82±12.45	0.847	4.05±3.95	6.74±9.94	0.112
EL(W/m3)	7607±12065	18543±38272	0.062	4446±8564	10813±24876	0.154

An=aneurysm number; AR=aspect ratio; EI=ellipticity index; EL=energy loss; LSA=low wall shear stress area; MWSS=maximum wall shear stress; NSI=nonsphericity index; OSI=oscillatory shear index; PLc=pressure loss coefficient; RRT=relative residence time; SR=size ratio; UI=undulation index; WSS=wall shear stress; WSSG=wall shear stress gradient

Table 2.

Comparison of ruptured and unruptured clinical features for small and large IAs.

	Small IAs (≤5mm)			Large IAs (>5mm)
	Unruptured n=206 Total(%)	Ruptured n=63 Total(%)	p-value	Unruptured n=105 Total(%)	Ruptured n=39 Total(%)	p-value
Flow Mode Classification
Jet Breakdown	22(11%)	22(35%)	<0.001	29(28%)	23(59%)	0.002
Patient Features
Female	167(81%)	44(70%)	0.058	75(71%)	23(59%)	0.154
Hypertension	114(55%)	35(56%)	0.976	56(53%)	22(56%)	0.742
Smoking	98(48%)	23(37%)	0.122	58(55%)	19(49%)	0.486
IA Family History	29(14%)	6(10%)	0.367	10(10%)	6(15%)	0.320
Previous SAH	17(8%)	11(17%)	0.036	4(4%)	8(21%)	0.001
CAD	20(10%)	8(13%)	0.496	11(10%)	4(10%)	0.956
Dyslipidemia	54(26%)	14(22%)	0.524	23(22%)	7(18%)	0.603
Diabetes	15(7%)	9(14%)	0.126	12(11%)	4(10%)	0.829
Cocaine	4(2%)	2(3%)	0.627	0(0%)	3(8%)	0.019
PKD	5(2%)	1(2%)	1.000	1(1%)	2(5%)	0.122
Multiple IAs	78(38%)	8(13%)	<0.001	26(25%)	10(26%)	0.914
Aneurysm Location
ACA	38(18%)	28(44%)	<0.001	8(8%)	14(36%)	<0.001
ICA	104(50%)	17(27%)	0.001	58(55%)	7(18%)	<0.001
MCA	29(14%)	5(8%)	0.199	12(11%)	5(13%)	0.818
PCOM	7(3%)	5(8%)	0.127	8(8%)	10(26%)	0.004
Posterior	28(14%)	8(13%)	0.855	19(18%)	3(8%)	0.123

ACA=anterior cerebral artery; CAD=coronary heart disease; ICA=internal carotid artery; MCA=middle cerebral artery; PCOM=posterior communicating artery; PKD=polycystic kidney disease; SAH=subarachnoid hemorrhage

Size Cutoff Defining Small and Large Aneurysms

To determine if small and large IAs intrinsically separate, hierarchal cluster analysis was performed on the training cohort. Morphologic and hemodynamic features, excluding IA size, determined clustering. All features were standardized on a scale from 0 to 1. To assess the ability of an IA size cutoff to determine cluster assignment, we built a receiver operating characteristic (ROC) curve. If the ROC analysis showed good performance (area under the curve [AUC]>0.7), it would be determined that separating the population into 2 groups based on IA size is reasonable. The size cutoff would be determined by the Youden Index (J),²³ which gives equal weight to sensitivity and specificity.

Construction of Small, Large, and Aggregate Rupture Discrimination Models

To select candidate morphologic, hemodynamic, and clinical features for rupture discrimination models, we first compared ruptured and unruptured IAs by univariate analyses in the small IA, large IA, and aggregate groups. Binary features were compared by chi-square or Fisher’s exact tests; continuous features were first tested for normality, followed by a Student’s t-test (for normally distributed data) or a Mann-Whitney U test (for non-normally distributed data). Statistically significant features (p<0.05) were considered for logistic regression analysis. Features were also tested for collinearity and were considered for logistic regression if they were independent (p>0.05, correlation coefficient <0.8).

To build rupture discrimination models for small IAs, large IAs, and the aggregate group, we performed multivariate logistic regression. Using a backwards conditional stepwise method, a single rupture discrimination model was built for each group that included morphologic, hemodynamic, and clinical features of IAs. Continuous morphologic and hemodynamic characteristics were scaled to a range of 0 to 10 to ease the comparison of odds ratios (ORs). Binary factors were included in the equation as absent (0) or present (1). Statistical analyses were performed using IBM SPSS Statistics Version 22.0 (IBM Corporation, Armonk, NY).

Assessment of Model Performances

We evaluated the performance of the size-dichotomized and aggregate models in the training cohort by comparing the AUCs that were the result of the logistic regression analysis. We predicted that an IA was ruptured when the probability was greater than the cost-effective cutoff (sensitivity weighted twice more than specificity).²⁴

To test the ability of the models to predict rupture status in an independent cohort of IAs, we applied them to the testing cohort. We treated the small and large IA models as a unified, size-dichotomized model and compared it to the aggregate model. The AUC, sensitivity, specificity, and accuracy (percentage of IAs with correctly predicted rupture status) of each model was determined.

Results

Patient Cohorts

Figure 1 shows the distributions of IAs by size and location in the training and testing cohorts. The training cohort consisted of 413 IAs (102 ruptured) from 345 patients with an average IA size of 4.84±3.26mm. The testing cohort consisted of 129 IAs (14 ruptured) from 107 patients with an average size of 4.92±2.95mm.

Figure 1.

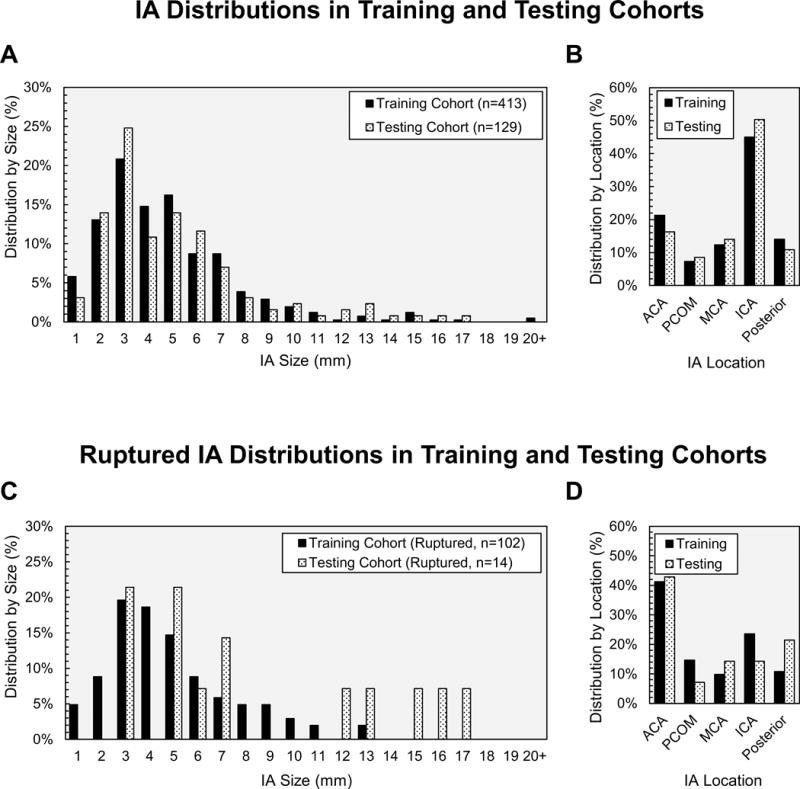
Distributions of all IAs in the training and testing cohorts based on (A) size and (B) location. Distribution of ruptured IAs based on (C) size and (D) location.

Size Cutoff Defining Small and Large Aneurysms

Hierarchal cluster analysis shows the 413 IAs separated into two primary clusters (Cluster A and Cluster B) (Figure 2A). Ellipticity index (EI), or the deviation of the IA convex hull from a perfect hemisphere, was the most important feature for determining cluster assignment (Figure 2B). Cluster A tended to have IAs that were more hemispherical and smaller (Figure 2C). Further, ROC analysis revealed that size was a good determinant of cluster assignment (AUC=0.81) and the best size cutoff to separate small and large IAs was 5.04mm (Figure 2D). Similar size cutoffs were found when ruptured and unruptured IAs were analyzed independently (5.24mm and 4.55mm) (Supplemental Figure). Therefore, 5mm was adopted as a cutoff to dichotomize the training cohort into 269 small (63 ruptured) and 144 large (39 ruptured) IAs. When the morphologic and hemodynamic features of the two groups were compared, 13 of 16 features were statistically different (Supplemental Table II).

Figure 2.

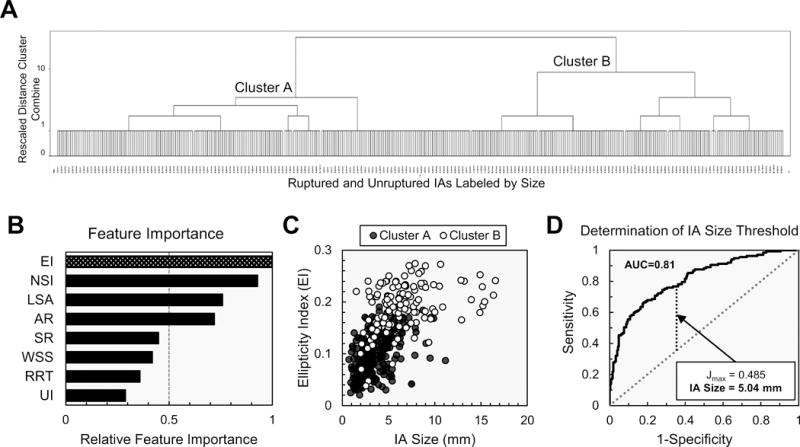
Results of hierarchal cluster analysis. (A) The IAs, labeled by size, and separated into two clusters. (B) EI was the most important feature in separating the two clusters. (C) A scatter plot of EI versus IA size indicated that more hemispherical and smaller IAs tended to be assigned to Cluster A. (D) ROC analysis showed that IA size was a good indicator of cluster assignment (AUC=0.81) and the best size cutoff to separate small and large IAs was 5.04mm.

AR=aspect ratio; EI=ellipticity index; LSA=low wall shear stress area; NSI=nonsphericity index; RRT=relative residence time; SR=size ratio; UI=undulation index; WSS=wall shear stress

Rupture Characteristics of Small and Large Aneurysms

Tables 1 and 2 show descriptive statistics from the univariate comparison of ruptured and unruptured IAs for small (<5mm) and large (≥5mm) IAs in the training cohort. Small and large IAs had several similar rupture discriminants. In both groups, ruptured IAs had higher size ratio (SR), undulation index (UI), EI, nonsphericity index (NSI), oscillatory shear index (OSI), relative residence time (RRT), low wall shear stress area (LSA), and lower normalized wall shear stress (WSS), compared to unruptured IAs. Additionally, ruptured IAs more often had Jet Breakdown Mode, occurred more frequently in patients with previous SAH and at the anterior cerebral artery (ACA) location, and occurred less frequently at the internal carotid artery (ICA) location.

Small and large IAs have some different rupture discriminants. Small ruptured IAs had higher aneurysm number (An), and were less frequent in the presence of multiple IAs when compared to small unruptured IAs. Large ruptured IAs had a higher maximum WSS, occurred in younger patients, and a higher frequency at the posterior communicating artery (PCOM) location than large unruptured IAs. The results of univariate analysis for the aggregate group are provided in Supplemental Tables III, IV, and V.

Rupture Discrimination Models

Multivariate logistic regression analysis yielded three rupture discrimination models for small IAs, large IAs, and the aggregate group:

$$\mathit{odd}{s}_{\mathit{small}\mathit{IAs}}=\mathit{exp}[0.38\left(UI\right)+0.97\left(\mathit{OSI}\right)+1.35(\mathit{PriorSAH})-1.08\left(\mathit{MultipleIAs}\right)-3.27]$$

$$\mathit{odd}{s}_{\mathit{large}\mathit{IAs}}=\mathit{exp}[0.38\left(UI\right)-0.34\left(\mathit{WSS}\right)+2.03(\mathit{PriorSAH})+1.98\left(\mathit{ACA}\right)+1.75\left(\mathit{PCOM}\right)-2.02]$$

$$\mathit{odd}{s}_{\mathit{aggregate}}=\mathit{exp}[0.37\left(UI\right)+1.47\left(\mathit{OSI}\right)-0.12\left(\mathit{WSS}\right)+2.26(\mathit{PriorSAH})+1.40\left(\mathit{ACA}\right)+1.44\left(\mathit{PCOM}\right)-0.79\left(\mathit{MultipleIAs}\right)-2.91]$$

where $\mathit{odd}s$ is the ratio of the probability of ruptured status ( $p$) to the probability of unruptured status ( $1-p$) of a given IA.

Independently significant discriminants of small IA rupture included UI, OSI, previous SAH, and the absence of multiple IAs. Discriminants of large IAs included UI, low WSS, previous SAH, and ACA or PCOM location. The aggregate model retained all previously mentioned small and large IA rupture discriminants.

Figure 3 shows examples of ruptured and unruptured small and large IAs with statistics for the 269 small and 144 large IAs in the training cohort. We found that both small and large IA rupture discrimination models contain UI, or the degree of IA surface irregularity. We also found that high OSI predicted rupture in small IAs, whereas low WSS predicted rupture in large IAs.

Figure 3.

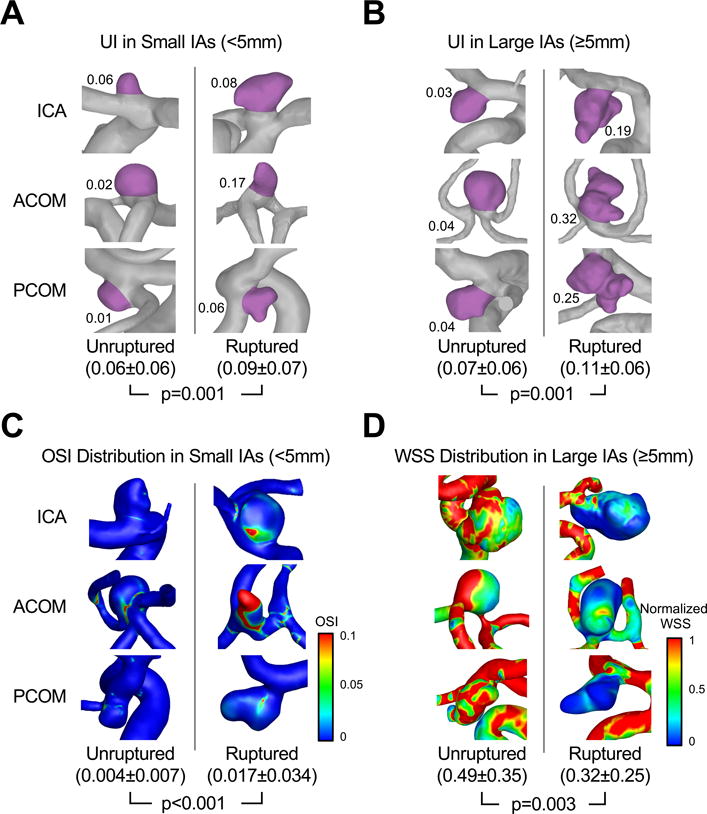
Representative unruptured and ruptured IAs with statistics for all 269 small and 144 large IAs in the training cohort. The aneurysm sac was highlighted to illustrate UI (significant for both small and large IAs) in (A) small IAs and (B) large IAs. (C) OSI distributions in small IAs. (D) Normalized WSS distributions in large IAs.

For all 3 models, previous SAH had a higher odds ratio [OR] than any other model parameter (small IAs OR=3.86, 95% confidence interval [CI] 1.29-11.51; large IAs OR=7.65, 95% CI 1.28-45.69; aggregate OR=9.55, 95% CI 3.61-25.23). The ORs for model parameters are given in Supplemental Table V.

Assessment of Rupture Discrimination Models

The ROC curves for the size-dichotomized and the aggregate models for small and large IAs in the training cohort were compared (Figure 4A-B). For small IAs, the AUC of the size-dichotomized model was marginally higher compared to the aggregate model (0.84, 95% CI 0.78-0.88 vs. 0.82, 95% CI 0.77-0.88). For large IAs, the AUC of the size-dichotomized model was also marginally higher when compared to the aggregate model (0.87, 95% CI 0.82-0.93 vs. 0.83, 95% CI 0.75-0.90). From the ROC curves, we predicted that IAs would be ruptured at a probability greater than 0.23, 0.34, and 0.21 for the small, large, and aggregate models respectively.

Figure 4.

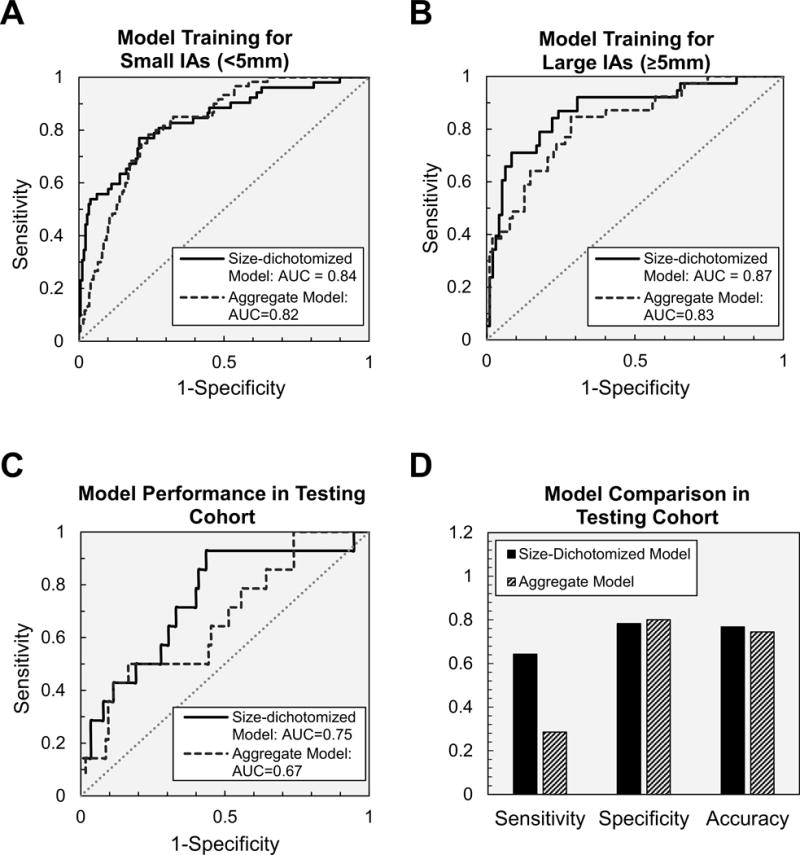
ROC analysis of size-dichotomized and aggregate models for (A) small IAs and (B) large IAs in the training cohort. (C) Model performance in the testing cohort showing the higher AUC of the size-dichotomized model compared to the aggregate model. (D) The size-dichotomized model also had higher sensitivity, and accuracy compared to the aggregate model.

Lastly, the performance of the size-dichotomized and aggregate models in the independently analyzed testing cohort was assessed (Figure 4C-D). The size-dichotomized model has higher sensitivity (64% vs. 29%) and accuracy (77% vs. 74%), marginally higher AUC (0.75, 95% CI 0.61-0.88 vs. 0.67, 95% CI 0.52-0.82), and similar specificity (78% vs. 80%) compared to the aggregate-based model.

Discussion

Identifying the risk of IA rupture is challenging. Many longitudinal and cross-sectional studies have attempted to identify rupture risk predictors, with size being the most widely accepted metric. In the PHASES study,¹ pooled analysis of six longitudinal studies including ISUIA³ and UCAS⁴ found that the estimated risk of aneurysm rupture increases with aneurysm size. For IAs between 7mm and 10 mm, the risk is 2.7 times that of small IAs (<5mm); and for those >20mm, the risk increases to 14.3 times.¹ This suggests that small IAs are least likely to rupture. However, clinical reports show that a substantial percentage of ruptured aneurysms are small. In some reports, 35%⁸ or 47%⁵ of ruptured IA are <5mm; in another report, 66% of ruptured IA are <7mm.⁶ The disparity between the reported low rupture risk and high rupture presentation of small IAs illustrates a gap in our understanding of small IA rupture.

The high percentage of ruptured small IAs among ruptured IAs clearly indicates that small IAs can rupture without becoming large IAs, but we do not know how long it has taken for them to reach the point of rupture. Given that longitudinal studies, such as those surveyed by the PHASES study,¹ tend to follow low-risk IAs that are slated for observation and any sign of increased risk would usually result in treatment, findings from these studies may not represent the true rupture risk of small IAs. In this light, there are some merits in cross-sectional studies that include both small and large ruptured IAs.^{15–17, 19, 21, 25}

Most previous studies, including both longitudinal and cross-sectional ones, have examined IAs without dichotomizing them by size, but small and large IAs could be different phenotypes or even different pathologies.^11–14 In our study, hierarchal cluster analysis resulted in two primary IA groups separated at 5mm in size. This suggests that there are some intrinsic differences between small and large IAs in morphologic and hemodynamic features. We found that large IAs (≥5mm) were more irregular in shape with lower WSS, and small IAs (<5mm) were more spherical with higher WSS.

We inquired whether small and large IAs might have different rupture risk profiles. We found that they have some shared and some distinct rupture discriminants. The shared discriminants include: (1) a history of SAH, consistent with previous studies,^{1, 3, 9} and (2) higher UI (surface irregularity), and this is also in line with previous studies.^{9, 19, 25, 26} Irregular shapes may reflect the presence of daughter aneurysms. These geometries tend to harbor secondary vortices which may promote inflammatory cell infiltration.¹⁷ This type of local disturbed flow environment may also be conducive to thrombus formation, which can exacerbate inflammatory cell infiltration and increase the proteolytic degradation of the IA wall.^{12, 14, 27}

The distinct discriminants of small and large IAs include their hemodynamic environment. Although low WSS predicted large IA rupture, high OSI predicted small IA rupture. Meng et al.¹⁴ proposed two distinct hemodynamic-biological pathways that are responsible for IA growth and rupture: low WSS and high OSI in the aneurysm sac could trigger inflammatory-cell-mediated destructive remodeling, while a high-flow condition could trigger mural-cell-mediated destructive remodeling. Furthermore, it was proposed that the dominance of the inflammatory-cell-mediated pathway could give rise to large, irregular, and atherosclerotic IAs and the dominance of a mural-cell-mediated pathway could be responsible for the genesis of small, smooth-walled IAs.¹⁴

In our study, we found that low WSS predicted rupture status in large IAs. This could indicate the dominance of the inflammatory-cell-mediated pathway in these IAs. On the other hand, high OSI predicted rupture status in small IAs in our study. Meng et al. suggested that jet impingement on the wall could lead to growth and rupture in small IAs.¹⁴ In our study, we found that Jet Breakdown Mode, which is a result of an impingement jet, was associated with rupture. To determine if Jet Breakdown Mode was associated with high OSI, we performed a post-hoc analysis on the training cohort. Our analysis revealed that OSI was significantly higher in IAs with Jet Breakdown Mode than in IAs with Continuous Jet Mode (Supplemental Table VI). This may be because the breakdown of an inflow jet creates a more unsteady flow at the aneurysm wall, thus resulting in high OSI. We also suspect that high OSI plays a bigger role in small IAs compared to large IAs due to a relatively larger surface area being affected by jet impingement.

In addition to hemodynamics, small and large IAs also had distinct rupture discriminants in IA locations and multiplicity of IAs. Large IAs had a higher frequency of rupture at ACA and PCOM locations, as in previous studies.^{1, 4, 26} In small IAs, IA multiplicity was negatively associated with rupture status. This is consistent with previous findings that in the presence of multiple IAs, the ruptured one is most likely the largest aneurysm.²⁸

This study has several limitations. First, our patient population was from a single center, and we do not know how applicable the results are to different populations. Second, we adopted several commonly used assumptions to make CFD tractable. Due to a lack of patient-specific information, we assumed a generic inlet waveform and a constant, location-based inlet flow rate. The inlet velocities were scaled by the inlet diameter. We also assumed blood as a Newtonian fluid and that IAs have rigid walls. Lastly, our rupture discrimination models were based on cross-sectional data, and we cannot address whether they can predict impending rupture in unruptured IAs. Specifically, evidence suggests that the post-rupture IA geometry may be different from the pre-rupture geometry.^{29, 30} Therefore, the observed phenomenon may represent the change in an IA geometry secondary to rupture.

Conclusions

In this study of 542 IAs, hierarchal cluster analysis showed that small and large IAs fell into two clusters based on morphologic and hemodynamic features, with 5mm being the best cutoff. Small (<5mm) and large (≥5mm) IAs have different hemodynamic and clinical, but not morphologic, rupture discriminants. Furthermore, size-dichotomized rupture discrimination models based on morphologic, hemodynamic, and clinical parameters had a higher sensitivity and accuracy than such a model built from the aggregate cohort with no size distinction. These results may indicate that small and large IAs have different paths to rupture.