Abstract
The traits of the primary case of an infectious disease outbreak, and the circumstances for their aetiology, potentially influence the trajectory of transmission dynamics. However, these dynamics likely also depend on the traits of the individuals with whom the primary case interacts.
We used the social spider Stegodyphus dumicola to test how the traits of the primary case, group phenotypic composition and group size interact to facilitate the transmission of a GFP-labelled cuticular bacterium. We also compared bacterial transmission across experimentally generated “daisy-chain” vs. “star” networks of social interactions. Finally, we compared social network structure across groups of different sizes.
Groups of 10 spiders experienced more bacterial transmission events compared to groups of 30 spiders, regardless of groups’ behavioural composition. Groups containing only one bold spider experienced the lowest levels of bacterial transmission regardless of group size. We found no evidence for the traits of the primary case influencing any transmission dynamics. In a second experiment, bacteria were transmitted to more individuals in experimentally induced star networks than in daisy-chains, on which transmission never exceeded three steps. In both experimental network types, transmission success depended jointly on the behavioural traits of the interacting individuals; however, the behavioural traits of the primary case were only important for transmission on star networks.
Larger social groups exhibited lower interaction density (i.e. had a low ratio of observed to possible connections) and were more modular, i.e. they had more connections between nodes within a subgroup and fewer connections across subgroups. Thus, larger groups may restrict transmission by forming fewer interactions and by isolating subgroups that interacted with the primary case.
These findings suggest that accounting for the traits of single exposed hosts has less power in predicting transmission dynamics compared to the larger scale factors of the social groups in which they reside. Factors like group size and phenotypic composition appear to alter social interaction patterns, which leads to differential transmission of microbes.
Keywords: primary case, social network, social spider, trait variation, transmission heterogeneity
1 | INTRODUCTION
Hosts’ traits are important determinants of individuals’ propensity to acquire and transmit microbes which may be infectious agents of disease (Martin, Burgan, Adelman, & Gervasi, 2016; Salje et al., 2016). Thus, differences among individuals in traits like immunocompetence (Gopinath, Lichtman, Bouley, Elias, & Monack, 2014) and behavioural tendencies (Barron, Gervasi, Pruitt, & Martin, 2015) can have implications for the nature and magnitude of host–microbe interactions. In the most extreme cases, certain individuals can be the tipping point upon which epidemics arise or halt (Lloyd-Smith, Schreiber, Kopp, & Getz, 2005). However, the influence of a single individual on its social group or population will be, at least in part, mediated by the traits of nearby individuals with whom the focal individual interacts. Unfortunately, reliably detecting and tracking transmission among individuals is one of the most difficult problems in disease ecology (Buhnerkempe et al., 2015; Fenton, Fairbairn, Norman, & Hudson, 2002; Haydon et al., 2003; Read, Edmunds, Riley, Lessler, & Cummings, 2012). Furthermore, the traits of pairs or groups of interacting individuals are rarely studied empirically or in unison. Thus, a more complete understanding of how individual traits unite with group traits to explain epidemiological dynamics will require (i) a priori characterization of important host traits; (ii) analyses of social interaction networks; and (iii) information regarding how microbes are transmitted through different structures of social networks.
Many emerging infectious disease outbreaks begin with a single individual contracting an infection, although inferring the origin of an epidemic (i.e. the “primary case” or “patient zero”) does not establish their aetiology (Lokhov, Mézard, Ohta, & Zdeborová, 2014). It is tempting to expect that the traits of the primary case will predict the likelihood and magnitude of the ensuing outbreak, and some empirical evidence supports this expectation (Adelman, Moyers, Farine, & Hawley, 2015). However, this is not always the case (Keiser, Howell, Pinter-Wollman, & Pruitt, 2016), and we propose that the effects of the traits of the primary case will depend on factors of the group in which they reside (e.g. group size) and the traits of the individuals with whom it interacts. For instance, the spread of infectious pathogens may be halted if the primary case resides in a small social group, or interacts with a large number of individuals of low infection competence (Barron et al., 2015). In the 2002–2004 SARS outbreak, simulations showed that two identical communities can experience vastly different outbreaks if the primary cases differed in their social contact patterns (Meyers, Pourbohloul, Newman, Skowronski, & Brunham, 2005). Even after a successful transmission event from the primary case to the primary cases of infection, the propensity to transmit infectious agents to secondary cases will depend on the traits of the interacting individuals. Thus, studying individuals’ traits in isolation is likely a less powerful predictor of disease dynamics relative to more comprehensive analyses of group traits. We therefore reason that the degree to which infectious microbes travel through a social network will depend on the series of host individuals through which the microbe is transmitted.
There are several non-mutually exclusive paths through which microbes may be transmitted from a single exposed individual to its social partners (Pinter-Wollman, Keiser, Wollman, & Pruitt, 2016). For example, the microbe could follow a daisy-chain or diffusion chain pattern (i.e. a “line network”), where the primary case transmits to a secondary individual, who then transmits to a third individual, and so on. However, models have suggested that transmission along daisy-chains may be altered by the traits of its members (Moussaïd, Brighton, & Gaissmaier, 2015; Moussaïd & Yahosseini, 2016). Alternatively, the primary case alone may transmit to multiple individuals simultaneously or in succession (i.e. via a “star or “radial” network; Perkins, Cagnacci, Stradiotto, Arnoldi, & Hudson, 2009). These two opposing transmission patterns are rarely differentiated experimentally, although evidence for each exists distinctly. For example, the transmission of entomopathogenic fungal spores through interaction chains of cabbage maggot flies and tephritid fruit flies has been shown to extend to at least six and three hosts respectively (Dimbi, Maniania, & Ekesi, 2013; Meadow, Vandenberg, & Shelton, 2000). Alternatively, the superspreader concept in epidemiology represents an extreme case of the star network structure, where a single individual of very high transmission competence can spread pathogens to a large number of susceptible individuals (Lloyd-Smith et al., 2005; Paull et al., 2012).
Here, we use the social spider Stegodyphus dumicola as a model to evaluate how individual traits, group phenotypic composition and social network structure influence the degree of group-wide transmission of a GFP-labelled cuticular bacterium (Pantoea sp.). Individual Stegodyphus vary in a diagnostic behavioural trait, “boldness,” that is consistent across long periods and is associated with individuals’ propensity to participate in several collective behaviours (Beleyur, Bellur, & Somanathan, 2015; Grinsted, Pruitt, Settepani, & Bilde, 2013; Keiser, Jones, Modlmeier, & Pruitt, 2014; Wright, Keiser, & Pruitt, 2015). Previous experiments demonstrate that transmission of cuticular bacteria between pairs of individuals is biased and directional: more likely to occur from bolder to shyer spiders (Keiser, Pinter-Wollman, et al., 2016), and the degree of group-wide transmission depends on the phenotypic composition of the unexposed individuals in a colony (Keiser, Howell, et al., 2016). Thus, boldness is a measure of individuals’ behavioural tendencies that influence their interaction patterns within colonies and likely the transmission of cuticular microbes (Pinter-Wollman et al., 2016). Here we ask (i) whether the traits of the primary case influence bacterial transmission across groups of different sizes and phenotypic compositions; (ii) to what degree transmission dynamics are a product of different social interaction patterns, specifically “daisy-chains” vs. “star networks”; and (iii) whether network attributes that may be important for transmission vary across groups of different sizes.
2 | MATERIALS AND METHODS
2.1 | Animal collection and maintenance
Stegodyphus dumicola is a group-living spider from arid southwestern African that lives in female-biased colonies of two to several hundred age-structured individuals. Adult females in these societies cooperate in several group behaviours like alloparental care, collective foraging and web-building (Avilés, Varas, & Dyreson, 1999; Bilde et al., 2007; Henschel, 1998; Henschel, Lubin, & Schneider, 1995; Keiser et al., 2014). For the bacterial transmission experiments, we collected 19 S. dumicola colonies from Acacia trees in the Northern Cape of South Africa in March 2015, transported them to the laboratory, and maintained colonies on an ad libitum diet of domestic crickets in 500-ml plastic containers. For the social network observations, colonies were collected from the field in May 2016. We isolated adult females, measured their prosoma width and body mass, and housed them in 30-ml plastic cups during individual behavioural assays. We estimated spiders’ body condition (a measure of health or nutritional status) by the residuals of a linear regression of individuals’ body mass on body size (prosoma width) (Jakob, Marshall, & Uetz, 1996). Thus, greater values of body condition indicate that individuals weigh more than expected based on their body size, an indication of positive health status.
2.2 | Boldness assays
We characterized individuals’ boldness (a behavioural traits associated with individuals’ propensity to engage in risky behaviour; Sloan Wilson, Clark, Coleman, & Dearstyne, 1994) by placing each spider in a clear plastic arena (diameter = 12 cm), allowing a 30-s acclimation period, and administering two rapid puffs of air atop the spider using an infant nose-cleaning bulb. Spiders responded by halting movement and huddling their legs close to their body. We then measured their latency to resume activity after this aversive stimulus, and we designated bold individuals as those that resumed movement within 1–200 s and shy individuals required ≥600 s to resume activity (similar to Keiser & Pruitt, 2014).
2.3 | Bacterial exposure, transmission and sampling
We exposed spiders to Pantoea + pGLO by submerging them individually in 1 ml of a liquid bacterial solution (c. 109 CFU/ml in phosphate buffered saline) for 3 s and allowing it to dry for 24 hr before transferring the spider to a colony (see below). Topical application of GFP-labelled Pantoea does not appear to be harmful nor alter spiders’ boldness (Keiser, Shearer, et al., 2016), thus these transmission patterns may be thought of as a “null model” for transmission in the absence of infection, sickness behaviours and mortality, similar to studying prey behaviour in the absence of predation (e.g. Bastille-Rousseau et al., 2016). To differentiate the primary case from other spiders, we tagged the experimentally exposed individuals with a small green paint dot atop their dorsal abdomen. All susceptible individuals were marked with a blue dot. After allowing the spiders to interact for 24 hr, we sampled the susceptible spiders’ cuticles for the presence of Pantoea + pGLO by vortexing each spider separately in 1 ml of sterile selective growth media (LB broth with 100 μg/ml ampicillin, 20% arabinose; Data S1) for 10 s, removing and euthanizing the spider, and incubating the solution for 20 hr at 30°C. Then, we checked each solution for green fluorescence under long-wave UV light. Here, we measured transmission solely in the context of a “susceptible-infected model”-type epidemiological framework, where we consider the transition of hosts from unexposed to exposed and disregarded intensity (i.e. bacterial load) (Hethcote, 1976).
2.4 | Bacterial transmission within colonies
To examine bacterial transmission dynamics, we constructed 93 experimental groups of 10 spiders or 30 spiders each containing either all shy spiders (n = 23 for groups of 10, n = 6 for groups of 30), one bold spider (n = 26 for groups of 10, n = 5 for groups of 30) or three bold spiders (n = 24 for groups of 10, n = 9 for groups of 30) with the remaining spiders in the colony being shy. These group sizes and colony compositions are within natural distributions (Keiser & Pruitt, 2014). Colonies were housed in 500-ml plastic containers with a wire substrate for web-building for 48 hr before adding a randomly selected primary case exposed to Pantoea + pGLO as described above (latency to resume movement for primary cases ranged from 1 s to 600 s). After interacting with the primary case for 24 hr, we sampled each susceptible spider in the colony for the presence of fluorescing bacteria as described above. A previous study in this system showed that exposure to bacteria via these methods can increase cuticular bacterial load by multiple orders of magnitude and remain elevated for several days (Keiser, Wright, & Pruitt, 2016). The degree of bacterial transmission in each colony was quantified as the number of individuals on which we identified the transformed bacteria, excluding the primary case.
2.5 | Transmission via daisy-chains or star networks
We exposed individuals to Pantoea + pGLO, and then 24 hr later, they were split into two experiments for “daisy-chain” or “star networks” social interactions. For the daisy-chain interactions (n = 39), primary cases of known boldness and body condition were isolated for 24 hr in their own housing container, and then moved into the housing container of a primary individual. After 24 hr, the primary individual was moved to the housing container of a secondary individual, and the primary case was checked for the presence of Pantoea. Twenty-four hours later, the secondary individual was moved into the container of a tertiary individual, and the primary individual was checked for Pantoea. This process was continued until the tenth individual was reached (e.g. Figure 3a).
FIGURE 3.
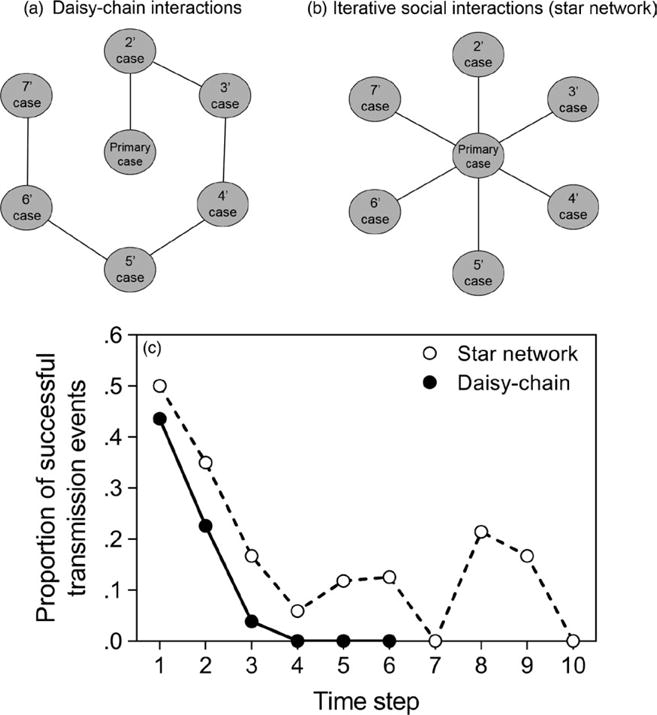
Schematic depiction of (a) daisy-chain interactions and (b) star network interactions. Each interaction was separated by 24 hr. (c) The proportion of social interactions which resulted in successful transmission events across 10 days of interactions in each network type. Note that the star networks can reach steps of completely unsuccessful transmission (e.g. time point = 7) and then recover because the same primary case is interacting with new individuals, whereas the daisy-chain transmission cannot recover from an unsuccessful transmission because the bacterial source is lost
For the star networks (n = 20), an primary case was moved into the housing container of a primary individual for 24 hr, and then the primary case was moved into the housing container of a secondary individual and the primary individual was checked for the presence of bacteria (Figure 3b). This process was continued until the tenth individual was reached. For these pairwise interactions, we calculated the difference in boldness between interacting spiders by subtracting the “latency to move” value of the unexposed individual from the “latency to move” value of the exposed individual, where positive values denote pairs where the exposed spider was bolder (an important predictor of transmission; Keiser, Pinter-Wollman, et al., 2016).
2.6 | Social contact networks and network analysis
To determine the social network structure of intact colonies, we observed resting interactions among spiders in laboratory colonies. Twenty-four colonies each consisting of 10–11 adult female spiders, individually marked with acrylic paint dots atop their dorsal abdomen, were kept in 710-ml round plastic containers with chicken wire that allowed them to build a retreat and a capture web. Individuals in each group came from the same source colony (we used three source colonies which produced 10, 9 and 5 experimental colonies each). We manually noted the resting interaction patterns of all individuals in each colony. We defined interactions between resting group members as a physical contact between any body parts of two spiders. Each group was observed for 6.5 weeks. Resting interactions were observed three times a week with 2–3 days separating each observation. Thus, we obtained 19 resting networks for each group totalling 456 networks. Because groups were tracked for almost 2 months and mortality occurred over time, we obtained interaction networks of groups of different sizes.
To quantify interaction patterns within colonies, we used three network measures calculated using the IGRAPH package in R version 3.1.2 (Csardi & Nepusz, 2006; R Core Team, 2014): (i) network density, the ratio between the number of observed links and all possible links, which quantifies how tightly connected the individuals are in the group; (ii) clustering coefficient, the ratio of observed links connecting a node’s neighbours to each other and the maximum possible number of such links, which quantifies the likelihood that an individual’s neighbours are also connected to one another; and (iii) Modularity (Q), which quantifies the separation of the network into densely connected subgroups, defined using the “leading eigenvector” clustering algorithm (Newman, 2006). To compare whether the above network measures differed from those expected if individuals interacted randomly, we performed simulations which generated random networks with a given degree sequence, using the degree.sequence.game R function (Molloy & Reed, 1995), and compared these simulated values to those for our observed networks (Data S1).
2.7 | Statistical analyses
2.7.1 | Bacterial transmission within colonies
We used a generalized linear mixed model with a log-link function for count data (number of spiders exposed) with the following independent variables: the number of bold spiders in the group (0, 1 or 3; categorical variable), group size (10 or 30; categorical variable), the boldness value of the primary case (continuous variable), body condition of the primary case (continuous variable), group mean body condition (continuous variable), and the interaction between the number of bold spiders in the groups and group mean body condition (all non-significant interaction terms were removed for model simplification; Crawley, 2012; see Data S1). Experimental colony ID nested in source colony ID was included as a random intercept in the model (see details in Data S1). For groups that contained both bold and shy spiders, we also performed a univariate nominal logistic regression model predicting the likelihood of an individual acquiring the bacteria based on their own behavioural phenotype (shy vs. bold), where we also included individual ID nested in experimental group ID as a random effect.
2.7.2 | Transmission via daisy-chain and star networks
To analyse whether successful transmission took place at each step, we used nominal logistic regressions with the following independent variables: transmission step, difference in boldness between interacting individuals, primary case body condition, susceptible individual body condition, and the pairwise interaction between these variables and transmission step (Table 1). Then, we removed non-significant interaction terms for model simplification and present the simplified model here (Crawley, 2012).
TABLE 1.
Results from a general linear mixed model predicting the number of individuals that became exposed to the GFP-transformed cuticular bacteria Pantoea within 24 hr of interacting with an experimental primary case. Significant p-values are denoted with an asterisk
| Effect | Parameter estimate (95% CI) | df | χ2 | p-value |
|---|---|---|---|---|
| Number of individuals exposed to bacteria | ||||
| Number of bold spiders in colony | −0.48 (−0.74 to −0.245) | 2 | 17.22 | .0002* |
| Group size | −0.08 (−0.12 to −0.043) | 1 | 27.01 | <.0001* |
| Primary case boldness | 0.0002 (−0.0004 to 0.0008) | 1 | 0.55 | .46 |
| Primary case body condition | −35.41 (−81.74 to 10.45) | 1 | 2.28 | .13 |
| Mean group body condition | 162.71 (94.93–232.12) | 1 | 22.81 | <.0001* |
| Group body condition × Number bold spiders in colony | −79.41 (−156.01 to −4.81) | 2 | 7.09 | .03* |
2.7.3 | Social network analysis
To determine the effect of group size on network density, clustering coefficient and modularity, we ran three linear mixed effects models (LMM) because the distribution of all the response variables was close to normal. Our dependent variables were network density, clustering coefficient or modularity, and number of individuals in the group was the fixed effect in all three models. We further included group identity nested in colony of origin as a random effect and time point as another random effect to control for any variation caused by these variables. LMMs were implemented using the LME4 package (Bates, Mächler, Bolker, & Walker, 2014) in R version 3.1.2 (R Core Team, 2014). To determine the confidence of our estimates, we ran a Wald chi-squared test using the ANOVA R function on the LMM results.
3 | RESULTS
3.1 | Bacterial transmission within colonies
Groups of 10 spiders experienced approximately five times more transmission events compared to groups of 30 spiders (GLMM: χ2 = 27.01, df = 1, p < .0001; Table 1, Figure 1). Groups containing only one bold susceptible spider experienced over 50% fewer transmission events than groups containing three or zero bold spiders (GLMM: χ2 = 17.22, df = 2, p = .0002; Table 1, Figure 1). Groups containing spiders in better body condition experienced an increased incidence of bacteria transmission (GLMM: χ2 = 22.81, df = 1, p < .0001; Table 1, Figure 2). However, this trend differed for groups depending on their phenotypic composition (interaction term: χ2 = 7.09, df = 2, p = .03; Table 1, Figure 2): this trend was strongest in colonies containing three bold spiders (R2 = 0.25) compared to those with one or zero bold spiders (R2 = 0.03 and R2 = 0.05 respectively). Neither the boldness value (χ2 = 0.55, df = 1, p = .46) nor the body condition (χ2 = 2.28, df = 1, p = .13) of the primary case was associated with the degree of bacterial transmission in their social group. Lastly, averaged across all groups containing one or three bold spiders and both group sizes, the per capita likelihood of acquiring bacteria was four times greater for bold spiders (12/87) compared to shy spiders (20/591) (univariate nominal logistic regression: χ2 = 11.66, df = 1, p = .0006).
FIGURE 1.
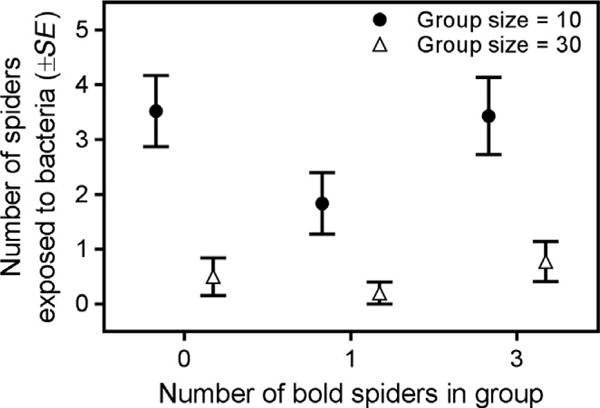
Groups of 10 spiders experienced more bacterial transmission compared to groups of 30 spiders, regardless of group composition. However, groups containing only one bold spider experienced the least bacterial transmission in each group size
FIGURE 2.
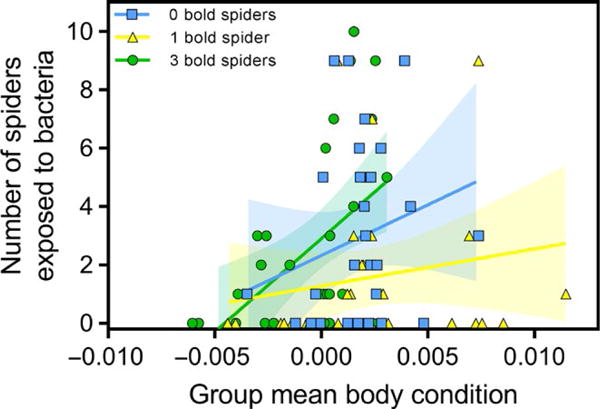
Groups containing spiders in better body condition experienced greater bacteria transmission. This trend was strongest in colonies containing three bold spiders (R2 = 0.25) compared to those with one or zero bold spiders (R2 = 0.03 and R2 = 0.05 respectively). [Colour figure can be viewed at wileyonlinelibrary.com]
3.2 | Transmission via daisy-chain vs. star networks
For each interaction network structure, the likelihood of transmission decreased over each step of transmission (nominal logit: p < .0001; Table 2, Figure 3). For daisy-chain interactions (nominal logit: χ2 = 6.28, df = 1, p = .01) and star networks (χ2 = 10.41, df = 1, p = .001), transmission was more likely to take place when the exposed spider was bolder than the susceptible spider with whom it interacted, as previously reported (Keiser, Pinter-Wollman, et al., 2016). For star networks, we found that the rate of transmission across time steps was strongly influenced by the body conditions of both the exposed individual (nominal logit: χ2 = 15,309.73, df = 6, p < .0001) and the susceptible spiders with which they interacted (nominal logit: χ2 = 1,302.41, df = 5, p < .0001). That is, bacterial transmission was more likely to occur between spiders in better body condition, although this trend was stronger during earlier steps in the interaction chain.
TABLE 2.
Results from nominal logistic regressions predicting the number of individuals that became exposed to bacteria via daisy-chain social interactions or iterative social interactions
| Effect | df | χ2 | p-value |
|---|---|---|---|
| Daisy-chain interactions | |||
| Transmission step | 3 | 50.62 | <.0001* |
| Primary case body condition | 1 | 1.96 | .16 |
| Susceptible individual’s body condition | 1 | 0.41 | .52 |
| Difference in boldness | 1 | 6.28 | .01* |
| Star network interactions | |||
| Transmission step | 9 | 9,388.29 | <.0001* |
| Exposed individual’s body condition | 1 | 3.33 | .0681 |
| Susceptible individual’s body condition | 1 | 0.31 | .5798 |
| Difference in boldness value | 1 | 10.41 | .001* |
| Transmission step × Exposed body condition | 6 | 15,309.73 | <.0001* |
| Transmission step × Susceptible body condition | 5 | 1,302.41 | <.0001* |
| Transmission step × Difference in boldness | 8 | 901.85 | <.0001* |
Significant p-values are denoted by an asterisk.
3.3 | Social network analysis
Interaction density decreased with group size and network modularity increased with group size. Network density was negatively associated with group size (LMM: χ2 = 192.17, df = 1, p < .0001; Figure 4), while network modularity was positively associated with group size (LMM: χ2 = 134.47, df = 1, p < .0001; Figure 4). We did not detect a relationship between network clustering coefficient and group size (LMM: χ2 = 0.21, df = 1, p = .65).
FIGURE 4.
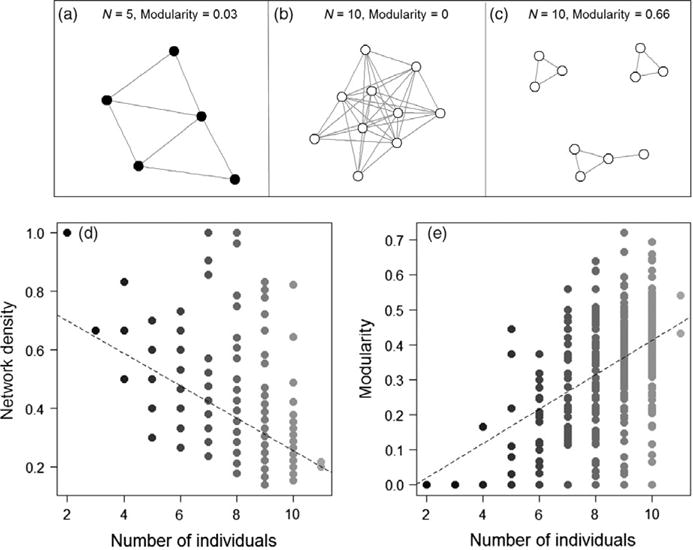
Examples of empirical networks differing in groups size and modularity: observed interaction network of (a) 5 spiders with low modularity; (b) 10 spiders with low modularity; and (c) 10 spiders with high modularity. (d) Larger networks were less dense and (e) more modular than their smaller counterparts
4 | DISCUSSION
The traits of the first individual to become exposed to a novel microbe (e.g. the primary case of an infectious disease outbreak) can impact the trajectory of transmission dynamics. However, the magnitude of their influence undoubtedly depends jointly on their traits and the individuals with whom they interact (Salje et al., 2016). Here, we found that group-wide transmission of a benign GFP-labelled cuticular bacterium is greater in groups of 10 individuals compared to 30 in colonies of the social spider S. dumicola, and that groups containing only one bold individual experienced the least transmission, regardless of the traits of the primary case. Furthermore, we found that bacteria were transmitted to more individuals along a star network of social interactions than along daisy-chains, although transmission depended on the traits of both interacting individuals. Finally, by observing the contact networks of colonies of varying sizes, we infer that the greater incidence of transmission in groups of 10 spiders may be a product of their greater density and lower modularity.
Group size and phenotypic composition have both been independently demonstrated as important predictors of groups’ susceptibility to disease outbreaks (Gao, Bidochka, & Thompson, 2012). Here, we observed more bacterial transmission in groups of 10 individuals compared to groups of 30. This seems counterintuitive, as spiders could transmit bacteria along star networks to at least six other individuals and up to three steps away along daisy-chains, and both transmission dynamics may have played out simultaneously in social groups. In general, transmission often increases with host density for directly transmitted microbes (i.e. density-dependent transmission: Begon et al., 2002; Côté & Poulin, 1995). However, this trend is not universal (Nunn, Jordán, McCabe, Verdolin, & Fewell, 2015), and may be due to the more modular network structure of larger groups (Sah, Leu, Cross, Hudson, & Bansal, 2017). We also found that groups containing only one bold spider experienced fewer transmission events, regardless of the traits of the primary case, recapitulating the findings of an earlier study on this species (Keiser, Howell, et al., 2016). It may be that the role of a single bold spider plays in structuring the colony has important consequences for group-wide transmission (Pinter-Wollman et al., 2016). Although bold spiders were more likely to become exposed than shy spiders overall, the difference in per capita exposure was minute in groups with only one bold spider. Thus, the reduction in exposure rate in these groups is unlikely to be a product of phenotype-biased exposure. Theory incorporating both group phenotypic composition and size to predict transmission patterns is currently absent from the literature, possibly because the dynamics differ based on the focal phenotype and system under consideration (e.g. social insect caste ratio vs. the ratio of demonstrators to observers in a fish school). Nevertheless, the patterns by which individuals within a group interact (i.e. social network structure) will undoubtedly determine transmission dynamics (Hock & Fefferman, 2012; Stroeymeyt, Casillas-Pérez, & Cremer, 2014), especially if interaction patterns change across different group sizes or compositions.
We found that network modularity increased with group size, a trend commonly reported and often suggested to reduce parasite transmission in larger groups (Nunn et al., 2015; Sah et al., 2017). High network modularity suggests that because social interactions within larger groups are broken into several smaller subgroups with few connections between subgroups, transmission in large groups (e.g. of 30 spiders) may have been restricted to individuals within a subgroup. However, more transmission events may have eventually taken place had there been time for individuals to move between subgroups (Eubank et al., 2004). In Belding’s ground squirrels, for example, juvenile males that move between groups increase the overall incidence of intestinal parasite infections by connecting individuals from different subgroups (VanderWaal, Atwill, Hooper, Buckle, & McCowan, 2013). Furthermore, smaller groups were denser, meaning their interactions networks were closer to interaction saturation compared to larger groups, thus providing more opportunities for transmission among all group members. Similarly, a positive relationship between network density and parasite transmission has been described in bumblebee colonies (Otterstatter & Thomson, 2007). Taken together, group size appears to play a large role in dictating transmission dynamics because it influences network structure, which is the organizing force that determines how many and which individuals will interact.
Our experimental manipulations of social interaction patterns further suggest that network structure may be the most important force in shaping transmission dynamics in this system. More transmission occurred in star networks than along daisy-chains. That is, auxiliary cases of bacterial exposure are more likely to arise from a series of individuals interacting directly with the primary case, rather than transmission occurring along a chain of interacting individuals. This suggests that transmission may be dose-dependent, where recipients of cuticular bacteria harbour smaller and smaller bacterial loads at each step of transmission, as has been observed in some systems (Pulkkinen, 2007). Yet, we observed that the primary case harbours a bacterial load large enough to transmit bacteria to many social partners, even many days after exposure (Figure 3). Thus, transmission along star networks appears to mimic that of “stuttering chains” that cannot initiate self-sustaining epidemics, but rather follows stochastic transmission chains that stutter towards extinction (Blumberg & Lloyd-Smith, 2013). The transmission data arising from our star networks and daisy-chains suggest that one can predict the proportion of successful transmission events for a given step in the daisy-chain via the proportion of successes in the previous time from both networks (Pdct and Pst, respectively, where t is the time step under consideration). At any given time step, one can calculate Pdct as:
Using this equation, we can predict the probability of transmission on a daisy-chain with high accuracy (Table 3). We hope that future studies will experimentally manipulate interaction patterns to compare transmission along these types of networks in regard to infectious diseases with variable transmission modes (Read et al., 2012).
TABLE 3.
Observed and predicted proportions of successful transmission events across four time steps in a daisy-chain network. The predicted values are calculated based on the proportion of successful transmission events from daisy-chain and star networks in the previous time step (i.e. Pdcn = Pdcn−1…Psn−1…Pdcn−2 · Psn−2…)
| Time step | Star network observed | Daisy-chain observed | Daisy-chain predicted |
|---|---|---|---|
| 1 day | 0.50 | 0.44 | — |
| 2 days | 0.35 | 0.23 | 0.22 |
| 3 days | 0.17 | 0.04 | 0.02 |
| 4 days | 0.06 | 0.00 | 0.0001 |
The transmission dynamics we observed are of a benign cuticular bacteria lacking infection-induced sickness behaviours and mortality. Transmission dynamics could differ when studying coevolved host– pathogen systems or emerging disease with which hosts have no experience. Still, our study can inform the modes by which microbes are shared among hosts of social species and shape resident microbiome communities (Ezenwa, Gerardo, Inouye, Medina, & Xavier, 2012; Song et al., 2013). Our methods represent a step forward for experimental studies tracking transmission across social contacts because of our ability to connect individual traits and group properties (e.g. group size, composition) with network structure and transmission rates, and further experimentally manipulate network structure itself. We therefore hope that these data will prompt other researchers to use similar methods for evaluating the transmission of disease-causing infectious agents and/or beneficial microbes that defend against infection (e.g. chytridiomycosis; Harris et al., 2009; Rebollar, Simonetti, Shoemaker, & Harris, 2016). In conclusion, our data show that reliable and vigilant tracking of social contacts in the initial stages of an outbreak may be vital for controlling disease outbreaks (Meyers et al., 2005), and that such interactions are likely to change based on the social context of the primary case rather than its own traits, potentially due to consequences on social network structure.
Supplementary Material
Acknowledgments
We thank the South Africa Department of Tourism, Environment, and Conservation for providing permits for animal collection (FAUNA 1690/2015). We thank Sara Geary for laboratory assistance in the bacterial transmission experiments and Brian Mi, Camila Fernandez, and Brandyn Wong for assistance in collecting social network data. We thank Jamie Lloyd-Smith and Patrick Clay for helpful comments on interpreting these data. Funding for this research was provided by the University of Pittsburgh and by NSF IOS grants 1352705, 1455895 to J.N.P., 1456010 to N.P.W., and NIH GM115509 to N.P.W. and J.N.P.
Funding information
Division of Integrative Organismal Systems, Grant/Award Number: 1352705, 1455895 and 1456010; National Institutes of Health, Grant/Award Number: GM115509
Footnotes
Handling Editor: Andy Fenton
[Correction added after online publication on 22 January 2018: ‘index case’ changed to ‘primary case’ throughout the paper]
AUTHORS’ CONTRIBUTIONS
C.N.K. designed the experiments; C.N.K., M.J.Z. and K.S.K. performed the experiments; N.P.W. performed social network observations and analyses; C.N.K. performed statistical analyses and prepared the manuscript with assistance from J.N.P.
DATA ACCESSIBILITY
Data available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.47p7c (Keiser, Pinter-Wollman, Ziemba, Kothamasu, & Pruitt, 2017).
SUPPORTING INFORMATION
Additional Supporting Information may be found online in the supporting information tab for this article.
References
- Adelman JS, Moyers SC, Farine DR, Hawley DM. Feeder use predicts both acquisition and transmission of a contagious pathogen in a North American songbird. Proceedings of the Royal Society of London B: Biological Sciences. 2015;282:20151429. doi: 10.1098/rspb.2015.1429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avilés L, Varas C, Dyreson E. Does the African social spider Stegodyphus dumicola control the sex of individual offspring? Behavioral Ecology and Sociobiology. 1999;46:237–243. [Google Scholar]
- Barron D, Gervasi S, Pruitt J, Martin L. Behavioral competence: How host behaviors can interact to influence parasite transmission risk. Current Opinion in Behavioral Sciences. 2015;6:35–40. [Google Scholar]
- Bastille-Rousseau G, Gibbs JP, Yackulic CB, Frair JL, Cabrera F, Rousseau LP, Blake S. Animal movement in the absence of predation: Environmental drivers of movement strategies in a partial migration system. Oikos. 2016;126:1004–1019. [Google Scholar]
- Bates D, Mächler M, Bolker B, Walker S. Fitting linear mixed-effects models using lme4. arXiv. 2014;1406:5823. [Google Scholar]
- Begon M, Bennett M, Bowers RG, French NP, Hazel S, Turner J. A clarification of transmission terms in host-microparasite models: Numbers, densities and areas. Epidemiology and Infection. 2002;129:147–153. doi: 10.1017/s0950268802007148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beleyur T, Bellur DU, Somanathan H. Long-term behavioural consistency in prey capture but not in web maintenance in a social spider. Behavioral Ecology and Sociobiology. 2015;69:1019–1028. [Google Scholar]
- Bilde T, Coates K, Birkhofer K, Bird T, Maklakov A, Lubin Y, Aviles L. Survival benefits select for group living in a social spider despite reproductive costs. Journal of Evolutionary Biology. 2007;20:2412–2426. doi: 10.1111/j.1420-9101.2007.01407.x. [DOI] [PubMed] [Google Scholar]
- Blumberg S, Lloyd-Smith JO. Inference of R0 and transmission heterogeneity from the size distribution of stuttering chains. PLoS Computational Biology. 2013;9:e1002993. doi: 10.1371/journal.pcbi.1002993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buhnerkempe MG, Roberts MG, Dobson AP, Heesterbeek H, Hudson PJ, Lloyd-Smith JO. Eight challenges in modelling disease ecology in multi-host, multi-agent systems. Epidemics. 2015;10:26–30. doi: 10.1016/j.epidem.2014.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Côté IM, Poulin R. Parasitism and group size in social animals: A meta-analysis. Behavioral Ecology. 1995;6:159–165. [Google Scholar]
- Crawley MJ. The R book. Chichester, UK: John Wiley; 2012. [Google Scholar]
- Csardi G, Nepusz T. The igraph software package for complex network research. InterJournal, Complex Systems. 2006;1695:1–9. [Google Scholar]
- Dimbi S, Maniania NK, Ekesi S. Horizontal transmission of Metarhizium anisopliae in fruit flies and effect of fungal infection on egg laying and fertility. Insects. 2013;4:206–216. doi: 10.3390/insects4020206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eubank S, Guclu H, Kumar VA, Marathe MV, Srinivasan A, Toroczkai Z, Wang N. Modelling disease outbreaks in realistic urban social networks. Nature. 2004;429:180–184. doi: 10.1038/nature02541. [DOI] [PubMed] [Google Scholar]
- Ezenwa VO, Gerardo NM, Inouye DW, Medina M, Xavier JB. Animal behavior and the microbiome. Science. 2012;338:198–199. doi: 10.1126/science.1227412. [DOI] [PubMed] [Google Scholar]
- Fenton A, Fairbairn JP, Norman R, Hudson PJ. Parasite transmission: Reconciling theory and reality. Journal of Animal Ecology. 2002;71:893–905. [Google Scholar]
- Gao Q, Bidochka MJ, Thompson GJ. Effect of group size and caste ratio on individual survivorship and social immunity in a subterranean termite. Acta Ethologica. 2012;15:55–63. [Google Scholar]
- Gopinath S, Lichtman JS, Bouley DM, Elias JE, Monack DM. Role of disease-associated tolerance in infectious superspreaders. Proceedings of the National Academy of Sciences of the United States of America. 2014;111:15780–15785. doi: 10.1073/pnas.1409968111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grinsted L, Pruitt JN, Settepani V, Bilde T. Individual personalities shape task differentiation in a social spider. Proceedings of the Royal Society B: Biological Sciences. 2013;280:20131407. doi: 10.1098/rspb.2013.1407. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Harris RN, Brucker RM, Walke JB, Becker MH, Schwantes CR, Flaherty DC, Vredenburg VT. Skin microbes on frogs prevent morbidity and mortality caused by a lethal skin fungus. The ISME Journal. 2009;3:818–824. doi: 10.1038/ismej.2009.27. [DOI] [PubMed] [Google Scholar]
- Haydon DT, Chase–Topping M, Shaw D, Matthews L, Friar J, Wilesmith J, Woolhouse M. The construction and analysis of epidemic trees with reference to the 2001 UK foot–and–mouth outbreak. Proceedings of the Royal Society of London B: Biological Sciences. 2003;270:121–127. doi: 10.1098/rspb.2002.2191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henschel JR. Predation on social and solitary individuals of the spider Stegodyphus dumicola (Araneae, Eresidae) Journal of Arachnology. 1998;26:61–69. [Google Scholar]
- Henschel J, Lubin Y, Schneider J. Sexual competition in an inbreeding social spider, Stegodyphus dumicola (Araneae: Eresidae) Insectes Sociaux. 1995;42:419–426. [Google Scholar]
- Hethcote HW. Qualitative analyses of communicable disease models. Mathematical Biosciences. 1976;28:335–356. [Google Scholar]
- Hock K, Fefferman NH. Social organization patterns can lower disease risk without associated disease avoidance or immunity. Ecological Complexity. 2012;12:34–42. [Google Scholar]
- Jakob EM, Marshall SD, Uetz GW. Estimating fitness: A comparison of body condition indices. Oikos. 1996;77:61–67. [Google Scholar]
- Keiser CN, Howell KA, Pinter-Wollman N, Pruitt JN. Personality composition alters the transmission of cuticular bacteria in social groups. Biology Letters. 2016;12:20160297. doi: 10.1098/rsbl.2016.0297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keiser CN, Jones DK, Modlmeier AP, Pruitt JN. Exploring the effects of individual traits and within-colony variation on task differentiation and collective behavior in a desert social spider. Behavioral Ecology and Sociobiology. 2014;68:839–850. [Google Scholar]
- Keiser CN, Pinter-Wollman N, Augustine DA, Ziemba MJ, Hao L, Lawrence JG, Pruitt JN. Individual differences in boldness influence patterns of social interactions and the transmission of cuticular bacteria among group-mates. Proceedings of the Royal Society of London B: Biological Sciences. 2016;283:20160457. doi: 10.1098/rspb.2016.0457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keiser CN, Pinter-Wollman N, Ziemba MJ, Kothamasu KS, Pruitt JN. Data from: The primary case is not enough: Exploring trait variation among individuals and social groups in bacterial transmission dynamics. Dryad Digital Repository. 2017 doi: 10.1111/1365-2656.12729. https://doi.org/10.5061/dryad.47p7c. [DOI] [PMC free article] [PubMed]
- Keiser CN, Pruitt JN. Personality composition is more important than group size in determining collective foraging behaviour in the wild. Proceedings of the Royal Society of London B: Biological Sciences. 2014;281:20141424. doi: 10.1098/rspb.2014.1424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keiser CN, Shearer TA, DeMarco AE, Brittingham HA, Knutson KA, Kuo C, Pruitt JN. Cuticular bacteria appear detrimental to social spiders in mixed but not monoculture exposure. Current Zoology. 2016;62:377–384. doi: 10.1093/cz/zow015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keiser CN, Wright CM, Pruitt JN. Increased bacterial load can reduce or negate the effects of keystone individuals on group collective behaviour. Animal Behaviour. 2016;114:211–218. [Google Scholar]
- Lloyd-Smith JO, Schreiber SJ, Kopp PE, Getz W. Superspreading and the effect of individual variation on disease emergence. Nature. 2005;438:355–359. doi: 10.1038/nature04153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lokhov AY, Mézard M, Ohta H, Zdeborová L. Inferring the origin of an epidemic with a dynamic message-passing algorithm. Physical Review E. 2014;90:012801. doi: 10.1103/PhysRevE.90.012801. [DOI] [PubMed] [Google Scholar]
- Martin LB, Burgan SC, Adelman JS, Gervasi SS. Host competence: An organismal trait to integrate immunology and epidemiology. Integrative and Comparative Biology. 2016;56:1225–1237. doi: 10.1093/icb/icw064. [DOI] [PubMed] [Google Scholar]
- Meadow R, Vandenberg JD, Shelton AM. Exchange of inoculum of Beauveria bassiana (Bals.) Vuill. (Hyphomycetes) between adult flies of the cabbage maggot Delia radicum L. (Diptera: Anthomyiidae) Biocontrol Science and Technology. 2000;10:479–485. [Google Scholar]
- Meyers LA, Pourbohloul B, Newman ME, Skowronski DM, Brunham RC. Network theory and SARS: Predicting outbreak diversity. Journal of Theoretical Biology. 2005;232:71–81. doi: 10.1016/j.jtbi.2004.07.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molloy M, Reed B. A critical point for random graphs with a given degree sequence. Random Structures and Algorithms. 1995;6:161–180. [Google Scholar]
- Moussaïd M, Brighton H, Gaissmaier W. The amplification of risk in experimental diffusion chains. Proceedings of the National Academy of Sciences of the United States of America. 2015;112:5631–5636. doi: 10.1073/pnas.1421883112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moussaïd M, Yahosseini KS. Can simple transmission chains foster collective intelligence in binary-choice tasks? PLoS ONE. 2016;11:e0167223. doi: 10.1371/journal.pone.0167223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman ME. Finding community structure in networks using the eigenvectors of matrices. Physical Review E. 2006;74:036104. doi: 10.1103/PhysRevE.74.036104. [DOI] [PubMed] [Google Scholar]
- Nunn CL, Jordán F, McCabe CM, Verdolin JL, Fewell JH. Infectious disease and group size: More than just a numbers game. Philosophical Transactions of the Royal Society B. 2015;370:20140111. doi: 10.1098/rstb.2014.0111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otterstatter MC, Thomson JD. Contact networks and transmission of an intestinal pathogen in bumble bee (Bombus impatiens) colonies. Oecologia. 2007;154:411–421. doi: 10.1007/s00442-007-0834-8. [DOI] [PubMed] [Google Scholar]
- Paull SH, Song S, McClure KM, Sackett LC, Kilpatrick AM, Johnson PT. From superspreaders to disease hotspots: Linking transmission across hosts and space. Frontiers in Ecology and the Environment. 2012;10:75–82. doi: 10.1890/110111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perkins SE, Cagnacci F, Stradiotto A, Arnoldi D, Hudson PJ. Comparison of social networks derived from ecological data: Implications for inferring infectious disease dynamics. Journal of Animal Ecology. 2009;78:1015–1022. doi: 10.1111/j.1365-2656.2009.01557.x. [DOI] [PubMed] [Google Scholar]
- Pinter-Wollman N, Keiser CN, Wollman R, Pruitt JN. The effect of keystone individuals on collective outcomes can be mediated through interactions or behavioral persistence. The American Naturalist. 2016;188:240–252. doi: 10.1086/687235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pulkkinen K. Microparasite transmission to Daphnia magna decreases in the presence of conspecifics. Oecologia. 2007;154:45–53. doi: 10.1007/s00442-007-0805-0. [DOI] [PubMed] [Google Scholar]
- R Core Team. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; 2014. [Google Scholar]
- Read JM, Edmunds WJ, Riley S, Lessler J, Cummings DAT. Close encounters of the infectious kind: Methods to measure social mixing behaviour. Epidemiology and Infection. 2012;140:2117–2130. doi: 10.1017/S0950268812000842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rebollar EA, Simonetti SJ, Shoemaker WR, Harris RN. Direct and indirect horizontal transmission of the antifungal probiotic bacterium Janthinobacterium lividum on green frog (Lithobates clamitans) tadpoles. Applied and Environmental Microbiology. 2016;82:2457–2466. doi: 10.1128/AEM.04147-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sah P, Leu ST, Cross PC, Hudson PJ, Bansal S. Unraveling the disease consequences and mechanisms of modular structure in animal social networks. Proceedings of the National Academy of Sciences of the United States of America. 2017;114:4165–4170. doi: 10.1073/pnas.1613616114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salje H, Lessler J, Paul KK, Azman AS, Rahman MW, Rahman M, Cauchemez S. How social structures, space, and behaviors shape the spread of infectious diseases using chikungunya as a case study. Proceedings of the National Academy of Sciences of the United States of America. 2016;113:13420–13425. doi: 10.1073/pnas.1611391113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sloan Wilson D, Clark AB, Coleman K, Dearstyne T. Shyness and boldness in humans and other animals. Trends in Ecology and Evolution. 1994;9:442–446. doi: 10.1016/0169-5347(94)90134-1. [DOI] [PubMed] [Google Scholar]
- Song SJ, Lauber C, Costello EK, Lozupone CA, Humphrey G, Berg-Lyons D, Nakielny S. Cohabiting family members share microbiota with one another and with their dogs. Elife. 2013;2:e00458. doi: 10.7554/eLife.00458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stroeymeyt N, Casillas-Pérez B, Cremer S. Organisational immunity in social insects. Current Opinion in Insect Science. 2014;5:1–15. doi: 10.1016/j.cois.2014.09.001. [DOI] [PubMed] [Google Scholar]
- VanderWaal KL, Atwill ER, Hooper S, Buckle K, McCowan B. Network structure and prevalence of Cryptosporidium in Belding’s ground squirrels. Behavioral Ecology and Sociobiology. 2013;67:1951–1959. [Google Scholar]
- Wright CM, Keiser CN, Pruitt JN. Personality and morphology shape task participation, collective foraging and escape behaviour in the social spider Stegodyphus dumicola. Animal Behaviour. 2015;105:47–54. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


