Two-dimensional IR spectroscopy can be designed to eliminate the diagonal peaks and expose only the crosspeaks needed for structure determination

Abstract

The power of two-dimensional (2D) IR spectroscopy as a structural method with unprecedented time resolution is greatly improved by the introduction of IR polarization conditions that completely eliminate diagonal peaks from the spectra and leave only the crosspeaks needed for structure determination. This approach represents a key step forward in the applications of 2D IR to proteins, peptides, and other complex molecules where crosspeaks are often obscured by diagonal peaks. The technique is verified on the model compound 1,3-cyclohexanedione and subsequently used to clarify the distribution of structures that the acetylproline-NH₂ dipeptide adopts in chloroform. In both cases, crosspeaks are revealed that were not observed before, which, in the case of the dipeptide, has led to additional information about the structure of the amino group end of the peptide.

Heterodyned 2D IR experiments have recently been reported that are the IR analogues of pulsed correlated spectroscopy and nuclear Overhauser effect spectroscopy in 2D NMR (1–5). Like 2D NMR spectra that exhibit diagonal peaks at frequencies determined by one-dimensional spectra and crosspeaks between coupled nuclear spins, 2D IR spectra contain diagonal peaks and crosspeaks that represent coupled vibrational transitions. The 2D IR crosspeak intensities and splittings depend on the angles and distances between the vibrational modes and can be used to characterize the structures of peptides (3, 6, 7). One advantage (8) of 2D IR over other structure-determining methods is the time scale; 2D IR can monitor structures on a picosecond timescale, which allows transient protein dynamics to be followed. However, structural information is lost when the crosspeaks overlap with the more intense diagonal peaks. Methods have been developed in 2D NMR to minimize the overlap of diagonal and crosspeaks (9, 10). Here we report a technique based on quite different principles that completely eliminates the diagonal peaks from 2D IR spectra and allows the crosspeaks and hence structures to be more easily and better characterized.

A useful characteristic of IR transitions is that the directions of their transition dipoles in the molecular frame are often predictable. For example, modes that are mainly localized on two atoms such as N—H, C—H, or C⩵O stretches usually have transition dipole vectors near the bond axis, and the amide I modes of peptide units have transition dipoles whose directions are given by the positions of the amide atoms (11). The four polarized IR pulses in the 2D IR experiments successively interact with four transition dipoles of each molecule, and thus polarized 2D IR measurements can yield information on the geometric arrangements of the dipoles. The diagonal peaks are generated when the IR pulses all interact with the same mode and therefore interrogate only a single location in the structure. The crosspeaks are generated when the IR pulses interact with modes in different locations. The results are couplings and relative orientations that can be used to determine the structure. This paper reports on the discovery of useful polarization conditions (listed in Table 1) for IR laser pulses several of which completely eliminate the diagonal peaks from the 2D IR spectra. These conditions allow significantly more information to be gathered about the coupling between different spatial regions of the molecule and about the dynamics of the structural changes for these regions.

Table 1.

Some polarization conditions for 2D-IR spectroscopy

α*	β	γ	δ	Tensor element†
0	π/4	−π/4	0	1/2(〈xxyy〉 + 〈xyxy〉)
π/4	0	−π/4	0	1/2(〈xxyy〉 + 〈xyyx〉)
π/4	−π/4	0	0	1/2(〈xyyx〉 + 〈xyxy〉)
π/3	−π/3	0	0	1/4(〈xxxx〉 − 3〈xxyy〉)
0	π/3	−π/3	0	1/4(〈xxxx〉 − 3〈xyyx〉)
θ	−θ	π/2	0	1/2sin2θ(〈xyxy〉 − 〈xyyx〉)
π/2	θ	−θ	0	1/2sin2θ(〈xxyy〉 − 〈xyxy〉)
circ	circ	0	0	1/2(〈xxxx〉 + 〈xxyy〉)
circ	0	circ	0	1/2(〈xxxx〉 + 〈xyxy〉)

^*The angles measured with respect to one of the polarization axes; circ means circularly polarized light of a given sense, and results are obtained from laboratory fixed field unit vectors that are complex. For example, for a process generating a macroscopic polarization P_δ = χ_αβγδE_αE^*_βE^*_γ, the general tensor element would be 〈α_iβ^*_jγ^*_kδ_l〉. 

^† Subscripts have been removed, e.g. 〈xyxy〉 = 〈x_iy_jx_ky_l〉, because the relations are true for all paths i,j,k,l. In our experiment, x and y are orthogonal polarization axes perpendicular to the direction of pulse propagation, z. 

We have chosen two simple systems to demonstrate this approach. The first is 1,3-cyclohexanedione, which has two C⩵O groups giving symmetric and antisymmetric stretching bands in the linear IR spectrum, but whose coupling is not known. This molecule thus serves as a model system to develop the method. The second system is acetylproline-NH₂, which has been studied previously with heterodyned 2D IR spectroscopy (3, 4). Acetylproline-NH₂ is a dipeptide and also has two C⩵O groups that give rise to two amide I bands and one observable amide II band. The dipeptide was found to adopt two different conformations in CDCl₃, and its 2D IR spectrum has been assigned. We show here that the structural information content of the 2D IR spectrum is significantly enhanced with the information gained from the polarization measurements.

Materials and Methods

The laser system developed to perform the 2D IR experiments consists of an amplified titanium sapphire laser that pumps a difference frequency optical parametric amplifier. The resulting tunable IR pulses of 1 μJ in energy and 120 fs full width half maximum form the three excitation pulses with wavevectors k₁, k₂, and k₃ (≈300 nJ each) and a local oscillator pulse (k_LO, ≈3 nJ). The excitation pulses impinge on the sample in a box configuration, and the local oscillator pulse passes outside the sample, where it is overlapped and heterodyned with the emitted photon echo signal in the phase matching direction k_LO = −k₁ + k₂ + k₃. The pulses k₁ and k₂ are separated by time τ, k₂ and k₃ are separated by T that is set to zero for a two-pulse echo, and k_LO arrives a time t after k₂ and k₃. The heterodyned photon echo is collected as a function of τ and t. For the 1,3-cyclohexanedione experiments, τ and t were stepped from 0 to 2,500 fs, and for acetylproline-NH₂, τ and t were stepped from 0 to 1,800 fs. The t and τ signals were undersampled by collecting data in 18-fs increments (the fundamental period is ≈10 fs). The resulting spectra are aliased and corrected by addition of the spectral width (3). The polarizations of all of the pulses are controlled with wire-grid polarizers (Specac; 12900) placed before the sample; a polarizer after the sample selects the polarization of the photon echo. Three polarization conditions are used in this report: (0, 0, 0, 0), (0, π/2, π/2, 0), and (π/4, −π/4, π/2, 0), listed in the order that the pulses follow in the experiment (k₁, k₂, k₃, k_LO), and 0 ≡ vertical. The samples are about 100 mM in CDCl₃ and are held between two CaF₂ windows that are spaced 50 μm apart. The (0, π/2, π/2, 0) measurement of acetylproline-NH₂ is consistent with previously published spectra (3), although the signal strength is improved by a factor of 10.

The 1,3-cyclohexanedione spectrum taken with (π/4, −π/4, π/2, 0) polarization (see Fig. 1b below) consists of eight peaks whose peak positions are determined by the frequencies and anharmonicities (see Eq. 2 below). It is a straightforward task to determine these parameters for well-separated peaks (5), but when the separations are less than the linewidths, as is the case here, an accurate fit requires a known lineshape (2). The lineshape is calculated from the dephasing time, T₂, and the inhomogeneous broadening, σ. These parameters were determined from two-pulse photon echo measurements and a 2D IR spectrum by using (0, 0, 0, 0) polarization and gave T₂ = 575 ± 50 fs and σ = 7 cm⁻¹. To determine the frequencies and anharmonicities, the (π/4, −π/4, π/2, 0) spectrum was least-squares fit to eight peaks. The parameters were constrained to reproduce the frequencies in the linear spectrum,† and the intensities and signs of the peaks in the 2D IR spectrum were allowed to vary. The resulting frequencies and anharmonicities are listed below.

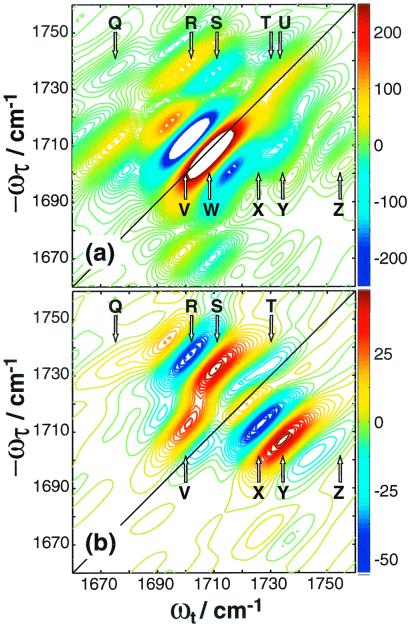
Figure 1.

2D IR spectra for 1,3-cyclohexanedione. (a) Re{S̃[0,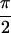, , 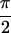0]}, (b) Re{S̃[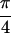,−,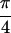 , 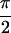0]},. The peaks are labeled Q through Z. U and W lie on the diagonal.

After the incident pulse, an echo field, analogous to the free induction decay of NMR, is emitted that is combined with the local oscillator pulse on a detector to give the meas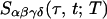ured signal as a function of the time intervals; the subscripts follow the polarization condition (α, β, γ, δ). The 2D IR spectrum is generated from the time-domain data by calculating the 2D Fourier transform of the measured signal,

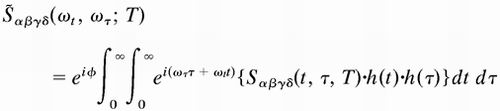1

where h(t) is a window function, and φ is a phase factor, described previously (2).S̃_αβγδ(ω_t, ω_τ; T), hereafter written S̃[αβγδ], is a complex function, and in this paper the magnitude Abs{S̃[αβγδ]} and the real spectrum Re{S̃[αβγδ]} are reported.

Results

1,3-Cyclohexanedione.

The linear-IR spectrum for 1,3-cyclohexanedione in CDCl₃ has two peaks located at 1,711 and 1,735 cm⁻¹, which are the symmetric and antisymmetric C⩵O stretch modes. The ratio of their areas is ≈2.9:1. Fig. 1a shows Re{S̃[0, 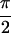, , 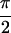0]}. Ten peaks contribute to the 2D spectra, labeled Q through Z. The two peaks in the linear spectrum each produce a positive peak on the diagonal, labeled U and W, and a negative peak that is shifted to lower frequencies along ω_t, labeled T and V. The pattern that each linear peak produces a pair of out-of-phase peaks near the diagonal is typical for 2D IR spectra (2). Peaks R/S and X/Y are crosspeaks that correlate the diagonal peaks to one another, and each pair of crosspeaks consists of one positive and one negative peak, similar to the diagonal pairs. However, the signs of the crosspeaks are reversed for this molecule as compared with the diagonal peaks; the lower-frequency peaks R and X are positive, and the higher-frequency peaks S and Y are negative. This phase reversal is because the angle between the transition dipoles of the symmetric and antisymmetric stretch is 90°, which is larger than the magic angle (54.7°) (3, 12). Peaks Q and Z arise from transitions that are expected to be very weak. Some peaks are not so evident in Fig. 1a, but they are more apparent in Re {S̃[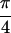, −, 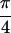, 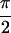0]}, shown in Fig. 1b. The relative intensities of the peaks are dramatically different in the Re {S̃[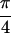, −, 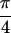, 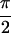0]}, spectrum. Peaks U and W have been eliminated in this spectrum, and peaks T and V are only a few percent of their original intensity. Crosspeaks R/S and X/Y are now the dominant features. Peaks Q and Z are also more apparent.

Acetylproline-NH₂.

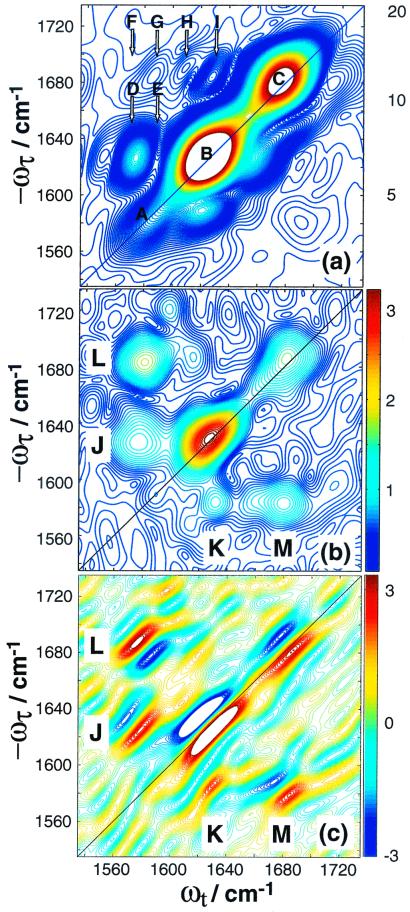
The linear-IR spectrum of acetylproline-NH₂ in CDCl₃ has three peaks that arise from the amide I and II modes (3). The three peaks each produce a pair of peaks along the diagonal similar to 1,3-cyclohexanedione, which are observed in Re{S̃[0,0,0,0]} as previously reported (3). Because the pairs are split by less than their linewidths, they appear as single peaks in Abs{S̃[0,0,0,0]}, shown in Fig. 2a. The diagonal peaks are labeled A, B, and C in Fig. 2a. Peaks A and C are from the amide II and I vibrational modes located on the amino end of the molecule. Peak B is the amide I band on the acetyl end. Six crosspeaks are observed above the diagonal, labeled D through I. Each of these consists of a pair of unresolved and out-of-phase peaks (like the pairs in 1,3-cyclohexanedione) and results from coupling between the amide I and II modes. As has been determined previously by using 2D IR spectroscopy (3), acetylproline-NH₂ adopts two configurations in CDCl₃. The six peaks in the magnitude spectrum result from each configuration having three crosspeaks above the diagonal. Crosspeaks D and E correlate the two amide II bands with the two acetyl amide I bands, crosspeaks F and G correlate the two amide II bands with the two amino amide I bands, and crosspeaks H and I correlate the two acetyl and amino amide I bands. In general, the crosspeaks do not appear as intense on the lower half of the spectrum. The positions of peaks D-I indicate that the two configurations have degenerate amino amide I frequencies, but different acetyl amide I and amino amide II frequencies. From previous polarization measurements (3), the angles between the transition dipoles for all of the crosspeaks are known.

Figure 2.

2D IR spectra for acetylproline-NH₂. (a) Abs{S̃[0,0,0,0]}, (b) Abs{S̃[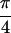, −, 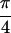, 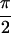0]} and (c) Re{S̃[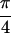, −, 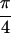, 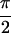0]}. In a, the diagonal peaks are labeled A, B, and C, and the crosspeaks are labeled D through I. Each of these features is a pair of out-of-phase peaks, as determined from Re{S̃[0,0,0,0]}, published previously (3). In b, the remaining crosspeak features are labeled J through M, and the out-of-phase components of each feature are visible in c.

Fig. 2b shows Abs{S̃[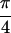, −, 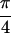, 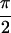0]}, where the diagonal peaks A, B, and C are suppressed by about 90–95%. The crosspeaks are now clearly visible on the lower half of the spectrum as well. The peaks in Fig. 2b are labeled J, K, L, and M. Clearly J and K are a set of crosspeaks, as are L and M. It will be shown below that J results from crosspeaks D and E, and L from F and G. Re {S̃[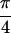, −, 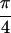, 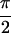0]} is shown in Fig. 2c. The out-of-phase pairs of peaks are now clearly visible for each of the crosspeaks in Fig. 2a. However, the phase of the pairs is not the same for all of the peaks. The set of peaks that form J and K have the same phase on either side of the diagonal, but L and M are out-of-phase.

Analysis and Discussion.

First, we account for the peak positions in the 2D IR spectra and predict their relative contributions and signs depending on the polarizations of the pulses. The 1,3-cyclohexanedione spectra are then fit to determine the frequencies and anharmonicities. In the final section, the peak intensities observed in the {S̃[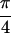, −, 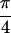, 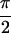0]} spectrum for acetylproline-NH₂ are explained with previously measured transition dipole angles, and a simulation is presented that accounts for the phases of the observed crosspeaks.

2D IR Signals.

In principle, all of the vibrational states of a molecule having vibrational quantum numbers 1 and 2 can be accessed in a third-order photon echo experiment. As a result, the fundamentals, overtones, and combination bands all contribute. For a single vibrator, the two-or three-pulse echo involves a fundamental and an overtone state (2). For a system with N oscillators, there will be N one-quantum states and N(N + 1)/2 states that can have the excitations on different oscillators (combination modes). The vibrational energy for a two-mode system up to second order in the vibrational quantum numbers υ_i and υ_j is

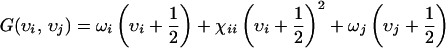2

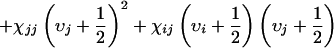where ω_i and ω_j are the frequencies of the fundamentals and are the anharmonicities. The shifts between the υ = 0 to 1 χ_ab and their υ = 1 to 2 transitions are Δ_i = −2χ_ii, and the off-diagonal anharmonicity is Δ_ij = −χ_ij. For the 1,3-cyclohexanedione system, the one-quantum states are the symmetric and antisymmetric stretching modes of the molecule. For the acetylproline-NH₂ system, the one-quantum states are the acetyl and amino amide I vibrations and the amide II vibration of the amino.

For a two-mode system, the 2D IR spectrum can be schematically written as the 2D Fourier transform (2DFT) of the superposition of 18 contributions as follows,

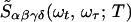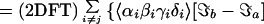3

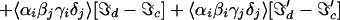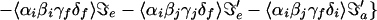A more general form of this equation is given in refs. 3 and 13. Each pulse in the IR sequence can in principle excite a different mode of the molecule, so up to four different transition dipoles may be involved in any one term. The ℑ terms represent the various ways the IR pulses can excite the vibrational states. Each term includes the transition dipole amplitude factors that determine the strength of the transition, the dynamics and frequency factors for that pathway. The 〈....〉 symbolizes an average over the orientations of the transition dipoles involved in each path whose modes are labeled with the indices i and j. States that do not participate in transitions unless there is some coupling between modes are labeled f for “forbidden.” ℑ_a and ℑ_b both involve all of the IR pulses successively interacting with only a single mode of the system, and the dynamics are for only that mode; ℑ_c and ℑ_d arise from the pulses interrogating different modes, and the dynamics involve both modes. Other paths would be needed if pulses other than k₂ and k₃ were to overlap, which is not the case for the spectra reported here. These factors are all discussed in previous reports (4). The contributions of each ℑ term to the signal depends on 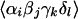, which depend on the polarization of the IR pulses, the angles between the transition dipoles associated with different modes of the molecule, and the rotational dynamics. Manipulating these factors to enhance or suppress specific terms in Eq. 3 is the main topic of this paper.

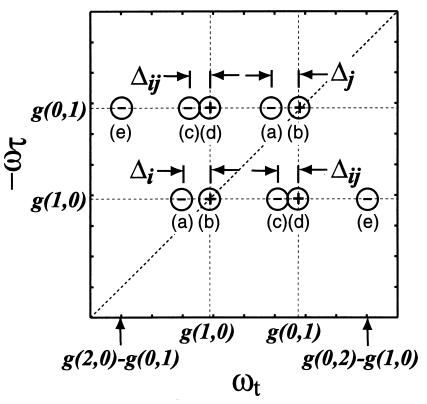
The 2D IR spectrum predicted by Eq. 3 is shown in Fig. 3. Each of the ℑ terms produces a peak in the 2D IR spectrum indicated by its subscript. Thus, for a two-oscillator system, each oscillator i will have a row of five peaks along the ω_t axis. Positive and negative amplitude peaks are labeled as “+” and “−.” The second line of Eq. 3 produces the diagonal peaks a and b, which have different signs. The third line gives rise to crosspeaks c and d, also out-of-phase. Lines 4 produces peaks at e and a, respectively, which are expected to be much weaker than those from the other lines in Eq. 3. The present analysis assumes that the vibrational and overall rotational dynamics are statistically independent. Furthermore, spontaneous energy and coherence transfer are neglected.

Figure 3.

A schematic representation of the 2D IR spectrum predicted by Eqs. 2 and 3. The peak positions are referenced to G(0,0) by using g(i,j) = G(υ_i,υ_j) − G(0,0). The ℑ and ℑ′ paths in Eq. 3 produce 2D IR peaks at the same frequencies.

Polarization Effects.

In this section, we introduce a number of polarization configurations to select the pathways, ℑ. Each contribution to the third-order nonlinear response depends on a fourth-rank polar tensor that describes the orientation of the four-molecule fixed transition dipole moments defining the path, i, j, k, and l, and the laboratory fixed set of polarization directions α, β, γ, and δ. A typical factor is 〈α_i(0)β_j(τ)γ_k(τ + T)δ_l(τ + T + t)〉 ≡ 〈α_iβ_jγ_kδ_l〉, where the time arguments are implicit in the last expression. From known properties of polar fourth-rank tensors in isotropic media, the general tensor element is the product of two factors, one that depends on the polarizations of the exciting fields and another that includes only the time-dependent relative orientations of the dipoles (12).

In isotropic media, only three independent macroscopic observables are obtainable from variations in the polarizations of the incident fields (14). If we choose x and y as any two of the three orthogonal directions in the lab frame, the following condition is maintained between the nonvanishing tensor elements for each of the paths:

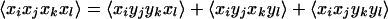4

Note that there are no terms having only one x or one y. From these general relations, it is straightforward to write down the specific tensor elements that are measured in any chosen polarization condition. Some useful examples are given in Table 1, showing that different linear combinations of the tensor elements can be obtained by judicious choices of polarizations of the four pulses. Depending on the specification of the molecular dipole axes, some of these linear combinations may exist, and others may not. Therefore the polarization conditions may be used to examine specific microscopic contributions to the 2D IR spectrum. Such procedures have been used in many other forms of nonlinear spectroscopy, such as in coherent anti-Stokes Raman and Raman-induced Kerr effect measurements (15).

The fourth to seventh entries in Table 1 are particularly useful in 2D IR, because the signals vanish for certain pathways involved in the interaction of a molecule with IR pulses. We consider a molecule having two vibrations, 1 and 2, and hence two possible transition dipole directions in the molecule frame. These could correspond to excitations of the two amide I groups in acetylproline-NH₂, or the symmetric and asymmetric stretches of 1,3-cyclohexanedione. The polarization condition (π/4, −π/4, π/2, 0), which maximizes the signal given in the sixth row of Table 1, allows the measurement of the tensor combination 〈xyxy−xyyx〉 which for the various possible paths is given by:

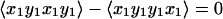5a

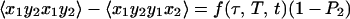5b

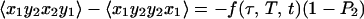5c

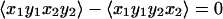5d

where P₂ = ½(3〈cos²θ₁₂〉 −1), and θ₁₂ is the angle between the transition dipoles and the average is over any fixed distribution of structures. The internal motions and overall rotations are considered to be independent. All of the terms in Eq. 5 vanish when the transition dipoles are parallel (P₂ = 1). The diagonal contributions to the 2D IR spectrum vanish (Eq. 5a), whereas the crosspeaks in the spectra will remain whenever P₂ ≠ 1 (Eq. 5 b and c). When the molecules are not rotating during the experiment, which is commonly the case when the coherence dynamics are faster than the orientational relaxation time, we find f = 1/9. The values of f(τ, T, t) depend on the specific models for the rotational dynamics (16). Eq. 5a was recently proven for a symmetric diffuser even with the transition dipole not parallel to a principal diffusion axis (17). The values of f(τ, T, t) for a spherical rotor are tabulated in ref. 12. If the transition dipoles are parallel to principal diffusion axes, such as with 1,3-cyclohexanedione, the calculations are greatly simplified and yield the inequalities in Eq. 5 by straightforward application of known principles (16). The ensemble averages needed to obtain f(τ, T, t) in the case of asymmetric rotors are functions of the diffusion of the molecule about its principal axes but can be calculated easily by standard methods for all possible cases (16).

The (π/4, −π/4, π/2, 0) polarization condition from line 6 of Table 1 completely removes peaks arising from diagonal regions when internal motions are neglected. Thus, the signal from the first line of Eq. 3 should be completely eliminated from 2D IR spectra by using (π/4, −π/4, π/2, 0) polarization. Hence peak b is removed from the spectra in Fig. 3, and peak a should be greatly diminished because only the forbidden term remains.

Simulation of the Polarized 2D IR Spectrum of 1,3-Cyclohexanedione.

The origin of the peaks in the 1,3-cyclohexanedione spectra is immediately apparent from Fig. 3; all 10 peaks predicted by Eq. 3 are present in Re{S̃[0, , , 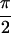0]} of Fig. 1a. Peaks T/U and V/W correspond to peaks a and b in Fig. 3, peaks R/S and X/Y correspond to peaks c and d, and peaks Q and Z correspond to peak e. As predicted above, the (π/4, −π/4, π/2, 0) measurement does indeed remove peaks arising from parallel transitions, as evidenced by the elimination of peaks U and W and the suppression of peaks T and V in Fig. 1b.

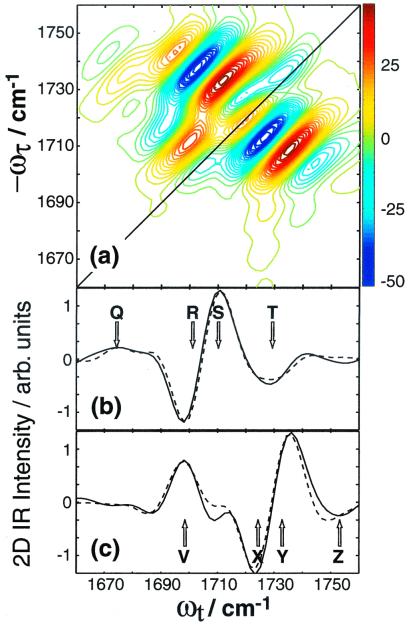
The peak positions are determined by the one- and two-quantum eigenstate energies, which need to be extracted from the 2D IR spectra to determine the frequencies and anharmonicities in Eq. 2. The simulated spectrum is shown in Fig. 4 a–c, which models the data extremely well, and the resulting frequencies and anharmonicites are ω₁ = 1,730.2, ω₂ = 1,746.5, Δ₁ = 13.1, Δ₂ = 5.5, Δ₁₂ = 12.4 cm⁻¹.

Figure 4.

Fit to Re{S̃[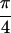, −, 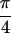, 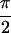0]} of 1,3-cyclohexanedione (a), and comparison of slices along ω_t for ω_τ = 1,735 (b), and 1,711 cm⁻¹ (c). Experiment is shown solid and fit, dashed.

The question of how to provide the frequencies and anharmonicities with a structural basis remains. In peptides and proteins, the C⩵O stretches, or the amide I modes, are mechanically localized on each peptide unit and only weakly perturbed from their zero-order energies by electrostatic coupling to other amide I modes (11). In such a picture, the zero-order modes must convert into the eigenmodes of the whole system by a simple perturbation calculation within each nearly degenerate group. If the calculation of the eigenmodes were to require coupling among zero-order modes of different types, the exciton model would be wrong. This appears to be the case for 1,3-cyclohexanedione, whose spectra are not predicted by a simple exciton model. The construction of its symmetric and antisymmetric stretch modes must require the participation of other modes, so there is not a simple approximation in which the C⩵O excitations are localized and from which the eigenmodes are retrieved by a perturbation calculation. Thus, the C⩵O modes are determined by the motions of the entire molecule, and the force constant matrix needs to be diagonalized to ascertain their energies. The frequencies and anharmonicities are still sensitive to the structure of the molecule, but a simple electrostatic coupling model based on isolated modes, such as used for peptides, does not apply for 1,3-cyclohexanedione. The 2D IR and linear IR measurements on peptides and 1,3-cyclohexanedione support the aforementioned differences.

Simulation of the 2D IR Spectrum of Acetylproline-NH₂.

The (π/4, −π/4, π/2, 0) polarization experiment in Fig. 2b substantially improves the spectral discernability of the crosspeaks.‡ The relative crosspeak intensities also change according to Eq. 5 because of their differing angular dependencies (3). For instance, crosspeak F, which is very weak in the Abs{S̃[0,0,0,0]} spectra of Fig. 2a, has significant intensity in Fig. 2b as peak L, because the two transition dipoles involved are almost at 90°. Crosspeak G in Fig. 2a also contributes to peak L (see below). The transition dipoles that form peak H, which is not very intense in Fig. 2b, are at 35°. The signal corresponding to peak I is not visible in Fig. 2b, because the transition dipoles involved are nearly parallel (P₂ = 1).

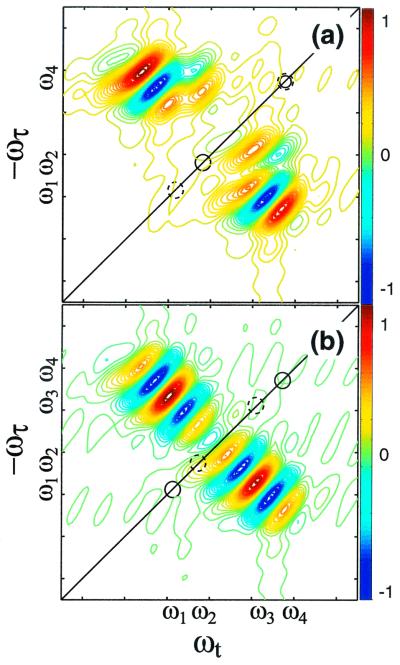
The phases of the crosspeaks also help to distinguish the different conformers. For example, peaks L and M are about 180° out-of-phase with each other in Fig. 2c, whereas peaks J and K are in-phase. Fig. 5 simulates two distributions that could arise from two sets of coupled oscillators representing two conformers. In Fig. 5a, one set has frequencies ω₁ and ω₄, the other ω₂ and ω₄, and the structures are chosen such that the angles between the transition dipoles of ω₁ and ω₄ produce a crosspeak that is twice as intense as the other with half the coupling. In the second case, Fig. 5b, the two pairs have the same intensity and coupling but different frequencies. The first case results in interference between the two sets of peaks that lead to crosspeaks that are out-of-phase above and below the diagonal; the second case gives rise to peaks that are in-phase. Clearly the conditions of Fig. 5a simulate the effects seen in the experiments for peaks L and M, whereas the conditions of Fig. 5b apply to peaks J and K.

Figure 5.

Simulation of crosspeaks for two cases when two conformers have overlapping frequencies. (a) The frequencies of the diagonal peaks are ω₁ and ω₄ (solid circles) for one set of coupled oscillators and ω₂ and ω₄ (dashed circles) for the other. The ω₁/ω₄ pair has half the coupling but twice the intensity of the ω₁/ω₄ pair. (b) The pairs of frequencies are now ω₁/ω₄ and ω₂/ω₃, and the crosspeaks have equal intensities and couplings.

The crosspeaks below the diagonal were not previously observed, nor were the amino II bands correlated with their corresponding acetyl amide I bands (3). The (π/4, −π/4, π/2, 0) measurement indicates that the lower amide II band is correlated to the higher acetyl amide I band and clarifies that two structures do indeed exist for acetylproline-NH₂ in CDCl₃. Our previous work characterized the two structures by the angles between the amino and acetyl amide I transition dipoles on opposite ends of the dipeptide. It is clear here that L and M arise from coupling between the amide I and II transition dipoles that are both located on the amino end. Thus, the peaks give local structural information. Furthermore, the structure of the amino end must differ for the two known conformations, because crosspeaks F and G yield different angles. The structure differences are likely caused by two amino group geometries, because the amide II normal mode is mostly due to NH₂ motions (3). An extended structure like C₅, observed in our previous work, and an internal hydrogen bonded structure like C₇ could account for the differences.

The Use of Polarized IR Pulses in Structure Determination.

The structural information of 2D IR comes from the angular and coupling information. The angles between transition dipoles in peptides have been measured by polarization in double resonance 2D IR and heterodyned 2D IR experiments (3, 6, 18). Usually two separate measurements are compared: one where the laser pulses have the same polarization, and another where they do not. In heterodyned and double resonance 2D IR experiments, the measurements in the two polarization conditions can be subtracted to yield difference spectra with the diagonal peaks removed (3, 6), if the molecule does not rotate. In practice, there is always some overall or internal rotation, so the method contains intrinsic uncertainties. Furthermore, it can be difficult to normalize the two spectra recorded in different polarizations, especially when the crosspeaks and diagonal peaks overlap. These difference spectra can be measured directly by using (π/3, −π/3, 0, 0) and (π/3, 0, −π/3, 0) polarizations (Table 1), without the need to normalize or collect multiple spectra, but the diagonal peaks are eliminated for spectra collected by using (π/4, −π/4, π, 0), even if the molecule rotates; rotation simply diminishes the signal. Thus the shapes and positions of the crosspeaks are made much clearer. The next step of analyzing the peaks to understand how the pieces of the structure move with respect to one another (4) is now possible.

Abbreviation

2D

two-dimensional