Abstract
Recent advances in mobile technology have created a shift towards using battery-driven devices in remote monitoring settings and smart homes. Clinicians are carrying out diagnostic and screening procedures based on the electrocardiogram (ECG) signals collected remotely for outpatients who need continuous monitoring. High-speed transmission and analysis of large recorded ECG signals are essential, especially with the increased use of battery-powered devices. Exploring low-power alternative compression methodologies that have high efficiency and that enable ECG signal collection, transmission, and analysis in a smart home or remote location is required. Compression algorithms based on adaptive linear predictors and decimation by a factor are evaluated based on compression ratio (CR), percentage root-mean-square difference (PRD), and heartbeat detection accuracy of the reconstructed ECG signal. With two databases (153 subjects), the new algorithm demonstrates the highest compression performance ( and ) and overall detection accuracy (99.90% sensitivity, 99.56% positive predictivity) over both databases. The proposed algorithm presents an advantage for the real-time transmission of ECG signals using a faster and more efficient method, which meets the growing demand for more efficient remote health monitoring.
Keywords: wearable sensors, telemedicine, digital medicine, smart healthcare, wireless systems, remote healthcare, mobile health, e-Health
1. Introduction
The World Health Organization (WHO) cites Cardiovascular Diseases (CVDs) as the number one cause of death worldwide [1]. Given the gravity of these diseases, many researchers have focused their research on cardiovascular disease and heart health. Additionally, an intense focus has been placed on studying the ways in which conventional cardiovascular diagnosis technologies can be improved for use in hospitals, clinics, and other related health care facilities. Increased efforts in this research area have led to several advances in technology for cardiac function screening and diagnostics. A variety of cardiac abnormalities are screened and assessed using a simple, risk-free and inexpensive cardiac test known as the electrocardiogram (ECG) analysis [2]. Each ECG heartbeat signal contains three prominent waves: the P wave, the QRS complex, and the T wave. The detection of these waves over a short period of time (<30 min) has been accomplished with great success and accuracy for acute screening and diagnostics [3,4,5]. Early detection of CVDs, on the other hand, necessitates long-term monitoring of ECG signals via ECG electrodes that are connected to wearable devices, mobile phones, smart clothes, and point-of-care (POC) devices in a smart home setting [6]. Devices used in remote monitoring typically rely on wireless communication and could require extensive power resources [7].
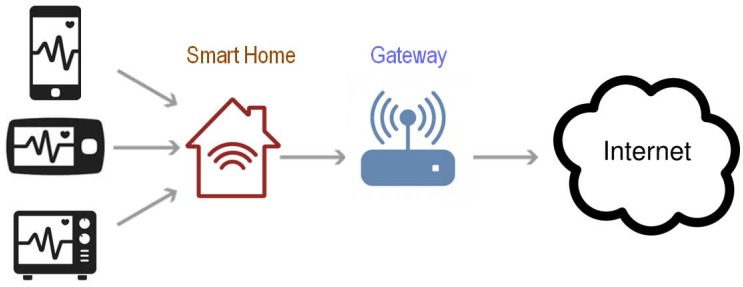
A remote system with real-time monitoring for the elderly can provide a timely alarm when patients need urgent help [6,8]. This technology may relieve some of the pressure on hospitals to monitor patients on-site. The architecture proposed in Figure 1 includes: biosensors, connected through a Bluetooth wireless technology to a unit (referred to as a gateway) that mainly interfaces the user with the healthcare center. The gateway unit can carry out signal processing and data storage before transmitting the data over the internet. A gateway can be an independent device or a personal computer. Several studies have developed smart gateways and have proposed different health care system models based on these gateways [9,10,11]. Bansal et al. [12] and Jung et al. [13] proposed health care monitoring systems that rely on mobile gateways, similar to smart phones. Spinsante and Gambi [14] and Lin et al. [15] proposed TV-based mode of home care using a WiFi set-top box as a gateway.
Figure 1.
A smart home with electrocardiogram (ECG) monitoring system.
Rahmani et al. [16] developed a smart home gateway and a corresponding monitoring system based on embedded technology, which can monitor multi-physiological signals. Although each of these methods has their own advantages, there are also some drawbacks. The mobile gateway cannot guarantee long-term and continuous measurements. The set-top-box-based system does not provide measurement of ECG signals, which is the most important physiological signal for assessing patients with cardiovascular diseases, and thus cannot offer comprehensive services for patients.
Smart homes [17,18,19] are becoming an effective solution that allows the growing number of elderly patients, as well as physically impaired patients such as the deaf and blind, to remain in the comfort of their homes with healthcare monitoring that supports their lifestyles. With several sensors, cameras, biomedical devices, and wearable health trackers installed throughout the home, the health conditions of residents can be continuously monitored. The assistance-required feature is triggered when an unusual or critical situation is detected, helping patients during emergencies. Local and remote alarms generated by the system alert the patient of critical situations, and can call healthcare service providers for help depending on how the system is programmed. A smart home can enable the elderly and people with disabilities to have full control over their living environments and perform daily activities on their own, while monitoring patient safety and well-being to reduce hazard risks. Having this level of independence improves patients’ sense of dignity and reduces costs imposed on the healthcare system [20,21].
Energy consumed in remote monitoring systems and smart homes during the transmission of biomedical signals, such as ECG signals, needs to be reduced with a proper compression method that preserves the main ECG events. Notably, there are high-performance compression lossless-based methods [22] that are very complex, require high computational resources, and thus not suitable for remote monitoring [23,24]. We have therefore developed a simple, efficient, and sufficient lossy compression method that is suitable for remote monitoring and smart homes.
2. Methods
2.1. Data Used
Training Database: All 48 ECG recordings from the MIT-BIH arrhythmia database were used in the training phase, totaling 109,984 heartbeats [25]. The MIT-BIH database is widely used to evaluate the performance of ECG compression methods and QRS detection algorithms as it contains different types of noise and various QRS morphologies [26]. The annotations of R peaks are provided within each ECG recording.
Testing Database: All 105 ECG recordings from the QT database were used in the testing phase, totaling 111,301 heartbeats [27] for evaluation of the performance of our proposed compression algorithm.
2.2. Benchmark Method I: Adaptive Linear Prediction
In the literature, researchers have used forward-prediction based approaches to detect QRS complexes in ECG signals [28,29,30]. Typically, the use of linear forward prediction is for the estimation of the current ECG sample n based on its past m samples:
| (1) |
where is the output of estimating , represents the predictor coefficients, and is the prediction error that is calculated as follows:
| (2) |
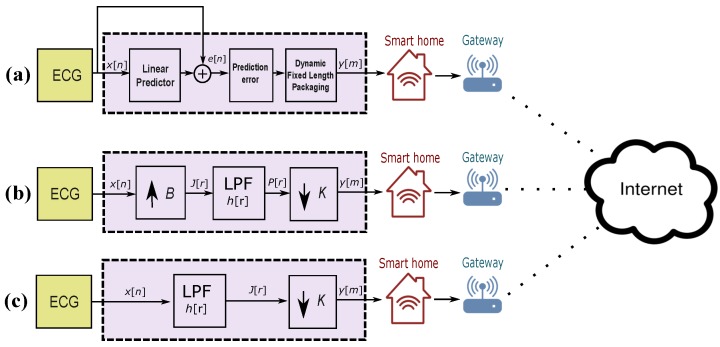
The schematic representation of Method I is shown in Figure 2a. The prediction error signal is used to detect QRS complexes instead of using the ECG signal itself. For consistency and easy comparison between methods, we have used the variable h to refer to the impulse response in this paper.
Figure 2.
Schematic diagram of ECG compression methods. (a) benchmark lossless method I (b) benchmark lossy method II (c) proposed lossy method III.
2.3. Benchmark Compression Method II: Decimating by a Factor
Method II converts the sampling rate by interpolation factor of B, followed by a decimating factor of K [31,32]. Figure 2b illustrates the idea of decimation by factor . The interpolation step can be expressed as follows:
| (3) |
Then, the output signal passes through low-pass filter (LPF) as follows:
| (4) |
Then, the output signal of the decimator is
| (5) |
where m is the data samples of the compressed ECG signals. In this paper, r refers to the ECG sample point generated after the filtering step while m refers to the compressed ECG sample point.
2.4. Proposed Compression Method III: Decimating by Factor K
The decimator is an improved version of a downsampler as it avoids aliasing (defined as reconstructing a signal that is completely distorted and does not include the original signal main events [31]). The first step of the decimator is to reduce the bandwidth of to , which is equivalent to in frequency domain, and then downsample by K. The block diagram of decimation is shown in Figure 2c. The ECG signal is passed through an LPF, characterized by the impulse response and frequency response , which satisfies the following:
| (6) |
Therefore, the LPF eliminates the spectrum of in the range . In other words, only the frequency components of within the range will be downsampled. The output of the LPF can be written as follows:
| (7) |
Thus, the output signal of the decimator is:
| (8) |
Given that the LPF operation on is linear and time invariant, the combination of LPF with the downsampler produces a time-variant system. Thus, decimation is suitable for analysis of the ECG signal, as it is a time-varying signal.
We have one variable K to compress the ECG signal to K. An optimization step is needed to determine the optimal value for K. We have three objective functions: , , and to be optimized simultaneously, as follows:
| (9) |
where g is the F-score (the harmonic mean of sensitivity and positive predictivity). The optimization process is time-consuming at the training phase, but once it is achieved, the optimal parameter K will be used as is in the implementation phase.
2.5. QRS Detection
In this paper, a QRS detector is needed to evaluate the compression performance. To our knowledge, the recently published QRS detection algorithm [3,26] is the most reliable as it was tested on 11 different ECG databases, making it an efficient algorithm. The QRS detector in [26] was validated multiple times in the literature, and it is called the two-event-related moving averages (TERMA) algorithm [33]. The TERMA-based QRS detector is fast, reliable, and efficient, and better-suited for remote monitoring and battery-operated mobile devices [3,26,33]. Therefore, TERMA-based QRS detectors are used in combination with Method III to improve the overall ECG signal analysis, reduce memory capacity, and improve signal transmission as recommended in [22].
The function of a TERMA-based QRS detector [33] has five inputs: starting frequency (), end frequency (), first window size (), second window size (), and rejection threshold (). The processing flow of TERMA begins by passing an ECG signal through a third-order Butterworth – bandpass filter. The output signal is then squared, followed by two moving averages (with two window sizes and ), and then applying threshold is applied for blocks of interest generation. The optimization phase of TERMA is discussed in [26], and the optimal value for these five parameters is found to be Hz, Hz, ms, ms, and . Therefore, we use a TERMA-based QRS detector with these optimized values.
The TERMA-based QRS detector is applied after compressing ECG signals using Method III. The lossless benchmark in Method I has it is own QRS detector that begins by removing high-frequency noise from the prediction error signal. Then, it passes the output signal to a Savtizky–Golay filter to smooth the signal with a window of size W and a polynomial of order O, treating the QRS detection as a least-squares problem. Method II uses a TERMA-based QRS detector as in Method III.
2.6. Compression Ratio
The bit compression ratio (BCR) was calculated as follows:
| (10) |
where and refer to the bit widths of compressed and uncompressed samples, respectively.
3. Results and Discussion
The MIT-BIH arrhythmia database is used for evaluating all compression algorithms. This benchmark database contains 48 ECG recordings, each of which is 30 min in length. The ECG signals have 11-bit resolution over 10 mV and are sampled at 360 Hz.
For the evaluation of all compression methods, two statistical measures are used, sensitivity () and positive predictivity (), which are calculated as follows:
| (11) |
| (12) |
The benchmark lossless Method I uses two parameters during the process of compression and detection of QRS complexes: W and q. The optimal values for W and q are determined in [30]; after applying Pareto optimization, W ranged from 3 to 6 and q ranged from 9 to 17. It was found that optimal values are and .
The benchmark lossy Method II also uses two parameters B and K. The optimization process is determined in [22], where the value of B varies from Hz to Hz, and the value of K varies from Hz to Hz. The optimal value of Hz and the optimal value of Hz.
The proposed lossy Method III uses only one parameter, K. The optimization process was carried out using the training database (MIT-BIH Arrhythmia database) and the value of K varied from Hz to Hz. The optimal value of K was found to be 60 Hz, as shown in Table 1. Then, the value of was used on the testing database (QT database). Note that researchers can use the optimal value for compressing any ECG signals, and there is no need to redo the optimization phase again unless a certain abnormality or noise is investigated.
Table 1.
Determining the optimal K value for Method III based on the QRS detection accuracy. Results were sorted in descending order according to the K value. stands for true positives (QRS complexes detected as QRS complexes), stands for false negatives (QRS complexes that have not been detected), stands for false positives (non-QRS complexes detected as QRS complexes), stands for sensitivity, stands for positive predictivity, and g is the F-score.
| K | No. Beats | TP | FP | FN | SE | PP | g |
|---|---|---|---|---|---|---|---|
| 360 | 109,985 | 109,742 | 126 | 250 | 99.78 | 99.87 | 99.83 |
| 180 | 109,985 | 109,756 | 144 | 236 | 99.79 | 99.85 | 99.83 |
| 120 | 109,985 | 109,786 | 167 | 223 | 99.80 | 99.83 | 99.82 |
| 90 | 109,985 | 109,788 | 204 | 212 | 99.81 | 99.79 | 99.81 |
| 72 | 109,985 | 109,786 | 259 | 219 | 99.80 | 99.73 | 99.78 |
| 60 | 109,985 | 109,818 | 196 | 208 | 99.81 | 99.80 | 99.82 |
| 51 | 109,985 | 109,867 | 252 | 197 | 99.83 | 99.75 | 99.80 |
| 45 | 109,985 | 109,800 | 217 | 222 | 99.80 | 99.78 | 99.80 |
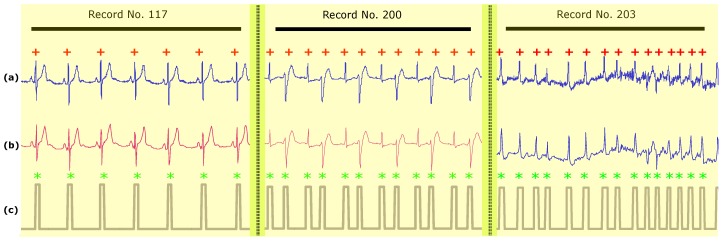
The QRS detection results of all ECG recordings using Method III with are shown in Table 2. Figure 3 shows the performance of Method III under different conditions from Record 117, Record 200, and Record 203. The upper plots (a) for each recording show the original ECG signal. The middle plots (b) show the compressed ECG signal for each recording using Method III. The bottom plots (c) show the result for each recording of the two-event-related moving-average(TERMA)-based QRS detector based on the compressed signals shown in the second row signals (b). Figure 3 (Record 117) shows the performance of the QRS detector on a compressed ECG signal using Method III over T waves with large amplitudes. Method III succeeded in detecting irregular beats, as shown in Figure 3 (Record 201) and detecting beats in the presence of noise and baseline wandering, as shown in Figure 3 (Record 203).
Table 2.
Performance of the proposed compression of Method III using the MIT-BIH Arrhythmia Database. The results were obtained using the optimal value of Hz. stands for true positives (QRS complexes detected as QRS complexes), stands for false negatives (QRS complexes that have not been detected), stands for false positives (non-QRS complexes detected as QRS complexes), stands for sensitivity, and stands for positive predictivity.
| Record | No. of Beats | TP | FP | FN | SE(%) | +P(%) | g(%) |
|---|---|---|---|---|---|---|---|
| 100 | 2274 | 2274 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 101 | 1866 | 1866 | 3 | 0 | 100.00 | 99.84 | 99.92 |
| 102 | 2187 | 2187 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 103 | 2084 | 2084 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 104 | 2229 | 2231 | 27 | 0 | 100.00 | 98.80 | 99.40 |
| 105 | 2602 | 2602 | 5 | 0 | 100.00 | 99.81 | 99.90 |
| 106 | 2026 | 2025 | 4 | 1 | 99.95 | 99.80 | 99.88 |
| 107 | 2136 | 2137 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 108 | 1763 | 1791 | 42 | 2 | 99.89 | 97.71 | 98.79 |
| 109 | 2533 | 2533 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 111 | 2123 | 2123 | 3 | 0 | 100.00 | 99.86 | 99.93 |
| 112 | 2539 | 2539 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 113 | 1794 | 1794 | 3 | 0 | 100.00 | 99.83 | 99.92 |
| 114 | 1890 | 1881 | 9 | 9 | 99.52 | 99.52 | 99.52 |
| 115 | 1953 | 1953 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 116 | 2395 | 2395 | 1 | 0 | 100.00 | 99.96 | 99.98 |
| 117 | 1535 | 1535 | 1 | 0 | 100.00 | 99.93 | 99.97 |
| 118 | 2278 | 2278 | 1 | 0 | 100.00 | 99.96 | 99.98 |
| 119 | 1988 | 1988 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 121 | 1863 | 1863 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 122 | 2476 | 2476 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 123 | 1519 | 1519 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 124 | 1619 | 1619 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 200 | 2601 | 2601 | 6 | 0 | 100.00 | 99.77 | 99.88 |
| 201 | 1949 | 1949 | 13 | 0 | 100.00 | 99.34 | 99.67 |
| 202 | 2138 | 2133 | 0 | 5 | 99.77 | 100.00 | 99.88 |
| 203 | 2988 | 2979 | 10 | 11 | 99.63 | 99.67 | 99.65 |
| 205 | 2656 | 2655 | 0 | 1 | 99.96 | 100.00 | 99.98 |
| 207 | 2324 | 2163 | 3 | 167 | 92.83 | 99.86 | 96.22 |
| 208 | 2953 | 2947 | 0 | 6 | 99.80 | 100.00 | 99.90 |
| 209 | 3006 | 3006 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 210 | 2652 | 2650 | 1 | 2 | 99.92 | 99.96 | 99.94 |
| 212 | 2748 | 2748 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 213 | 3250 | 3249 | 0 | 1 | 99.97 | 100.00 | 99.98 |
| 214 | 2262 | 2260 | 1 | 2 | 99.91 | 99.96 | 99.93 |
| 215 | 3362 | 3362 | 1 | 0 | 100.00 | 99.97 | 99.99 |
| 217 | 2208 | 2208 | 1 | 0 | 100.00 | 99.95 | 99.98 |
| 219 | 2154 | 2154 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 220 | 2048 | 2048 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 221 | 2427 | 2427 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 222 | 2485 | 2485 | 4 | 0 | 100.00 | 99.84 | 99.92 |
| 223 | 2604 | 2604 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 228 | 2060 | 2059 | 39 | 1 | 99.95 | 98.14 | 99.04 |
| 230 | 2256 | 2256 | 1 | 0 | 100.00 | 99.96 | 99.98 |
| 231 | 1571 | 1571 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| 232 | 1783 | 1783 | 14 | 0 | 100.00 | 99.22 | 99.61 |
| 233 | 3077 | 3077 | 1 | 0 | 100.00 | 99.97 | 99.98 |
| 234 | 2751 | 2751 | 2 | 0 | 100.00 | 99.93 | 99.96 |
| 48 Records | 109,985 | 109,818 | 196 | 208 | 99.81 | 99.80 | 99.81 |
Figure 3.
Heartbeat (QRS complex) detection over Records 117, 200, and 203 of the MIT-BIH Arrhythmia Database. (a) raw ECG signal (b) compressed ECG signal using Method III (c) compressed ECG signal using Method III. Record 117 contains regular beats with large T waves, Record 200 contains irregular beats (specifically premature ventricular contractions), and Record 203 contains severe baseline drift and noise. The y-axis represents manipulated signal amplitudes. Here, the red + represents the annotated R peak based on the MIT-BIH Arrhythmia Database while the green * represents the detected R peak using the two-event-related-moving-average(TERMA)-based QRS detector.
The QRS detection performance of the proposed compression methods and well-known QRS detectors is shown in Table 3. As shown, Method III (along with a TERMA-based QRS detector) outperformed most of the well-known algorithms, such as Hamilton and Tompkins [34], Poli et al. [35], Afonso et al. [36], Martínez et al. [37], Chen et al. [38], Ieong et al. [39], and Nallathambi and Principe [40]. Interestingly, Method III scored identical results as the multiscale morphology technique, which is highly computationally complex. In contrast, the proposed Method III is simple, faster, and more efficient, more suitable for smart homes and remote monitoring. Method III outperformed Method I and provided similar (though slightly lower) results to Method II.
Table 3.
Performance of QRS detectors on the MIT-BIH Arrhythmia Database. SE stands for sensitivity, while +P stands for positive predictivity. N/R stands for Not Reported.
| Ref. | Method | (%) | (%) |
|---|---|---|---|
| Hamilton and Tompkins [34] | Band-pass filter/Search-back | 99.69 | 99.77 |
| Poli et al. [35] | Genetic Algorithm | 99.60 | 99.51 |
| Afonso et al. [36] | Filter Banks | 99.59 | 99.56 |
| Martínez et al. [37] | Wavelet Delineation | 99.66 | 99.56 |
| Chen et al. [38] | Wavelet De-noising | 99.55 | 99.49 |
| Zhang and Lian [41] | Multiscale Morphology | 99.81 | 99.80 |
| Ieong et al. [39] | Quadratic Spline wavelet | 99.31 | 99.70 |
| Nallathambi and Principe [40] | Pulse Train | 99.58 | 99.55 |
| Method I | Adaptive Predictor | 99.64 | 99.81 |
| Method II | Decimating By A Factor | 99.78 | 99.92 |
| Method III | Decimating By A Factor K | 99.81 | 99.80 |
Table 4 compares the performance of Methods I, II, and III with other compression schemes implemented for remote monitoring. Method III scored the highest BCR at 6 with low PRD of 1.88 over the whole MIT-BIH Arrhythmia Database, outperforming existing well-known compression methods. Note that Method III outperformed the delta predictor/Rice–Golomb coding [42], adaptive predictor/Huffman coding [43], simple predictor/Huffman coding [44], slope predictor/fixed-length packaging methods [45], Compressive Sensing [46], Nonuniform Binary Matrices [47], and Encoding with Modified Thresholding [48], as well as Method I and Method II.
Table 4.
Performance comparison of compression methods. BCR stands for bit compression ratio, PRD stands for percentage root-mean-square difference, N/R stands for Not Reported, and the symbol ≈ means nearly equal.
| Compression Type | Method | Year | No. Records Used | BCR | PRD | Ref. |
|---|---|---|---|---|---|---|
| Simple Predictor/Huffman Coding | 2009 | N/R | 1.92 | ≈0 | [44] | |
| Delta Predictor/Rice Golomb Coding | 2011 | N/R | 2.38 | ≈0 | [42] | |
| Lossless | Adaptive Predictor/Huffman Coding | 2013 | N/R | 2.43 | ≈0 | [43] |
| Slope Predictor/Fixed-length Packaging | 2013 | N/R | 2.25 | ≈0 | [45] | |
| Method I | 2015 | All records in MIT-BIH Arrhythmia DB | 2.28 | ≈0 | [30] | |
| Simultaneous Orthogonal Matching Pursuit | 2011 | One record from MIT-BIH Arrhythmia DB | 7.23 | 2.57 | [50] | |
| Compressive Sensing | 2011 | All records in MIT-BIH Arrhythmia DB | 3.44 | 9 | [46] | |
| Wavelet Transform | 2012 | 10 records from MIT-BIH Arrhythmia DB | 4.0 | 1.66 | [51] | |
| Nonuniform Binary Matrices | 2012 | N/R | 5.0 | 8.58 | [47] | |
| Compressive Sensing | 2012 | 3 records from MIT-BIH Arrhythmia DB | 2.5 | 2.6 | [52] | |
| Lossy | Encoding with Modified Thresholding | 2013 | 4 records from MIT-BIH Arrhythmia DB | 5.4 | 2.7 | [48] |
| Compressive Sampling | 2013 | One record from MIT-BIH Arrhythmia DB | 2.5 | 9 | [53] | |
| Compressive Sensing | 2015 | 11 records from MIT-BIH Arrhythmia DB | 6.4 | 3.75 | [49] | |
| Method II | 2017 | All records from MIT-BIH Arrhythmia DB | 4.5 | 0.53 | [22] | |
| Method III | 2017 | All records in MIT-BIH Arrhythmia DB | 6 | 1.88 | – |
On the other hand, Method III scored a BCR similar to the Compressive Sensing method [49]; however, Method III scored a lower PRD of 1.88, which makes it superior. The only method that may compete with Method III is the Simultaneous Orthogonal Matching Pursuit [50]; however, these results were based on only one record from the MIT-BIH database, unlike Method III, which was validated over the entire database.
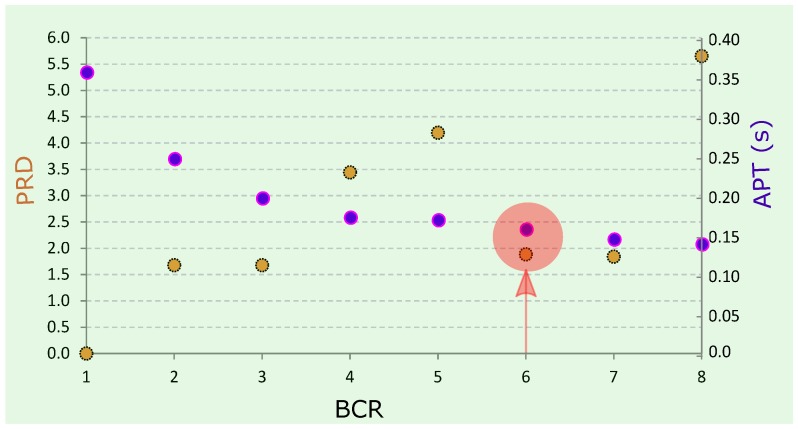
In this work, the proposed Method III along with the TERMA-based QRS detector were implemented in MATLAB 2012a (MathWorks, Inc., Natick, MA, USA) on an Intel ™ i5 CPU with 2.27 GHz (Santa Clara, California, United States). Figure 4 shows the BCR versus PRD and the average processing time (APT) for a TERMA-based QRS detector. As expected, the APT decreased as the BCR increased. The TERMA-based detector took an APT of 0.15 s to achieve a BCR of 6. The compression of Method III took an APT of 0.10 s to compress Record 100 from the MIT-BIH Arrhythmia database.
Figure 4.
Performance of proposed Method III. Here, BCR stands for bit compression ratio, PRD stands for percentage root-mean-square difference, and APT stands for average processing time. The red arrow shows the optimal combination of BCR, APT, and PRD.
3.1. Methods Implementation
To date, researchers have focused only on the ECG lossless compression methods, as seen in Method I. The lossless compression methodology tries to achieve a PRD of value 0. However, the lossy methods have no yet been investigated as extensively as the lossless methods [22]. We have therefore developed Method III to improve the CR of the lossy method that was recently published in [22].
Method I uses the prediction error signal to detect the QRS complexes in ECG signals. Method II and Method III detect the QRS complexes from the filtered ECG signal, and therefore they do not need a linear predictor. The advantage of using the prediction error signal is its low amplitude values and its center around zero amplitude, except for the QRS complex areas. However, a lossless coding step is required to preserve the main events within ECG signals. It is known that the use of lossless coding scheme would affect the signal quality and increase consumption of energy and computational resources.
The CR (downsampling factor) in Method III ranges from 1 to 8. If we downsample by a factor greater than 8, then the corresponding frequency band will be ≤40 Hz. In other words, if the downsampling factor is 9, then the corresponding sampling frequency is 40 Hz (the original sampling frequency of the ECG signals is 360 Hz). When applying the bandpass filter of the QRS detection algorithm, there will be an error, as the cutoff frequencies must be within the interval of 0–1. For example, the QRS detection algorithm uses Hz. If the factor is 9, then the sampling frequency will be 40 Hz; if the cutoff frequency is , then it will equal exactly one, which the filter will fail to implement. Therefore, the maximum factoring for Method III is 8. In other words, the sampling frequency of ECG signals is recommended to be greater than or equal to 40 Hz.
Method II was developed to compress ECG signals and focused on achieving a high QRS detection rate and a high PRD. In comparison, Method III was developed to focus on increasing the CR with a strong emphasis on the QRS detection method, rather than emphasizing the PRD method. The main objective of Method III was to create a method that could be applied to smart homes and remote monitoring, where long-term (over several days) ECG signals need to be collected in a fast and efficient manner. In other words, if we have the computational resources, and the ECG processing speed is not crucial, then Method II can be used; otherwise, Method III needs to be used to achieve high processing speeds.
3.2. Method Performance
The comparison of the compression performance of Methods I, II, and III with well-known compression techniques can be seen in Table 4. There are more compression techniques that achieve higher BCR, but these techniques are not suitable for low-power wearable applications [54,55], and are therefore not included in the table. Note that low complexity compression algorithms that achieve high BCR result in energy savings for both the compression process and the wireless transmission [46]. The overall energy consumption is more efficient when compared to transmitting the original signal with more complex algorithms [56,57,58].
Method III achieved a BCR of 6 without the need for linear predictor, coding, or packaging. The compression performance of Method III is substantially higher than all the algorithms, especially when the value PRD is considered. Moreover, applying the TERMA-based QRS detector validates the proposed Method III based on QRS detection accuracy. This step is crucial for developing a compression methodology for smart homes and remote monitoring applications.
Most of the published ECG compression methods are typically not validated by a QRS detection step, which makes it more difficult to assess compression quality. Method III succeeds in preserving the main features of the ECG signal morphology given its lossy nature, as shown in Figure 3. It is clear that Method III is a fast, efficient, and sufficient technique for remote monitoring.
The performance of different QRS detectors published in the literature is shown in Table 2. Unfortunately, some researchers have excluded records from the MIT-BIH arrhythmia database due to noise or arrhythmia, and, consequently, their algorithms appear to achieve higher performance levels. Other researchers have excluded specific segments from each recording [37,59]. In contrast, we tested the TERMA-based QRS detector over the output of Method III without excluding any records or segments making the results more robust and meaningful [3].
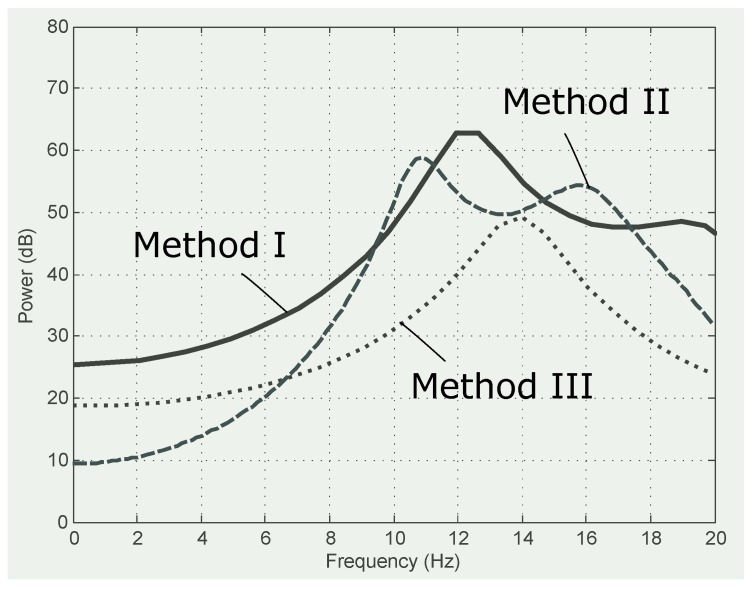
Figure 5 shows that Method III smooths the frequencies with a power spectrum capturing the main frequencies in the range of 10 Hz to 18 Hz. This observation confirms the findings in [26,60,61,62]. Method II also enhances the ECG frequencies, creating a bimodal distribution and improving the frequency spectra of Method I.
Figure 5.
Comparison of power spectra for compression methods. The first 60 s of Record 100 from the MIT-BIH Arrhythmia Database.
The detection performance of Method III on the QT database on a record-by-record basis is shown in Table 5, while Table 6 shows the overall comparison of our results with the existing QRS detection algorithms on the QT database. The performance of each algorithm was reported in terms of number of beats, SE, and +P. The proposed algorithm performed higher in terms of SE and +P when compared to Pan–Tompkins [26] and Elgendi [26] over the same number of beats. Moreover, Method III scored an overall performance similar to Method II with a higher compression rate () when compared to the recently published Method II. We applied Method III to the QT database without changing the value of any parameter and without re-training the algorithm. It is clear that the results of Method III are promising (with the fixed parameter Hz) and can be applied over different databases with different sampling frequencies.
Table 5.
Performance of Method III using Hz on the QT Database. The stands for true positives (the number of QRS complexes detected as QRS complexes), stands for false negatives (the number of QRS complexes that have not been detected), stands for the number of false positives (non-QRS complexes detected as QRS complexes), stands for sensitivity, and stands for positive predictivity.
| Record | No. of Beats | TP | FP | FN | SE(%) | +P(%) |
|---|---|---|---|---|---|---|
| 100 | 1134 | 1134 | 0 | 0 | 100.00 | 100.00 |
| 102 | 1088 | 1088 | 0 | 0 | 100.00 | 100.00 |
| 103 | 1048 | 1048 | 0 | 0 | 100.00 | 100.00 |
| 104 | 1109 | 1118 | 0 | 0 | 100.00 | 100.00 |
| 114 | 867 | 866 | 3 | 1 | 99.88 | 99.65 |
| 116 | 1186 | 1186 | 0 | 0 | 100.00 | 100.00 |
| 117 | 766 | 766 | 0 | 0 | 100.00 | 100.00 |
| 123 | 756 | 756 | 0 | 0 | 100.00 | 100.00 |
| 213 | 1641 | 1641 | 0 | 0 | 100.00 | 100.00 |
| 221 | 1247 | 1247 | 1 | 0 | 100.00 | 99.92 |
| 223 | 1309 | 1309 | 0 | 0 | 100.00 | 100.00 |
| 230 | 1077 | 1077 | 0 | 0 | 100.00 | 100.00 |
| 231 | 732 | 732 | 0 | 0 | 100.00 | 100.00 |
| 232 | 866 | 866 | 2 | 0 | 100.00 | 99.77 |
| 233 | 1532 | 1532 | 0 | 0 | 100.00 | 100.00 |
| 301 | 1352 | 1352 | 0 | 0 | 100.00 | 100.00 |
| 302 | 1501 | 1501 | 0 | 0 | 100.00 | 100.00 |
| 306 | 1040 | 1040 | 0 | 0 | 100.00 | 100.00 |
| 307 | 853 | 853 | 0 | 0 | 100.00 | 100.00 |
| 308 | 1294 | 1294 | 3 | 0 | 100.00 | 99.77 |
| 310 | 2012 | 2012 | 0 | 0 | 100.00 | 100.00 |
| 803 | 1026 | 1026 | 0 | 0 | 100.00 | 100.00 |
| 808 | 903 | 903 | 5 | 0 | 100.00 | 99.45 |
| 811 | 704 | 704 | 0 | 0 | 100.00 | 100.00 |
| 820 | 1159 | 1159 | 0 | 0 | 100.00 | 100.00 |
| 821 | 1557 | 1557 | 0 | 0 | 100.00 | 100.00 |
| 840 | 1180 | 1180 | 0 | 0 | 100.00 | 100.00 |
| 847 | 803 | 801 | 8 | 2 | 99.75 | 99.01 |
| 853 | 1113 | 1113 | 0 | 0 | 100.00 | 100.00 |
| 871 | 917 | 917 | 1 | 0 | 100.00 | 99.89 |
| 872 | 990 | 990 | 0 | 0 | 100.00 | 100.00 |
| 873 | 859 | 859 | 0 | 0 | 100.00 | 100.00 |
| 883 | 892 | 892 | 0 | 0 | 100.00 | 100.00 |
| 891 | 1267 | 1267 | 0 | 0 | 100.00 | 100.00 |
| 16265 | 1031 | 1031 | 0 | 0 | 100.00 | 100.00 |
| 16272 | 851 | 851 | 0 | 0 | 100.00 | 100.00 |
| 16273 | 1112 | 1112 | 0 | 0 | 100.00 | 100.00 |
| 16420 | 1063 | 1063 | 0 | 0 | 100.00 | 100.00 |
| 16483 | 1087 | 1087 | 0 | 0 | 100.00 | 100.00 |
| 16539 | 922 | 922 | 0 | 0 | 100.00 | 100.00 |
| 16773 | 1008 | 1008 | 0 | 0 | 100.00 | 100.00 |
| 16786 | 925 | 925 | 0 | 0 | 100.00 | 100.00 |
| 16795 | 761 | 761 | 0 | 0 | 100.00 | 100.00 |
| 17453 | 1047 | 1047 | 0 | 0 | 100.00 | 100.00 |
| 104 | 804 | 804 | 0 | 0 | 100.00 | 100.00 |
| 106 | 897 | 897 | 17 | 0 | 100.00 | 98.14 |
| 107 | 823 | 822 | 25 | 1 | 99.88 | 97.05 |
| 110 | 872 | 872 | 15 | 0 | 100.00 | 98.31 |
| 111 | 908 | 907 | 161 | 1 | 99.89 | 84.93 |
| 112 | 684 | 684 | 12 | 0 | 100.00 | 98.28 |
| 114 | 698 | 698 | 1 | 0 | 100.00 | 99.86 |
| 116 | 560 | 560 | 16 | 0 | 100.00 | 97.22 |
| 121 | 1434 | 1434 | 2 | 0 | 100.00 | 99.86 |
| 122 | 1414 | 1414 | 0 | 0 | 100.00 | 100.00 |
| 124 | 1121 | 1121 | 0 | 0 | 100.00 | 100.00 |
| 126 | 945 | 945 | 0 | 0 | 100.00 | 100.00 |
| 129 | 672 | 671 | 184 | 1 | 99.85 | 78.48 |
| 133 | 840 | 838 | 2 | 2 | 99.76 | 99.76 |
| 136 | 810 | 810 | 0 | 0 | 100.00 | 100.00 |
| 166 | 813 | 813 | 4 | 0 | 100.00 | 99.51 |
| 170 | 897 | 897 | 0 | 0 | 100.00 | 100.00 |
| 203 | 1246 | 1246 | 1 | 0 | 100.00 | 99.92 |
| 210 | 1063 | 1063 | 5 | 0 | 100.00 | 99.53 |
| 211 | 1575 | 1575 | 0 | 0 | 100.00 | 100.00 |
| 303 | 1045 | 1045 | 0 | 0 | 100.00 | 100.00 |
| 405 | 1216 | 1216 | 0 | 0 | 100.00 | 100.00 |
| 406 | 959 | 959 | 3 | 0 | 100.00 | 99.69 |
| 409 | 1737 | 1737 | 0 | 0 | 100.00 | 100.00 |
| 411 | 1202 | 1202 | 0 | 0 | 100.00 | 100.00 |
| 509 | 1028 | 1028 | 0 | 0 | 100.00 | 100.00 |
| 603 | 869 | 869 | 0 | 0 | 100.00 | 100.00 |
| 604 | 1031 | 1031 | 1 | 0 | 100.00 | 99.90 |
| 606 | 1442 | 1442 | 0 | 0 | 100.00 | 100.00 |
| 607 | 1184 | 1184 | 0 | 0 | 100.00 | 100.00 |
| 609 | 1127 | 1127 | 0 | 0 | 100.00 | 100.00 |
| 612 | 751 | 751 | 1 | 0 | 100.00 | 99.87 |
| 704 | 1094 | 1094 | 0 | 0 | 100.00 | 100.00 |
| 30 | 1018 | 1018 | 4 | 0 | 100.00 | 99.61 |
| 31 | 1087 | 1087 | 0 | 0 | 100.00 | 100.00 |
| 32 | 1196 | 1197 | 2 | 0 | 100.00 | 99.83 |
| 33 | 527 | 527 | 0 | 0 | 100.00 | 100.00 |
| 34 | 897 | 897 | 0 | 0 | 100.00 | 100.00 |
| 35 | 882 | 882 | 101 | 0 | 100.00 | 89.73 |
| 36 | 948 | 948 | 1 | 0 | 100.00 | 99.89 |
| 37 | 682 | 682 | 62 | 0 | 100.00 | 91.67 |
| 38 | 1563 | 1563 | 0 | 0 | 100.00 | 100.00 |
| 39 | 1171 | 1171 | 3 | 0 | 100.00 | 99.74 |
| 40 | 1069 | 1069 | 1 | 0 | 100.00 | 99.91 |
| 41 | 1366 | 1366 | 0 | 0 | 100.00 | 100.00 |
| 42 | 1247 | 1247 | 0 | 0 | 100.00 | 100.00 |
| 43 | 1430 | 1430 | 0 | 0 | 100.00 | 100.00 |
| 44 | 1337 | 1340 | 6 | 0 | 100.00 | 99.55 |
| 45 | 971 | 971 | 0 | 0 | 100.00 | 100.00 |
| 46 | 856 | 856 | 1 | 0 | 100.00 | 99.88 |
| 47 | 886 | 886 | 0 | 0 | 100.00 | 100.00 |
| 48 | 1398 | 1398 | 0 | 0 | 100.00 | 100.00 |
| 49 | 833 | 833 | 2 | 0 | 100.00 | 99.76 |
| 50 | 661 | 661 | 0 | 0 | 100.00 | 100.00 |
| 51 | 749 | 749 | 0 | 0 | 100.00 | 100.00 |
| 52 | 1411 | 1411 | 0 | 0 | 100.00 | 100.00 |
| 17152 | 1628 | 1628 | 0 | 0 | 100.00 | 100.00 |
| 14046 | 1260 | 1260 | 0 | 0 | 100.00 | 100.00 |
| 14157 | 1081 | 1081 | 0 | 0 | 100.00 | 100.00 |
| 14172 | 663 | 663 | 0 | 0 | 100.00 | 100.00 |
| 15814 | 1036 | 1036 | 0 | 0 | 100.00 | 100.00 |
| 105 Records | 111,201 | 111,206 | 656 | 8 | 99.99 | 99.31 |
Table 6.
Comparison of the QRS detection with other published algorithms on the QT database. SE stands for sensitivity, while +P stands for positive predictivity.
Method III scored a BCR of 6, whereas Method II scored a BCR of 4.5, demonstrating that Method III outperformed Method II given the fact that Method III does not require the upsampling step as seen in Method II. Method III provided reconstructed ECG signals that were as informative as the reconstructed ECG signals in Method II. The accuracy of detecting QRS using Method III was more balanced in terms of SE and +P; additionally, Method III achieved an SE of 99.81% and a +P of 99.80%, while Method II achieved an SE of 99.78% and a +P of 99.92%.
It is known that more complex algorithms consume more energy and take more time, when compared to simpler algorithms [63,64]. Our results demonstrate that Method III took only 0.08 s on average to process one 30-min ECG recording, while Method II took 0.157 s. In other words, Method III took less than half of the processing time when compared to Method II. Thus, we can conclude that Method III consumes half of the power. Objectively, if we only look at the algorithm complexity, the time complexity of Method III is an algorithm, which is less than the algorithm complexity of Method II [] and Method I [)].
One of our next steps is to test Method III in a wireless healthcare system to confirm the findings. Given the fact that we implemented the algorithm on Matlab, the results are promising and give an approximation of real-world application. Mamaghanian et al. [46] found that the processing time of compression method provided by the TI MSP430 microcontroller and the CC2420 radio chip-set, which operates on a Li-ion battery, is close to the processing time estimated by Matlab.
3.3. Smart Homes
This proposed lossy algorithm aims at developing a smart home solution based on ECG signals that is environmentally friendly, maintains and enhances occupant lifestyles, and cares for users both physiologically and psychologically. There are several technical challenges that exist in remote monitoring, health, wellness, and home operations. Through this paper, we investigate the possibility of overcoming the technical challenges associated with transmitting and processing ECG signals as part of a smart home system.
To provide a long-range remote monitoring, several gateway devices can be deployed to interface with the existing wireless systems in healthcare [65]. These gateway devices will mainly be used to provide communications between the sensor unit and the remote computers or mobile devices [8]. Two scenarios can be considered:
Scenario 1: The lossy compression method is applied on the sensor unit and the analysis of ECG signals such QRS detection can be implemented on the gateway(s) or the processing unit (computers, internet, etc.). This will depend on the gateway computational capability in terms of processing and memory.
Scenario 2: The lossy compression method is applied on the gateway unit and the analysis of ECG signals such QRS detection can be implemented on the processing unit (computers, internet, etc.).
We believe that the key to establishing a smart home system lies in developing and enabling hybrid technologies that are user-friendly, affordable, and allow for a seamless transition as new technologies evolve, such as cloud computing, the Internet of Things, 5G wireless networking, and sensor networks. Such an integrated system can augment current healthcare methods and empower healthcare professionals and patients with an advanced personalized smart home for continuous monitoring, quality diagnosis and prognosis, and assessment of rehabilitation efficacy for better treatment, well-being, and smart care. The proposed ECG compression algorithm will facilitate health care cost reduction, early release from hospitals, quality patient care through continuous monitoring, reduced pressure on health care providers, and accessibility to care for underserved populations in remote areas.
3.4. Global Health
Method III potentially plays a major role in the development of ECG-based point-of-care technologies to assist in the prediction and diagnosis of diseases in low- and middle-income countries (LMICs). It is known that LMICs struggle to attain high quality and universally accessible healthcare. Many factors need to be considered when developing robust medical monitoring technologies, one of the most important parts being data collection and transmission. A framework was created to standardize the way of tackling this issue in [66], and Method III achieves all the requirements of the global health framework in [66]: simplicity, mining, connecting, reliability, affordability, and scalability. Simpler algorithms that achieve the same or even higher accuracy than complex algorithms are necessary for global health application [66].
In LMICs, mobile network penetration has reached 89% [66], and, consequently, the use of mobile devices in these countries has increased. This gives researchers an opportunity to collect ECG signals using mobile phones as a gateway for transmitting ECG data. Some analysis can be done locally on point-of-care devices, phones, and wearable devices before transmission; however, this step requires a large amount of energy. Investigating efficient ECG compression methods for local analysis and transmission is valuable in these scenarios.
4. Conclusions
We discuss in this paper the lossy compression Method III, which is suitable for remote health monitoring systems. The proposed Method III is validated with QRS detection and is scalable for smart homes, wearable devices, and point-of-care devices. It can provide long-term and continuous monitoring for the elderly and other patients whose mobility and access to healthcare is limited. Given the considerable data collection, transmission, and analysis involved in the monitoring process, Method III achieves a compression ratio that is six times faster with a high QRS detection accuracy (an SE of 99.90% and a +P of 99.56% using the MIT-BIH arrhythmia and QT databases). The results demonstrate system readiness, and effectiveness for real-time healthcare monitoring.
Acknowledgments
This work was made possible by NPRP grant # 7-684-1-127 from the Qatar National Research Fund (a member of Qatar Foundation). The work of Mohamed Elgendi was partially supported by Kind Saud University and Qatar University under GCC Co-Funding Program Grant no. GCC-2017-009. The findings achieved herein are solely the responsibility of the authors.
Author Contributions
Mohamed Elgendi, Amr Mohamed, and Rabab Ward designed the experiment. Mohamed Elgendi, Amr Mohamed, Abdulla Al-Ali, and Rabab Ward performed the statistical analysis. Mohamed Elgendi, Amr Mohamed, Abdulla Al-Ali, and Rabab Ward conceived of the study and drafted the manuscript. The authors approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Alwan A. Global Status Report on Noncommunicable Diseases 2010. World Health Organization; Geneva, Switzerland: 2011. [Google Scholar]
- 2.Dilaveris P.E., Gialafos E.J., Sideris S.K., Theopistou A.M., Andrikopoulos G.K., Kyriakidis M., Gialafos J.E., Toutouzas P.K. Simple electrocardiographic markers for the prediction of paroxysmal idiopathic atrial fibrillation. Am. Heart J. 1998;135:733–738. doi: 10.1016/S0002-8703(98)70030-4. [DOI] [PubMed] [Google Scholar]
- 3.Elgendi M., Eskofier B., Dokos S., Abbott D. Revisiting QRS Detection Methodologies for Portable, Wearable, Battery-Operated, and Wireless ECG Systems. PLoS ONE. 2014;9:1–18. doi: 10.1371/journal.pone.0084018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Elgendi M., Jonkman M., De Boer F. Improved QRS detection algorithm using dynamic thresholds. Int. J. Hybrid Inf. Technol. 2009;2:65–80. [Google Scholar]
- 5.Elgendi M., Jonkman M., De Boer F. Premature atrial complexes detection using the Fisher Linear Discriminant; Proceedings of the 7th IEEE International Conference on Cognitive Informatics (ICCI 2008); Stanford, CA, USA. 14–16 August 2008; pp. 83–88. [Google Scholar]
- 6.Scilingo E.P., Valenza G. Recent Advances on Wearable Electronics and Embedded Computing Systems for Biomedical Applications. Electronics. 2017;6:12. doi: 10.3390/electronics6010012. [DOI] [Google Scholar]
- 7.Fanucci L., Saponara S., Bacchillone T., Donati M., Barba P., Sánchez-Tato I., Carmona C. Sensing devices and sensor signal processing for remote monitoring of vital signs in CHF patients. IEEE Trans. Instrum. Meas. 2013;62:553–569. doi: 10.1109/TIM.2012.2218681. [DOI] [Google Scholar]
- 8.Saponara S., Donati M., Fanucci L., Celli A. An Embedded sensing and communication platform, and a healthcare model for remote monitoring of chronic diseases. Electronics. 2016;5:47. doi: 10.3390/electronics5030047. [DOI] [Google Scholar]
- 9.Donati M., Bacchillone T., Fanucci L., Saponara S., Costalli F. Operating protocol and networking issues of a telemedicine platform integrating from wireless home sensors to the hospital information system. J. Comput. Netw. Commun. 2013;2013:781620. doi: 10.1155/2013/781620. [DOI] [Google Scholar]
- 10.Chen M., Wan J., González-Valenzuela S., Liao X., Leung V.C. A Survey of Recent Developments in Home M2M Networks. IEEE Commun. Surv. Tutor. 2014;16:98–114. doi: 10.1109/SURV.2013.110113.00249. [DOI] [Google Scholar]
- 11.Baig M.M., GholamHosseini H., Connolly M.J. Mobile healthcare applications: System design review, critical issues and challenges. Australas. Phys. Eng. Sci. Med. 2015;38:23–38. doi: 10.1007/s13246-014-0315-4. [DOI] [PubMed] [Google Scholar]
- 12.Bansal A., Kumar S., Bajpai A., Tiwari V.N., Nayak M., Venkatesan S., Narayanan R. Remote health monitoring system for detecting cardiac disorders. IET Syst. Biol. 2015;9:309–314. doi: 10.1049/iet-syb.2015.0012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jung S.J., Myllylä R., Chung W.Y. Wireless machine-to-machine healthcare solution using android mobile devices in global networks. IEEE Sens. J. 2013;13:1419–1424. doi: 10.1109/JSEN.2012.2236013. [DOI] [Google Scholar]
- 14.Spinsante S., Gambi E. Remote health monitoring by OSGi technology and digital TV integration. IEEE Trans. Consum. Electron. 2012;58 doi: 10.1109/TCE.2012.6415017. [DOI] [Google Scholar]
- 15.Lin B.S., Hsiao P.C., Cheng P.H., Lee I.J., Jan G.E. Design and Implementation of a Set-Top Box–Based Homecare System Using Hybrid Cloud. Telemed. e-Health. 2015;21:916–922. doi: 10.1089/tmj.2014.0244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rahmani A.M., Thanigaivelan N.K., Gia T.N., Granados J., Negash B., Liljeberg P., Tenhunen H. Smart e-health gateway: Bringing intelligence to internet-of-things based ubiquitous healthcare systems; Proceedings of the 2015 12th Annual IEEE Consumer Communications and Networking Conference (CCNC); Las Vegas, NV, USA. 9–12 January 2015; pp. 826–834. [Google Scholar]
- 17.Martin S., Kelly G., Kernohan W.G., McCreight B., Nugent C. Smart Home Technologies for Health and Social Care Support. John Wiley & Sons, Ltd.; Hoboken, NJ, USA: 2008. The Cochrane Collaboration. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Vashist S.K., Schneider E.M., Luong J.H. Commercial smartphone-based devices and smart applications for personalized healthcare monitoring and management. Diagnostics. 2014;4:104–128. doi: 10.3390/diagnostics4030104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Baig M.M., Gholamhosseini H. Smart health monitoring systems: An overview of design and modeling. J. Med. Syst. 2013;37:9898. doi: 10.1007/s10916-012-9898-z. [DOI] [PubMed] [Google Scholar]
- 20.Jacobson N. Dignity and health: A review. Soc. Sci. Med. 2007;64:292–302. doi: 10.1016/j.socscimed.2006.08.039. [DOI] [PubMed] [Google Scholar]
- 21.Collins A., Leier B. Can medical assistance in dying harm rural and remote palliative care in Canada? Can. Fam. Physician. 2017;63:186–190. [PMC free article] [PubMed] [Google Scholar]
- 22.Elgendi M., Mohamed A., Ward R. Efficient ECG Compression and QRS Detection for E-Health Applications. Sci. Rep. 2017;7:459. doi: 10.1038/s41598-017-00540-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kannan R., Eswaran C. Lossless compression schemes for ECG signals using neural network predictors. EURASIP J. Appl. Signal Process. 2007;2007:102. doi: 10.1155/2007/35641. [DOI] [Google Scholar]
- 24.Calhoun B.H., Lach J., Stankovic J., Wentzloff D.D., Whitehouse K., Barth A.T., Brown J.K., Li Q., Oh S., Roberts N.E., et al. Body sensor networks: A holistic approach from silicon to users. Proc. IEEE. 2012;100:91–106. doi: 10.1109/JPROC.2011.2161240. [DOI] [Google Scholar]
- 25.Moody G.B., Mark R.G. The impact of the MIT-BIH Arrhythmia Database. IEEE Eng. Med. Biol. Mag. 2001;20:45–50. doi: 10.1109/51.932724. [DOI] [PubMed] [Google Scholar]
- 26.Elgendi M. Fast QRS Detection with an Optimized Knowledge-Based Method: Evaluation on 11 Standard ECG Databases. PLoS ONE. 2013;8:e73557. doi: 10.1371/journal.pone.0073557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Laguna P., Mark R.G., Goldberg A., Moody G.B. A database for evaluation of algorithms for measurement of QT and other waveform intervals in the ECG. IEEE Comput. Cardiol. 1997;24:673–676. [Google Scholar]
- 28.Kyrkos A., Giakoumakis E., Carayannis G. QRS detection through time recursive prediction techniques. Signal Process. 1988;15:429–436. doi: 10.1016/0165-1684(88)90061-8. [DOI] [Google Scholar]
- 29.Lin K.P., Chang W.H. QRS feature extraction using linear prediction. IEEE Trans. Biomed. Eng. 1989;36:1050–1055. doi: 10.1109/10.40806. [DOI] [PubMed] [Google Scholar]
- 30.Deepu C.J., Lian Y. A Joint QRS detection and data compression scheme for wearable sensors. IEEE Trans. Biomed. Eng. 2015;62:165–175. doi: 10.1109/TBME.2014.2342879. [DOI] [PubMed] [Google Scholar]
- 31.Kovacevic J., Vetterli M. Perfect reconstruction filter banks with rational sampling factors. IEEE Trans. Signal Process. 1993;41:2047–2066. doi: 10.1109/83.210873. [DOI] [PubMed] [Google Scholar]
- 32.Tao R., Deng B., Zhang W.Q., Wang Y. Sampling and sampling rate conversion of band limited signals in the fractional Fourier transform domain. IEEE Trans. Signal Process. 2008;56:158–171. doi: 10.1109/TSP.2007.901666. [DOI] [Google Scholar]
- 33.Elgendi M. TERMA Framework for Biomedical Signal Analysis: An Economic-Inspired Approach. Biosensors. 2016;6:55. doi: 10.3390/bios6040055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hamilton P., Tompkins W. Quantitative investigation of QRS detection rules using the MIT/BIH arrhythmiac database. IEEE Trans. Biomed. Eng. 1986;33:1157–1165. doi: 10.1109/TBME.1986.325695. [DOI] [PubMed] [Google Scholar]
- 35.Poli R., Cagnoni S., Valli G. Genetic design of optimum linear and nonlinear QRS detectors. IEEE Trans. Biomed. Eng. 1995;42:1137–1141. doi: 10.1109/10.469381. [DOI] [PubMed] [Google Scholar]
- 36.Afonso V., Tompkins W., Nguyen T., Luo S. ECG beat detection using filter banks. IEEE Trans. Biomed. Eng. 1999;46:192–202. doi: 10.1109/10.740882. [DOI] [PubMed] [Google Scholar]
- 37.Martínez J.P., Almeida R., Olmos S., Rocha A.P., Laguna P. A wavelet-based ECG delineator: Evaluation on standard databases. IEEE Trans. Biomed. Eng. 2004;51:570–581. doi: 10.1109/TBME.2003.821031. [DOI] [PubMed] [Google Scholar]
- 38.Chen S.W., Chen H.C., Chan H.L. A real-time QRS detection method based on moving-averaging incorporating with wavelet denoising. Comput. Methods Progr. Biomed. 2006;82:187–195. doi: 10.1016/j.cmpb.2005.11.012. [DOI] [PubMed] [Google Scholar]
- 39.Ieong C.I., Mak P.I., Lam C.P., Dong C., Vai M.I., Mak P.U., Pun S.H., Wan F., Martins R.P. A 0.83-QRS detection processor using quadratic spline wavelet transform for wireless ECG acquisition in 0.35-CMOS. IEEE Trans. Biomed. Circuits Syst. 2012;6:586–595. doi: 10.1109/TBCAS.2012.2188798. [DOI] [PubMed] [Google Scholar]
- 40.Nallathambi G., Principe J.C. Integrate and fire pulse train automaton for qrs detection. IEEE Trans. Biomed. Eng. 2014;61:317–326. doi: 10.1109/TBME.2013.2282954. [DOI] [PubMed] [Google Scholar]
- 41.Zhang F., Lian Y. QRS detection based on multiscale mathematical morphology for wearable ECG devices in body area networks. IEEE Trans. Biomed. Circuits Syst. 2009;3:220–228. doi: 10.1109/TBCAS.2009.2020093. [DOI] [PubMed] [Google Scholar]
- 42.Chua E., Fang W.C. Mixed bio-signal lossless data compressor for portable brain-heart monitoring systems. IEEE Trans. Consum. Electron. 2011;57:267–273. doi: 10.1109/TCE.2011.5735512. [DOI] [Google Scholar]
- 43.Chen S.L., Wang J.G. VLSI implementation of low-power cost-efficient lossless ECG encoder design for wireless healthcare monitoring application. Electron. Lett. 2013;49:91–93. doi: 10.1049/el.2012.3505. [DOI] [Google Scholar]
- 44.Chen S.L., Lee H.Y., Chen C.A., Huang H.Y., Luo C.H. Wireless body sensor network with adaptive low-power design for biometrics and healthcare applications. IEEE Syst. J. 2009;3:398–409. doi: 10.1109/JSYST.2009.2032440. [DOI] [Google Scholar]
- 45.Deepu C.J., Zhang X., Liew W.S., Wong D., Lian Y. An ECG-SoC with 535nW/channel lossless data compression for wearable sensors; Proceedings of the IEEE Asian Solid-State Circuits Conference; Singapore. 11–13 November 2013; pp. 145–148. [Google Scholar]
- 46.Mamaghanian H., Khaled N., Atienza D., Vandergheynst P. Compressed sensing for real-time energy-efficient ECG compression on wireless body sensor nodes. IEEE Trans. Biomed. Eng. 2011;58:2456–2466. doi: 10.1109/TBME.2011.2156795. [DOI] [PubMed] [Google Scholar]
- 47.Ansari-Ram F., Hosseini-Khayat S. ECG signal compression using compressed sensing with nonuniform binary matrices; Proceedings of the 2012 16th CSI International Symposium on Artificial Intelligence and Signal Processing; Shiraz, Iran. 2–3 May 2012; pp. 305–309. [Google Scholar]
- 48.Kumar R., Kumar A., Pandey R.K. Beta wavelet based ECG signal compression using lossless encoding with modified thresholding. Comput. Electr. Eng. 2013;39:130–140. doi: 10.1016/j.compeleceng.2012.04.008. [DOI] [Google Scholar]
- 49.Polania L.F., Carrillo R.E., Blanco-Velasco M., Barner K.E. Exploiting prior knowledge in compressed sensing wireless ECG systems. IEEE J. Biomed. Health Inform. 2015;19:508–519. doi: 10.1109/JBHI.2014.2325017. [DOI] [PubMed] [Google Scholar]
- 50.Polania L.F., Carrillo R.E., Blanco-Velasco M., Barner K.E. Compressed sensing based method for ECG compression; Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing; Prague, Czech Republic. 22–27 May 2011; pp. 761–764. [Google Scholar]
- 51.Mishra A., Thakkar F., Modi C., Kher R. ECG signal compression using Compressive Sensing and wavelet transform; Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society; San Diego, CA, USA. 28 August–1 September 2012; pp. 3404–3407. [DOI] [PubMed] [Google Scholar]
- 52.Casson A.J., Rodriguez-Villegas E. Signal agnostic compressive sensing for body area networks: Comparison of signal reconstructions; Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society; San Diego, CA, USA. 28 August–1 September 2012; pp. 4497–4500. [DOI] [PubMed] [Google Scholar]
- 53.Chae D.H., Alem Y.F., Durrani S., Kennedy R.A. Performance study of compressive sampling for ECG signal compression in noisy and varying sparsity acquisition; Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing; Vancouver, BC, Canada. 26–31 May 2013; pp. 1306–1309. [Google Scholar]
- 54.Arnavut Z. ECG signal compression based on Burrows-Wheeler transformation and inversion ranks of linear prediction. IEEE Trans. Biomed. Eng. 2007;54:410–418. doi: 10.1109/TBME.2006.888820. [DOI] [PubMed] [Google Scholar]
- 55.Miaou S.G., Chao S.N. Wavelet-based lossy-to-lossless ECG compression in a unified vector quantization framework. IEEE Trans. Biomed. Eng. 2005;52:539–543. doi: 10.1109/TBME.2004.842791. [DOI] [PubMed] [Google Scholar]
- 56.Zhang Z., Jung T.P., Makeig S., Rao B.D. Compressed sensing of EEG for wireless telemonitoring with low energy consumption and inexpensive hardware. IEEE Trans. Biomed. Eng. 2013;60:221–224. doi: 10.1109/TBME.2012.2217959. [DOI] [PubMed] [Google Scholar]
- 57.Fauvel S., Ward R.K. An energy efficient compressed sensing framework for the compression of electroencephalogram signals. Sensors. 2014;14:1474–1496. doi: 10.3390/s140101474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Zhang J., Gu Z., Yu Z.L., Li Y. Energy-Efficient ECG Compression on Wireless Biosensors via Minimal Coherence Sensing and Weighted \ell_1 Minimization Reconstruction. IEEE J. Biomed. Health Inform. 2015;19:520–528. doi: 10.1109/JBHI.2014.2312374. [DOI] [PubMed] [Google Scholar]
- 59.Moraes J.C.T.B., Freitas M.M., Vilani F.N., Costa E.V. A QRS complex detection algorithm using electrocardiogram leads. IEEE Comput. Cardiol. 2002:205–208. doi: 10.1109/CIC.2002.1166743. [DOI] [Google Scholar]
- 60.Elgendi M., Jonkman M., De Boer F. Frequency Bands Effects on QRS Detection; Proceedings of the International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSIGNALS 2010); Valencia, Spain. 20–23 January 2010; pp. 428–431. [Google Scholar]
- 61.Elgendi M., Eskofier B., Abbott D. Fast T wave detection calibrated by clinical knowledge with annotation of P and T waves. Sensors. 2015;15:17693–17714. doi: 10.3390/s150717693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Elgendi M., Meo M., Abbott D. A Proof-of-Concept Study: Simple and Effective Detection of P and T Waves in Arrhythmic ECG Signals. Bioengineering. 2016;3:26. doi: 10.3390/bioengineering3040026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Liu X., Zheng Y., Phyu M.W., Endru F., Navaneethan V., Zhao B. An ultra-low power ECG acquisition and monitoring ASIC system for WBAN applications. IEEE J. Emerg. Sel. Top. Circuits Syst. 2012;2:60–70. doi: 10.1109/JETCAS.2012.2187707. [DOI] [Google Scholar]
- 64.Mazomenos E.B., Biswas D., Acharyya A., Chen T., Maharatna K., Rosengarten J., Morgan J., Curzen N. A low-complexity ECG feature extraction algorithm for mobile healthcare applications. IEEE J. Biomed. Health Inform. 2013;17:459–469. doi: 10.1109/TITB.2012.2231312. [DOI] [PubMed] [Google Scholar]
- 65.Yuce M.R. Implementation of wireless body area networks for healthcare systems. Sens. Actuators A Phys. 2010;162:116–129. doi: 10.1016/j.sna.2010.06.004. [DOI] [Google Scholar]
- 66.Elgendi M., Howard N., Lovell N., Cichocki A., Brearley M., Abbott D., Adatia I. A Six-Step Framework on Biomedical Signal Analysis for Tackling Noncommunicable Diseases: Current and Future Perspectives. JMIR Biomed. Eng. 2016;1:e1. doi: 10.2196/biomedeng.6401. [DOI] [Google Scholar]