Biophysics Model of Heavy-Ion Degradation of Neuron Morphology in Mouse Hippocampal Granular Cell Layer Neurons

Abstract

Exposure to heavy-ion radiation during cancer treatment or space travel may cause cognitive detriments that have been associated with changes in neuron morphology and plasticity. Observations in mice of reduced neuronal dendritic complexity have revealed a dependence on radiation quality and absorbed dose, suggesting that microscopic energy deposition plays an important role. In this work we used morphological data for mouse dentate granular cell layer (GCL) neurons and a stochastic model of particle track structure and microscopic energy deposition (ED) to develop a predictive model of high-charge and energy (HZE) particle-induced morphological changes to the complex structures of dendritic arbors. We represented dendrites as cylindrical segments of varying diameter with unit aspect ratios, and developed a fast sampling method to consider the stochastic distribution of ED by δ rays (secondary electrons) around the path of heavy ions, to reduce computational times. We introduce probabilistic models with a small number of parameters to describe the induction of precursor lesions that precede dendritic snipping, denoted as snip sites. Predictions for oxygen (¹⁶O, 600 MeV/n) and titanium (⁴⁸Ti, 600 MeV/n) particles with LET of 16.3 and 129 keV/μm, respectively, are considered. Morphometric parameters to quantify changes in neuron morphology are described, including reduction in total dendritic length, number of branch points and branch numbers. Sholl analysis is applied for single neurons to elucidate dose-dependent reductions in dendritic complexity. We predict important differences in measurements from imaging of tissues from brain slices with single neuron cell observations due to the role of neuron death through both soma apoptosis and excessive dendritic length reduction. To further elucidate the role of track structure, random segment excision (snips) models are introduced and a sensitivity study of the effects of the modes of neuron death in predictions of morphometric parameters is described. An important conclusion of this study is that δ rays play a major role in neuron morphological changes due to the large spatial distribution of damage sites, which results in a reduced dependence on LET, including modest difference between ¹⁶O and ⁴⁸Ti, compared to damages resulting from ED in localized damage sites.

INTRODUCTION

Whole- and partial-brain irradiation has been studied extensively, and significant disruption of a wide array of learning and memory functions has been documented, as well as drastic inhibition of hippocampal proliferation and neurogenesis (1-6). It has also been found that radiation affects the medial prefrontal cortex (mPFC), which involves executive function and decision making (7, 8). One mechanism contributing to the progressive dementia experienced after cranial irradiation is the persistent reduction in the structural complexity of mature neurons throughout the brain (9-16). Radiation exposure has been shown to reduce dendritic complexity and spine density, and alters the density of specific spine types (9-16) that represent the structural correlates of learning and memory, which are critical for proper cognitive functioning.

Heavy-ion irradiation is used in the treatment of brain cancers (17) and occurs during galactic cosmic ray exposures of astronauts in space (18). Recently published studies have shown that heavy-ion irradiation leads to changes in dendritic spine morphogenesis and synaptic plasticity at low dose (<0.5 Gy), which is likely to directly contribute to radiation-induced cognitive impairment (14-16). The differences observed between X rays and protons in granular cell layer (GCL) neurons in the hippocampus (13) and heavy ions of different linear energy transfer (LET) in PFC neurons (16) demonstrates the radiation quality dependence of these effects. Here we postulate that descriptions of microscopic energy deposition (ED) events in neuron cells for different radiation qualities (19, 20) will be fundamental to elucidating these observations, and to support the determination of relative biological effectiveness (RBE) factors for normal tissue injury. Other than descriptive statistics and visual presentations of neurons, to our knowledge there are no published underlying biophysics models that describe changes in morphology at a given dose and radiation quality for any type of neuron.

In this work, we developed an empirical model that postulates that changes to neuronal morphology can be predicted using mechanistically based radiation-dependent patterns of high-ED sites that are potentially “snipped”, reducing the length of dendritic arbors of GCL neurons. We use the terminology “snip” to distinguish those lesions from the biological program of dendritic pruning. Snip sites are formed from high-ED lesions along dendritic arbors. In contrast, the underlying mechanisms of dendritic pruning have not been fully elucidated and could include dendrite retraction (21-24) and degradation by activated microglial cells (25-27). Notably, the regulation of dendrites and spines is influenced by changes to cognition (28, 29), and it is not known at this time if microscopic ED is causative of morphological changes, or if the dose and radiation quality dependence of these changes are manifested in a distinct manner. However, the methods developed herein, although empirical in part, can form the basis for more detailed models at the time the underlying radiobiology of radiation modifications to dendrite growth and retraction, pruning and spine stability are understood.

Experimental techniques to visualize morphological changes have been reported using single cell methods as well as scoring of cell populations in tissues from brain slices. Structural parameters to be considered define dendritic complexity without and with radiation exposure through quantification of neuronal cell bodies (N_N), total dendritic length (DL_T), the number of dendritic branch points (BP_T) and branch number (BN_T) and dendritic spines normalized to DL_T. Single neuron observations can be achieved by neuro-tracers (30, 31) or traditional Golgi staining (32-34). Tissues prepared with green fluorescent protein expressing (GFP) neurons have the advantage of presenting a population of neurons on thin slices (~60 μm depth) of brain sections (12, 35, 36). A reliable method to determine the number of neurons in a slice is to count neuronal cell bodies (soma). Nuclear DNA staining of differentiating soma structure (spherical or stereotypical for some types of neurons, such as pyramidal neurons) can be counted by image processing tools. In contrast, Sholl analysis (37) considers a single neuron, while measuring the contribution of total dendritic length and branch points in concentric circles centered at the soma, thus providing a quantitative method to compare damaged and control neuron morphologies. Both Golgi staining and GFP expressing neurons in confocal images have provided quantitative data on dendritic spine density and spine classification.

The focus on this study was to consider the detailed track structure of particle irradiation in realistic in silico neuronal structures to predict morphological changes for low to moderate absorbed doses of heavy ions. Computational methods investigated earlier to find dose to neuronal segments (19, 20) are based in stochastic particle track structure predictions of ED events that are quantized in nanoscopic voxels, including coordinate and magnitude of ED to a media (water), and the scoring of coincidences of ED events in a large number of segments from individual or multiple particle tracks. A challenge in this approach is computational time as ED in each voxel per particle and segments per neuron are determined. Satisfying electronic equilibrium due to δ-ray (secondary electron) kinematics requires encapsulating a target neuron with particle tracks that extend to ~1,000 microns in each (x,y,z) coordinate. The maximum δ-ray energy and radial ED events depend on charge particle kinetic energy per nucleon (MeV/n) and the mean number of charged particles intersecting a relatively large neuron volume (~10⁶ μm³) at low doses increases as square of the radial range. A mathematical approach is applied in this work to shorten computational time by analytically calculating the mean number of δ-ray track crossings per primary ion track and utilizing numerically calculated ED for δ-ray crossings of cylindrical segments.

The methods developed herein are applied to mouse dentate GCL neurons for high-energy oxygen (¹⁶O) and titanium (⁴⁸Ti) irradiation, while future studies will focus on more complex neurons such as pyramidal neurons as well as other brain regions and radiation types. Modeling the geometric extension of dendrites and high-energy particle tracks while using stochastic Monte Carlo computer codes requires extensive computational power. The calculations reported herein use parallel processing techniques on a 48-core computer workstation, while requiring several weeks of CPU time for each particle type considered. Current data on morphological changes after particle or X-ray irradiation have not considered early times points (<10 days) and used only 1 or 2 absorbed dose values (9-16). Also, there have been no reported studies that have considered both X rays and heavy ions in the same brain region or neuron type. Observations at such later time points (>10 days or more) are likely influenced by activated microglia. Thus, the current approach is more reflective of earlier morphological changes, however, it could form a basis to consider how morphological changes evolve with time after irradiation.

MATERIALS AND METHODS

In this work, we utilize as our test neuron a complete reconstruction of a mouse GCL neuron from the open source Neuromorpho.org site (ID no. NMO 06176) (38, 39). Neuronal reconstruction based on microscopy studies represents segments on dendritic branches as right circular cylinders that have continuously varying diameter determined by the biology of branches and axes lengths. The in silico neuron has continuous segments of a specified radii, r, which are modified by 1 −Exp[−r^1.5/0.85] to obtain segment diameters that reach 0.4 μm at the dendritic tips with approximately 11.95 μm diameter at the soma. The (mean, median, minimum) segment radii of (0.66, 0.62, 0.55) μm of the test neuron are reduced to (0.47, 0.44, 0.38) μm after the radii correction. This procedure is motivated by analysis of unpublished GCL neurons of mice brain slices and evaluation reported at http://neuromorpho.org/ by different authors (38, 39).

To evaluate microscopic ED in any segment we consider segment diameters and axis lengths of unit aspect ratio = 1, as discussed in our previously published work (20). A computational program was written to re-segment dendritic branches to keep the total branch volume and branch length optimally constant and have new segment coordinates along the original reconstruction with equal diameters and axes lengths for any segments. Variations in diameters along a branch of the original data are also included in the re-segmentation program. The DL₀, BN₀ and BP₀ of the test neuron are (1,793.8 μm, 23, 11), respectively, where the subscript represents the unperturbed neuron. The re-segmented neuron has 3,049 segments including a single soma segment. The mean and standard deviation (SD) values of dendritic segment volumes are (0.259, 0.902) μm³ and the soma volume is 1,340 μm³.

Snip Formation on Dendritic Trees

The model assumes that, dependent on the magnitude of the ED to a neuronal segment, a local damage is marked as a candidate snip site. A probabilistic model (described below) determines if a given site would be snipped with higher probability found for larger ED. If a segment is decided to be snipped, as shown in Fig. 1A, all branches and their segments in the soma-to-tip direction supported by the cut branch shown in Fig. 1B are eliminated from the original neuron, as shown in Fig. 1C. An alternative model, whereby intrabranch deletions result from multiple snips, could be considered in future work using a similar approach. There can be many segments that are determined to be snipped in a neuron, including one on the same branch at a given absorbed dose. Surviving segments and the end point of branches are determined by the snipped segments closest to the soma on the tip-to-soma direction pathway. The new total dendritic length, number of branch points and branch numbers are then calculated on the remaining neuron. The Sholl analysis is also recorded for a given distribution per trial. The presentation of dose responses in this work include normalized neuromorphometric parameters; DL = DL_T/DL₀, BP = BP_T/BP₀, BN = BN_T/BN₀. Error bars representing standard deviations generated over many Monte Carlo trials are quantified for morphometric parameters and Sholl analysis.

FIG. 1.

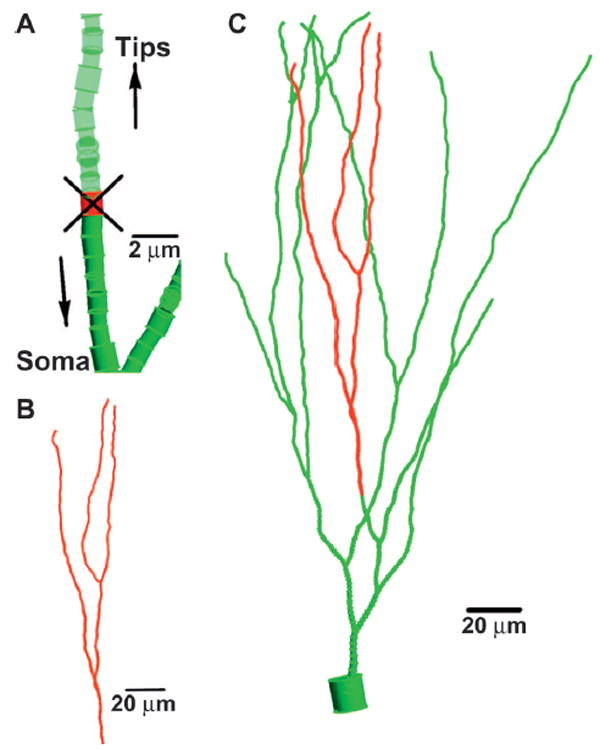
Model for snips and reduction in dendritic complexity. Panel A: A segment (shown in red) is determined to be the snip site on a dendritic branch due to a large energy deposition occurrence. All the segments supported by the snipped segment (panel B), indicated in red, are deleted from the green dendritic structure (panel C).

Approach to Score ED in Neuronal Segments

The method of finding ED to neuronal segments are defined elsewhere (19, 20). Briefly, a neuron with a large number of segments is exposed to a stochastic track structure with the number of particles corresponding to a given absorbed dose, and the ED events in individual segments recorded as a trial outcome. Many Monte Carlo trials with random particle track directions are sampled to generate a particle beam library of stochastic histories. The number of trials for a given absorbed dose or corresponding particle fluence to the media is determined while correlated ED events in each segment are sampled from the library. The orientation of the neuron is not specified and we therefore assume isotopic irradiation.

In this work, the macroscopic or absorbed dose is denoted as D_F (in units of Gy) to indicate its relationship to the average particle fluence, F. All other doses described refer to microscopic doses (also in units of Gy) for the small volumes considered. Table 1 lists the key variables and parameters used in the model. Stochastic track structures are generated by the RITRACKs software with track length of 20 μm and voxel sizes at 20 nm (40, 41). Track structures are used to find radial ranges, radial dose profiles and LET values from generated histories of 30,000 and 20,000 stochastic tracks of ¹⁶O (600 MeV/n) and ⁴⁸Ti (600 MeV/n), respectively. The LET values for ¹⁶O and ⁴⁸Ti are 16.3 and 129 keV/μm, respectively. Because the kinetic energy per nucleon for both particles is the same, the same maximum electron energies (1,740.6 keV) and theoretical δ-ray radial ranges (2,125 μm) are found (42, 43). As a result of analysis of track structure and voxel coordinates (20), a larger radial range (2,434 μm) is used in the simulations to adjust for the additional dimension of voxel coordinate in track histories.

TABLE 1.

Summary of Parameters Used in the Track Structure Model of Changes to Dendritic Morphology

Parameter	Symbol	Units
Mean particle fluence	F	Number per μm2
Linear energy transfer	LET	keV/μm
Absorbed dose	DF	Gy
Impact parameter (radial distance from particle to dendritic segment or soma)	b	Microns (μm)
Radial dose	D(b)	Gy
Dendritic segment diameter	dCyl	Microns (μm)
Dendritic segment volume	Vcyl	Cubic microns (μm3)
Frequency mean specific energy in dendrite cylindrical segment	zF(b, dCyl)	Gy
Absorbed dose corresponding to reduction in dendritic length by one-half	DHV	Gy
Damage response-sensitivity parameters
Sensitivity parameter for soma apoptosis	DTH,S	Gy
Sensitivity parameter for dendrite snip	DTH,D	Gy
Sensitivity for neuron death due to dendritic length reduction	DL	Unitless

Note. Other model parameters specifically related to random damage models are described in the discussion of Eqs. (7–9).

The radial dose profile per charged particle, D(b), where b (in microns) is the impact parameter, is obtained for 20-μm-long-particle track histories as described elsewhere (20). Radial dose profiles are well known to decrease as one over the distance squared for most radial distances, as shown in Fig. 2, with deviations from an inverse-square law both close to the particles’ path and near the maximum radial distance (42, 43), which corresponds to the range of the highest energy δ rays produced through ionization. To reduce computational times, radial profiles were thus interpolated over b using Eq. (1) for ¹⁶O (600 MeV/n) and ⁴⁸Ti (600 MeV/n),

$$D(b)=\frac{c_1{e}^{-c_2\times b_i^2}}{(c_3+c_4{b}_i^{-1})b_i^2}\mathrm{Gy},$$ (1)

where numerical values of (c₁, c₂, c₃, c₄) are (0.02748, 2.411 × 10⁻⁶, 1.256, 10⁻⁷) for ¹⁶O and (0.20784, 2.411 × 10⁻⁶, 1.256, 10⁻⁷) for ⁴⁸Ti particles, respectively.

FIG. 2.

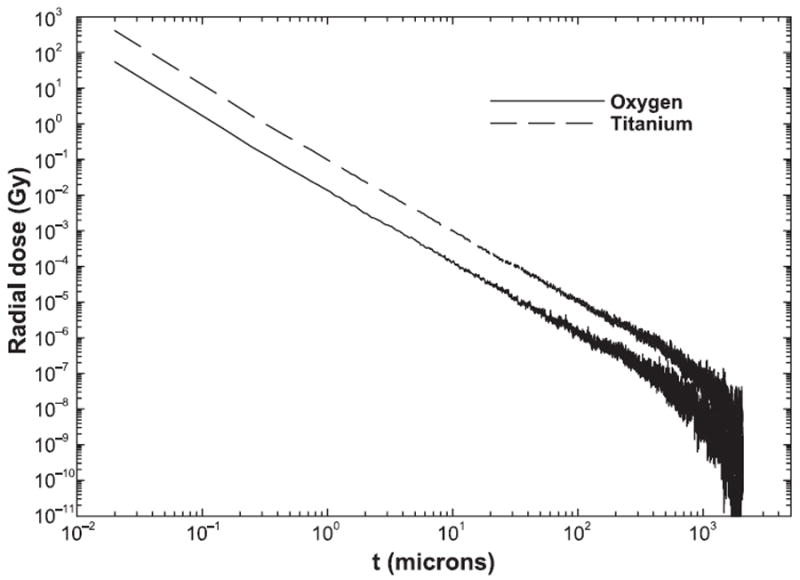
Radial dose profiles versus impact parameter for ¹⁶O and ⁴⁸Ti particles at 600 MeV/n.

The ED to a segment has both primary beam (core track with low-energy electrons) and δ-ray contributions, with the determination of ED due to δ rays leading to large computational times to sample the volume juxtaposed with large radial and longitudinal track lengths. Two modifications are applied in this study to shorten the simulation times. First, the neuron is fixed in space and uniform random track structures target the neuronal segments, as described elsewhere (19, 20). A direct hit by a primary track to a segment i is determined by finding the normal distance (impact parameter, b_i) between a line approximation of the beam and the segment center. If b_i is less than an additional distance (0.4 μm) plus one-half of the diagonal length of the segment, then a 20 μm random selected track is chosen in the identical direction of beam propagation, and the ED to the segment of interest is found as the primary beam contribution. The additional distance of 0.4 μm is chosen to cover the densely ionizing core region of a track.

Microscopic Dose due to Delta Rays in Cylindrical Segments

Microscopic dose to a segment by random δ-ray crossings per particle beam is found using statistical methods, first by finding the number of δ-ray crossings to the segment, then by determining ED to the segment. The mean number of δ-ray hits, P_Scnd to a segment, i depends on the impact parameter b_i for given segment and track dose at b_i, D(b_i) in Eq. (1).

The procedure to find the ED, as represented by the frequency mean specific energy, z_F (in units of Gy) arising from random δ-ray track crossing to any segment volume, V_Cyl,i at b_i is as follows. First, a coordinate point of a voxel, r_vox that is nearest to a predefined b_i value is found for a track history. A random point, c_seg in a sphere of radius dia_Cyl,j centered at r_vox is found to represent the center of V_Cyl,i, as follows. The dia_Cyl,j is the diagonal length of a cylindrical segment with diameter and axis length of d_Cyl,j. Then, a random length, d_seg, which is the one-third power of a random number in a uniform distribution between (0, dia_Cyl,j), is used to account for selecting a random radius in a sphere. The initial segment center point, c_seg,ini at c_seg,ini = r_vox + (0,0,d_seg) is randomly rotated by θ₁ (Fig. 3A), which represents 3-dimensional random rotation angles. The test cylindrical segment with diameter and axis length d_Cyl,j centered at c_seg is randomly rotated by θ₂, which represents 3-dimensional rotation angles. If there are any voxels bound by the rotated cylinders, their total energy is calculated as frequency-specific energy and random dose to the cylinder is found. We use a total of 11 b_i distances and 10 d_Cyl,j size segments to interpolate the random ED events by δ-ray tracks. The b_i samples are in the radial range of 10–2,400 μm and d_Cyl,i is between 0.3–6 μm, with smaller distances treated with the primary track contributions.

FIG. 3.

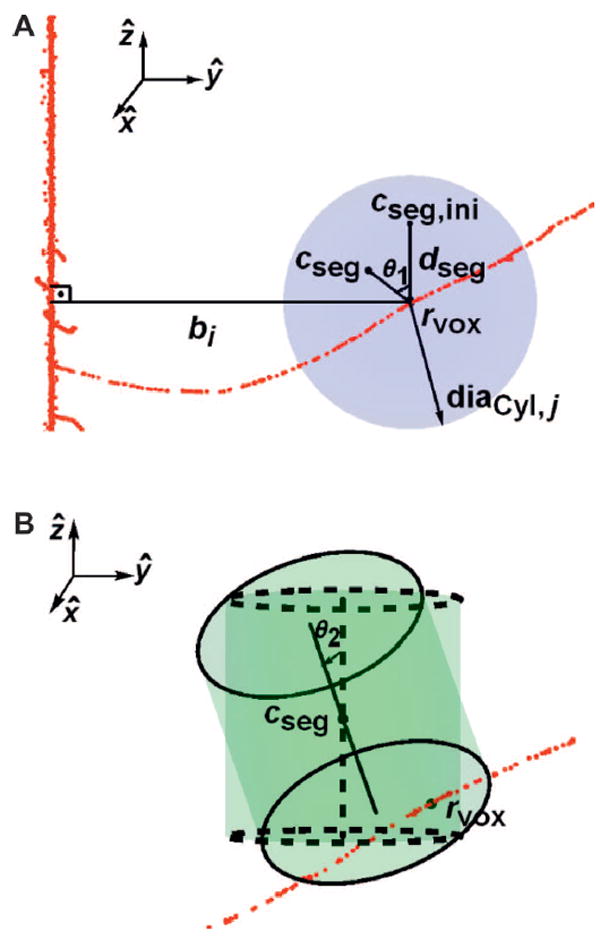
Panel A: A random point c_seg is selected as the center of the test volume, by first finding a random length d_seg while randomly rotating around a fixed point r_vox by θ₁. Panel B: The test cylindrical segment with diameter and axis length d_Cyl,j centered at c_seg is randomly rotated by θ₂, and total ED to the cylinder is calculated.

Using the RITRACKs code, the frequency mean specific energy z_F(b, d_Cyl) in Gy (ED per segment mass) in Fig. 4 is found to change slowly for increasing impact parameter and segment diameter. Therefore, we introduced the following parameterization to improve computational times data.

$${\mathit{log}}_{10}{z}_F(b,d_{\mathit{Cyl}})=a_1+a_2{(a_3-{\mathit{log}}_{10}b)}^2+a_4{\mathit{log}}_{10}b+a_5{\mathit{log}}_{10}{d}_{\mathit{Cyl}},$$ (2)

where numerical values of (a₁, a₂, a₃, a₄, a₅) are (−1.9787, 0.146693, 3.61922, 0.20436, −2.04264) with b and d_Cyl. The mean number of δ-ray hits, P_Scnd, to a segment depends on the impact parameter b for the given segment and track dose, D(b) is calculated by:

$$P_{\mathit{Scnd}}=\frac{D(b)}{Z_F(b,d_{\mathit{Cyl}})}.$$ (3)

The random number of crossings, N_Scnd for a given segment is determined by a Poisson process with mean P_Scnd.

FIG. 4.

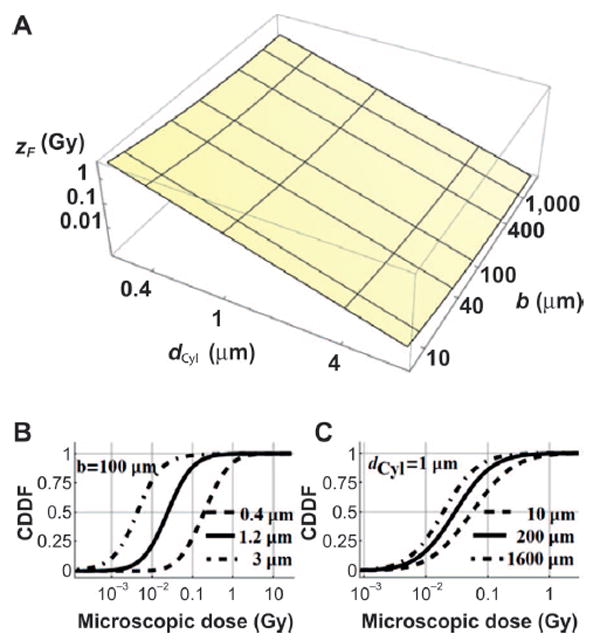
Panel A: Surface plots for frequency mean specific energy z_F as a function of segment diameter d_Cyl and impact parameter b. Panels B and C: Cumulative dose distribution function (CDDF) of δ-ray ED to a given cylinder with (panel B) varying axis lengths d_Cyl (0.4, 1.2 and 3 μm) (dashed, solid, dot-dashed lines) at b = 100 μm; and (panel C) at varying b (10, 200 and 1,600 μm) (dashed, solid, dot-dashed lines) at d_Cyl = 1 μm.

A random δ-ray dose per hit, $D_{\mathit{Scnd}}^1(b,d_{\mathit{Cyl}})$ is calculated by the δ-ray crossing fitted values by drawing a uniform random number between (0, 1) in Eq. (4),

$$\mathit{RND}=\frac{1}{1+e^{-(d_1({\mathit{log}}_{10}{D}_{\mathit{Scnd}}^1-d_0)+d_2{({\mathit{log}}_{10}{D}_{\mathit{Scnd}}^1-d_0)}^2+d_3{({\mathit{log}}_{10}{D}_{\mathit{Scnd}}^1-d_0)}^3)}},$$ (4)

where RND is a random number from a uniform distribution, and the b- and d_Cyl-dependent variables are:

$$\begin{array}{lll}{d}_0& =& f_1+f_2{\mathit{log}}_{10}{d}_{\mathit{Cyl}}+f_3{\log }_{10}b\mathrm{;}\\ d_1& =& g_1+g_2{\mathit{log}}_{10}{d}_{\mathit{Cyl}}+g_3{\mathit{log}}_{10}b\mathrm{;}\\ d_2& =& h_1+h_2{\mathit{log}}_{10}{d}_{\mathit{Cyl}}+h_3{\mathit{log}}_{10}b\mathrm{;}\\ d_3& =& j_1+j_2{\mathit{log}}_{10}{d}_{\mathit{Cyl}}+j_3{\mathit{log}}_{10}b+j_4{(j_5-\mathit{log}10d_{\mathit{Cyl}})}^2\mathrm{;}\end{array}$$

where (f₁, f₂, f₃) are (−1.02255, −1.85849, −0.21713) and (g₁, g₂, g₃) are (3.07646, 0.13306, 0.09597) and (h₁, h₂, h₃) are (0.13252, 1.26433, −0.07845) and (j₁, j₂, j₃, j₄, j₅) are (0.04562, −1.27628, −0.02858, 0.75681, −0.47213), respectively.

Stochastic Dose Model (SDM) for Single and Population of Neurons

A library of segment hits per track is generated for ¹⁶O and ⁴⁸Ti for a large number of trials (1.6 × 10⁷ and 6 × 10⁶, respectively) with the highest absorbed doses considered of 2.24 and 6.65 Gy, respectively. The mean number of random particle beams drawn per Gy from the library are then calculated. This approach is denoted as the SDM. To obtain sampling statistics to generate a dose response, we use a trial number, N_Trial, which is larger than 1,000/D_F.

For considering a population of neurons we assume the mean number of dentate GCL neurons on a brain slice is 100 and a random number of neurons at each trial is chosen assuming Poisson statistics for the distribution of neuron cell number in the slice. Then, the dose response for each neuron per trial is tested and the population total of DL, BN and BP values for a slice are calculated. The mean and SD values are plotted over N_Trial outcomes. Single neuron sampling statistics, including the Sholl analysis (mean and SD at each distance from soma), are represented over a single trial while repeating the analysis on the test neuron N_Trial times.

Probability Model for Snip Occurrences

Snip sites on dendritic segments undergo excision processes at given cumulative segment microscopic dose, D_Seg, and probability of snip occurrence, P_Snip, which is modeled by an exponential response function,

$$P_{\mathit{Snip}}=1-\mathit{Exp}(-D_{\mathit{seg}}/D_{\mathit{TH}}),$$ (5)

where D_TH is a parameter representing a quasi-threshold dose. Values for soma and dendritic segments are denoted by D_TH,S and D_TH,D. Note the value for the soma is related to cell apoptosis, while the data for the much smaller dendritic segments represent structural component damage sites. A single D_TH,D for all the neuronal dendritic segments independent of radiation type or absorbed dose, and their segment geometric size and location on dendrites is chosen in this model based on our library of segment hits and sizes described above.

Modes of Neuronal Death

There are two pathways for neuronal death after irradiation in the model. First, a stochastic model assuming an exponential survival curve is assumed for soma death, which leads to collapse of the dendritic arbor, precluding its observation in experiments of morphological changes. The value of D_TH,S is varied in the sensitivity analysis (see Results), however, it can be estimated based on dose responses for apoptosis in neuronal cells, which suggest values of a few Gy for heavy ions (44-46).

A second mode of neuronal death is assumed due to excessive DL shortening as a result of dendritic snips, which promotes neuronal death. The total DL of a survived neuron (DL_T,survived) is calculated at given absorbed dose, D_F for each trial. The probability of survival (P_survive) is expressed in terms of the Gaussian error function (Erf) as

$$P_{\mathit{survive}}=\frac{1}{2}(1+\mathit{Erf}\left[\frac{D{L}_{\mathit{ratio}}-D{L}_{\mathit{TH}}}{\sqrt{2\sigma }}\right]),$$ (6)

where DL_ratio is the ratio of surviving and unperturbed total dendritic lengths (DL_ratio= DL_T,survived/DL_T), and DL_TH is the normalized dendritic length threshold value of DL_ratio corresponding to a 50% probability that the neuron survives due to reduction in D_LT after irradiation (see Fig. 5). The σ value is the width of underlying Gaussian function provided survival approaches unity for an unperturbed neuron.

$$\sigma =\frac{1-D{L}_{\mathit{TH}}}{3}$$

A random decision on neuron survival and death for given survival probability is assumed. There is no contribution of neuron death to morphometric parameter evaluation since neurons are assumed to have survived to the time of observation.

FIG. 5.

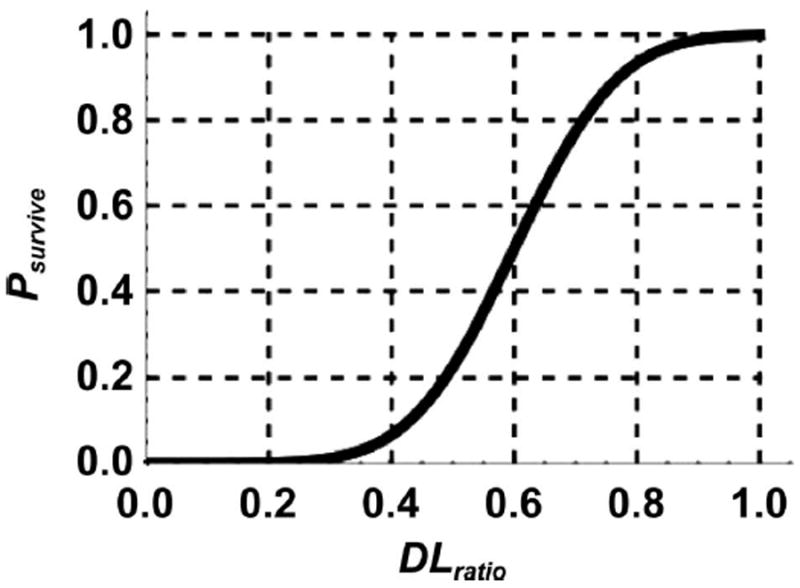
The ratio of shortened to control total dendritic length, DL_ratio, which is utilized to find a neuron survival probability after dendrites are snipped. The DL_TH of 0.6 in the figure satisfies 50% chance of survival. A uniform random number (between 0, 1) determines neuron survival and death at a given trial for given survival value, as described by Eq. (5).

Random Snip Models

To elucidate the role of particle track structure and importance of deviations from random ED events in dendritic arbors, two random snip models, which are independent of track structure and the stochastic microscopic dose to segments, but are dependent on geometrical parameters of neuronal segments, are introduced, which are compared to the SDM.

The first random snip model, denoted as Rnd1, depends on segment cross section areas in random particle hits. A particle track is approximated by a line and the mean number of hits, n_Hit,1, to a segment with cross section area A_segment given by

$$n_{\mathit{Hit},1}=\frac{D_F{A}_{\mathit{Segment}}}{0.16\mathit{LET}},$$ (7)

where D_F is in Gy, LET is in keV/μm and 0.16 is a unitless number. The second random snip model, denoted as Rnd2, assumes that the probability of a segment hit depends on its axis length, d_segment and the mean number of hits, n_Hit,2 is calculated by

$$n_{\mathit{Hit},2}=\frac{D_F}{0.16\mathit{LET}}\frac{A_{T,\mathit{segment}}}{D{L}_T}{d}_{\mathit{segment},}$$ (8)

where A_T is the total cross section summed over all the segments A_segment. The prefactor for n_Hit,2 provides the equivalence for total mean number of hits between the Rnd1 and Rnd2 models.

In both random snip models the number of hits to each segment including the soma is found from a Poisson distribution with mean number of hits, n_Hit,1 or n_Hit,2. The dose per hit to any segment is defined by a mean dose per hit, D_seg,mean,

$$D_{\mathit{seg},\mathit{mean}}=\frac{D_F}{n_{\mathit{Hit}}}.$$

Both random models follow the same snip decision process in Eq. (5), and comparative quantitative analysis is presented for models SDM, Rnd1 and Rnd2. The Rnd1 can be interpreted as snips due to random hits to targets with particles, and probability of hits are proportional to cross section area.

RESULTS

Our model predicts radiation-induced changes in morphological parameters of a single neuron and a population of neurons, while exploring results for ¹⁶O and ⁴⁸Ti irradiation at LET values of 16.3 and 129 keV/μm, respectively. We consider possible differences between observations from single neuron cell and population type experiments. Here, experiments on morphological changes in a population of neurons could show differential results from single cell analysis due to the loss of cells through soma or dendritic arbor damage, which may influence the density of dendritic arbors observed. Reduction in DL, BP and BN for a single neuron and a population of neurons is quantified for a given absorbed dose and model parameter values D_TH,S, D_TH,D and DL_TH. The reduction of morphological parameters are fitted to variable = 2^−D_F^/D_HV, where variable refers to the mean values of normalized DL, BN and BP (DL_T/DL₀, BP_T/BP₀, BN_T/BN₀) and D_HV is the resulting half-value for DL reduction.

The dose response for DL, BP and BN based on the Sholl analysis for ⁴⁸Ti is shown in Fig. 6 for (D_TH,S, D_TH,D and DL_TH) variables set at (7 Gy, 350 Gy and 0.6), respectively. There are higher reductions for DL, BP and BN for ⁴⁸Ti than ¹⁶O irradiation (not shown) for both single neuron and neuron population analysis predicted at all absorbed doses considered. The same conclusion is reached by D_HV values. The D_HV values presented for (DL, BP and BN) for single neurons are (2.32, 5.00, 5.26) Gy for ¹⁶O and (2.15, 4.66, 4.91) Gy for ⁴⁸Ti. The same D_HV values of (DL, BP and BN) for population of neurons are (0.63, 0.73, 0.74 Gy) for ¹⁶O and (0.56, 0.65, 0.65 Gy) for ⁴⁸Ti. Further investigation of possible differences in the ¹⁶O and ⁴⁸Ti dose responses are found in the number of snip occurrences on dendrites, which follow a linear dose response with slopes of (8.50, 8.80) snips/Gy for (¹⁶O, ⁴⁸Ti), respectively. The larger number of snip occurrences in ⁴⁸Ti compared to ¹⁶O irradiation leads to increased neuron death by both dendritic shortening and soma death mechanisms. The Sholl analysis quantifies changes in DL for increasing 10 μm co-centric circles with the soma, and provides a useful comparison of single neuron DL reduction for given parameter sets. Sholl analysis of a single neuron (see Fig. 6D for ⁴⁸Ti) for absorbed dose, D_F, of 0.5 Gy did not identify any systematic difference between ¹⁶O and ⁴⁸Ti radiation in the model. In addition, the bar charts that quantify the reduction in DL, BP and BN at given D_F, shown in Fig. 6E, for ⁴⁸Ti are similar for ¹⁶O.

FIG. 6.

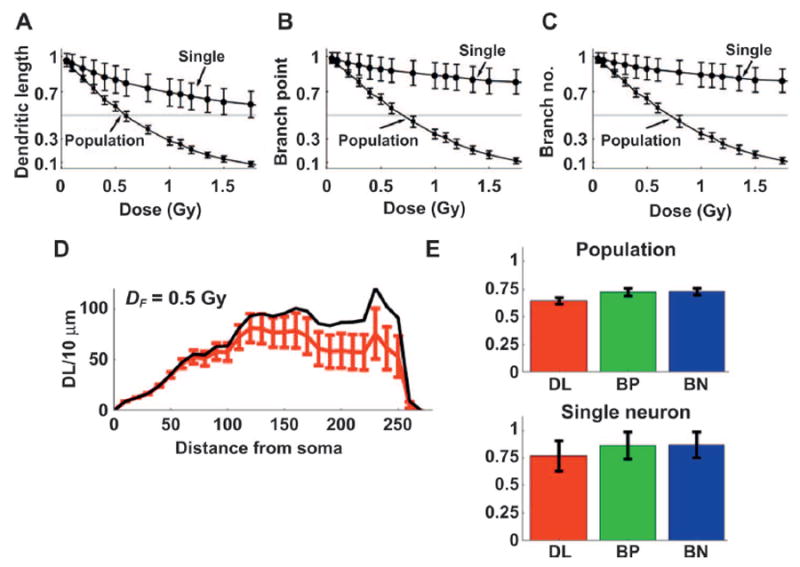
Absorbed dose D_F response of morphometric parameters in dendritic length (panel A), branch point (panel b) and branch number (panel C), respectively, for ⁴⁸Ti irradiation for single neuron (single) and population of neurons (population) with mean of 100 neurons. Panel D: Sholl analysis at D_F = 0.5 Gy is shown for 10-μm thick annuli from the soma. Black line is unperturbed test neuron and red line with error bars represents the change in the test neuron at given distances from soma. Panel E: Bar graphs show reductions in dendritic length (DL), branch point (BP) and branch number (BN) are given for single and population of neurons, respectively, at D_F = 0.5 Gy. Mean (± SD), values of population of neurons for DL, BP and BN are 0.65 ± 0.03, 0.73 ± 0.04 and 0.73 ± 0.03, respectively; and for single neuron, the values are 0.77 ± 0.14, 0.86 ± 0.12 and 0.87 ± 0.1, respectively.

Effects of Neuronal Death on Neuron Morphology Changes

Two modes of neuronal death arising from ED to soma and dendrites are investigated. Neuron death by excessive dendritic reduction requires excision of dendritic segments at snip points that depend on the parameter D_TH,D and a decision of neuron death by the functional form of Eq. (6). It is assumed that neuron loss does not contribute to single neuron morphometric parameters (DL, BP, BN) and Sholl analysis, but does contribute to population statistics. The dependence of neuron death and predicted reduction in total DL for single neuron and population of neurons as a function of D_TH,S for a set of variables, D_TH,D and DL_TH value, is shown in Fig. 7 for ¹⁶O radiation. For identical values of D_TH,D and DL_TH, differences between the ¹⁶O and ⁴⁸Ti results are small. The contribution of soma death to total neuron death leveling to (2⁻¹, e⁻¹) occurs at D_TH,S = (0.75, 1.12 Gy), respectively, see Fig. 7A for ¹⁶O radiation. Likewise, the contribution to neuronal death by dendritic shortening reaching the (2⁻¹, 1 – e⁻¹) of the maximum contribution level (=0.20) occurs at (0.73, 1.12 Gy), see Fig. 7A.

FIG. 7.

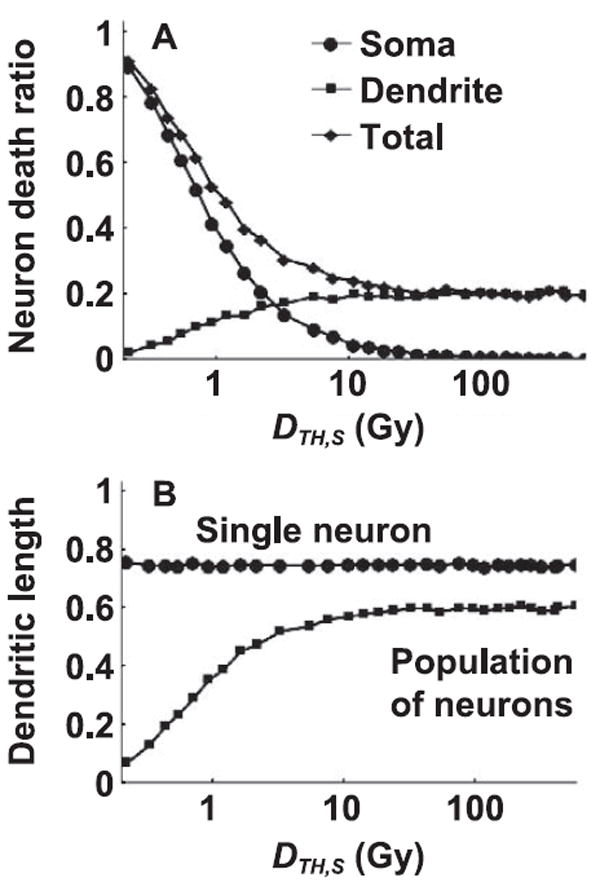
Panel A: Total neuron death caused by soma death (soma) and dendritic snipping (dendrite) for absorbed dose, D_F = 0.5 Gy by ¹⁶O (600 MeV/n) irradiation using model parameters, D_TH,D = 250 Gy and DL_TH = 0.5. Equilibrium value of total neuron death at large D_TH,S (>10 Gy) leads to an asymptote to 0.20. Panel B: Total dendritic length of a single neuron is independent of D_TH,S and mean value is DL = 0.74. For the DL value for normalized population of neurons, mean value reaches 0.59 when soma death is negligible.

The reduction in single neuron morphology (Fig. 7B) with a constant value of DL = 0.74 is not affected by D_TH,S, since single neuron morphometric values are determined only for survived neurons. Morphometric values for a single neuron depend on both D_TH,D and DL_TH, which are considered in the next section. Soma apoptosis does not occur for large D_TH,S (D_TH,S ≫ D_F) values such that any neuron death would be attributed to dendritic reduction in model predictions. The resultant population statistics reach the equilibrium value DL = 0.59, see Fig. 7B. Reduction in total dendritic length is the only mode of neuronal death (e.g., D_TH,S > 10 Gy; see Fig. 7), and a correlation between measured single neuron and population of neurons indicates that DL values (0.74, 0.59; see Fig. 7B) are tied to the total neuron death probability of 0.20 in Fig. 7A by a simple arithmetic product of 0.59 = (1 – 0.20) ×0.74. As absorbed dose increases, the half-values of D_TH,S also increase. For example, neuron death reaches (2⁻¹, e⁻¹) half-values of (0.15, 0.22 Gy), (0.75, 1.12 Gy) and (3.00, 4.80 Gy) at absorbed doses of (0.1, 0.5, 2 Gy), respectively.

Effects of D_TH,D and DL_TH on Single Neuron and Neuron Population Morphology

The values of D_TH,D and DL_TH modify both the single neuron and population of neurons morphometric parameters. For smaller D_TH,D in Eq. (5), more snips occur and dendritic reduction is promoted. In Fig. 8A, for ¹⁶O irradiation, dose response for normalized mean DL at constant DL_TH (=0.5) is investigated, while keeping the D_TH,S value large enough such that soma damage-induced apoptosis does not occur. Higher reduction in DL for single neurons with smaller D_TH,D, see Fig. 8A, independent of constant DL_TH, highlights that surviving single neuron morphometric parameters are not just a function of an intrinsic dose-dependent survival parameter as modeled in Fig. 5, but that the probability of reduced DL in surviving neurons increases as a higher number of snips occurs.

FIG. 8.

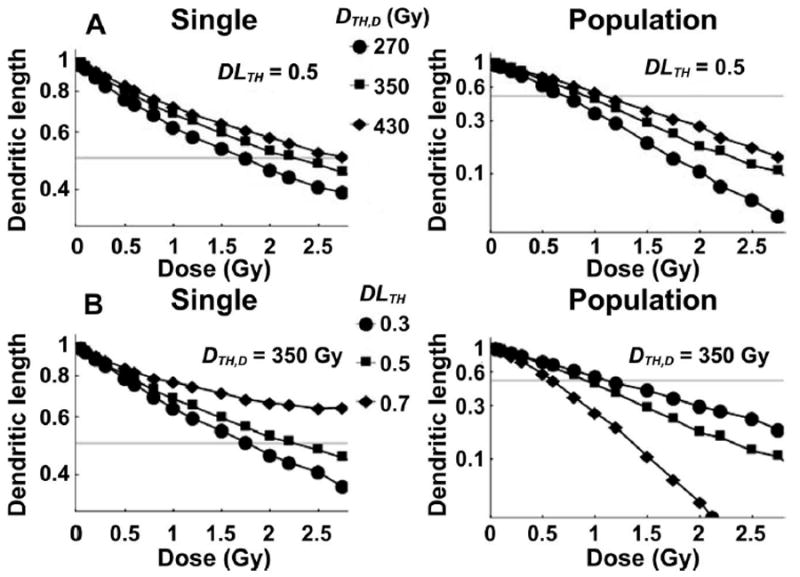
Dose response for ¹⁶O radiation of the dendritic length for single neuron and population of neurons are compared for different model parameter values. Panel A: Varying D_TH,D with DL_TH = 0.5. Panel B: Varying DL_TH with D_TH,D = 350 Gy.

Neurons with lower DL reduction, shown in Fig. 5, can support more of their viability by truncated dendrites in the model. This conclusion is predicted at the single neuron level shown in Fig. 8B; the mean DL of single neuron measurements is shorter for lower DL_TH values at given constant D_TH,D. If the neurons can survive with reduced DL, then less neuron death due to dendritic shortening takes place. As a result, the mean population values of DL are higher for lower DL_TH (see Fig. 8B). These predictions indicate that differences between single neuron and population of neuron morphometric parameters are reduced for lower DL_TH values.

Absorbed Dose Dependence of Morphological Changes

It is expected that the number of snip occurrences and reduction in DL, BP and BN increase with absorbed dose. Dendritic snips in the model depend on the dendritic segment ED and the value of D_TH,D in Eq. (5). The DL response parameter DL_TH determines if the neuron survives under a damaged dendritic structure [Eq. (5)]. The number of snips at given absorbed dose D_F is found to be larger for ⁴⁸Ti than ¹⁶O radiation over a range of D_TH,D values. The dendritic snips per Gy at D_TH,D (180, 250, 350, 450 Gy) for ¹⁶O and ⁴⁸Ti are (15.7, 11.4, 8.2, 6.4) and (15.7, 11.8, 8.6, 6.8), respectively. Responses of DL, BP and BN for single neuron statistics with respect to number of snips are shown in Fig. 9. The results shown in Fig. 9 were obtained by first simulating absorbed dose responses for D_TH,D over (180, 250, 350, 450 Gy) for DL_TH (0.3, 0.5, 0.7), then plotting resultant mean values of DL, BP, BN for the corresponding number of snips. The model predicts that the snip response does not depend strongly on D_TH,D, as different values generate the same snip response at given DL_TH as shown in Fig. 9A. The snip half-values, S_HV, (e.g., DL = DL₀ 2^{number of snips/SHV}) for (DL, BP, BN) are (14.5, 18.2, 27.6) snips under ⁴⁸Ti irradiation, see Fig. 9A. The same snip response curves for ¹⁶O are (15.4, 19.0, 29.0) snips. Evaluation of half-values and snip response of DL, BP, BN suggests that ⁴⁸Ti is more effective per unit dose in shortening the DL, BP and BN than ¹⁶O, as the number of snips per Gy is larger for ⁴⁸Ti (3.5%) and DL response requires less snips (5.3%) for ⁴⁸Ti than ¹⁶O to reach the same reduced DL levels. The dose responses for DL, BP and BN, as in Fig. 6, for a given D_F are more effective for ⁴⁸Ti than ¹⁶O irradiation in our simulations.

FIG. 9.

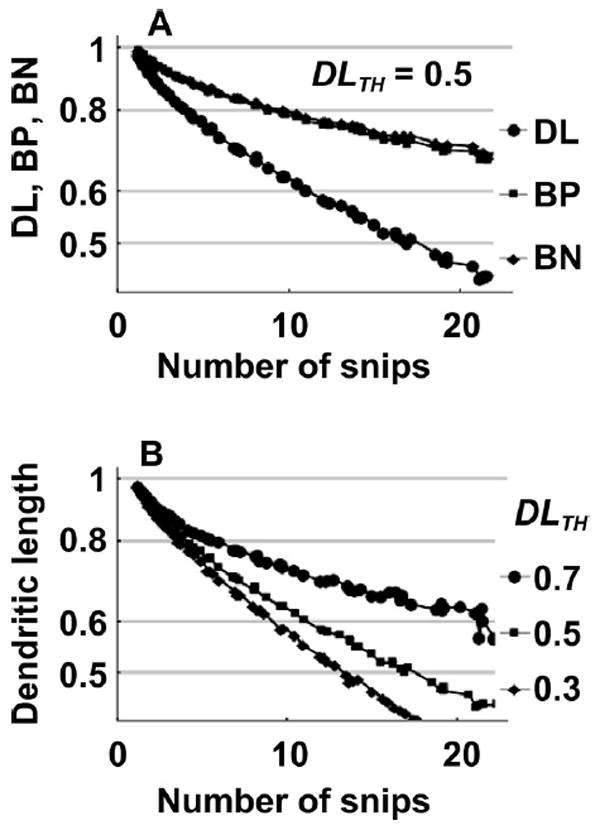
Panel A: Change in single neuron DL, BP and BN for given number of snip occurrences on the test neuron is plotted for ⁴⁸Ti radiation. A range of D_TH,D values, (180, 250, 350 and 450 Gy) gives the same snip response for DL, BP and BN, but the final results depend on DL_TH (=0.5). Panel B: Change in dendritic length for single neuron statistics with given number of snips is shown for DL_TH (0.7, 0.5, 0.3). To highlight the effects of snip numbers on morphometric parameters predictions with negligible soma dose death (D_TH,D > 1,000 Gy) are shown, and single neuron statistics over the surviving neurons are chosen.

The change in DL with the number of snips for single neurons are shown for different DL_TH values over the same range of D_TH,D values shown in Fig. 9B. Because neurons with smaller DL can survive with smaller DL_TH values and contribute to sampling statistics in the model, DL is smaller for smaller DL_TH at a given number of snips.

Random Snip Models Predict Similar Reduction in Morphometric Parameters

The SDM initiates random hits to segments by primary and δ-ray tracks, while allowing for correlated ED along the radial and longitudinal directions of a heavy-ion path. In contrast, the random hit models (Rnd1, Rnd2) are reduced to spatially random hits scaled by cross section areas (Rnd1) and axes lengths (Rnd2) of segments and constant dose proportional to absorbed dose per hit. The reduction in DL of single neurons and population of neurons are compared for the three models. Dose half-values for reduction in DL and the number of snips per Gy are given in Tables 2 and 3 for threshold values (D_TH,S, D_TH,D) set at DL_TH = 0.5 as (>1,000, 300 Gy) and (5, 600 Gy), respectively. Because random models use mean dose per hit scaled by the LET of the particles, LET of 0.4 keV/μm, for example, representing protons at ~240 MeV, are added to the tables to compare results of random models over a range of LET values.

TABLE 2.

Comparison of Model Predictions for Absorbed Doses for DL Half-Values Number of Snips per Gy Assuming High Soma Survival Rates

	Model	DL half-values (Gy)		No. of snips/Gy
		Single	Population
48Ti (129 keV/μm)	SDM	1.616	0.660	10.03
	RND1	1.801	0.756	9.17
	RND2	1.630	0.723	12.33
16O (16.3 keV/μm)	SDM	1.754	0.744	9.61
	RND1	1.718	0.720	10.0
	RND2	1.554	0.687	13.53
0.4 keV/μm	RND1	1.691	0.699	10.17
	RND2	1.537	0.670	13.74

Notes. The half-values in Gy are calculated for DL reduction per Gy of absorbed dose in the SDM, RDM1 and RDM2 models using (D_TH,S, D_TH,D and DL_TH) set at (>1,000 Gy, 300 Gy, 0.5). The LET of 0.4 keV/μm is representative of δ rays and is used in the simulations performed in the RND1 and RND2 models. The number of snips per Gy shown in the last column is identical in the single and population analysis.

TABLE 3.

Comparison of Model Predictions for DL Half-Values and Number of Snips per Gy for Average Soma Survival Rates

	Model	DL half-values (Gy)		No. of snips/Gy
		Single	Population
48Ti (129 keV/μm)	SDM	2.663	0.976	14.51
	RND1	3.031	1.088	15.37
	RND2	2.707	1.412	17.83
16O (16.3 keV/μm)	SDM	2.629	0.930	15.8
	RND1	2.558	0.925	16.03
	RND2	2.265	1.142	18.68
0.4 keV/μm	RND1	2.927	1.057	15.57
	RND2	2.603	1.364	18.12

Notes. The half-values in Gy are calculated for DL reduction per Gy of absorbed dose in the SDM, RDM1 and RDM2 models for parameters (D_TH,S, D_TH,D, DL_TH) set at (5 Gy, 600 Gy, 0.5). The LET of 0.4 keV/μm is representative of d rays and is used in the simulations of the RND1 and RND2 models. The number of snips per Gy shown in the last column is identical in the single and population analysis.

Table 2 underscores the effects of dendritic reduction in models solely causing the neuronal death and resultant population statistics. In addition to the earlier observation of more effective DL reduction by ⁴⁸Ti than ¹⁶O radiation in the SDM indicated by the presented half-values, the random models tend to show an opposite trend; ¹⁶O is more effective than ⁴⁸Ti in shortening DL at a given absorbed dose. The RND2 shows a larger number of snips per Gy and a higher reduction in DL at a given absorbed dose than SDM and RND1 models. The results shown in Table 2 verify a similarity between SDM and RND1 models particularly for ¹⁶O irradiation. This indicates that when soma death is negligible and dendrite segment doses are calculated by stochastic secondary dose for given segment [Eq. (4)], a similar dose response occurs when the secondary dose per hit is determined by constant values [Eq. (9)].

Table 3 introduces neuron death by soma apoptosis by lowering the D_TH,S with the contribution of dendrite shortening and direct soma death to the total neuron death of the same order (unpublished results). The response of the SDM model indicates reversal in ¹⁶O and ⁴⁸Ti effectiveness compared to Table 2. This is due to the effectiveness of DL reduction by smaller half-values for ¹⁶O than ⁴⁸Ti in Table 3. Random models show a higher dose response in dendritic reduction for ¹⁶O as well. These results imply variable effects of LET on reduction of neuromorphic parameters when the total neuron death is weighted by dendritic shortening and soma apoptosis. The correlation of more snips per Gy providing more reduction in DL holds among all models considered.

DISCUSSION

Dendritic complexity influences many aspects of neuronal function, including excitatory and inhibitory post-synaptic potentials and information processing (47, 48). Notably, alterations in neuronal branching and dendritic spine morphology, including the shape, size and number of spines, have been found in several brain disorders, suggesting that dendritic spines may serve as a common factor in the pathogenesis of neurodegenerative disorders (49). Changes in dendritic complexity can affect the geometry of neural connections, the formation of synapses and the overt function of neurons (50, 51). It is well known that changes in neuronal and spine structure as well as in the expression of various neurotransmitters contribute to the cognitive decline observed in aging and in the early stages of neurodegenerative diseases such as Alzheimer’s and Parkinson’s disease (49, 52). Many of the consequences of the foregoing insults can be linked to alterations in the outgrowth and elongation of dendrites, branching of the dendrites, number of dendritic endings and cell body area (53, 54). Morphometric changes in neurons reflect the amount of remodeling and neurite outgrowth that occurs in response to specific stimuli. These changes are modulated by intrinsic and extrinsic stimuli such as signaling cascades, trophic factors, dendritic arborization, synaptogenesis electrical activity, functional maturation and differentiation of neurons (55-57), as well as radiation exposure (10-16, 58, 59). These observations highlight the need for understanding the effects of radiation-induced morphological changes, with the focus of this work on the understanding of heavy-ion-induced changes.

The current work focuses on heavy-ion radiation, where changes to dendritic morphology have been reported at low to moderate doses (11, 13-16). Experiments with X-ray radiation have shown inconsistent findings, with both positive (9, 10, 12, 58, 59) and negative (60, 61) results for morphological changes reported. However, interpretation is difficult due to differences in animal models, brain regions, doses and time after irradiation used in the various experiments. Microscopic energy deposition in small volumes such as dendrite segments is qualitatively distinct from X rays due to the heavy-ion track core where very large ED events occur, while such large ED is not possible for X-ray doses less than ~100 Gy.

The biophysics model we have developed integrates detailed morphological data on dendritic structure with a stochastic model of heavy-ion track structure including δ rays. The model has only three free parameters, D_TH,S, D_TH,D and DL_TH, which, once determined, allow for detailed predictions of changes in neuron morphology for different doses of any charged particle. Quantitative descriptors of neuron morphology tied to experimental data outcomes are DL, BP and BN for delineated single neurons or population of neurons in imaged brain slices. Sholl analysis was used to compare projection of spatial dependence of snips at the single neuron level. Experimental data evaluation in light of model predictions can search for fitted model parameters by a top-down approach to compare model outputs to experimental outcomes. Experiments showing changes to neuron morphology have used differential postirradiation time points, particle beam types (O, Ti and Fe) at only one or two absorbed doses, while studying distinct brain regions and neuronal cell types with additional differences in animal age and strain, and morphological scoring approaches (11, 13-16). These factors limit the usefulness of their data compared to the current results. The results described here show great flexibility in describing such data with only a small number of model parameters. Future work will extend this approach to consider the time dependence of morphological changes induced by particle radiation.

The range of values considered for D_TH,S, D_TH,D are reflective of neuronal apoptosis (44-46) and protein damage (62, 63), respectively. For the latter, much less is known. However, we suggest that clusters of damaged microtubule, membrane lipids, cytoskeleton and other proteins would trigger one or more biochemical responses such as sustained reactive oxygen pathways, mitochondria, to name a few. The activation of microglia several weeks after both low-and high-LET irradiations has been shown in several studies (6, 46, 64, 65). Activated microglia play a role in synaptic pruning, but less is known about their function in dendrite reduction (66). Dendritic cytoskeletal proteins are polymers exhibiting rapid turnover (67) and sensitivity to calcium (68) and magnesium concentrations along with ATP and GTP availability. Membrane lipid damage and ion concentrations are important in controlling the polymerization/ depolymerization equilibrium. In vitro studies aimed at identifying these changes after particle beam irradiation would be useful to help elucidate the most likely mechanisms. In addition, clusters of damaged spines, including excessive damage to neuro-receptors, could also trigger dendrite degeneration and such damage would be reflected in large ED events in the segments considered in this work. We have assumed such damages lead to snips and loss of dendritic branch segment resulting in DL reduction, however, retraction, regrowth and deletions are also possible. The ED model developed here can serve to investigate such possibilities when further experimental data are obtained. Single neuron degeneration could also contribute to degeneration of adjacent neurons with active synaptic contacts; however, this requires further investigation.

A technical limitation in the observations of brain slices is poor identification of single neuron structures due to the absence of information of the number of soma in the slice. This leads to the presentation of statistics in changes of morphological structure for a population of neurons. In contrast, identification of single neurons can be achieved by indicator dye loading and Golgi staining of single neurons, or delineation of principal neurons for a sparse population of brain regions and neuron types. When technical issues of image processing are overcome, these approaches can provide solutions for quantitative evaluation, although experimental drawbacks like incomplete Golgi staining can skew quantitative data evaluation. The modeling approach used here can guide statistics for single neuron or neuron population studies, as well as aid in distinguishing predicted changes among different types of neurons in evaluating brain slices in future studies. Results showed differences between single neuron and population approaches dependent on the extent of neuron cell death.

Parameter estimates related to neuronal loss can be optimized with additional experimental data. If total neuron survival (Fig. 7) can be determined experimentally, e.g., by counting the number of somas and soma density as the ratio of nonirradiated and irradiated neurons in slices of brain sections, then the contribution of soma apoptosis and excessive dendrite reduction to neuron death can be elucidated. Potential biological markers or microscopic studies indicating variation in time course of neuron death by soma collapse or dendritic snips is another potential tool to unfold these two pathways in experimental studies.

The parameters D_TH,D and DL_TH are tied to dendritic snipping. Smaller DL_TH fosters the survival of snipped neurons as shown in Fig. 8, which can be observed by Sholl analysis, and reverse outcomes in the reduction of DL are predicted in single neuron and population of neuron statistics. The number of dendritic segment snips with reduction in DL increase as numerical D_TH,D value is reduced (Fig. 8A). Neurons can survive with shorter mean DL if their DL_TH value decreases, which is observed by reduced dendritic lengths of surviving single neurons and less neuronal death. As a result of increased neuronal survival, the neuron population of DL is higher at low DL_TH (Fig. 8B). In contrast, a larger DL_TH value leads to less reduction in DL of single neurons, more neuron death promoted by dendritic snips and a larger reduction of morphometric parameters in population statistics. Predicted number of snip occurrences and reduction in DL can also be a tool to determine DL_TH.

One of the predictions of the model is that ⁴⁸Ti irradiation with eightfold-higher LET value causes more reduction of morphometric parameters compared to ¹⁶O. However, the difference was not observed for lower values (D_TH,D < 150 Gy) or when soma apoptosis dominates the total neuron death (Table 3). Future studies of other test neurons with varying dendritic structures will provide valuable insight. Because the random snip models do not require particle track information but only LET, absorbed dose and segment cross section areas, our numerical analysis using smaller LET particles (e.g., LET = 0.4 keV/μm) results in higher snip occurrence and higher reduction in morphometric parameters, since neuron death is governed by dendritic shortening and reversal in response, as neuron death is dominated by soma death. These predictions can be tested in the future. Because of the large number of particle types and energies present in primary and secondary galactic cosmic ray exposures (69), random snip models will be useful, given the significant reduction in computational times compared to the SDM model. Both models agreed to within approximately 20% with the detailed stochastic model (SDM), while we could not find significant criteria to favor RND1 or RND2 at this time.

The microscopic dose dependence of dendritic snipping and neuron death pathways are mechanistic models used to hypothesize that energy deposition in dendrites initiates the snipping processes at the same spatial location, while the probability of occurrences can be represented by simple probabilistic models. Targeted pruning (70, 71) rather than random dose deposition to dendrites can help us understand neuron-specific DL reductions under dendrite injuries. Molecular programs for dendrite degeneration may be independent of the age-related pruning of neurons as well as caspase-dependent apoptosis (21). However, in Drosophila, it has been reported that neurons complete regeneration after dendrite removal (72) along with degeneration (73). Much more is known about axon regeneration after damage, due to the difficulties in following dendrites in individual neurons in the time after damage induction.

The in silico model in this work utilizes a single test neuron and allows for predictions on experimentally quantifiable outcomes. The model can be extended to other types of neurons; however, longer computational times will be required for most neuron types due to length and volume considerations. Of note, model parameters found from experimental data evaluation can be fitted to one type of primary neuron class in animal models. The usefulness of this modeling approach is not limited to making predictions for other types of neurons with the same parameter set. Dependence of age, sex and time postirradiation in the same class of neurons in the same animal model can be explored to investigate possible differences. Likewise, parameter values in the model could be compared for different types of neurons or animal models.