Succinct colored de Bruijn graphs

Abstract

Motivation

In 2012, Iqbal et al. introduced the colored de Bruijn graph, a variant of the classic de Bruijn graph, which is aimed at ‘detecting and genotyping simple and complex genetic variants in an individual or population’. Because they are intended to be applied to massive population level data, it is essential that the graphs be represented efficiently. Unfortunately, current succinct de Bruijn graph representations are not directly applicable to the colored de Bruijn graph, which requires additional information to be succinctly encoded as well as support for non-standard traversal operations.

Results

Our data structure dramatically reduces the amount of memory required to store and use the colored de Bruijn graph, with some penalty to runtime, allowing it to be applied in much larger and more ambitious sequence projects than was previously possible.

Availability and Implementation

https://github.com/cosmo-team/cosmo/tree/VARI

Contact

martin.muggli@colostate.edu

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

In the 20 years since it was introduced to bioinformatics by Idury and Waterman (1995), the de Bruijn graph has become a mainstay of modern genomics, essential to genome assembly (Compeau et al., 2011; Muggli et al., 2015; Ronen et al., 2012). The near ubiquity of de Bruijn graphs has led to a number of succinct representations, which aim to implement the graph in small space, while still supporting fast navigation operations. Formally, a de Bruijn graph constructed for a set of strings (e.g. sequence reads) has a distinct vertex v for every unique (k – 1)-mer (substring of length k – 1) present in the strings, and a directed edge (u, v) for every observed k-mer in the strings with (k – 1)-mer prefix u and (k – 1)-mer suffix v. A contig corresponds to a non-branching path through this graph. See (Compeau et al., 2011) for a more thorough explanation of de Bruijn graphs and their use in assembly.

Iqbal et al. (2012) introduced the colored de Bruijn graph, a variant of the classical structure, which is aimed at ‘detecting and genotyping simple and complex genetic variants in an individual or population.’ The edge structure of the colored de Bruijn graph is the same as the classic structure, but now to each vertex ((k – 1)-mer) and edge (k-mer) is associated a list of colors corresponding to the samples in which the vertex or edge label exists. More specifically, given a set of n samples, there exists a set $\mathcal{C}$ of n colors $c_1,c_2,\mathrm{..},c_n$ where c_i corresponds to sample i and all k-mers and (k – 1)-mers that are contained in sample i are colored with c_i. A bubble in this graph corresponds to an undirected cycle, and is shown to be indicative of biological variation by Iqbal et al. (2012). Cortex, the implementation of Iqbal et al. (2012), uses the colored de Bruijn graph to develop a method of assembling multiple genomes simultaneously, without losing track of the individuals from which (k – 1)-mers (and k-mers) originated. This graph is derived from either multiple reference genomes, multiple samples, or a combination of both.

Variant information of an individual or population can be deduced from structure present in the colored de Bruijn graph and the colors of each k-mer. As implied by Iqbal et al. (2012), the ultimate intended use of colored de Bruijn graphs is to apply it to massive, population-level sequence data that is now abundant due to next generation sequencing technology (NGS) and multiplexing. These technologies have enabled production of sequence data for large populations, which has led to ambitious sequencing initiatives that aim to study genetic variation for agriculturally and bio-medically important species. These initiatives include the Genome 10K project that aims to sequence the genomes of 10 000 vertebrate species (Genome 10K Community of Scientists, 2009), the iK5 project (Robinson et al., 2011), the 150 Tomato Genome ReSequencing project (Causse et al., 2013; Kobayashi et al., 2014) and the 1001 Arabidopsis project, a worldwide initiative to sequence cultivars of Arabidopsis (Weigel and Mott, 2009). Hence, the succinct colored de Bruijn graph is applicable in the context of these projects, in that it can assist in variation discovery within a species by analyzing all the data in these projects at once.

In addition to species-specific initiatives, scientific and regulatory agencies are showing increased interest in shotgun metagenomic sequences for public health purposes (EMBL-EBI Metagenomics, 2016; Miller et al., 2013), specifically monitoring for antimicrobial resistance (AMR) (Baquero et al., 2012; Port et al., 2014). AMR is considered one of the top public health threats, with fears that the spread of AMR will lead to increased morbitiy and mortality for many bacterial illnesses (Food and Agricultural Organization of the United Nations, 2016; The White House, 2015). AMR occurs when bacteria express genetic elements that render them impervious to antibiotic treatments. Importantly, these genetic resistance elements can be exchanged between distantly-related bacteria via multiple genetic mechanisms, which makes AMR an inherently population-level phenomenon (Baquero et al., 2013). Shotgun metagenomic sequencing allows access to the entire microbial population in a sample (the ‘metagenome’), which is of immense value for tracking and understanding the evolution of resistance elements within and across diverse bacteria(MacLean et al., 2010). This metagenomics approach to AMR surveillance has been applied in both human and agricultural settings (King et al., 2016; Noyes et al., 2016), generating hundreds of samples with terabytes of sequence data for relatively small studies. Given the large number of samples and large size of sequence data involved in these whole-genome and metagenomic projects, it is imperative that the colored de Bruijn graph can be stored and traversed in a space- and time-efficient manner.

Our contribution. We develop an efficient data structure for storage and use of the colored de Bruijn graph. Compared to Cortex, the implementation of Iqbal et al. (2012), our new data structure dramatically reduces the amount of memory required to store and use the colored de Bruijn graph, with some penalty to runtime. We demonstrate this reduction in memory through a comprehensive set of experiments across the following three datasets: (i) four plant genomes, (ii) 3765 Escherichia coli assemblies and (iii) 87 sequenced metagenomic samples from commercial beef production facilities. We show our method, which we refer to as Vari (Finnish for color), has better peak memory usage on all these datasets. Our plant reference genomes dataset required 101 GB of RAM for Cortex to represent while Vari required only 4 GB. And our largest two datasets contain too many k-mers and colors for Cortex’s data structure to represent in the 512 GB of RAM available on our bioinformatics servers. Vari is a novel generalization of the succinct data structure for classical de Bruijn graphs due to Bowe et al. (2012), which is based on the Burrows-Wheeler transform of the sequence reads, and thus, has independent theoretical importance.

In addition to demonstrating the memory and runtime of Vari, we validate its output using the E.coli reference genome and a simulated variant.

Related work. As noted above, maintenance and navigation of the de Bruijn graph is a space and time bottleneck in genome assembly. Space-efficient representations of de Bruijn graphs have thus been heavily researched in recent years. One of the first approaches was introduced by Simpson et al. (2009) as part of the development of the ABySS assembler. Their method stores the graph as a distributed hash table and thus requires 336 GB to store the graph corresponding to a set of reads from a human genome (>38× depth paired-end reads from Illumina Genome Analyzer II, HapMap: NA18507 (https://www.ncbi.nlm.nih.gov/sra/?term=SRA010896)).

Conway and Bromage (2011) reduced space requirements by using a sparse bitvector (by Okanohara and Sadakane, 2007) to represent the k-mers (the edges), and used rank and select operations (to be described later) to traverse it. As a result, their representation took 32 GB for the same dataset. Minia, by Chikhi and Rizk (2013), uses a Bloom filter to store edges. They traverse the graph by generating all possible outgoing edges at each node and testing their membership in the Bloom filter. Using this approach, the graph was reduced to 5.7 GB on the same dataset. Contemporaneously, Bowe et al. (2012) developed a different succinct data structure based on the Burrows-Wheeler transform (Burrows and Wheeler, 1994) that requires 2.5 GB. The data structure of Bowe et al. (2012) is combined with ideas from IDBA-UD (Peng et al., 2012) in a metagenomics assembler called MEGAHIT (Li et al., 2015). In practice MEGAHIT requires more memory than competing methods but produces significantly better assemblies. Chikhi et al. (2014) implemented the de Bruijn graph using an FM-index and minimizers. Their method uses 1.5 GB on the same NA18507 data. Holley et al. (2015) released the Bloom Filter Trie, which is another succinct data structure for the colored de Bruiin graph; however, we were unable to compare our method against it since it only supports the building and loading of a colored de Bruijn graph and does not contain operations to support our experiments. SplitMEM (Marcus et al., 2014) is a related algorithm to create a colored de Bruijn graph from a set of suffix trees representing the other genomes. Lastly, Lin et al. (2014) point out the similarity between the breakpoint graph, which is traditionally viewed as a data structure to detect breakpoints between genome rearrangements, and the colored de Bruijn graph.

Roadmap. In the next section, we describe our succinct colored de Bruijn graph data structure, generalizing the stucture for classic de Bruijn graphs presented by Bowe et al. (2012). Section 3 then elucidates the practical performance of the new data structure, comparing it to Cortex. Section 4 offers some concluding remarks.

2 Materials and methods

Our data structure for colored de Bruijn graphs is based on the succinct representation of individual de Bruijn graphs introduced by Bowe et al. (2012)—which we refer to as the BOSS representation from the authors’ initials—so we start by describing that representation. We note that BOSS is itself a generalization of FM-indexes (Ferragina and Manzini, 2005) obtained by extending the Burrows-Wheeler transform (BWT) from strings to the multisets of edge-labels of de Bruijn graphs. We then give a general explanation of how we add colors, and finally give details of our implementation.

2.1 BOSS representation

Consider the de Bruijn graph $G=(V,E)$ for a set of k-mers, with each k-mer $a_0\cdots a_{k-1}$ representing a directed edge from the node labelled $a_0\cdots a_{k-2}$ to the node labelled $a_1\cdots a_{k-1}$, with the edge itself labelled $a_{k-1}$. Define the nodes’ co-lexicographic order to be the lexicographic order of their reversed labels. Let F be the list of G’s edges sorted co-lexicographically by their ending nodes, with ties broken co-lexicographically by their starting nodes (or, equivalently, by their k-mers’ first characters). Let L be the list of G’s edges sorted co-lexicographically by their starting nodes, with ties broken co-lexicographically by their ending nodes (or, equivalently, by their own labels). If two edges e and $e\prime$ have the same label, then they have the same relative order in both lists; otherwise, their relative order in F is the same as their labels’ lexicographic order. Defining the edge-BWT (EBWT) of G to be the sequence of edge labels sorted according to the edges’ order in L, so $\mathrm{label}(L[h])=\mathrm{EBWT}(G)[h]$ for all h, this means that if e is in position p in L, then in F it is in position

$$\left|\right\{d\hspace{0.17em}:\hspace{0.17em}d\in E,\hspace{0.17em}\mathrm{label}(d)\prec \mathrm{label}(e)\left\}\right|+\mathrm{EBWT}(G).\mathrm{ran}{\mathrm{k}}_{\mathrm{label}(e)}(p)-1\hspace{0.17em},$$

where $\mathrm{EBWT}(G).\mathrm{ran}{\mathrm{k}}_{\mathrm{label}(e)}(p)$ is the number of times $\mathrm{label}(e)$ appears in $\mathrm{EBWT}(G)[1,p]$. It follows that if we have, first, an array storing $\left|\right\{d\hspace{0.17em}:\hspace{0.17em}d\in E,\hspace{0.17em}\mathrm{label}(d)\prec c\left\}\right|$ for each character c and, second, a fast rank data structure on $\mathrm{EBWT}(G)$ then, given an edge’s position in L, we can quickly compute its position in F.

Let B_F be the bitvector with a 1 marking the position in F of the last incoming edge of each node, and let B_L be the bitvector with a 1 marking the position in L of the last outgoing edge of each node. Given a character c and the co-lexicographic rank of a node v, we can use B_L to find the interval in L containing v’s outgoing edges, then we can search in $\mathrm{EBWT}(G)$ to find the position of the one e labelled c. We can then find e’s position in F, as described above. Finally, we can use B_F to find the co-lexicographic rank of e’s ending node. With the appropriate implementations of the data structures, we can store G in $(1+o(1))\left|E\right|(\lg \sigma +2)$ bits, where σ is the size of the alphabet (i.e. 4 for DNA), such that when given a character c and the co-lexicographic rank of a node v, in $\mathcal{O}(\text{log}\hspace{0.17em}\hspace{0.17em}\text{log}\hspace{0.17em}\sigma )$ time we can find the node reached from v by following the directed edge labelled c, if such an edge exists.

If we know the range $L[i\mathrm{..}j]$ of k-mers whose starting nodes end with a pattern P of length less than (k– 1), then we can compute the range $F[i\prime \mathrm{..}j\prime ]$ of k-mers whose ending nodes end with $Pc$, for any character c, since

$$\begin{array}{c}i\prime =\left|\right\{d\hspace{0.17em}:\hspace{0.17em}d\in E,\hspace{0.17em}\mathrm{label}(d)\prec c\left\}\right|+\mathrm{EBWT}(G).\mathrm{ran}{\mathrm{k}}_c(i-1)\\ j\prime =\left|\right\{d\hspace{0.17em}:\hspace{0.17em}d\in E,\hspace{0.17em}\mathrm{label}(d)\prec c\left\}\right|+\mathrm{EBWT}(G).\mathrm{ran}{\mathrm{k}}_c(j)-1\hspace{0.17em}.\end{array}$$

It follows that, given a node v’s label, we can find the interval in L containing v’s outgoing edges in $\mathcal{O}(k\hspace{0.17em}\text{log}\hspace{0.17em}\hspace{0.17em}\text{log}\hspace{0.17em}\sigma )$ time, provided there is a directed path to v (not necessarily simple) of length at least k – 1. In general there is no way, however, to use $\mathrm{EBWT}(G)$, B_F and B_L alone to recover the labels of nodes with no incoming edges.

To prevent information being lost and to be able to support searching for any node given its label, Bowe et al. add extra nodes and edges to the graph, such that there is a directed path of length at least k – 1 to each original node. Each new node’s label is a (k – 1)-mer that is prefixed by one or more copies of a special symbol $not in the alphabet and lexicographically strictly less than all others. Notice that, when new nodes are added, the node labelled ${\$}^{k-1}$ is always first in co-lexicographic order and has no incoming edges. Bowe et al. also attach an extra outgoing edge labelled $, that leads nowhere, to each node with no original outgoing edge. The edge-BWT and bitvectors for this augmented graph are, together, the BOSS representation of G.

2.2 Adding color

We cannot represent the colored de Bruijn graph for a multiset $\mathcal{G}=\{G_1,\dots ,G_t\}$ of individual de Bruijn graphs satisfactorily by simply representing each individual graph separately, for two reasons: first, the memory requirements would quickly become impractical and, second, we should be able to answer efficiently queries such as ‘which individual graphs contain this edge?’ Therefore, we set G to be the union of the individual graphs and build the BOSS representation only for G. As long as most of the k-mers are common to most of the individual graphs, the memory needed to store G is comparable to that need to store an individual graph.

To indicate which edges of G are in which individual graphs, we build and store a two-dimensional binary array C in which $C[i,j]$ indicates whether the ith edge in G is present in the jth individual de Bruijn graph (i.e. whether that edge has the jth color). (Recall from the description above of BOSS that we consider the edges in G to be sorted lexicographically by the reversed labels of their starting nodes, with ties broken lexicographically by their own single-character labels.) If the individual graphs are sufficiently similar, then we can compress C effectively and store it in such a way that we can still access its individual bits quickly and support fast rank and select queries on the rows. (A $\mathrm{select}$ query on the ith row takes an argument r and returns the index j of the rth individual graph that contains the ith edge in G.) In the next subsection we give details of some relatively simple compression strategies that support fast access, rank and select. With these data structures, we can navigate efficiently in any of the individual graphs and switch between them. For example, we can efficiently check whether an edge has a particular color (with an access), count the number of colors it has (with a $\mathrm{rank}$ query) or list them (with repeated $\mathrm{select}$ queries). We have not yet considered more sophisticated compression schemes that could still offer fast queries while taking advantage of, e.g. correlations among the variations or grouping of the individual graphs by subpopulation.

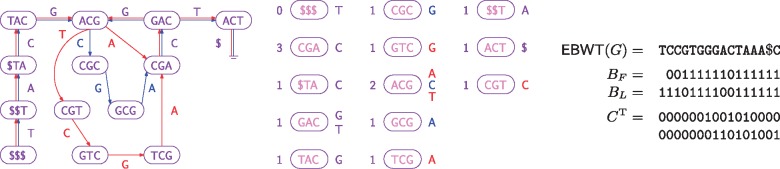
Figure 1 shows an example of how we represent a colored de Bruijn graph consisting of two individual de Bruijn graphs. Suppose we are at node ACG in the graph, which is the co-lexicographically eighth node. Since the eighth 1 in B_L is $B_L[10]$ and it is preceded by two 0s, we see that ACG’s outgoing edges’ labels are in $\mathrm{EBWT}[\mathrm{8..10}]$, so they are A, C and T. Suppose we want to follow the outgoing edge e labelled C. We see from $C[9,\mathrm{0..1}]$ (i.e. the tenth column in $C^{\mathrm{T}}$) that e appears in the second individual graph but not the first one (i.e. it is blue but not red). There are four edges labelled A in the graph and three Cs in $\mathrm{EBWT}(G)[\mathrm{0..9}]$, so e is $F[6]$. (Since edges labelled $ have only one end, they are not included in L or F.) From counting the 1s in $B_F[\mathrm{0..6}]$, we see that e arrives at the fifth node in co-lexicographic order that has incoming edges. Since the first node, $$$, has no incoming edges, that means e arrives at the sixth node in co-lexicographic order, CGC.

Fig. 1.

Left: A colored de Bruijn graph consisting of two individual graphs, whose edges are shown in red and blue. (We can consider all nodes to be present in both graphs, so they are shown in purple.) Center: The nodes sorted into co-lexicographic order, with each node’s number of incoming edges shown on its left and the labels of its outgoing edges shown on its right. The edge labels are shown in red or blue if the edges occur only in the respective graph, or purple if they occur in both. Right: Our representation of the colored de Bruijn graph: the edge-BWT and bitvectors for the BOSS representation for the union of the individual graphs, and the binary array C (shown transposed) whose bits indicate which edges are present in which individual graphs

2.3 Implementation

We now give some details of how our data structure is implemented and constructed in practice.

2.3.1 Data structure

The arsenal of component tools available to succinct data structures designers has grown considerably in recent years (Navarro, 2016), with many methods now implemented in libraries. We chose to make heavy use of the succinct data structures library (SDSL) (https://github.com/simongog/sdsl-lite) in our implementation.

$\mathrm{EBWT}(G)$, the sequence of edge labels, is encoded in a wavelet tree, which allows us to perform fast rank queries, essential to all our graph navigations. The bitvectors of the wavelet tree and the B bitvector are stored in the Raman-Raman-Rao (RRR) encoding (Raman et al., 2007). The rows of the color matrix, C, are concatenated (i.e. C is stored in row-major order) and this single long bit string is then compressed. It is either stored with RRR encoding, or alternately Elias-Fano encoding (Elias, 1974; Fano, 1971; Okanohara and Sadakane, 2007) which supports online construction. Online construction is important for datasets where C is too large to fit in memory in uncompressed form, such as our metagenomic sample dataset. These encodings reduce the size of C considerably because we expect rows to be very sparse and both encodings exploit this sparseness.

2.3.2 Construction

In order to convert the input data to the format required by BOSS (that is, in correct sorted order, including dummy edges and bit vectors), we use the following process. We take care to ensure only subsets of data are needed in RAM at any one time during construction.

Our construction algorithm takes as input the set of (k-mer, color-set) pairs present in the input sets of reads, or alternately, k-mer counts for each color which we convert to the former ourselves. Here, color-set is a bit set indicating which samples the k-mer occurs in. We provide the option to use the Cortex frontend to generate the (k-mer, color-set). Unfortunately, this also limits the datasets to those that would run through Cortex. To overcome this, we provide the option to use a list of KMC2 (Deorowicz et al., 2015) sorted k-mer counts as input. With this option, the k-mers from each k-mer count file in native KMC2 binary format are streamed through a priority queue to produce the union of all k-mer sets; initially one k-mer from each file is tagged with which file it originated from, and the (k-mer, file ID) pair is added to the queue. The priority queue ensures the lexicographically smallest k-mer instances across all files can be popped off the queue consecutively. All of the k-mer count files contributing a particular k-mer value have their corresponding color recorded as ‘1’ bits in the bit set for that k-mer. Both the k-mer and the bit set are then appended to vectors which optionally are allocated in external memory using the STXXL (http://http://stxxl.sourceforge.net/) library. As each k-mer is popped off the queue, another k-mer is added to the queue to take the old k-mer’s place (i.e. using the file identified by the popped k-mer’s tag). This process continues until all files are read in their entirety. By both streaming data from the source files and streaming it to the external vectors, only a small amount of the data need exist in memory at a time; the priority queue will only contain the number of samples and only one row of the color matrix needs to exist in memory before being written out to disk.

After constructing the initial union set of k-mers and their corresponding color rows, BOSS construction mostly continues as originally described by Bowe et al. The changes from the original construction algorithm are that most of the data optionally resides in external memory and the rows of the color matrix are permuted with their corresponding k-mers as they are sorted. For each of the k-mers we generate the reverse complement (giving it the same color-set as its twin). Then, for each k-mer (including the reverse complements), we sort the (k-mer, color-set) pairs by the first k – 1 symbols (the source node of the edge) to give the F table (from here, the colors are moved around with rows of F, but otherwise ignored until the final stage). Independently, we sort the k-mers (without the color-sets) by the last k – 1 symbols (the destination node of the edge) to give the L table.

With F and L tables computed, we calculate the set difference F – L (comparing only the $(k-1)$-length prefixes and suffixes respectively), which tells us which nodes require incoming dummy edges. Each such node is then shifted and prepended with $signs to create the required incoming dummy edges (k – 1 each). These incoming dummy edges are then sorted by the first k – 1 symbols. Let this table of sorted dummy edges be D. Note that the set difference L – F will give the nodes requiring outgoing dummy edges, but these do not require sorting, and so we can calculate it as is needed in the final stage.

Finally, we perform a three-way merge (by first k – 1 symbols) D with F, and L – F (calculated on the fly). For each resulting edge, we keep track of runs of equal k – 1 length prefixes, and $k-2$ length suffixes of the source node, which allows us to calculate the $B_F\hspace{0.17em}\text{and}\hspace{0.17em}{B}_L$ bit vectors, respectively. Next, we write the bit vectors, symbols from last column, and count of the second to last column to a packed file on disk, and the colors to a separate file. The color file is then either buffered in RAM and RRR encoded or optionally streamed from disk and then Elias-Fano encoded online (i.e. only the compressed version is ever resident). The time bottleneck in the above process is clearly in sorting the D and F tables, which are of the same size, and are made up of elements of size $O(k)$. Thus, overall, construction of the data structure takes $O(k(\left|F\right|\hspace{0.17em}\text{log}\hspace{0.17em}\left|F\right|))$ time.

2.3.3 Traversal

We implemented two traversal methods based on those of Cortex with a modification in light of our intention to apply Vari to metagenomic reads looking for AMR gene presence.

The first, bubble calling, is a simple algorithm to detect sequence variation in genomic data. It consists of iterating over a set of k-mers in order to find places where bubbles start and terminate. When combined with the k-mer color (in a colored de Bruijn graph), this enables identification of places where genomic sequences diverge from one another. The differing region of the two sequences will form the two arms of a bubble, each colored with only one of the two sequence’s colors. A bubble is identified when a vertex has two outgoing edges. Each edge is followed in turn to navigate a non-branching path until reaching a vertex with two incoming edges. If the terminating vertex is the same for both paths, we call this a bubble. Colors for the bubbles are determined by looking at the color assignment of the corresponding $(k)$-mers. Our implementation in Vari closely follows the pseudocode given by Iqbal et al. (2012).

Cortex’s traversal algorithms were designed for single isolates. For the beef safety experiments, which use metagenomic samples, we implemented a traversal inspired by Cortex’s path divergence algorithm. In the original Cortex path divergence algorithm, bubbles are identified where a user-supplied reference sequence prescribes a walk through a (possibly tangled) sections of the graph in one arm of a bubble while the alternative arm must be branch free. This branch free requirement on the second arm could be a problem for metagenomic data. Due to the presence of tangle inducing homologous genomes and risk of inferring erroneous, chimeric sequences (which comprise reads from a mix of genomes in the sample), variant detection in metagenomic data is more complex. In the absence of a simple metagenomic-aware traversal algorithm, we implemented a variation of the path divergence algorithm which addresses a simpler problem, primarily for the purpose of measuring performance. This algorithm uses a reference guided approach and allows us to measure the memory footprint at traversal time as well as the time savings of not traversing the entire dataset. For this purpose, we focus specifically on the presence of AMR genes (our reference sequence) rather than variants of those genes; in our derived algorithm we ignore sample path segments leading away from and returning to the AMR gene path. This avoids some of the problems with tangles, incomplete coverage, or read errors. Thus as we traverse the gene path, we simply count the number of samples in each sample group that color the current edge. We note that keeping C in row major order allows us to compute this count in constant time as the difference between two $\mathrm{rank}$ queries.

3 Results

We evaluated Vari performance on three different datasets, described below. For this evaluation, we compare peak memory, which was measured as the maximum resident set size, and CPU core time, measured as the user + system process time as our metrics. In addition to evaluating performance, we also validated Vari by the ability to correctly call bubbles known to be present in a simulated dataset.

Our software supports a variety of options. It can consume k-mer counts from either Cortex’s binary files or KMC2. For all experiments, we use the KMC2 flow because using Cortex as a front end limits designs to only those that would fit in memory with Cortex. Next, our software can compress the color matrix using either RRR or Elias-Fano encodings. The SDSL-light implementation allows the color matrix to be compressed in an on-line fashion only using the Elias-Fano encoding. This allows us to process larger designs, as the uncompressed matrix need never fit in RAM, and thus we use this option for all experiments. Finally, STXXL (which holds temporary vectors during data structure construction) allows using internal or external memory. Again, we used the more scalable external memory option for all experiments. All experiments were performed on a machine with AMD Opteron model 6378 processors, having 512 GB of RAM and 64 cores.

3.1 Datasets

The three different datasets were chosen in order to test and evaluate the performance of Vari on a variety of diverse yet realistic data types that are likely to be used as input into Vari. For the first two datasets which comprise single isolates, we use preassembled genomes. Assembly serves to try correct sequencing errors which could otherwise falsely be detected as variants. To this end, Cortex includes its own optional data cleaning operations. However, by using instead the output of third party assembly software we can compare the colored de Bruijn graph performance on identical graphs. Characteristics about these datasets are provided in Table 1.

Table 1.

Characteristics of our datasets

Name	Accession numbers	Aprox. size	GC Content
Plant species	Rice (NC_008394 to NC_008405)	430 Mbp	43.42%
	Tomato (NC_015438 to NC_015449)	950 Mbp	43.42%
	Corn (NC_024459 to NC_024468)	2.07 Gbp	35.70%
	Arabidopsis (NC_003070 to NC_003076)	135 Mbp	47.4%
E.coli strains	N/A	avg=5.1 Mbp min=2.9 Mbp max= 7.7 Mbp	50.5%
Beef safety	PRJNA292471	N/A	44.3%

The E.coli dataset represents 3765 strains and hence only summary statistics for size and GC content are given. Accession numbers for this dataset as well as download procedure can be found in assembly_summary.txt as discussed in the main text.

Our first performance dataset comprises reference genomes for four different plant species: Oryza sativa Japonica (rice) (http://rice.plantbiology.msu.edu/annotation_pseudo_current.shtml) (Tanaka et al., 2008), Solanum lycopersicum (tomato) (ftp://ftp.solgenomics.net/tomato_genome/assembly/build_2.50/SL2.50ch00.fa.tar.gz) (Causse et al., 2013; Kobayashi et al., 2014), Zea mays (corn) (ftp://ftp.ncbi.nlm.nih.gov/genomes/all/GCF/000/005/005/GCF_000005005.1_B73_RefGen_v3/GCF_000005005.1_B73_RefGen_v3_genomic.fna.gz) (Schnable et al., 2009) and Arabidopsis thaliana (Arabidopsis) (ftp://ftp.ensemblgenomes.org/pub/plants/release-34/fasta/arabidopsis_thaliana/dna/) (Swarbreck et al., 2008). This represents a sufficiently large dataset for comparing the performance of Vari with Cortex.

Our second performance dataset consists of the set of all 3765 NCBI GenBank assemblies (ftp://ftp.ncbi.nlm.nih.gov/genomes/genbank/bacteria/assembly_summary.txt; https://www.ncbi.nlm.nih.gov/genome/doc/ftpfaq/) having the organism_name field equal to ‘Escherichia coli’ as of March 22, 2016. To evaluate the effects of varying k-mer size, we ran this dataset with $k=32,48,64$. The union of all assemblies contains 158 501 209 k-mers for k = 32, 205 938 139 k-mers for k = 48 and 251 764 413 k-mers for k = 64. The minimum, maximum and average assembly lengths are 2 911 360 bp, 7 687 202 bp and 5 156 744 bp, respectively.

Our third performance dataset consists of 87 metagenomic samples (https://www.ncbi.nlm.nih.gov/bioproject/292471) taken at various timepoints during the beef production process from eight pens of cattle in two beef production facilities by Noyes et al. (2016). Sequentially, these timepoints were feedlot arrival, feedlot exit, slaughter transport truck, slaughter holding and slaughter trimmings and sponges. Sample reads were preprocessed using trimmomatic v0.36 by Bolger et al. (2014). Although further assembly or error correction would have been possible, it would reduce the biological variation which may be useful for some queries. Furthermore, building the data structure on uncorrected data better stresses our representation method. Samples were then arranged into groups based on the sample timepoints. The original study used these samples to demonstrate the advantages of shotgun metagenomic sequencing in tracking the evolution of antimicrobial resistance longitudinally within a complex environment like beef production; the results suggested that selective pressures occurred within the feedlot, but that slaughter safety measures drastically reduced both bacterial and AMR levels. In addition to the metagenomic samples, we included 4062 AMR genes from the previously mentioned gene databases (https://meg.colostate.edu/MEGaRes/). 23 genes in the databases containing IUPAC codes other than the four bases were filtered out as KMC2 and the succinct de Bruijn graph were configured with a four symbol alphabet. Because we have the reference to guide the traversal, all AMR genes were combined into a single color. By combining AMR genes, the uncompressed color matrix that exists on disk during sorting and as intermediate file is much smaller (still occupying 1.2 TB), thus accelerating the permutation during construction and reducing the external memory and disk space requirements. The union of all samples and genes contains 40 995 794 366 32-mers and the GC content is 44.3%. While our server has enough RAM to represent a dataset with twice the memory footprint, this dataset nearly exhuasted the approximately 10 TB of disk space available when intermediate files were preserved. Thus this dataset is on the order of the upper limit for Vari in practice.

Finally, for validation purposes, we generated a dataset (https://github.com/cosmo-team/cosmo/tree/VARI/experiments/ecoli_validation) comprising two genomes: (i) E.coli K-12 substraing MG 1655 reference genome, and (ii) a copy of the reference genome to which we applied various simulated mutations. We simulated mutations by choosing 100 random loci and either inserting, deleting, or replacing a region of random length ranging from 200 to 500 bp. For each mutation locus, we record the flanking regions and the two variants (original reference and simulated) as a ground truth bubble.

3.2 Time and memory usage

To measure Vari’s resource use and compare with Cortex by Iqbal et al. (2012) where possible, we constructed the colored de Bruijn graph for the plant dataset, the E.coli assembly dataset and the beef safety dataset. Construction time and memory is detailed in Supplementary Table 2. We performed bubble calling on the first two and recorded peak memory usage and runtime. Direct resource comparison with Cortex was only possible on the smallest dataset, as the largest two have too many k-mers and colors to fit in memory on our machine with Cortex. Based on the data structure defined in Cortex’s source as well as the supplementary information provided by Iqbal et al., it would have required more than 3 TB of RAM and more than 18 TB of RAM for its hash table entries alone, respectively.

In order to test query performance characteristics, various experiments were performed on all three performance datasets described in the previous subsection. Datasets varied in the number of k-mers in the graph from 158 million to over 40 billion, the number of colors, from 4 to 3765, and degree of homology from disperate plants to the single E.coli species. This diversity shows the space savings achievable when the population is largely homologous, as is the case with the E.coli dataset, where the graph component is relatively small, in contrast to the plant dataset, where the graph component is relatively large. As can be seen in Table 2, where directly comparable, Vari used an order of magnitude less than the peak memory that Cortex required but required greater running time. This memory and time trade-off is important in larger population level data. This is highlighted by our largest two datasets which could not be run with Cortex. Hence, lowering the memory usage in exchange for higher running time deserves merit in contexts where there is data from large populations.

Table 3.

Comparison between the peak memory and time usage required to store all the k-mers and run bubble calling on the data in Cortex and Vari

			Cortex		Vari
Dataset	No. of k-mers	Colors	Memory	Time	Memory	Time
Plants (k=32)	1 709 427 823	4	100.93 GB	2 h 18 m	3.53 GB (sdBG=0.89 GB, sC = 1.95 GB)	32 h 39 m
E. coli (k=32)	158 501 209	3765	N/A	N/A	42.17 GB (sdBG=0.09 GB, sC = 38.35 GB)	3 h 57 m
E. coli (k=48)	205 938 139	3765	N/A	N/A	42.26 GB (sdBG=0.11 GB, sC = 38.42 GB)	4 h 38 m
E. coli (k=64)	251 764 413	3765	N/A	N/A	42.32 GB (sdBG=0.13 GB, sC = 38.45 GB)	5 h 28 m
Beef safety (k=32)	40 995 794 366	88	N/A	N/A	245.54 GB (sdBG=27.08 GB, sC = 200.34 GB)	N/A

The peak memory is given in megabytes (MB) or gigabytes (GB). The running time is reported in seconds (s), minutes (m) and hours (h). The succinct de Bruijn graph and compressed color matrix components of the memory footprint are listed in parenthesis as sdBG and sC, respectively.

Table 2.

Comparison between the peak memory and time usage required to store all the k-mers and run bubble calling on the data in Cortex and Vari

			Cortex		Vari
Dataset	No. of k-mers	Colors	Memory	Time	Memory	Time
Plants (k=32)	1 709 427 823	4	100.93 GB	2 h 18 m	3.53 GB (sdBG=0.89 GB, sC = 1.95 GB)	32 h 39 m
E. coli (k=32)	158 501 209	3765	N/A	N/A	42.17 GB (sdBG=0.09 GB, sC = 38.35 GB)	3 h 57 m
E. coli (k=48)	205 938 139	3765	N/A	N/A	42.26 GB (sdBG=0.11 GB, sC = 38.42 GB)	4 h 38 m
E. coli (k=64)	251 764 413	3765	N/A	N/A	42.32 GB (sdBG=0.13 GB, sC = 38.45 GB)	5 h 28 m
Beef safety (k=32)	40 995 794 366	88	N/A	N/A	245.54 GB (sdBG=27.08 GB, sC = 200.34 GB)	N/A

The peak memory is given in megabytes (MB) or gigabytes (GB). The running time is reported in seconds (s), minutes (m) and hours (h). The succinct de Bruijn graph and compressed color matrix components of the memory footprint are listed in parenthesis as sdBG and sC, respectively.

3.3 Validation on simulated E.coli

We ran the implementations of bubble calling from both Vari and Cortex, using k = 32 on the simulated E. coli dataset. Both tools reported the same set of 223 bubbles, 55 of which were in the ground truth set. This ensures our software faithfully implements the original data handling capabilities of Cortex. For biological implications of colored de Bruijn graph variant calls and in particular with parameter choices such as k see Iqbal et al. (2012).

3.4 Observations on beef safety dataset

While the beef safety dataset was primarily used for measuring the scalability of Vari and to determine if representing a dataset of this type and size was possible, we used Vari to additionally make observations about the presence of AMR genes in the beef production dataset. As previously described, during our path divergence derived algorithm, we compute a count of how many k-mers in each AMR gene are found across all samples within a sample group. This algorithm need only traverse the AMR genes, so despite the size of the overall dataset, it only took 20 minutes to load and access the necessary parts of the data structure. In contrast, if bubble calling were to run at the same rate for this dataset as for the E.coli assembly dataset, it would take 3001 hours to complete, thus suggesting value in a targeted inquiry approach on datasets of this size.

Since longer genes have more k-mers, the counts are likely to be larger, as are those from larger sample groups. To make these counts comparable, we normalize by both gene length and sample group size. We can then examine the number of genes having a disproportionately large (>3 std. dev. above mean) shared k-mer count for each gene and sample group combination. The number of such genes with disproportionately large normalized counts in each sample group were: feedlot arrival—304, feedlot exit—93, transport truck—230, slaughter holding—16 and slaughter trimmings and sponges—0. This observation supports the conclusion of Noyes et al. (2016), namely, that antimicrobial interventions during slaughter were effective in reducing AMR gene presence in the trimmings and sponge samples, which represent the finished beef products just before they are shipped to retail outlets for human consumption.

4 Concluding remarks

We presented Vari, which is an implementation of a succinct colored de Bruijn graph that significantly reduces the amount of memory required to store and use the colored de Bruijn graph. In addition to the memory savings, we validated our approach using E.coli. Moreover, we introduced the use of colored de Bruijn graph for accurately identifying the presence of AMR genes within metagenomic samples, which is an important advance as public health officials increasingly move towards a metagenomic sequence-based approach for surveillance and identification of resistant bacteria (Baquero et al., 2012; Food and Agricultural Organization of the United Nations, 2016; Port et al., 2014). Possible nontrivial extensions to our work include (i) using multi-threading to speed up the bubble calling, (ii) compressing the color array C more effectively by taking advantage of correlations among the variations and (iii) applying more sophisticated approaches to metagenomic data.

Funding

MDM, NRN, PSM, KEB, and CB are funded by USDA-NIFA grant 2016-67012-24679. NRN is also funded by USDA-NIFA grant 2015-68003-23048. SJP and TG are funded by Academy of Finland grants 294143 and 268324, respectively.

Conflict of Interest: none declared.