Collective motion of rod-shaped self-propelled particles through collision

Abstract

Self-propelled rods, which propel by themselves in the direction from the tail to the head and align nematically through collision, have been well-investigated theoretically. Various phenomena including true long-range ordered phase with the Giant number fluctuations, and the collective motion composed of many vorices were predicted using the minimal mathematical models of self-propelled rods. Using filamentous bacteria and running microtubules, we found that the predicted phenomena by the minimal models occur in the real world. This strongly indicates that there exists the unified description of self-propelled rods independent of the details of the systems. The theoretically predicted phenomena and the experimental results concerning the phenomena are reviewed.

Significance.

The investigation of collective motion of moving objects, called active matter physics, is the relatively new field of physics. One of the major studies pertaining to active matter physics is the quest for unified descriptions independent of details of systems. Although various phenomena were predicted using simple minimal models with a given symmetry, which are expected to be observed in various experimental systems, many of them had been unobserved in any experimental systems. We found in the experimental systems the various phenomena observed with the minimal models. Our results strongly indicate that there exist unified simple descriptions of the collective motion of moving objects including living objects.

Emergent ordered structures in groups of motile living things such as a flock of birds [1], a school of fish [2], and cell wound healing [3] are ubiquitous. Although there is no external force and no boundary around group, living things form huge structures containing a large number of moving units through the interaction with the neighbors. Not only motile living things but motile inanimate objects such as colloids driven by electric fields [4,5] or chemical reaction [6], droplets driven by Marangoni effect [7,8], and vibrated granular rods [9,10] move in rotationally symmetric systems and the collective motions of them have been studied. One of common characteristics of animate and inanimate motile objects, so-called self-propelled particles, is that they are both “active” objects which consume free energy inside themselves or ambient environment. There are expected to be unified simple descriptions for the collective motion of both animate and inanimate active objects like the Ising model in equilibrium systems. Including the quest of the unified descriptions, nonequilibrium physics focusing on the dynamics of the structures composed of a large number of active units, which is known as active matter, is relatively new field of physics [11,12].

Active matter is classified into two types, wet active matter and dry active matter [13]. To model wet active matter like suspension of swimming bacteria in a thick cell, the momentum conservation should be considered since the flow field around bacteria is significant. In the model of dry active matter such as herds of animals on land, suspension of swimming bacteria in a thin cell, and vibrated granular particles on a plate, momentum conservation is not in general considered. The momentum is exchanged with the outside through the friction from wall. In dry active matter, head to head and tail to tail alignment, called polar alignment, is permitted after collision of two motile particles. In 1995, Vicsek et al. reported the phase transition to the orientationally ordered phase in two-dimensional space governed by motility and polar alignment with neighbors using the representative agent-based model, which is called Vicsek model [14]. Using continuum model with the same symmetry as the Vicsek model, Toner and Tu reported that the phase with true long-range orientational order in two-dimensional space, which is prohibited in equilibrium systems [15], can exist [16]. In true long-range ordered phase, average of the direction of motion is the same at any place in an infinite space. This result implies that regardless of way of propulsion, self-propulsion expands the effective range of interaction, which leads to the true long-range order [17]. Due to rotational symmetry of systems, long-wavelength modes of orientation are easily excited and decay slowly. The slowly decaying fluctuations of orientation and the conservation of number of particles make bizarre density fluctuations with long-range correlation in the ordered phase [16–19]. The fluctuations can be detected as the Giant number fluctuations (GNF) [20]. Since the Vicsek model and the Toner-Tu model are minimal models with the collective motion of self-propelled particles with polar interactions, it is expected that these are the unified descriptions and the true long-range ordered phase with GNF is observed universally. The active matter having the motility and the nematic alignment to neighbors, during which one particle turn to its head to the head or the tail of the other, was studied by Ginelli et al. using the similar agent-based model to the Vicsek model [21]. The particles in this type of active matter are called self-propelled rods (SPR). Bacillus subtilis in a soap film [22], and running actin filaments [23] and running microtubules in an in vitro motility assay [24] are known to behave like SPR. In two-dimensional active matter composed of SPR, Ref. [21] reported the phase with true long-range orientational order and GNF as was in the Vicsek model case. Although true long-range order in two dimension and GNF are the significant characteristics, especially from the view of statistical physics, no experimental systems which show both of these had not been reported until 2017.

Recently, using elongated E. coli, the true long-range ordered collective motion with GNF was realized [25]. We also found that even minimal agent-based model like the model in [21] well reproduced the collective motion microtubules driven by dyneins grafted to a glass plate [24,26]. The main topic in this review is the introduction of these recent experimental results which can be interpreted with the minimal mathematical descriptions without the consideration of details of systems.

Self-propelled rods

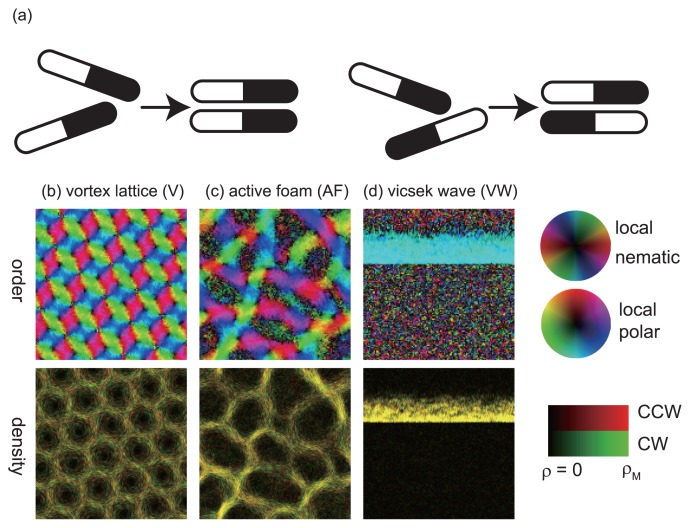
A minimal discrete-time agent-based model concerning collective motion of self-propelled rods was constructed by Ginelli et al [21]. In this model, all particles move at constant speed v₀ in two dimensions. Each particle nematically aligns to the particles within unit distance, that is, the head turns to the heads or the tails of neighbors (Fig. 1 (a)). At each time step t, the position of particle j, ${\mathbf{r}}_j^t$, and the direction of motion, ${\theta }_j^t$, are updated according to

Figure 1.

Self-propelled rods. The short-range nematic interaction of SPR is schematically illustrated in (a). The black (white) region is the head (the tail). (b–d) Collective motion of smoothly rotating self-propelled particles with the same symmetry as SPR. Upper: local orientational order [nematic (b), (c); polar (d)]. Bottom: superimposed density of clockwise (green) and counterclockwise (red) particles. Adapted from Nagai et al. (2015).

$$\begin{array}{l}{\theta }_j^{t+1}=\text{arg}\left[\sum _{k~j}\text{sign}[\text{cos}({\theta }_k^t-{\theta }_j^t)]e^{i{\theta }_k^t}\right]+\eta {\xi }_j^t\\ {\mathbf{r}}_j^{t+1}={\mathbf{r}}_j^t+v_0{e}^{i{\theta }_k^{t+1}},\end{array}$$

where k~j means all particles k within the unit circle centered at ${\mathbf{r}}_j^t$, and ζ is a white noise uniformly distributed in $\left[-\frac{\pi }{2},\frac{\mathrm{\pi }}{2}\right]$. Each particle moves with a constant speed (v₀) when it is isolated. The first term in the upper equation leads to alignment of close particles. The noise amplitude η and the particle density ρ is the two main parameters of this model.

When ρ=1/8 and v₀=1/2, at the low η value, the ordered phase with spatially homogeneous density was formed. The order parameter, $S(t)=\mid {\langle \text{exp}(i2{\theta }_j^t)\rangle }_{\text{j}}\mid$, was measured varying the system size, and found S converged to a finite value with the increase of system size, which indicates that the nematic order was true long-range order. In other words, almost all particles aligned in parallel or in antiparallel. They measured the variance of the number of particles in a square of linear size ℓ, Δn², in the case of the largest system size. Δn² algebraically depends on the average number in the area, 〈n〉=ρℓ², as $\sqrt{\mathit{\Delta }{n}^2}~{\langle n\rangle }^{\alpha }$. If the fluctuation is normal, α is expected to be 0.5 from the prediction of the central limit theorem. In the homogeneous ordered phase of SPR, the estimated value of α is larger than 0.5, which indicates that the fluctuations with long-range correlation, called Giant number fluctuations, exist. The estimated α is close to the predicted value of α in Toner-Tu model (4/5) [16,18,19] although the symmetry of the alignment of SPR is different from Toner-Tu model. Since the model in Ref. [21] is described with only the minimal rules determined by the symmetry of self-propulsion and alignment, it is expected that the homogeneous true longrange ordered phases with GNF will be observed in various experimental systems with the same symmetry; nevertheless, there had been no experimental reports of the phase having both true long-range order and GNF until our report [25].

In the above equations, a white noise is added to the direction of motion, which means no smooth turn. In the real world, birds and fish cannot turn abruptly since rotational inertia works. Furthermore, various self-propelled particles such as C. elegans [27], Mycoplasma [28], and E. coli near a substrate [29] show circular trajectories. To obtain a simple description corresponding to much more kinds of active matter in the real world, we investigated the collective motion of smoothly turning self-propelled rods using the minimal agent-based model. Our model reported in [26] is continuous-time model obeying following equations:

$$\begin{array}{l}\frac{\text{d}{\mathbf{x}}_i}{\text{d}t}=(\text{cos}{\theta }_i,\text{sin}\hspace{0.17em}{\theta }_i)\\ \frac{\text{d}{\theta }_i}{\text{d}t}={\omega }_i+\frac{\alpha {\sum }_{j~i}\text{sin}[2({\theta }_j-{\theta }_i)]}{n_i},\end{array}$$

where x_i and θ_i are the position and the direction of motion of particle i, respectively, and j~i means all particles j within the unit circle centered at x_i. ω_i is an Ornstein-Uhlenbeck process, where the correlation time is τ and the variance is τσ²/2, namely,

$$\frac{\text{d}{\omega }_i}{\text{d}t}=-\frac{{\omega }_i}{\tau }+{\sigma }^2{\xi }_i(t).$$

Here, ζ_i(t) is a zero-mean white Gaussian process with unit variance. Since an Ornstein-Uhlenbeck process keeps its value for around τ, the turning of each particle is smooth. To avoid too strong alignment interaction, the interaction term is normalized by the number of the particles in the unit circle around particle i, n_i. The collective motion dependence on the correlation time of rotation rate, τ, and the number density, ρ, is elaborated in the next paragraph.

At small density region, noise always overcame the alignment interaction, so that a homogeneous disordered phase was formed. When τ was low enough, homogeneous nematic phase was formed with larger density than the critical density as was in [21]. On the other hand, hexagonal lattice of large vortices was observed in the region with high τ and large ρ (Fig. 1(b)). At large density, spatiotemporally disordered cellular structure, an “active foam”, emerged with the middle value of τ (Fig. 1(c)). At low τ region, trains of dense traveling bands, called Vicsek waves, was observed (Fig. 1(d)). We confirmed that the smectic pattern was the asymptotic state in the subregion of the region where Vicsek waves was observed. This result means that globally polar order can emerge through purely nematic interaction, when the correlation time of rotation rate is finite.

Collective motion of elongated E. coli

Although there had been various experimental reports about the system with the same symmetry as SPR, no systems showed true long-range order and GNF simultaneously. Rather, disordered phases are often reported such as the chaotic phase with vortices, so-called bacterial turbulence, of suspensions of B. subtilis in three-dimensional space and quasi two-dimensional space [30]. This is partially due to the destabilization of order by long-range hydrodynamic interactions and too short length of objects to lead to strong alignment. For experimental verification of the prediction in [21], we avoid these two pitfalls by using filamentous non-tumbling E. coli in a very thin fluid layer. The filamentous E. coli were obtained by incubating the cells of nontumbling chemotactic mutant strain RP4979 with the antibiotic cephalexin, which inhibits cell division. The average length of used E. coli was 19±5 μm. The suspension of filamentous cells was sandwiched between a coverslip and a polydimethylsiloxane (PDMS) plate without any spacers to make a thin chamber. The number density of bacteria was in the order of 10⁴ per millimeter square. The use of PDMS was the key technique of this experiment since PDMS has high oxygen permeability.

To estimate the alignment interaction by collisions of bodies, binary collisions of bacteria was analyzed. The difference between incoming and outgoing angles is on average negative (positive) when the incoming angle is smaller (larger) than π/2. Incoming (outgoing) angle was defined as a difference between directions of motion of two E. coli before (after) a collision. From this analysis of binary interaction, it was confirmed that the filamentous E. coli has the head-tail direction and the short-range nematic interaction, that is, the same symmetry as SPR.

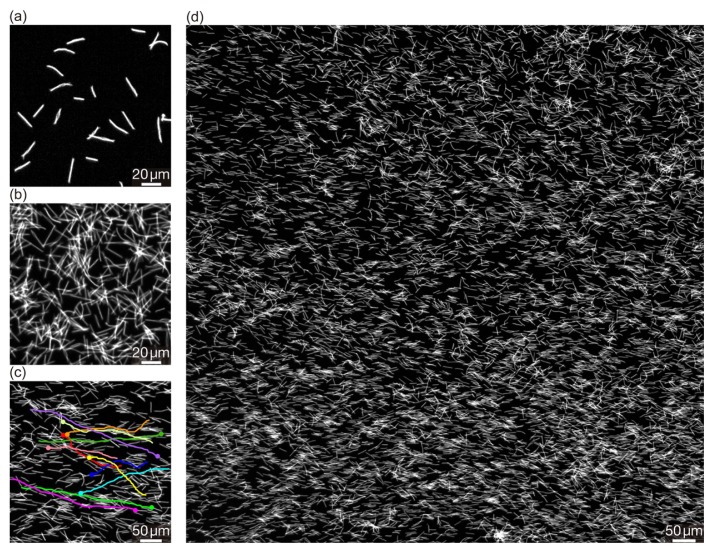
As for collective motion, at low density of cells or with a larger spacing (~10 μm), cells do not align enough to order in large area (Fig. 2(a) and 2(b)). Unlike bacterial turbulence, no vortices were formed in the disordered phase. But at high concentrations (average area fraction of ~0.25) with a smaller spacing (~2 μm), their collisions are so frequent that global nematic order emerged. This ordered phase was homogeneous without clusters (Fig. 2(c) and 2(d)). Since it is very difficult to measure the direction of each bacterium, the “structure tensor” method [31] was used to analyze the nematic order of the collective motion. This method is very strong method since it gives the estimate of the scaler nematic order parameter in a region of interest (ROI), called the “coherency parameter”, C, with an easy image processing. When E. coli have no nematic order in a ROI, C is zero, and when E. coli are ordered more nematically in a ROI, C is larger.

Figure 2.

Collective motion of elongated E. coli. Disordered phase with (a) the low density, and (b) in the thick cell. (c), (d) Ordered phase with true long-range order and the Giant number fluctuations. Colored lines in (c) are the 10-s trajectories of bacteria. Adapted from Nishiguchi et al. (2017).

We have measured the average of C over both space and time for square ROIs of various areas S. In the disordered phases in Figure 2(a) and (b), we find that $C~\sqrt{S}$, as is expected in the case of finite spatial correlation length of alignment. In the ordered phase in Figure 2(d), on the other hand, a decay of C slower than a power law was observed. This is the signature of true long-range order. Indeed, the data is well-fitted with an algebraic approach to a finite asymptotic value of C–C_∞~S^β with C_∞=0.505 and β=−0.66.

To quantify number fluctuations, we binarized our images and counted the number of pixels N(t) covered by bacteria at time t varying the size of ROI. ROI was centered at the field of view. The binarization has the advantage of correcting for the slight differences in intensity resulting from variations of the height of bacteria or fluctuations in the overall light intensity. As number fluctuations, the standard deviation $\mathit{\Delta }N=\sqrt{\langle {[N(t)-\langle N\rangle ]}^2\rangle }$ averaged over time was calculated. In the disordered phase, we find normal fluctuations ΔN~〈N〉^0.5. On the other hand, in the dense nematically ordered phase, ΔN~〈N〉^α with α>0.5 i.e., GNF due to the presence of longrange correlations in the system was rigorously observed as was predicted in Ref. [21]. The estimated α was 0.63(2)>0.5, which is a bit smaller than the exponent estimated in [21].

Collective motion of microtubules in in vitro motility assay

Some of the collective motions of smoothly turning SPR reported in [26] were observed in various experimental systems. One of the examples is the hexagonal lattice of vortices of microtubules driven by dyneins grafted to a glass plate [24]. In the experiment, inner-arm dynein subspecies c (dynein c) purified from Chlamydomonas flagella was used. The dyneins fixed to a glass plate drove the microtubules whose average length was 15.6±7.3 μm. Since relatively many, randomly oriented, dyneins were attached at any time to a microtubule, smooth and isotropic motion was observed.

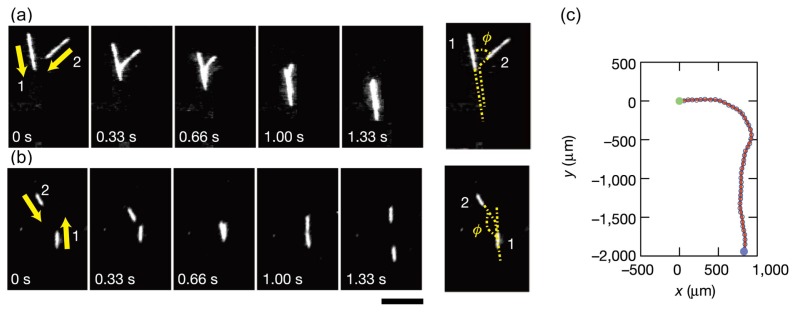
With low density of microtubules (0.5–1 μg/ml), the binary interactions of microtubules were analyzed. We examined 393 binary collision events. As shown in Figure 3(a) and (b), on collision, strong steric interactions occurred in the almost all events (80%), leading either to alignment or anti-alignment (70%) or to the stoppage of one microtubule (10%). 20% of the microtubules crossed each other with little effect on their trajectories. In aligning and anti-aligning collisions, the trajectory of one microtubule undergoes a sharp turn and alignment was near perfect. Thus, the outgoing angle was near 0 or π in aligning events, irrespective of the value of the incoming angle. In other words, near-perfect nematic alignment was induced by a collision. As is in the E. coli case, incoming (outgoing) angle was defined as a difference between directions of motion of two microtubules before (after) a collision.

Figure 3.

(a, b) Binary interaction of microtubules and (c) trajectory of an isolated microtubule. ϕ is the difference between the directions of motion of two microtubules before the collision. Scale bar is 10 μm. Adapted from Sumino et al. (2012).

To measure the correlation time of rotation rate of microtubules, the trajectories of isolated microtubules were analyzed using the microtubule concentration of 4.8 ng/ml. The trajectories composed of circular trajectories as is in Figure 3(c), which indicates that the rotation rate has long-time correlation, were observed. After the appropriate filtering, based on the Savitzky–Golay method [32], to eliminate the small-amplitude transverse oscillations of trajectories, we obtained the curvature as a function of distance along the trajectory and calculated its autocorrelation. Fitting the result with the exponential function, we found the persistent length of curvature to be of the order of 500 μm. Since the average speed of microtubules wad 8.75 μm/s, the correlation time was estimated as 61.9±0.5 s. The distribution of curvature was roughly Gaussian with the mean of −7.1×10⁻⁴ μm⁻¹ and the standard deviation of 1.8×10⁻³ μm⁻¹.

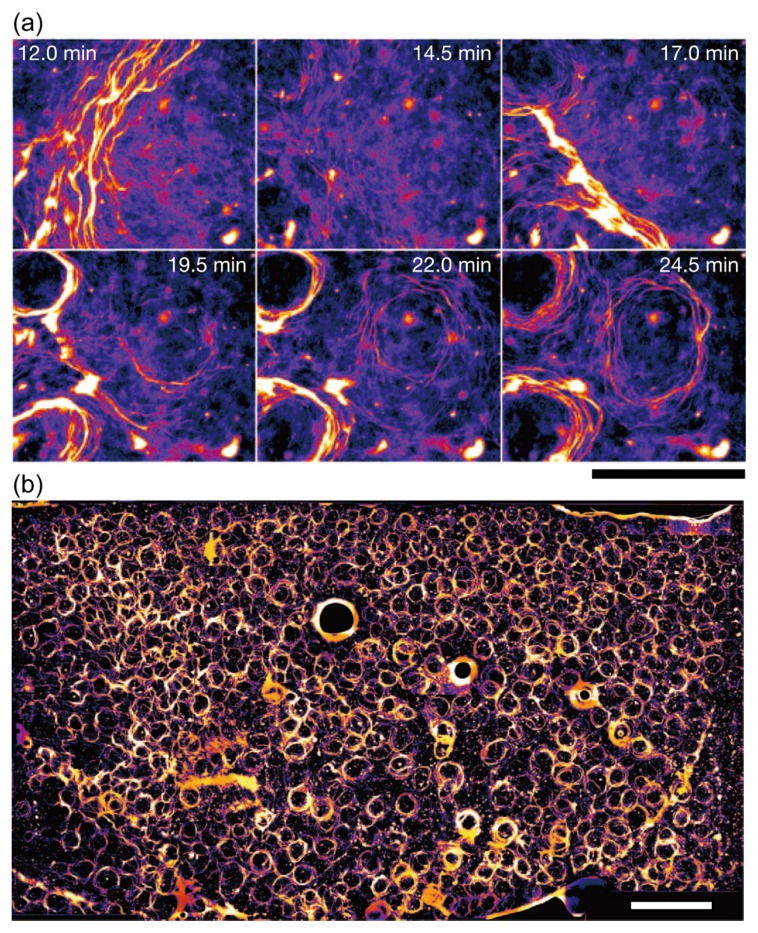
Using high microtubule concentration (40 μg/ml), the collective motion of running microtubules was observed. On addition of ATP (at 0 min), streams along which dozens of microtubules moved in both directions were formed. The width of a stream got thicker and thicker (the upper-left figure in Fig. 4(a)), then streams started to meander (the middle and the right figures in the upper row of Fig. 4(a)). At 10–20 min, some vortices appeared (the lower row of Fig. 4(a)) and eventually covered the flow cell almost entirely (Fig. 4(b)). The shape of the vortices gradually changed over time but their diameters were almost constant, at 400 μm. It is noted that the standard deviation of curvature of isolated microtubules, which has the same order of magnitude as the average of absolute value of curvature, is of the same order as the vortex diameter. At this late stage, the vortices showed a tendency to arrange their positions into a hexagonal lattice. Inside the peripheral annulus of a given vortex, microtubules rotated both clockwise and anticlockwise and slid past each other. Microtubules were never trapped in a single vortex: they circulated inside one vortex for some time before moving to a neighboring one or travelling farther and starting to revolve around a more distant vortex. The hexagonal lattice of vortices with the same characteristics emerged in the simulation with the parameters estimated from the analysis of isolated microtubules.

Figure 4.

Collective motion of microtubules running on glass plate. (a) Vortex formation. Scale bar is 500 μm. (b) Lattice of vortices. Scale bar is 2 mm. Adapted from Sumino et al. (2012).

Perspective

Self-propelled rods are the particles which move in the direction from the tail to the head and have short-range nematic interactions through collision, such as asymmetric vibrated granular rods (~1 cm) [9,10], confined bacteria in two-dimensional space (~1 μm) [22,25,30], and running filamentous proteins in an in vitro motility assay (~10 μm) [23,24]. Since it is expected that there exists the unified description of SPR, SPR has been well-investigated. Using filamentous bacteria and running filamentous proteins, we indeed found the various phenomena which were observed in the minimal models of SPR. This fact strongly indicates the existence of the unified description of SPR, which are independent of the details of systems such as the structure of proteins used for motility, the conditions of substrate, and whether particles are animate or inanimate.

Although we found GNF in the ordered collective motion of filamentous E. coli, the estimated exponent was smaller than the one estimated in [21]. This may be due to the limitation of analyzed area. To clarify the actual value of exponent, more careful analysis of the collective motion with broader observed area is needed. The dynamics of transition to the ordered phase should also be analyzed using the system with better control of the density of bacteria. Using the models with excluded volume of particles, not only nematically ordered phase but clusters and turbulent phase were observed depending on aspect ratio of particles [30,33]. The investigation of the dependence of collective motion of E. coli on aspect ratio will give more knowledges about the fundamental principles governing collective behaviors of self-propelled particles, including collective motions related to biological functions such as biofilm formations and wound healing.

Unified descriptions should reproduce the dynamics of various experimental systems; therefore, inanimate self-propelled colloids with high aspect ratio will also have true long-range order and GNF. As for smoothly turning self-propelled particles, the collective motion composed of vortices like that of the microtubule were observed in the various experimental systems in various scales such as C. elegans (~500 μm) and motile cyanobacteria (~10 μm) (Sugi, T., Ito, H. & Nagai, K. H. in preparation, and Iwasaki, H., Fukasawa, Y., Kato, H., Takiguchi, M., & Nagai, K. H. in preparation). Our minimal model can reproduce the various aspects of these collective motions, therefore, our model may be the unified description of the collective motion of smoothly turning self-propelled particles.