Influence of cavitation and high shear stress on HSA aggregation behavior

Abstract

Neither the influence of high shear rates nor the impact of cavitation on protein aggregation is fully understood. The effect of cavitation bubble collapse‐derived hydroxyl radicals on the aggregation behavior of human serum albumin (HSA) was investigated. Radicals were generated by pumping through a micro‐orifice, ultra‐sonication, or chemically by Fenton's reaction. The amount of radicals produced by the two mechanical methods (0.12 and 11.25 nmol/(L min)) was not enough to change the protein integrity. In contrast, Fenton's reaction resulted in 382 nmol/(L min) of radicals, inducing protein aggregation. However, the micro‐orifice promoted the formation of soluble dimeric HSA aggregates. A validated computational fluid dynamic model of the orifice revealed a maximum and average shear rate on the order of 10⁸ s⁻¹ and 1.2 × 10⁶ s⁻¹, respectively. Although these values are among the highest ever reported in the literature, dimer formation did not occur when we used the same flow rate but suppressed cavitation. Therefore, aggregation is most likely caused by the increased surface area due to cavitation‐mediated bubble growth, not by hydroxyl radical release or shear stress as often reported.

Abbreviations

CFD

Computational fluid dynamics

HSA

Human serum albumin

hTPA

Hydroxyterephthalic acid

SEC

Size exclusion chromatography

TPA

Terephthalic acid

VOF

Volume of fluid

1. Introduction

Irreversible mechanical stretching of proteins due to shear stress and the resulting aggregation behavior is unclear in the literature. From the early stages of bioprocess engineering until now, mechanical stress has been thought to be a real harm in processing proteins 1, 2, 3, 4. However, more recent studies 5, 6 have not supported these assumptions, and some studies have attributed protein aggregation during processing to conformational changes in the protein at the air‐liquid interface rather than to shear stress 7, 8. It has been hypothesized that, at really high shear rates, the effect of cavitation may be overlooked and the possible effect misattributed to shear stress 9, 10. In bioprocesses, protein solutions are often pumped through narrow orifices (e.g., high pressure homogenizers, valves, or gear pumps). As a result of the velocity increase in these gaps, the local pressure decreases as described by the Bernoulli equation Eq. (1), where v is velocity, p the hydrostatic pressure, and ρ the density of the liquid.

$$p+\frac{\rho }{2}{v}^2=const.$$ (1)

Cavitation occurs when the local static pressure falls below the vapor pressure of the liquid, resulting in the liquid boiling at ambient temperatures. When the pressure increases downstream of the orifice, these vapor cavities are unstable and collapse under high pressure and temperature 11, resulting in the formation of hydroxyl radicals 12. The destructive nature of these radicals generated by X‐ray radiolysis of water or Fenton's reaction on certain amino acid side chains was reported previously 13, 14, 15, 16. The Fenton reaction is induced when ferrous iron (Fe(II)) is present together with hydrogen peroxide at low pH 17. When studying the influence of hydroxyl radicals on proteins, Fenton's reaction can be used as a positive control due to the high radical generation rate.

An alternative source of hydroxyl radicals is ultra‐sonication 12. In this method, ultrasound waves are transmitted through the medium, compressing and stretching the molecular spacing of the medium. Thus, the average distance between the molecules varies as they oscillate about their mean position. When the distance between water molecules is extremely large, the local pressure undercuts the vapor pressure of the liquid and cavitation occurs 18. Hydroxyl radicals occurring from ultra‐sonication were already associated with DNA degradation 19.

Cavitation can be detected and quantified in biopharmaceutical processes by the well‐established terephthalic acid (TPA) dosimeter 20, 21. Generated hydroxyl radicals react with TPA, forming hydroxyl terephthalic acid (hTPA), a stable fluorescence‐active, heat‐resistant 22 chemical. We applied this technique to compare cavitation intensity between an ultra‐sonic homogenizer, a micro‐orifice, and Fenton's reaction.

In fluid dynamics, the dimensionless cavitation number (Ca) is used to predict cavitation Eq. (2). The equation relates the local static pressure in a liquid (p) to the vapor pressure of the liquid (p_v), the density (ρ), and the flow velocity (v). Below 0.2 cavitation can be expected 23.

$$Ca=\frac{2\left(\mathrm{p}-{\mathrm{p}}_v\right)}{\rho \ast v^2}$$ (2)

According to this engineering correlation, a micro‐orifice and flow conditions were selected to achieve velocities high enough to generate cavitation 24. We also wanted to describe the shear rate inside the micro‐orifice. For laminar flow, the maximum shear rate near the wall can be calculated using a stress approximation Eq. (3) 25, where Q is the volumetric flowrate, r is the radius of the tube, and y is the shear rate.

$$\gamma =\frac{4\mathrm{Q}}{\pi {\mathrm{r}}^3}$$ (3)

However, this equation is only valid when calculating maximum wall shear stress in laminar flow with a single velocity component parallel to the wall. Reynolds equation Eq. (4) is used to evaluate whether laminar flow is present, where ρ is the density of the liquid, v the linear flow velocity, d the diameter of the tube, and μ the dynamic viscosity.

$$Re=\frac{\rho \mathrm{vd}}{\mu }$$ (4)

We show that laminar flow conditions were not present for our desired flow rates. Thus, a validated computational fluid dynamics (CFD) simulation was set up to reliably calculate an average shear rate for the whole micro‐orifice cross‐section.

The aim of the present study was to evaluate whether hydroxyl radicals generated by cavitation resulting from a micro‐orifice are a possible source of protein aggregation. The radical generation rate was compared to that of ultra‐sonication and Fenton's reaction. In addition, the influence of extremely high shear rates with and without cavitation on HSA aggregation behavior was studied.

2. Materials and methods

2.1. Protein standard

We selected HSA as the model protein due to its ability to form soluble aggregates in buffered solutions. It was purchased as highly pure lyophilized powder (A3782, Sigma‐Aldrich, St. Louis, MO, USA). We prepared 0.25 mg/mL HSA in 10 mM sodium phosphate and 5 mM sodium chloride (pH 6.5) as standards. Standards were 0.2 μm filtrated and degassed with sterile rapid flow units (566‐0020, Thermo Fisher Waltham, MA, USA). Every experiment was carried out in triplicate.

2.2. Size exclusion chromatography

The soluble aggregate content and concentrations of HSA samples were analyzed by high performance size exclusion chromatography. The runs were performed on an Agilent 1290 LC system (Santa Clara, CA, USA). We used a TSKgel G3000SWXL column (5 μm, 7.8 mm id x 300 mm + 6 mm id x 40 mm guard) from Tosoh (Shiba, Minato‐Ku, Tokyo, Japan). Phosphate running buffer (13 g/L KH₂PO₄, 9.4 g/L K₂HPO₄, 14.61 g/L sodium chloride pH 6.5) was used at a flow rate of 0.4 mL/min. Protein samples were filtered using a 0.2 μm filter and 20 μl directly injected without any dilution.

2.3. Terephthalic acid dosimeter

TPA was purchased from Sigma‐Aldrich (185361) and used as a 30 mM stock solution in 0.2 M NaOH adjusted to pH 6.5 or 9 with phosphoric acid. To establish the relationship between fluorescence signal and hydroxyl radicals, hTPA was purchased from Sigma‐Aldrich (752525) and three independent dilution series prepared. For each dilution, 10 mg of hTPA was dissolved in 100 g of 0.2 M NaOH previously adjusted to pH 6.5 using phosphoric acid. The resulting 549 μM hTPA solution was diluted 1:10 twice, followed by dilution 1:3 six times. Finally, the fluorescence signal was measured for the last five dilutions.

2.4. Fluorescence measurements

To evaluate different cavitation intensities with the TPA dosimeter, we used an Infinite® 200 PRO fluorescence detector (TECAN, Maennedorf, Zuerich, Switzerland). Triplicate 150 μL aliquots of each sample were measured in a Nunclon Delta Black 96 Microwell plate (137101, ThermoFisher) at excitation and emission wavelengths of 315 and 425 nm, respectively. The electrical gain was adjusted to 150 to easily compare results between different plates.

2.5. Fenton's reaction

For Fenton's reaction, we mixed 1 mL of 0.12 M TPA in 0.25 M NaOH, 1 mL of 0.5 M phosphate buffer (pH 9.0; pH 3.0 for protein experiments), and 1 mL of 8 mM iron(II)chloride‐tetrahydrate in a 5 mL Eppendorf tube. To initiate the reaction, we added 1 mL of 4% hydrogen peroxide (v/v). For protein aggregation experiments, the TPA solution was replaced with 1 mg/mL HSA in 0.3 M phosphate (pH 9.0 or 3.0).

2.6. Ultra‐sonication

A UP100H ultra‐sonic homogenizer (Hilscher, Teltow, Brandenburg, Germany) with an MS3 sonotrode was used at 60% intensity in continuous mode to generate cavitation. Sample solutions (60 mL) were sonicated in a jacketed 100 mL glass beaker constantly cooled to 25°C by a F12‐ED circulator (Julabo, Seelbach, Baden‐Wuerttemberg, Germany) connected with silicon tubes.

2.7. Micro‐orifice

T‐4‐SS micro‐orifices (Fig. 1) were purchased from O'Keefe Controls Co. (Monroe, CT, USA). These devices were delivered with a barb connector on each side, which allowed an easy connection to 1/16‘’ tubes. The diameter reduction to 99 μm generated a back pressure of up to 30 bar at a flow rate of 26 mL/min. To ensure a continuous flow rate with the described requirements, we integrated the micro‐orifice into the flow path of an ÄKTA P‐901 piston pump (GE Healthcare, Chicago, IL, USA) (Fig. 1). At different flow rates through the micro‐orifice, 60 mL of protein or TPA solution was recirculated for 90 and 1440 min. To evaluate the influence of the pump on protein aggregation the micro‐orifice was replaced by a 2 m 0.75 μm id tube. Hence, the effect of the pump can be subtracted from the combined effect pump and orifice. To suppress cavitation we increased the backpressure behind the micro‐orifice with a 31.5 cm tube 0.25 mm id PEEK tube (1/16 ‘’ od) (GE) glued into the tube exiting the micro‐orifice (1/16 ‘’ id).

Figure 1.

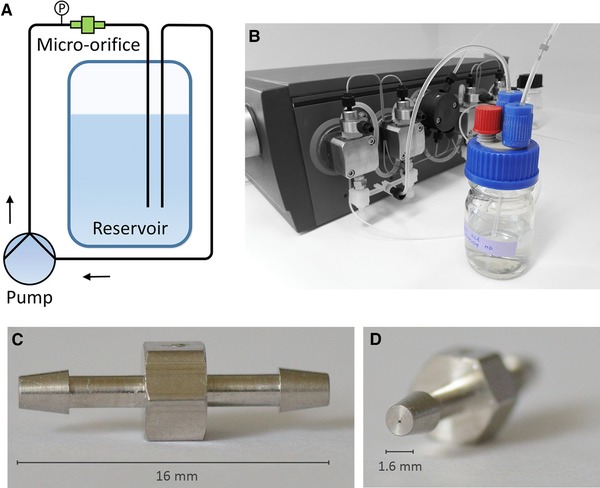
The protein stressing setup with the integrated micro‐orifice. (A) Schematic drawing. (B) Photograph. The micro‐orifice is located at the top right. (C) side view onto the orifice. (D) Front view of the flow reduction.

2.8. Computational fluid dynamic simulation

To simulate the flow inside the micro‐orifice and calculate an average shear rate over the flow reduction, a CFD simulation was set up using the computer program Star‐CCM+® (CD‐adapco, Melville, NY, USA). The geometry of the orifice was obtained from a technical drawing by the manufacturer. The inlet diameter through the barb connector was set to 1.2 mm. A continuous conical narrowing from 1.2 mm to 99 μm was adjusted in 0.25‐mm increments. The orifice length itself was set to 0.33 mm. After the reduction, the diameter instantly expanded to the diameter of the connected transparent Fluoroethenepropene tube (1/16‘’, which is equal to 1.59 mm). We chose a three‐dimensional, steady, Eulerian multiphase including volume of fluid (VOF) and cavitation‐segregated flow, realized K‐Epsilon turbulence with Reynolds averaged Navier‐Stokes model. The minimum allowable wall distance and reference pressure were set to 1.0 × 10⁻⁹ m and 1013 mbar, respectively. We picked a cubic mesh to better resolve the contribution of both liquid and vapor in each cell derived from the VOF model. Therefore, we focused on reducing the cell size in the critical regions, including the orifice reduction or the free jet region, after the device.

3. Results and discussion

3.1. Selection of a micro‐orifice

We compared different methods to study the effect of hydroxyl radicals on protein aggregation behavior. We used Fenton's reaction for a high radical generation rate per time, ultra‐sonication as a well‐established method for the generation of detectable amounts of radicals 18, 26, 27, and a micro‐orifice with an unknown generation rate. A stirring device to simulate protein mixing processes at high revolution rates was also taken into account but considered to not be feasible due to the resulting vortex and air entrapment in the protein solution. Using a micro‐orifice integrated into a pumping flow path overcomes the issue of air inclusion due to the closed system. In addition, this setup mimics the conditions downstream of a high pressure homogenizer quite well, or the slit between the rotor and the wall of a fast rotating gear pump. We used the dimensionless cavitation number (Ca) to roughly predict the required flow. Estimating a downstream pressure of 106.3 kPa, assuming an orifice diameter of 100 μm, vapor pressure of water at 20°C of 2338 Pa, and a density of water of 998 kg/m³, a linear flow rate of 33 ms⁻¹ (15.6 mL/min) was required to be below the cavitation number threshold of 0.2, ensuring the occurrence of cavitation 23. Thus, the T‐4‐SS micro‐orifices with a nominal diameter of 99 μm was suitable for generating cavitation with an ÄKTA system pump. We further increased the flow rate up to 56.3 m/s (26 mL/min) to increase the cavitation strength.

3.2. CFD simulation of shear rates

The prevailing flow inside a tube or orifice can be estimated by the Reynolds number Eq. (4). A simple calculation of shear rate is only possible when the flow is laminar 28, 29, 30. Assuming a liquid density of 998 kg/m³, a linear velocity of 56.3 m/s, a micro‐orifice diameter of 9.9 × 10⁻⁵ m, and a dynamic viscosity of 8.9 × 10⁻⁴ Pa, the resulting Reynolds number was 6250, indicating turbulent flow. Additionally, the occurrence of a defined vena contracta complicates the flow profile, requiring a numerical solution by CFD 31. To simplify the complex time‐ and location‐dependent turbulent flow, we used a steady simulation approach that averaged the turbulence over time. The CFD simulation was validated by comparing the simulated and experimentally determined pressure drops at several different flow rates (Fig. 2). The accuracy of the pump was evaluated with ±1.3% in the range of 8 to 30 mL/min. We accurately predicted the pressure drop with the CFD simulation. Although our simulations underestimated the measured pressure drop by 4% at 26 mL/min and overestimated the pressure by 9% at 8 mL/min, we were able to precisely predict the minimum flow rate for cavitation (online supporting data Table 1). We observed both an increase in fluorescence signal when using the TPA dosimeter and the occurrence of noise produced by the implosion of vapor cavities. The implemented cavitation model predicted a realistic number of cells with vapor content at the corresponding flow rates in the CFD simulation, concluding that cavitation was occurring. However, at a flow rate of 11 mL/min, the simulation demonstrated some cells with vapor content, but we did not notice any noise or increase in hTPA signal. Either the fluorescence assay was not sensitive enough to detect this minor cavitation level, or the simulation simply overestimated the reality. As the simulation matched our experiments very well, we generated 110 cross‐sections through the whole orifice reduction (every 3.2 μm) in silico to estimate shear rates.

Figure 2.

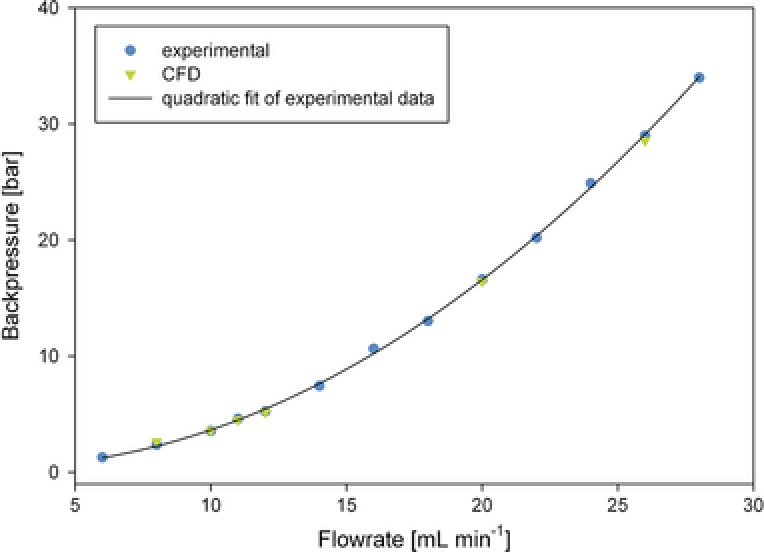
Pressure curve for the micro‐orifice integrated into the ÄKTA flow path and CFD calculation at six different flow rates. Experimentally measured data (blue) and a quadratic fit of the data (black) are shown. Simulation data are in green.

A plane section is a virtual two‐dimensional space located inside the geometry used to display physical values, such as pressure or velocity, for all of the cells it contains (Fig. 3). For the calculation of shear rates, we wrote a user script in Star CCM+ that derived the velocity vector perpendicular to the wall of each cell to the next cell located closer to the center of the reduction according to Eq. (5), where $\dot{\gamma }$ is the shear rate, Δv the velocity difference between two cells, and h the distance between these cells.

$$\dot{\gamma }=\frac{\mathrm{\Delta }v}{h}$$ (5)

Figure 3.

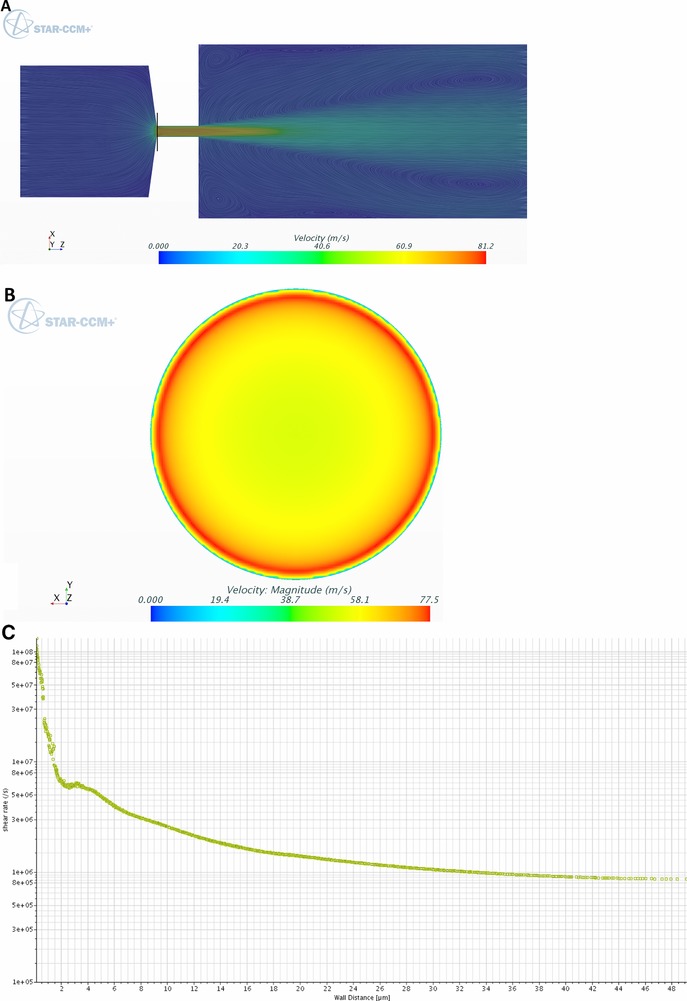
Velocity and shear profiles indicated by plane section through the micro‐orifice. (A) Color represents the flow velocity, whereas the lines give information about the direction. (B) Plane section indicated by the black line in (A). (C) Shear rates across the plane section in (B) from the wall to the center.

We showed at the beginning of the vena contracta that the maximum obtained wall shear rate was in the order of 10⁸ s⁻¹ (Fig. 3). Although studies on high shear rate‐dependent aggregation have been reported 5, 9, 32, 33, 34, 35, the values from our simulation exceed these values by a factor of at least 10. In addition, the maximum shear rate was 22‐times higher than one would expect from the laminar flow profile at the wall (4.5 × 10⁶ s⁻¹), which further indicates the importance of a validated CFD simulation. However, the mass flow rate at the wall and, thus, the amount of proteins sensing this extremely high shear stress is rather low. Therefore, a mass flow‐averaged shear rate over the whole orifice reduction was required. We additionally picked the velocity and density profiles of each cell, allowing us to calculate the average shear rate ($\dot{\gamma }$) Eq. (6) by taking into account the overall mass flow from all sections and cells (${\dot{M}}_t$) the shear rate contribution (${\gamma }_i$), and the mass flow of each individual cell, given by the velocity ($v_i$), density (${\rho }_i),$ and cell size $(A_i$).

$${\displaystyle \dot{\gamma }=\frac{1}{{\displaystyle {\sum }_i{\dot{M}}_i}}\sum _i{v}_i{\rho }_i{A}_i{\gamma }_i}$$ (6)

This calculation enabled a detailed average description of the shear rate inside the micro‐orifice, which was not possible with ordinary theoretical assumptions due to the focusing effect of the vena contracta and the resulting complex velocity profile 31. However, we calculated an extremely high average shear rate of 1.2 × 10⁶ s⁻¹. We obtained 5 × 10⁶ s⁻¹ when averaging the shear rate for all of the cells of the 110 cross‐sections without taking into account the reduced mass flow rate at the wall. Hence, the mass flow averaged calculation provides a more realistic picture because the averaged shear rate would have been overestimated by a factor of 4. As we used a static simulation, the local shear rates could even be higher due to fluctuations in the turbulence, whereas our steady simulation averaged velocity and shear rates over time.

3.3. Suppressing cavitation with a flow restrictor

To separate the influence of cavitation from the high demonstrated shear rates, we suppressed cavitation by increasing the downstream pressure of the orifice with a flow restrictor. We used a 31.5 cm Teflon tube with a diameter of 0.25 mm, increased the downstream pressure to 21 bar. The resulting cavitation number was 1.3 and no increase in fluorescence signal was obtained after 24 hours of pumping with TPA solution. We performed another CFD simulation and obtained an average shear rate of 1.6 × 10⁶ s⁻¹. The 33% increase in the average shear rate can be explained by the higher mass flow rate near the wall because no gas phase is transported.

3.4. Calibration of hydroxyl radical formation with hTPA

To investigate hydroxyl radical‐mediated protein aggregation by cavitation, we correlated the arising fluorescence signals of the micro‐orifice, the ultra‐sonication homogenizer and Fenton's reaction with hydroxyl radical concentrations by analyzing the reactant of the TPA reaction, hTPA. We obtained a linear correlation for the stock solution and found that a gain of one fluorescence unit corresponded to 59.3 ± 3.8 pmol/L hydroxyl radicals.

3.5. Hydroxyl radical formation by micro‐orifice and ultra‐sonication treatment

Hydroxyl radical generation by the ultra‐sonication sonotrode and the micro‐orifice was tested with the TPA dosimeter after 60 and 1440 min, respectively. With both devices, we visually detected cavitation (Fig. 4) by the characteristic bubble formation at the exit of the orifice or the apex of the ultra‐sonication tip. The micro‐orifice and ultra‐sonic homogenizer generated 2.09 and 189.7 fluorescence counts per minute. With the micro‐orifice, the flow rate determined the cavitation intensity, whereas the time constant and power input were relevant for the ultra‐sonic homogenizer. The oscillating tip of the ultra‐sonic homogenizer resulted in a 90‐times higher signal due to the high local energy input 36. Converting the fluorescence signals to moles of hydroxyl radicals using the calibration curve, we found that 0.124 nmol/(L min) was generated by the micro‐orifice, whereas the ultra‐sonication sonotrode was capable of generating 11.25 nmol/(L min) which is in good agreement with expectations from the literature 37. We expected that the same amount of hydroxyl radicals will result in similar levels of protein aggregation. To investigate hydroxyl radical‐mediated HSA aggregation, we picked an incubation time of 1 and 90 min for the ultra‐sonic homogenizer and micro‐orifice, respectively.

Figure 4.

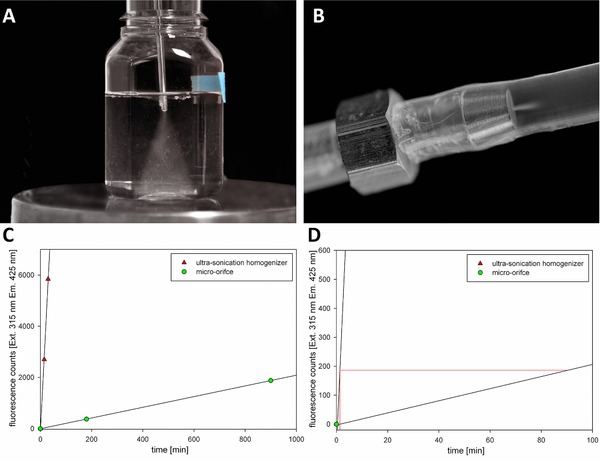
Visualization of cavitation. (A) Ultra‐sonication. (B) micro‐orifice. (C) Generation of hydroxyl radicals measured as fluorescence counts by the terephthalic acid dosimeter. Data are presented as the means of three experiments ± SD which is within the color marking. (D) Zoomed in view of (C) to calculate time when the same amount of radicals is generated by the different methods.

3.6. Hydroxyl radical formation by Fenton's reaction

To investigate the influence of high concentrations of hydroxyl radicals on protein aggregation, we used Fenton's reaction as an additional radical source. Fe(II) reacted with hydrogen peroxide to form ferric iron (Fe(III)), one hydroxyl radical, and one hydroxide ion 38. To measure hydroxyl radical formation with TPA, the pH was set to 9 to prevent TPA precipitation. In addition, the catalytic back reaction of Fe(III) to Fe(II) was prevented due to the high pH, resulting in the formation of insoluble iron(III) hydroxide (K_sp 2.7 × 10⁻³⁹ mol⁴/L⁴ 39). Therefore, hydroxyl radicals were the only radical species, which was necessary to avoid misinterpreting the results. Although Fenton's reaction is normally conducted at pH 3, some researchers have shown that an even faster hydroxyl radical release occurs at pH 9 40. After initiation of the reaction, we measured the fluorescence signal at 10, 30, and 60 min. The fluorescence signal did not change after 10 min, indicating that the reaction was over after a few minutes. A total of 381.56 nmol/(L min) hydroxyl radicals were formed by this reaction, which was 34‐times higher than ultra‐sonication and 3067‐times higher than with the micro‐orifice (Table 1). The reaction might have been over after several seconds but sample mixing and repeated plate reader analysis required several minutes, hence the generation rate per minute was probably even higher.

Table 1.

Comparison of hydroxyl radical formation by different methods

Treatment	nmol/(L min)	Proportion
Pumping + micro‐orifice	0.12 ± 0.01
Ultra‐sonic homogenizer	11.25 ± 1.68	90
Fenton's reaction, pH 9	381.56 ± 81.25	34/3067

Data are presented as mean ± SD. The proportion between different treatments also indicated.

3.7. Protein stress

The HSA solution was stressed by the micro‐orifice, ultra‐sonication, and hydroxyl radicals generated by Fenton's reaction. We used a low protein concentration of 0.25 g/l in all experiments. With this concentration structural analytics like HP‐SEC are less error prone because no dilutions have to be done which decreases sample to sample deviations. Further, in case dilutions are done it is well know that a protein could refold and then we could make a false conclusion. Therefore, a direct injections is less critical regarding interpretation. The concentration of HSA monomers in the supernatant did not change with ultra‐sonication (Fig. 5). Treatment with the micro‐orifice reduced the HSA monomers by 3.3 ± 0.3 %, and the dimeric form increased by the same amount (Fig. 6). Although both systems generated the same amount of radicals, the aggregation behavior was different. We also increased the incubation time for the ultra‐sonication homogenizer to 30 min. After 30 min the hydroxyl radical concentration was similar to the Fenton's reaction after 1 min but we did not find increased HSA aggregation. The Intensity of hydroxyl radicals per time is most reasonable not high enough. However, we also processed a HSA sample with the ultra‐sonication homogenizer for 1 h. After this time we could notice increased aggregation. Although we used a circulation bath to cool the sample, the homogenizer produced a lot of heat. We measured the tip temperature after 1 h and obtained 58°C. Therefore, aggregation in samples treated longer than 30 min with this specific setup is most likely generated by the hot sonication tip and not related to cavitation. In contrast, Fenton's reaction at pH 9 resulted in 9.5 % ± 1.6 % protein aggregation (Fig. 5). However, at alkaline pH we also lose a certain amount of HSA due to co‐precipitation with iron hydroxide 41, 42. We showed that this effect occurred without the addition of hydrogen peroxide at pH 9; thus, under the prevailing buffer conditions, oxidation of Fe(II) to Fe(III) occurs spontaneously. We lost 41.7 ± 2.1% of the HSA due to this treatment, which is more than the amount obtained from the effect of hydroxyl radicals. However, when adding hydrogen peroxide to the protein solution, the additional 9.5% protein loss was most likely due to the fast release of hydroxyl radicals in Fenton's reaction. Although a maximum of 2 mM iron was available in the reaction solution, the spontaneous oxidation of Fe(II) to Fe(III) without peroxide 43 may explain the rather low generation rate of 3.82 μmol/L after 10 min. We also performed Fenton's reaction at pH 3, which resulted in total protein aggregation without any undesired iron hydroxide (Fig. 5). Unfortunately, we were not able to measure hydroxyl radical formation due to the insolubility of TPA at acidic pH. We assume that the amount of hydroxyl radicals generated by cavitation is most reasonable not high enough to cause relevant protein aggregation. Although the generation of hydroxyl radicals by cavitation is evident it is unclear if these radicals are the driving force for protein aggregation or DNA fragmentation 12. Protein aggregation by cavitation was already described for an antibody and recombinant human growth hormone (rhGH) 44. No chemical modifications was found for the antibody while the data for rhGH was inconsistent. Recent research on cavitation did also not find radial associated oxidation of an antibody by cavitation events 45. However, in both studies protein aggregation could be noticed, which indicates that the driving force behind cavitation induced aggregation is more reasonable the generated surface area and not hydroxyl radicals. Additionally the described aggregation could be suppressed with surfactant. Hence we suggest that the aggregation mechanism towards air/liquid interfaces by shaking and cavitation is similar. Further, we could suppress cavitation inside the micro‐orifice by inserting a flow restrictor downstream of the micro‐orifice, which allowed us to investigate the influence of isolated high shear rates on protein aggregation (Fig. 5). No additional HSA dimers were formed and the monomer content did not change. Therefore, the described generation of dimers obtained by the micro‐orifice was most likely due to the additional surface area generated by the device. We observed that, although the cavitation intensity was higher for the ultra‐sonic homogenizer, the stability of vapor cavities was higher with the micro‐orifice; several bubbles were still visible several centimeters downstream from the orifice. Although the protein solution was degassed, the described stabilization of vapor cavities downstream of the orifice was most likely due to the protein. Thus, the aggregating effect of cavitation is likely less correlated with hydroxyl radical intensity, but rather with the surface area and stability of vapor cavities. Mechanical stress in form of extensional flow was recently proposed as mechanism for aggregation 4. However, the most relevant control experiment has not been conducted, namely the influence of the plunger. Protein aggregation in those experiments most reasonable occured due to the friction between the plunger and the wall. In our experiments the impact of the shear, cavitation, friction between the piston and sealing, and particle formation by abrasion by the position of the pumps was corrected in order to be able to observe the impact of the orifice. Although we did not calculate the extensional flow strain due to the higher velocity gradient it is above the described value. Hence, we think that neither shear nor extensional force is able to unfold proteins under isolated conditions. On the other side we came to the conclusion that the increase in vapor/liquid interfaces generated by cavitation is a reasonable mechanism for aggregation. However, for future work the focus should be set to analyze cavitation mediated protein aggregation with additional methods. Dynamic light scattering analysis could be used to track insoluble particle formation while circular dichroism could be used to get a better insight into secondary structural alterations.

Figure 5.

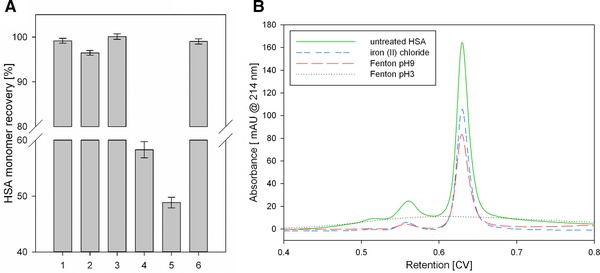
(A) HSA recovery of soluble HSA monomer before and after different treatments. 1: pumping (control); 2: pumping through the micro‐orifice; 3: ultra‐sonication; 4: iron(II)chloride at pH 9; 5: Fenton's reaction at pH 9; 6: suppressed cavitation. Error bars represent the standard deviation of three independent experiments. (B) SEC chromatograms of different HSA samples. Untreated HSA (green) was compared to an HSA solution containing iron(II)chloride (blue), HSA treated with Fenton's reaction at pH 9 (red), and Fenton's reaction at pH 3 (black dotted).

Figure 6.

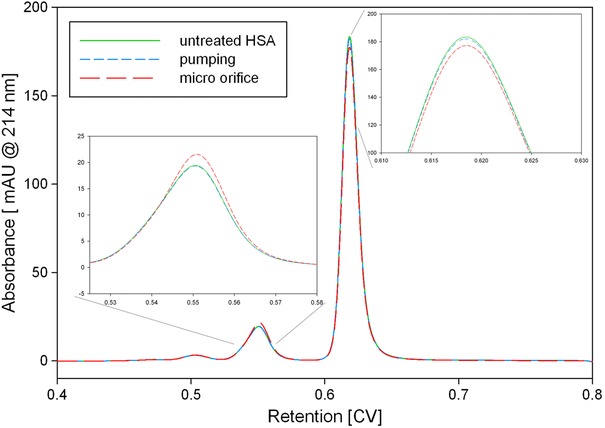
HP‐SEC samples of HSA treated with the micro‐orifice. Untreated HSA (green) was compared to an experiment with (red) and without the micro‐orifice (blue). The decrease in monomeric HSA and the increase in dimeric HSA by the micro‐orifice treatment is visible.

4. Concluding remarks

In the present study, we demonstrated that HSA did not aggregate due to cavitation‐mediated hydroxyl radicals, as insufficient radicals were generated. Although hydroxyl radicals belong to the most aggressive radical species, even the high energy input of the ultra‐sonic homogenizer did not have a high enough generation rate to alter HSA aggregation level. However, a change in HSA aggregation behavior was observed when pumping through the micro‐orifice. Due to our validated CFD simulation, we calculated an average shear rate and stress of 1.2 × 10⁶ s⁻¹ and 1200 Pa, respectively. Although the shear stress applied to the proteins was higher than reported elsewhere in the literature, when cavitation was suppressed and the pumping rate the same, HSA aggregation did not occur. We conclude that the impact of isolated shear conditions on protein integrity is low. Nevertheless, we observed HSA aggregation when cavitation occurred. Therefore, the increased surface area due to cavitation bubble growth was identified to be responsible for aggregation. Our future work will evaluate the effect of cavitation on the behavior of structurally different proteins at different concentrations. Further, we want to compare protein aggregation behavior during cavitation with air/liquid interfaces and address the aggregation mechanism.

Practical application

The influence of high shear rates and cavitation on the aggregation/destruction of proteins is not fully understood. We developed a methodology to mimic both cavitation and extremely high shear rates to investigate protein behavior. The method is able to discriminate the effects of both mechanical shear stress and cavitation and will serve as a tool for root cause analysis when proteins aggregate during bioprocessing, as well as to predict if a protein is resistant to cavitation and shear stress.

The authors have declared no conflict of interest.

Nomenclature

A [m²]

area of a certain mesh face front

Ca [‐]

dimensionless cavitation number

d [m]

diameter of a tube

h [h]

distance between two mesh cells

$\dot{\mathrm{M}}$ [kg/s]

mass flow average

p [kg/(m s²)]

local pressure

p_v [kg/(m s²)]

vapor pressure of a liquid

Q [m³/s)]

volumetric flow rate

r [m]

radius of a tube

Re [‐]

Reynolds number

v [m/s]

velocity

Greek symbols

ρ [kg/m³]

density

γ [s⁻¹]

shear rate

μ [kg/(m s)]

dynamic viscosity

Supporting information

Supporting information