Encoding Time in Feedforward Trajectories of a Recurrent Neural Network Model

Abstract

Brain activity evolves through time, creating trajectories of activity that underlie sensorimotor processing, behavior, and learning and memory. Therefore, understanding the temporal nature of neural dynamics is essential to understanding brain function and behavior. In vivo studies have demonstrated that sequential transient activation of neurons can encode time. However, it remains unclear whether these patterns emerge from feedforward network architectures or from recurrent networks, and, furthermore, what role network structure plays in timing. We address these issues using a recurrent neural network (RNN) model with distinct populations of excitatory and inhibitory units. Consistent with experimental data, a single RNN could autonomously produce multiple functionally feedforward trajectories, thus potentially encoding multiple timed motor patterns lasting up to several seconds. Importantly, the model accounted for Weber’s law, a hallmark of timing behavior. Analysis of network connectivity revealed that efficiency—a measure of network interconnectedness—decreased as the number of stored trajectories increased. Additionally, the balance of excitation and inhibition shifted towards excitation during each unit’s activation time, generating the prediction that observed sequential activity relies on dynamic control of the E/I balance. Our results establish for the first time that the same RNN can generate multiple functionally feed-forward patterns of activity as a result of dynamic shifts in the E/I balance imposed by the connectome of the RNN. We conclude that recurrent network architectures account for sequential neural activity, as well as for a fundamental signature of timing behavior: Weber’s law.

1 Introduction

The ability to accurately tell time and generate appropriately timed motor responses is essential to most forms of sensory and motor processing. However, the neural processes used to encode time remain unknown (Mauk and Buonomano, 2004; Buhusi and Meck, 2005; Ivry and Schlerf, 2008; Merchant et al., 2013). While the brain tells time across many scales, ranging from microseconds to days, it is on the scale of tens of milliseconds to a few seconds that timing is most relevant to sensory-motor processing and behavior. Several neural mechanisms have been proposed to account for temporal processing in this range (for reviews see Hardy and Buonomano, 2016; Hass and Durstewitz, 2016), including pacemaker/counter internal clocks (Treisman, 1963; Gibbon et al., 1984), ramping firing rates (Durstewitz, 2003; Simen et al., 2011), the duration of firing rate increases (Gavornik et al., 2009; Namboodiri et al., 2015), models that rely on the inherent stochasticity of sensory signals and neural responses (Ahrens and Sahani, 2008; Ahrens and Sahani, 2011), and finally “population clocks”, in which timing is encoded in the evolving patterns of activity within recurrent circuits (Buonomano and Mauk, 1994; Mauk and Donegan, 1997; Medina and Mauk, 1999; Buonomano and Laje, 2010).

The theory that time is encoded in the dynamics of large populations of neurons has received experimental support in several brain regions including the cortex (Crowe et al., 2010; Merchant et al., 2011; Harvey et al., 2012; Kim et al., 2013; Crowe et al., 2014; Bakhurin et al., 2017), basal ganglia (Jin et al., 2009; Gouvea et al., 2015; Mello et al., 2015), hippocampus, (Pastalkova et al., 2008; MacDonald et al., 2011; Kraus et al., 2013; Modi et al., 2014), and area HVC in songbirds (Hahnloser et al., 2002; Long et al., 2010). Some of these studies report relatively simple, apparently feedforward, sequential patterns of activity in brain regions containing significant recurrent connectivity. A fundamental question is whether these patterns of activity are generated by truly feed-forward circuits, or rather by recurrent circuits generating “functionally feedforward” patterns of activity (Banerjee et al., 2008; Goldman, 2009). Here we define functionally feedforward trajectories as those generated by recurrent neural networks, and that are characterized by sequential patterns of activation (“moving bumps”) in which any given unit only fires once during a pattern.

Synfire chains are perhaps the simplest network-based model that could account for the reports of functionally feedforward patterns of activity. Typically, synfire chain models consist of many pools of neurons connected in a feedforward manner such that activation of one pool results in the sequential activation of each downstream pool (Abeles, 1991; Diesmann et al., 1999). However, cortical circuits, where functionally feedforward activity is often observed, are characterized by recurrent connections and local inhibition, features that standard synfire chain models generally lack (Harvey et al., 2012). Moreover, the capacity of these synfire networks is limited because any given neuron generally participates in only one pattern (Herrmann et al., 1995). To address these issues, we use a model of recurrent neural networks (RNNs) to examine how they might produce functionally feedforward patterns of activity that encode time.

Previous studies of timing using RNNs have not sought to simulate experimentally observed patterns of neural activity and have used RNNs that do not follow Dale’s law. We expand on previous work (Laje and Buonomano, 2013; Rajan et al., 2016) by training RNNs that follow Dale’s Law to emulate experimentally observed activity patterns. In addition, unlike standard RNN models, the networks in this study only have positive value firing rates. The networks are trained using the innate-training learning rule to autonomously produce stable activity for up to five seconds, two orders of magnitude greater than the time constant of the units (Laje and Buonomano, 2013; Rajan et al., 2016). Our results demonstrate that RNNs can robustly encode time by generating functionally feedforward patterns of activity. Importantly, these networks account for a characteristic of motor timing known as Weber’s Law (Gibbon, 1977; Gibbon et al., 1997), and can encode multiple feedforward patterns. Analysis of trained networks revealed changes in the balance of excitation and inhibition that account for the production of this feedforward activity, thus generating an experimentally testable prediction.

2 Results

2.1 Recurrent Neural Networks Produce Functionally Feedforward Trajectories

We first examined if recurrent neural networks can generate the sequential patterns of activity observed in the cortex and hippocampus (Pastalkova et al., 2008; Crowe et al., 2010; MacDonald et al., 2011; Crowe et al., 2014). Typically, in these areas any neuron participating in a sequence is active for periods of hundreds of milliseconds to a few seconds. We used a modified version of standard firing-rate RNNs in which units are sparsely and randomly connected to one another (Sompolinsky et al., 1988). Specifically, to more closely mimic neural physiology we incorporated separate populations of excitatory and inhibitory units (Fig. 1A). Furthermore, the firing rate of each unit was bounded between 0 and 1 (see Materials and Methods).

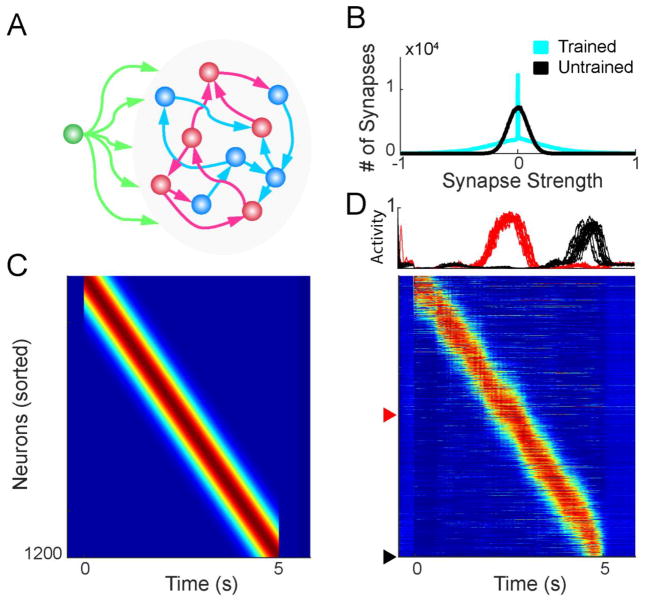
Figure 1. Generation of feedforward trajectories within a RNN.

A. Schematic of network architecture. The networks were composed of 600 excitatory (blue) and 600 inhibitory (red) firing rate units (N^Rec = 1200), with sparse recurrent connections. Neurons at the beginning of a sequence received input (green) during a 50 ms window to trigger the trajectory. B. Connection weights were initialized with a Gaussian distribution. After training to produce a single feedforward sequence, a large number of weights were pruned to zero, and some weights became stronger, resulting in a long tailed distribution. C. Example five second feedforward sequence target. D. After training, the RNN can produce a five second feedforward trajectory. Top: two units trained to activate in the middle and end of the trajectory, highlighted below. Each trace represents one of 15 trials. Bottom: Example network activity from a single trial.

We used a supervised learning rule to adjust the recurrent weights and train the network to produce a functionally feedforward trajectory in response to a brief (50 ms) input. Specifically, the networks were trained to produce a 5 second long target sequence of feedforward activity such that each unit in the network was transiently activated without being driven by external input (Fig. 1C). This activity pattern can be thought of as a moving bump of neural activity. After training, the network was able to reproduce the 5 sec long neural trajectory in response to the brief input (Fig. 1D). Importantly, after the end of the trajectory the RNN returned to an inactive rest state—thus in contrast to RNNs in high-gain regimes these networks were silent at rest. Training dramatically altered the distribution of synaptic weights in the network: the weight of many synapses converged to 0 (in part as a consequence of the boundaries imposed by Dale’s law) while others were strengthened resulting in long tails (Fig. 1B). These long-tails of the synaptic weight distribution is in line with experimentally observed distributions of synaptic weights (Song et al., 2005) and observations in previous models of neural dynamics in RNNs (Laje and Buonomano, 2013; Rajan et al., 2016).

2.2 RNNs can Encode Multiple Sequences

Many motor behaviors such as playing the piano or writing require the use of the same muscle groups activated in distinct temporal patterns. If the motor cortex is to drive these motor patterns, it must produce distinct well-timed trajectories of neural activity using the same sets of neurons activated in different orders. Traditional models of sequential neural activity (e.g. standard feedforward synfire chains) do not account for this because each unit generally participates in only a single sequence.

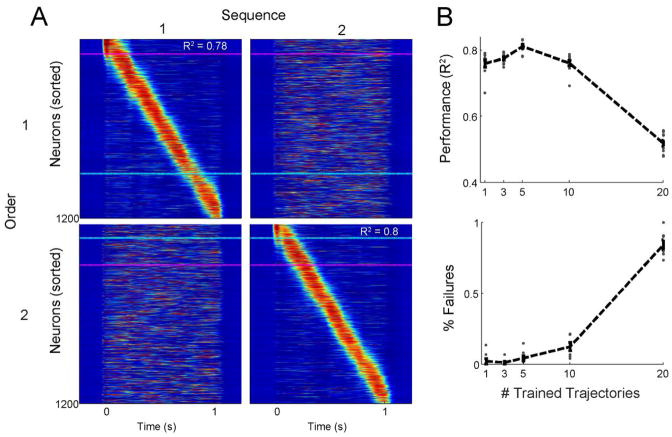
To examine the capacity of recurrent networks to encode multiple functionally feedforward trajectories, we trained RNNs to learn patterns in which all units participated in each trajectory. RNNs were trained to learn 1, 3, 5, 10, or 20 distinct sequences. Each sequence lasted one second, and was triggered by a distinct input. As shown in Fig. 2A, an RNN can generate multiple distinct patterns in response to distinct inputs. Importantly, each pattern recruits all the units in the network. To quantify the network capacity, we calculated the correlation between the evoked activity on each test trial and the corresponding target. We used the average correlation across targets as a measure of performance. Trained networks could reliably produce ten 1-second sequences with relatively little decrement in performance. However, when RNNs were trained on 20 patterns they showed a large decrease in performance (one-way ANOVA, F_4,45= 193, p < 10⁻²⁷, n = 10 networks; Fig. 2B) and increased failure rate (number of trials in which the input did not evoke a pattern or generated a partial sequence; one-way ANOVA, F_4,45= 419, p < 10⁻³⁵, n = 10 networks).

Figure 2. A single RNN can encode many different feedforward trajectories.

A. The units of the same trained RNN in response to two different inputs. Each column shows the spatiotemporal pattern of activity triggered by a single input. Each row shows the activity sorted according to feedforward trajectory #1 (top row) or #2 (bottom row). Blue and pink dashed lines highlight the same two units in all panels. B. Performance (top) and failure rate (bottom) for ten networks trained to produce up to 20 trajectories. Each dot represents the average across 15 trials per target for a single network. Each network can reliably produce up to ten feedforward sequences before performance decreases. Error bars show the mean ± SEM

2.3 Functionally Feedforward Trajectories Account for Weber’s Law

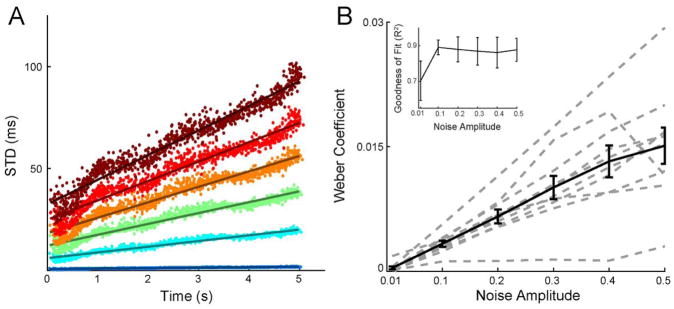
A defining feature of behavioral timing is that there is an approximately linear relationship between the standard deviation and mean of a timed response (Gibbon, 1977; Gibbon et al., 1997)—referred to as the scalar property or Weber’s law. The ability to account for Weber’s law is often taken as a benchmark for models of timing, and does not generally emerge spontaneously in many models (Ahrens and Sahani, 2008; Hass and Herrmann, 2012; Hass and Durstewitz, 2014). To examine whether the RNNs studied here obey Weber’s law, we measured the temporal variability of each unit within a single feedforward pattern at different levels of noise. We fit the activity of each unit on every test trial with a Gaussian function, and calculated the standard deviation and mean of the peak time of each unit’s fit across trials (see Materials and Methods). We used Weber’s generalized law to fit the standard deviation as a function of time, and refer to the slope of this linear fit as the Weber coefficient (Ivry and Hazeltine, 1995; Merchant et al., 2008)—note that Weber’s generalized law allows for a positive intercept. In each of ten trained networks, we found that the standard deviation of a unit’s peak firing time across trials increased linearly with its mean activation time (Fig. 3A). This property was highly robust: while the Weber coefficient increased with the amount of noise injected into the network, the scalar property was preserved even at large noise amplitudes (Fig. 3B)—thus Weber’s law was not limited to any specific noise parameter choice.

Figure 3. The timing generated by the RNN obeys Weber’s law.

A. Temporal variability increases linearly with elapsed time. Each dot shows the standard deviation of the activation time of a unit of an example network plotted against its mean. The activation time of each unit on each trial was determined from the center of a Gaussian fit of that unit’s activity. Each color represents one of six amplitudes of injected noise. Lines show the linear fit. B. The Weber law is robust to noise. The Weber Coefficient (slope of the linear fit shown in panel A) is shown across six noise amplitudes for ten trained networks. Each dotted line represent a single network, the solid black line represents the mean with error bars showing ± SEM. Inset: mean ± SEM of the goodness of fit (R²) for the linear fits.

2.4 Sequences are Generated by Dynamic Shifts in the Balance of Excitation and Inhibition

Experimental studies have conclusively demonstrated that functionally feedforward patterns of activity occur in vivo, but these studies have not been able to explore the neural and network mechanisms underlying these patterns (Pastalkova et al., 2008; Harvey et al., 2012; MacDonald et al., 2013). Computational models allow us to address this question and generate experimental predictions. To determine how RNNs generate sequential activity, we first examined the balance of excitation and inhibition in the units during the trained patterns. This analysis parallels experimental studies which have examined the relative balance of excitatory and inhibitory currents (Shu et al., 2003; Froemke et al., 2007; Heiss et al., 2008). We examined the balance of excitation and inhibition by separately summing the total excitatory and inhibitory input onto each unit at all time points. Fig. 4A shows the relationship between the E/I balance and firing rate in a single example unit. Interestingly, when cells were not active they still received significant excitation and inhibition, and these inputs were usually approximately balanced (E/I ≅ 1), similar to a recent in vitro study of temporal processing (Goel and Buonomano, 2016). This balance shifted towards excitation (E/I > 1) primarily during a unit’s target activity period. By plotting the E/I ratio of all the neurons in the network during a trajectory it is possible to visualize the progressive shift in the E/I balance during a feedforward sequence (Fig. 4B). These observations are consistent with experimental studies during up-state activity showing excitatory and inhibitory currents are balanced, and that changes in activity consist of subtle shifts towards excitation (Shu et al., 2003; Haider et al., 2006; Sun et al., 2010), as well as recent work showing timing-specific shifts in E/I balance in vitro (Goel and Buonomano, 2016).

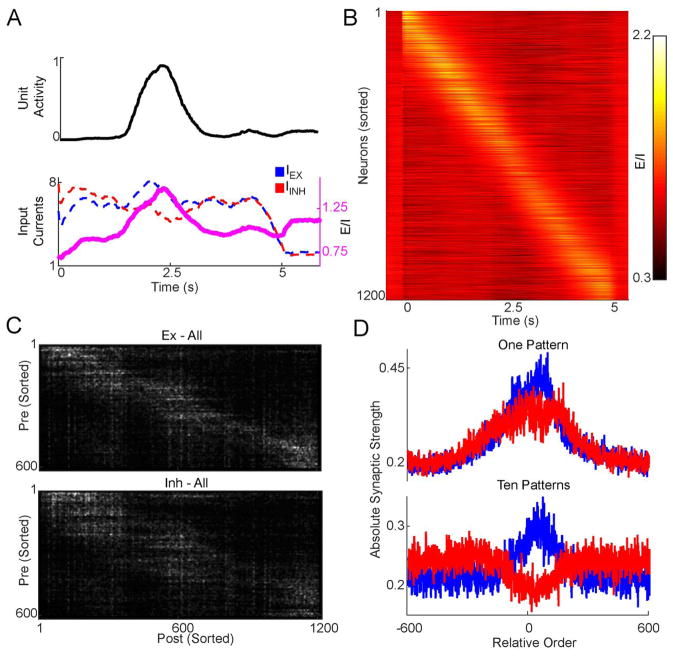
Figure 4. Feedforward trajectories are generated by dynamic shifts in the E/I balance.

A. The excitation/inhibition (E/l) ratio peaks around a unit’s activation time. Top: the activity of an example unit which peaked in the middle of a five seconds trajectory. Bottom: Inhibitory (red) and excitatory (blue) inputs are high but usually balanced throughout the trajectory, but the balance shifts towards excitation when the unit is active. E/I ratio shown in pink. B. A heat-map of the E/I ratio of the same network showing a shifting peak of the E/I ratio along the trajectory (during one trial). C. Excitatory (top) and inhibitory (bottom) weight matrices of a network sorted according to the activation order. Note the peak in synaptic strength following the activation order along the diagonal. Weights are smoothed for visualization. D. Averaging along the feedforward trajectory reveals a peak in excitatory weights pointing forward, bounded by inhibition. The absolute value of the weight matrix was centered along the feedforward sequence and averaged according to excitatory and inhibitory units. Top: Weights of a network trained for one pattern. Bottom: The same initial network, but trained for ten feedforward patterns.

To examine the origins of the dynamic shift in the E/I balance, we analyzed the synaptic connectivity matrix. When sorted according to activation order, connections from both inhibitory and excitatory units displayed a pattern of peak connection strength along the sequence of activation (Fig. 4C). To examine the structure of the connectome we shifted the sorted weight matrix to align the window of activity of each postsynaptic cell within the trajectory. Taking the mean across all cells of this shifted weight matrix revealed a peak of excitation pointing forward along the trajectory (that is, the excitatory weights are asymmetrically shifted to the right), bounded by peaks of inhibition (Fig. 4D, upper panel). Despite the rightward shift of the peak—and in contrast to feedforward networks—the excitatory units are clearly connected in the “forward” and “backward” directions. This anatomical feature allows for the local mutual excitation necessary to keep units active for durations of up to a second. This “Mexican hat” connectivity pattern, has been observed in other studies of sequence generation (Itskov et al., 2011; Rajan et al., 2016) and accounts for the moving bump of activation in feedforward RNNs. Interestingly, for a single pattern the shift of the E/I balance towards excitation was primarily driven by an increase in excitation (Fig 4D upper panel). However, when the same analysis is performed for networks that learned 10 patterns, the E/I shift driving activity forward was generated by both an increase in excitation and a decrease in inhibition (Fig. 4D, lower panel). Taken together, these results predict that recurrent networks in the cortex generate functionally feedforward sequences of activity using asymmetries in the connectivity patterns between neurons, and dynamic shifts in the E/I balance.

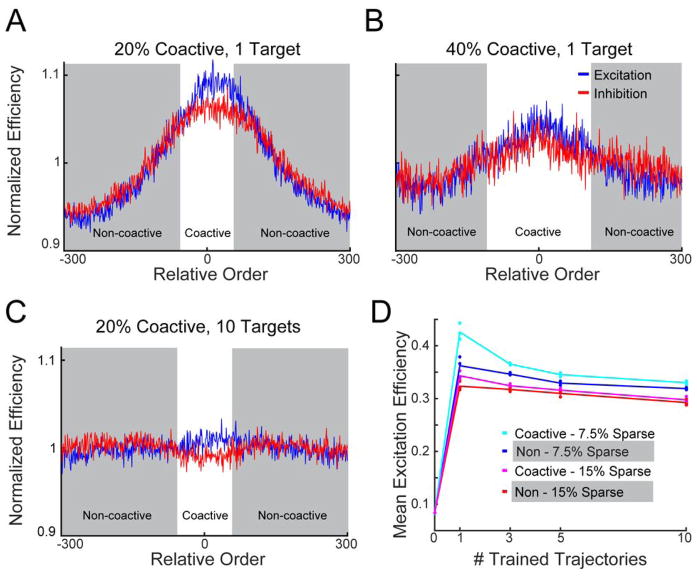
2.5 Connectivity of RNNs Reflects the Number of Encoded Trajectories

There is increasing emphasis on characterizing the microcircuit structure, or the connectome, of biological neural circuits. To further examine the relationship between the microcircuit structure in our model, and potentially generate experimental predictions, we calculated network efficiency—a standard measure from graph theory that captures the “interconnectedness” of the units in a graph (Boccalettii et al., 2006). Specifically, it measures the minimal weighted path length between units, such that a larger efficiency value corresponds to a shorter path (see Materials and Methods). Because we were interested in the relationship between structure and function we compared efficiency measures of coactive and non-coactive units. Furthermore, since the activity in any unit is the result of the interaction between excitatory and inhibitory inputs we separately calculated the net excitatory and inhibitory connection strengths between pairs of units—generating topological representations of recurrent excitation and inhibition. We then calculated the weighted efficiency index of these connections in trained untrained networks.

As expected, when averaged along a single trained sequence of feedforward activity, we observed that units that co-activate (i.e, active at neighboring points in time) had a higher than average efficiency value (Fig. 5A), similar to the observed “Mexican hat” architecture in Fig. 4D. However, when networks were trained for sustain more coactive units (Fig. 5B), or were trained to produce a larger number of targets (Fig. 5C), the connection efficiency between coactive and non-coactive units approached the network mean. Finding the average disynaptic efficiency between coactive and non-coactive units revealed that efficiency sharply increased when networks were trained for a single target, with coactive efficiency exceeding non-coactive (Fig. 5D). As more trajectories were encoded, this difference decreased, indicating that efficiency became uniform with respect to unit pairs’ active relationship. Moreover, networks with more coactive units (40% active) were initially more uniform than those with fewer coactive units (i.e, the efficiency between coactive and non-coactive units was more similar), consistent with the notion that higher local efficiency may be necessary to maintain temporally sparser trajectories in order to support more local positive feedback between coactive units.

Figure 5. Multiple feedforward pat terns are embedded via uniform path lengths between units.

A. Average disynaptic efficiency between coactive (unshaded) and non-coactive (shaded) unit pairs in an RNN trained for a single feedforward target. Units that are coactive during a trajectory have a higher mean efficiency compared to non-coactive pairs. Efficiency values were normalized to the mean to aid visualization. B. Same as A but showing the same initial network trained such that more units are coactive at a given time (lower temporal sparsity). The efficiency across the network is more uniform. C. Same as in A now trained for 10 targets. In A–C, postsynaptic efficiency values were aligned according to the activation order of the presynaptic unit within the same target order and averaged across units. D. Average efficiency of connections between coactive and non-coactive units according to the number of trained trajectories. Efficiency increases sharply from the naive weights. As more trajectories are encoded, efficiency becomes uniform across the network, i.e. the difference between coactive and non-coactive units decreases.

3 Discussion

Functionally feedforward patterns of activity have been observed in a wide range of different brain areas (Pastalkova et al., 2008; MacDonald et al., 2011; Kraus et al., 2013; Mello et al., 2015; Bakhurin et al., 2017). These patterns have been proposed to underlie a number of different behaviors, including memory, planning, and motor timing. Here we have focused primarily on the potential role of such patterns in timing, specifically in tasks which animals must learn to generate timed motor patterns or anticipate when external events will occur on the scale of hundreds of milliseconds to seconds. Our results show that even though many of these experimentally reported patterns of sequential activation are apparently accounted for by feedforward architectures, recurrent neural networks are more consistent with the data. Furthermore, recurrent architectures are computationally more powerful in that they can store many different trajectories in which each unit participates in each trajectory. We propose that networks with recurrent excitation underlie the functionally feedforward trajectories observed in cortical areas.

A number of models have proposed mechanisms for generating functionally feedforward patterns within recurrent networks (Buonomano, 2005; Liu and Buonomano, 2009; Fiete et al., 2010; Itskov et al., 2011; Rajan et al., 2016). These studies have used both spiking and firing rate models, and relied on a number of different mechanisms, but they have not explicitly addressed a standard benchmark for behavioral timing—Weber’s law. One recent model developed by Rajan et al. (2016) also trained RNNs using the an RLS-based learning rule, and our results complement their findings: specifically that by tuning the recurrent weights of an initially randomly connected network it is possible to robustly encode multiple functionally feedforward patterns of activity. That study, however, focused primarily on sequence generation and encoding memory-dependent motor behaviors, and did not encode time per se as the network was driven in part by time-varying inputs (that is, external information about the time from trial onset was present).

3.1 Weber’s Law

Here we show that an RNN can encode time and account for Weber’s law, more specifically Weber’s generalized law, which states that the standard deviation of a timer increases linearly with elapsed time (Ivry and Hazeltine, 1995; Merchant et al., 2008; Laje et al., 2011). The origins of Weber’s law in timing models is a longstanding and vexing problem, because according to the simplest model in which an accumulator integrates the pulses of a noisy oscillator, the standard deviation of the latency of a neuron, or of a motor output, should increase as a function of the square root of total time (Hass and Herrmann, 2012; Hass and Durstewitz, 2014; Hass and Durstewitz, 2016). In contrast, the current model naturally captures Weber’s law (at least within the parameter regimes used here), even at high noise amplitudes. Major issues remain, such as the properties underlying Weber’s law in recurrent networks and why the brain “settles” for the observed linear relationship (Hass and Herrmann, 2012). We hypothesize that these properties may be related: 1) recurrency may inherently amplify internal noise, producing long-lasting temporal correlations (Hass and Herrmann, 2012), and 2) evolutionarily speaking, the tradeoff was adaptive because it increased computational capacity.

The current model also establishes that RNNs can robustly store multiple patterns, in which each neuron participates in every pattern. This feature is consistent with experimental findings demonstrating that the same neuron can participate in multiple patterns of network activity, firing within different windows in each (Pastalkova et al., 2008; MacDonald et al., 2013). Thus the experimental data and the current model are consistent with stimulus-specific timing, in which time codes are generated in relation to each stimulus or task condition as opposed to an absolute time code. The capacity of the RNNs described here appears to be fairly large. But as demonstrated in a previous study, the true capacity of RNNs is likely to be strongly dependent on model assumptions, most notably noise levels (Laje and Buonomano, 2013).

Within this population clock framework, the same RNN does not function as a single clock, but rather implements many event-specific timers. That is, the network does not encode absolute time but elapsed time from stimulus onset, and there is an entirely different time code for each stimulus. This computational strategy ensures that the activity vector at any given instant not only encodes elapsed time, but also provides a dynamic memory of the current stimulus.

3.2 RNN Connectome

In order for sequences to propagate in a defined trajectory through a network, activity must generate imbalances that simultaneously push the activity forward and prevent it from deviating from the proper activation order (Ben-Yishai et al., 1995; Fiete et al., 2010). Here we find that training an RNN composed of distinct excitatory and inhibitory populations produces synaptic connectivity resembling an asymmetric “Mexican hat” architecture, with excitation propagating and maintaining network activity and inhibition bounding this activity to prevent off-target activation. Importantly, the recurrency of the network enables multiple “Mexican hats” to be embedded in a single connectivity matrix, allowing multiple functional feedforward patterns to be produced by a single network.

An important characteristic of the connectome of a network is how efficiently individual units exchange information. Surprisingly, we found that the weighted efficiency of a feedforward RNN was negatively correlated with the number of sequences stored, and that this change was largely driven by reduced efficiency between coactive units. Indeed, multi-trajectory networks exhibited uniform path lengths between units, regardless of their relative activation order. This “flattening” of the efficiency within a network is likely necessary to allow units that are highly separated in one sequence to also co-activate in another. Thus a prediction that emerges from this study is that learning may induce an overall decrease in the efficiency of cortical circuits, as the networks embed more uniform connection structures, making individually learned patterns difficult to distinguish using connectomics.

Reports of sequential patterns of activity in multiple brain areas appear to be superficially consistent with feedforward synfire-like architectures. However, recurrent networks are likely responsible for generating the experimentally observed patterns for two reasons. First, although the patterns of activity comprise sequential activation of neurons, the duration of activity over which a neuron fires (in the range of hundreds of millisecond to a few seconds) likely relies on local positive feedback maintained by recurrent connections; and second, purely feedforward network architectures are unlikely to account for the ability of networks to generate multiple trajectories in which any given neuron can participate in many different patterns.

4 Materials and Methods

4.1 Network Structure and Dynamics

The network dynamics were governed by the standard firing rate equations (Abeles, 1982; Sompolinsky et al., 1988; Jaeger and Haas, 2004):

$$\tau \frac{{dx}_i}{dt}=-x_i+\sum _{j=1}^{N^{\mathit{Rec}}}{W}_{ij}^{\mathit{Rec}}{r}_j+\sum _{k=1}^{N^{In}}{W}_{ik}^{In}{y}_k+I_i^{\mathit{Noise}}$$ (1)

Where x_i represents the state of unit i. The sparse, N^Rec x N^Rec matrix W^Rec describes the recurrent connectivity, with nonzero values initially drawn from a Gaussian distribution of μ = 0 and $\sigma =g/\sqrt{p_c\ast N^{\mathit{Rec}}}$, where g = 1.6 is the synaptic scaling constant and p_c = 0.3 is the probability a given unit will connect to another unit in the network (autapses were eliminated). The firing rate, r_i, of unit i is given by the logistic function:

$$r_i=\frac{1}{1+e^{-a·x_i+b}}$$ (2)

where a = 2 and b = 4 correspond to the gain and “threshold” of the units, respectively. Compared to the traditional tanh function, this provides a more biologically plausible model in which activity is low at “rest” (i.e. without input), and rates are bounded between 0 and 1.

After initialization, the efferent synapses from a randomly selected half of the recurrent units were set to be positive and the other half set to be negative to create inhibitory and excitatory populations. The N^Rec x N^In matrix W^In describes the input connections from input units y to the recurrent units, and is set to stimulate only those units active at the start of a functionally feedforward sequence with weight equal to each unit’s target activity at t = 0. The activity of the input units was set to 0 except during the 50 ms input window at the beginning of a trial when it was set to 3. N^Rec = 1200 is the network size, and τ = 25 ms is the time constant of the units. The random noise current (I^Noise) was drawn from a Gaussian distribution of μ = 0 and σ = 0.5 (noise amplitude) unless otherwise indicated. A single unit of the RNN contacted all other units and was tonically active, providing a “bias” to each unit, but containing no temporal information as its activity was set to 1 at all times.

4.2 Training the RNNs

The RNNs were trained to generate target patterns of sequential activity designed to mimic the functionally feedforward activity observed in neural circuits during temporal tasks (Hahnloser et al., 2002; Pastalkova et al., 2008; MacDonald et al., 2011; Harvey et al., 2012). These targets were generated by setting each unit to activate briefly in sequence so the entire population tiled the interval defined by t_max (Fig. 1C). The activation order was generated randomly for each target pattern and constrained so that the order of inhibitory and excitatory units was interleaved. The pattern of activation for each unit was set by a Gaussian with a μ equal to the unit’s activation time. The temporal sparsity of the pattern, defined by $\frac{N^{\mathit{Active}}}{N^{\mathit{Rec}}}$, where N^Active represents the number of units in the target pattern that are active at any given point in time, was set to approximately 20% by making the σ of the Gaussian target function 7.5% of t_max (Rajan et al., 2016).

Training was performed using the innate-training learning rule which tunes the recurrent weights based on errors generated by each unit (Laje and Buonomano, 2013), similar to the learning rule used in Rajan et al. 2016. The error was determined by taking the difference between the activity of the unit r_i and it’s target activity at time t and used to update its weights using the recursive least squares (RLS) algorithm (see also, Haykin, 2002; Jaeger and Haas, 2004; Sussillo and Abbott, 2009; Mante et al., 2013; Carnevale et al., 2015; Rajan et al., 2016). As described previously (Laje and Buonomano, 2013) the weights onto a given unit were updated proportional to its error, the activity of its presynaptic units, and the inverse cross-correlation matrix of the network activity. To maintain Dale’s law, efferent weights from all units were bounded so that they could not cross zero (i.e. negative weights were prevented from becoming positive and vice versa). The weights were bounded to a maximum value of $g+5/\sqrt{N^{\mathit{Rec}}}$ of the appropriate sign to prevent overfitting. Training was conducted at a noise amplitude of 0.5 and all recurrent units were trained.

4.3 Weber Analysis

To determine if the timing of the network obeyed Weber’s law, we tested each network 15 times at six different I^Noise amplitudes. For each trial, we fit the activity of each unit with a Gaussian curve and used the center of that curve as a measure of the unit’s activation time. Because each unit activates only once, time can be measured directly from the activity state of the network (Abeles, 1982; Long et al., 2010). Only units whose Gaussian fit had an R² > 0.9 where used for the Weber analysis. For a given noise level and network, we calculated the standard deviation (std_i) and mean (t_i) of these activation times for each unit i and found a linear fit of these values. We then used the slope of the linear fit as the Weber coefficient, std/t (excluding units outside a 95% confidence interval of the linear fit; Fig. 1).

4.5 Performance

Network performance was measured by a performance index, calculated as the correlation (R²) between network activity on a given trial and the corresponding target pattern. The overall performance of a network was calculated as the network’s mean performance index across all trials for all trained patterns. Particularly at high noise levels and numbers of trained targets, networks sometimes failed to complete a feedforward sequence; thus we also used the percentage of these failures to quantify capacity (Fig. 2B).

4.6 Network Efficiency

In graph theory, network efficiency measures the shortest path between two nodes of a network, and can be thought of as a measure of interconnectedness of the units (Boccalettii et al., 2006). Efficiency was calculated by determining the minimum weighted disynaptic excitatory and inhibitory path length between pairs of excitatory units in the network, with weights normalized to the maximum weight. Disynaptic connection strengths were calculated by taking matrix products W_{Ex Ex}W_{Ex Ex} for the excitatory path and W_{Ex Inh}W_{Inh Ex} for inhibitory path, creating two N^Ex × N^Ex matrices. The path length between two units was determined by finding the series of edges that connected the units with the smallest summed inverse weight. For example, if unit A is connected to unit B with a strength of 0.2, the path length will be 5; if unit A is also connected to unit C with a strength 0.5 and unit C connects to B with a strength of 0.5, then the length from A to B is 4 (2 + 2). Thus the minimum weighted path between A and B would be through unit C. This path length was calculated for all possible pairs in the disynaptic matrices, inverted, and normalized by the total number of possible connections (N^Rec * (N^Rec − 1)) to generate an efficiency value. Therefore, a network with 100% maximal connections would have an efficiency value of 1.