Classification of calcium in intravascular OCT images for the purpose of intervention planning

Abstract

The presence of extensive calcification is a primary concern when planning and implementing a vascular percutaneous intervention such as stenting. If the balloon does not expand, the interventionalist must blindly apply high balloon pressure, use an atherectomy device, or abort the procedure. As part of a project to determine the ability of Intravascular Optical Coherence Tomography (IVOCT) to aid intervention planning, we developed a method for automatic classification of calcium in coronary IVOCT images. We developed an approach where plaque texture is modeled by the joint probability distribution of a bank of filter responses where the filter bank was chosen to reflect the qualitative characteristics of the calcium. This distribution is represented by the frequency histogram of filter response cluster centers. The trained algorithm was evaluated on independent ex-vivo image data accurately labeled using registered 3D microscopic cryo-image data which was used as ground truth. In this study, regions for extraction of sub-images (SI’s) were selected by experts to include calcium, fibrous, or lipid tissues. We manually optimized algorithm parameters such as choice of filter bank, size of the dictionary, etc. Splitting samples into training and testing data, we achieved 5-fold cross validation calcium classification with F₁ score of 93.7±2.7% with recall of ≥89% and a precision of ≥97% in this scenario with admittedly selective data. The automated algorithm performed in close-to-real-time (2.6 seconds per frame) suggesting possible on-line use. This promising preliminary study indicates that computational IVOCT might automatically identify calcium in IVOCT coronary artery images.

1. INTRODUCTION

Vascular disease, which extracts a terrible toll on health in the developed world, is being treated percutaneously using a variety of methods that could be improved with the use of intravascular imaging. Heart attack and stroke are the major causes of human death, and almost twice as many people die from cardiovascular diseases than from all forms of cancer combined. Coronary calcified plaque (CP) is an important marker of atherosclerosis and as such, it is important to gain understanding into CP lesion formation, as it is associated with higher rates of complications and lower success rates after percutaneous coronary intervention (PCI).^{[1, 2]} The CP lesion can provide an estimate of total coronary plaque burden for a patient^[3–9], thus, concise analysis may be used to prevent and treat occlusions, which are caused by CP as soon as it is discovered.

An automatic method to segment and quantify CP in medical images would facilitate our understanding of its role in the clinical cardiovascular disease risk assessment.^[3] Furthermore, current concepts in interventional cardiology highlight the need for IVOCT. First, there is a need to guide plaque modification. The presence of calcium is the strongest factor affecting “stent expansion,” a well-documented metric for clinical outcome.^{[10, 11]} IVOCT provides the location, circumferential extent, and thickness of calcium. Angiography gives no such details. IVUS detects calcium but gives no information about thickness, as the signal reflects from the front surface. As interventional cardiologists tackle ever-more complex vascular lesions and use bioresorbable stents, there is a recent growing interest in using atherectomy devices for lesion “preparation.” Since there is a substantial economic cost and risk of complications with atherectomy^[12], we should un-blind physicians with IVOCT and provide them with improved assessment of the need for atherectomy and with angular location for “directed” atherectomy. Second, there can be a geographic miss, where the stent either misses the lesion along its length or is improperly expanded, affecting its ability to stabilize the lesion and/or provide appropriate drug dosage. There is well-documented impact on restenosis.^[13] Plaque dissections at the edge of a stent clearly visible in IVOCT were detected by angiography in only 16% of cases.^[14] Edge dissection happens almost exclusively in areas with eccentric calcium/lipid^[14], characteristics only available with intravascular imaging. Under IVOCT guidance, one can use a longer stent or apply a second stent to reduce effects of geographic miss. Third, plaque sealing is the treatment of a remote lesion that is hemodynamically insignificant (<50% stenosis) but that may appear vulnerable under intravascular imaging. Because approximately 50% of coronary events after stenting happen at remote, non-stented sites, plaque sealing is an attractive concept under investigation in trials. IVOCT’s high sensitivity for lipid plaque will be advantageous for guidance of plaque sealing.

To meet this unmet clinical need, we will develop a methodology for automatic detection of calcified plaques. The methodology we propose is a new approach for CP segmentation and is intended to perform robustly with IVOCT images encountered in the clinical environment, in real time, without the need for user interaction. In previous study done in our lab^[15] we came to the realization that, in the case of plaque characterization, due to the complexity of the different plaque compositions, when attempting to discriminate a specific, well defined plaque type (positive), all positive examples are alike, yet each negative example is negative in its own way. This led to our proposed algorithm, where we use a one-plaque classifier that tries to identify CP amongst all other plaques.

A CP region appears as a signal-poor or heterogeneous region with a sharply delineated border (leading, trailing, and/or lateral edges).^[16] Calcium is darker than fibrous plaque with greater variation in intensity level inside the region. A few major contributors to the variance in appearance of the different plaques are also artifacts as discussed in^[17] including multiple reflection, saturation, motion etc.

In our approach, a CP image is modelled by the joint distribution of filter responses combined with edge data as derived by using a canny edge detector. This distribution is represented by texton (cluster center) distribution. Classification of a new image proceeds by mapping the image to a texton distribution and comparing this distribution to the learned models. We further enhance this unique approach by increasing robustness by introducing methods novel to plaque analysis. First, we created a dictionary using images containing all possible variations of calcium encountered in a clinical environment. In addition, we introduced an approach that minimizes the reliance on edge orientation and avoids the reliance on visible structures. In the next section, we describe the algorithms in detail. Then, we describe the validation experiments, and analyze results of the comparison with human experts.

2. ALGORITHMS

Classification algorithms based on distribution of filter responses have been used in the past with various level of success.^{[18, 19]} Our algorithm enhances this concept by adding various features at various stages of the algorithm. Specifically, when extracting features, we add a very plaque-specific feature set we name DGAS (stands for Distance, Gradient, Average and Smoothness) as described below. Our algorithm is divided into four main steps: processing for extraction of image-wide features, dictionary creation, model creation (training) and classification (prediction).

Image Processing for extraction of DGAS features

In the initial step, before the SI’s are extracted, all images are passed through canny edge detector^[20] preceded by blood vessel mask extraction (the mask includes all pixels between the lumen border and the back border^[21] and guidewire artifact removal.^[22] This enables each pixel to be assigned a global edge feature vector (features of edges extending over a length in the image) set referred to as DGAS feature set (these are five real-valued features). The DGAS feature set includes distance of the pixel from the lumen, continuous edge gradient magnitude, continuous edge gradient direction (together, they express the acutance of the edge), average edge intensity and edge smoothness computed as the second derivative of the image (i.e. Laplacian).^[23] Notice that these features are assigned based on edge which are found by processing the complete frame, thus, continuity across SI’s is preserved. Following this step, SI’s are extracted as described below.

Calcium Texton Dictionary Creation

In the dictionary creation step (Algorithm, part 1), we obtain a finite set of local structural features that can be found within a large collection (40 randomly selected from the CA-DS set describe below) of calcium SI’s from various pullback images. We follow the hypothesis that this finite set, which we call the calcium texton dictionary, closely represents all possible local structures for every possible calcium instance in a pullback.

Textons

We characterize a calcium SI by its responses to a set of linear filters (filter bank, F) combined with edge features (DGAS feature set). We seek a set of local structural features (filter responses) which is targeted towards having largest response representing the calcium specifically. This approach leads to our main four-part proposal: First, to use a filter bank containing edge and line filters in different orientations and scales. Second, optionally, select a subset taking into account only the strongest responses across all orientations (thus providing orientation invariance). Third, based on the concept of textons and its generalizations introduced by Malik et al.^[24] we use the concept of clustering the pixel responses into a small set of prototype response vectors we refer to as textons. Note that by adding to each filter response vector the DGAS feature set, we enable the addition of spatial relationships between adjacent SI’s in the form of continuous borders within the image.

Algorithm, part 1.

Dictionary creation

Init split CA-DS into 2 disjoint sets: dictionary, training&testing (for model creation)

input 40 calcium sub-images.

output dictionary of textons (∈ ℝK×n)

for each sub-image { Create filter bank, F Convolve with filter bank, F (∈ □nf) and record convolution value. Combine with DGAS feature set - ℝn for each pixel

}

Concatenate all calcium pixel responses

Create K clusters for each group via K-means (Identify K via “elbow” method).

Output dictionary

Filter bank, F

We designed a special filter bank, in an attempt to capture the qualitative description of calcium as signal-poor or heterogeneous region with a sharply delineated border.^{[17, 25]} We then investigate the maximum response filters over the orientation (MR8) versus the entire filter bank. It is shown that by doing that we reduce computation effort significantly with minimal loss in performance. The full filter bank (Figure 1) consists of a Gaussian and a Laplacian of Gaussian filters, an edge filter at three scales and six orientations and a bar filter (a symmetric oriented filter) at the same three scales and orientations, giving a total of 38 filters. When using the maximum response filters, the output dimensionality is reduced by recording only the maximum filter responses across all scales, therefore, yielding one response for each of the upper six rows in Figure 1, where the Gaussian and Laplacian of Gaussian are recorded always, hence MR8. In the MR8 case, the final vector of filter responses consists of eight numbers.

Figure 1.

Filter bank designed to capture the calcium characteristics. Each row represents a different scale, where the upper three rows are bar filters in 6 orientations, the three middle rows are edge filters in six orientations and in the last row, Gaussian and Laplacian of Gaussian filters. To generate the MR8 filter responses, only 8 responses are recorded by taking maximal response at each orientation, the Gaussian, and the Laplacian of Gaussian.

Model Creation

In the model creation step (Algorithm, part 2), the remaining m_t SI’s subset from the CA-DS is used. Each of these training SI’s is convolved with F, generating a vector of filter responses which is concatenated with the DGAS feature set, thus creating a pixel response vector (∈ ℝⁿ) for each of the SI’s pixels. This vector is compared with the dictionary described above using k-nearest neighbors (k-NN) thus each pixel of the SI’s pixels is assigned a label creating a label vector whose length is the number of pixels in the SI. We then quantized this label vector into a histogram (with L bins) of texton frequencies. Finally, the texton frequency histogram is converted into a texton probability distribution, by normalizing the texton frequency histogram to sum to unity. The reason we normalize the histogram is to avoid the need of the various SI’s to have the same size or shape. This process is repeated for all m_t training SI’s, thus the final outcome of this process is a matrix whose dimension is m_t x L which is used as the training dataset for one class Support Vector Machine classifier (OC-SVM) as described below.

Texton probability distribution (normalized histograms)

The histogram of image textons is used to encode the global distribution of the local structural attributes (i.e. the filter bank’s responses and the DGAS feature set) over the calcium texture image while ensuring that every shape and size of SI can be part of the experiment. This representation, denoted by H(l), is a discrete function of the labels l derived from the texton dictionary. Each SI is filtered using the same filter bank, F, and its DGAS feature set is computed the same way. Each pixel within the SI is represented by a one-dimensional (∈ ℝⁿ) feature vector which is labeled (i.e. assigned a texton number) by determining the closest image texton using k-NN algorithm. The spatial distribution of the representative local structural features over the image is approximated by computing the normalized texton histogram.

The dimensionality of the histogram is determined by the size of the texton dictionary, K, which should be comprehensive enough to include large range of calcium appearances and the number of bins, L, used to create the histogram. Therefore, the histogram space is high dimensional and a compression of this space is suitable since computation time is a factor at the event of on-line processing. This may be an essential requirement, provided that the properties of the histogram are preserved.

Algorithm, part 2.

Model creation.

input dictionary & training sub-images

output calcium plaque model

For each training sub-image { Convolve with filter bank, F and record convolution value. Combine with DGAS feature set (ℝn for each pixel) Label each pixel response by comparing to the dictionary (using k-NN) Create histogram of label frequencies Normalize to get distribution (hence, sub-images do not need to be of the same size)

}

Assemble all histogram vectors into a single matrix (∈ ℝmt×k)

Train a one-class SVM to get the model

Algorithm, part 3.

Classification rule for new data.

input test sub-images, dictionary, model.

output label (calcium, non-calcium)

For each new sub-image { Convolve with filter bank, F and record convolution value. Combine with DGAS feature set (ℝn for each pixel) Label each pixel response by comparing to the dictionary (using k-NN) Create a histogram of label frequencies Normalize to get distribution (hence, sub-images do not need to be the same size) Predict using OC-SVM model

}

Classification Rule: One-class Support Vector Machine (OC-SVM)

For classifying new data, we use a one-class classifier. In this step, (Algorithm, part 3), we do not have stand-alone SI’s since the only input to the automated algorithm is an IVOCT pullback. We scan the pullback within the blood vessel mask, one frame after the other in (r-θ) view, with a window whose size was determined by the size of smallest calcium region required for measurement (100×100 in our experiments) and with a step which is equal to half the window size (ensuring 50% overlap). Each window is treated as an SI. The same procedure as done in the training step is followed to build a histogram corresponding to the new SI. This histogram is the new data point, which is used by the trained OC-SVM classifier for classification, producing the final SI’s classification as calcium or non-calcium as described below.

There is a reason for selecting the one-class paradigm: The traditional multi-class classification paradigm aims to classify an unknown data object into one of several pre-defined categories (two in the simplest case of binary classification). A problem arises when the unknown data object does not belong to any of those categories. When analyzing plaque in IVOCT images, it is challenging to decide what the plaque type is, especially because there are many plaques types other than the main three plaque types typically being analyzed (calcium, lipid, fibrous). One-class classification algorithms aim to build classification models when the negative class is absent, either poorly sampled, or not well defined (where the latter describes our case). This unique situation constrains the learning of efficient classifiers by defining class boundary just with the knowledge of positive class. In our problem, the calcium plaque type is defined as positive and everything else is negative. We decided to use one-class-SVM (implemented using libsvm library^[26]) because of the following reasons: First, it is effective in high dimensional spaces even in cases where number of dimensions is greater than the number of samples, second, it is very versatile since different kernel functions can be specified for the decision function including custom kernels.

One-class SVM was suggested by Scholkopf et al.^[27] where the approach is to adapt the binary support vector machine classifier (SVM) methodology to one-class classification problem, which only uses examples from one-class, instead of multiple classes, for training. The one-class SVM algorithm first maps input data into a high dimensional feature space via a kernel function, Φ(·), and treats the origin as the only example from other classes. Then the algorithm learns the decision boundary (a hyperplane) that separates the majority of the data from the origin. Only a small fraction of data points, considered outliers, are allowed to lie on the other side of the decision boundary. The hyperplane is found iteratively such that it best separates the training data from the origin. The kernel that guarantees the existence of such a decision boundary is the Gaussian kernel^[27] and, therefore, was selected to be the kernel used in this study.

Considering that our training dataset x₁, x₂, …, x_l ∈ X, Φ(·) is the feature mapping X→F to a high-dimensional space. We can define the kernel function as:

$$k(x,y)=\mathrm{\Phi }(x)•\mathrm{\Phi }(y)$$

Using kernel functions, the feature vectors need not be computed explicitly, greatly improving computational efficiency since we can directly compute the kernel values and operate on their images. We used the radial basis function (RBF) kernel:

$$k(x,y)=e^{-{\Vert x-y\Vert }^2/2{\sigma }^2}$$

Solving the one-class SVM problem is equivalent to solving the dual quadratic programming (QP) problem:

$$\text{min}\frac{1}{2}{\Vert w\Vert }^2+\frac{1}{\nu l}\sum _{i=1}^i{\xi }_i-\rho$$

subject to

$$(w•\mathrm{\Phi }(x_i))>\rho -{\xi }_i,i=1,2,\dots ,l,{\xi }_i>0$$

where ρ is the bias term and w is the vector perpendicular to the decision boundary. ξ_i is the slack variable for point i that allows it to lie on the other side of the decision boundary. ν is a parameter that controls the trade-off between maximizing the number data points contained by the hyperplane and the distance from the hyperplane to the origin. It has two main functions: it sets an upper bound on the fraction of outliers (training examples regarded out-of-class) and, it is a lower bound on the number of training examples used as support vectors. Finally, the following function is the decision rule of the OC-SVM: It returns a positive value for normal examples x_i points (i.e. positive) and negative otherwise.

$$f(x)=\mathit{\text{sign}}((w•\mathrm{\Phi }(x))-\rho )$$

3. EXPERIMENTAL METHODS

IVOCT Image Acquisition and selection of regions for SI extraction

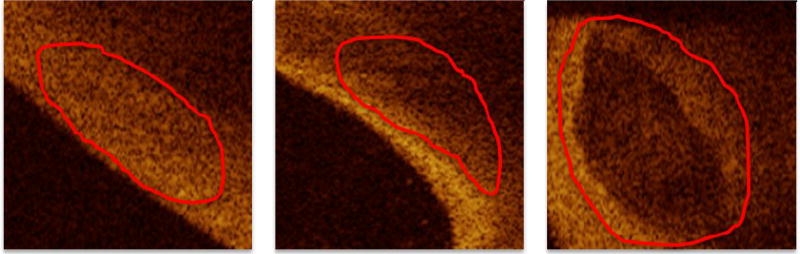
Images were collected on the C7-XR system from St. Jude Medical Inc., Westford, MA. It has an OCT Swept Source having a 1310 nm center wavelength, 110 nm wavelength range, 50 kHz sweep rate, 20 mW output power, and ~12 mm coherence length. The pullback speed was 20 mm/s and the pullback length was 54 mm. A typical pullback consisted of 271 image frames spaced ~200 µm apart. Images used in this study were selected from the database available at the Cardiovascular Core Lab of University Hospitals Case Medical Center (Cleveland OH). They consisted of 35 IVOCT pullbacks of the Left Anterior Descending (LAD) and the Left Circumflex (LCX) coronary arteries of patients acquired prior to stent implantation. These images were manually analyzed by an expert from the Core Lab to identify images of calcium, lipid, and fibrous plaques. See Figure 2 for a few examples of the CP appearance as compared to the other plaque types in a typical pullback (r-θ) view.

Figure 2.

Images in (r-θ) view showing the different appearance of the main three plague types: left, fiber; middle, lipid; right, calcium. It is shown that the calcium has a few distinctive characteristics which are apparent in the images: sharp borders with low average intensity and low attenuation (beam goes from left to right) within the calcified region.

The training dataset was created from de-identified clinical images in the set described above. An expert reviewed pullbacks and identified regions containing plaques (fibrous, lipid, or calcified) utilizing consensus criteria descried.^[16] This was followed by identifying sub-images (SI’s) which were generated by cropping a region in the image and the rest of the image was regarded as background data which was discarded. All processing is done on these cropped regions we refer to as sub-images (SI’s).

For validation testing, we created an independent (not used in training) image dataset with each voxel accurately labeled and validated by 3D cryo-imaging.^[28] To create this dataset, we obtained coronary arteries (LADs) of human cadavers within 72 hours of death and stored at 4 °C. Arteries were treated and stored in accordance with federal, state, and local laws by the Case Institutional Review Board. To prepare for IVOCT imaging, arteries were trimmed to approximately 10 cm in length. A luer was then sutured to the proximal end of each vessel which was flushed with saline to remove blood from the lumen. Major side branches and the distal end of each artery were sutured shut. Using super glue, the artery was adhered to the sides and bottom of a rig that was used to minimize motion between cryo and IVOCT imaging procedures. IVOCT imaging conditions mimicked the in-vivo acquisitions described above. Sutures were placed on the vessel to identify ROIs (1.5–2cm in length) that would later be analyzed using cryo-imaging. Following IVOCT imaging, the entire imaging rig containing the artery was flash frozen in liquid nitrogen, and stored at −80 °C until cryoimaging was performed. Prior to cryo-imaging, arteries were cut into blocks corresponding to the ROIs determined during IVOCT imaging. Blocks were placed in the cryo-imaging system and allowed to equilibrate to the −20 °C cutting temperature. The ROIs were then alternately sectioned and imaged at 20 µm cutting intervals and color and fluorescent cryo-images were acquired at each slice. The process was repeated until the whole specimen was imaged.

Training, Testing and Dictionary Datasets

The following four datasets, which were assembled from the above pool of SI’s, were used in the experiments: CA-DS (stands for Calcium Data Set) composed of 316 calcium-only SI’s, LI-DS composed of 250 lipid-only SI’s, FI-DS composed of 250 fiber-only SI’s and NON-DS, composed of approximately 750 SI’s which are neither one of the main plaque types.

In addition, we also created an independent (in the sense that data from it were not part of the training or any other experiment) dataset which is extracted from a cadaver where each pixel is annotated using cryo-based ”ground-truth” images as a confirmation of annotation, thus removing reliance on expert’s interpretation of qualitative plaque description. We name this dataset “validation dataset”.

Experiments

We compare the performance of the method using two filter banks, the full filter bank and the MR8 version of it (see below for a full description). In the following experiments, a positive example is an example that came from calcified dataset and a negative example is an example that is drawn from any dataset other than calcified dataset.

1. Stratified five-fold cross validation (SFV-CV) experiment: In one-class classifier, class boundary (model) is determined by just using the knowledge of the positive class, allowing some outliers (negatives) to be present.^[29] To create the one-class model, we combine the CA-DS with 15 negative examples (2–3 from each type). Then perform stratified 5-fold cross validation.

2. Leave-one-pullback-out (LOPO): The idea is to quantify the generalization capability of the classifier to new pullbacks. Although this approach repeats the same logic as the SFV-CV approach described above, there is one important difference: the left out set is not randomly selected from the dataset but is chosen such that all samples belong to the same pullback are held out. This represents a much more realistic condition in our application, thus is a better indication of the estimator’s ability to. We use 35-fold (because we have data from 35 different pullbacks) cross validation where we use the CA-DS set combined with a small number (2–3) examples from each of the other sets. For each of the folds, the dataset corresponding to one pullback’s images is held out and constitutes the cross validation set, while the other datasets constitute the training set. Note that this is a much more stringent and realistic condition as opposed to randomly partitioning the dataset as done in the SFV-CV experiment, since in real usage, we expect the system to see and classify plaque types from entirely new pullbacks.

3. Next experiment is intended to measure the confusion between calcium and the other plaque types. We combine the CA-DS with each of the other datasets described above and run a classification experiment. We create two mixed sets (CA-DS and FI-DS when testing against fiber and CA-DS and LI-DS when testing against lipid) and we perform internal stratified 5-fold cross validation. We divide the CA-DS into 5 folds and the mixed set into 5 folds. In each of the folds, we use a fold which is composed of only CA-DS examples for training and then we do the prediction on the rest of the CA-DS folds combined with the FI-DS/LI-DS folds. This gives a better balanced dataset and enables us to create accuracy results (as opposed to F₁ score) since the data is minimally skewed. The goal of this experiment is to quantify the amount by which the calcium can be discriminated from the other main plaque types. This also helps focus our attention on the more “problematic” plaque type, thus increase the overall performance of the classifier.

4. Finally, we use the validation dataset to classify never-seen-before datasets.

As performance measure, we use F₁ score, which can be interpreted as a weighted average of the precision and recall values. We follow standard nomenclature where we use TP (true positives), FN (false negative), FP (false positive), and TN (true negative) to make assessments of (P)recision = TP/(TP+FP), (R)ecall = TP/(TP+FN), F₁ = 2PR/(P+R). (ACC)uracy = (TP+TN)/(TP+FN+FP+TN).

4. RESULTS

Before analyzing the algorithm’s performance, it is essential to determine all of its parameters to ensure good performance. We show that using the MR8 as opposed to the full filter bank, does not impact significantly the final outcome, yet the speed is improved.

Algorithm Parameters

We optimized algorithm parameters in multiple steps. First, we determined the two OC-SVM parameters to be used in all subsequent analyses. These parameters are σ, the RBF kernel’s bandwidth and ν, which according to^[27] can be viewed as either the upper bound on the fraction of outliers (in our case, we simply set this value to be the number on non-calcium SI’s used in the training divided by the total number of training SI’s). Or, it can also be viewed as a lower bound on the number of training examples used as support vectors. This good initial value enables us to perform an efficient grid search for best parameters for the OC-SVM. In this grid search we were able to find the best σ for the radial basis function (RBF) and fine-tune the initial ν. The final values were: ν=0.0896 and σ=0.0313.

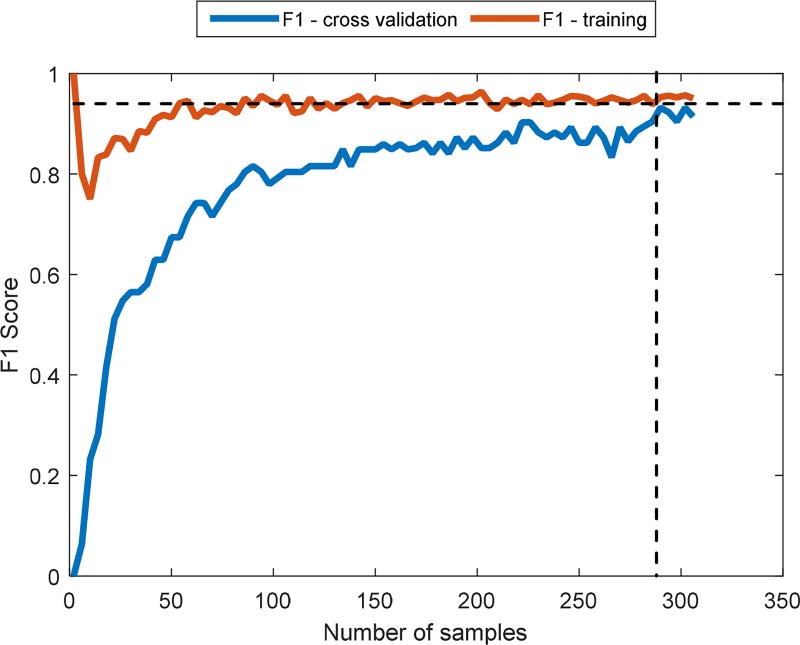
Second, we verified that the number of training examples was sufficient to enable efficient training of the OC-SVM. We performed a learning curve analysis where we varied the number of samples and compared the training and the cross validation F₁ score until they converged (Figure 3). This gave us a good starting point to ensure minimal over/under fitting is minimized. We selected to use the F₁ score as performance matrix, since, as it is typical with one-class classification, the number of negative examples is very small compared to the positive examples, causing the overall dataset to be skewed. It is shown that for cross validation F₁ score to reach that of training F₁ score, approximately 280 examples are sufficient (each point is a point in feature space, meaning, it represents a single SI).

Figure 3.

Learning curve analysis for a OC-SVM. Here we use F₁ score as performance measure. The vertical dashed line is the minimal number of data points which will enable high enough performance (280). The horizontal dashed line represents the steady state F₁ score which is the best possible performance given the current training data.

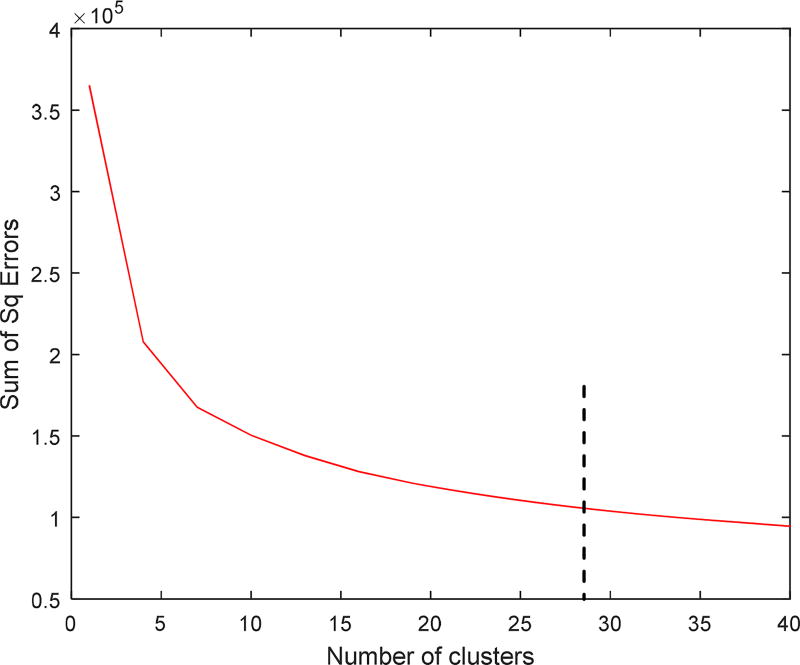
Third, to find the best number of textons to be used in the dictionary, we used the “elbow” approach by plotting the sum of the within-cluster square of Euclidean distances versus increasing number of clusters and observed where the “elbow” occurred. As shown in Figure 4, the optimal number of textons for the calcium dictionary was K=29. This value was used in all subsequent processing of SI’s.

Figure 4.

Finding the optimal number of textons by plotting the within-cluster sum of squared distances vs. the number of clusters.

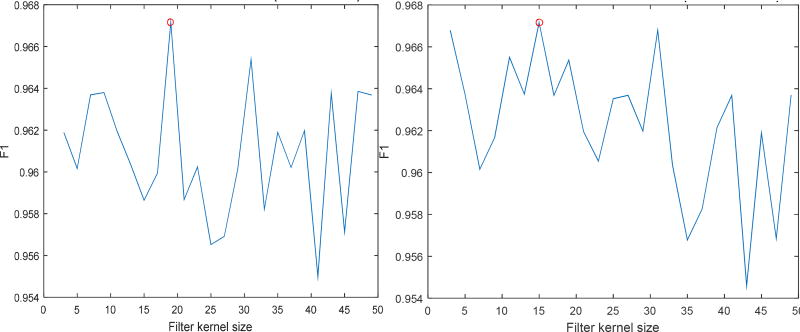
Fourth, we determined the optimal size of the kernel to be used in the filter bank. To do that, we created a dictionary of 29 calcium clusters and then ran the classification algorithm on CA-DS set using the full kernel and then using the MR8 version of the filter bank’s responses. The idea was to be able to derive the best kernel size rather than get the optimal performance measure. We ran 5-fold cross validation of the created datasets for varying values of filter kernel (Figure 5). The optimal kernel size, which was found in this experiment, was 19 × 19 for full filter bank and 15 × 15 for the MR8 filter bank.

Figure 5.

Determination of filter bank’s kernel size. 5-fold cross validation performance (using F₁ score as a statitical measure) performed by varying filter kernel size. (left) plot of F₁ score variation for full kernel filter bank. (right) F₁ score variation for MR8 filter bank. Red circles indicate the location of best performance size (full kernel, kernel is 19×19, MR8 kernel is 15 × 15).

Training and Model Creation using Regions from Clinical Dataset

Results of the SFV-CV and the LOPO experiments are shown in Table 1. First, we note that, the MR8 performs as well as the full filter bank. This is a clear indicator that orientation invariant description is not a disadvantage (i.e. salient information for classification is not lost). Second, the fact that MR8 does as well as the full filter bank is also evidence that it is detecting the most distinctive features. These results are encouraging since reduction of the features space down to 8 from 38 is a significant computational advantage, making the process more suitable for on-line usage.

Table 1.

Performance statistics for the two experiments (showing mean±sd), SFV-CV and LOPO.

	SFV-CV		LOPO
	Full filter bank	MR8	Full filter bank	MR8
F1 Score	0.929±0.026	0.933±0.027	0.815±0.265	0.825±0.258
Precision	0.986±0.015	0.975±0.016	0.899±0.274	0.894±0.273
Recall	0.879±0.046	0.896±0.048	0.785±0.278	0.866±0.266

In the next experiment, we tested the calcium against each of the other main plaque types (Table 2). It is evident that calcium and fibrous are more easily discriminated compared to calcium and lipid. It suggests that we should consider designing additional filters that not only favor the calcium plaque characteristics but also favor the lipid characteristics. Moreover, we see that the results when using the responses of the full filter are better than when we just use the maximum responses.

Table 2.

Performance of calcium classification versus classification of the other main plaque types.

	5-fold cross validation
	Full filter bank	MR8
	mean±sd	mean±sd
Ca-v-lipid	0.762±0.07	0.743±0.004
Ca-v-fiber	0.835±0.016	0.814±0.018
Ca-v-all	0.778±0.012	0.759±0.010

Evaluation on Independent Validation Dataset

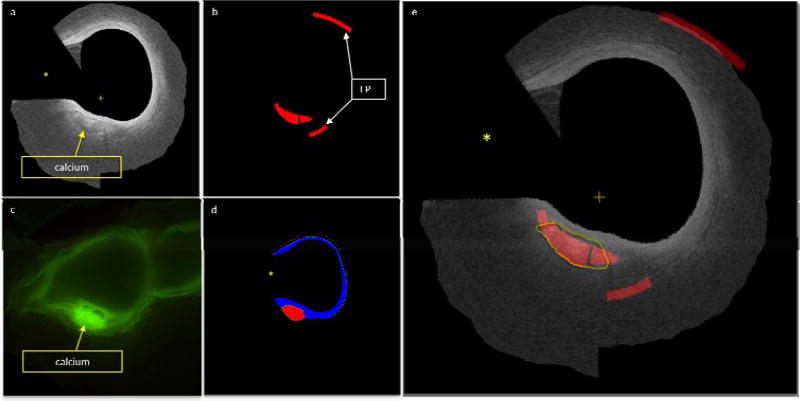
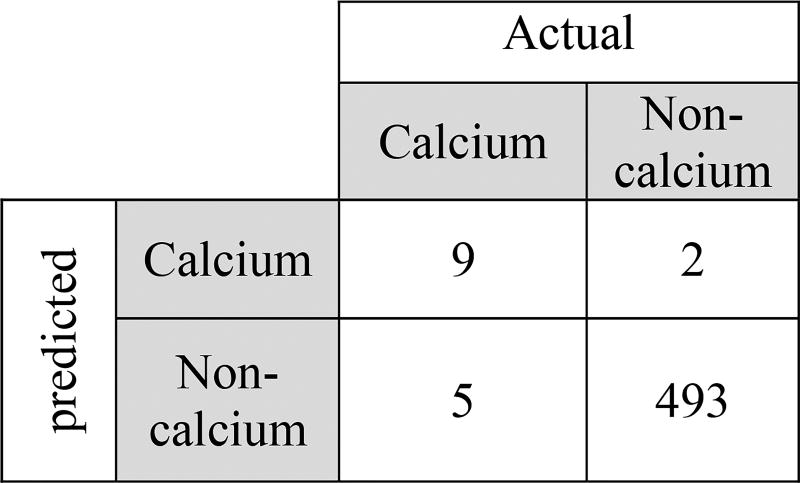
We evaluated our algorithm performance on the independent validation dataset confirmed with cryo-imaging. Example result (Figure 7) show cryo and IVOCT input images, manual plaque annotations, and classifier outputs. For the purpose of quantifying the automatic calcification on the validation dataset, we counted the number of SI’s scanned where classification is considered TP if more than 25% of the SI covered a true calcified region. Using this criterion, the performance of the scanned image shown in Figure 7 is shown in the form of a confusion table (Figure 6). Clearly, due to the fact that the majority of the SI’s scanned, using accuracy will not reflect the performance accurately, so we choose to compute the F₁ score as described above, yielding F₁ = 0.72;

Figure 7.

Independent validation classification. a) Original IVOCT imaged where the guidewire (marked by yellow asterisk) and data beyond lumen and back border are masked out. Notice the calcified region with sharp borders. b) Results of automated classification. C) Corresponding registered cryo-image. Notice how the calcified region is much brighter when using fluoroscopy. D) Expert annotation of the plaque types present in the image (blue is fiber and red is calcium). e) IVOCT image with automated classification overlay. The yellow line represents the experts annotation of the calcified region (can also be seen in part a). Red represents the classification and the blue represents fiber, the “+” sign represents the center of the image.

Figure 6.

Confusion table showing independent validation image classification results (Figure 7)

Finally, in terms of time performance, the MR8 yielded a classifier which is more than 30% faster, yet, as can be seen in the results above, the accuracy measurements are not significantly affected. When using MR8 filter bank, the average time to compute features (histogram) for a single frame is 2.6 seconds and for full filter bank 3.7 seconds (measured by running Matlab). This means that the feature creation using MR8 filter bank is 30% less expensive than full filter bank, thus making the algorithm suitable for on-line application.

5. DISCUSSION

The presence of calcium in the coronary arteries is an indication of intimal atherosclerosis.^[30] Because of the demonstrated value of coronary calcium detection in predicting significant coronary disease and because of its independent predictive value for coronary events^[31], it is important to be able to precisely and efficiently detect and quantify coronary calcium.

Automated calcium plaque classification, represents the key step to help in treatment decision making in clinical settings and reduce the human interaction during post-procedure analyses. We have presented a novel approach for completely automatic intravascular calcium classification in close to real time performance which significantly improves on the state of the art.^[32] It presents the following advantages. First, our model representation captures efficiently “texture like” visual structures where we do not impose any constraints on, or requiring any a priori knowledge of, the catheter type, IVOCT machine type or any other conditions under which the images were acquired. The second is the learning algorithm which does not require manual extraction of objects or features. The third is the independence of region segmentation and feature extraction, which are never perfect. Finally, we have shown that the results of the reduced filter bank (MR8) do not significantly affect the performance, yet speed is improved by more than 30%, a very important parameter to consider when an on-line application is required.

In Figure 7, we note two important “artifacts” which are caused by the scanning algorithm: First, the classifier’s output looks bulky. This is due to the way we extract SI’s from a new pullback: we scan the image with a scanning window that is being labeled in its entirety as calcium or non-calcium, there is no partial-window labeling. This results in over estimation of the calcified region however, it preserves the ratio between different sizes of circumferential calcified regions. Second, the farther the scanning window is from the catheter in r-θ view, the larger the size in Cartesian view is (a square in r-θ view is transformed into an arc in Cartesian view). This causes the area in Cartesian view to look as if it is larger. This characteristic is also shown in the false positives (part b). Another thing to note is the fact that the classifier can discriminate calcium from any other plaque type (in this case, fiber). This emphasizes the advantage of using a one-class classifier, where the classifier does not have to classify one class or the other, but it simply indicates if a plaque belong to the class of interest (calcium) or not, a very elegant solution to a problem other researchers encountered.^{[21, 32–34]}

Our choice of one-class classifier approach can be proven useful in another aspect. Because a one-class classifier defines class boundary just with the knowledge of positive class (“positive” being the class of interest, calcium in our case), we can use its parameter such that they reflect expert annotation quality. For example, we can create a one-class classifier model, using cryo-imaging as annotation tool (as done in our study as escribed above). We can then compare the classifier results to, say, three experts, and quantify the quality of their annotation according to their deviation from the model. Since we assume that cryo-based-imaging is a reliable ground truth, this quantification can be used a scoring mechanism for expert annotation.

Finally, we are continuously working to improve the results in several ways: We will improve the visualization of the scanning window such that when switching between r-θ view and Cartesian view, the classified area is preserved. Pixel-based feature set will be improved using a different or enhanced feature set (i.e. improved dictionary). SI-based feature set will be enhanced by modifying histogram creation combined with additional SI-specific features. Dimension reduction will be addressed to adjust the method to cope with very large pullbacks. In addition, we will address the incorporation of a post-processing step in the third dimension (i.e. along the pullback direction). This way, the impact of the spatial variability of coronary cross-sectional morphology will be reduced, thus increase the accuracy of the classification.

6. CONCLUSION

We have demonstrated an automatic method for calcified plaque segmentation. The promising results show that the method has the potential to be used in the clinic to facilitate quantitative analysis of intravascular IVOCT images. Although additional validation is needed, the presented method holds great promise for reliable, robust, and clinically applicable segmentation of calcium in IVOCT image sequences on and off line, thus change clinical practice.