Modelling and Predicting Backstroke Start Performance Using Non-Linear and Linear Models

Abstract

Our aim was to compare non-linear and linear mathematical model responses for backstroke start performance prediction. Ten swimmers randomly completed eight 15 m backstroke starts with feet over the wedge, four with hands on the highest horizontal and four on the vertical handgrip. Swimmers were videotaped using a dual media camera set-up, with the starts being performed over an instrumented block with four force plates. Artificial neural networks were applied to predict 5 m start time using kinematic and kinetic variables and to determine the accuracy of the mean absolute percentage error. Artificial neural networks predicted start time more robustly than the linear model with respect to changing training to the validation dataset for the vertical handgrip (3.95 ± 1.67 vs. 5.92 ± 3.27%). Artificial neural networks obtained a smaller mean absolute percentage error than the linear model in the horizontal (0.43 ± 0.19 vs. 0.98 ± 0.19%) and vertical handgrip (0.45 ± 0.19 vs. 1.38 ± 0.30%) using all input data. The best artificial neural network validation revealed a smaller mean absolute error than the linear model for the horizontal (0.007 vs. 0.04 s) and vertical handgrip (0.01 vs. 0.03 s). Artificial neural networks should be used for backstroke 5 m start time prediction due to the quite small differences among the elite level performances.

Introduction

Competitive swimming start effectiveness has been typically measured using the time from the acoustic signal until the 15 m mark and divided into wall/block, flight, entry and underwater phases (Vantorre et al., 2014). In fact, 15 m time is a good predictor of overall race performance in the four conventional swimming techniques (Cossor and Mason, 2001), although shorter distances have also been considered when evaluating start skills (e.g. 5 m, de Jesus et al., 2016; Nguyen et al., 2014). There is, inclusively, a trend that proposes shorter distances to assess start performance better, which minimises the confounding effects of swimmers’ abilities during the glide and underwater swimming (Fischer and Kibele, 2016; Garcia-Ramos et al., 2015).

Since short distance swimming events can be decided by margins as small as .01 s, an effective start is essential (de Jesus et al., 2014), forcing coaches and competitors to search for and use newer and sometimes innovative solutions in the training process (Wiktorowicz et al., 2015). The application of predictive models has been a supporting solution to this process, being used in swimming starts analysis through the linear regression tool (e.g. Tor et al., 2015). Researchers have been using linear mathematical models (LM) to identify relevant kinematic and kinetic swimming start time related variables, mainly characterizing ventral start technique (Fischer and Kibele, 2016; Garcia-Ramos et al., 2015; Tor et al., 2015).

The backstroke start is more complex than the ventral start techniques since swimmers have to position themselves above the water surface level to perform a reduced water resistance start motion (Takeda et al., 2014). Previous studies, based on out-dated rules, sustained that linearly modelling backstroke start performance has evidenced the centre of mass (CM) horizontal setup positioning, take-off horizontal velocity and horizontal impulse as determinant for start time reduction (de Jesus et al., 2011; Nguyen et al., 2014). The actual start block configurations authorized by the Fédération Internationale de Natation (FINA, FR 2.7. and 2.10) have allowed backstrokers to increase the centre of mass (CM) set-up position and take-off angle (de Jesus et al., 2015), reducing overall start time (Ikeda et al., 2016). Despite the current backstroke start wedge has been pointed out as decisive for an effective backstroke start performance (e.g. Ikeda et al., 2016), no study has considered the implementation of modelling techniques using this new technology, yet.

There is a current paradigm shift to a view of sports training as a nonlinear dynamical process, which has triggered the abandonment of general linear data analysis methods in favour of computational intelligence algorithms such as artificial neural networks – ANN (Maszczyk et al., 2012; Pion et al., 2016; Silva et al., 2007). Previous modelling studies conducted in competitive swimming have pointed out the ANN as more suitable than the LM (Edelmann-Nusser et al., 2002) and nonlinear multiple regression models (Maszczyk et al., 2014), although it has never been applied in swimming starts. The aim of the current study was to compare the accuracy of ANNs and LM to performance prediction of two backstroke start technique variants using kinematic and kinetic variables. It was hypothesized that artificial neural networks would produce more accurate backstroke start performance prediction than LM.

Methods

Participants

Ten male well-trained backstroke swimmers (age 21.1 ± 5.36 years, body height 1.78 ± 0.04 m, body mass 72.82 ± 10.06 kg, training experience 12.6 ± 6.13 years and mean performance on 100 m backstroke in short course, 59.67 ± 2.89 s representing 78.67 ± 3.63% of the World Record) volunteered to participate. All swimmers were healthy (no serious injury or illness occurred in the last six months), ablebodied and had participated in national level competitions. Data collection was approved according to the local research ethics committee and all experimental procedures were carried out in accordance with The Code of Ethics of the World Medical Association (Declaration of Helsinki) for experiments involving humans. Swimmers and parents and/or guardians (when subjects were under 18) provided written informed consent before data collection.

Backstroke start variants

Two backstroke start technique variants were performed, both with feet parallel and positioned over a wedge (0.04 m above water level, FINA rule FR 2.10), but with hands on the highest horizontal (0.56 m above water surface level) or vertical handgrips. The selection of those starting variants was based on the highest number of swimmers that had elected them in competition (c.f. de Jesus et al., 2015).

Backstroke start trials

Body height and mass of swimmers were measured, and then they performed a standardised warm-up consisting of a 600 m front crawl and backstroke swimming in a 25 m indoor and heated (27ºC) swimming pool, followed by a familiarisation period of each start variant (c.f. de Jesus et al., 2015; Hardt et al., 2009; Nguyen et al., 2014). Each start variant was verbally described, visually depicted through video recordings, with the swimmers being given verbal instructions and feedback during familiarisation, thus ensuring that they were performed correctly (de Jesus et al., 2015; Nguyen et al., 2014). Swimmers performed randomly eight maximal 15 m repetitions, four with each backstroke start variant with a 2 min rest period in-between.

Data collection

A bi-dimensional (2D) kinematical set-up consisting of two (one surface and one underwater) stationary digital video cameras (HDR CX160E, Sony Electronics Inc., Japan), operating at a 50 Hz sampling frequency and at a 1/250 s exposure time was used to record starts from the auditory signal until the 5 m mark (de Jesus et al., 2015). Cameras were enclosed in a waterproof housing (SPK-CXB, Sony Electronics Inc., Japan) and fixed on a custom-built support, which was arranged on the lateral pool wall, 2.6 m from the starting wall and 6.78 m away from the start trajectory, perpendicularly to the swimmers motion. Surface and underwater cameras were aligned and located 0.15 m above and 0.20 m below water level (respectively).

A prism to calibrate starting space (4 m length [horizontal axis], 2.5 m height [vertical axis], 2 m width - [lateral axis]) was used and was placed 0.80 m above water level with the horizontal axis aligned towards the starting direction (de Jesus et al., 2015). A pair of light emitting diodes visible in each camera field of view was fixed to this frame. To enable swimmers’ tracking, 13 anatomical landmarks were identified (cf. de Jesus et al., 2011), defining a 10 segment anthropometric model (de Leva, 1996): the head vertex (using a swim cap), mid-gonion, right acromion, lateral epicondyle of the humerus, ulnar styloid process of the wrist, 3^rd hand distal phalanx, xyphoid process, iliac crest, great trochanter of the femur, lateral epicondyle of the femur, lateral malleolus of the fibula, calcaneus and 1^st foot distal phalanx.

Start trials were performed on an instrumented block complying with the FINA facility rules (FR. 2.7 and 2.10; cf. de Jesus et al., 2016), which included one surface and one underwater force plate pair used for force measurements exerted on hands and feet (300 and 200 Hz resonance frequency, respectively), both with sensitivity of 0.5 N, error < 5%, displaying accurate and reliable measurements. All strain outputs were converted to digital data through an analogue to digital converter via strain gauge input modules NI 9237 connected to a chassis CompactDAQ USB-9172 and to an Ethernet-9188 (National Instruments Corporation, USA). Data processing software was created in Lab View 2013 (SP1, National Instruments Corp., USA) to acquire, plot and save the two force plate pair data in real time (2000 Hz sampling rate). Dynamical calibration previously followed had described the methodologies used by means of rigid body falling (Mourão et al., 2015), revealing the homogeneity of static calibrations.

The start signal complying with the FINA rules (SW 4.2 and 6.1) was produced through an official device (OMEGA StartTime IV acoustic start, Swiss Timing Ltd., Switzerland) and delivered simultaneously to a light towards digital cameras and to a pulse in the direction of the force plates with convenient signal conditioning.

Data processing

The surface and underwater video images were independently digitised frame-by-frame by the same operator using the Ariel Performance Analysis System (Ariel Dynamics Inc., USA) (e.g. Sanders et al., 2016). Image coordinates were transformed into 2D object-space coordinates with a Direct Linear Transformation algorithm (Abdel-Aziz and Karara, 1971) with six calibration points (de Jesus et al., 2013, 2015) and a 5 Hz cut-off value has been selected for data filtering (2^nd order low-pass digital filter; de Jesus et al., 2015) according to residual analysis (residual error vs. cut-off frequency). The calibration and digitising accuracy calculations had been detailed in previous studies (de Jesus et al., 2015).

Two processing custom-designed routines created in the MatLab R2014a (The MathWoks Incorporated, USA) computational environment were used to: (i) convert strain readings (με) into force values (N); (ii) forces offset removal; (iii) filter right and left force exerted on the hands and feet (4^th order zero-phase digital Butterworth low-pass filter with a 10 Hz cut-off frequency); and (iv) sum right and left upper and lower limb force data and normalize each force curve to individual swimmer’s weight (N/N) and time in a vector to maximum time value (s/s).

Data analysis

Backstroke start variants were divided into four phases (de Jesus et al., 2011): (i) handsoff - from the start signal to swimmers’ hands left the handgrips (1^st positive horizontal swimmers’ hand 3^rd distal phalanx coordinate); (ii) take-off - from hands-off until swimmers’ foot left the wall (1^st positive horizontal swimmers’ foot 1^st distal phalanx coordinate); (iii) flight - from take-off until swimmers’ CM immersion (1^st negative swimmers’ CM vertical coordinate); and (iv) entry - from final instant of the flight phase until swimmers’ foot immersion (1^st negative swimmers’ foot 1^st distal phalanx vertical coordinate). The studied kinematic and kinetic variables are presented and described in Table 1.

Table 1.

Linear and angular kinematic and linear kinetic variables selected in each start variation, respective units and definition.

Parameters	Definition
Hands-off phase relative time (%)	Time from the auditory signal until swimmers’ hands left the handgrips normalized to 5 m start time
Take-off phase relative time (%)	Time from hands-off until swimmers’ feet left the starting wall normalized to 5 m start time
Flight phase relative time (%)	Time from the take-off until the CM water immersion normalized to 5 m start time
Entry phase relative time (%)	Time from CM water immersion until full swimmers’ immersion normalized to 5 m start time
Resultant take-off velocity (m·s-1)	Resultant (horizontal and vertical) CM velocity at take-off
Resultant flight velocity (m·s-1)	Resultant (horizontal and vertical) CM velocity in centre of mass water immersion
Resultant entry velocity (m·s-1)	Resultant (horizontal and vertical) CM velocity in swimmers’ full immersion
5 m start time (s)	Time between the acoustic signal until swimmers’ vertex achieves the 5 m mark
Wrist entry angle (º)	Angle formed between the forearm and horizontal axis in the first fingertip water contact
Shoulder entry angle (º)	Angle formed between the upper trunk and horizontal axis in acromion water immersion
Hip entry angle (º)	Angle formed between the thigh and horizontal axis in greater trochanter water immersion
Back arc angle (º)	Angle formed between the medium and lower trunk and the horizontal axis in the first fingertip water contact
Upper limb force at starting position (N/N)	Horizontal upper limb force at the acoustic signal
Maximal upper limb force and time (N/N; %)	Horizontal upper limb force before hands-off and respective normalized time
Upper limb horizontal and vertical impulse $\begin{array}{l}(\frac{N/N}{S/S})\end{array}$	Upper limbs time integral normalized of horizontal and vertical force component from the acoustic signal until hands-off
Lower limbs force at starting position (N/N)	Horizontal lower limbs force at the acoustic signal
1st maximal lower limb force and time (N/N; %)	1st maximal lower limb horizontal force before the hands-off instant and respective normalized time
Intermediate lower limb force and time (N/N; %)	1st minimum lower limb horizontal force between the 1st and 2nd maximal value before hands-off and take-off and respective normalized time
2nd maximal lower limb force and time (N/N; %)	2nd maximal horizontal lower limb horizontal force before the take-off and respective normalized time
Lower limb horizontal, vertical and medio-lateral impulse $\begin{array}{l}(\frac{N/N}{S/S})\end{array}$	Lower limb time integral normalized of horizontal, vertical and medio-lateral force from the acoustic signal until take-off

Statistical procedures

Multilayer perceptron, an ANN model, designed using Matlab’s Neural Network Toolbox (v. 4.0.3, The MathWorks, Incorporated, USA), was adopted to model the backstroke start nonlinear behaviour. Eleven kinematic and 15 kinetic variables from 35 valid start trials were inputted to the development of a feed-forward ANN with four neurons in a single hidden layer for modelling and predicting the 5 m backstroke start time (output variable). The model complexity was arbitrarily chosen until a reasonable performance had been achieved and the Levenberg-Marquardt optimisation algorithm (Allen et al., 2015; Maszczyk et al., 2012; Novatchkov and Baca, 2013) was used for training procedures and measure performance regarding the precision of training and the validation phase outputs (50 models randomly sorted, with 90 and 10% of data, respectively). Results were analysed based on each model output accuracy by mean absolute percentage error calculation (MAPE; Tsai et al., 2013). ANN results were compared with LM, which is a linear combination of the same inputs used in ANN, being the least squares problem solved by means of QR factorization to estimate the LM variables.

The coefficient of variation (CV) of the four backstroke start trials for each swimmer and for each variant was calculated for kinematic and kinetic variables.

Results

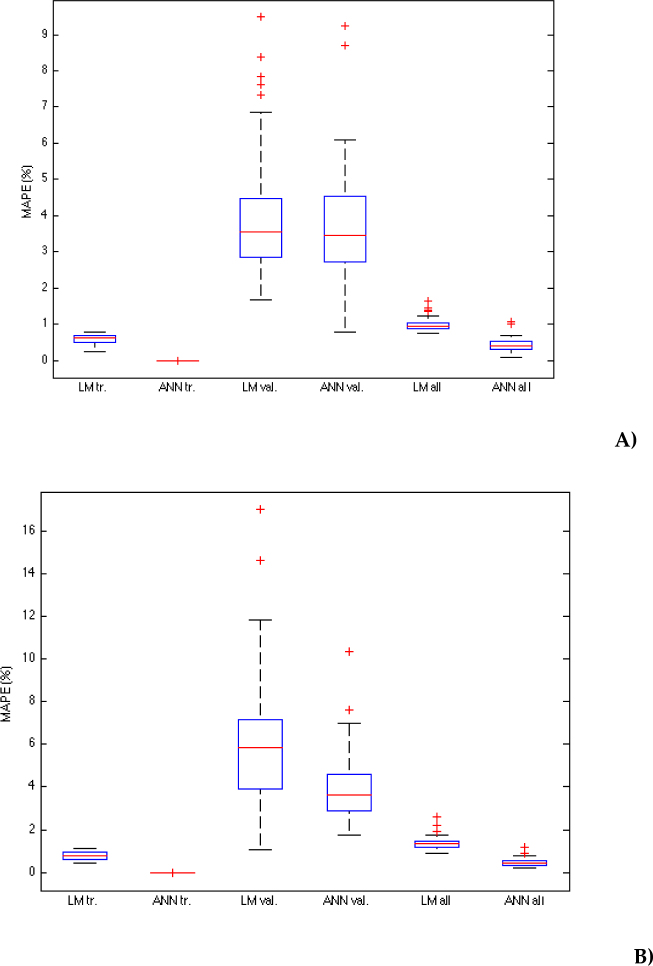
The average and standard deviation of MAPE values evidenced that the ANN often obtained smaller prediction errors (Table 2). In Figure 1, the MAPE statistics for all simulations are analysed. It is possible to see that, with the exception of the validation phase in the horizontal variant (Figure 1, panel A), ANNs perform better than LM, being more robust with respect to changing the training and validation datasets (Figure 1, panel A and B).

Table 2.

Average ± standard deviation of the mean absolute percentage error in training and validation phases, overall data and the best validation for both start variations obtained by the artificial neural network (ANN) and the linear model (LM).

Start variant	Model type	Training (%)	Validation (%)	All data (%)	Best Validation (%)
Horizontal	ANN	0.000000878 ± 0.00000199	3.73 ± 1.62	0.43 ± 0.19	0.77
	LM	0.58 ±0.13	4.06 ± 1.81	0.98 ±0.19	4.68
Vertical	ANN	0.000000828±0.0000015	3.95 ±1.67	0.45 ± 0.19	1.74
	LM	0.79 ± 0.18	5.92 ± 3.27	1.38 ± 0.30	3.72

Figure 1.

Box plot showing the mean absolute percentage error (MAPE) distribution of the backstroke start trials used in linear models (LM) and artificial neural networks (ANN) during training (LM tr. and ANN tr.) and validation phases (LM val. and ANN val.), as well as all start trials (LM all and ANN all) for both start variants, horizontal (panel A) and vertical (panel B) handgrip. The outliers are presented (+) above the upper extreme values in the dataset.

True 5 m time obtained values of both start variants were confronted with mean and standard deviation of both models for each sample. Through the mean of predictions, Figure 2 evidenced that ANNs captured more precisely the 5 m time information in both variants, horizontal (Figure 2, panel A) and vertical handgrips (Figure 2, panel B), when compared to LM based on kinematic and kinetic data.

Figure 2.

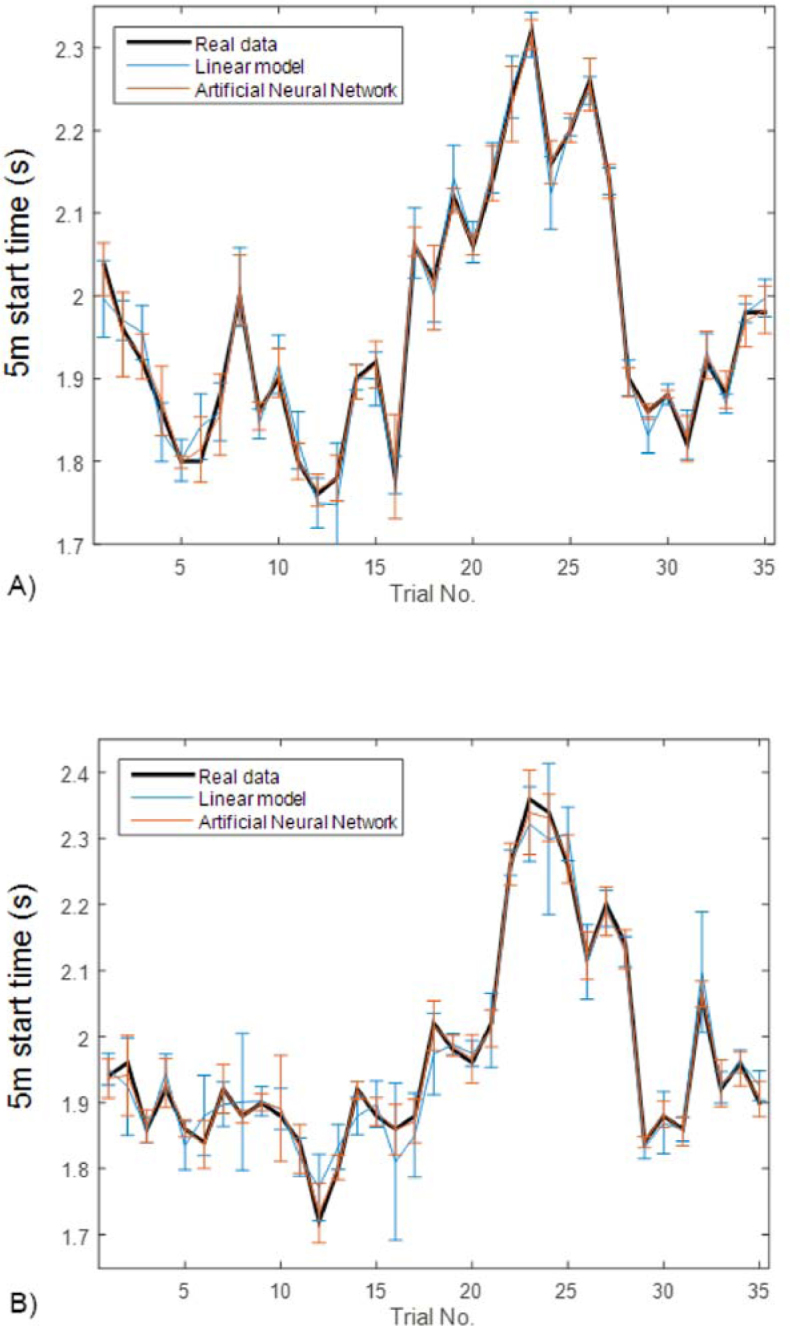
Real measured 5 m backstroke start times (black line) and model predicted output, linear model (LM; blue line) and artificial neural networks (ANN; red line), for backstroke start variations with horizontal (panel A) and vertical (panel B) handgrips. The variances observed from real and each model predictions are also presented.

The intra-trials variability assessed using a CV evidenced values between: 0.007 and 0.25, 0.006 and 0.13, 0.006 and 0.24 and 0.003 and 0.19 for the backstroke start variant with hands horizontal and vertically positioned for kinematic and kinetic variables, respectively

Discussion

The established hypothesis that ANN would generate more precise performance prediction of the backstroke start variants was confirmed, having the results analysed both graphically and by the MAPE calculation. Despite both, non-linear and linear methods had evidenced values lower than 10% (Tsai et al., 2013), ANN outperformed LM throughout training and validation phases with reduced prediction errors, except the validation phase of the horizontal start variant. In times of ubiquitous information technology, coaches and athletes are able to use advanced mathematical methods in modelling the training process (Przednowek et al., 2016). From a coach’s point of view, the prediction of results is very important in the sports training process (Przednowek et al., 2016; Wiktorowicz et al., 2015), since backstroke start performance modelling can show how kinematic and kinetic changes will influence the start time.

Currently, backstroke start is performed with different handgrips and a feet support, which might allow swimmers to position their CM as high out of the water as possible and, consequently, reduce drag, since they need to move through the take-off, flight and entry phases (de Jesus et al., 2013, 2014). In fact, it has been previously mentioned that coaches should focus on strategies that would improve flight and entry phase biomechanics, guaranteeing a shorter backstroke start time (Takeda et al., 2014). It is consensual in backstroke (e.g. de Jesus et al., 2015) and ventral start techniques (e.g. Fischer and Kibele, 2016) that wall/block phase parameters as horizontal and vertical impulses are considered the basis for successful mastering the other motion phases in the swim start. In the present study, modelling and predicting the 5 m backstroke start time were conducted using kinematics and kinetics from the start signal until full immersion, which have already been pointed out as performance determinants (de Jesus et al., 2011; Nguyen et al., 2014; Takeda et al., 2014).

The use of ANN in swimming allowed researchers to create high realistic models of swimming performance (Edelmann-Nusser et al., 2002; Pfeiffer and Hohmann, 2012; Silva et al., 2007). A high correspondence between network response and swimmers’ performance compared to LM has also reinforced previous study results (Edelmann-Nusser et al., 2002). In both start variants, ANN depicted mean absolute errors of 0.004 s between real and estimated 5 m start time (considering all data sets) compared to ~0.01 s of LM. The importance of higher ANN predictive accuracy is further emphasized by the observation that the differences between the individual performances of high-level swimmers are quite small.

Notwithstanding the research question had been adequately addressed, some limitations should be pointed out. Firstly, ten swimmers is a reasonable sample size as this type of experiment requires swimmers’ availability and highly methodological testing protocols; yet, larger samples regardless of the variance level are desired to increase ANN and LM accuracy (Hahn, 2007; Markham and Rakes, 1998). This drawback was compensated by the inclusion of four randomised trials for each participant, totalizing 35 valid trials in each start variant, thereby increasing the available dataset for modelling. Secondly, start variants performed over the wedge and hands on the highest horizontal and vertical handgrip have been extensively applied in backstroke events (de Jesus et al., 2015), but, nowadays, swimmers might adopt different start configurations, which should be analysed in further studies. Finally, when comparing ANN and LM, the balance between usability and accuracy becomes critical. ANN resulted in greater prediction accuracy, yet, the software used may restrict practical application. This study used MATLAB software, however, the same models could be run on recently available nonproprietary software, allowing the trained networks to be more usable to a broader range of individuals.

Conclusions

Despite both ANN and LM depicted prediction errors lower than 10%, indicating excellent modelling, the first method often evidenced smaller backstroke start performance prediction errors for the variant performed with hands positioned at the highest horizontal and vertical handgrip. As the margins between success and failure in short distance events are often measured in hundredths of a second, this study outlines the importance of combining relevant kinematic and kinetic data and ANNs to successfully predict backstroke start performance.