Phenotypic diversity and ecosystem functioning in changing environments: A theoretical framework

Abstract

Biodiversity plays a vital role for ecosystem functioning in a changing environment. Yet theoretical approaches that incorporate diversity into classical ecosystem theory do not provide a general dynamic theory based on mechanistic principles. In this paper, we suggest that approaches developed for quantitative genetics can be extended to ecosystem functioning by modeling the means and variances of phenotypes within a group of species. We present a framework that suggests that phenotypic variance within functional groups is linearly related to their ability to respond to environmental changes. As a result, the long-term productivity for a group of species with high phenotypic variance may be higher than for the best single species, even though high phenotypic variance decreases productivity in the short term, because suboptimal species are present. In addition, we find that in the case of accelerating environmental change, species succession in a changing environment may become discontinuous. Our work suggests that this phenomenon is related to diversity as well as to the environmental disturbance regime, both of which are affected by anthropogenic activities. By introducing new techniques for modeling the aggregate behavior of groups of species, the present approach may provide a new avenue for ecosystem analysis.

Tilman (1) proposed that understanding the role of species diversity for ecosystem functioning lies in quantifying interspecific tradeoffs that organisms face within the constraints of their environment. Species may, for example, exhibit tradeoffs in the types of resources they use or the environmental conditions under which they have their optimum growth rate. To focus on key functional relationships and rates of biogeochemical processes, ecosystem studies often aggregate species into functional groups on the basis of their role in these processes. Species within a functional group share similar resources and predators, whereas differences among species within a group are mainly expressed as variation in the efficiency of resource use or predator avoidance and/or sensitivity to other environmental variables (2) (e.g., temperature). It follows from this definition that species within functional groups compete more strongly with each other for resources, whereas those in different functional groups, though still potentially competing, either are relatively more complementary in resource use or interact through trophic interactions.

In this study, we focus on the functional group as the basic unit of ecosystems and explore how diversity may affect its functioning. The dynamics of a functional group consisting of n species may be modeled by accounting for the dynamics of each separately. However, constructing models of aggregate group behavior instead has several advantages. Species distinctions are sometimes imprecise, and in any case a species-based approach necessarily ignores intraspecific variation. In contrast, a continuum approach that accounts for the distribution of response characteristics within a functional group may incorporate such variation and thereby allow for better understanding of group behavior. Moreover, such an aggregated approach for functional groups can facilitate incorporation into more complex ecosystem models. We will present a theoretical framework inspired by recent moment approaches in ecology (3–7) to derive equations that describe the aggregate properties of a group of species in changing environments.

Species within functional groups share some essential analogies with alleles in a haploid species, which allows us to apply the fundamental theory of natural selection (8) to describe aspects of their behavior. Just as the fitness of a genotype affects that genotype's frequency in future populations, relative productivity of a species will affect its future proportion of the total biomass of a functional group.

Barton and Turelli (9) used a moment closure technique to approximate genetic variance and the effects of disruptive selection in a diploid population. The approach suggested here is to model the moments of a group of species (biomass, and the means, variances, and higher moments of phenotypic characters). Most genetic studies have focused on equilibrium behavior (10, 11) or transient behavior of the genetic variance (12). In ecology, researchers have summarized the role of species richness for ecosystem functioning for the equilibrium case (13, 14) and treated the general statistical properties for group performance with heterogeneous species in a varying environment (14–16). Our approach uses quantifiable interspecific tradeoffs to predict the dynamics of functional group properties in nonequilibrium situations.

Model

Consider a local group of species competing for the same resource and assume that growth rates are a function of a time-varying environmental factor, E, which can be either abiotic or biotic—for example, temperature, resource concentration, or predator abundance. Certain morphological or physiological traits of the species, such as structures facilitating uptake at low resource densities or antipredatory defenses, can influence the severity of the imposed limitation. Because of energy and time constraints, species face tradeoffs. Those that allocate internal resources to traits that reduce the impact of a limiting factor necessarily incur a disadvantage with respect to another limiting factor.

We introduce a variable, x, which we call the species phenotype, to represent this dependency. Every species, j, is defined by a unique value of x_j, and the spectrum of all species (x₁, x₂, … , x_j, … , x_N) comprises the whole group. The growth function of the jth species, i.e., its per capita instantaneous growth rate, is influenced by its phenotype (x_j), the present value of the environmental variable (E), and the total biomass of the group (C_T = ∑C_j) because of density-dependent effects. The dynamics of a group of N species can be described by

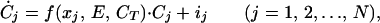1

where Ċ_j denotes the rate of change in the biomass of the jth species (C_j), and i_j is the input from external sources such as dispersal from adjacent patches.

The multispecies model (Eq. 1) serves the purpose of representing the dynamics of the biomass of every species in the functional group in terms of endogenous processes (e.g., competition for resources) and exogenous processes (e.g., immigration). Each species, j, has a fixed rate of external biomass input, i_j. If no intrinsic growth occurs, i.e., f(x_j, E, C_T) = 0, and the input rates are held constant, each species will settle into a steady-state biomass determined by the input rate and the sum of all loss rates. Intrinsic growth redistributes biomass away from this externally driven distribution.

We focus on three macroscopic properties to characterize intrinsic patterns, which can be calculated from the distribution of biomass over the phenotype aspect: total biomass, C_T, average phenotype, x_avg, and phenotypic variance, V:

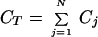2

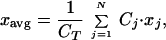3

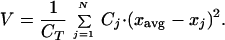4

Results

First we explore the basic response of the multispecies model (Eq. 1) to different rates of environmental variability. The first case we consider is that of a constant directional rate of change in the environmental variable. Such a constant directional change is very unrealistic but allows us to explore the basic behavior of the system. To do this, one can use either a very long transect with a large number of species or a circular boundary condition with fewer species. We have chosen the latter because it allows us to run the simulation for as long as needed for the system to stabilize. We let E(t) = mod[ψ⋅t; E_max], where ψ is the rate of change of the environmental variable, and E_max is the maximum environmental value and species type. We are here assuming that we have appropriately scaled the species type into the units of the environmental variable. The distance from the optimum, on the circle, can be calculated as:

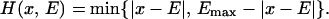5

We fix the functional form of f(x, E, C_T) and simulate the system numerically. For simplicity, we chose a Gaussian growth function:

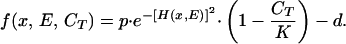6

The parameter p represents the per capita fertility of the species in the absence of density effects, whereas d is the mortality (or dilution) rate. For any value of E, the species characterized by the phenotype x_opt = E is the one with the highest growth rate at that time. We define the distance between the optimal and the average phenotype as Δx = x_opt − x_avg.

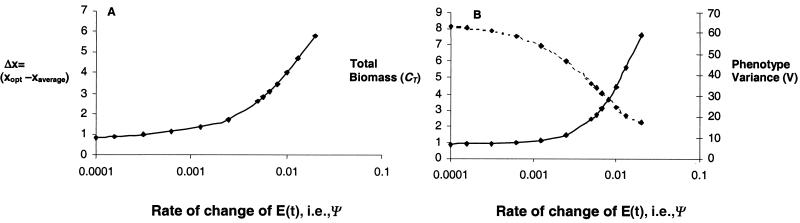
During the simulation, the biomass distribution will follow the environmentally determined optimum with a certain lag, Δx, and travel at constant speed, forming a traveling wave along the phenotype axis with a stable shape. This means that, even though species are constantly replaced in the community, the group properties reach equilibrium, and we can examine the relationships among these properties. As shown in Fig. 1, the higher the rate of change of the environmental variable, the lower C_T and the higher both Δx and V.

Figure 1.

Solutions for numerical simulations of the multispecies model (Eq. 1) with constant rate of change of the environmental variable E. (A) The difference between the optimal type and the current average type. (B) The total biomass (dotted line) and the species type variance (solid line). The points on the lines indicate for which values the model was evaluated numerically. Parameters of growth function (Eq. 6) were: p = 0.6, K = 10, and d = 0.1. The value of immigration, i_j, was equal for all species and set to 0.01. All initial biomasses were set to 0.1, and we used 100 species with a range of phenotypes between 0 and 20.

If E changes at variable rates, more complex dynamics result. To simulate a seasonal environment, we let E(t) oscillate around a fixed value, χ, with frequency ω, as:

7

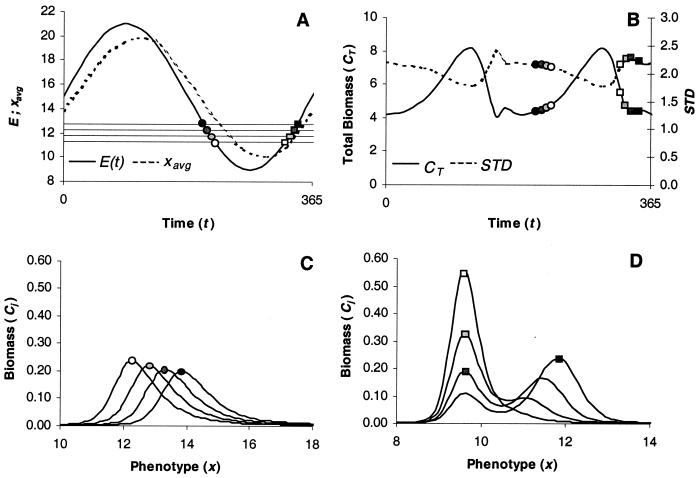
Such an environmental signal could represent annual or diurnal temperature, for example. Because there is no need of any boundary condition in this more realistic case, we redefine H(x, E) = x − E and again use Eq. 6 as the growth function. In slowly changing phases of the cycle of E near its limits, Δx decreases, which causes V to decrease accordingly, while the total biomass increases, implying that the best competitor is dominating the community at the expense of all other species. During the subsequent acceleration phase of E, however, the species distribution fails to track the accelerating optimum species type set by E(t). A new separated peak occurs in the distribution, which thereby becomes bimodal (see Fig. 2B). We have also done simulations that show that similar abrupt transitions may be caused by directional environmental change, if the change is accelerating through time. Biologically speaking, this means that an abrupt transition of species occurs in the community within a very short time. This phenomenon deserves further attention, because ongoing global changes may very well cause accelerating environmental changes (17, 18), which are too rapid for existing phenotypic variances and thus might lead to abrupt turnovers in species compositions.

Figure 2.

The general behavior of model (Eq. 1) in the case of a seasonally changing environment. (A) The average phenotype x_avg (dashed line) tracks the environmental sinusoidal factor E(t) = 15 + 6* sin(2*pi/365*t) (solid line) over the period of one year. (B) The period of oscillation of the other two macroscopic characteristics of the system, the total biomass C_T (solid line), and the standard deviation σ = sqrt(V) (dashed line), is 6 months. (C) Four snapshots of the species distribution obtained during the decreasing phase of the environmental factor (see A) when it equals 12.75 (black circle), 12.25 (dark gray circle), 11.75 (light gray circle), and 11.25 (white circle). All these distributions are unimodal. The circle denotes the dominating species, i.e., with the maximum abundance. (D) During the subsequent increasing phase of E(t), the distributions of species appear to be bimodal, and the transition of the dominating species is far from being smooth. The simulation has been run by using the Gaussian growth function (Eq. 6) and 250 species whose phenotypes uniformly range from 0 to 30. Other parameter values are set to: p = 0.6, K = 10, d = 0.1, and l = 0.1.

Deriving an Aggregate Model.

The multispecies model described in Eq. 1 has the disadvantage that it needs many equations, and that no understanding regarding the aggregated properties can be derived without simulations. Using moment approximation methods, however, we can reduce the multispecies model to three equations that capture the dynamics of the macroscopic characteristics of the group, such as the total biomass in the community, the average phenotype, and the phenotypic variance (i.e., a measure of species diversity). The simplified system elucidates the mechanisms underlying the influence of phenotypic variance on ecosystem characteristics. Inspired by a variety of recent moment closure approaches in ecology (3–7), we use a moment closure technique to approximate the dynamics of model (Eq. 1) in terms of centralized moments. Truncating the power series for f, and making an approximation for skewness and kurtosis, we obtain the following aggregate model (terms in curly brackets are related to external input dynamics; see Appendix for the derivation and parameter estimation):

The rate of change of the total biomass is given as

8

where f_i = [(dⁱ/dxⁱ)f(x)]/i! are scaled derivatives of f (see Appendix), and I is the total external input of biomass. Here we use f_i as shorthand for f_i(x_avg). Note that, because the growth function has a maximum at x_opt, we expect the second derivative, f₂, to be negative, as long as x_avg is in the neighborhood of x_opt. The term in square brackets represents the productivity of the whole group of species. Productivity is thus determined by the growth rate of the average species (represented by f) and a negative term (because f₂ is less than zero) proportional to phenotypic variance. Thus, for large V, the average growth rate of the whole group is lower because of a higher proportion of suboptimal species. In agriculture, the functional group (crop) is often represented by one single species to minimize V and thus to optimize productivity by choosing a species close to the optimum. The drawback of low phenotypic variance is elucidated in the next equation for the rate of change of the average phenotype of the group:

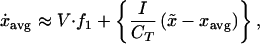9

where x̃ is the average phenotype of the external input of biomass. Eq. 9 represents an analogy to the fundamental theorem of natural selection: the succession of the average phenotype of the group towards the one with optimal productivity is determined by phenotypic variance V. Note that f₁ will have the same sign as (x_opt − x_avg), and thus the first term tends to move the average phenotype towards the currently optimal phenotype with a rate determined by the phenotypic diversity. Thus, high phenotypic variance means fast successional response of this functional group in response to a change in the environment.

The following equation shows the closure scheme we use to approximate the rate of change of the phenotypic variance using the average phenotype and a rough approximation of the skewness, which seems to be sufficient in most cases. The positive constants α and β are estimated by fitting the first term to the actual skewness and the second term to the actual kurtosis (see Appendix):

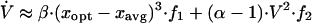10

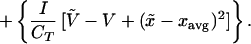Note that f₁ always has the same sign as (x_opt − x_avg), so the first term is always positive (zero exactly at the optimum). The second term is always negative, because f₂ < 0 and α > 1 (19) and thus when x_opt = x_avg, i.e., when the average type is also the optimal type and environmental conditions are constant, the phenotypic variance will decline because of competitive exclusion. Changes in the environment cause x_opt to differ from x_avg, and thus the first term increases above zero thereby increasing the phenotypic variance. Simulations have shown that over time, changing environments alone cannot generally sustain phenotypic variance without the external input of seed biomass. Thus, the importance of the amount and phenotypes of external inputs—seeds, immigrants, or propagules—becomes obvious.

An Example.

To provide an example of the proposed approach, we use a growth function based on the tradeoff between predator defense and growth, such as displayed in phytoplankton communities (20, 21). In this case, the main environmental factor, E(t), represents predator density, and we use a reddened noise time series to mimic natural population fluctuations (22):

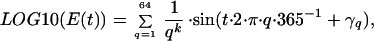11

where γ_f is a vector with values chosen from a uniform random distribution [0, 2π], q is the frequency, and k determines the “color” of the variation (we used k = 1). Note that this time series repeats its pattern with a period of 365.

On the basis of energy-allocation theory, we assume that an investment in a beneficial trait, such as the ability to lower predator selectivity s(x), has a metabolic cost r(x). To incorporate self-limitation, we use a traditional logistic function, in which density dependence is taken into account via the total group biomass, C_T. The per capita growth rate of species x can be given as:

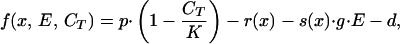12

where g represents the specific grazing rate, and d is the system dilution rate. If we interpret x as the investment in predator defense, x is constrained to be positive, and we define the metabolic cost as r(x) = r⋅x, r being a constant. The benefit of this investment is a decrease in predator selectivity, and we choose a negative exponential s(x) = e^−x to reflect this effect. Note that the optimal species type can be found by setting the first derivative of Eq. 12 equal to zero and solving for x, giving

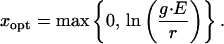13

We simulate the multispecies model (Eq. 1, using Eq. 12 as the growth function) with 100 species and calculate C_T, x_avg, and V over time from the resulting species distribution. These calculated values are then compared to those obtained by simulating the approximated Eqs. 8–10 and to a homogeneous model with a single phenotype chosen to represent the whole group and the value of x chosen to maximize productivity over the course of the simulation. All models were driven by an identical environmental time series E(t), as described above.

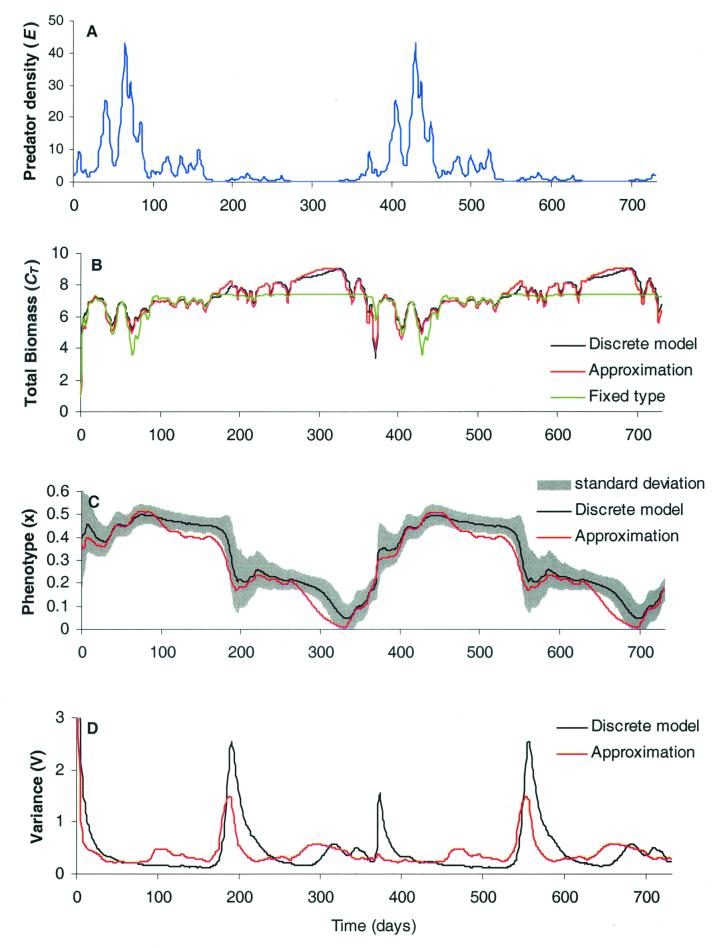
The comparison between the results obtained via the multispecies model (Eq. 1), the aggregate model (Eqs. 8–10), and the homogeneous model are shown in Fig. 3. These simulations show that our approximation well represents the dynamics with decreasing precision for higher moments. Even though the variance approximation is rather crude, it still provides a sufficiently good estimate to approximate average species type and total biomass successfully. We hope that further refinements will improve this estimate in the future. Note how the increasing predation peaks at time 380, 400, and 440 cause biomass of the single-species model to decrease more sharply than the adaptive model, where the community moves towards more predation-tolerant species. This important feature is well captured by the approximation.

Figure 3.

Simulation results of a group of prey with tradeoffs in predator defense vs. net growth (Eq. 12). The multispecies model was an implementation of Eq. 1. The approximation was based on Eqs. 8–10. (A) The forcing function of the model was a red-noise time series simulating predator density over 2 successive years with yearly repeating patterns (see Methods). (B) Prey group total biomass over time. For the fixed type model, the value of the species type was chosen to minimize the error relative to the multispecies model. (C) The succession of the average phenotype over time. The approximation captures quite accurately the dynamics of a changing community consisting of 100 species, by using only two additional equations for the average phenotype and the phenotypic variance. Note that we show the standard deviation instead of the variance. (D) The approximate vs. the reference variance. Although not perfect, our approximation captures most of the dynamics of the variance and provides a simple closure scheme for obtaining C_T and x_avg. We used 100 species with a uniform distribution of x between 0 and 8. Parameters for the growth function Eq. 12 were: p = 2, g = 1, r = 0.1, d = 0.1, and K = 10. Immigration was set to 0.001 for each species, and initial biomasses were 0.01. Coefficients for approximating the skewness and the kurtosis were α = 2.122 and β = 0.015, respectively.

Discussion

The theoretical framework we present here allows us to relate an important component of diversity, phenotypic variance within functional groups, to crucial aspects of ecosystem function. Most intriguing is the balance between short-term productivity with low variance and optimal phenotypes, and long-term productivity in changing environments with higher phenotypic variance causing better adaptive capacity. The adaptive model had about 6% higher productivity than the model with a fixed phenotype, which was chosen iteratively to yield the highest possible long-term productivity for a single-species model. Any other phenotype would have performed worse under the given environmental scenario. Thus even if short-term productivity is hampered by suboptimal species being present, long-term productivity may be higher for a system with adaptive possibilities. This conclusion relates to the recent debate regarding whether observed relationships between species richness and ecosystem functioning is because of sampling effects (23) rather than overyielding (13, 24). This work shows that, whatever the outcome of that debate, the presence of such a “sampling effect” can itself lead to higher functional group efficiency in a fluctuating environment.

The importance of external inputs for sustaining phenotypic variance in this simple model highlights the fact that no site is independent of the surrounding area, and that a metacommunity approach is necessary to understand adaptive phenomena of ecosystems over larger spatial scales. Davis and Shaw (25) suggest that adaptive responses of vegetation to climate change occur at many levels, including phenotypic plasticity, genetic adaptation, succession, and migration processes, stressing that genetic variation is linked to migration and dispersal processes. Spatiotemporal heterogeneities give the advantage to different species at different times, and dispersal can compensate for the local loss of species, phenotypes, or genotypes. Evolutionary processes act to moderate the effect of unfavorable growing conditions. All of these factors act as buffers against extinction by increasing the potential for greater phenotypic diversity and will result in better long-term productivity of the functional group.

In conclusion, we have suggested an approach for ecosystem theory that extends previous equilibrium-type analyses to dynamic environments and focuses on the properties of the basic ecosystem unit, the functional group. Furthermore, we suggest that the phenotypic variance may be a more appropriate measure of diversity when attempting to relate diversity to ecosystem functioning. We have provided a simple example that uses a measure of phenotypic diversity explicitly as a state variable and have derived simple and intuitive equations to describe the effect of diversity on ecosystem function. The result is an approach that is simple enough to analyze theoretically, but which captures aspects of the inherent nature of ecosystems as complex adaptive systems.

Moment derivations:

To derive our moment closure, we consider species continuously distributed over aspect space. The model, which is directly analogous to Eq. 1, is:

The same derivation can be done with the original discrete-species system. We approximate the response function using a Taylor expansion around the average type x_avg:

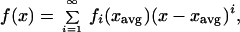where f_i(x) = [(dⁱ/dxⁱ)f(x)]/i!.

The rate of change of total biomass, C_T, can then be written:

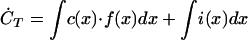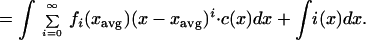Using the central moments M_i = (1/C_T)∫(x − x_avg)ⁱ⋅c(x)dx, we can write the previous equation as a function of higher moments

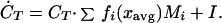The corresponding equation for mean species type, x_avg, can be found by defining S = x_avg⋅C_T. Then we have:

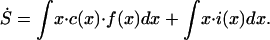Expanding yields:

where x̃ is the average type of immigrating species.

By the quotient rule we have:

We can derive the higher moments in a similar fashion, recalling that x_avg changes with time:

where M̃_i is the distributional moment of order i for immigrating species. Expanding, and recalling that M₀ = 1 and M₁ = 0, we have:

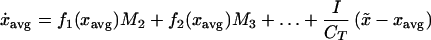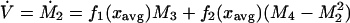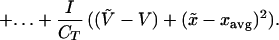To close the system, we approximate the moments higher than order two by using the lower level moments. A common approximation for the 4th-order moment is the square of the second order moment multiplied by a factor, here α (a factor equal to three gives an exact result for the Gaussian distribution). The distribution of species types is usually skewed as a result of the optimally growing species being on either side of the current average species type as the forcing function varies over time. The best estimate we have found so far for the skewness is (x_opt − x_avg)³ β. We estimate factors α and β by finding the minimum of the following functions:

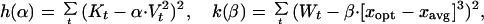where K is the kurtosis, W is the skewness, and V is the variance of the distribution, all estimated from simulation results. The contributions of the skewness and the kurtosis to the change in V are important, whereas their contributions to total biomass and average type are negligible and can be omitted for simplicity. Substituting our approximations for M₃ and M₄ yields Eqs. 8–10.