New tricks for old dogs: Improving the accuracy of biomolecular force fields by pair-specific corrections to non-bonded interactions

Abstract

In contrast to ordinary polymers, the vast majority of biological macromolecules adopt highly ordered three-dimensional structures that define their functions. The key to folding of a biopolymer into a unique 3D structure or to assembly of several biopolymers into a functional unit is a delicate balance between the attractive and repulsive forces that also makes such self-assembly reversible under physiological conditions. The all-atom molecular dynamics (MD) method has emerged as a powerful tool for studies of individual biomolecules and their functional assemblies, encompassing systems of ever increasing complexity. However, advances in parallel computing technology have outpaced development of the underlying theoretical models—the molecular force fields, pushing the MD method into untested territory. Recent tests of the MD method have found the most commonly used molecular force fields to be out of balance, overestimating attractive interactions between charged and hydrophobic groups, which can promote artificial aggregation in MD simulations of multi-component protein, nucleic acid, and lipid systems. One route to improving the force fields is through the NBFIX corrections method, in which the intermolecular forces are calibrated against experimentally measured quantities such as osmotic pressure by making atom pair-specific adjustments to the non-bonded interactions. In this article, we review development of the NBFIX corrections to the AMBER and CHARMM force fields and discuss their implications for MD simulations of electrolyte solutions, dense DNA systems, Holliday junctions, protein folding and lipid bilayer membranes.

1 Introduction

Since the 9.2 ps molecular dynamics (MD) simulation of the 58 residue bovine pancreatic trypsin inhibitor (BPTI)¹, the MD simulation method has been developing in sync with the computer power that doubles every two years according to the Moore's law^2,3. Over the history of MD simulations, the ever-increasing computer power has been putting the underlying theoretical models—empirical molecular force fields—under evermore stringent tests, stimulating force field development that has made the next-generation simulations possible. The most popular biomolecular models, the CHARMM and AMBER force fields, have had several major updates to improve description of proteins^4–8, lipids^9,10, and nucleic acids^4,11–18. Presently, microsecond simulations of monomeric proteins can be readily obtained using commodity computers^19–22. The emergence of the special purpose hardware and massively parallel computer systems has pushed the time scale of all-atom MD simulations into milliseconds^23,24 and has made simulations of large biomolecular systems, such as an HIV virus, possible²⁵.

Recent spectacular improvements in single-node performance of the MD codes^26,27 have dramatically lowered the cost of ensemble simulations, making it computationally feasible to probe not only near-native conformations of biomolecules but also their conformations in transient states including those where the biomolecules are partially or completely denatured. The growing recognition of the functional roles played by denatured conformations, exemplified by intrinsically disordered proteins, have made the sampling of denatured ensembles even more important²⁸. However, MD characterization of denatured conformations remains challenging in part because of the inaccuracies of the molecular force fields that have been calibrated to reproduce properties of folded biomolecules. For example, long time-scale simulations of small proteins and nucleic acids have shown that ensembles of denatured conformations obtained using either CHARMM or AMBER force fields are overly compact in comparison to the conformations observed in experiment^29–43.

The advent of massively parallel supercomputers have enabled simulations of large biomolecular assemblies^25,44–48 where multiple biomolecules—proteins, nucleic acids, lipids and polyglycans—form a functional unit that is held together by non-covalent interactions. All-atom simulations of such biomolecular assemblies have been an important milestone for the development of the MD method, setting the stage for truly molecular-level description of the most fundamental biological processes, such as transcription, translation, virus maturation, etc. However, quantitative studies of DNA–protein and DNA–DNA interactions revealed considerable problems with the standard parameterization of the molecular force field, which typically produce unrealistic aggregation of biomolecules^{31,41,43,48–50}.

Largely, the MD community is in agreement that the approximate description of molecular interactions employed by the fixed-charge models strengthens attractive solute–solute interactions, which causes artificial aggregation of denatured proteins or multimeric assemblies^{29,32,35,39,41,42,53,54,60}. There is, however, no agreement on the best way for improving the force field models. One possibility is that the overly attractive interactions between solutes derive from the shortcomings of the standard water models, such as TIP3P and its variants⁶¹. Realizing that the older water models generally underestimate the solute–water binding affinity and instead promote solute–solute bindings, several new water models have been developed^39,62 while the older water models have been modified^32,35,63. Using these improved water models in MD simulations produces more realistic conformations of denatured proteins³⁹ and intrinsically disordered peptides³⁵ and reduces artificial aggregation of amino acid monomers^32,54. However, modification of the water model requires significant validations as it affects all solute–solute interactions. Indeed, the improved water models that produce expanded conformations of denatured proteins also destabilize the folded conformations of the proteins^32,39 and may prevent protein folding⁴². In the case of nucleic acids, the effect might be amplified by the already underestimated strength of hydrogen bond interactions⁶⁴.

In this perspective, we discuss an alternative approach for improving the MD force fields that surgically corrects pair-specific Lennard-Jones (LJ) parameters without modifying solute–water interactions. This approach is usually referred as NBFIX (Non-Bonded FIX) following the convention of the CHARMM package⁵⁵, although NBFIX equivalents also exist for the AMBER and Gromacs packages (LJEDIT and nonbond_param, respectively). The need for NBFIX arises from the parameterization of LJ interactions employed in the biomolecular force fields^4,66. An empirical force field defines more than a hundred different atom types to described biomolecules. For example, the CHARMM36 force field has 124 atom types in total (53, 42, and 29 atom types for proteins⁷, nucleic acids¹⁴, and lipids¹⁰, respectively), and thus requires 7,626 sets of LJ parameters to describe all possible pair-wise LJ interactions. For convenience, only 124 atom-specific sets of LJ parameters are used to described solute–water interactions that directly affect the hydration free energy, whereas LJ parameters for solute–solute atom pairs are estimated according to the atom-specific LJ parameters and the Lorentz-Berthelot combination rule^67,68. The LJ parameters for the AMBER force fields have been developed in a similar manner. The NBFIX correction overrides the default assignment of the LJ parameters and allows one to assign custom values to the LJ parameters of a specific atom pair. For example, Bernèche & Roux used NBFIX to correct LJ interactions between Na⁺ and K⁺ ions with carbonyl oxygen to simulate ion selectivity of the KcsA channel⁵⁵.

Development of NBFIX corrections requires reference experimental data. Osmotic pressure data for binary solutions^63,69,70 have been used extensively for NBFIX development as such data can be easily and accurately obtained both experimentally and computationally. Experimentally, osmotic pressure can be determined using either a conventional semipermeable membrane osmometer or modern osmometers based on the freezing point or vapor pressure measurements⁷¹. Computationally, osmotic pressure can be determined through an MD simulation using a two-compartment setup (see Section 2.1)⁷⁰. Experimental osmotic pressure is known for most common solutions of electrolytes⁶⁹ and amino acids^72–76.

Thus, realizing that binding affinity of the Na–Cl and K–Cl ion pairs is overestimated, Luo and Roux calibrated the Na–Cl and K–Cl ion pair LJ interactions to reproduce the experimental osmotic pressure of the NaCl and KCl solutions⁵⁶, a procedure that we refer hereinafter as the NBFIX approach. Subsequently, osmotic pressure-calibrated NBFIX corrections have been developed for several other interaction types as summarized in Fig. 1 and Table 1 and 2^{31,41,51,53,54,59}. The advantage of the NBFIX approach is that the calibration is surgically applied only to specific atom pairs, making the introduction of side effects, such as unintended destabilization of hydrogen bonds^32,35,39, unlikely. Thus, NFBIX calibration has been shown to have no affects on the hydration free energy, solution density, interactions with other solutes, and bonded parameters (e.g., backbone torsions and NMR J coupling parameters in proteins)⁴². Below, we review the improvements brought to the MD method by the NBFIX approach and discuss its limitations and challenges.

Fig. 1.

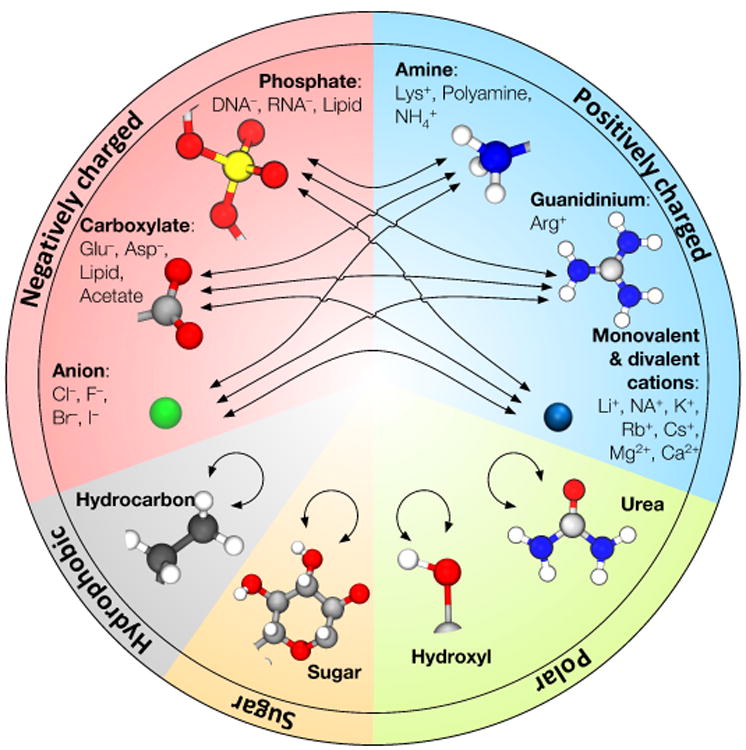
Visual summary of NBFIX corrections to the AMBER99 and CHARMM force fields. Tables 1 and 2 summarize efforts of various groups in this area. Tables 3 and 4 provide specific values of the Champaign-Urbana NBFIX (CUFIX) corrections to the AMBER99 and CHARMM force fields.

Table 1.

Summary of NBFIX corrections for the AMBER ff99-derivative force fields. COO, PO₄, and SO₄ indicate carboxylate, phosphate, and sulfate groups, respectively.

Reference	Type of NBFIX corrections
Yoo & Aksimentiev, 201231	Li/Na/K/Mg–Cl/COO/PO4
Yoo & Aksimentiev, 201641	Amine–COO/PO4/SO4
Yoo & Aksimentiev, 201641	Urea–urea
Yoo & Aksimentiev, 201642	Hydrocarbon–hydrocarbon
Yoo, Wilson, Aksimentiev, 201651	Ca–Cl/COO/PO4
Lay, Miller, Elcock, 201752	Carbohydrate–carbohydrate
Miller, …, Elcock, 201753,54	Hydroxyl–hydroxyl
This article (Fig. 5A)	Guanidinium–COO
This article (Figs. S1 to S5)	Ion pairs including Cs/Rb/Br/I

Table 2.

Summary of NBFIX corrections for the CHARMM force fields. COO, PO₄, and SO₄ indicate carboxylate, phosphate, and sulfate groups, respectively.

Reference	Type of NBFIX corrections
Bernèche & Roux, 200155	Na/K–carbonyl
Luo & Roux, 201056	Na/K–Cl
Yoo & Aksimentiev, 201231	Li/Na/K/Mg–Cl/COO/PO4
Venable, …, Pastor, 201357	Na–COO
Yoo & Aksimentiev, 201641	Amine–COO/PO4/SO4
Yoo & Aksimentiev, 201641	Urea–urea
Yoo, Wilson, Aksimentiev, 201651	Ca–Cl/COO/PO4
Huang, ï, MacKerell, 201758	Guanidinium–COO
Lay, Miller, Elcock, 201659	Carbohydrate–carbohydrate
This article (Fig. 5B)	Guanidinium–COO
This article (Figs. S6, S7)	Ion pairs including Rb/Cs

2 Physical chemistry of the NBFIX approach

In the case of an ideal solution where osmolytes (e.g., solutes or ions) do not interact with each other, osmotic pressure, π, is linearly proportional to the solute concentration, c: π(c) = cRT where R and T are the gas constant and temperature, respectively. In the case of interacting osmolytes, the osmotic pressure of a solution can be related to its concentration by introducing a concentration-dependent factor, the osmotic coefficient ϕ(c), π(c) = ϕ(c)cRT. Broadly speaking, ϕ values smaller than 1 indicate attractive interactions between the osmolytes, which decrease the effective osmolyte concentration to ϕc as the osmolytes form complexes⁷¹. Conversely, ϕ values larger than 1 indicate repulsive interactions that effectively increase the solute concentration to ϕc. Thus, osmotic pressure (or equivalently osmotic coefficient) data present a convenient target for the calibration of solute–solute interactions.

2.1 Calibration of solute–solute interactions using osmotic pressure data

The first step in the calibration procedure is choosing a target interaction. For an illustrative example, here we choose the interaction between positively charged amine and negatively charged carboxylate groups,⁴¹ which are common functional groups of amino acids (e.g., lysine, glutamate, and aspartate) and lipids (e.g., phosphatidylserine), Fig. 2A. First we note that using entire amino acids or lipid molecules for calibration is not ideal because the amine–carboxylate interaction are not guaranteed to dominate the overall inter-solute interactions. A much better alternative is using a methylammonium–acetate or glycine solution where amine–carboxylate interactions dominate over all other interactions. Here, we chose the glycine solution because experimental osmotic pressure data are available for a range of solution concentrations⁷². Similarly, methylguanidinium and dimethylphosphate can serve as good models for calibration of interactions between arginine side chain and phosphate groups of lipids or nucleic acids, respectively Fig. 2A, whereas carbohydrate monomers can be used to calibrate the interactions between carbohydrate groups of the nucleic acid backbone⁵⁹.

Fig. 2.

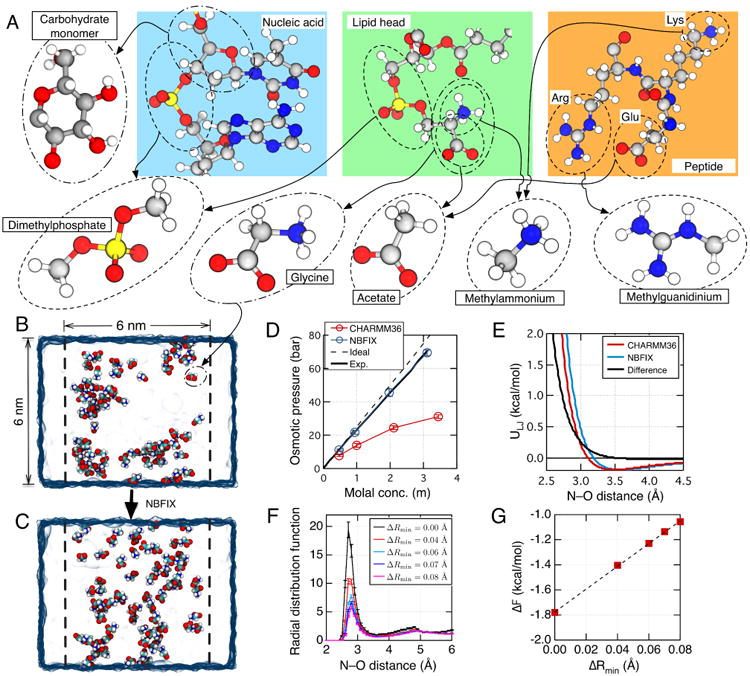
NBFIX calibration using model compounds. (A) To perform NBFIX calibration, complex biological molecules are represented by simpler model compounds. The compounds are chosen to isolate a specific type of inter-solute interactions, which can be modulated by the NBFIX correction. The figure shows a possible decomposition of three representative biomolecules—a nucleic acid fragment, a lipid molecule and a peptide. Molecular structures are shown using the ball-and-stick representation where each atom is colored according to its type: hydrogen, white; carbon, gray; nitrogen, blue; oxygen, red; phosphorus, yellow. (B,C) Calibration of amine–carboxylate interactions using the osmotic pressure of a glycine solution. The simulated system includes a volume of water (blue semi-transparent surface) divided into two compartments by two planar half-harmonic potentials (depicted by dashed lines). Glycine monomers (shown as spheres colored by atom: carbon, cyan; hydrogen, white; oxygen, red; nitrogen, blue) are confined to remain within one compartment by the half-harmonic potentials while water can exchange between the compartments freely. The difference in the glycine concentration between the two compartments generates osmotic pressure. The equilibrium osmotic pressure value is determined from the average force exerted by the confining potentials on the glycine molecules and the cross-section area of the system. Panels B and C illustrate instantaneous configurations of a 3 m glycine solution observed at the end of two 25 ns simulations performed using the standard CHARMM36 force field without (B) and with (C) the NBFIX correction. (D) Osmotic pressure of a glycine solution as a function of its concentration obtained from MD simulations performed using the CHARMM force field with (blue) and without (red) the NBFIX corrections. Experimentally determined⁷² and ideal solution (osmotic coefficient = 1) dependences are shown as solid and dashed black lines, respectively. (E) The effect of an NBFIX correction (ΔR_min = 0.08 Å) on the LJ interaction potential between amine nitrogen and carboxylate oxygen. The LJ potentials are plotted using the standard CHARMM force field with (blue) and without (red) the NBFIX correction. The difference between the NBFIX and standard potentials is shown as a black line. (F) Inter-molecular radial distribution function (RDF) of glycine nitrogen with respect to glycine oxygen in MD simulations of a ∼3 m glycine solution at several values of ΔR_min. Error bars indicate standard error. The value of ΔR_min affects the height of the first peak, g₁. (G) Correlation between ΔR_min and ΔF = −k_BTlog(g₁). Dashed line indicates a linear fit. Figures in panels B–D were adapted with permission from Ref. 41.

The osmotic pressure of a solution can be computed using a two-compartment simulation setup, Fig. 2B,C, where a rectangular simulation volume is divided, under periodic boundary conditions, into two compartments separated by two virtual semi-permeable membranes (dashed lines in Fig. 2B,C). The effect of the two semi-permeable membranes is typically realized by using two planar half-harmonic potentials that exert forces on non-hydrogen atoms of the solutes. The presence of solutes only in one of the two compartments—the solute compartment—generates the osmotic pressure. At equilibrium, the pressure exerted by the semi-permeable membrane on the atoms of solutes equals to the osmotic pressure in the solute compartment^56,70 and can be conveniently evaluated by recording the forces applied to the solutes by the half-harmonic potentials.

When simulated using the standard CHARMM36 force field, a ∼3 m glycine solution is observed to form clusters, Fig. 2B, which is inconsistent with the high experimental solubility of glycine that exceeds 3 M at room temperature and the near-ideal dependence of the experimental osmotic pressure on glycine concentration, Fig. 2D. Accordingly, the simulated osmotic pressure is half or even less of the experimental value over a range of glycine concentration, Fig. 2D, indicating an overestimation of the attractive interaction between amine and carboxylate groups. Although the attractive interaction is of the electrostatic nature, modifying the partial charges of the amine or carboxylate groups would lead to uncontrolled changes in the solvation energy and charge–charge interactions with other groups of the force field. An alternative approach is to change the interaction that opposes the electrostatic attraction—the steric repulsion between the amine nitrogen (N) and carboxylate oxygen (O) described by the LJ potential:

$$U_{\text{LJ}}=\varepsilon [{(R_{min}/r)}^{12}-{(R_{min}/r)}^6]=4\varepsilon [{(\sigma /r)}^{12}-{(\sigma /r)}^6]$$ (1)

where r indicates the N–O distance and R_min (= 2^1/6σ) and ε are pair-specific LJ parameters. Indeed, increasing the LJ R_min (or equivalently σ) parameter for amine nitrogen-carboxylate oxygen pairs gradually increases the osmotic pressure of a glycine solution at a fixed concentration and alleviates the clustering problem, Fig. 2C⁴¹. Increasing the R_min value by only 0.08 Å brings the simulated osmotic pressure values in agreement with experiment Fig. 2D⁴¹. Fig. 2E displays the amine nitrogen–carboxylate oxygen LJ potentials before and after the NBFIX correction. Fig. 2F characterizes the effect of NBFIX correction on the radial distribution function (RDF) of the inter-molecular nitrogen-oxygen pair: increasing R_min monotonically decreases the height of the first RDF peak, g₁. By plotting −k_BTlog(g₁) as a function of ΔR_min, we obtain an estimate of the free energy change introduced by the NBFIX correction, Fig. 2G. Thus, ΔR_min of 0.08 Å increases the free energy of a contact ion pair by about 0.7 kcal/mol with respect to the standard value.

2.2 Why NBFIX works?

Although the NBFIX correction does not explicitly alter the solute-water interactions, it affects the behavior of water molecules in proximity of the solutes. Specifically, the NBFIX correction affects the ability of water molecules to mediate the solute-solute interaction, controlling the relative abundance of contact ion pairs (CIP), Fig. 3A, and solvent-shared ion pairs (SIP), Fig. 3B. We illustrate this effect here by analyzing the simulations of an ammonium–acetate pair, for which the NBFIX correction was derived in Ref. 41. Fig. 3C shows the potential of mean force (PMF) between an ammonium and acetate in pure water computed using the umbrella sampling method ^78,79 and the AMBER ff99 force field with and without the NBFIX correction. In the absence of NBFIX, the free energy of a CIP configuration is about 1 kcal/mol lower than that of a SIP configuration, Fig. 3C, whereas the two configurations have similar energy in the NBFIX-optimized simulation. Thus, the NBFIX correction destabilizes the CIP state, increasing the population of SIP states. NBFIX corrections to the CHARMM force field have similar effects on the energetics of CIP to SIP⁴¹.

Fig. 3.

The effects of NBFIX on ion pair formation. (A, B) Ammonium and acetate ions forming a contact ion pair (CIP, panel A) and a solvent-shared ion pair (SIP, panel B)⁷⁷. Nitrogen, oxygen, carbon, and hydrogen atoms are shown in blue, red, gray, and white colors. Hydrogen bonds are depicted as dotted lines. (C) Potential of mean force (PMF) between ammonium and acetate in pure water computed using the standard (red) and NBFIX-optimized (blue) force field models (data taken from Ref. 41). The PMF was computed using the umbrella sampling method; the force constants of the umbrella restraints were 10 kcal/mol·Å². The reaction coordinate was the distance between the ammonium nitrogen (N) and carboxylate carbon (CC) atoms. (D,E) Variations of the N–CC distance in the simulations performed using the standard (D) and NBFIX-optimized (E) force field models. Each plot illustrates the last 1 ns segment of a 30 ns simulation performed having the N–CC distance harmonically constrained to 4.2 Å using a weak harmonic potential (0.5 kcal/mol·Å² force constant). The instantaneous N–CC distance was recorded every 20 fs. The unnormalized probability density functions computed from the entire 30 ns trajectories are shown at the right vertical axis of each panel. (F) Correlations between the N–CC distance and the number of shared water molecules. Each data point represents a 200 ps average. Here, a water molecule is considered to be shared if it simultaneously forms hydrogen bonds with both ammonium and acetate (see panel B). The occurrence of a hydrogen bond was determined using the g_hbond program of the Gromacs package with the distance and angle cutoffs of 3.5 Å and 30°, respectively. The bar graphs at the right and the top axes show the unnormalized probability distributions of the N–CC distance and the number of shared water molecules. All data reported in this figure were obtained using the AMBER ff99 force field.

To examine the destabilization of CIP by the NBFIX correction more quantitatively, we simulated the ammonium–acetate system having the distance between the ammonium nitrogen (N) and carboxylate carbon (CC) restrained to 4.2 Å using a weak harmonic potential (spring constant k = 0.5 kcal/mol·Å²). The equilibrium restrain distance (4.2 Å) chosen for these simulations corresponds to a local maximum in the PMF that separates the CIP and SIP states, Fig. 3C. During the simulations, the system was observed to undergo frequent transitions between the CIP and SIP states, Fig. 3D,E. In the simulation performed using the standard force field model, the CIS state was dominant (72% of all conformations). The application of the NBFIX correction changed the relative occupancy of the CIS and SIP states, making the SIP state more probable (60% of all conformations), Fig. 3E.

To elucidate the role of water, we counted the number of water molecules that simultaneously formed hydrogen bonds with both ammonium and acetate groups, Fig. 3B. The average number of such shared water molecules exhibits a strong correlation with the N–CC distance, Fig. 3F. Most data points obtained using the NBFIX correction have the number of shared water molecules larger than 0.3 (140 out of 154 points) and N–CC distance larger than 4.2 Å (146 out of 154 points), Fig. 3F. Thus, our analysis suggests that the primary effect of the NBFIX correction on a solute pair is in changing the probability of having a water molecule between the two solutes. Consequently, the presence of a shared water molecule between the solutes increases the solute–solute distance roughly by the size of a water molecule.

2.3 Potential concerns with the NBFIX approach

Although the NBFIX corrections developed using the experimental osmotic pressure data of model solutes have so far been found to be transferable to larger biomacromolecules, e.g., nucleic acids^31,41,43, proteins^42,58, and lipid bilayer membranes^41,57, there are several potential concerns about the NBFIX approach.

First, the NBFIX corrections might be overfitted to the osmotic pressure data and hence require careful cross-validation against diverse experimental data sets. Potential target data sets for NBFIX validation include Ramachandran plots, NMR J-coupling parameters, and X-ray scattering data^8,35,42. Second, all current NBFIX corrections (see Table 1 and 2) are applied to pair-specific LJ interactions, not partial charges, largely for the convenience. Given the fact that both CHARMM and AMBER force fields have a well-defined procedure for the derivation of solute partial charges and solute–water LJ parameters whereas solute–solute LJ parameters are largely estimated without validation, modifying pair-specific solute–solute LJ parameters appears to be a logical approach. It is, nevertheless, true that a better optimization can be achieved by modifying both LJ parameters and partial charges. Third, the transferability of the NBFIX corrections from one chemical context to the other is not guaranteed and requires additional validation. For example, although the standard CHARMM and AMBER force fields prescribe the same LJ parameters for the car-boxylate and phosphate oxygen atoms, reproducing osmotic pressure data for both required different sets of NBFIX corrections⁴¹. Thus, NBFIX corrections for the same chemical groups can be different depending on their chemical context.

3 Improvements and challenges

3.1 Biological electrolyte solutions

The physical properties of electrolyte solutions is a topic of growing interest for both physical chemists and biophysicists⁷¹. Many inorganic and organic salts dissociate in water into positively and negatively charged ions, cations and anions, making the electrolyte solution electrically conducting. The interaction of cations and anions with water molecules and with each other affects the structure and dynamics of the electrolyte solutions and determine their physical properties such as ionic conductivity, osmotic and activity coefficients. Furthermore, the valence and concentration of ions are known to considerably affect the properties of biomacromolecules. For example, the strength of salt bridges in proteins is determined by the complex interactions of ionizable side chains, cations, and anions⁸⁰. Below, we discuss the application of the NBFIX approach toward improving the classical MD description of ion effects and discuss remaining challenges.

3.1.1 NBFIX corrections improve description of ion pairing

The key process determining the structure and dynamics of an electrolyte solution is ion pair formation^63,77,81. Although various spectroscopic and scattering methods have provided important insights into the behavior of ions and water leading to ion pair formation^82–84, these methods cannot presently provide direct information about the structural dynamics of ion pairs as it occurs at the picosecond and angstrom time and length scales⁸⁵. The all-atom MD method can thus provide unique information about the process of ion pair formation, including the properties of the ions' hydration shells^63,81,86,87. Here, we examine the effect of NBFIX corrections on ion pairs containing functional analogs of biomolecules such as ionizable side chains and nucleic acid backbone. Following that, we briefly discuss the present status of NBFIX corrections for monatomic ions.

As previously discussed (see Section 2.2 and Fig. 3), the effective interaction between two oppositely charged ion species sensitively depends on the microscopic configuration of water molecules at short (2–5 Å) ion–ion separations. At such separations, the microscopic configurations adopted by an ion pair can be classified as either forming a direct contact (CIP) or sharing a water molecule (SIP). Furthermore, the energetics of an ion pair formation is conditioned by the relative abundance of the CIP and SIP states. Fig. 4 shows the free-energy of an ion pair as a function of ion–ion distance computed using the standard CHARMM36 force field for six biologically relevant ion pairs: sodium–acetate (Fig. 4A), methylammonium–acetate (Fig. 4B), methylguanidinium–acetate (Fig. 4C), sodium–dimethylphosphate (Fig. 4D), methylammonium–dimethylphosphate (Fig. 4E), and methylguanidinium–dimethylphosphate (Fig. 4F). Note that acetate, methylammonium, and methylguanidinium, and dimethylphosphate ions are analogous to functional groups of ionizable side chains, nucleic acid backbone, and lipid head groups, Fig. 2A. Just as with ammonium–acetate (Fig. 3), the standard parameterization favors the CIP state over the SIP state for all ion pairs except sodium–dimethylphosphate, with the maximum free energy difference of −2 kcal/mol, Fig. 4C. The excessive stability of CIPs leads to artificial clustering of ions in MD simulations performed using standard force fields^31,41.

Fig. 4.

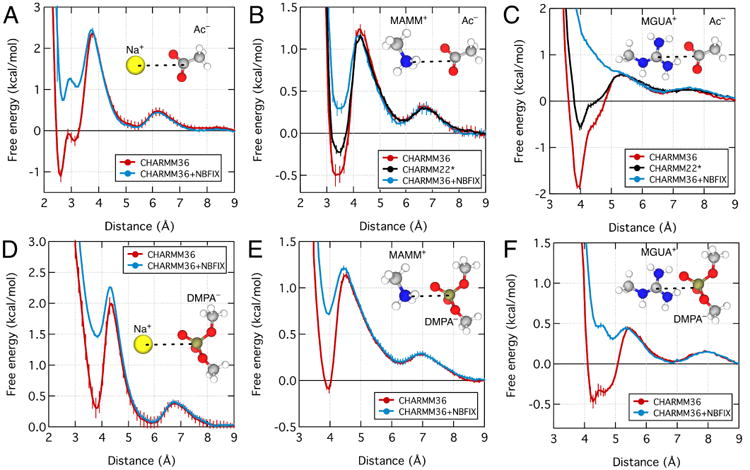
Effect of NBFIX corrections on the PMF between sodium and acetate (A), methylammonium and acetate (B), methylguanidinium and acetate (C), sodium and dimethylphosphate (D), methylammonium and dimethylphosphate (E), and methylguanidinium and dimethylphosphate (F). The reaction coordinate was defined as the distance between the following atoms of the ion pairs: sodium, nitrogen of methylammonium, nitrogen of methylguanidinium, carboxylate carbon of acetate, and phosphorus of dimethylphosphate. Each panel shows the PMFs computed using the standard CHARMM36⁶⁶ (red) and the CHARMM36 force field with the NBFIX correction⁴¹ (blue). In panels B and C, the black lines show the PMFs computed using CHARMM22*³⁰. The inset of each plot shows the chemical structure of the ion pair. Except for panel C, all NBFIX-corrected data were obtained using parameters developed in Ref. 41. Fig. 5 and Section 3.1.2 describe the development of the NBFIX correction for the guanidinium–carboxylate pair.

For comparison, we plot in Fig. 4 the free energy of the ion pairs computed using the NBFIX corrections to the CHARMM36 force field. The application of corrections reduces stability of CIPs by 1 – 3 kcal/mol but does not affect stability of SIPs. As a result of the corrections, the SIP state is energetically more stable than the CIP state for all six ion pairs. Because of the reduced energy barrier between CIP to SIP, the application of the NBFIX corrections also increases the exchange rate between the two states.

An alternative approach to correcting the artificially strong attraction between molecular ion pairs is the modification of their partial atomic charges. Thus, the Shaw group modified the partial charges of the side chains of guanidinium, acetate, and glutamate residues in the CHARMM22 force field to reduce the attractive interactions of arginine side chain with as-partate and glutamate side chains, producing a force field variant known as CHARMM22*³⁰. To determine how the two approaches compare, we computed the PMF for methylguanidinium–acetate and methylammonium–acetate pairs using CHARMM22*; the results are shown as black curves in Fig. 4B,C. Similar to the effect of the NBFIX corrections to CHARMM36, the charge reduction in CHARMM22* reduces stability of CIPs without affecting stability of SIPs, however, the CIP states remains the global energy minimum for both ion pairs. At the quantitative level, the free energy of the CIP state is 0.5 and 2 kcal/mol more favorable in CHARMM22* than in NBIFX-CHARMM36 for the methylammonium–acetate, Fig. 4B, and methylguanidinium–acetate, Fig. 4C, pairs, respectively. Thus, the two calibration approaches produce qualitatively similar results that nevertheless differ substantially at a quantitative level.

For a pair of monatomic ions, the refinement of ion-ion interactions using the NBFIX approach is straightforward because each ion carries a well-defined electrical charge. The NBFIX corrections for ion pairs involving a Cl⁻ ion and one of the monovalent cations (Li⁺, Na⁺, K⁺) were previously reported for both CHARMM36 and AMBER99 force fields^31,56. The NBFIX corrections for ion pairs containing larger monatomic ions such as Rb⁺, Cs⁺, Br⁻, and I⁻ are reported in this article, see Fig. S1 to S7 for the results of the calibration simulations. For divalent monoatomic cations such as Mg²⁺ and Ca²⁺, addressing the polarization effect of first solvation water molecules was as important as the refinement of Lennard-Jones parameters⁸⁸. Treating Mg²⁺ and Ca²⁺ as hexahydrate and heptahydrate complexes, respectively, and adjusting the dipole moment of the first solvation shell water molecules turned out to be an effective approach for implementation of the polarization effects in the framework of non-polarizable force fields^31,51. Further optimization of the hydrated Mg²⁺ and Ca²⁺ ion models was done by adjusting the LJ parameters describing the interactions of the first solvation shell oxygen and anions^31,51. Table 3 and 4 provides a summary of all NBFIX corrections developed by Yoo and Aksimentiev.

Table 3.

Pair-specific NBFIX corrections to AMBER ff99-derivative force fields. The table lists corrections to the LJ a parameters of the specified atom pairs. The corrections are given relative to the standard force field values and have units of Angstroms. The standard σ values for monovalent ions are those of Joung and Cheatham⁶⁵. The standard σ values for the divalent cations are from the CHARMM36 force field ¹⁴. Mg²⁺ and Ca²⁺ ions are described as permanent hexahydrate and heptahydrate complexes, respectively. The dipole moment of each water molecule within each Mg²⁺ hexahydrate or Ca²⁺ heptahydrate complex is set to be 1 or 0.5 Debye, respectively larger than the standard value of TIP3P water^31,51. The NBFIX corrections are for the atom pairs formed by monovalent ions, water oxygens of Mg²⁺ hexahydrates and Ca²⁺ heptahydrates, nitrogen atom of a positively charged amine group (N–H), nitrogen atom of a guanidinium group (N=C), acetate oxygen (O=C), phosphate oxygen (O=P), sulfate oxygen (O=S), and methyl carbon (C–H). Superscripts §, ¶, *, and ‡ correspond to Refs. 31, 41, 51, and 42, respectively, which detail validation of the specific corrections. The value of 0.00 indicates that no NBFIX correction is needed to reproduce the osmotic pressure experiment using the standard parameter set. The CUFIX-corrected parameter sets in the Gromacs, AMBER, and Anton formats are available at http://bionano.physics.illinois.edu/CUFIX.

	Li+	Na+	K+	Rb+	Cs+	Mg2+	Ca2+	N–H	N=C	C–H
Cl−	0.12§	0.015§	0.02§	0.02 Fig. S1A	0.00 Fig. S1A	0.02§	0.01*	0.00¶	0.00¶	N/A
Br−	0.15 Fig. S2A	0.00 Fig. S2B	0.02 Fig. S2C	0.00 Fig. S2D	0.00 Fig. S2E	0.00 Fig. S5A	0.00 Fig. S5C	N/A	N/A	N/A
I−	0.00 Fig. S3A	0.00 Fig. S3B	0.00 Fig. S3C	0.00 Fig. S3D	−0.04 Fig. S3E	−0.08 Fig. S5B	0.00 Fig. S5D	N/A	N/A	N/A
O=C	0.17§	0.10§	0.30§	0.15Fig. S4A	0 10Fig. S4B	0.06§	0.07*	0.08¶	0.20Fig. 5A	N/A
O=P	0.17§	0.10§	0.30§	0.15 Fig. S4A	0.10 Fig. S4B	0.06§	0.07*	0.14¶	0.14¶	N/A
O=S	0.17§	0.10§	0.30§	0.15 Fig. S4A	0.10 Fig. S4B	0.06§	0.07*	0.14¶	0.14¶	N/A
C–H	N/A	N/A	N/A	N/A	N/A	N/A	N/A	N/A	N/A	−0.40‡

Table 4.

Pair-specific NBFIX corrections to the CHARMM36 force field¹⁴. The table lists corrections to the LJ R_min parameters of the specified atom pairs. The corrections are given relative to the standard force field values and have units of Angstroms. Mg²⁺ and Ca²⁺ are modeled as permanent hexahydrate and heptahydrate complexes, respectively, with the water dipole moments increased by 1 or 0.5 Debye, respectively, above the standard TIP3P value^31,51. The NBFIX corrections are for the atom pairs formed by monovalent ions, water oxygens of Mg²⁺ hexahydrates and Ca²⁺ heptahydrates, nitrogen atom of a positively charged amine group (N–H), nitrogen atom of a guanidinium group (N=C), acetate oxygen (O=C), phosphate oxygen (O=P), and sulfate oxygen (O=S). Superscripts §, ¶ and * correspond to Refs. 31, 41, and 51, respectively, which detail validation of the specific corrections. The value of 0.00 indicates that no NBFIX correction is needed to reproduce the osmotic pressure experiment using the standard parameter set. Br⁻ and I⁻ anions are not listed because they are not included in the standard CHARMM36 force field. The CUFIX-corrected parameter set in the CHARMM format is available at http://bionano.physics.illinois.edu/CUFIX.

	Li+	Na+	K+	Rb+	Cs+	Mg2+	Ca2+	N–H	N=C
Cl−	0.23§	0.06§	0.05§	0.022 Fig. S6A	0.00 Fig. S6B	0.015§	0.011*	0.03¶	0.03¶
O=C	0.19§	0.09§	0.08§	0.056 Fig. S7A	0.00 Fig. S7B	0.055§	0.079*	0.08¶	0.20 Fig. 5B
O=P	0.19§	0.09§	0.08§	0.056 Fig. S7A	0.00 Fig. S7B	0.055§	0.079*	0.16¶	0.16¶
O=S	0.19§	0.09§	0.08§	0.056 Fig. S7A	0.00 Fig. S7B	0.055§	0.079*	0.16¶	0.16¶

3.1.2 Parameterization of guanidinium group leaves room for improvement

To illustrate the limitation of the NBFIX approach, here we review NBFIX calibration of the guanidinium–acetate interaction—a proxy for evaluation of non-bonded interactions between positively charged arginine side chains and anionic moieties, such as the side chains of aspartic or glutamic acids. The calibration was performed using a two-compartment system similar to that shown in Fig. 2B,C. The osmotic pressure computed using the standard CHARMM36 force field (red marks in Fig. 5A) was significantly lower than prescribed by experiment⁸⁹. For example, 139 bar was measured in experiment at 2 m concentration whereas the simulated osmotic pressure was only 18 bar. The NBFIX correction was introduced by gradually increasing the LJ R_min (or equivalently σ) parameter for the guanidinium nitrogen–carboxylate oxygen atom pair.

Fig. 5.

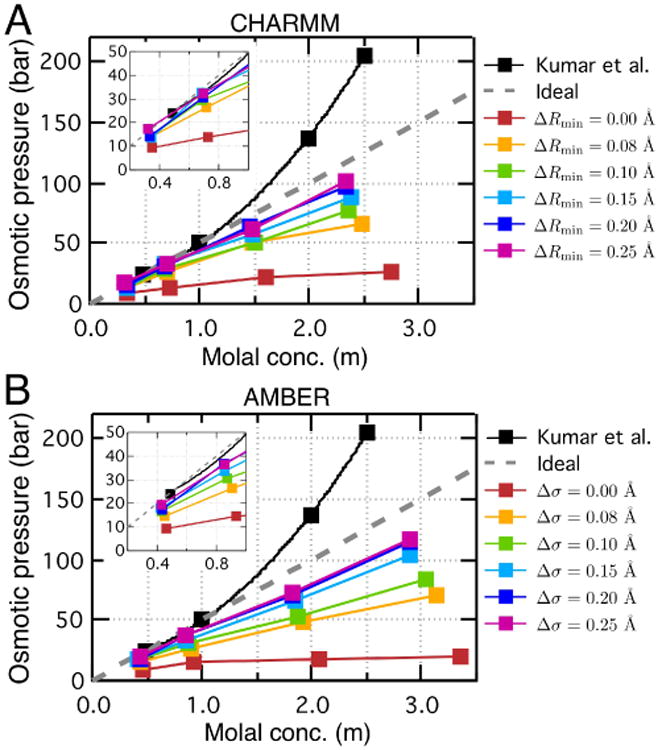
Calibration of the guanidinium–acetate interaction using the osmotic pressure method. (A) Osmotic pressure of the guanidinium–acetate solution as a function of the solution molality obtained using the CHARMM36 force field with the specified value of the NBFIX correction (colored symbols) and experiment⁸⁹ (black symbols). Gray dashed line shows the dependence of an ideal 1:1 solution. For the purpose of calibration, the LJ R_min parameter describing the interactions between the guanidinium nitrogen and acetate oxygen was increased by ΔR_min. The inset shows a zoomed-in view of the dependences at concentrations lower than 1 m. (B) Same as in panel A but for the AMBER99 force field. To be consistent with the AMBER parameterization convention, the calibration of the LJ interaction is done by adjusting the σ parameter (R_min = 2^(1/6)σ).

Increasing R_min by 0.08 Å, which was sufficient to bring the non-bonded interaction between amine and carboxylate groups in accord with experiment (see Table 4), markedly increased the osmotic pressure of the guanidinium–acetate solution (orange marks in Fig. 5A), however, the simulated pressure remained less than a half of the experimental value (black marks in Fig. 5A). Increasing the R_min value further increased the simulated osmotic pressure, however, no change in osmotic pressure was observed beyond ΔR_min = 0.20 Å, Fig. 5A. The saturation occurs because of the finite range of the effect of NBFIX corrections on the formation of contact ion pairs: once all contact ions pairs have been removed, further increase in R_min value has little effect on the behavior of the system (see Section 3.1.1). At concentrations lower than 1 m, ΔR_min of 0.20 Å is seen to produce a reasonable agreement with experiment, see inset of Fig. 5A. Thus, the NBFIX correction alone was not sufficient to bring the simulated osmotic pressure of the system in accordance with experiment at higher electrolyte concentrations.

The calibration simulations performed using the AMBER99 force field, Fig. 5B, revealed similar limitations of the NBFIX approach. The significantly underestimated osmotic pressure obtained using the standard parameterization (red marks in Fig. 5B) could be gradually increased by increasing the σ parameter of the LJ potentail. However, no further improvement could be made beyond Δσ = 0.20 Å.

Importantly, the experimental osmotic pressure of the guanidinium–acetate solution is much higher than that of an ideal solution, Fig. 5A, suggesting that guanidinium and carboxylate groups at least do not form tight CIP complexes. Accordingly, the CIP state of the methylguanidinium–acetate pair is not even a local minimum of the ion pair's PMF computed using the NBFIX correction, blue line in Fig. 4C. At the same time, the osmotic pressure of the glycine solution is slightly lower than that of an ideal solution, Fig. 2D, suggesting that the interaction between ammonium and carboxylate groups is slightly more attractive than in the ideal non-interacting case. Accordingly, we find the CIP state to be a local minimum of the methylammonium–acetate PMF, blue line in Fig. 4B. Thus, our NBFIX corrections capture the overall difference between interactions of acetate with guanidinium and amine groups. To describe such a difference more accurately, it might be necessary to explicitly consider the sphere–plane and plane–plane geometry of ammonium–acetate and guanidinium–acetate interactions.

The discrepancy between the computed and experimental osmotic pressure of the guanidinium–acetate solution at a higher concentration highlights the limitations of the NBFIX appoach. The similarity of limitations observed for both AMBER99 and CHARMM36 force fields suggests that the problem could be intrinsic to the standard water models, TIP3P and modified TIP3P for the AMBER99 and CHARMM36 force fields, respectively. Calibration simulation using different water models could be essential for simulations of high-concentration guanidinium–acetate solutions. Another possible source of discrepancy is the fundamental limitation of the non-polarizable models in describing the π–π stacking interactions^90–92 between guanidiniums in planar configurations⁹³. Computing the osmotic pressure of the guanidinium–acetate solution using a polarizable force field model^94,95 is an interesting direction for future research efforts in this area. Corrections that affect formation of solvent-shared ion pairs might also be necessary to address the remaining discrepancy.

In summary, recent MD studies demonstrate that all-atom MD simulations equipped with a refined force field can quantitatively reproduce the thermodynamic properties of electrolyte solutions (e.g., osmotic pressure^31,63,86) and some thermodynamics effects of ions on biomolecules (e.g., condensation of DNA^31,41). However, it is still an open question whether MD simulations can provide an atomistic description of a thermodynamic observation. An outstanding challenge is the simulation of the Hofmeister series^96,97. Although the “salting in” and “salting out” phenomena have been known and used in practice for more than a hundred of years, we still do not have a complete theoretical model explaining their physical origin⁹⁷. A careful parameterization of all ions in the Hofmeister series using the NBFIX approach could provide an opportunity for resolving this long-standing puzzle.

3.2 Nucleic acid systems

For efficient storage and gene regulation, DNA in living cells and viruses is present in a highly condensed state^98,99. Experimental studies of DNA condensation in vitro have provided invaluable insights into the physics of DNA–DNA interactions, revealing surprising effects that originate from the DNA's polymer-like behaviors and complex electrostatics^100–105. As each nucleotide of a DNA strand contains a negatively charged phosphate group at the strand's backbone, screening of the DNA charge by counter ions and ion mediation of DNA–DNA interactions are the key effects determining the structure and dynamics of DNA systems^106,107. Below, we discuss development and application of NBFIX corrections for MD simulations of condensed DNA systems and illustrate remaining challenges using the Holliday junction (HJ) system.

3.2.1 NBFIX corrections increase realism of DNA simulations

DNA condensation in vitro can be produced through the application of external pressure or by condensing agents such as positively charged polyamine ions. Regardless of the condensation method, the DNA helices adopt an ideal hexagonal packing in the condensed state, with the average inter-DNA distance being a well-defined function of the external pressure and ionic condition^100,101. Unlike the DNA structure, the concentration and arrangement of couterions within such in vitro condensates is not experimentally known, which makes them an attractive target for MD studies¹⁰⁸.

Prior to the development of NBFIX corrections to ion–DNA phosphate interactions^31,41,51, MD characterization of DNA condensates had been challenging. At the level of a single DNA helix, both standard CHARMM and AMBER force fields overestimate the binding affinities of cations to DNA phosphate groups, which is a consequence of overstabilization of the CIP states³¹. For a pair of DNA helices, the artificially strong interactions between cations and DNA phosphates facilitate formation of phosphate–cation–phosphate bridges and produce attractive inter-DNA forces even for monovalent and divalent electrolytes¹⁰⁹ that do not condense DNA in experiment¹⁰⁰. In the simulations of DNA array systems⁴³, such as the one shown in Fig. 6A, the overly favorable interaction between DNA helices produces artificial clustering of DNA helices and significantly underestimate the internal pressure, Fig. 6B–D, inconsistent with experimental observations^100,101.

Fig. 6.

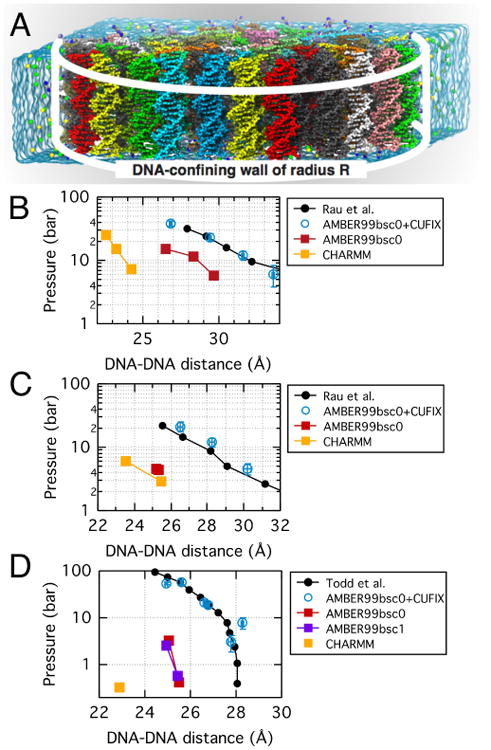
Effect of NBFIX corrections on MD simulations of DNA array systems ^41,43. (A) DNA array system containing 64 20-bp double-stranded DNA molecules (each shown in distinct color) confined to a cylinder of radius R (white lines) by a half-harmonic potential^31,43. Under periodic boundary conditions, each DNA molecule is effectively infinite. The blue semi-transparent surface indicates the volume occupied by electrolyte in a unit simulation cell; water and ions are not subject to external potential and can exchange between buffer and DNA array volumes. The internal pressure of a DNA array is measured from the total force applied to DNA by the confining potential divided by the array's area. A set of simulations carried out at different values of R yields a dependence of the internal pressure on the inter-DNA distance. (B) Experimentally determined (black) and simulated (colors) pressure in a DNA array as a function of the mean distance between the nearest DNA helices. Both experimental and simulated dependences were obtained at 250 mM Na^{+ 43,100}. (C) Same as in panel B but for MgCl₂ solution. The experimental dependence was measured at 20 mM concentration of Mg²⁺ ions¹⁰⁰. The simulated pressure was obtained at 20 mM Mg²⁺ and 200 mM Na^{+ 43}. (D) Same as in panel B but in the presence of spermine. The experimental dependence was obtained at 2 mM spermine concentration¹⁰¹. The charge of the spermine molecules in the MD systems was equal by magnitude to the charge of the DNA array and no additional ions were introduced to the system⁴³.

The application of NBFIX corrections brings MD description of ion atmosphere of DNA in agreement with experiment. In comparison to standard parameterization, the NBFIX corrections reduce the number of cations directly bound to the phosphate groups of the DNA backbone, increasing the population of loosely bound ions in the atmosphere. Direct quantitative validation of ion atmosphere description is obtained through comparison of the simulation results to the ion counting data obtained using the buffer equilibration and atomic emission spectroscopy (BE-AES)¹⁰⁶. Specifically, NBFIX-enabled MD simulations were found to reproduce results of the BE-AES measurements even in the case when two cation species, such as Li⁺, Na⁺, K⁺, and Mg²⁺, compete for DNA binding¹⁰⁷. MD simulations of DNA translocation through solid-state nanopores^51,110 provided additional validation of ion type-dependent cation–DNA interactions^51,110.

NBFIX-enabled simulations of DNA array systems reproduce the experimental dependence of the internal pressure on the inter-DNA distance for a range of electrolyte compositions and concentrations Fig. 6B–D^31,43. Inside an array, DNA helices are found to arrange on a regularly spaced hexagonal lattice⁴³, as prescribed by experiment^100,101. Most importantly, the simulations identified indirectly bound bridging cations as the source of cohesive interactions that give rise to DNA condensation and characterized translational and rotational diffusion of DNA in such arrays, which is critical for modeling virus packaging and ejection⁴³. The balanced description of ion binding to DNA enabled characterization of more subtle effects, such as sequence and methylation dependence of inter-DNA forces. Thus, simulation predicted AT-rich DNA helices to attract stronger than CG-rich ones and methylation of cytosines to strengthen such attraction. These predictions were validated by single molecule experiment¹¹¹.

Another example of dense DNA systems are self-assembled DNA nanostructures (e.g., DNA origami¹¹²) that consist of many DNA helices joined through multiple HJs. In such systems, overly strong inter-DNA interactions can cause mechanical distortions including excessive twisting or bending. It has been shown that the MD method equipped with NBFIX corrections can be used to characterize structural and mechanical properties of DNA origami¹¹³ and DNA bricks¹¹⁴ objects. Such simulations are particularly suitable for characterization of the transport properties of DNA channels^115–119, where NBFIX corrections are essential to capture the ionic conductivity, electro-osmosis, and diffusion of small solutes.

3.2.2 MD simulations of Holliday junctions exemplify challenges in capturing conformation dynamics

MD simulation of a HJ system, Fig. 7A¹²¹, presents a stringent yet straightforward test of an MD force field. In this system, four DNA double helix arms interact with one another through two types of interactions: ion-mediated electrostatics of side-by-side DNA duplexes and base-stacking at the crossing of the four duplexes. Depending on ionic conditions, a HJ is known to adopt several conformations that are well characterized through biochemical¹²¹ and single-molecule^122,123 studies, Fig. 7B–D. At a low concentration of monovalent cations and in the absence of multivalent cation, electrostatic side-by-side repulsion wins over base-stacking attraction. As a result, a HJ adopts an open conformation, in which four arms are fully extended in a square-planar configuration, Fig. 7C^122,124,125. At a high concentration of monovalent cations (> 1 M) or in the presence of multivalent cation, side-by-side electrostatic repulsion is screened while the base-stacking interactions remain unaffected, Fig. 7B,D. As a result, a HJ adopts a right-handed antiparallel stacked-X configuration, Fig. 7B,D¹²⁶. Depending on the the stacking partner, two isomeric stacked-X configurations (iso I and II) are possible ^121,123

Fig. 7.

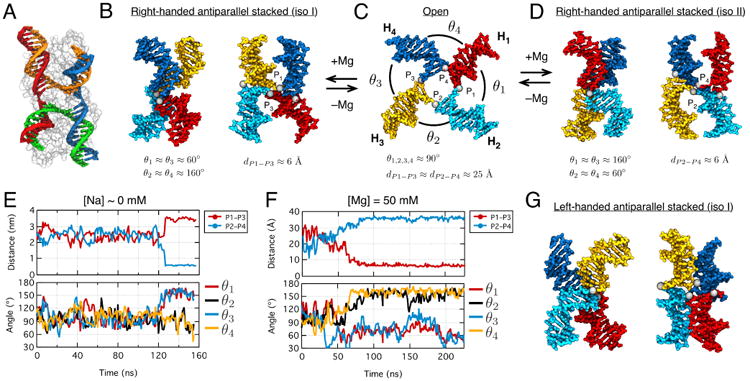
MD simulation of conformational transitions in a Holliday junction (HJ). (A) Crystal structure (PDB: 2QNC) of an open HJ conformation (each DNA strand uniquely colored) co-crystallized with a T4 endonuclease (semitransparent surface)¹²⁰. (B–D) Cation-dependent conformational transitions in HJ. At low ionic strength, HJ forms an open conformation (C). At high ionic strength, HJ forms one of the two, panels B and D, right-handed antiparallel stacked-X conformations. The HJ conformations can be described using the distances d_P1–P3 and d_P2–P4 between the phosphate groups P₁, …,P₄ (gray spheres) at the junction, and angles θ₁, …,θ₄ between the neighboring arms. Typical values of d_P1–P3, d_P2–P4 and θ₁, …,θ₄ are shown at the bottom of each panel. (E) The inter-phosphate distances d_P1–P3 and d_P2–P4 (top) and the θ₁, …,θ₄ angles (bottom) in an MD simulation initiated from an open HJ conformation and carried out at 0 mM Na⁺. (F) Same as in panel E but for a simulation that began from an open HJ conformation but was carried out at 50 mM Mg²⁺. (G) An example of a left-hand antiparallel stacked-X conformation found in an MD simulation.

Using the AMBER ff99bsc0 force field¹³ and the NBFIX corrections for ion-phosphate interactions³¹, we investigated the effect of ion conditions on the conformation of a HJ. Starting from the crystal structure of an open configuration of a HJ (PDB: 2QNC)¹²⁰, Fig. 7A, we built an all-atom model of the junction having the nucleotide sequence of the experimentally studied system¹²³. The all-atom model was submerged in a dodecahedron volume of TIP3P water⁶¹ (a = b = c = 10 nm α = β = 60° γ = 90°) containing a neutralizing amount (84) of sodium ions, which corresponds to a low ion concentration condition that, in experiment, strongly favors an open configuration of the junction. During the first 120 ns, the junction maintained its open configuration, Fig. 7E, but soon after underwent an unexpected conformational transition to a stacked-X conformation, Fig. 7E. A much more rapid transition to a stacked conformation was observed in fourteen additional simulations carried out in 50 mM Mg electrolyte, Fig. 7F. The initial conformations for these simulations were randomly selected from the first 120 ns of the HJ trajectory at low Na concentrations. In 13 out 14 such simulations, the con-formational change to stacked-X conformations occurred within 10–50 ns. Among the 13 stacked-X conformations, we found 3 right-handed iso I, 4 right-handed iso II, 3 left-handed iso I, and 3 left-handed iso II conformers.

The above simulations of the HJ system revealed two problems. First, a stable stacked conformation was observed in MD simulations at low sodium conditions whereas experiment indicates the dominance of open conformation even at 400 mM Na^121–123. Second, six out of thirteen stacked conformations at 50 mM Mg (and the stacked conformation at low sodium) were left-handed, whereas experiment found left-handed stacked conformations to be unlikely^121,126. Previously, we found NBFIX-enabled ion-mediated electrostatic interactions between DNA helices to provide quantitatively accurate description of experiments, Fig. 6⁴³. Thus the disagreement between simulation and experiment is likely to originate from inaccurate description of stacking forces between DNA bases^34,127–129. Indeed, an overestimation of base-stacking forces can increase the population of left-handed stacked-X conformations that have more steric contacts between the DNA arms than the right-handed or open conformations.

A potential problem with the present parameterization of the nucleic acids is the description of the nonbonded interactions of their sugar groups. Recently, the Elcock group showed that carbohydrate monomers attract one another too strongly when simulated using standard parameters and developed a set of NBFIX corrections for both the CHARMM and AMBER force fields that brought such interactions in agreement with experimental observations^52,59. It is thus possible to improve the description of the nucleic acid carbohydrate groups in the CHARMM and AMBER force fields by adopting the NBFIX corrections developed by the Elcock group. A combination of NBFIX corrections describing non-bonded interactions of backbone phosphates^31,41, sugars^52,59 and base-stacking³⁴ together with refinement of bonded interactions^13,14,130 may produce the most accurate computational model of nucleic acids.

3.3 Protein folding

The all-atom MD method has been instrumental in elucidating the mechanisms of protein folding-unfolding transitions^23,24 and even prediction of the folded structure of short globular proteins¹³¹. It has been, however, established that conformations of unfolded or disordered proteins are too compact in MD simulations in comparison to experimental conformations^29–42.

Several types of molecular interactions drive folding of a polypeptide chain into a unique 3D structure¹³². Among those interactions, salt bridges between amine and carboxylate groups^80,133 and hydrophobic interactions between nonpolar residues^134,135 have been found to be too strong in the standard CHARMM and AMBER force fields^32,41 whereas interactions between polar groups appear to be accurate⁴¹.

To elucidate the effect of NBFIX corrections on protein simulations, we used the replica-exchange MD (REMD) method⁴² to simulate folding of a villin head piece¹³⁶ and WW domain¹³⁷. Our simulations demonstrated that the NBFIX corrections to AMBER ff99sb-ildn-phi force field reduce artificial aggregation of both proteins in their disordered states⁴². Despite such reduction, both proteins fold into correct 3D structures, whereas the folding time is reduced by a factor of two, on average, in comparison to the results obtained using the standard force field⁴².

Although corrections to non-bonded parameters have improved sampling of disordered conformations^37,42, it has been argued that the radius of gyration, R_g, of a disordered protein is still smaller in an MD simulation than in experiment^37,38. In particular, the Shaw group found the simulated R_g values of unfolded proteins to be roughly half the value of chemically denatured ones for proteins containing from 10 to 90 residues¹³⁹. For example, the experimental R_g value of a 76-residue ubiquitin protein is 27 Ź³⁹ at 6 M GuHCl whereas the R_g value of unfolded ubiquitin at 390 K computed using the CHARMM22* force field is only ∼12 Å^37,140.

It is, however, unclear if the above comparison is fair as the conditions realized in experiment and simulation differ substantially. Unlike an MD simulation of an unfolded protein, which typically is performed at an elevated temperature^37,140, an experimental ensemble of denatured proteins is realized through addition of detergent at high concentration (typically in excess of 5 M). For a better comparison, we performed an REMD simulation of unfolded ubiquitin in pure water (0 M urea) and in 8 M urea solution using the AMBER ff99sb-ildn-phi force field and NBFIX corrections^41,42. The R_g value in the absence of urea converged to a value slightly below 20 Å (blue line in Fig. 8), which is about 10 Å smaller than the experimental R_g value at 6 M GuHCl¹³⁹ (black line in Fig. 8). However, simulated R_g of ubiquitin at 8 M urea is close to the experimental value, Fig. 8. Although the above result is encouraging, it is still possible that NBFIX-enabled force fields underestimate R_g values of unfolded or intrinsically disordered proteins⁴⁰.

Fig. 8.

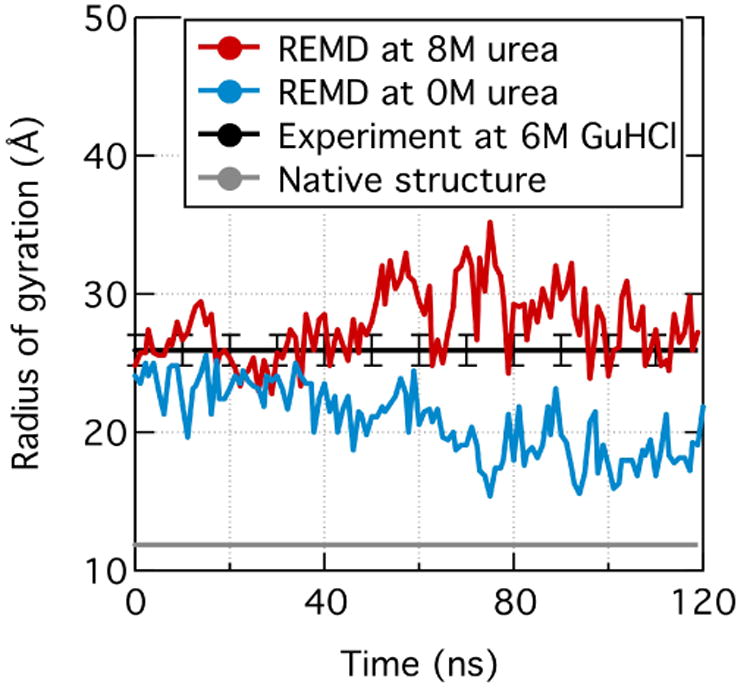
Experimental and simulated radius of gyration, R_g, of an unfolded ubiquitin. R_g values observed in the simulations carried out at 0 and 8 M urea concentrations are shown in blue and red, respectively. The R_g values shown were measured using the 300 K replica of a 53-temperature replica-exchange MD (REMD) simulation. Experimental R_g values for the folded (gray) and unfolded (black, 6 M GuHCl) ubiquitin were taken from PDB 1UBQ¹³⁸ and Ref. 139, respectively.

3.4 Lipid membranes

Phospholipid is a major class of lipids that are the building blocks of cell membranes. Each phospholipid (hereinafter lipid for brevity) contains two hydrophobic hydrocarbon tails and a polar or charged head group. The head groups in particular are known to interact with membrane and membrane-associated proteins through electrostatic interactions involving negatively charged phosphate and carboxylate groups and positively charged amine and choline groups. Thus, it is natural to expect NBFIX corrections to have a major effect on the simulations of lipid bilayers and protein–lipid systems.

Indeed, we found the application of the NBFIX corrections to amine–phosphate and amine–carboxylate interactions to loosen the packing of lipid molecules in a lipid bilayer membrane⁴¹. The CHARMM27r lipid force field is known to underestimate the simulated area per lipid molecule, suggesting that the head groups of the lipid molecules attract one another too strongly⁹. The application of the NBFIX corrections reduces attraction between the head groups, bringing the simulated area per lipid molecule in close agreement with experiment for both phosphatidylethanolamine (PE) and phosphatidylserine (PS) lipid bilayers⁴¹. As all lipid types contain electronegative groups at high concentrations, their structure and dynamics is affected by the presence of cations. As the introduction of NBFIX corrections improves description of cation–carboxylate and cation–phosphate interactions, it can contribute to more accurate simulations of the cation effects on lipid membrane structure and dynamics^41,57.

Just like with development of corrections to amino acid side chains (recall Fig. 4B,C and related paragraphs), there could be multiple different approaches for improving parameterization of lipid head groups. One such approach is development of NBFIX corrections^41,57. An alternative approach is modification of partial charges, similar to that used by the Shaw group for development of CHARMM22*. With regard to simulations of lipid bilayers, Berger and coworkers have shown that modifications of head group partial charges in the Gromos lipid force field brings the simulated area per lipid in agreement with experiment¹⁴¹. Yet another approach is modification of torsion parameters, which was used in the development of the CHARMM36 lipid force field¹⁰. As all three approaches can reproduce the correct area per lipid values, it is premature to conclude which of the specific approaches is better than the others. A next generation lipid force field might as well be produced through combination of all these approaches after systematic validation against experimental data.

3.5 Molecular recognition and signaling

Regulation of biochemical processes is paramount to survival, growth, and development of living cells. At the molecular level, regulation of cellular processes relies on physical recognition of signaling ligands by their biomolecular targets. Molecular mechanisms of such recognition have been an area of active research for the MD community¹⁴⁴. Because molecular recognition is largely electrostatic in nature, the application of NBFIX corrections to charge-charge interactions could have a major effect on the outcome of a molecular recognition simulation.

The application of NBFIX corrections can be expected to provide more accurate simulations of ligand docking or protein–protein assembly, especially when mediated by salt bridges between amine and carboxylate groups. For example, the stability of β-amyloid fibrils implicated in the Alzheimer disease¹⁴⁵ and the ligand binding behavior of the extracellular domain of G-protein coupled receptors (GPCR)^146,147 are highly regulated by salt bridges between lysine and aspartate residues. The salt bridge formation is also essential for the function of ligand-gated ion channels and transporters¹⁴². For example, Fig. 9A shows the structure of a dopamine transporter (PDB: 4XP9), in which the bound dopamine is in direct contact with the carboxylate group of an aspartate side chain¹⁴². Several important neurotransmitters such as AMPA (α-amino-3-hydroxy-5-methyl-4-isoxazole propionic acid), NMDA (N-methyl-D-aspartate), GABA (γ-aminobutyric acid), glutamate, and serotonin contain multiple amine and carboxylate groups^148,149, Fig. 9B. Based on our simulation data^41,42, we expect that the standard CHARMM and AMBER force fields are likely to overestimate the binding affinity of such ligands to their respective target sites and that applying NBFIX corrections may improve the simulation outcomes.

Fig. 9.

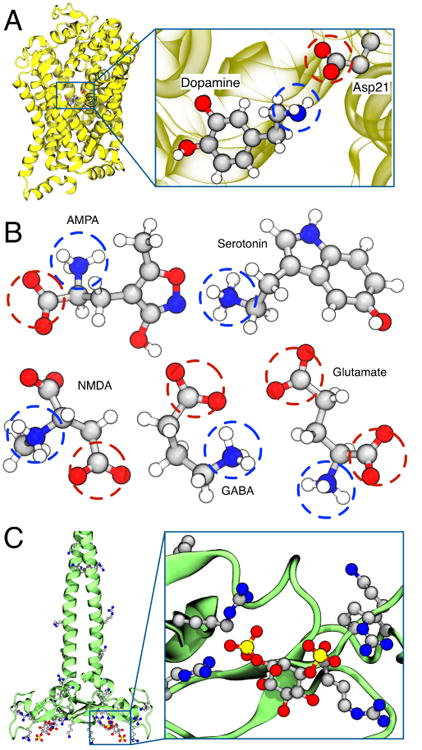
Interactions between charged groups in cell signaling. (A) Crystal structure of a dopamine transporter having a dopamine molecule bound to the binding site (PDB: 4XP9)¹⁴². The inset shows a close-up view of the dopamine molecule and the interacting aspartate side chain. (B) Structures of five representative neurotransmitters: AMPA (α-amino-3-hydroxy-5-methyl-4-isoxazole propionic acid), NMDA (N-methyl-D-aspartate), GABA (γ-aminobutyric acid), serotonin, and glutamate. The chemical structures are shown using the ball-and-stick representation colored by the atom type: carbon, gray; oxygen, red; nitrogen, blue; hydrogen, white. Charged amine and carboxylate groups are indicated by blue and red circles, respectively. (C) Crystal structure of EEA1 homodimer of C-terminal FYVE domain bound to inositol 1,3-diphosphate (PDB: 1JOC)¹⁴³. The inset shows the structure of inositol 1,3-diphosphate coordinated by four neighboring arginine side chains.

In the case of protein–DNA complexes, electrostatic interactions play an important role in sequence-specific binding of transcription factors via leucine zipper, zinc finger and helix-turn-helix mechanisms^150,151, DNA-binding domains of ATP-driven motor proteins¹⁵², and DNA–histone assembly of nucle-osomes^153,154. One can thus expect that NBFIX corrections to interactions between positively charged residues (Lys, Arg, His) and the phosphate groups of a DNA backbone will improve the accuracy of protein–DNA complex simulations. Indeed, we observed such improvement in simulations of lysine-mediated interactions between DNA molecules⁴¹. In qualitative disagreement with experiment¹⁵⁵, the simulations carried out using the standard CHARMM and AMBER models predict attractive interaction between DNA helices in the presence lysine monomers or trimers⁴¹, which derive primarily from the overestimation of amine–phosphate attraction. Applying NBFIX corrections to the same simulations considerably improved the realism of the simulation outcome, reproducing, for example, a crossover from repulsive to attractive interactions with increasing length of polylysine peptides⁴¹.

Considering that charged groups are functional moieties of the molecules involved in cell signaling, the NBFIX corrections to amine–carboxylate and amine–phosphate interactions might be of relevance to simulations of cell signaling. The interactions between charged amino acids and lipid head groups are essential for maintaining the structure^156–158 and biological function^159,160 of channel proteins. One celebrated example is the voltage sensor of potassium or sodium channels, in which guanidinium–phosphate interactions play a central role^159,161.

Lipid molecules containing phosphatidylinositide (PI) groups have been implicated in cell signaling^{160,162–165} and have recently become a subject of MD studies^166,167. Accurate simulations of such systems will require validation of interactions between the phosphate groups of PI lipids and the charged side chains of the signaling proteins. For example, the crystal structure of inositol 1,3-diphosphate bound to EEA1 homodimer of C-terminal FYVE domain shows a coordination of a PI group by four different arginine side chains, Fig. 9C. The NBFIX corrections developed to describe the amine–phosphate and guanidinium–phosphate interactions should provide a reasonable initial parameterization for the MD study of PI lipid molecules and cell signaling.

4 Conclusion

Over the past decades, the field of MD simulations has been experiencing a tremendous growth, fueled by continuous efforts of the MD community to improve accuracy and efficiency of the MD method. Until recently, significant efforts were put into refinement of the chemical bond interactions through systematic quantum mechanical calculations and comparison to experimental structural data. Presently, the MD community recognizes the urgent need for refinement of the non-bonded interactions. One particular challenge is to balance the strength of non-bonded interactions without compromising stability of the native structures. In this perspective, we reviewed one of the possible solutions to that challenge—the NBFIX approach, which has the advantage of offering a significant improvement to the force field accuracy by introducing minimal adjustments to the force field parameterization. However, it remains to be seen if the NBFIX approach can indeed offer solutions to the majority of the remaining force field problems or if the MD community will need to build a drastically different force field model. Answering this open question will require critical assessment of force fields accuracy, development of experimental approaches tailored to the force field parameterization and a framework for systematic force field refinement and validation.