Mining Major Transitions of Chronic Conditions in Patients with Multiple Chronic Conditions

Summary

Objectives

Evolution of multiple chronic conditions (MCC) follows a complex stochastic process, influenced by several factors including the inter-relationship of existing conditions, and patient-level risk factors. Nearly 20% of citizens aged 18 years and older are burdened with two or more (multiple) chronic conditions (MCC). Treatment for people living with MCC currently accounts for an estimated 66% of the Nation’s healthcare costs. However, it is still not known precisely how MCC emerge and accumulate among individuals or in the general population. This study investigates major patterns of MCC transitions in a diverse population of patients and identifies the risk factors affecting the transition process.

Methods

A Latent regression Markov clustering (LRMCL) algorithm is proposed to identify major transitions of four MCC that include hypertension (HTN), depression, Post-Traumatic Stress Disorder (PTSD), and back pain. A cohort of 601,805 individuals randomly selected from the population of Iraq and Afghanistan war Veterans (IAVs) who received VA care during three or more years between 2002-2015, is used for training the proposed LRMCL algorithm.

Results

Two major clusters of MCC transition patterns with 78% and 22% probability of membership respectively were identified. The primary cluster demonstrated the possibility of improvement when the number of MCC is small and an increase in probability of MCC accumulation as the number of comorbidities increased. The second cluster showed stability (no change) of MCC overtime as the major pattern. Age was the most significant risk factor associated with the most probable cluster for each IAV.

Conclusions

These findings suggest that our proposed LRMCL algorithm can be used to describe and understand MCC transitions, which may ultimately allow healthcare systems to support optimal clinical decision-making. This method will be used to describe a broader range of MCC transitions in this and non-VA populations, and will add treatment information to see if models including treatments and MCC emergence can be used to support clinical decision-making in patient care.

1. Introduction

All complex systems including human beings are subjected to degradation [1]. Chronic conditions that are persistent or otherwise long-lasting in their effects [2], are principal examples of degradation in humans. For example, obesity is associated with coronary artery disease, high blood pressure, stroke, and type II diabetes. Analytic methods for monitoring chronic conditions are also primarily focused on single chronic conditions [3]. For instance Markov Decision Processes (MDP) have been used to guide disease manage for conditions including, heart disease [4], Kidney and liver transplant [5], HIV [6], hepatitis C [7], breast cancer [8], diabetes and hyperlipidemia [9, 10], pneumonia [11, 12], and others [13, 14]. However, when the number of (disease) states increases, as happens frequently in chronic disease management, MDP methods become infeasible. Reinforcement learning, which is also known as approximate dynamic programming, has been successfully applied to some of these cases including cancer treatment [15], psychotic disorders [16, 17], and HIV monitoring [18].

Chronic conditions not only affect patients’ daily life, but they also compete with, interact with, and sometimes result in additional comorbidities [19]. In fact, having two or more (multiple) chronic physical and mental health conditions is among top challenges of healthcare at this time. Approximately one in four Americans and 75% of Americans aged 65 years are burdened with Multiple Chronic Conditions (MCC) [20]. People with MCC have increased risk of mortality and reduced functional status and diminished quality of life. Furthermore, as the number of chronic conditions increases so does frailty/disability and avoidable hospitalizations [21]. MCC are associated with substantial healthcare costs in the United States, which accounts for approximately 66 percent of the total healthcare [20].

Given the importance of the problem, several aspects of MCC have been studied: (1) prevalence and rate of increase [22, 23], (2) cost and quality of life [23, 24], (3) health consequences and complications [23, 25], (4) patient support, intervention and healthcare design [25, 26], and (5) assessment, prediction and decision-making [24, 27]. Nonetheless, the majority of studies on chronic conditions are focused on individual diseases such as cardiovascular diseases (CVD), chronic obstructive pulmonary diseases (COPD), chronic kidney diseases (CKD), diabetes, etc. [28, 29]. However, most patients suffering from a chronic disease either have, or will eventually develop, other conditions resulting in MCC [30, 31].

Because MCC adds layers of complexity to various aspects of healthcare management, there has been an increasing emphasis on prognosis and effective monitoring of MCC [31]. Most of the existing literature on MCC prognosis either investigates the association between known risk factors for a specific chronic condition, or studies the effect of an existing condition on the emergence of another condition [32, 33]. The few analytic studies that consider MCC are also not suitable for prognostic purposes [27, 34]. In terms of the analytic tools, various methods have been used in the literature which include, Latent Class Analysis (LCA) [35], Group-Based Trajectory Modeling (GBTM) [36], Growth Curve Modeling (GCM) [37], Generalized Linear Models (GLM) [38], Correlation Analysis [39], the Markov Model [40], the Hidden Markov Model [41], the Hidden Semi Markov Model [42], and Graphical Models [43].

While there has been a large body of literature describing MCC, little is known about the emergence of MCC over time as existing studies tend to be cross sectional, and examine patterns of comorbidity in older adults [21]. The cornerstone of the Strategic Framework for MCC presented by the Department of Health and Human Services (HHS) in 2010 was to focus on prevention of or delaying onset of MCC [31]. Nonetheless, existing methods do not provide a clear picture of how MCC emerge and variables associated with progression, which is important to optimize preventive efforts and address the goals of the MCC Framework. While concern about MCC has focused on multi-morbidity in older adults, understanding the emergence of MCC over time requires longitudinal evaluation of populations beginning in young/middle adulthood. The proposed study addresses these critical gaps by investigating the risk factors associated with the emergence and progression of MCCs and predicting MCC transitions at both individual and population levels. Models developed in this study will be the foundation for incorporating data to identify optimal timing and treatment approaches that prevent/slow progression of comorbidity accumulation (HHS Strategic Framework Goals 1, 3, 4) [31].

2. Methods

2.1. Study design

This retrospective cohort study used healthcare system data to identify common psychiatric/physical comorbidities and demographic characteristics to describe emergence and progression of a limited number of comorbidities over time. We used randomly selected derivation and validation cohorts to test and evaluate the models.

2.2. Study population

Because chronic disease tends to develop over time, we selected a population for which we had access to inpatient and outpatient data from which comorbid conditions could be identified, and that was relatively young allowing observation of MCC emergence. Our dataset included a cohort of Iraq and Afghanistan war veterans (IAV) who were first seen in the Department of Veterans Affairs (VA) between 2002-2015 and who received care in each of three or more years during that period (n=601,805) (See Fig. 1). From that sample, we use multiple imputation based on K-nearest neighbor algorithm [44] to substitute values for individuals with missing risk factors (n=16,079), and then used 10-fold cross-validation with approximately 60,180 patients in each validation set for model development and analysis.

Fig 1.

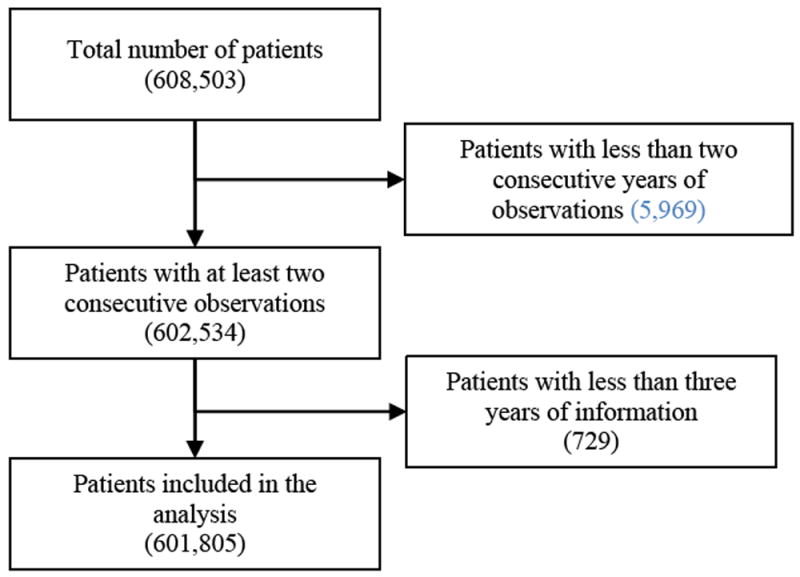
Flow diagram of sample selection and final number of patients included in the analysis

2.3. Data source

Using the roster of Iraq and Afghanistan Veterans (IAV) including Operation Enduring Freedom (OEF), Operation Iraqi Freedom (OIF), and Operation New Dawn (OND) veterans [12] we identified individuals from all over the US who met inclusion criteria described above from VA’s central data repository which is located in Austin Texas. Inpatient and outpatient files include patient age, sex, race/ethnicity, poverty status, date and type of care received (e.g. primary care, specialty care), and ICD-9-CM diagnostic codes to identify conditions for which care was received [27, 45, 46].

The specific chronic conditions included in our analyses included one chronic medical condition expected to be relatively consistent in medical records after diagnosis (hypertension (HTN)), and three conditions that are common in the IAV population and which may have periods of remission and recurrence of symptoms once diagnosed (depression, PTSD, and back-pain). These conditions were also identified by HHS as MCC of importance based on the Medicare population [31]. We identified diagnosis of back pain, hypertension, PTSD and depression each year using ICD-9-CM codes identified by validated algorithms [47] (See Appendix II). Data are available from the Veterans Health Administration Institutional Data Access / Ethics Committee for researchers who meet the criteria for access to confidential data.

Covariates included in the model were age during the first year of care, sex, race/ethnicity, marriage status (married or not), education, and age. Race/ethnicity was classified as White, Black, Hispanic, Asian, and Native American. Education at the time of military discharge or last deployment was classified as less than high school, high school, some college, college, and post baccalaureate.

2.4. Developing MCC transition matrix

In modeling MCC, we consider addition, subtraction and stability in the conditions for which care is received. Considering n = 4 possible MCC in the population, i.e. depression, PTSD, back pain, hypertension (HTN), there will be M= 2ⁿ⁼⁴ possible combinations that can change from one year to another. The transition between these combinations of MCCs in the population can be effectively modeled under Markov models using a transition matrix. We estimated the transition probabilities by calculating the percent of patients who transit from a specific MCC in a year to another MCC in the following year [48].

2.5. Identifying MCC cluster

To account for heterogeneity in the population, we placed the Markov chain model within a mixture model framework to identify subpopulations that share the same MCC patterns. These Markov models have distinct- and independent-model parameters that are recovered from the data.

In order to model population-specific risk factors we used a Latent Regression Markov Mixture Model (LRMM) to incorporate subject–specific covariates (e.g., age, sex, race/ethnicity, etc.) into Markov mixture models, allowing them to influence the mixing proportion through a regression model. To specify the mixing proportions we used logit model [49] which has been previously applied for observed-outcome analysis in the substantive areas [50].

To optimize the LRMM model parameters we adapted a hybrid Expectation Maximization [51] and Newton-Raphson algorithm [52]. The procedure starts with introducing a dummy variable to the likelihood function, which indicates the latent group to which each individual belongs. The procedure then iteratively updates the estimates through two steps of: expectation (E-step) which calculates the expected value of the log likelihood function, given the current estimate of the parameters and maximization, and Maximization (M-Step) which finds the parameters that maximize the model estimated in E-step.

Additionally, to identify the possible patterns of MCC progression, we applied Markov clustering algorithm (MCL) to LRMM. MCL algorithm is an iterative process of applying two operators - expansion and inflation - until convergence. Here we add MCL expansion and inflation steps to expectation maximization steps in LRMM estimation to extract the major patterns of MCC transitions while the learning the model parameters. We call this model latent regression Markov mixture clustering (LRMCL). The analysis was done in MATLAB R2016a 64 bit.

After using imputation to substitute values for the patients with missing information (n=16,079), we used 10-fold cross-validation with approximately 60,180 patients in each validation set to identify the optimal number of clusters and determine the predictive accuracy. We use c-statistic as the performance metric.

3. Result

Table 1 shows the distribution of the five major risk factors considered in this study in the full cohort: patient’s sex, marital status, education, race/ethnicity, and age. Table 2 illustrates the prevalence of MCC conditions in the final dataset based on first year of care in the VA.

Table 1.

Characteristics of the sample including demographic and socio economic information

Risk factors	Level	Overall	%
Sex	Male	523,411	87%
Marriage status	Married	269,183	45%
Education	Less than high sch.	7,744	1%
	High school	465,109	77%
	Some college	59,791	10%
	College	45,671	8%
	Post baccalaureate	15,406	3%
	Missing value	8,084	1%
Race/ethnicity	White	391,886	65%
	Black	106,626	18%
	Hispanic	70,797	12%
	Asian	15,728	3%
	Native American	8,634	1%
	Missing value	8,134	1%
Age	Mean	31.84
	Standard deviation	9.11

The information shown are: (1) before imputation, (2) after removing records with less than three years of information, (3) after removing records with less than 2 consecutive observations

Table 2.

Prevalence of MCC conditions in the dataset in year one of VA care

MCC Condition				Count	%
DEP	PTSD	HTN	BP
0	0	0	0	379,393	63%
1				22,754	4%
	1			38,479	6%
		1		22,114	4%
			1	58,330	10%
1	1			23,478	4%
1		1		2,500	0%
1			1	7,604	1%
	1	1		3,375	1%
	1		1	17,240	3%
		1	1	6,297	1%
1	1	1		2,843	0%
1		1	1	1,167	0%
	1	1	1	2,015	0%
1	1		1	12,329	2%
1	1	1	1	1,887	0%

Dep=depression; PTSD=Po Posttraumatic stress disorder, HTN=Hypertension, LBP=Low back Pain

3.1. Patterns of MCC

Fig. 2, shows the original transition matrix of MCC over (any two) consecutive years throughout the 14-year study period. In general, we found that the highest likelihood of transition (>40%) was to continue with the same condition or combination of conditions (i.e. no change) as seen on the red diagonal in Fig. 1. For individuals with one MCC in year t there was an increased likelihood (range 19-29%) of not having that diagnosis the subsequent year. Individuals with two MCC in year t also were also had an increased likelihood of having only one MCC (<18%) or no MCC (range 8-13%) the following year. However, individuals with three MCC had an increased likelihood of adding a fourth condition (range 3-11%) the subsequent year.

Fig 2.

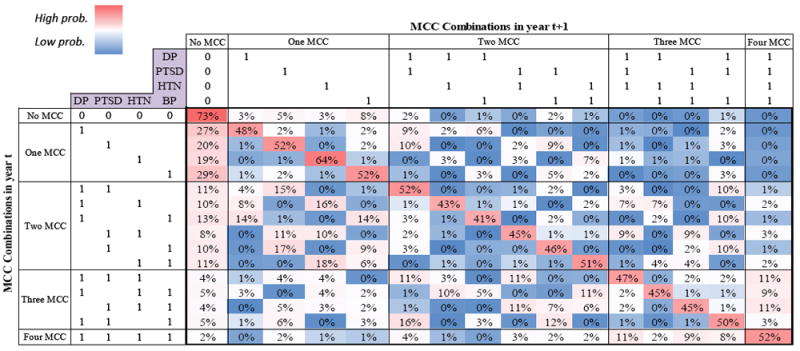
The original transition matrix

In order to investigate the possibility that subpopulations exist within the initial transition matrix that may bias the trends, we performed cluster analysis incorporating associated risk factors using the LRMCL algorithm. Table 3 compares the effect of number of clusters on average c-statistic performance of the LRMCL across different MCC combinations over the next five years. For all models, accuracy decreased for longer-term predictions. We found that performance was best when using more than one cluster, but did not improve when using more than two. After considering optimal performance and parsimony we chose to use the two-cluster model for the remainder of analyses.

Table 3.

Average c-statistic performance of the LRMCL across different MCC combinations based on various numbers of clusters

	1 yr ahead	2 yrs ahead	3 yrs ahead	4 yrs ahead	5 yrs ahead
1 Cluster	0.6150	0.5435	0.5042	0.4832	0.4697
2 Clusters	0.6985	0.5961	0.5365	0.5035	0.4841
3 Clusters	0.6470	0.5614	0.5154	0.4943	0.4770
4 Clusters	0.6035	0.5256	0.4930	0.4764	0.4658

The c-statistic illustrated in Table 3 is across all 16 possible MCC combinations, which is equivalent to a 16-class classification problem, with 1/16=0.0625 correct classification rate using random guess strategy. Meanwhile, the predictive accuracy of the LRMCL algorithm and its degradation over time can be further improved by using higher order Markov chains in LRMCL. However, this strategy significantly increases the number of states and consequently the computational complexity of the algorithm, and hence not adopted for our analysis.

3.2. Population risk factors

Five demographic and socioeconomic risk factors (see Table 1) were used for the latent variable regression. Table 4 shows the estimated parameters of the latent variable regression for the LRMCL with 2 clusters based on the logit model $\pi \left(X_{\mathrm{j}}\right)=\frac{\exp \left({\sum }_{i=1}^6{B}_{\mathrm{i}}{X}_{\mathrm{ij}}\right)}{1+\exp \left({\sum }_{i=1}^6{B}_{\mathrm{i}}{X}_{\mathrm{ij}}\right)}$, where π(X_j) represents the jth patient’ probability of membership in the first cluster (1-π(X_j) shows the probability of membership in the second cluster), X_ijdenotes the values of the i^th risk factors for the j^th patient, and B_i represents the estimated parameter for the i^th risk factor. Given the structure of logit model, positive coefficients in Table 4 are associated with an increase in the probability of membership to the first cluster, while negative coefficients are associated with an increase in the probability of membership to the second cluster. In addition, the size of coefficients shows the relative contribution of each variable to cluster membership with respect to the comparison group (baseline variable). Analyzing the P-value column, we found that age followed by Marriage status (Married) were the strongest factors that contributed to assignment of patients to clusters.

Table 4.

The estimated parameters of the proposed LRMCL model

	Risk factors	Coefficient	P-value
Intercept		0.497
Sex	Male	0.007	0.021
Marriage status	Married	0.109	0.000
	Less than high sch.	0.294	0.089
	High sch.	0.322	0.067
Education	Some college	0.147	0.371
	College	0.001	0.997
	Post baccalaureate	-0.151	0.352
	White	0.154	0.603
	Black	0.298	0.327
Race/ethnicity	Hispanic	0.215	0.469
	Asian	0.060	0.837
	Native	0.250	0.402
		0.609	0.000

^*Significance Level 0.01

3.3. Cluster analysis

Figs. 3.a and 3.b show the resulting transition matrices of LRMCL algorithm and the emergence of two general patterns (clusters) of MCC trajectories. Cluster 1 (Figs. 3.a and 3.b) accounts for 78% of the membership probability, with two dominant patterns: stability and change. The pattern of stability was similar to that found in cluster two. The patterns of change include remission of conditions (improvement) which is illustrated as red/pinks under the diagonal and addition of conditions (decline) which are shown as pinks above the diagonal. When the only chronic condition was depression, or back pain there was more than 49% chance of improvement; however, those with hypertension remained mostly stable. Those with two MCC showed more variability in their year-to-year transition: some remained stable (30% for those with hypertension and back pain), some showed possibility of improvement (23% for those with depression and PTSD), and still others showed possibility of decline (16% for those with depression and back pain). Those with three MCC shows more patterns of stability and decline (19% for those with PTSD, hypertension, and back pain) where a fourth condition (depression) is added the following year.

Fig 3.

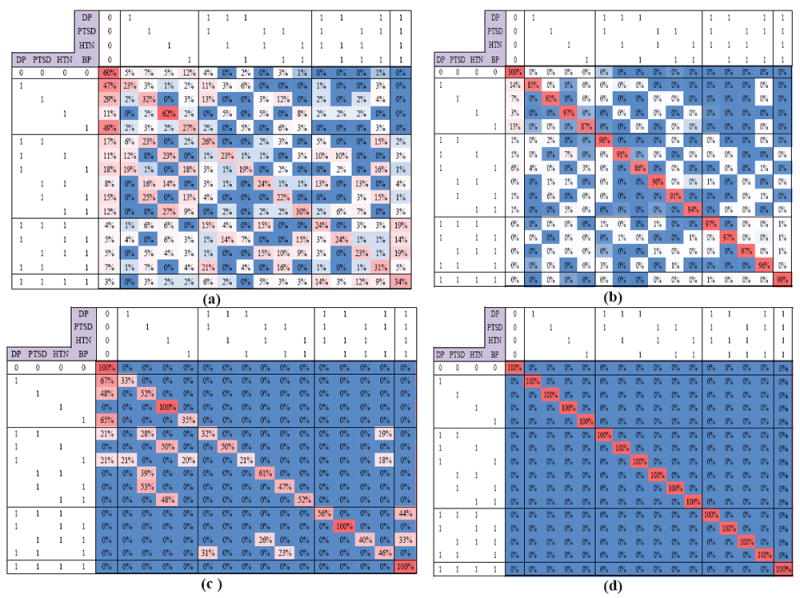
(a-b) Final LRMCL result for cluster 1 and 2, (c-d) LRMCL result after Thresholding 0.15 (c-statistic is used as the accuracy metric).

There was also a 22% chance of membership probability for Cluster 2, which illustrates a dominant pattern of stability of MCC conditions for the following year. Regardless of the type and number of conditions, those individuals represented by cluster one were more likely to retain those same conditions in the following year (red blocks on the diagonal). Figs. 3.c and 3.d summarizes major transitions of LRMCL results after pruning less likely transitions (less than 15%). One may use other thresholds values for pruning transitions to achieve the desired level of summarization in Fig. 3; Increasing the threshold value will result in sparser transition matrices, while decreasing the threshold value will result in more nonzero transitions in each cluster. For instance, Fig. 3.a and 3.b can be considered as the transition matrices of cluster one and two, when applying the threshold of 100% (less than 100%). The standard deviation of the estimated transition matrices of LRMCL algorithm is provided in the Appendix I.

4. Discussion

4.1. Overall findings

We developed a novel data analytic approach to identify temporal patterns of multi-morbidity using data that is increasingly available from healthcare systems. Using a cohort of IAV who received VA care at least three different years between 2002-2015, we found that the LRMCL approach was feasible and could generate predictive patterns of comorbidity. In our cohort of deployed US veterans, we found 2 major subpopulations: one was characterized by stability in disease states over time, while the other revealed dynamic variability in disease burden as a function of the number of diseases. That is, as the number of diseases increased, the likelihood of retaining or adding another disease also increased. This approach could be implemented on the population level and with a larger number of conditions.

There are a few reasons why we developed the proposed LRMCL as a combinatorial approach based on Markov modeling: (1) it is common to use a set of discrete states for modeling and monitoring chronic conditions [5], (2) Markovian structure as proposed in this research, can be effectively integrated with Markov decision Process (MDP) which is among most advanced and successful practices in clinical decision making (CDM), (3) it provides a straightforward yet effective predictive framework for estimating the risk of future MCC development, and therefore enables clinicians to develop more effective screening and treatment plans

Markov clustering algorithm (MCL) models have been successfully applied to many fields such as protein interaction networks [53, 54], and event mining video surveillance [55], etc. Here we extended the MCL algorithm to a mixture framework controlled by exogenous risk factors. We successfully applied the proposed algorithm to modeling of MCC in a diverse population over time. Given the importance of matrix partitioning, numerous solutions have been investigated in the literature, which range from spectral clustering and multi-level graph partitioning to divisive/agglomerative approaches and heuristic approaches. Here, we focused on the class of flow-based graph clustering algorithms known as Markov Clustering (MCL) because of its several advantages including: (1) an elegant approach based on the natural phenomenon of flow, or transition probability, in graphs, (2) robustness to topological noise effects, and (3) while not being completely nonparametric, varying a simple parameter can result in clustering of different granularities.

Prior studies have used latent class analysis (LCA) to examine complex comorbidity among IAV and identified clusters with distinct patterns of comorbidities [27, 46]. Other studies examining the trajectories of these clusters also found stability in patterns of comorbidities over time [56]. Those studies described six general patterns of MCC diagnosed in year 1-3 of VA care. There was a relatively large group (~40%) with a low probability of modeled conditions at any time (healthy), and groups that exhibited chronic disease (e.g., hypertension, diabetes), mental health conditions (depression, PTSD, substance use disorder), pain (headache, back pain), and multimorbidity (traumatic brain injury, mental health, and pain)[45]. However, the LCA approach does not show patterns within person and the transition between MCC combinations over time. Unlike latent class, the LRMCL considers the temporal transitions of MCC and directly associates them with risk factors. This study using four conditions suggests that LRMCL may be a useful tool to patterns of MCC transition using a larger number of conditions.

In this limited group of conditions, we found that the most common state among our cohort was to have none of the four conditions, which may be related to their relatively young age and therefore overall good health (mean 32 years, SD 9). This finding is consistent with prior LCA studies in this population [45].

The dynamic variability seen in older IAV (Cluster 1) included increases and decreases in MCC. Decreases in comorbidity were more evident among individuals with fewer conditions indicating that lower disease burden in some individuals may indicate a lower likelihood of chronicity. Some of our findings can be understood in light of the specific condition. We found that hypertension alone or in combination with other conditions had a high probability of persisting the subsequent year. In combinations of MCC that included hypertension, loss or addition of a condition usually included a comorbidity other than hypertension. This likely reflects the fact that hypertension is a chronic medical condition requiring regular follow-up care and treatment. Thus, the finding that individuals with a hypertension diagnosis are likely to have the diagnosis in year T+1 is not surprising (Cluster 1; see Fig. 3d). However, this consistency provides an internal validation of this approach as we would expect more dynamic patterns for the other conditions that have symptoms that resolve with treatment or reflect recurrence or new onset of symptoms.

We chose to study the complex temporal relationships between 4 distinct diseases (hypertension, PTSD, depression, low back pain) that are common comorbidities in this population [27]. These conditions do not always have directly linked causal (i.e. pathophysiological) pathways, but they do have interesting potential inter-correlation. For example, PTSD and hypertension are linked because of putative autonomic nervous system and hypothalamic-pituitary-adrenal axis involvement and dysfunction [57]. Furthermore, BP has been associated with depression and hypertension in multiple studies [58, 59], and individuals with PTSD are more sensitive to pain, including back pain. Among our cohort during the first year of VA care, BP was the most common diagnosis (10%) and among those with two MCC, the most common pattern was depression and PTSD (4%). For patients with three comorbidities, BP, PTSD, and depression were the most frequent MCC (3%); less than 1% of the cohort had all four conditions. While the links between these 4 conditions have been described previously, our data demonstrates the co-occurrence and emergence of them over time in a relatively young population. In particular, our goal was to examine conditions that are common and often times comorbid, but do not necessarily have temporal or overt physiological relationships. This approach allows us to identify relationships among comorbidities that emerge over time and that are not directly connected with our current understanding of the pathophysiology. For example, patients with PTSD are more sensitive to pain, but that does not necessarily infer that they will experience low back pain. Importantly, our approach may identify associations between conditions that could be further explored using more traditional and reductionist studies of pathopsysiology. This also supports the use of our approach for predictive purposes.

4.2. Significant transitions identified by LRMCL

While for cluster two, the dominant pattern of stability was observed (Fig. 3.d); the examination of cluster one revealed a few important transitions of non-stability (See Fig. 3.c). First, when examining cluster 1 for transitions associated with a single condition (Fig. 3.c), it appears that depression, PTSD, and BP, but not hypertension, are likely to be treated or go away. However, hypertension diagnoses persist in cluster 1, possibly because this condition tends to be chronic and requires regular long-term medical follow-up as mentioned above [60].

Second, we observed several patterns of variability in patients with two chronic conditions (Fig. 3.c). for instance, when one of the two MCC is hypertension, there are two possible paths of stability and improvement. Specifically, for patients with depression and hypertension other than a pattern of stability (50%), we found that 50% improved, where depression is dropped. This may indicate that for these individuals, depression symptoms were more adequately treated and/or resolved. Based on the stability of hypertension diagnoses for individuals with one MCC, we would expect the persistence of hypertension. Some evidence shows patients with depression are at risk for hypertension [61] and that some anti-hypertensive medications may lead to depression [62]. However, understanding of the association between hypertension and depression is complicated by studies that show a link between depression and low blood pressure and that antidepressant use is associated with hypertension [63]. Future studies should explore how medical management of these conditions (and which treatment options) results in resolution or persistence of these diagnoses. For patients with PTSD and hypertension in cluster 1, we also observed a possible path of improvement, and a path of stability. The pattern of improvement may be due to more adequate treatment of hypertension compared to PTSD. This may also suggest that some distinct comorbid conditions with biological links have better prognosis for ultimate resolution that would have been predicted when considered in isolated models. Those with hypertension and BP were also likely to lose one diagnosis the following year, which might be explained by the association between these two conditions. Additional studies exploring these transitions could result in improved clinical targeting, which ultimately optimizes medical management of comorbid patients.

Third, we found a general trend that as the number of MCC increases the chance of improvement decreases. Although we observed less significant improvement pattern for patients with three MCC in cluster 2 (Fig. 3.c), we did identify that for patients with depression, PTSD, and hypertension there was a 44% chance of adding the fourth condition (BP). Similarly, we observed that for patients with PTSD, hypertension, and BP there was a 33% chance of adding the fourth condition (DEP). Finally, we did not find any major pattern of improvement for patients with 4 MCC. Because we limited this study to 4 conditions, we weren’t able to investigate the transition patterns associated with addition of new conditions for patients with 4 MCC.

4.3. Limitations

One limitation of this study is that our data were derived from VA healthcare databases, and therefore only those who have received care in the VA are included and do not reflect diagnoses received by individuals in non-VA settings. The male/female ratio is skewed in our study population and might bias the findings; however, our prior study [56, 64] shows these trends are very similar. We found there was more “stability” with increasing age (see cluster 1), which may be due to the diagnoses we examined. A study of other conditions or more conditions overall may find more variability associated with age. For example, individuals over the age 65 with MCC may trend towards frail conditions where disease patterns are more complex and transitions more likely [65]. Another limitation of our study is that we utilize administrative data with the assumption that diagnostic codes represent a correct diagnosis made in year one and indicate that subsequent treatment will occur. Along with this limitation, we assumed the observed transition (especially resolution) of problems from one year to the next is due to actual changes in patients’ disease states versus incomplete documentation/billing. Although, we excluded years where patients didn’t have a visit, it’s still possible that patients may have sought care for other reasons and not had a diagnosis code documented for one of the four diseases of interest, but still had the disease. Furthermore, we identified conditions using dichotomous variables that may not capture all individuals with symptoms consistent with these conditions and does not provide information about condition severity. In addition, not all diagnosed conditions were included in this analysis. Therefore, the conditions not studied may have also had effect on the findings, which requires additional analyses. Finally, the LRMCL is developed based on the simplifying assumption of first order Markov property, which assumes the probability of transitions will remain the same over time. Therefore, the results do not consider the effect of time on transition probabilities.

5. Conclusions

We developed an algorithm that uses age, race/ethnicity, and education to identify clusters of patients with different MCC transition patterns within a population of patients. We tested the algorithm based on a dataset of 13,983 patients monitored for four MCC (depression, PTSD, Hypertension, and Low back pain) over 10 years in VA healthcare and identified two major clusters of stability and change within the population, achieving 61% accuracy in predicting future comorbidities. We also identified a number of major MCC transition patterns within the subpopulations and explored the possible reasons. In addition, we found that as the number of diseases increases, the likelihood of retaining or adding another disease also increases.