Structure of linkage disequilibrium and phenotypic associations in the maize genome

Abstract

Association studies based on linkage disequilibrium (LD) can provide high resolution for identifying genes that may contribute to phenotypic variation. We report patterns of local and genome-wide LD in 102 maize inbred lines representing much of the worldwide genetic diversity used in maize breeding, and address its implications for association studies in maize. In a survey of six genes, we found that intragenic LD generally declined rapidly with distance (r² < 0.1 within 1500 bp), but rates of decline were highly variable among genes. This rapid decline probably reflects large effective population sizes in maize during its evolution and high levels of recombination within genes. A set of 47 simple sequence repeat (SSR) loci showed stronger evidence of genome-wide LD than did single-nucleotide polymorphisms (SNPs) in candidate genes. LD was greatly reduced but not eliminated by grouping lines into three empirically determined subpopulations. SSR data also supplied evidence that divergent artificial selection on flowering time may have played a role in generating population structure. Provided the effects of population structure are effectively controlled, this research suggests that association studies show great promise for identifying the genetic basis of important traits in maize with very high resolution.

In plant genetic studies, recombinant inbred lines have been very successful for mapping quantitative trait loci (QTLs) to 10–30 cM regions (1, 2), but association studies based on linkage disequilibrium (LD) may allow identification of the actual genes represented by QTLs. Only polymorphisms with extremely tight linkage to a locus with phenotypic effects are likely to be significantly associated with the trait in a randomly mating population, providing much finer resolution than genetic mapping. Association methods have been especially important for studying the genetic basis of human diseases, for which controlled genetic experiments are not feasible. However, these methods also have great potential for resolving individual genes responsible for QTLs (3–5).

The resolution of association studies in a test sample depends on the structure of LD across the genome. LD, or the correlation between alleles at different sites, is generally dependent on the history of recombination between polymorphisms. However, factors such as genetic drift, selection within populations, and population admixture can also cause LD between markers and traits. [Following common practice (6, 7), we refer to gametic phase disequilibrium as LD whether or not it is caused by linkage.] Because many factors affect LD, its genomic structure in particular crop plants must be empirically determined before association studies can be applied. In maize, for example, divergent selection for adaptive traits such as time of maturation in different regions may have created LD among chromosomal regions containing major genes for these traits.

Our goal in this study was to evaluate patterns of LD among 102 maize inbred lines representing the diversity of both temperate and tropical sources and address its implications for association studies in maize. Our first objective was to evaluate the rates at which LD decays within genes, by using DNA sequence data from six candidate genes for important agronomic traits. Secondly, to explore the extent of LD between unlinked sites, we evaluated LD between sites in different candidate genes and between 47 simple sequence repeat (SSR) loci. Finally, we performed a number of statistical tests on the SSR LD data and SSR-trait associations to identify mechanisms by which selection on agronomic traits may have shaped LD in the maize genome. This evaluation of LD across maize breeding lines will show that association studies could be developed for maize to map quantitative traits at very high resolution.

Materials and Methods

Plant Materials.

One hundred two inbred maize lines, representing a broad cross section of breeding germplasm from temperate and tropical regions, were used in this study. These include 53 U.S. lines, 7 European and Canadian lines, and 42 tropical/semitropical (ST) lines. Thirteen of the combined U.S.-European-Canadian lines were primarily Iowa Stiff Stalk Synthetic in origin (SS), and the remaining 47 lines were non-stiff-stalk (NSS). The ST lines were as follows: A6, A272, A441-5, B103, CML5, CML10, CML61, CML91, CML247, CML254, CML258, CML261, CML277, CML281, CML287, CML333, D940Y, F2834T, I137TN, KUI3, KUI11, KUI21, KUI43, KUI44, KUI2007, M37W, M162W, NC296, NC298, NC300, NC304, NC338, NC348, NC350, NC352, NC354, Q6199, SC213R, Tzi8, Tzi10, Tzi18, and U267Y. SS lines were as follows: A632, B14A, B37, B68, B73, B84, B104, CM105, CM174, MS153, N28Ht, N192, and NC250. NSS lines were as follows: 38-11, A554, A619, B97, C103, CI187, CM7, CMV3, EP1, F2, F7, F44, Gt112, H95, H99, HP301, I29, I205, Ia2132, IDS28, Il14H, Il101, Il677a, K55, Ky21, Mo17, Mo24W, NC258, NC260, NC320, ND246, Oh43, Oh7B, P39, Pa91, SA24, SC55, Sg18, T232, T8, Tx601, Va26, W64A, W117Ht, W153R, W182B, and Wf9. Additional information on these lines is included in Table 4, which is published as supporting information on the PNAS web site, www.pnas.org.

Field Data.

Field tests were established at two sites, near Clayton, NC and Homestead, FL. A number of phenological and morphological traits were measured over three field seasons during 1998 and 1999 at one or both sites, for a total of five study environments. Details of test design and trait measurements have been described elsewhere (8). For this report, days to pollen (DPoll) and days to silking (DSilk) were selected as measures of flowering time, and ear height (EarHt) and total plant height (PlHt) were selected as measures of plant morphology.

Candidate Gene Sequence Data.

DNA sequence data were obtained from coding regions and flanking sequence of four genes: indeterminate1 (id1; chromosome 1, 175.0 cM), teosinte branched1 (tb1; chromosome 1, 197.6 cM), dwarf8 (d8; chromosome 1, 198.5 cM), and dwarf3 (d3; chromosome 9, 62.7 cM). These are considered candidate genes for variation in plant height and/or flowering time, based on mutant phenotypes and chromosomal locations near major QTLs. Sequence data were also obtained for 32 lines for two additional genes: shrunken1 (sh1; chromosome 9, 36.4 cM) and sugary1 (su1; chromosome 4, 60.2 cM). Gene fragments were PCR amplified by using primers designed from published sequences. Sequence data were obtained directly from PCR products or from pools of two to four clones of PCR products. Sequence chromatogram files were assembled into contigs by using seqman (DNAstar, Madison, WI), and consensus sequences were edited manually to resolve discrepancies. Consensus sequences for all lines were aligned by using the clustal alignment option in megalign (DNAstar), with further manual alignment. Polymorphisms appearing in only one or two lines were rechecked on chromatograms to distinguish true polymorphisms from probable polymerase or scoring errors. Well over 1.5 megabases of contiged sequence data were collected.

SSR Marker Data.

Development and scoring of SSR markers has been described elsewhere by Matsuoka (38). We used data from 47 highly polymorphic loci with a mean of 6.85 alleles per locus (range 2–16 alleles). These SSRs have been found to contain frequent indels outside of repeat units and are not evolving in a stepwise manner (38). Map positions for all candidate genes and SSRs were based on the Pioneer Composite 1999 linkage maps obtained from the MaizeDB website (www.agron.missouri.edu).

Statistical Analyses.

LD between pairs of sites in candidate genes (both SNPs and insertion-deletion polymorphisms, or indels) and in SSRs was evaluated by using the software package tassel (available at www.statgen.ncsu.edu/∼buckler/). Contiguous indel sites showing identical patterns of variation were treated as a single polymorphism. LD was estimated by using standardized disequilibrium coefficients (D′) per Hedrick (9), and squared allele-frequency correlations (r²) per Weir (7) for pairs of loci. D′ is affected solely by recombination and not by differences in allele frequencies between sites. r² is also affected by differences in allele frequencies at the two sites, and is therefore a better measure of potential allele-trait associations than D′. Only sites with a frequency of at least 0.10 for the rarer allele were included because D′ and r² have large variances with rare alleles. The probabilities of obtaining LD estimates at least as extreme as those observed under a hypothesis of linkage equilibrium (P values) were calculated by using Fisher's exact test (10) for site pairs with two alleles each. For site pairs with more than two alleles at one or both loci, empirical P values were obtained by repeatedly permuting the alleles at one of the loci as described by Weir (7). Complete LD data for pairs of candidate gene polymorphisms and SSR loci are included in Tables 5–7, which are published as supporting information on the PNAS web site.

Decay of LD with distance in base pairs (bp) between sites within the same candidate locus was evaluated by nonlinear regression (proc nlin in SAS software; ref. 11). The expected value of r² under drift-recombination equilibrium is E(r²) = 1/(1 + C), where N is the effective population size, c is the recombination fraction between sites, and C = 4Nc (12). With a low level of mutation and an adjustment for sample size n, the expectation becomes (13):

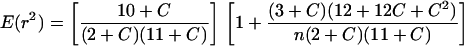1

The nonlinear models based on each of these expectations contain a single coefficient, which is the least-squares estimate for 4Nc per bp distance between sites. Distances were weighted to adjust for indels by averaging the number of base pairs separating the sites across all lines for which both sites were scored. Several factors may reduce precision or create bias in the model estimates, including non-independence of linked site pairs and non-equilibrium populations (14). Consequently, the models may not provide useful estimates of 4Nc, but are nonetheless useful for characterizing the rate of LD decay. The distribution of D′ and r² values for pairs of sites in different candidate loci was evaluated for d8, tb1, id1, and d3.

SSR haplotypes were used to evaluate population structure associated with the ST, NSS, and SS subpopulations. Lines were also subdivided based on data from the 47 SSRs by using a model-based approach with the software package structure (15). Several runs were made by using various sets of initial parameter values for 2, 3, 4, and 5 subpopulations. The run producing the highest log likelihood for the observed data was obtained when the number of subpopulations was set at 3, and was used to produce a new set of model-based subpopulations, designated ST_M, NSS_M, and SS_M. For analyses of structure within subpopulations, we assigned each line to the subpopulation with the largest estimated admixture contribution. Overall, individual-locus, and pairwise estimates of the correlation of alleles within subpopulations (F_ST) for both the origin-based and model-based groupings were calculated by using an AMOVA approach in arlequin version 2.0 (7, 16).

The significance of the overall matrix of pairwise LD P values among all 47 SSR loci was evaluated in tassel by repeatedly permuting the matrix of SSR genotypes at each locus, and computing pairwise LD P values for each permuted data set as described above. The numbers of site pairs with LD P values less than threshold values of 0.01, 0.001, and 0.0001 were counted for the observed data and for each permuted data set, and the total P value for the observed data was calculated as the proportion of permuted data sets with higher counts than the observed data.

Associations of individual SSR alleles with trait values across all five study environments were evaluated in tassel by simple regression. P values were obtained from the F value of effects of each allele on trait values. The P value of the most strongly associated allele (regardless of frequency) was used as a measure of the SSR-trait association for the locus. Differences in these measures among traits were evaluated by using SAS (proc glm). The effects of individual-locus F_ST values on SSR-trait associations were also evaluated by using proc glm. Simple linear correlations between SSR allele-trait associations and the distribution of SSR LD were evaluated by using SAS (proc corr).

Results

Linkage Disequilibrium Between Candidate Locus Polymorphisms.

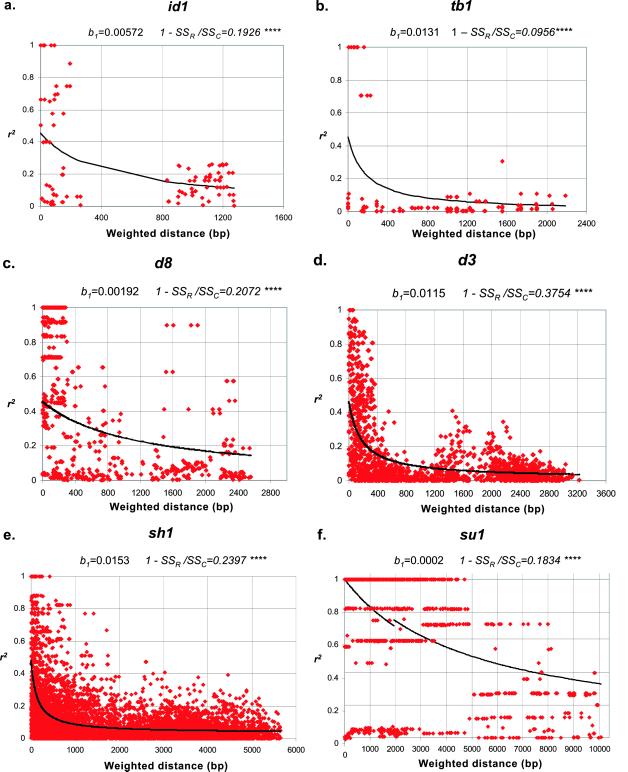
LD between pairs of sites within the six candidate loci is summarized in Fig. 1 a–f. A nonlinear model of LD decay that incorporated mutation (13) explained 9.6–37.5% of the variance in r² for all loci except su1. The model incorporating mutation explained more of the variance in r² than did a recombination-drift model (12) for d3, id1, tb1, and sh1. At su1, only the recombination-drift model explained more variation in r² than simply fitting a mean. The predicted value of r² declined to 0.1 or less within 1500 bp at d3, id1, tb1, and sh1. At su1, on the other hand, the predicted value of r² remained greater than 0.4 for more than 7,000 bp, and d8 showed an intermediate rate of decline. The degree of LD for sites a given distance apart was highly variable. Sites in strong LD with one another tended to occur in blocks, but pairs of sites in complete LD with each other often showed low LD with intervening sites as measured by both D′ and r².

Figure 1.

Plots of squared correlations of allele frequencies (r²) against weighted distance between polymorphic sites in six candidate genes: (a) id1, (b) tb1, (c) d8, (d) d3, (e) sh1, and (f) su1. Curves show nonlinear regression of r² on weighted distance, by using a recombination-drift model for su1 and a mutation-recombination drift model for all other loci. Regression coefficients (b₁) and the corrected percentage of variance explained by the models (SS_M/SS_C) are shown above each plot.

We also evaluated LD of interlocus site pairs between the four loci that were scored for the entire set of 102 lines. Three contrasting levels of linkage could be evaluated: tightly linked loci (tb1 with d8, which are ≈1 cM apart on chromosome 1), loosely linked loci (id1 with tb1 and d8, which are ≈22 cM apart), and unlinked loci (d3 on chromosome 9 with the other 3 loci; Table 1). Approximately 3.6% of site pairs were in significant LD at the comparison-wise 0.01 level. The pair of tightly linked loci showed by far the highest level of LD. This elevation is due primarily to a large number of polymorphic sites within the same large insertion in the d8 promoter, which are in LD with a cluster of sites in the 3′ untranslated region of tb1.

Table 1.

Comparison of LD values between pairs of polymorphic sites in different genes

Comparison	Degree of linkage*	Mean ± SD		f (P < 0.01)†	nobs
		r2	D′
d8 vs. tb1	Tightly-linked	0.046  ± 0.059	0.486  ± 0.325	0.157	624
d8/tb1 vs. id1	Loosely-linked	0.014  ± 0.021	0.237  ± 0.252	0.001	825
d8/tb1/id1 vs. d3	Unlinked	0.022  ± 0.030	0.334  ± 0.309	0.018	2,730
All unlinked site pairs		0.024  ± 0.001	0.338  ± 0.005	0.036	4,179

^*Tightly-linked loci are ≈1 cM apart; loosely-linked loci are ≈22 cM apart; unlinked loci are on different chromosomes. 

^† Percentage of site pairs with LD P value < 0.01. 

Population Structure.

When we grouped the lines into the ST, NSS, and SS subpopulations, the overall F_ST of 0.105 was highly significant, as were each of the three pairwise estimates of F_ST (Table 2). The pairwise comparisons show a low level of differentiation between the ST and NSS subpopulations, but the SS lines are much more highly diverged from the other two groups. The F_ST estimate for the three model-based subpopulations (ST_M, NSS_M, and SS_M) estimated from structure was only slightly higher at 0.122. All but 18 lines were predicted to have greater than 80% of their origin from one of the three inferred subpopulations in the highest-likelihood run. The model-based and origin-based subpopulations were in agreement for 88 of the 102 lines when each line was assigned to the subpopulation with the largest admixture proportion (see Table 4).

Table 2.

Overall and pairwise estimates of F_ST for 47 SSR loci, using (i) origin-based and (ii) model-based population subdivisions

Origin-based subdivision*				Model-based subdivision*
Subdivision*	ST	NSS	Overall	Subdivision*	STM	NSSM	Overall
NSS	0.069	—	—	NSSM	0.086	—	—
SS	0.202	0.132	—	SSM	0.224	0.149	—
Combined	—	—	0.105	Combined	—	—	0.122

^*ST/ST_M = tropical/semi-tropical lines. NSS/NSS_M = U.S./Northern NSS lines. SS/SS_M = U.S./Northern SS lines. 

Linkage Disequilibrium Between SSR Loci.

LD was significant at a comparison-wise 0.01 level in nearly 10% of the SSR marker pairs when all lines were included in the analysis, or nearly 10 times the number expected by chance (Table 3). This is nearly three times the percentage of intergenic site pairs that were in LD at this level. The proportion of sites in significant LD was reduced substantially within individual model-based subdivisions. Some of this reduction could be due to reduced power to detect LD with fewer lines. To test for this possibility, we evaluated the percentage of locus pairs showing significant LD in sets of 1,000 randomly chosen subpopulations, with each set containing the same numbers of lines as the original subpopulations. The observed percentages of LD in the random subpopulations were substantially higher than those in the origin-based and model-based ST and NSS subpopulations (Table 3), suggesting that the subpopulations themselves explain much of the LD. Nevertheless, each of the subpopulations still shows an excess of significant LD values. When 100 randomly permuted datasets were generated for each subpopulation, none showed more than the observed number of significant LD values at the 0.01 or the 0.001 levels. The low number of pairs with significant LD within the SS lines thus may be merely the result of limited power to detect significant deviations with such a small number of lines, but may also reflect the random-mated origin of the SS lines (17).

Table 3.

Numbers of SSR locus pairs showing LD at a P = 0.01 level, by population subdivision

Population subdivision	No. of lines	No. of locus pairs in LD	% of locus pairs	Expected % based on sample size*
All	102	105	9.7	—
Model-based subdivisions:
STM	37	26	2.4	3.0
NSSM	53	26	2.4	4.6
SSM	12	6	0.6	0.6

^*Empirically estimated percentage of locus pairs expected to show LD if population subdivision effect was due only to reduction in sample size, based on average percentage of all locus pairs showing LD in a random sample containing the same number of lines. 

SSR-Phenotype Associations.

We wanted to examine whether selection for maturation time in different environments may have been a factor in generating population structure and LD between unlinked genomic regions. Between 34% and 64% of SSRs showed strong associations (P < 0.01) with the four traits measured. The number of SSRs with strong trait associations for the two flowering time traits (DPoll and DSilk) directly related to maturation was significantly greater (P = 0.0007) than for the two morphological traits (EarHt and PlHt). Fewer SSRs showed strong trait associations when only the NSS_M lines were used in the analysis (15% to 30%). Within the NSS_M lines, the difference between SSR-flowering time and SSR-morphological trait associations was not significant (P = 0.17).

Next, we evaluated whether LD between SSRs was related to the strength of SSR-trait associations, which would be expected if selection on these traits helped generate population structure. SSR-trait associations for each of the four traits were correlated weakly but highly significantly (r = 0.11 to 0.16, P < 0.0001) with LD. When the same analysis was done by using only the NSS_M lines, none of the SSR-trait associations were significantly correlated with LD.

Third, we investigated whether selection on flowering time loci may have directly generated SSR LD. We compared flowering time associations for SSRs near known flowering time QTLs with those for the remaining SSRs. Twenty of the 47 SSR loci are within 20 cM of estimated map positions of flowering time QTLs in eight studies summarized in MaizeDB (18, 19). The mean P values of SSR-flowering time associations were not significantly different for these markers than for the remaining 27 SSRs.

Finally, we examined whether the SSRs showing strong associations with flowering time also showed greater levels of differentiation between subpopulations. We separately estimated overall and pairwise F_ST values for the model-based subpopulations for the 21 SSR loci showing strong flowering-time associations (P ≤ 0.001) and the remaining 26 loci. Overall F_ST values were consistently higher for the loci showing strong flowering time associations (0.161 vs. 0.085), as were all pairwise values among the three subpopulations. Individual-locus F_ST values were significant predictors of SSR associations with DPoll (R² = 0.176, F = 9.64, P = 0.003) and DSilk (R² = 0.149, F = 7.85, P = 0.008) but not with EarHt (R² = 0.034, F = 1.59, P = 0.215) and PlHt (R² = 0.001, F = 0.05, P = 0.824).

Discussion

Decay of LD with Distance Between Sites.

We found that LD generally decayed rapidly with distance between sites within loci, but there was substantial variation among genes. In four of the six genes sampled, predicted r² values declined to less than 0.1 within 2,000 bp, much less than the 50 kb predicted for the same degree of LD decay in humans (20). Recent studies in humans have shown that LD typically extends 60 kb in European populations, and may extend much farther (20–22). Only at su1 did we find evidence that LD might persist at anywhere near these distances in maize. This persistence may be caused in part by reduced recombination rates because of the location of su1 near the centromere of chromosome 4. Selection can also maintain elevated LD in localized regions (23), and may provide an explanation for the persistence of LD at su1 and to some extent at d8. Both loci are candidate genes for traits that have been under strong artificial selection; d8 for flowering time variation (8), and su1 for kernel sugar and starch levels (E.S.B. and S.R.W., unpublished results). LD appeared to decay rapidly at tb1, as has been reported previously (24), despite the selective sweep at this locus during maize domestication. The relatively poor fit of the nonlinear model with tb1 and su1 may be due in part to the effects of strong selective episodes on the frequency and distribution of polymorphisms. In some cases, sites separated by 1 kb or more were in complete LD, but had low D′ values (indicating recombination) with intervening sites. These anomalies reflect differences in the age and genealogy of the various mutations, and possibly the effects of gene conversion and admixture.

The unlinked candidate loci had extremely low levels of LD (r² = 0.024), and it was only modestly higher in one pair of loci 1 cM apart. To determine whether this slightly elevated level of LD at 1 cM is due to linkage or chance, sequencing of more genes and much longer contiguous regions will be necessary to evaluate the variability of LD decay over intermediate distances. These results are in sharp contrast with those recently reported for Dutch dairy cattle, in which LD has been found to persist over distances of many centiMorgans (25). LD has also been reported between loci as much as 4 cM apart in European human populations (23). The population recombination parameter C depends on both effective population size (N) and recombination frequency (c; refs. 26 and 27). High recombination frequencies have been reported for several maize genes (28–31). Other studies of recombination rates and levels of polymorphism in maize have found evidence of large population sizes as well, which suggests that the domestication bottleneck was either mild or of short duration (24, 32). Our average value for C from six loci was 0.0080. If the overall genomic value of ≈1 × 10⁻⁸ for c in maize is used, this suggests a value of ≈2 × 10⁵ for N, similar to estimates from sequence diversity at the Adh1 locus by Eyre-Walker et al. (32). This estimate would be biased upwards, however, if the recombination rate within the studied genes were abnormally high. If a much narrower set of lines had been chosen for this study, the rate of LD decay might have been substantially lower.

Candidate-Gene Polymorphisms vs. SSRs as Indicators of Genome-Wide LD.

The level of genome-wide LD indicated by the SSRs is much higher than that shown by the candidate genes. This discrepancy could be due to chance alone, because the small set of candidate genes may happen to share relatively little evolutionary history. It may also reflect the fact that these SSRs were initially chosen because they differentiated between a small set of U.S. inbred lines. Another possibility is that a higher percentage of SSR mutations than SNPs arose during the development of regional maize subpopulations. Maize and its wild progenitor, Zea mays ssp. parviglumis, share many of the same single-nucleotide polymorphisms at a number of loci, including adh1 (32), c1 (33), and tb1 (24), suggesting that SNP alleles tend to predate domestication. The high level of variability in the SSRs, however, suggests a high rate of mutation to new alleles (primarily indels rather than variation in repeat number), increasing the opportunity for unique length variants to have arisen in individual races during domestication (38). Consequently, the SSR polymorphisms may reveal the recent development of population structure in domesticated maize much better than SNPs.

Population Structure.

Despite the genome-wide LD revealed by the SSR loci, this broad cross section of maize breeding material shows a fairly low degree of population structure. Much of the differentiation we did detect was due to the rather divergent nature of the SS lines. The domestication and breeding history of maize may explain the low level of differentiation between the ST and NSS groups. The NSS lines are primarily Corn Belt dents, a diverse group that originated from the crossing of northern flints and southern dents and appears to consist predominantly of southern dent genetic material (34). The SS lines were developed from only 16 inbred Corn Belt ancestors, and their divergence from the NSS and ST lines is primarily due to genetic drift.

The degree of LD is lower within subpopulations, but it is still significantly elevated. The extent of within-subpopulation structure in domesticated maize is undoubtedly affected by the admixture origin of the Corn Belt dents, and probably by assortative mating and selection for divergent combinations of traits.

Role of Selection in Generating LD.

The population structure in maize appears to reflect the effects of selection on adaptive traits such as flowering time. SSR-phenotype associations and their relationship to population structure were stronger for flowering time than for correlated height traits. These relationships suggest that divergent selection on flowering time may have had an important role in the development of regional variation in maize germplasm. The most plausible explanation for the observed SSR-trait-F_ST associations is that SSRs with allelic variants that happen to distinguish subpopulations are consequently associated with differences in flowering time among subpopulations as well. SSR-trait associations among these lines are unlikely to reflect actual linkage to flowering time loci, because SSRs located near identified flowering time QTLs do not show stronger flowering time associations than other SSRs. Selection would have to generate LD over large chromosomal blocks to be detected through linkage to such a limited set of SSRs, which would probably require severe population bottlenecks generated by extremely strong selection and/or epistasis (23, 35, 36). In maize, however, the region affected by selective sweep at tb1, a major domestication locus, does not encompass the entire gene (24).

The significant relationship between SSR LD and SSR-trait associations also appeared to be an effect of population structure. These relationships disappeared entirely when the analysis was limited to the NSS_M subpopulation. Elevated levels of SSR LD, and SSR-flowering time associations, however, were apparent even within subpopulations, which suggests that assigning lines to subpopulations alone may not be adequate to control for nonfunctional LD. The structure analysis predicted 18 lines to be substantially admixed (<80% composition from a single population). Pritchard et al. (37) have developed a methodology that uses estimated subpopulation admixture proportions, not merely subpopulation assignments, to control for population structure in disease association studies. These methods have been adapted for quantitative traits and found useful for association testing in maize (8). In the future, pedigree information should also be integrated with overall population structure estimates. Such approaches will especially need to be used for traits under divergent selection such as flowering time.

Implications for Association Testing.

A rapid breakdown of LD because of linkage will be favorable for association testing of candidate genes that are located near mapped QTLs and have functional relevance to trait variation. The rate of LD decay is probably too rapid to permit genome-wide association testing with SNPs as has been proposed for human populations (22). However, a two-tiered strategy of QTL mapping followed by association testing of positional candidate genes shows substantial promise for localizing quantitative trait effects to individual genes or even subgenic regions (8). The rapid LD decay in maize provides an opportunity to map quantitative trait loci with up to 5,000-fold greater resolution than current mapping with F₂ or recombinant inbred populations. Statistical approaches will be needed to control for the effects of population structure, but suitable methods are now available (8). Mapping QTLs to the level of individual genes will provide new insights into the molecular and biochemical basis for quantitative trait variation, and identify specific targets for crop improvement for the 21st century.

Abbreviations

LD

linkage disequilibrium

SSR

simple sequence repeat

SNP

single nucleotide polymorphism

QTL

quantitative trait locus

indel

insertion/deletion

d3

dwarf3

d8

dwarf8

id1

indeterminate1

sh1

shrunken1

su1

sugary1

tb1

teosinte branched1

ST

semitropical

SS

stiff stalk

NSS

non-stiff stalk